Tomographic Description of a Quantum Wave Packet in an Accelerated Frame
Abstract
:1. Introduction
2. Formulation of the Problem
2.1. The Schrödinger Equation for a Single Particle in an Accelerated Frame
2.2. Reduction to Motion in the Presence of a Uniform Force Field
3. Gaussian Solution for an Arbitrary Acceleration
- (i).
- satisfies the normalization condition, i.e.,Therefore, represents the probability amplitude associated with the wave packet.
- (ii).
- The average of the spatial coordinate z (i.e., , the wave packet centroid), with respect to , defined assatisfies the property .
- (iii).
- The length of the wave packet, i.e., the rms of the probability density, defined assatisfies the property .
- (iv).
- Note that Equation (14) can be easily integrated without assigning the explicit time dependence of . Furthermore, by multiplying Equation (14) by , one finds the conserved quantity(i.e., energy conservation, ). Then, by expanding the quantity and by combining the result with Equation (14), we obtainwhich can be immediately integrated providingwhere we imposed the initial conditions, i.e., and . It is worth mentioning that the solution for does not depend on the force term appearing in Equation (8) and, therefore, it was integrated independently of the remaining differential equations of the system (10)–(14). This is due to the fact that the homogeneous force can act on the centroid of the wave packet but not on its rms.
- (v).
- Moreover, we can formally integrate Equation (13) for . Thus, imposing the initial conditions, i.e., and , we obtain the solutionThe double integration of can readily give, viz.
- (vi).
- System of Equations (10)–(14) can be cast in such a way to express all the quantities , , and in terms of , , , and only, i.e.,where . By substituting the solution and the formal solutions in Equation (11), we obtain the formal solutions , , and . In the next section, we find solutions for the latter in the case of constant acceleration.
- (vii).
- The quadratic phase term appearing in Equation (9) defines a parabolic phase. It can be cast as , where is the related bending radius; remarkably, it does not depend on the acceleration.
- (viii).
- The linear phase term represents a plane phase contribution and depends on the acceleration.
- (ix).
- The homogeneous phase term does not contribute to bending of the phase but depends on the acceleration.
3.1. Envelope Motion
3.2. Motion of Centroid
4. Gaussian Solution for Constant Acceleration
5. Tomographic Representation of the Quantum Wave Packet
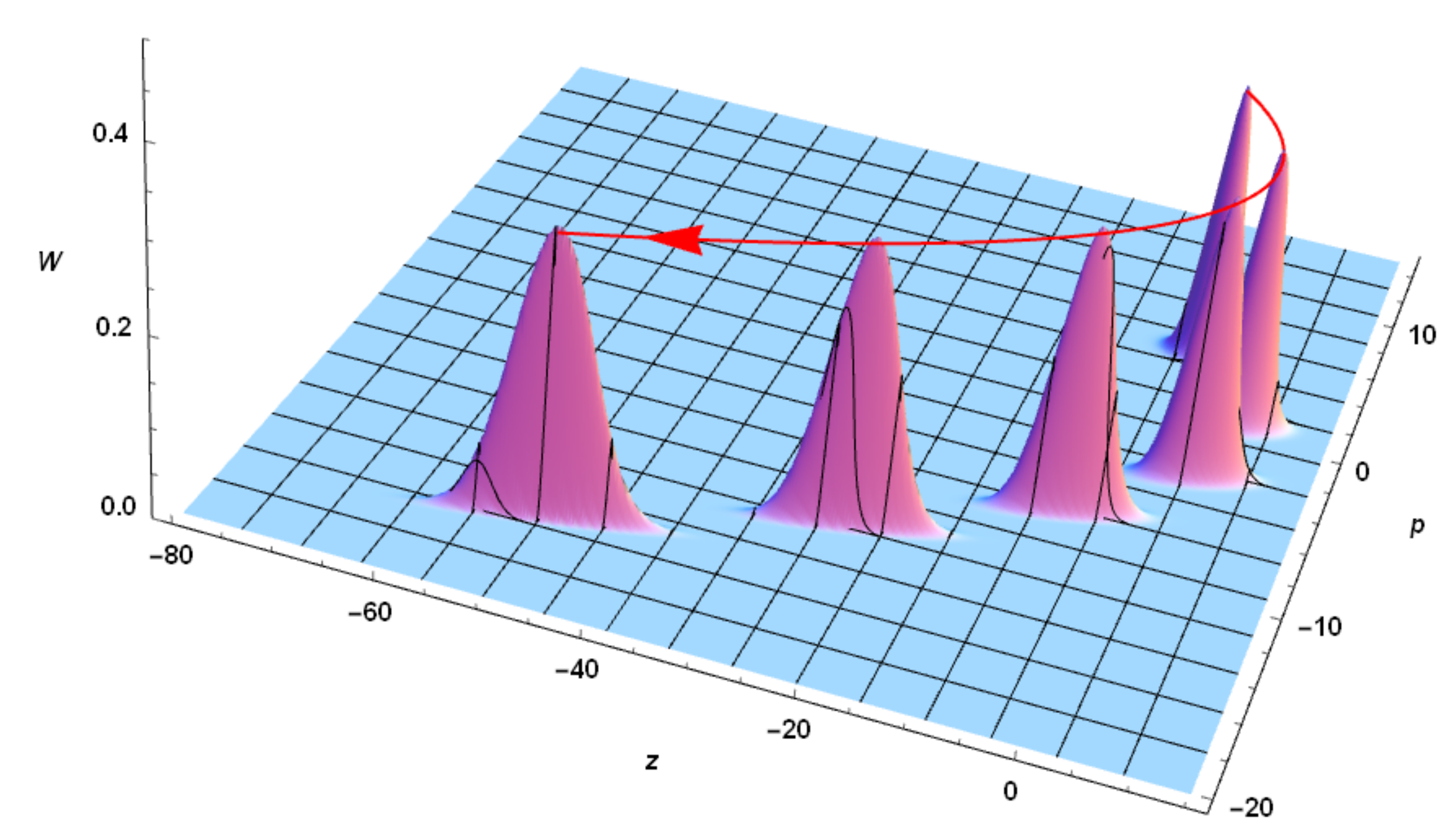
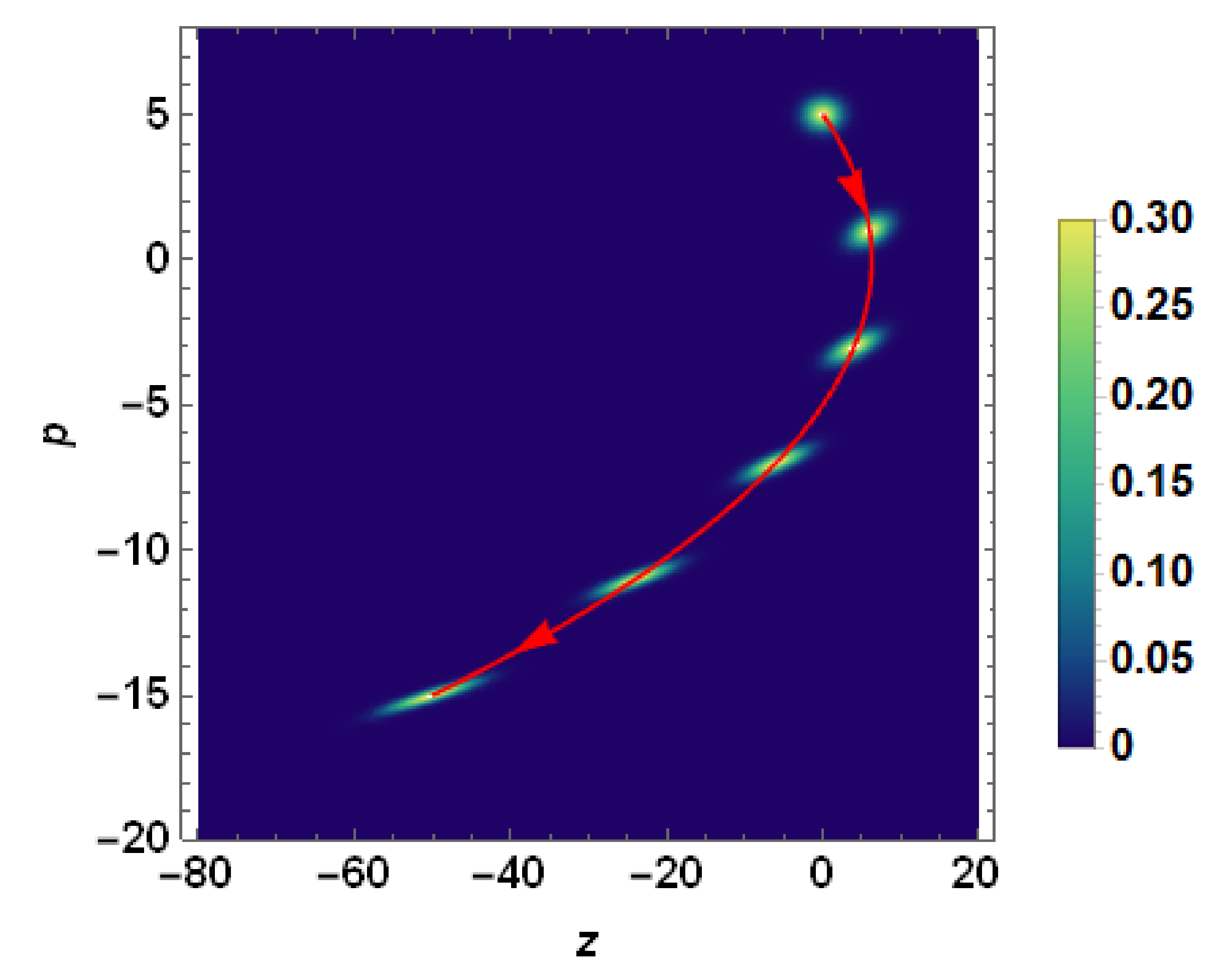
5.1. Density Matrix (i.e., Density Operator ) and Wigner Function W
5.2. Marginal Distribution
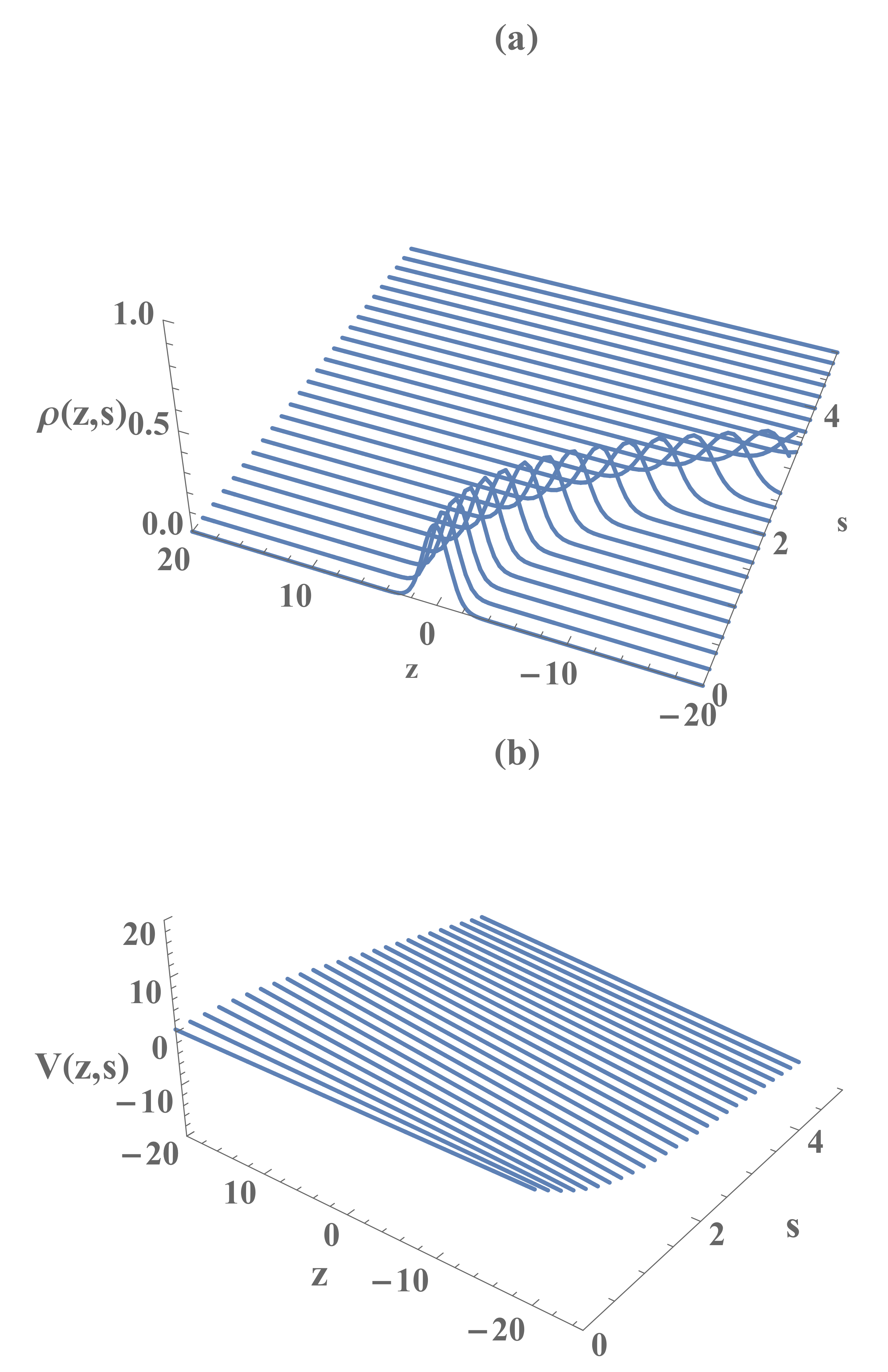
6. Tomographic Characterization of the Wave Packet
6.1. Configuration Space Analysis
6.2. Phase Space Analysis
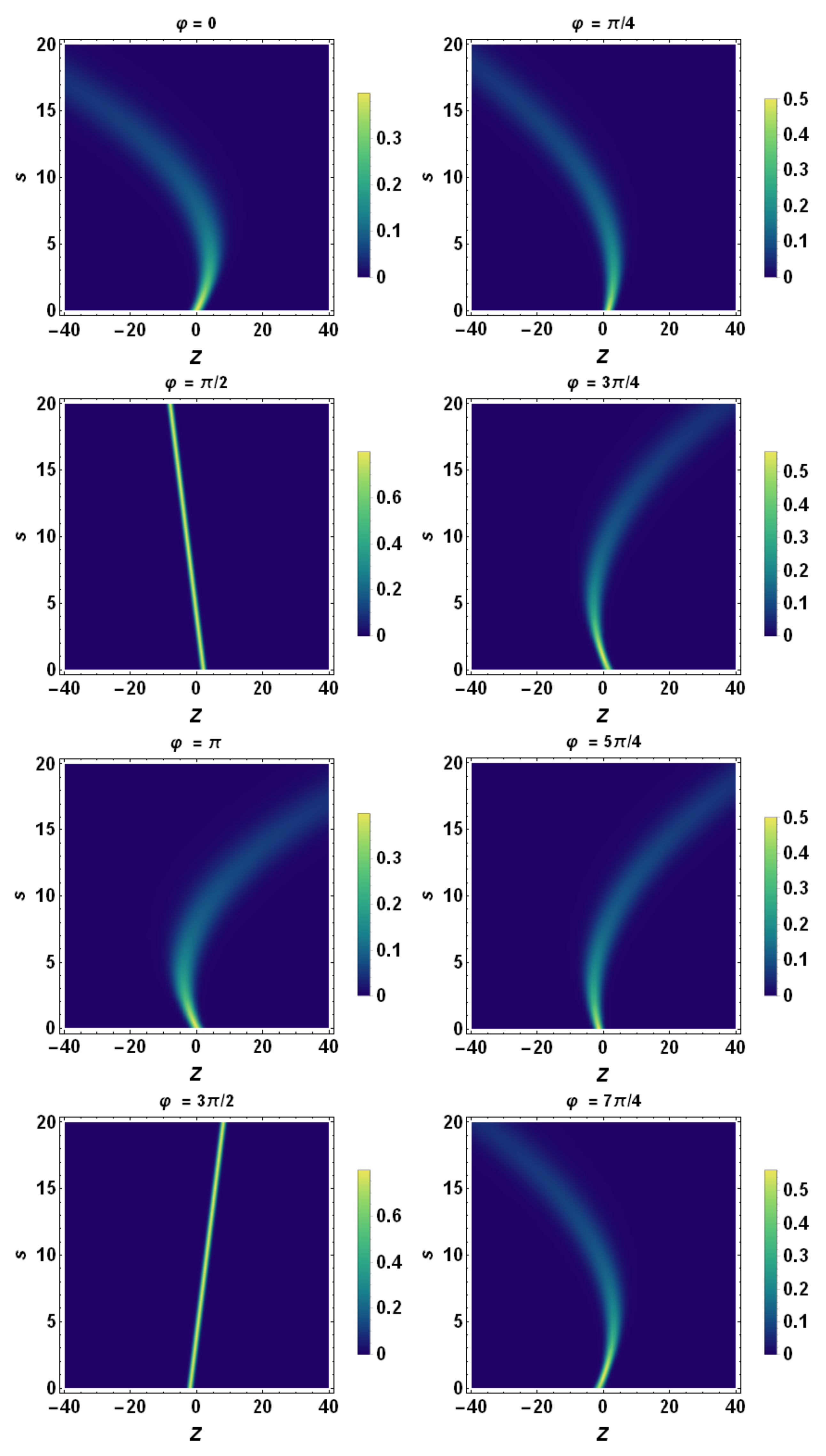
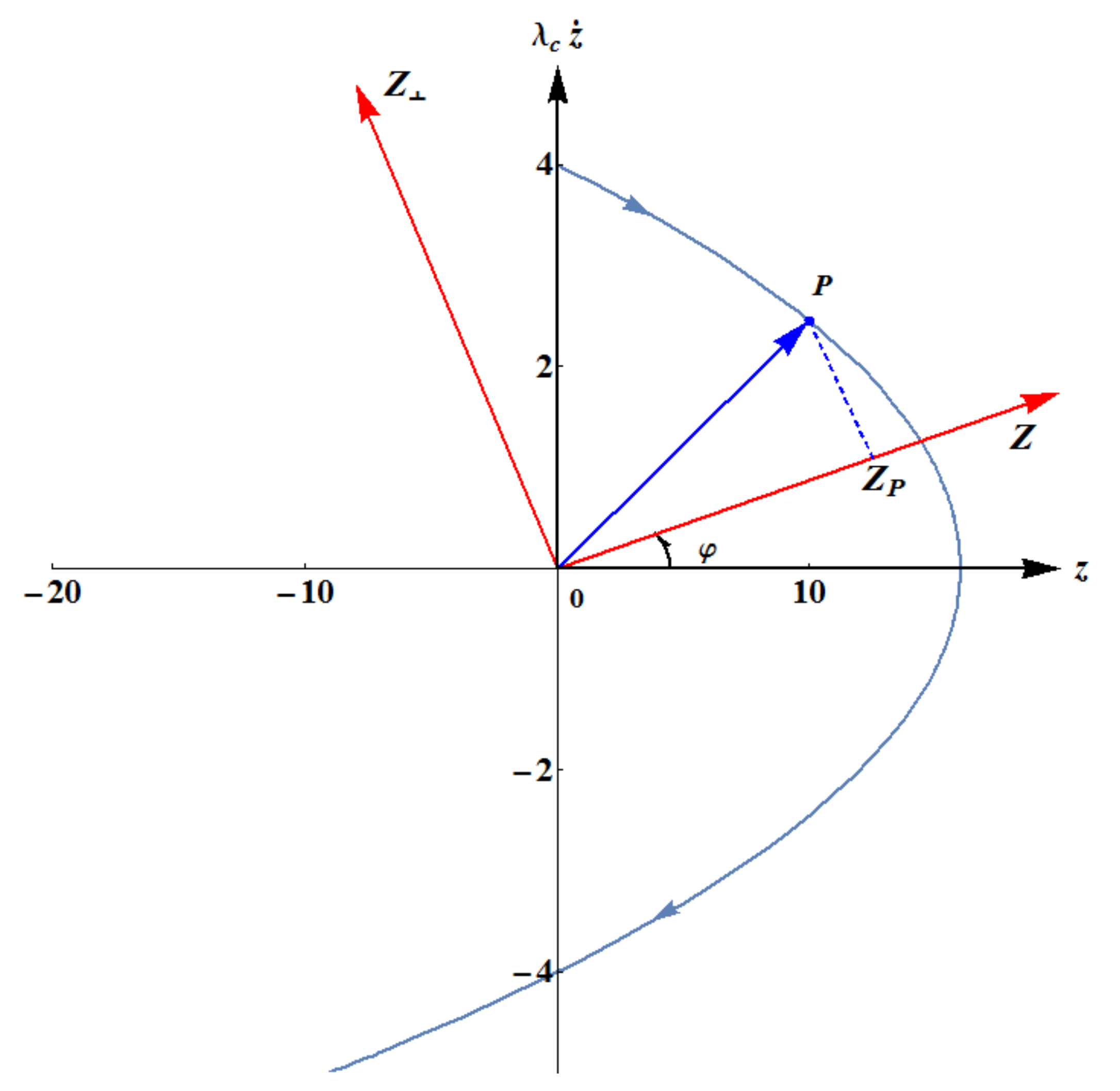
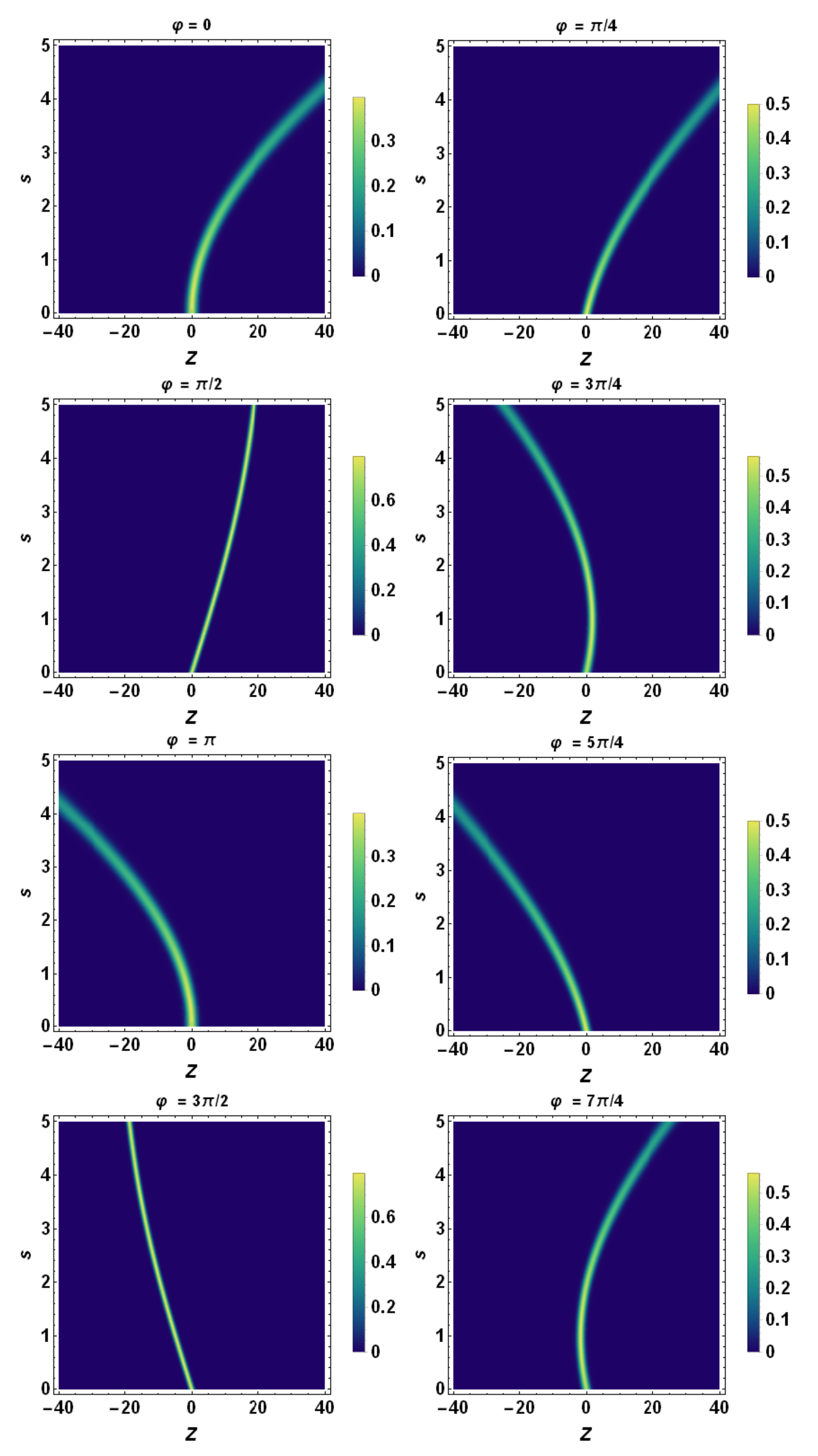
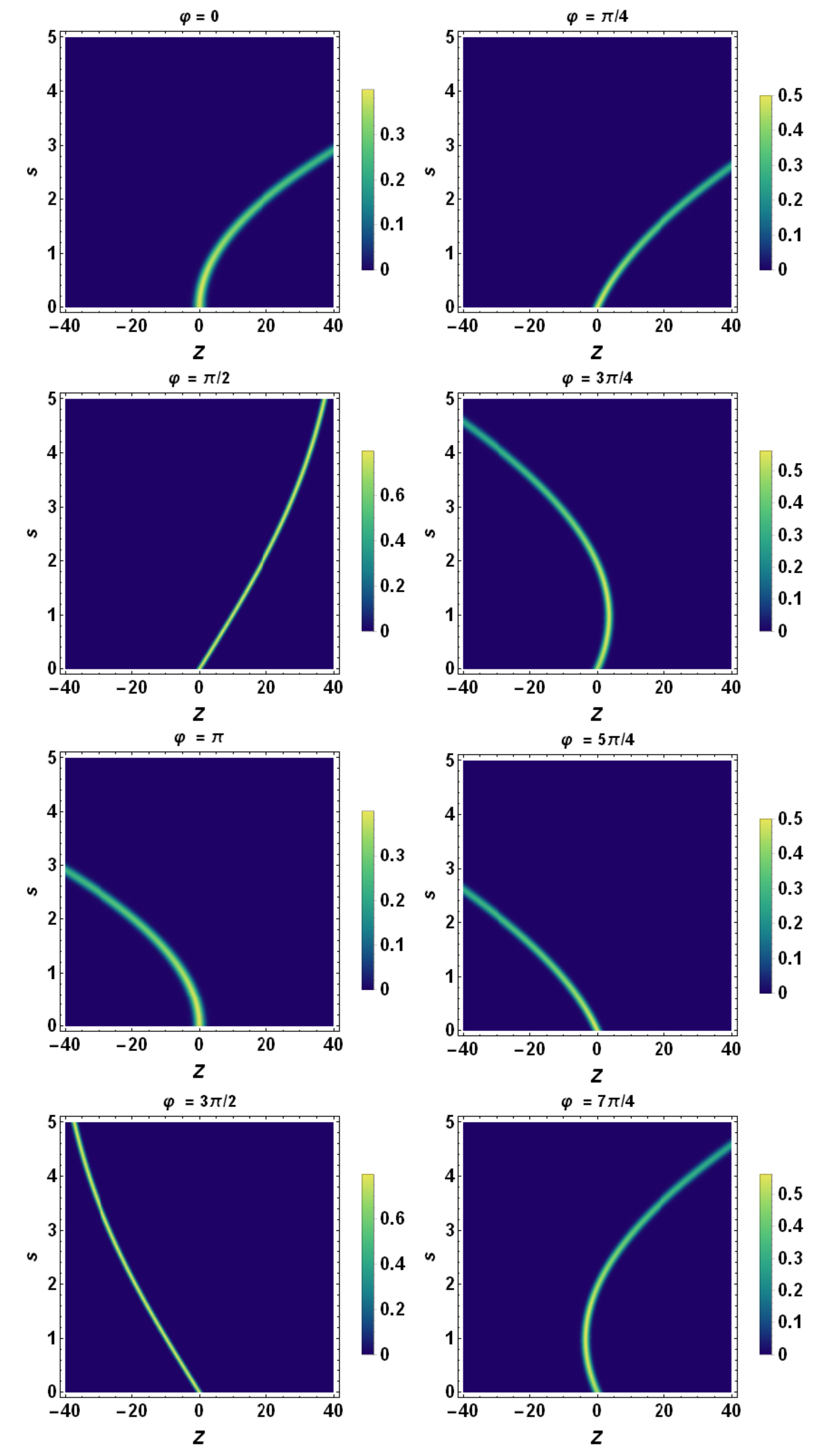
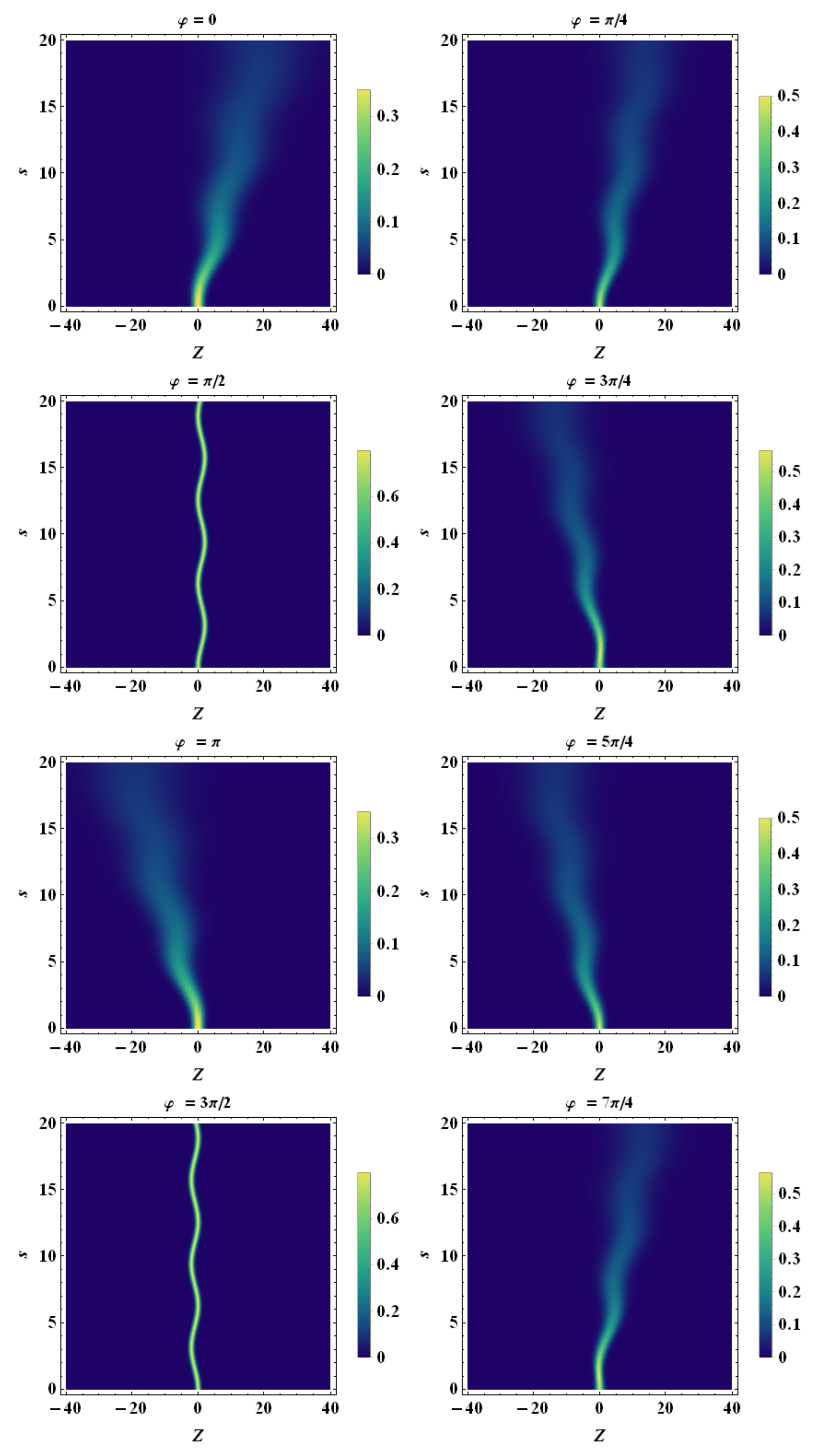
6.3. Tomographic Space
7. Gaussian Tomographic Description for Non-Constant Acceleration
7.1. Gaussian Temporal Burst of Acceleration
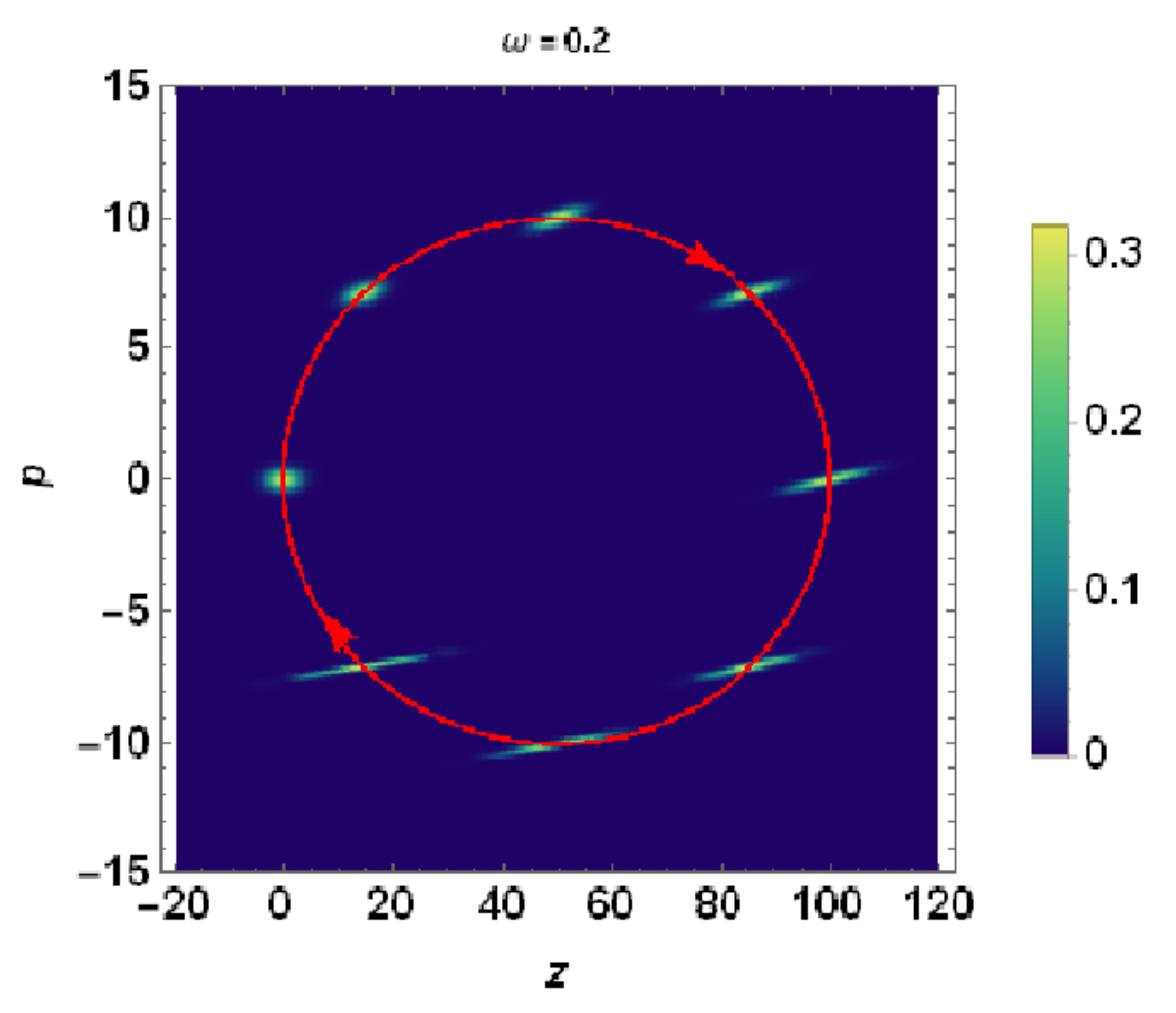
7.2. Sinusoidal Acceleration
8. Conclusions and Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mancini, S.; Man’ko, V.I.; Tombesi, P. Wigner Function and probability-distribution for shifted and squeezed quadratures. Quantum Semiclass. Opt. 1995, 7, 615–623. [Google Scholar] [CrossRef] [Green Version]
- Mancini, S.; Man’ko, V.I.; Tombesi, P. Symplectic tomography as classical approach to quantum systems. Phys. Lett. 1996, A213, 1. [Google Scholar] [CrossRef] [Green Version]
- Mancini, S.; Man’ko, V.I.; Tombesi, P. Classical-like description of quantum dynamics by means of symplectic tomography. Found. Phys. 1997, 27, 801. [Google Scholar] [CrossRef] [Green Version]
- Vogel, K.; Risken, H. Determination of quasiprobability distributions in terms of probability distributions for the rotated quadrature phase. Phys. Rev. 1989, A40, 2847. [Google Scholar] [CrossRef]
- Wigner, E. On the Quantum Correction For Thermodynamic Equilibrium. Phys. Rev. 1932, 40, 749. [Google Scholar] [CrossRef]
- Radon, J. Über die Bestimmung von Funktionen durch ihre Integralwerte längs gewisser Mannigfaltigkeiten. Berichte über die Verhandlungen der Königlich-Sächsischen Akademie der Wissenschaften zu Leipzig, Mathematisch-Physische Klasse [Reports on the proceedings of the Royal Saxonian Academy of Sciences at Leipzig, mathematical and physical section], Leipzig: Teubner (69), 277 (1917); Translation: J. Radon, P.C. Parks(translator), On the determination of functions from their integral values along certain manifolds. IEEE Trans. Med Imaging 1986, 5, 170–176. [Google Scholar]
- Glauber, R.J. Coherent and incoherent states of the radiation field. Phys. Rev. 1963, 131, 2766. [Google Scholar] [CrossRef]
- Sudarshan, E.C.G. Equivalence of semiclassical and quantum mechanical descriptions of statistical light beams. Phys. Rev. Lett. 1963, 10, 277. [Google Scholar] [CrossRef]
- Husimi, K. Some Formal Properties of the Density Matrix. Proc. Phys. Math. Soc. Jpn. 1940, 23, 264. [Google Scholar]
- Amosov, G.G.; Man’ko, V.I.; Orlov, Y.N. Evolution equation of quantum tomograms for a driven oscillator in the case of the general linear quantization. Phys. Scr. 2009, 79, 015004. [Google Scholar] [CrossRef] [Green Version]
- Auletta, G. Foundation and Interpretation of Quantum Mechanics; World Scientific: Singapore, 2000. [Google Scholar]
- De Nicola, S.; Fedele, R.; Man’ko, M.A.; Man’ko, V.I. Fresnel Tomography: A Novel Approach to Wave-Function Reconstruction Based on the Fresnel Representation of Tomograms. Theor. Math. Phys. 2005, 144, 1206. [Google Scholar] [CrossRef] [Green Version]
- De Nicola, S.; Fedele, R.; Man’ko, M.A.; Man’ko, V.I. Tomography of solitons. J. Opt. B Quantum Semiclass. Opt. 2003, 5, 95. [Google Scholar] [CrossRef]
- Leontovich, M.A. On a method of solving the problem of propagation of electromagnetic waves near the surface of the earth. Izv. Akad. Nauk SSSR Ser. Fiz. 1944, 8, 16. [Google Scholar]
- Leontovich, M.A.; Fok, V.A. About inconsistency of works by AA Vlasov on general theory of plasma and physics of solid body. Zh. Eksp. Teor. Fiz. 1946, 16, 557. [Google Scholar]
- De Nicola, S.; Fedele, R.; Man’ko, M.A.; Man’ko, V.I. Fresnel entropic characterization of optical Laguerre-Gaussian beams. Phys. Lett. 2011, A 375, 961. [Google Scholar] [CrossRef]
- Fedele, R.; Miele, G. A thermal-wave model for relativistic charged-particle beams. Il Nuovo C. D 1991, D13, 1527. [Google Scholar] [CrossRef] [Green Version]
- Fedele, R.; Shukla, P.K. Self-consistent interaction between the plasma wakefield and the driving relativistic electron beam. Phys. Rev. 1992, A 45, 4045. [Google Scholar] [CrossRef]
- Fedele, R.; Miele, G.; Palumbo, L.; Vaccaro, V.G. Thermal Wave Model for Nonlinear Longitudinal Dynamics in Particle Accelerators. Phys. Lett. 1993, A 179, 407. [Google Scholar] [CrossRef]
- Anderson, D.; Fedele, R.; Vaccaro, V.G.; Lisak, M.; Berntson, A.; Johansson, S. Modulational instabilities within the thermal wave model description of high-energy charged particle beam dynamics. Phys. Lett. A 1999, 244, 258. [Google Scholar] [CrossRef]
- De Nicola, S.; Fedele, R.; Man’ko, V.I. Coherent states for particle beams in the thermal wave model. Phys. Scr. 1995, 52, 191. [Google Scholar] [CrossRef]
- Fedele, R.; Man’ko, V.I. Quantum-like corrections and tomography in beam physics. In Proceedings of the European Particle Accelerator Conference EPAC98 (1998), Stockholm, Sweden, 22–26 June 1998; p. 1268. [Google Scholar]
- Fedele, R.; Man’ko, V.I. Quantumlike Corrections and Semiclassical Description of Charged-Particle Beam Transport. Phys. Rev. 1998, E58, 992. [Google Scholar] [CrossRef] [Green Version]
- De Nicola, S.; Fedele, R.; Man’ko, M.A.; Man’ko, V.I. Entropic uncertainty relations for electromagnetic beams. Phys. Scr. 2009, T135, 014053. [Google Scholar] [CrossRef] [Green Version]
- De Nicola, S.; Fedele, R.; Man’ko, M.A.; Man’ko, V.I. New inequalities for tomograms in the probability representation of quantum states. Theor. Math. Phys. 2007, 152, 1081. [Google Scholar] [CrossRef] [Green Version]
- Von Neumann, J. Mathematische Grundlagen der Quantenmechanik; Springer: Berlin/Heidelberg, Germany, 1932. [Google Scholar]
- Ermakov, V.P. Second-order differential equations, Conditions of complete integrability. Univ. Izv. (Kiev) 1880, 20, 1–25. [Google Scholar] [CrossRef] [Green Version]
- Pinney, E. The nonlinear differential equation y″ + p(x)y + cy−3 = 0. Proc. Am. Math. Soc. 1950, 1, 681. [Google Scholar] [CrossRef]
- Fiore, G.; Gouba, L. Class of invariants for the two-dimensional time-dependent Landau problem and harmonic oscillator in a magnetic field. J. Math. Phys. 2011, 52, 103509. [Google Scholar] [CrossRef] [Green Version]
- Landau, L.D.; Lifsits, E.M. Mechanics; Pergamon Press: Oxford, UK, 1957. [Google Scholar]
- Man’ko, V.I.; Mendes, R.V. Non-commutative time-frequency tomography. Phys. Lett. A 1999, 263, 53. [Google Scholar] [CrossRef] [Green Version]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Nicola, S.; Fedele, R.; Jovanović, D.; Man’ko, M.A.; Man’ko, V.I. Tomographic Description of a Quantum Wave Packet in an Accelerated Frame. Entropy 2021, 23, 636. https://doi.org/10.3390/e23050636
De Nicola S, Fedele R, Jovanović D, Man’ko MA, Man’ko VI. Tomographic Description of a Quantum Wave Packet in an Accelerated Frame. Entropy. 2021; 23(5):636. https://doi.org/10.3390/e23050636
Chicago/Turabian StyleDe Nicola, Sergio, Renato Fedele, Dušan Jovanović, Margarita A. Man’ko, and Vladimir I. Man’ko. 2021. "Tomographic Description of a Quantum Wave Packet in an Accelerated Frame" Entropy 23, no. 5: 636. https://doi.org/10.3390/e23050636
APA StyleDe Nicola, S., Fedele, R., Jovanović, D., Man’ko, M. A., & Man’ko, V. I. (2021). Tomographic Description of a Quantum Wave Packet in an Accelerated Frame. Entropy, 23(5), 636. https://doi.org/10.3390/e23050636







