Multi-Particle Interference in an Electronic Mach–Zehnder Interferometer
Abstract
1. Introduction
2. Theoretical Background
2.1. Floquet Scattering Theory
2.2. Voltage Pulses
2.3. Excess Correlation Function
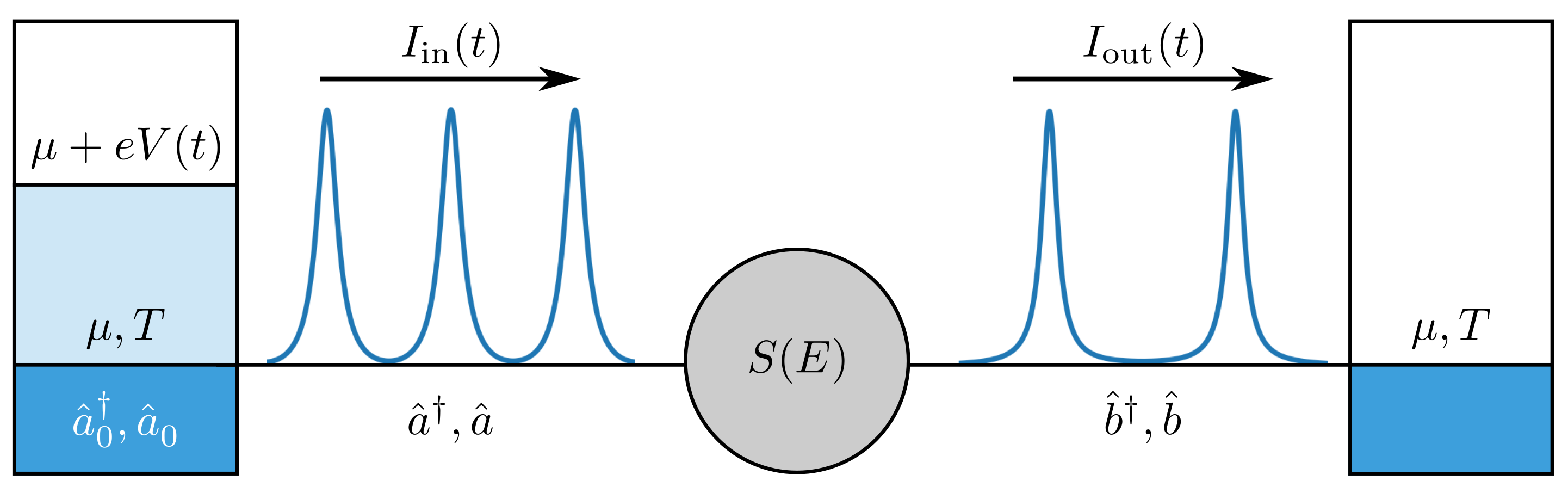
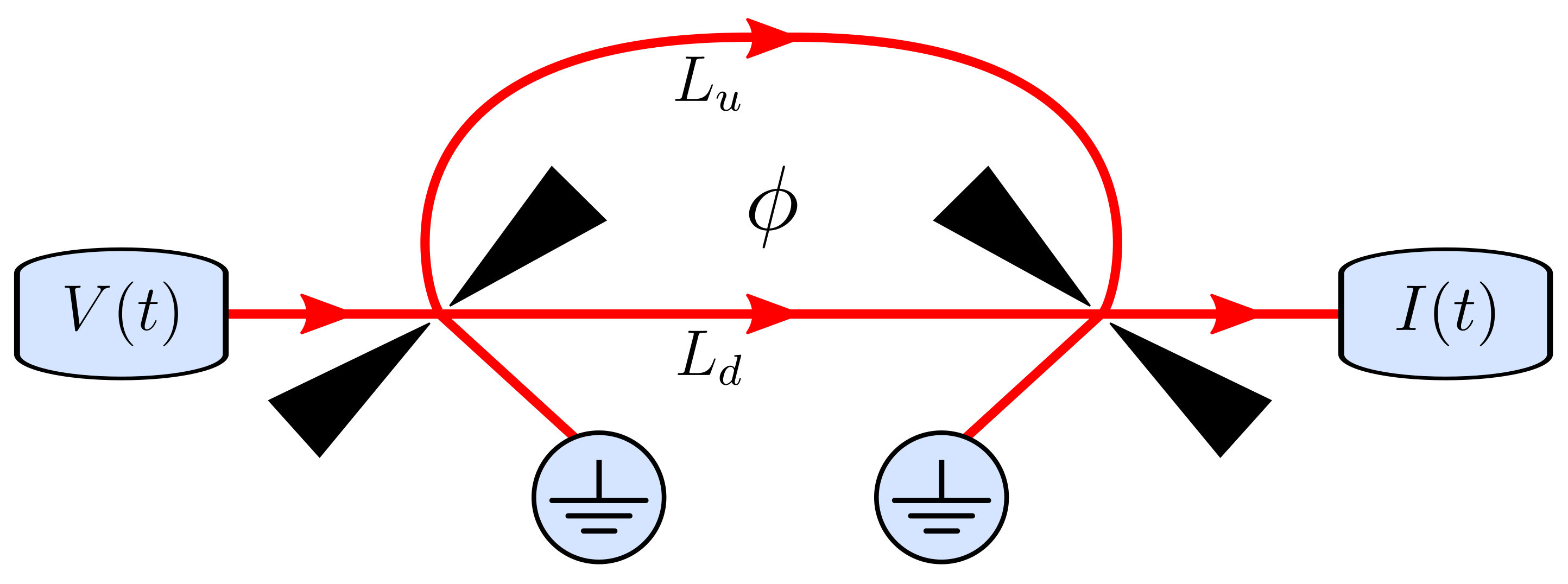
3. Mach–Zehnder Interferometer
3.1. Injected Current
3.2. Output Current
3.3. Transferred Charge
3.4. Visibility
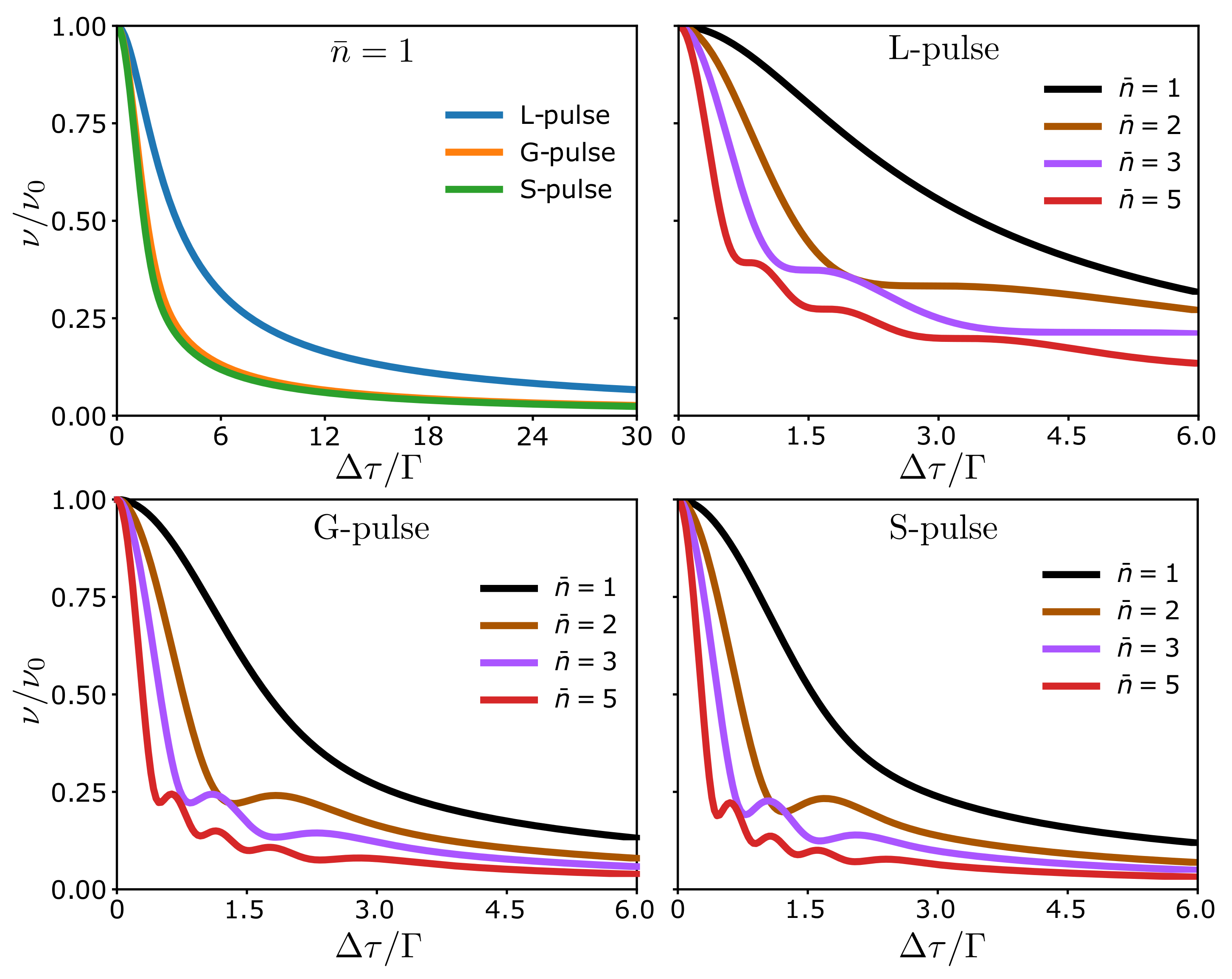
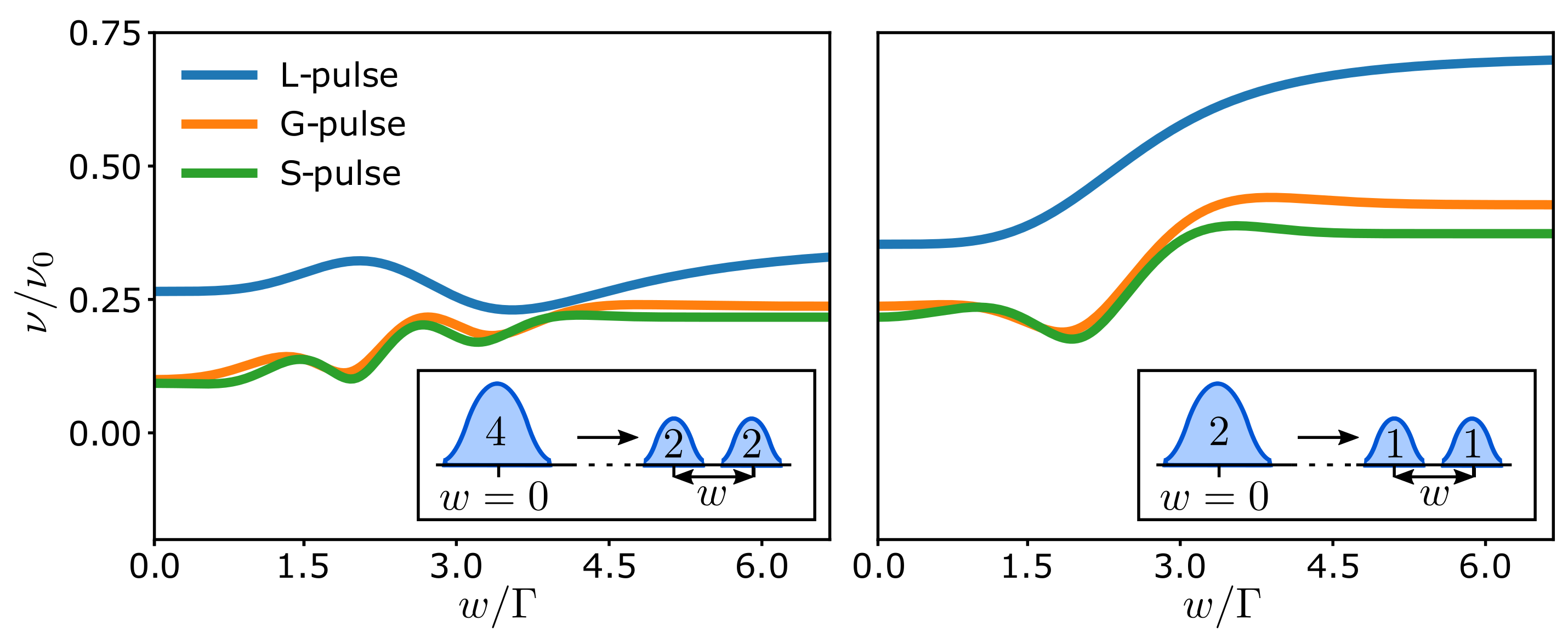
4. Results and Analysis
4.1. Fraunhofer-Like Diffraction Pattern
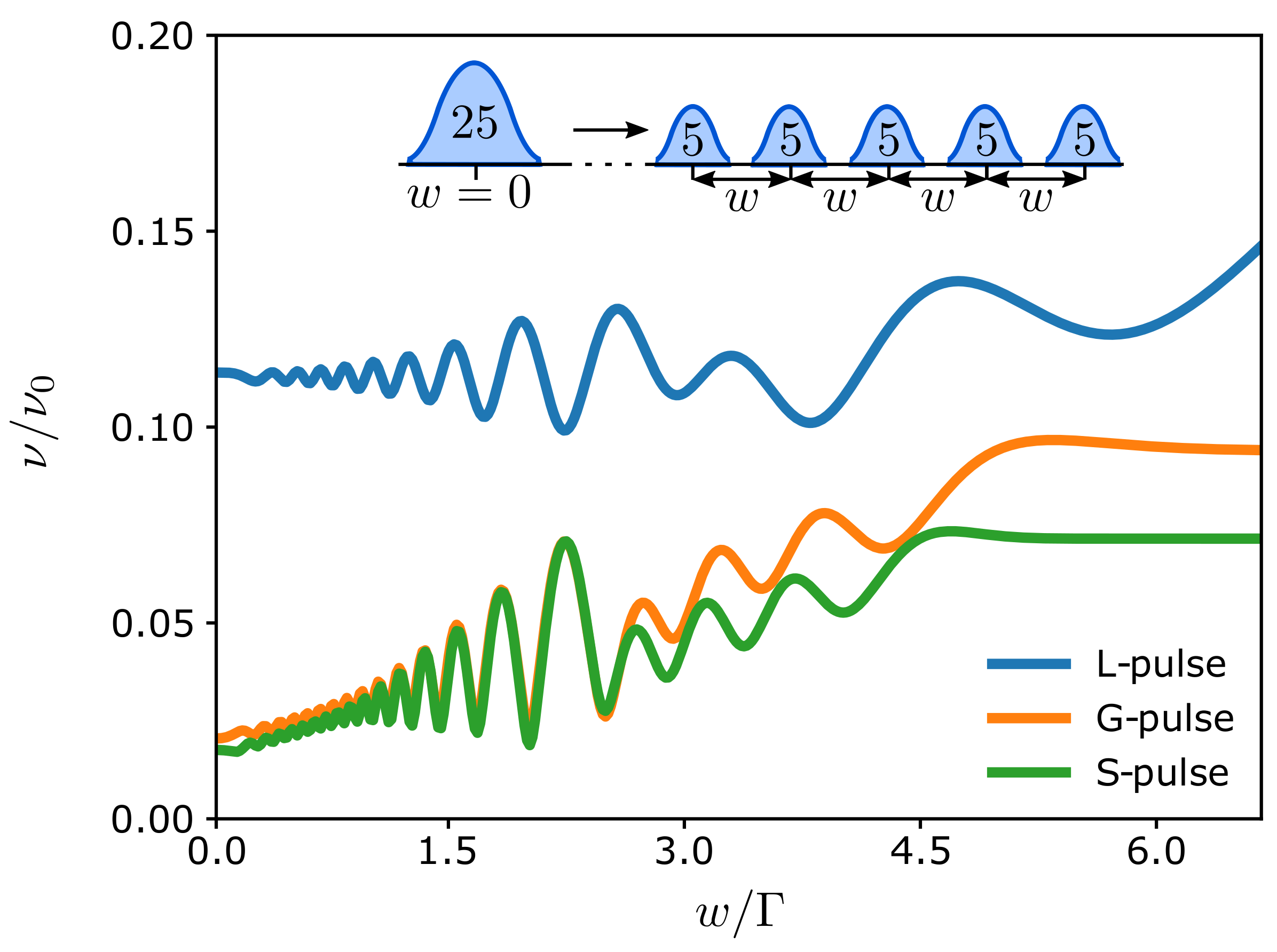
4.2. Diffraction Grid
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bocquillon, E.; Freulon, V.; Parmentier, F.D.; Berroir, J.M.; Plaçais, B.; Wahl, C.; Rech, J.; Jonckheere, T.; Martin, T.; Grenier, C.; et al. Electron quantum optics in ballistic chiral conductors. Ann. Phys. 2014, 526, 1. [Google Scholar] [CrossRef]
- Splettstoesser, J.; Haug, R.J. Single-electron control in solid state devices. Phys. Status Solidi 2017, 254, 1770217. [Google Scholar] [CrossRef]
- Bäuerle, C.; Glattli, D.C.; Meunier, T.; Portier, F.; Roche, P.; Roulleau, P.; Takada, S.; Waintal, X. Coherent control of single electrons: A review of current progress. Rep. Prog. Phys. 2018, 81, 056503. [Google Scholar] [CrossRef] [PubMed]
- Gabelli, J.; Fève, G.; Berroir, J.M.; Plaçais, B.; Cavanna, A.; Etienne, B.; Jin, Y.; Glattli, D.C. Violation of Kirchhoff’s Laws for a Coherent RC Circuit. Science 2006, 313, 499. [Google Scholar] [CrossRef]
- Fève, G.; Mahé, A.; Berroir, J.M.; Kontos, T.; Plaçais, B.; Glattli, D.C.; Cavanna, A.; Etienne, B.; Jin, Y. An On-Demand Coherent Single-Electron Source. Science 2007, 316, 1169. [Google Scholar] [CrossRef]
- Bocquillon, E.; Freulon, V.; Berroir, J.M.; Degiovanni, P.; Plaçais, B.; Cavanna, A.; Jin, Y.; Fève, G. Coherence and Indistinguishability of Single Electrons Emitted by Independent Sources. Science 2013, 339, 1054. [Google Scholar] [CrossRef]
- Dubois, J.; Jullien, T.; Portier, F.; Roche, P.; Cavanna, A.; Jin, Y.; Wegscheider, W.; Roulleau, P.; Glattli, D.C. Minimal-excitation states for electron quantum optics using levitons. Nature 2013, 502, 659. [Google Scholar] [CrossRef]
- Jullien, T.; Roulleau, P.; Roche, B.; Cavanna, A.; Jin, Y.; Glattli, D.C. Quantum tomography of an electron. Nature 2014, 514, 603. [Google Scholar] [CrossRef]
- Roussely, G.; Arrighi, E.; Georgiou, G.; Takada, S.; Schalk, M.; Urdampilleta, M.; Ludwig, A.; Wieck, A.D.; Armagnat, P.; Kloss, T.; et al. Unveiling the bosonic nature of an ultrashort few-electron pulse. Nat. Commun. 2018, 9, 2811. [Google Scholar] [CrossRef]
- Halperin, B.I. Quantized Hall conductance, current-carrying edge states, and the existence of extended states in a two-dimensional disordered potential. Phys. Rev. B 1982, 25, 2185–2190. [Google Scholar] [CrossRef]
- Büttiker, M. Absence of backscattering in the quantum Hall effect in multiprobe conductors. Phys. Rev. B 1988, 38, 9375–9389. [Google Scholar] [CrossRef]
- Büttiker, M.; Thomas, H.; Prêtre, A. Mesoscopic Capacitors. Phys. Lett. A 1993, 180, 364. [Google Scholar] [CrossRef]
- Blumenthal, M.D.; Kaestner, B.; Li, L.; Giblin, S.; Janssen, T.J.B.M.; Pepper, M.; Anderson, D.; Jones, G.; Ritchie, D.A. Gigahertz quantized charge pumping. Nat. Phys. 2007, 3, 343. [Google Scholar] [CrossRef]
- Fletcher, J.D.; See, P.; Howe, H.; Pepper, M.; Giblin, S.P.; Griffiths, J.P.; Jones, G.A.C.; Farrer, I.; Ritchie, D.A.; Janssen, T.J.B.M.; et al. Clock-Controlled Emission of Single-Electron Wave Packets in a Solid-State Circuit. Phys. Rev. Lett. 2013, 111, 216807. [Google Scholar] [CrossRef]
- Fletcher, J.D.; Johnson, N.; Locane, E.; See, P.; Griffiths, J.P.; Farrer, I.; Ritchie, D.A.; Brouwer, P.W.; Kashcheyevs, V.; Kataoka, M. Continuous-variable tomography of solitary electrons. Nat. Commun. 2019, 10, 5298. [Google Scholar] [CrossRef]
- Levitov, L.S.; Lee, H.; Lesovik, G.B. Electron counting statistics and coherent states of electric current. J. Math. Phys. 1996, 37, 4845. [Google Scholar] [CrossRef]
- Ivanov, D.A.; Lee, H.W.; Levitov, L.S. Coherent States of Alternating Current. Phys. Rev. B 1997, 56, 6839. [Google Scholar] [CrossRef]
- Keeling, J.; Klich, I.; Levitov, L.S. Minimal Excitation States of Electrons in One-Dimensional Wires. Phys. Rev. Lett. 2006, 97, 116403. [Google Scholar] [CrossRef]
- Hanbury Brown, R.; Twiss, R.Q. A Test of a New Type of Stellar Interferometer on Sirius. Nature 1956, 178, 1046. [Google Scholar] [CrossRef]
- Brown, R.; Twiss, R. Correlation between Photons in two Coherent Beams of Light. Nature 1956, 177, 27. [Google Scholar] [CrossRef]
- Hong, C.K.; Ou, Z.Y.; Mandel, L. Measurement of subpicosecond time intervals between two photons by interference. Phys. Rev. Lett. 1987, 59, 2044. [Google Scholar] [CrossRef] [PubMed]
- Glauber, R.J. Photon Correlations. Phys. Rev. Lett. 1963, 10, 84. [Google Scholar] [CrossRef]
- Glauber, R.J. Coherent and Incoherent States of the Radiation Field. Phys. Rev. 1963, 131, 2766. [Google Scholar] [CrossRef]
- Glauber, R.J. The Quantum Theory of Optical Coherence. Phys. Rev. 1963, 130, 2529. [Google Scholar] [CrossRef]
- Ursin, R.; Tiefenbacher, F.; Schmitt-Manderbach, T.; Weier, H.; Scheidl, T.; Lindenthal, M.; Blauensteiner, B.; Jennewein, T.; Perdigues, J.; Trojek, P.; et al. Entanglement-based quantum communication over 144 km. Nat. Phys. 2007, 3, 481. [Google Scholar] [CrossRef]
- Bocquillon, E.; Parmentier, F.D.; Grenier, C.; Berroir, J.M.; Degiovanni, P.; Glattli, D.C.; Plaçais, B.; Cavanna, A.; Jin, Y.; Fève, G. Electron Quantum Optics: Partitioning Electrons One by One. Phys. Rev. Lett. 2012, 108, 196803. [Google Scholar] [CrossRef] [PubMed]
- Glattli, D.C.; Roulleau, P. Pseudorandom binary injection of Levitons for electron quantum optics. Phys. Rev. B 2018, 97, 125407. [Google Scholar] [CrossRef]
- van Wees, B.J.; van Houten, H.; Beenakker, C.W.J.; Williamson, J.G.; Kouwenhoven, L.P.; van der Marel, D.; Foxon, C.T. Quantized conductance of point contacts in a two-dimensional electron gas. Phys. Rev. Lett. 1988, 60, 848. [Google Scholar] [CrossRef]
- Wharam, D.A.; Thornton, T.J.; Newbury, R.; Pepper, M.; Ahmed, H.; Frost, J.E.F.; Hasko, D.G.; Peacock, D.C.; Ritchie, D.A.; Jones, G.A.C. One-dimensional transport and the quantisation of the ballistic resistance. J. Phys. C Solid State Phys. 1988, 21, L209. [Google Scholar] [CrossRef]
- Henny, M.; Oberholzer, S.; Strunk, C.; Heinzel, T.; Ensslin, K.; Holland, M.; Schönenberger, C. The Fermionic Hanbury Brown and Twiss Experiment. Science 1999, 284, 296. [Google Scholar] [CrossRef]
- Oliver, W.D.; Kim, J.; Liu, R.C.; Yamamoto, Y. Hanbury Brown and Twiss-type experiment with electrons. Science 1999, 284, 299. [Google Scholar] [CrossRef]
- Oberholzer, S.; Henny, M.; Strunk, C.; Schönenberger, C.; Heinzel, T.; Ensslin, K.; Holland, M. The Hanbury Brown and Twiss experiment with fermions. Physica E 2000, 6, 314. [Google Scholar] [CrossRef]
- Ji, Y.; Chung, Y.; Sprinzak, D.; Heiblum, M.; Mahalu, D.; Shtrikman, H. An electronic Mach-Zehnder interferometer. Nature 2003, 422, 415. [Google Scholar] [CrossRef]
- Neder, I.; Ofek, N.; Chung, Y.; Heiblum, M.; Mahalu, D.; Umansky, V. Interference between two indistinguishable electrons from independent sources. Nature 2007, 448, 333. [Google Scholar] [CrossRef]
- Neder, I.; Heiblum, M.; Mahalu, D.; Umansky, V. Entanglement, Dephasing, and Phase Recovery via Cross-Correlation Measurements of Electrons. Phys. Rev. Lett. 2007, 98, 036803. [Google Scholar] [CrossRef]
- Roulleau, P.; Portier, F.; Roche, P.; Cavanna, A.; Faini, G.; Gennser, U.; Mailly, D. Direct Measurement of the Coherence Length of Edge States in the Integer Quantum Hall Regime. Phys. Rev. Lett. 2008, 100, 126802. [Google Scholar] [CrossRef]
- Litvin, L.V.; Helzel, A.; Tranitz, H.P.; Wegscheider, W.; Strunk, C. Edge-channel interference controlled by Landau level filling. Phys. Rev. B 2008, 78, 075303. [Google Scholar] [CrossRef]
- Zhang, Y.; McClure, D.T.; Levenson-Falk, E.M.; Marcus, C.M.; Pfeiffer, L.N.; West, K.W. Distinct signatures for Coulomb blockade and Aharonov-Bohm interference in electronic Fabry-Pérot interferometers. Phys. Rev. B 2009, 79, 241304. [Google Scholar] [CrossRef]
- Tewari, S.; Roulleau, P.; Grenier, C.; Portier, F.; Cavanna, A.; Gennser, U.; Mailly, D.; Roche, P. Robust Quantum Coherence above the Fermi Sea. Phys. Rev. B 2016, 93, 035420. [Google Scholar] [CrossRef]
- Huynh, P.A.; Portier, F.; le Sueur, H.; Faini, G.; Gennser, U.; Mailly, D.; Pierre, F.; Wegscheider, W.; Roche, P. Quantum Coherence Engineering in the Integer Quantum Hall Regime. Phys. Rev. Lett. 2012, 108, 256802. [Google Scholar] [CrossRef]
- Jo, M.; Brasseur, P.; Assouline, A.; Fleury, G.; Sim, H.S.; Watanabe, K.; Taniguchi, T.; Dumnernpanich, W.; Roche, P.; Glattli, D.C.; et al. Quantum Hall Valley Splitters and a Tunable Mach-Zehnder Interferometer in Graphene. Phys. Rev. Lett. 2021, 126, 146803. [Google Scholar] [CrossRef]
- Liang, W.; Bockrath, M.; Bozovic, D.; Hafner, J.H.; Tinkham, M.; Park, H. Fabry-Perot interference in a nanotube electron waveguide. Nature 2001, 411, 665. [Google Scholar] [CrossRef]
- Herrmann, L.G.; Delattre, T.; Morfin, P.; Berroir, J.M.; Plaçais, B.; Glattli, D.C.; Kontos, T. Shot Noise in Fabry-Perot Interferometers Based on Carbon Nanotubes. Phys. Rev. Lett. 2007, 99, 156804. [Google Scholar] [CrossRef]
- Kretinin, A.V.; Popovitz-Biro, R.; Mahalu, D.; Shtrikman, H. Multimode Fabry-Pérot Conductance Oscillations in Suspended Stacking-Faults-Free InAs Nanowires. Nano Lett. 2010, 10, 3439. [Google Scholar] [CrossRef]
- Gaury, B.; Waintal, X. Dynamical Control of Interference Using Voltage Pulses in the Quantum Regime. Nat. Commun. 2014, 5, 3844. [Google Scholar] [CrossRef]
- Grenier, C.; Dubois, J.; Jullien, T.; Roulleau, P.; Glattli, D.C.; Degiovanni, P. Fractionalization of minimal excitations in integer quantum Hall edge channels. Phys. Rev. B 2013, 88, 085302. [Google Scholar] [CrossRef]
- Ferraro, D.; Roussel, B.; Cabart, C.; Thibierge, E.; Fève, G.; Grenier, C.; Degiovanni, P. Real-Time Decoherence of Landau and Levitov Quasiparticles in Quantum Hall Edge Channels. Phys. Rev. Lett. 2014, 113, 166403. [Google Scholar] [CrossRef]
- Ferraro, D.; Rech, J.; Jonckheere, T.; Martin, T. Single quasiparticle and electron emitter in the fractional quantum Hall regime. Phys. Rev. B 2015, 91, 205409. [Google Scholar] [CrossRef]
- Rech, J.; Ferraro, D.; Jonckheere, T.; Vannucci, L.; Sassetti, M.; Martin, T. Minimal Excitations in the Fractional Quantum Hall Regime. Phys. Rev. Lett. 2017, 118, 076801. [Google Scholar] [CrossRef]
- Vannucci, L.; Ronetti, F.; Rech, J.; Ferraro, D.; Jonckheere, T.; Martin, T.; Sassetti, M. Minimal excitation states for heat transport in driven quantum Hall systems. Phys. Rev. B 2017, 95, 245415. [Google Scholar] [CrossRef]
- Ferraro, D.; Jonckheere, T.; Rech, J.; Martin, T. Electronic quantum optics beyond the integer quantum Hall effect. Phys. Status Solidi (b) 2017, 254, 1600531. [Google Scholar] [CrossRef]
- Cabart, C.; Roussel, B.; Fève, G.; Degiovanni, P. Taming electronic decoherence in one-dimensional chiral ballistic quantum conductors. Phys. Rev. B 2018, 98, 155302. [Google Scholar] [CrossRef]
- Ronetti, F.; Vannucci, L.; Ferraro, D.; Jonckheere, T.; Rech, J.; Martin, T.; Sassetti, M. Crystallization of levitons in the fractional quantum Hall regime. Phys. Rev. B 2018, 98, 075401. [Google Scholar] [CrossRef]
- Rodriguez, R.H.; Parmentier, F.D.; Ferraro, D.; Roulleau, P.; Gennser, U.; Cavanna, A.; Sassetti, M.; Portier, F.; Mailly, D.; Roche, P. Relaxation and revival of quasiparticles injected in an interacting quantum Hall liquid. Nat. Commun. 2020, 11, 2426. [Google Scholar] [CrossRef] [PubMed]
- Rebora, G.; Acciai, M.; Ferraro, D.; Sassetti, M. Collisional interferometry of levitons in quantum Hall edge channels at ν = 2. Phys. Rev. B 2020, 101, 245310. [Google Scholar] [CrossRef]
- Rebora, G.; Ferraro, D.; Rodriguez, R.H.; Parmentier, F.D.; Roche, P.; Sassetti, M. Electronic Wave-Packets in Integer Quantum Hall Edge Channels: Relaxation and Dissipative Effects. Entropy 2021, 23, 138. [Google Scholar] [CrossRef]
- Freulon, V.; Marguerite, A.; Berroir, J.M.; Plaçais, B.; Cavanna, A.; Jin, Y.; Fève, G. Hong-Ou-Mandel experiment for temporal investigation of single-electron fractionalization. Nat. Commun. 2015, 6, 6854. [Google Scholar] [CrossRef]
- Marguerite, A.; Bocquillon, E.; Berroir, J.M.; Plaçais, B.; Cavanna, A.; Jin, Y.; Degiovanni, P.; Fève, G. Two-particle interferometry in quantum Hall edge channels. Phys. Status Solidi (b) 2016, 254, 1600618. [Google Scholar] [CrossRef]
- Glattli, D.C.; Roulleau, P. Levitons for electron quantum optics. Phys. Status Solidi (b) 2016, 254, 1600650. [Google Scholar] [CrossRef]
- Glattli, D.C.; Roulleau, P. Hanbury-Brown Twiss noise correlation with time controlled quasi-particles in ballistic quantum conductors. Physica E 2016, 76, 216. [Google Scholar] [CrossRef]
- Marguerite, A.; Cabart, C.; Wahl, C.; Roussel, B.; Freulon, V.; Ferraro, D.; Grenier, C.; Berroir, J.M.; Plaçais, B.; Jonckheere, T.; et al. Decoherence and relaxation of a single electron in a one-dimensional conductor. Phys. Rev. B 2016, 94, 115311. [Google Scholar] [CrossRef]
- Grenier, C.; Hervé, R.; Bocquillon, E.; Parmentier, F.D.; Plaçais, B.; Berroir, J.M.; Féve, G.; Degiovanni, P. Single-electron quantum tomography in quantum Hall edge channels. New J. Phys. 2011, 13, 093007. [Google Scholar] [CrossRef]
- Bisognin, R.; Marguerite, A.; Roussel, B.; Kumar, M.; Cabart, C.; Chapdelaine, C.; Mohammad-Djafari, A.; Berroir, J.M.; Bocquillon, E.; Plaçais, B.; et al. Quantum tomography of electrical currents. Nat. Commun. 2019, 10, 3379. [Google Scholar] [CrossRef]
- Waldie, J.; See, P.; Kashcheyevs, V.; Griffiths, J.P.; Farrer, I.; Jones, G.A.C.; Ritchie, D.A.; Janssen, T.J.B.M.; Kataoka, M. Measurement and control of electron wave packets from a single-electron source. Phys. Rev. B 2015, 92, 125305. [Google Scholar] [CrossRef]
- Kataoka, M.; Johnson, N.; Emary, C.; See, P.; Griffiths, J.P.; Jones, G.A.C.; Farrer, I.; Ritchie, D.A.; Pepper, M.; Janssen, T.J.B.M. Time-of-Flight Measurements of Single-Electron Wave Packets in Quantum Hall Edge States. Phys. Rev. Lett. 2016, 116, 126803. [Google Scholar] [CrossRef]
- Fricke, L.; Wulf, M.; Kaestner, B.; Kashcheyevs, V.; Timoshenko, J.; Nazarov, P.; Hohls, F.; Mirovsky, P.; Mackrodt, B.; Dolata, R.; et al. Counting Statistics for Electron Capture in a Dynamic Quantum Dot. Phys. Rev. Lett. 2013, 110, 126803. [Google Scholar] [CrossRef]
- Ubbelohde, N.; Hohls, F.; Kashcheyevs, V.; Wagner, T.; Fricke, L.; Kästner, B.; Pierz, K.; Schumacher, H.W.; Haug, R.J. Partitioning of On-Demand Electron Pairs. Nat. Nanotech. 2014, 10, 46. [Google Scholar] [CrossRef]
- Johnson, N.; Emary, C.; Ryu, S.; Sim, H.S.; See, P.; Fletcher, J.D.; Griffiths, J.P.; Jones, G.A.C.; Farrer, I.; Ritchie, D.A.; et al. LO-Phonon Emission Rate of Hot Electrons from an On-Demand Single-Electron Source in a GaAs/AlGaAs Heterostructure. Phys. Rev. Lett. 2018, 121, 137703. [Google Scholar] [CrossRef]
- Samuelsson, P.; Sukhorukov, E.V.; Büttiker, M. Two-Particle Aharonov-Bohm Effect and Entanglement in the Electronic Hanbury Brown–Twiss Setup. Phys. Rev. Lett. 2004, 92, 026805. [Google Scholar] [CrossRef]
- Lebedev, A.V.; Lesovik, G.B.; Blatter, G. Generating spin-entangled electron pairs in normal conductors using voltage pulses. Phys. Rev. B 2005, 72, 245314. [Google Scholar] [CrossRef]
- Beenakker, C.W.J.; Titov, M.; Trauzettel, B. Optimal Spin-Entangled Electron-Hole Pair Pump. Phys. Rev. Lett. 2005, 94, 186804. [Google Scholar] [CrossRef]
- Samuelsson, P.; Büttiker, M. Dynamic generation of orbital quasiparticle entanglement in mesoscopic conductors. Phys. Rev. B 2005, 71, 245317. [Google Scholar] [CrossRef]
- Hofer, P.P.; Büttiker, M. Emission of time-bin entangled particles into helical edge states. Phys. Rev. B 2013, 88, 241308. [Google Scholar] [CrossRef]
- Dasenbrook, D.; Flindt, C. Dynamical generation and detection of entanglement in neutral leviton pairs. Phys. Rev. B 2015, 92, 161412. [Google Scholar] [CrossRef]
- Dasenbrook, D.; Hofer, P.P.; Flindt, C. Electron waiting times in coherent conductors are correlated. Phys. Rev. B 2015, 91, 195420. [Google Scholar] [CrossRef]
- Dasenbrook, D.; Bowles, J.; Bohr Brask, J.; Hofer, P.P.; Flindt, C.; Brunner, N. Single-electron entanglement and nonlocality. New J. Phys. 2016, 18, 043036. [Google Scholar] [CrossRef]
- Hofer, P.P.; Dasenbrook, D.; Flindt, C. On-demand entanglement generation using dynamic single-electron sources. Phys. Status Solidi (b) 2017, 254, 1600582. [Google Scholar] [CrossRef]
- Olofsson, E.; Samuelsson, P.; Brunner, N.; Potts, P.P. Quantum teleportation of single-electron states. Phys. Rev. B 2020, 101, 195403. [Google Scholar] [CrossRef]
- Moskalets, M.; Büttiker, M. Heat production and current noise for single- and double-cavity quantum capacitors. Phys. Rev. B 2009, 80, 081302. [Google Scholar] [CrossRef]
- Battista, F.; Moskalets, M.; Albert, M.; Samuelsson, P. Quantum Heat Fluctuations of Single-Particle Sources. Phys. Rev. Lett. 2013, 110, 126602. [Google Scholar] [CrossRef] [PubMed]
- Moskalets, M.; Haack, G. Heat and charge transport measurements to access single-electron quantum characteristics. Phys. Status Solidi (b) 2016, 254, 1600616. [Google Scholar] [CrossRef]
- Samuelsson, P.; Kheradsoud, S.; Sothmann, B. Optimal Quantum Interference Thermoelectric Heat Engine with Edge States. Phys. Rev. Lett. 2017, 118, 256801. [Google Scholar] [CrossRef] [PubMed]
- Dashti, N.; Misiorny, M.; Kheradsoud, S.; Samuelsson, P.; Splettstoesser, J. Minimal excitation single-particle emitters: Comparison of charge-transport and energy-transport properties. Phys. Rev. B 2019, 100, 035405. [Google Scholar] [CrossRef]
- Ronetti, F.; Vannucci, L.; Ferraro, D.; Jonckheere, T.; Rech, J.; Martin, T.; Sassetti, M. Hong-Ou-Mandel heat noise in the quantum Hall regime. Phys. Rev. B 2019, 99, 205406. [Google Scholar] [CrossRef]
- Dasenbrook, D.; Flindt, C.; Büttiker, M. Floquet Theory of Electron Waiting Times in Quantum-Coherent Conductors. Phys. Rev. Lett. 2014, 112, 146801. [Google Scholar] [CrossRef]
- Dasenbrook, D.; Flindt, C. Quantum theory of an electron waiting time clock. Phys. Rev. B 2016, 93, 245409. [Google Scholar] [CrossRef]
- Mi, S.; Burset, P.; Flindt, C. Electron waiting times in hybrid junctions with topological superconductors. Sci. Rep. 2018, 8, 16828. [Google Scholar] [CrossRef]
- Burset, P.; Kotilahti, J.; Moskalets, M.; Flindt, C. Time-Domain Spectroscopy of Mesoscopic Conductors Using Voltage Pulses. Adv. Quant. Technol. 2019, 2, 1900014. [Google Scholar] [CrossRef]
- Brange, F.; Schmidt, A.; Bayer, J.C.; Wagner, T.; Flindt, C.; Haug, R.J. Controlled emission time statistics of a dynamic single-electron transistor. Sci. Adv. 2021, 7, eabe0793. [Google Scholar] [CrossRef]
- Roussel, B.; Cabart, C.; Fève, G.; Thibierge, E.; Degiovanni, P. Electron quantum optics as quantum signal processing. Phys. Status Solidi (b) 2017, 254, 1600621. [Google Scholar] [CrossRef]
- Roussel, B.; Cabart, C.; Fève, G.; Degiovanni, P. Processing quantum signals carried by electrical currents. Phys. Rev. X Quantum 2021, 2, 020314. [Google Scholar] [CrossRef]
- Acciai, M.; Ronetti, F.; Ferraro, D.; Rech, J.; Jonckheere, T.; Sassetti, M.; Martin, T. Levitons in superconducting point contacts. Phys. Rev. B 2019, 100, 085418. [Google Scholar] [CrossRef]
- Averin, D.V.; Wang, G.; Vasenko, A.S. Time-dependent Andreev reflection. Phys. Rev. B 2020, 102, 144516. [Google Scholar] [CrossRef]
- Splettstoesser, J.; Ol’khovskaya, S.; Moskalets, M.; Büttiker, M. Electron counting with a two-particle emitter. Phys. Rev. B 2008, 78, 205110. [Google Scholar] [CrossRef]
- Splettstoesser, J.; Moskalets, M.; Büttiker, M. Two-Particle Nonlocal Aharonov-Bohm Effect from Two Single-Particle Emitters. Phys. Rev. Lett. 2009, 103, 076804. [Google Scholar] [CrossRef]
- Moskalets, M.; Büttiker, M. Spectroscopy of electron flows with single- and two-particle emitters. Phys. Rev. B 2011, 83, 035316. [Google Scholar] [CrossRef]
- Juergens, S.; Splettstoesser, J.; Moskalets, M. Single-particle interference versus two-particle collisions. Europhys. Lett. 2011, 96, 37011. [Google Scholar] [CrossRef]
- Ryu, S.; Kataoka, M.; Sim, H.S. Ultrafast Emission and Detection of a Single-Electron Gaussian Wave Packet: A Theoretical Study. Phys. Rev. Lett. 2016, 117, 146802. [Google Scholar] [CrossRef]
- Misiorny, M.; Fève, G.; Splettstoesser, J. Shaping charge excitations in chiral edge states with a time-dependent gate voltage. Phys. Rev. B 2018, 97, 075426. [Google Scholar] [CrossRef]
- Ferraro, D.; Ronetti, F.; Vannucci, L.; Acciai, M.; Rech, J.; Jockheere, T.; Martin, T.; Sassetti, M. Hong-Ou-Mandel characterization of multiply charged Levitons. Eur. Phys. J. Spec. Top. 2018, 227, 1345. [Google Scholar] [CrossRef]
- Moskalets, M.; Kotilahti, J.; Burset, P.; Flindt, C. Composite two-particle sources. Eur. Phys. J. Spec. Top. 2020, 229, 647. [Google Scholar] [CrossRef]
- Büttiker, M. Scattering theory of current and intensity noise correlations in conductors and wave guides. Phys. Rev. B 1992, 46, 12485. [Google Scholar] [CrossRef] [PubMed]
- Moskalets, M.; Büttiker, M. Floquet scattering theory of quantum pumps. Phys. Rev. B 2002, 66, 205320. [Google Scholar] [CrossRef]
- Moskalets, M.; Samuelsson, P.; Büttiker, M. Quantized Dynamics of a Coherent Capacitor. Phys. Rev. Lett. 2008, 100, 086601. [Google Scholar] [CrossRef]
- Moskalets, M.; Haack, G.; Büttiker, M. Single-electron source: Adiabatic versus nonadiabatic emission. Phys. Rev. B 2013, 87, 125429. [Google Scholar] [CrossRef]
- Moskalets, M. Two-electron state from the Floquet scattering matrix perspective. Phys. Rev. B 2014, 89, 045402. [Google Scholar] [CrossRef]
- Moskalets, M.; Haack, G. Single-electron coherence: Finite temperature versus pure dephasing. Physica E 2016, 75, 358. [Google Scholar] [CrossRef]
- Moskalets, M. Single-particle emission at finite temperatures. Low Temp. Phys. 2017, 43, 865. [Google Scholar] [CrossRef][Green Version]
- Moskalets, M. Single-particle shot noise at nonzero temperature. Phys. Rev. B 2017, 96, 165423. [Google Scholar] [CrossRef]
- Moskalets, M.V. Scattering Matrix Approach to Non-Stationary Quantum Transport; Imperial College Press: London, UK, 2011. [Google Scholar] [CrossRef]
- Chung, V.S.W.; Samuelsson, P.; Büttiker, M. Visibility of current and shot noise in electrical Mach-Zehnder and Hanbury Brown Twiss interferometers. Phys. Rev. B 2005, 72, 125320. [Google Scholar] [CrossRef]
- Chung, S.W.V.; Moskalets, M.; Samuelsson, P. Quantum pump driven fermionic Mach-Zehnder interferometer. Phys. Rev. B 2007, 75, 115332. [Google Scholar] [CrossRef]
- Hofer, P.P.; Flindt, C. Mach-Zehnder interferometry with periodic voltage pulses. Phys. Rev. B 2014, 90, 235416. [Google Scholar] [CrossRef]
- Moskalets, M.; Büttiker, M. Time-resolved noise of adiabatic quantum pumps. Phys. Rev. B 2007, 75, 035315. [Google Scholar] [CrossRef]
- Dubois, J.; Jullien, T.; Grenier, C.; Degiovanni, P.; Roulleau, P.; Glattli, D.C. Integer and fractional charge Lorentzian voltage pulses analyzed in the framework of photon-assisted shot noise. Phys. Rev. B 2013, 88, 085301. [Google Scholar] [CrossRef]
- Grenier, C.; Hervé, R.; Féve, G.; Degiovanni, P. Electron quantum optics in quantum Hall edge channels. Mod. Phys. Lett. B 2011, 25, 1053. [Google Scholar] [CrossRef]
- Haack, G.; Moskalets, M.; Büttiker, M. Glauber coherence of single-electron sources. Phys. Rev. B 2013, 87, 201302. [Google Scholar] [CrossRef]
- Moskalets, M. Single-electron second-order correlation function G(2) at nonzero temperatures. Phys. Rev. B 2018, 98, 115421. [Google Scholar] [CrossRef]
- Moskalets, M. First-order correlation function of a stream of single-electron wave packets. Phys. Rev. B 2015, 91, 195431. [Google Scholar] [CrossRef]
- Haack, G.; Albert, M.; Flindt, C. Distributions of electron waiting times in quantum-coherent conductors. Phys. Rev. B 2014, 90, 205429. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kotilahti, J.; Burset, P.; Moskalets, M.; Flindt, C. Multi-Particle Interference in an Electronic Mach–Zehnder Interferometer. Entropy 2021, 23, 736. https://doi.org/10.3390/e23060736
Kotilahti J, Burset P, Moskalets M, Flindt C. Multi-Particle Interference in an Electronic Mach–Zehnder Interferometer. Entropy. 2021; 23(6):736. https://doi.org/10.3390/e23060736
Chicago/Turabian StyleKotilahti, Janne, Pablo Burset, Michael Moskalets, and Christian Flindt. 2021. "Multi-Particle Interference in an Electronic Mach–Zehnder Interferometer" Entropy 23, no. 6: 736. https://doi.org/10.3390/e23060736
APA StyleKotilahti, J., Burset, P., Moskalets, M., & Flindt, C. (2021). Multi-Particle Interference in an Electronic Mach–Zehnder Interferometer. Entropy, 23(6), 736. https://doi.org/10.3390/e23060736






