GIS Partial Discharge Pattern Recognition Based on a Novel Convolutional Neural Networks and Long Short-Term Memory
Abstract
:1. Introduction
2. Basic Theory
2.1. Convolutional Neural Network
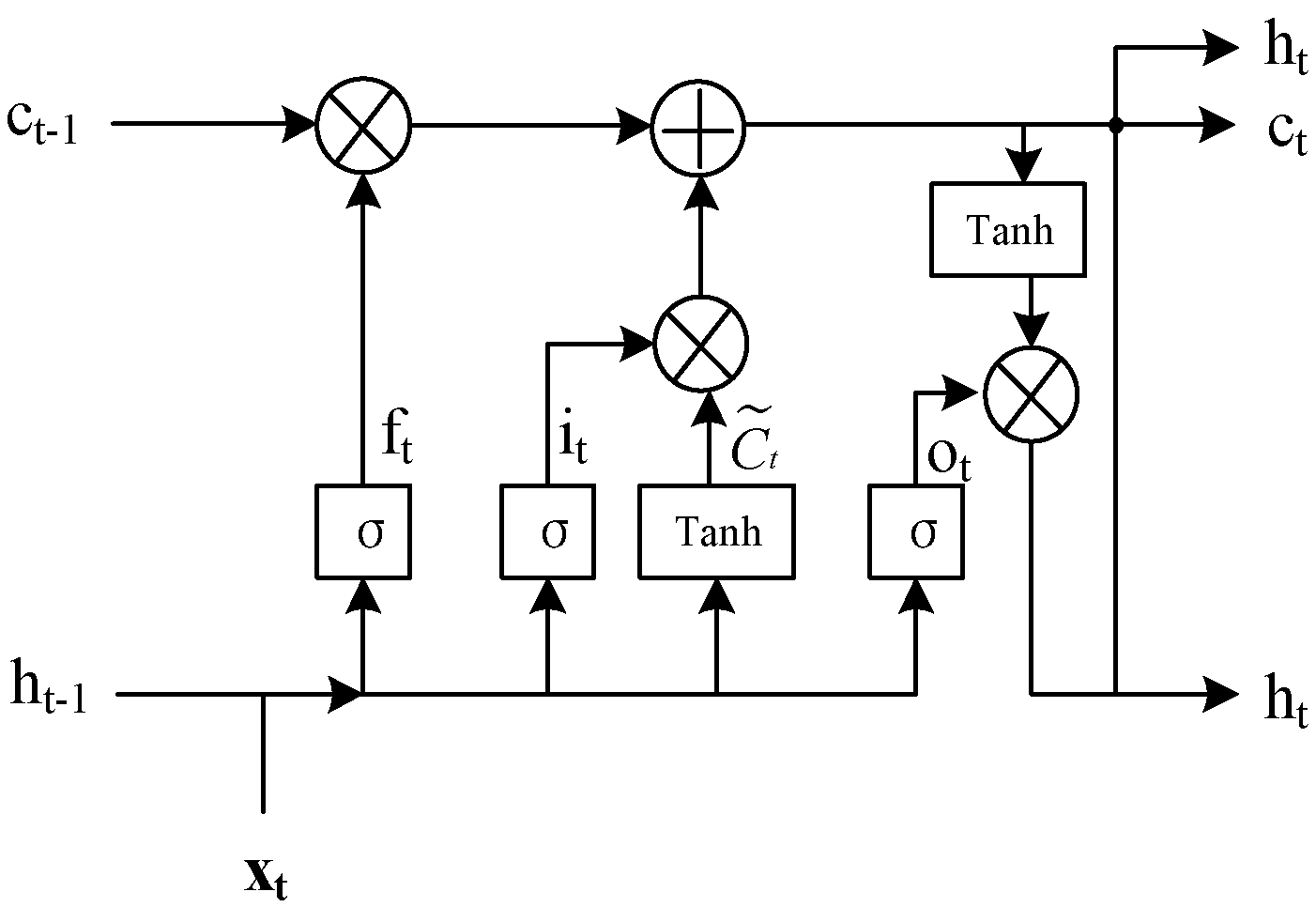
2.2. Long and Short-Term Memory
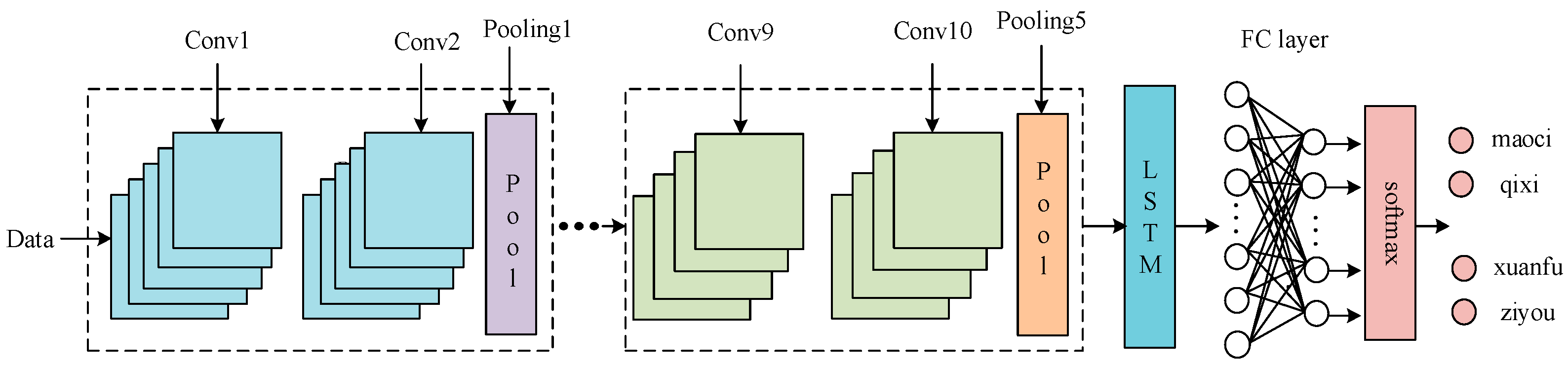
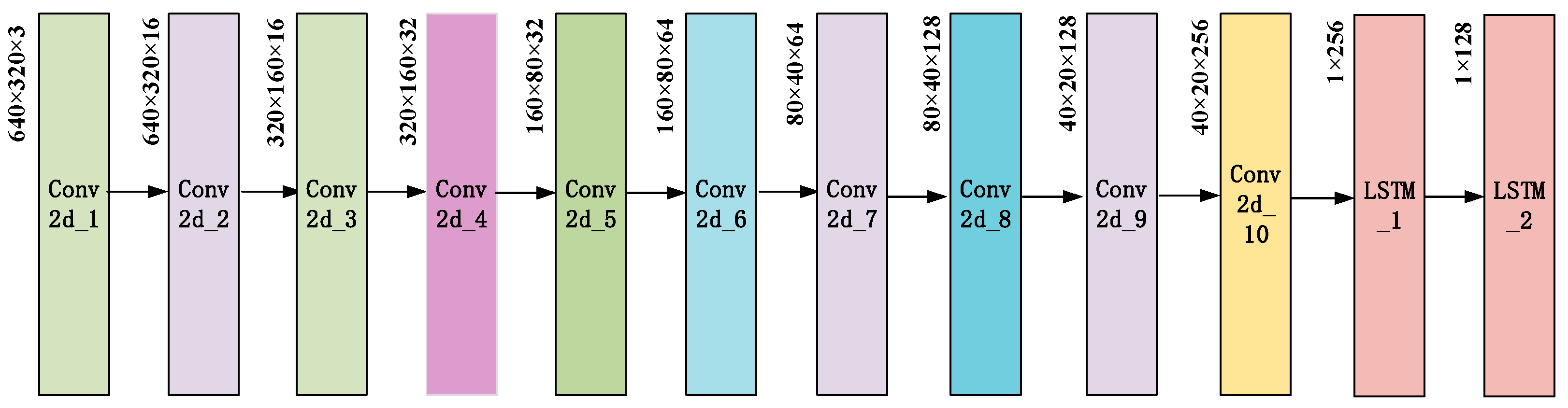
3. Proposed Method
4. Experimental Evaluation
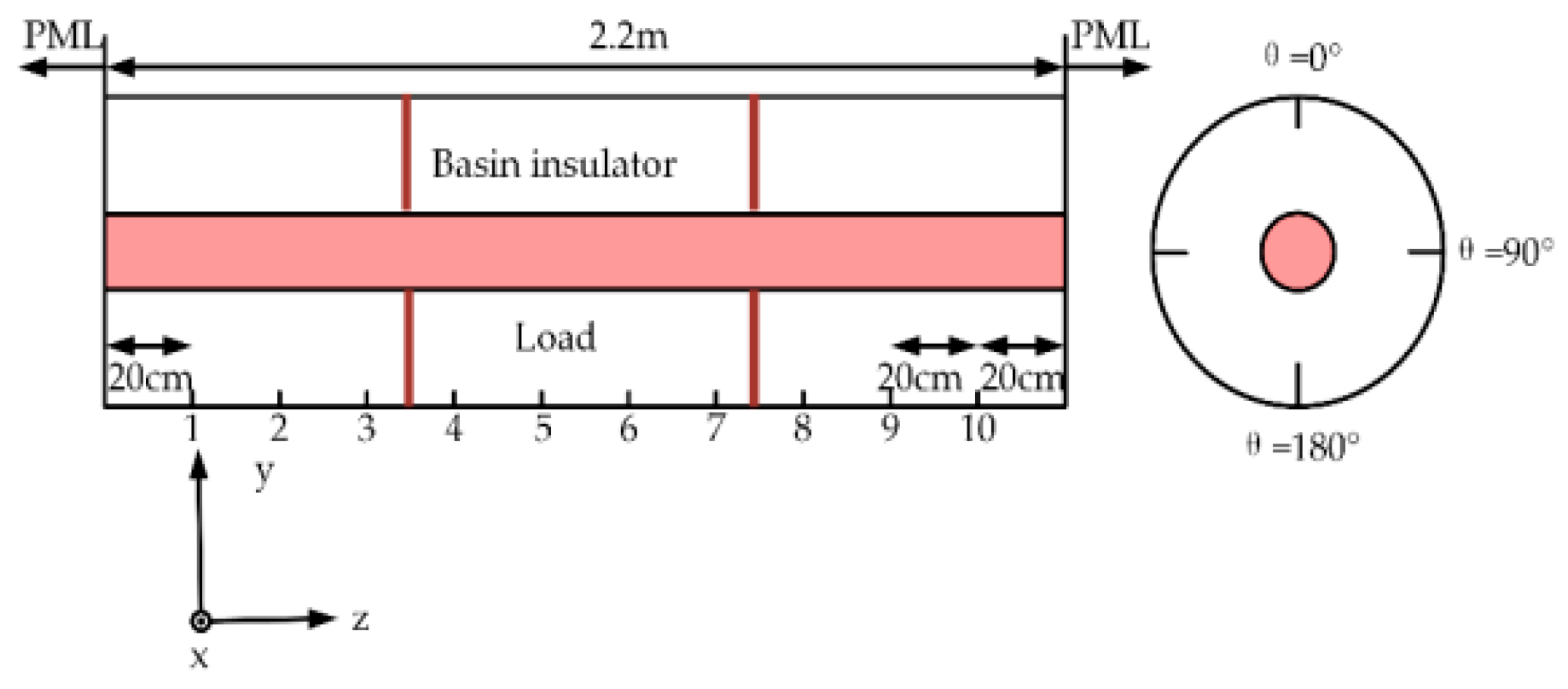
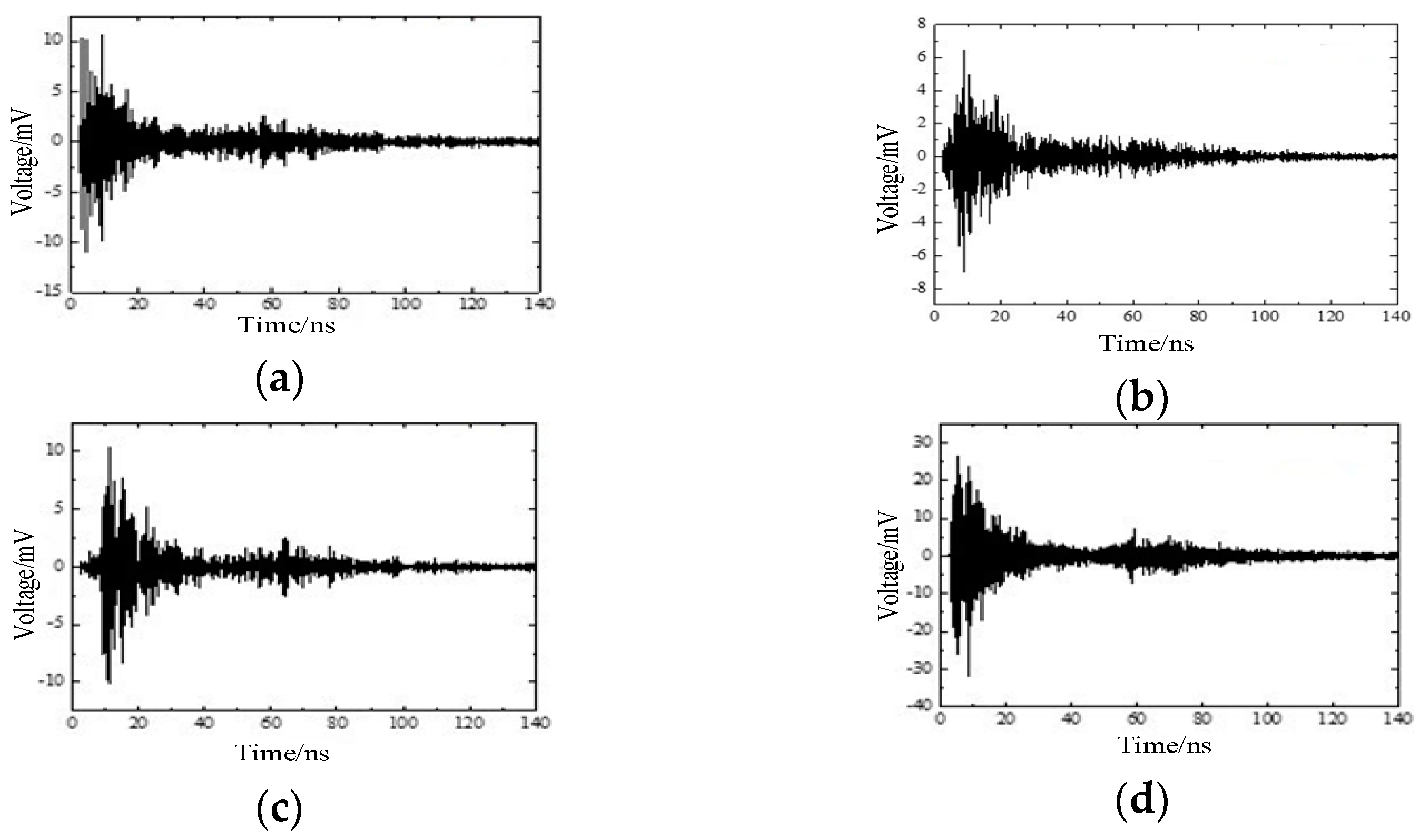
4.1. Data Acquisition
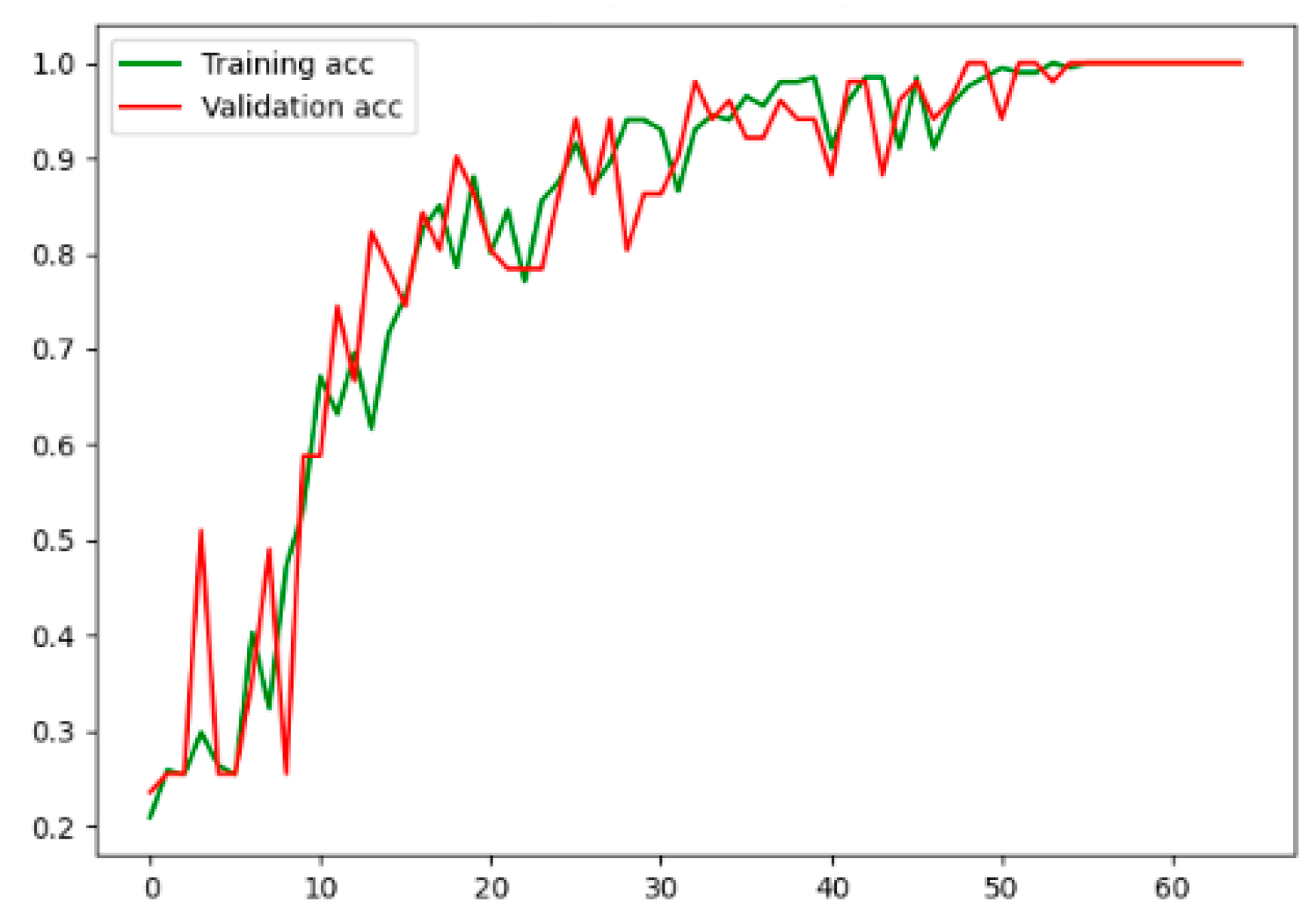
4.2. Training Process
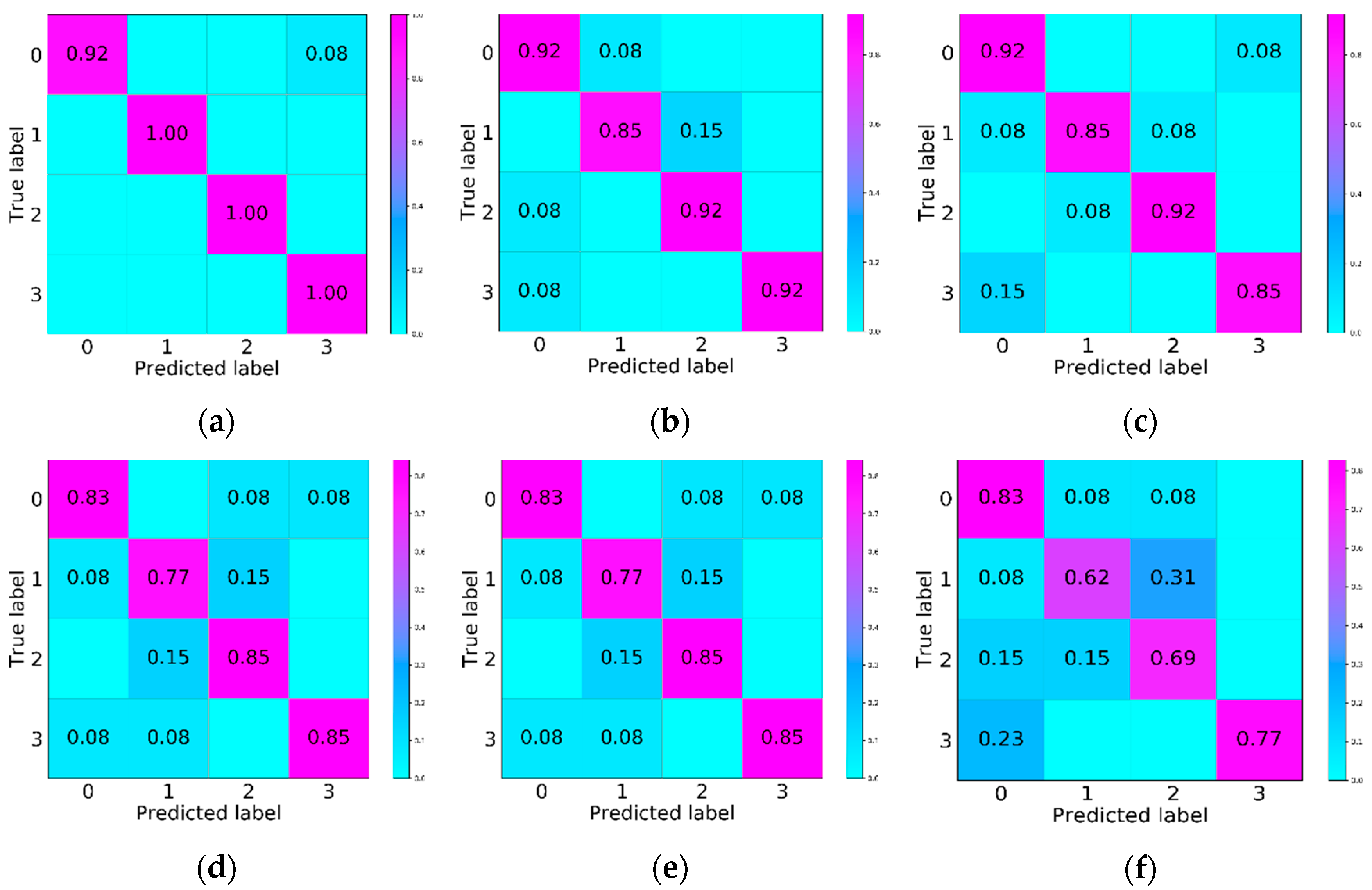
4.3. Results and Analysis
4.4. Comparison of Different Methods
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, Y.; Yan, J.; Sun, Q.; Jiang, Q.; Zhou, Y. Bearing Intelligent Fault Diagnosis in the Industrial Internet of Things Context: A Lightweight Convolutional Neural Network. IEEE Access 2020, 8, 87329–87340. [Google Scholar] [CrossRef]
- Fu, J.; Chu, J.; Guo, P.; Chen, Z. Condition Monitoring of Wind Turbine Gearbox Bearing Based on Deep Learning Model. IEEE Access 2019, 7, 57078–57087. [Google Scholar] [CrossRef]
- Guo, L.; Lei, Y.; Xing, S.; Yan, T.; Li, N. Deep Convolutional Transfer Learning Network: A New Method for Intelligent Fault Diagnosis of Machines With Unlabeled Data. IEEE Trans. Ind. Electron. 2019, 66, 7316–7325. [Google Scholar] [CrossRef]
- Wen, L.; Li, X.; Gao, L.; Zhang, Y. A New Convolutional Neural Network-Based Data-Driven Fault Diagnosis Method. IEEE Trans. Ind. Electron. 2018, 65, 5990–5998. [Google Scholar] [CrossRef]
- Principi, E.; Rossetti, D.; Squartini, S.; Piazza, F. Unsupervised electric motor fault detection by using deep autoencoders. IEEE/CAA J. Autom. Sin. 2019, 6, 441–451. [Google Scholar] [CrossRef]
- He, Z.; Shao, H.; Cheng, J.; Zhao, X.; Yang, Y. Support tensor machine with dynamic penalty factors and its application to the fault diagnosis of rotating machinery with unbalanced data. Mech. Syst. Signal Proc. 2020, 141. [Google Scholar] [CrossRef]
- Li, H.; Zhang, Q.; Qin, X.; Sun, Y. Fault diagnosis method for rolling bearings based on short-time Fourier transform and convolution neural network. J. Vibr. Shock 2018, 37, 124–131. [Google Scholar]
- Li, J.; Li, X.; He, D. A Directed Acyclic Graph Network Combined With CNN and LSTM for Remaining Useful Life Prediction. IEEE Access 2019, 7, 75464–75475. [Google Scholar] [CrossRef]
- Li, Y.; Wang, K. Modified convolutional neural network with global average pooling for intelligent fault diagnosis of industrial gearbox. Eksploat. Niezawodn. Maint. Reliab. 2020, 22, 63–72. [Google Scholar] [CrossRef]
- Chen, Z.; Gryllias, K.; Li, W. Intelligent Fault Diagnosis for Rotary Machinery Using Transferable Convolutional Neural Network. IEEE Trans. Ind. Inf. 2020, 16, 339–349. [Google Scholar] [CrossRef]
- Chen, Z.; Li, C.; Sanchez, R.-V. Gearbox Fault Identification and Classification with Convolutional Neural Networks. Shock Vibr. 2015, 2015. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.; Mauricio, A.; Li, W.; Gryllias, K. A deep learning method for bearing fault diagnosis based on Cyclic Spectral Coherence and Convolutional Neural Networks. Mech. Syst. Signal Proc. 2020, 140. [Google Scholar] [CrossRef]
- Ergen, T.; Kozat, S.S. Unsupervised Anomaly Detection With LSTM Neural Networks. IEEE Trans. Neural Netw. Learn Syst. 2020, 31, 3127–3141. [Google Scholar] [CrossRef] [Green Version]
- Song, Y.; Xia, T.; Zheng, Y.; Zhuo, P.; Pan, E. Remaining useful life prediction of turbofan engine based on Autoencoder-BLSTM. Comput. Integr. Manuf. Syst. 2019, 25, 1611–1619. [Google Scholar]
- Xie, G.; Shangguan, A.; Fei, R.; Ji, W.; Ma, W.; Hei, X. Motion trajectory prediction based on a CNN-LSTM sequential model. Sci. Chin. Inf. Sci. 2020, 63. [Google Scholar] [CrossRef]
- Wang, Y.; Yan, J.; Sun, Q.; Li, J.; Yang, Z. A MobileNets Convolutional Neural Network for GIS Partial Discharge Pattern Recognition in the Ubiquitous Power Internet of Things Context: Optimization, Comparison, and Application. IEEE Access 2019, 7, 150226–150236. [Google Scholar] [CrossRef]
- Zhu, X.; Hou, D.; Zhou, P.; Han, Z.; Yuan, Y.; Zhou, W.; Yin, Q. Rotor fault diagnosis using a convolutional neural network with symmetrized dot pattern images. Measurement 2019, 138, 526–535. [Google Scholar] [CrossRef]
- Tao, X.; Zhang, D.; Wang, Z.; Liu, X.; Zhang, H.; Xu, D. Detection of Power Line Insulator Defects Using Aerial Images Analyzed With Convolutional Neural Networks. IEEE Trans. Syst. Man. Cybern. Syst. 2020, 50, 1486–1498. [Google Scholar] [CrossRef]
- Wang, H.; Li, S.; Song, L.; Cui, L.; Wang, P. An Enhanced Intelligent Diagnosis Method Based on Multi-Sensor Image Fusion via Improved Deep Learning Network. IEEE Trans. Instrum. Meas. 2020, 69, 2648–2657. [Google Scholar] [CrossRef]
- Wang, S.; Xiang, J. A minimum entropy deconvolution-enhanced convolutional neural networks for fault diagnosis of axial piston pumps. Soft Comput. 2020, 24, 2983–2997. [Google Scholar] [CrossRef]
- Xu, G.; Liu, M.; Jiang, Z.; Shen, W.; Huang, C. Online Fault Diagnosis Method Based on Transfer Convolutional Neural Networks. IEEE Trans. Instrum. Meas. 2020, 69, 509–520. [Google Scholar] [CrossRef]
- Liu, T.; Yan, J.; Wang, Y.; Du, Y. Research on GIS Partial Discharge Pattern Recognition Based on Deep Residual Network and Transfer Learning in Ubiquitous Power Internet of Things Context. IEEE 2020, 207–211. [Google Scholar] [CrossRef]
- Kong, Z.; Tang, B.; Deng, L.; Liu, W.; Han, Y. Condition monitoring of wind turbines based on spatio-temporal fusion of SCADA data by convolutional neural networks and gated recurrent units. Renew. Energy 2020, 146, 760–768. [Google Scholar] [CrossRef]
- Liu, R.; Yang, B.; Hauptmann, A.G. Simultaneous Bearing Fault Recognition and Remaining Useful Life Prediction Using Joint-Loss Convolutional Neural Network. IEEE Trans. Ind. Inf. 2020, 16, 87–96. [Google Scholar] [CrossRef]

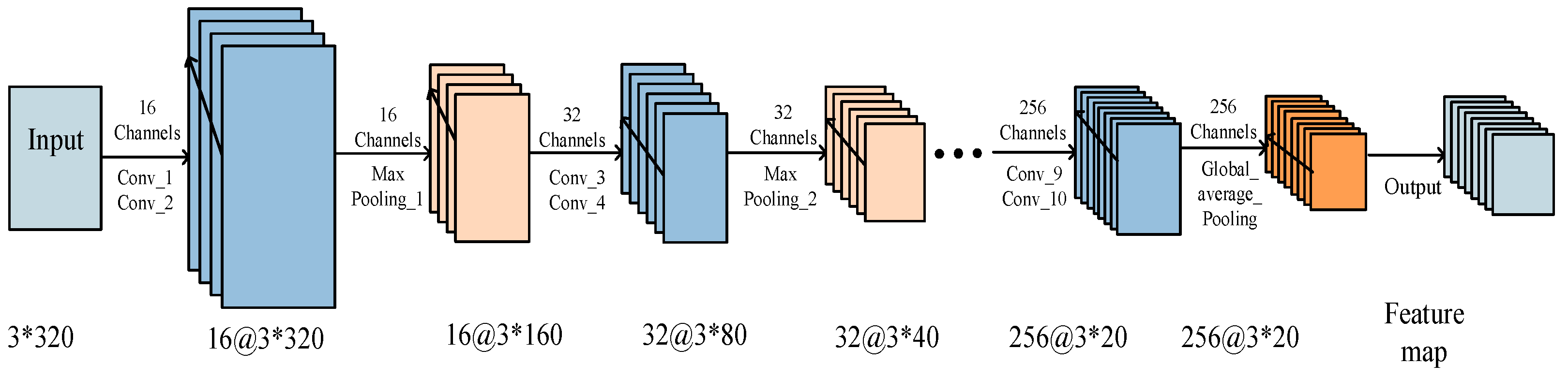

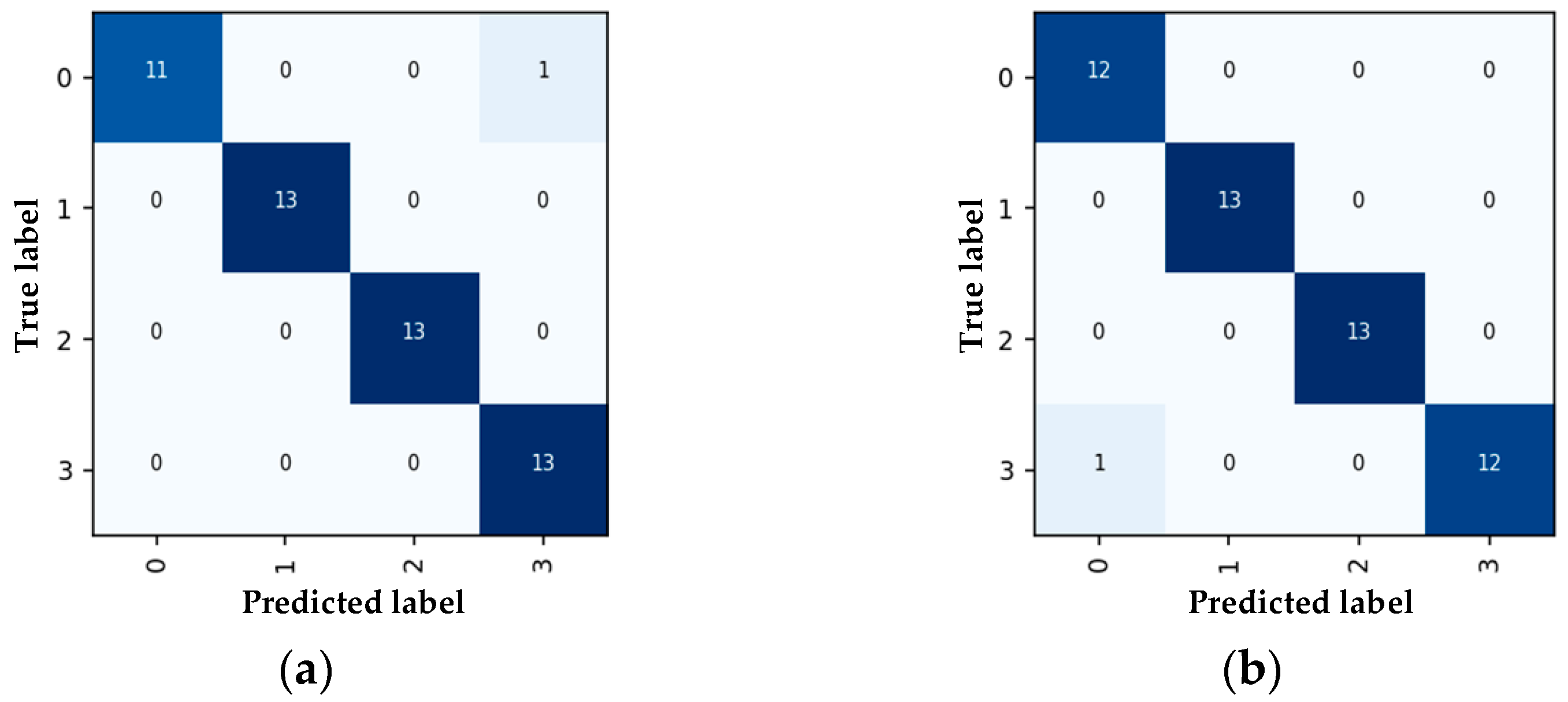
| Type | Precision (%) | Recall (%) | F1-Score (%) |
|---|---|---|---|
| 0 | 91.6 | 100 | 95.8 |
| 1 | 100 | 100 | 100 |
| 2 | 100 | 100 | 100 |
| 3 | 100 | 91.6 | 95.8 |
| Type | Model_1 | Model_2 | Model_3 | Model_4 | Model_5 |
|---|---|---|---|---|---|
| 0 | 91.6 | 100 | 91.6 | 100 | 100 |
| 1 | 100 | 92.3 | 92.3 | 92.3 | 100 |
| 2 | 92.3 | 92.3 | 100 | 100 | 100 |
| 3 | 100 | 92.3 | 100 | 92.3 | 91.6 |
| Overall | 96.0 | 94.2 | 96.0 | 96.2 | 97.9 |
| Type | CNN-LSTM | SVM | Resnet18 | BPNN | CNN | LSTM |
|---|---|---|---|---|---|---|
| 0 | 91.6 | 91.6 | 91.6 | 83.3 | 83.3 | 83.3 |
| 1 | 100 | 84.6 | 84.6 | 76.9 | 76.9 | 61.5 |
| 2 | 100 | 92.3 | 92.3 | 84.6 | 84.6 | 76.9 |
| 3 | 100 | 92.3 | 84.6 | 84.6 | 84.6 | 69.2 |
| Overall | 97.9 | 92.3 | 88.3 | 82.4 | 82.4 | 72.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, T.; Yan, J.; Wang, Y.; Xu, Y.; Zhao, Y. GIS Partial Discharge Pattern Recognition Based on a Novel Convolutional Neural Networks and Long Short-Term Memory. Entropy 2021, 23, 774. https://doi.org/10.3390/e23060774
Liu T, Yan J, Wang Y, Xu Y, Zhao Y. GIS Partial Discharge Pattern Recognition Based on a Novel Convolutional Neural Networks and Long Short-Term Memory. Entropy. 2021; 23(6):774. https://doi.org/10.3390/e23060774
Chicago/Turabian StyleLiu, Tingliang, Jing Yan, Yanxin Wang, Yifan Xu, and Yiming Zhao. 2021. "GIS Partial Discharge Pattern Recognition Based on a Novel Convolutional Neural Networks and Long Short-Term Memory" Entropy 23, no. 6: 774. https://doi.org/10.3390/e23060774
APA StyleLiu, T., Yan, J., Wang, Y., Xu, Y., & Zhao, Y. (2021). GIS Partial Discharge Pattern Recognition Based on a Novel Convolutional Neural Networks and Long Short-Term Memory. Entropy, 23(6), 774. https://doi.org/10.3390/e23060774






