In this section, we propose a sparse modeling method for extracting heterogeneous reactions. First, we introduce heterogeneous reactions, which depend on surface-area reactions between the liquid phase and the solid phase, and formulate a nonlinear state-space model of heterogeneous reactions with many candidate terms. Next, we employ the sequential Monte Carlo method in order to estimate the hidden variables of heterogeneous reactions from observable data. Finally, we adopt a sparse modeling approach to the framework of the sequential Monte Carlo method in order to extract important heterogeneous reactions from many candidates.
2.1. Nonlinear Dynamics of Heterogeneous Reactions of Fluid–Rock Interaction
In this study, we consider a general setting of heterogeneous reactions in fluid–rock interactions in which minerals (solid phase) dissolve and precipitate within a liquid phase. The fluid–rock interaction is one of the most important geoscientific processes in the earth. For example, serpentinization, a collection of heterogeneous reactions to generate serpentinite from peridotite and water, in the oceanic crust is known to be a key storage process of water brought into the earth’s deep region. In addition, it changes the physical properties of the earth’s interior significantly, and affects the occurrence of earthquakes in the subduction zone [
15]. It is important to specify the kinetics of heterogeneous reactions in order to understand the detailed processes of rock formation and predict the evolution of the earth system. However, estimating the heterogeneous reactions is difficult since observation data are limited, and there are many candidates for reaction types [
16,
17,
18,
19]. In addition, dominant reaction terms generally vary according to external conditions, such as temperature and pressure, hence it is very difficult to presumably predict which terms are active or inactive. Therefore, it is imperative to establish a method for estimating the reactions based on data-driven analysis using the data sets that are obtained from laboratory experiments and natural samples [
20].
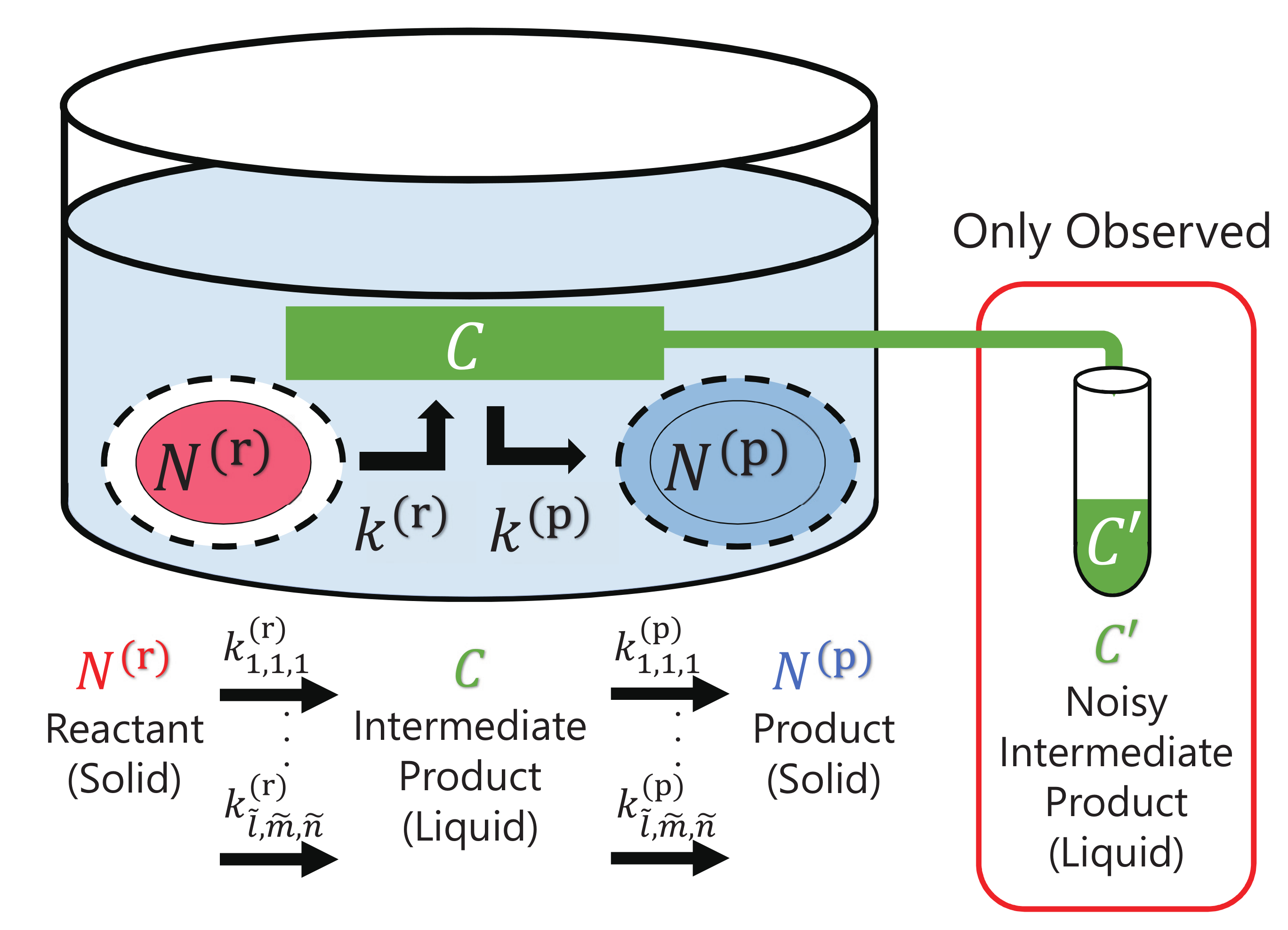
Here, we consider surface heterogeneous reactions in a hydrothermal laboratory experiment as an analogue of fluid–rock interactions in natural systems, as shown in
Figure 1. In the reactions, a solid reactant
dissolves into a liquid to form an intermediate product
C, and the intermediate product
C precipitates to form a solid product
.
Such dissolution and precipitation via an intermediate product within fluid is considered to be the most fundamental process, which describes the essence of heterogeneous reactions in fluid–rock interactions. Since there are many kinds of heterogeneous reactions that are linear or nonlinear related to surface-area reactions and reaction terms, and we cannot presumably assume effective specific reaction terms, we consider the amounts of reactant
, and those of product
obey the following general differential equations with a number of candidate reaction terms [
2]:
where
denotes time. Here,
and
are the rate constants governing the dynamics of heterogeneous reactions.
and
indicate the surface areas of the reactant and product, respectively.
is a type of surface area model.
and
are indices for the orders of an intermediate product
C and factor
of the reaction terms, respectively. Here,
,
and
are the total numbers of candidate surface models and candidate orders of the two factors. Note that Equations (1) and (2) contain
kinds of candidate reaction terms for each equation, and essential reaction terms are extracted from the candidates, using the framework of sparse modeling as described below.
The dynamics of heterogeneous reactions shown in Equations (1)–(3) depend on the rate constants
and
. The constants indicate how fast the reactants
dissolve and the products
precipitate. Therefore, rate constants
and
are important factors to determine what kind of mineral dissolves into a liquid intermediate product and precipitates into a solid product.
Figure 2 shows our problem setting for extracting important reactions from many reaction candidates. In
Figure 2, surface area is simply expressed as
rather than
and
.
indicates the surface area between two solid and liquid phases, and there are many types of surface-area reactions that highly influence heterogeneous surface reactions. Generally, a surface area
is expressed as follows:
where
is the order of the surface-area reaction. Note that the surface area
depends on the number
N of moles of the solid phase. As shown in Equation (4),
is proportional to the
-th power of
N. It is necessary to consider the kind of surface-area reaction that occurs since heterogeneous reactions change at the interface between the solid and liquid phases.
In this study, we consider three typical surface models (
Figure 2, horizontal line) as follows:
In
Figure 2, the blue area indicates the solid phase, whereas the red lines represent the surface between the solid phase (blue area) and liquid phase (white area). For
, the surface area does not change with an increase or decrease in the amount of the solid phase. For
, the geometrical shape of the solid phase does not change with an increase or decrease in the amount of the solid phase. For
, the bulk reaction occurs, and the surface area changes in proportion to the amount of solid phase.
As shown in the vertical line of
Figure 2, there are candidates for indices of nonlinearity
m and
n in the reaction terms, where
is a multiplier of the intermediate product
C.
is a multiplier of the reaction terms
. Both
and
are important for the dynamics of heterogeneous reactions.
Figure 3 shows a typical time course of the heterogeneous reaction when the type of surface-area model is
and the multipliers
,
in Equations (1) and (2). We simulate differential equations, Equations (1)–(3), with discretized time step
t and set the initial values
,
and
. As shown in
Figure 3, when the time is zero, the solid reactant
exists and dissolves into a liquid intermediate product
C with time. When the intermediate product
C dissolves sufficiently, it precipitates into a solid product
. After that, the solid reactant
almost disappears, and the intermediate product
C and solid product
become constant.
2.2. Estimating Heterogeneous Reaction Dynamics Based on Sequential Monte Carlo Method
In order to estimate the rate constants , it is necessary to estimate the solid reactant , liquid intermediate product C and solid product . We consider how the reactants , intermediate products C and products change over time.
Figure 4 shows the graphical model of surface heterogeneous reactions governed by Equations (1)–(3). Here, we consider discretized time steps for the states of surface heterogeneous reactions: the reactant
at time step
depends on the reactant
and the intermediate product
at the preceding time step
t. Additionally, the reactant
, the intermediate product
and the product
affect the intermediate product
and the product
. Moreover, since the intermediate product is assumed to be observable, the observed intermediate product
has a relationship with the intermediate product
at the respective time.
From
Figure 4, we propose a nonlinear state-space model for surface heterogeneous reactions. The state space model is a probabilistic model that describes the time evolution and observation process of the dynamical system, and was used in the time series analysis for estimating and predicting hidden variables in dynamical system from observable time-series data [
21,
22]. The state-space model consists of observation and system models [
23]. The observation model represents the relationship between hidden and observation variables, whereas the system model represents the relationship between hidden variables at two adjacent times. In this study, the solid reactant
, liquid intermediate product
C and solid product
are hidden variables, and the observed liquid intermediate product
is an observation variable.
First, we formulate the observation model by assuming that the observed liquid intermediate product
is obtained as a sum of the true liquid intermediate product
and an additive noise as follows:
where
denotes an observation noise. Assuming that the observation noise obeys the Gaussian distribution, the observation model is expressed by a probabilistic model as follows:
where
shows a standard deviation of the observation noise.
Next, we derive the system model that expresses the relationship among hidden variables. By discretizing Equations (1)–(3) at the time interval
, we obtain the following difference equation for each time step
t:
Furthermore, by assuming a system noise, we obtain the following equations:
where
and
denote the system noise obeying the white Gaussian noise: for time steps
t and
s,
,
, and
. Here,
is a Kronecker delta;
for
and
for
.
and
express the standard deviations of the system noise. Since Equations (13)–(15) have additive Gaussian noise, a probabilistic model of system model for heterogeneous reactions is derived as follows:
where we put
and
.
Here, we employ a sequential Monte Carlo method based on the state-space model of heterogeneous reactions. The sequential Monte Carlo method is a statistical method for estimating hidden variables of nonlinear dynamical systems by using a set of particles for posterior distributions of hidden variables [
22]. We derive a method for estimating time series of hidden variables
from the observed data
where
.
The predictive distribution of a hidden variable at time step
t, given time-series of observed data up to preceding time step
,
, is expressed as follows [
21,
22,
23,
24]:
where
is the system model, and
is the filtering distribution at time step
. Therefore, if we obtain the filtering distribution
at the time step
, we can calculate the prediction distribution
by integrating with respect to
. Moreover, the filtering distribution at time step
t,
, is expressed using the predictive distribution at time step
as follows:
where
is expressed as follows:
Note that
is the observation model. Thus, hidden variables can be estimated with forward recursion by alternatively calculating the predictive distribution and filtering distribution. Furthermore, the smoothing distribution of hidden variables at time
t(<
T) given the time-series of observation data up to time
T is expressed as follows:
where
indicates the filtering distribution at time step
t. Note that the smoothing distribution at a time step
t is obtained by that at time step
. Therefore, the smoothing distribution can be calculated using backward recursion.
To obtain the above conditional distributions, we express the distributions by using particle approximation. The particle approximation is employed to estimate predictive, filtering, and smoothing distributions numerically since it is difficult to conduct their updates shown in Equations (19)–(21) analytically when nonlinear dynamical systems are assumed [
22]. Each conditional distribution for the hidden variables
is assumed to be expressed by many particles. In the particle approximation, the predictive distribution
and the filtering distribution
are expressed as follows:
where
is the Dirac’s delta function and
I is the total number of particles. We substitute the approximated predictive and filtering distributions into Equations (18) and (19). By using the recursive relationship between the predictive and filtering distributions, we obtain a set of particles for the filtering distribution
from a set of particles for the predictive distribution
, and also obtain a set of particles for the predictive distribution
from that for the filtering distribution
. Based on the sequential Monte Carlo method, we estimate hidden variables by using particles
from the partially observed data
.
2.3. Sparse Modeling Algorithm for Estimating Rate Constants
Rate constants play a important role as determinants for reaction rates and surface-area reactions. Moreover, rate constants determine linearity or nonlinearity of reaction term and intermediate product C in Equations (1) and (2). According to Equations (1) and (2), there are types of reactant and product reactions. Therefore, there are reaction candidates of heterogeneous reactions.
We employ a sparse modeling approach in order to estimate rate constants
from many candidates. The sparse modeling is a framework for extracting only essential elements from candidates by assuming that the essential elements are
sparse compared with a number of candidates [
25,
26]. Based on Equations (1) and (2), there are
reaction candidates. By using the sparse modeling approach, we estimate each value of rate constants
and determine as zero unnecessary terms or non-zero for necessary terms. Then, we extract only the necessary heterogeneous reactions.
Figure 5 shows the schematic diagram of the estimation method for surface-area reaction in heterogeneous reactions by sparse modeling. The difference equations for heterogeneous reactions can be regarded as the following linear equation with respect to the rate constants
; each heterogeneous reaction is multiplied by the reaction rate coefficient
as follows:
Notably, the right-hand side of Equation (24) is expressed as a linear sum of the reaction term
with coefficients
corresponding to rate constants. To extract rate constant terms from a number of candidates, we use the Lasso framework (least absolute shrinkage and selection operator), which employs a sparse modeling approach [
6,
7,
27,
28]. By considering the
regularization term for rate constants, sparse modeling of heterogeneous reactions is formulated based on the Lasso framework as follows:
where
,
and
are represented by the following matrix and vectors:
In Equation (25),
is the regularization coefficient that controls the relative importance of a data-dependent error
and the regularization term
. The regularization term
is the sum of the absolute values of each rate constants
. When the regularization term
becomes smaller, the rate constants approach zero, and we can obtain a sparse solution. Here,
is a vector consisting of the averages of the differences
between intermediate products’ adjacent time steps, which are obtained by particles as the averages of the difference
.
denotes a matrix consisting of the average of reaction terms, which are obtained by particles
.
indicates a vector consisting of rate constants. We calculate the matrix
and vector
by using hidden variables
,
and
. To obtain an appropriate value of
, we employ nested cross-validation error since time-series data are used [
29].
To compare with the Lasso framework, we consider the Ridge framework, expressed by the following equation [
30]:
Namely, the Ridge framework introduces the
regularization term. Ridge and Lasso frameworks are different in terms of regularization terms.
Figure 6 shows a conceptual diagram of the Lasso and Ridge frameworks in two dimensions. Lasso yields a sparse solution because the part where the contour line of the error term and the boundary of the constraint condition meet is likely to be a corner since the constraint condition of Lasso is given by
. In
Figure 6,
is estimated to be a zero value by using Lasso. However, when Ridge is used, both
and
are estimated to be non-zero values. Therefore, the Lasso framework can obtain a sparse solution more effectively than the Ridge framework. Thus, we assume that the sparse modeling approach extracts only essential reactions from candidates in heterogeneous reactions by estimating each rate constant as either zero or non-zero.
However, in the case where we can observe few data or many candidates can be assumed, it may not be possible to extract only important reactions. Therefore, instead of uniform sparsity levels, we introduce non-uniform ones in order to extract only the important reactions more accurately. Here, a sparse modeling approach based on adaptive Lasso is introduced [
31]. The sparse modeling approach with non-uniform sparsity levels is expressed by the following equation:
where
is a consistent estimator, and it is determined by the least-squares method and the Ridge framework. Here,
is
j-th element of vector
shown in Equation (29). According to Equation (33),
is the reciprocal of the absolute value of
to the
power. Here, we employ the Ridge framework represented by Equation (30) to obtain
and put
. If the value of
is small, the values of
become large. Therefore, the sparsity tends to increase to realize
. In contrast, if the value of
is large, the value of
becomes small, and the sparsity tends to decrease to realize
.
Figure 7 shows a conceptual diagram of the sparse modeling approach with uniform and non-uniform sparsity levels for a two-dimensional vector. For the sparse modeling approach with non-uniform sparsity levels, the regularization term has non-uniformity, due to the weight vector obtained by the consistent estimator. The intersection of the contour line of the error term and regularization term of non-uniform sparsity is
. Therefore, non-uniform sparsity yields a sparse solution. However, for the sparse modeling approach with uniform sparsity levels, the intersection of the contour line of the error term and regularization term of uniform sparsity is
where both elements of the weight vector become non-zero (
and
). Therefore, sparse modeling with uniform sparsity may not yield a sparse solution. Thus, we employ the sparse modeling approach with non-uniform sparsity levels in order to extract only the important reactions more accurately.