Solutions of the Multivariate Inverse Frobenius–Perron Problem
Abstract
1. Introduction
2. Inverse Frobenius–Perron Problem and Lyapunov Exponent
2.1. Frobenius–Perron Operator
2.2. Inverse Frobenius–Perron Problem
2.3. Lyapunov Exponent
3. Solution of the IFPP in 1-Dimension
3.1. The Simplest Solution
3.2. Exploiting Symmetry in
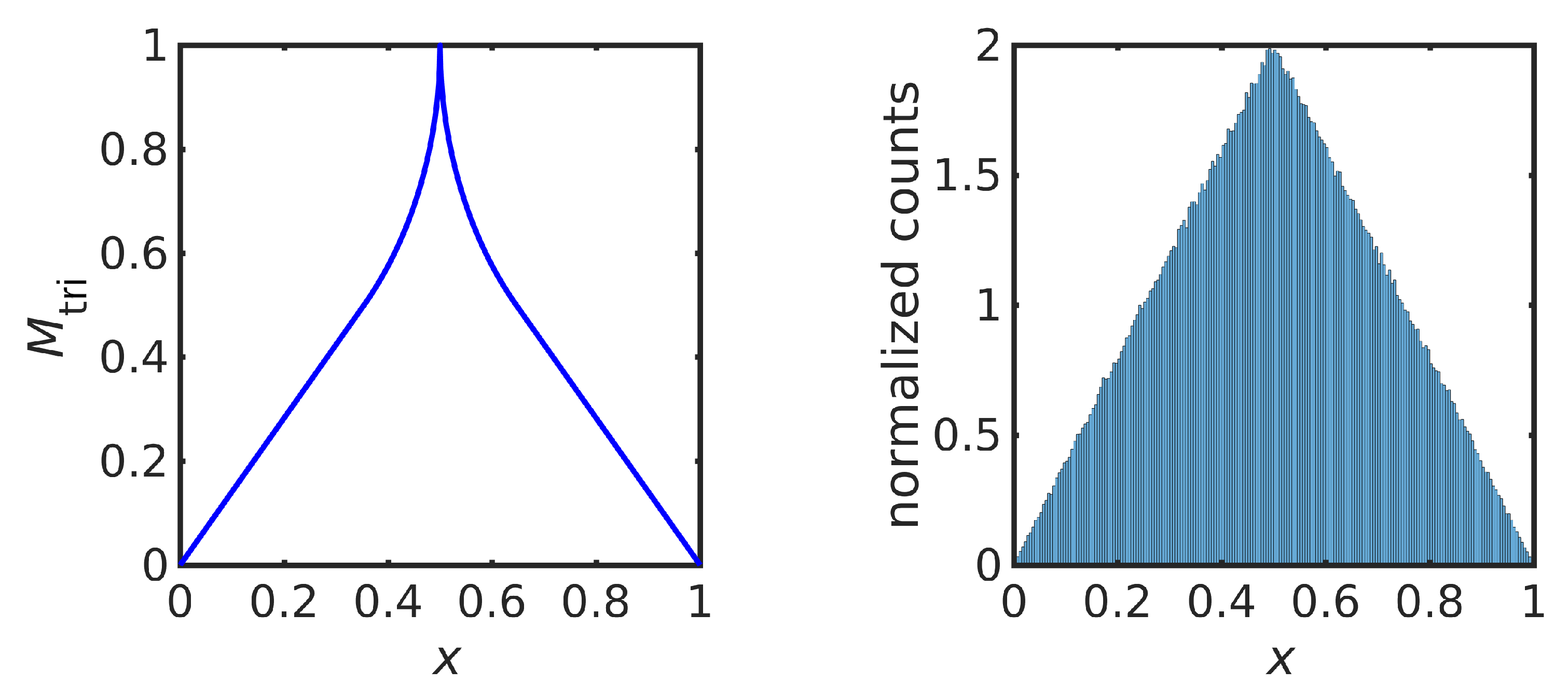
3.3. Symmetric Triangular Distribution
4. Solutions of the IFPP for General Multi-Variate Target Distributions
4.1. Forward and Inverse Rosenblatt Transformations
4.2. Factorization Theorem
4.3. Properties of M from U

5. Examples in One Dimension
5.1. Uniform Maps on
5.2. Ramp Distribution
5.3. The Logistic Map and Alternatives
6. Two Examples in Two Dimensions
6.1. Uniform Maps on
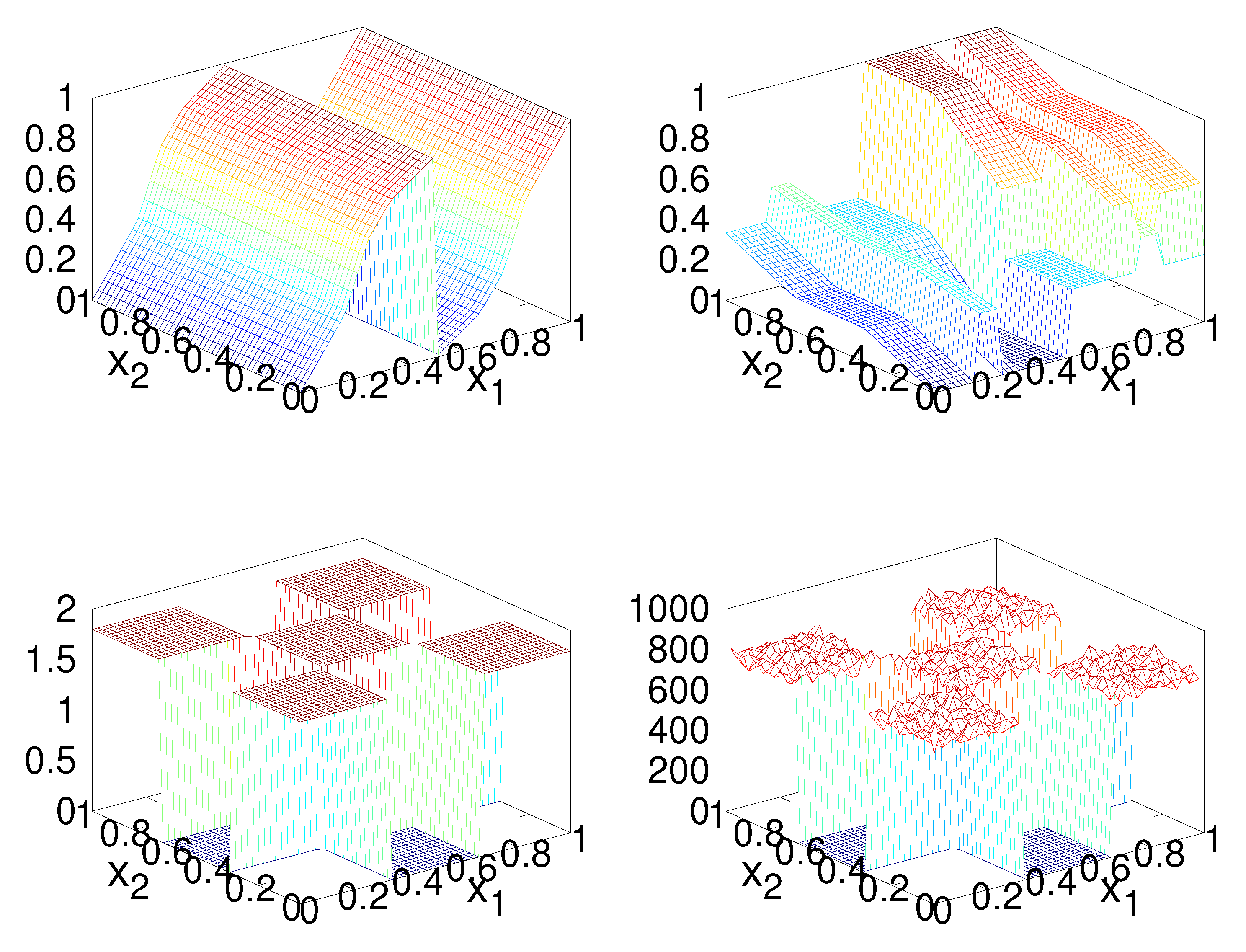
6.2. Checker-Board Distribution
6.3. A Numerical Construction
7. Summary and Discussion

Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Probability density function | |
| FP | Frobenius–Perron |
| IFPP | Inverse Frobenius–Perron problem |
| CDF | Cumulative distribution function |
| IDF | Inverse distribution function |
References
- Dorfman, J. Cambridge Lecture Notes in Physics: An Introduction to Chaos in Nonequilibrium Statistical Mechanics; Cambridge University Press: Cambridge, UK, 1999; Volume 14. [Google Scholar]
- Lasota, A.; Mackey, M.C. Chaos, Fractals, and Noise, 2nd ed.; Springer: New York, NY, USA, 1994. [Google Scholar]
- Ulam, S.; von Neumann, J. On Combination of Stochastic and Deterministic Processes. Bull. Am. Math. Soc. 1947, 53, 1120. [Google Scholar]
- May, R. Simple mathematical models with very complicated dynamics. Nature 1976, 261, 459–467. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.S. Monte Carlo Strategies in Scientific Computing; Springer: New York, NY, USA, 2001. [Google Scholar]
- Klus, S.; Koltai, P.; Schütte, C. On the numerical approximation of the Perron–Frobenius and Koopman operator. J. Comput. Dyn. 2016, 3, 51–79. [Google Scholar] [CrossRef]
- Grossmann, S.; Thomae, S. Invariant distributions and stationary correlation functions of one-dimensional discrete processes. Zeitschrift für Naturforschung A 1977, 32, 1353–1363. [Google Scholar] [CrossRef]
- Ershov, S.V.; Malinetskii, G.G. The solution of the inverse problem for the Perron–Frobenius equation. USSR Comput. Math. Math. Phys. 1988, 28, 136–141. [Google Scholar] [CrossRef]
- Diakonos, F.; Schmelcher, P. On the construction of one-dimensional iterative maps from the invariant density: The dynamical route to the beta distribution. Phys. Lett. A 1996, 211, 199–203. [Google Scholar] [CrossRef]
- Diakonos, F.; Pingel, D.; Schmelcher, P. A stochastic approach to the construction of one-dimensional chaotic maps with prescribed statistical properties. Phys. Lett. A 1999, 264, 162–170. [Google Scholar] [CrossRef]
- Pingel, D.; Schmelcher, P.; Diakonos, F. Theory and examples of the inverse Frobenius–Perron problem for complete chaotic maps. Chaos 1999, 9, 357–366. [Google Scholar] [CrossRef] [PubMed]
- Bollt, E.M. Controlling chaos and the inverse Frobenius–Perron problem: Global stabilization of arbitrary invariant measures. Int. J. Bifurc. Chaos 2000, 10, 1033–1050. [Google Scholar] [CrossRef]
- Nie, X.; Coca, D. A new approach to solving the inverse Frobenius–Perron problem. In Proceedings of the 2013 European Control Conference (ECC), Zurich, Switzerland, 17–19 July 2013; pp. 2916–2920. [Google Scholar]
- Nie, X.; Coca, D. A matrix-based approach to solving the inverse Frobenius–Perron problem using sequences of density functions of stochastically perturbed dynamical systems. Commun. Nonlinear Sci. Numer. Simul. 2018, 54, 248–266. [Google Scholar] [CrossRef] [PubMed]
- Rogers, A.; Shorten, R.; Heffernan, D.; Naughton, D. Synthesis of Piecewise-Linear Chaotic Maps: Invariant Densities, Autocorrelations, and Switching. Int. J. Bifurc. Chaos 2008, 18, 2169–2189. [Google Scholar] [CrossRef]
- Wei, N. Solutions of the Inverse Frobenius–Perron Problem. Master’s Thesis, Concordia University, Montreal, QC, Canada, 2015. [Google Scholar]
- Ulam, S.M. A Collection of Mathematical Problems; Interscience Publishers: Hoboken, NJ, USA, 1960. [Google Scholar]
- Rosenblatt, M. Remarks on a Multivariate Transformation. Ann. Math. Stat. 1952, 23, 470–472. [Google Scholar] [CrossRef]
- Gaspard, P. Chaos, Scattering and Statistical Mechanics; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Varberg, D.E. Change of variables in multiple integrals. Am. Math. Mon. 1971, 78, 42–45. [Google Scholar] [CrossRef]
- Györgyi, G.; Szépfalusy, P. Fully developed chaotic 1-d maps. Z. für Physik B Condens. Matter 1984, 55, 179–186. [Google Scholar] [CrossRef]
- Johnson, M. Multivariate Statistical Simulation; John Wiley & Sons: Hoboken, NJ, USA, 1987. [Google Scholar]
- Devroye, L. Non-Uniform Random Variate Generation; Springer: New York, NY, USA, 1986. [Google Scholar]
- Hörmann, W.; Leydold, J.; Derflinger, G. Automatic Nonuniform Random Variate Generation; Springer: New York, NY, USA, 2004. [Google Scholar] [CrossRef]
- Dolgov, S.; Anaya-Izquierdo, K.; Fox, C.; Scheichl, R. Approximation and sampling of multivariate probability distributions in the tensor train decomposition. Stat. Comput. 2020, 30, 603–625. [Google Scholar] [CrossRef]
- Dick, J.; Kuo, F.Y.; Sloan, I.H. High-dimensional integration: The quasi-Monte Carlo way. Acta Numer. 2013, 22, 133. [Google Scholar] [CrossRef]
- Rogers, A.; Shorten, R.; Heffernan, D.M. Synthesizing chaotic maps with prescribed invariant densities. Phys. Lett. A 2004, 330, 435–441. [Google Scholar] [CrossRef][Green Version]
- Huang, W. Characterizing chaotic processes that generate uniform invariant density. Chaos Solitons Fractals 2005, 25, 449–460. [Google Scholar] [CrossRef]
- Gentle, J.E. Random Number Generation and Monte Carlo Methods; Springer: New York, NY, USA, 2003; Volume 381. [Google Scholar]
- Parno, M.D.; Marzouk, Y.M. Transport map accelerated Markov chain Monte Carlo. SIAM/ASA J. Uncertain. Quantif. 2018, 6, 645–682. [Google Scholar] [CrossRef]








| ℓ | ||
|---|---|---|
| 1 | ||
| 2 | ||
| 4 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fox, C.; Hsiao, L.-J.; Lee, J.-E. Solutions of the Multivariate Inverse Frobenius–Perron Problem. Entropy 2021, 23, 838. https://doi.org/10.3390/e23070838
Fox C, Hsiao L-J, Lee J-E. Solutions of the Multivariate Inverse Frobenius–Perron Problem. Entropy. 2021; 23(7):838. https://doi.org/10.3390/e23070838
Chicago/Turabian StyleFox, Colin, Li-Jen Hsiao, and Jeong-Eun (Kate) Lee. 2021. "Solutions of the Multivariate Inverse Frobenius–Perron Problem" Entropy 23, no. 7: 838. https://doi.org/10.3390/e23070838
APA StyleFox, C., Hsiao, L.-J., & Lee, J.-E. (2021). Solutions of the Multivariate Inverse Frobenius–Perron Problem. Entropy, 23(7), 838. https://doi.org/10.3390/e23070838







