The Violation of Bell-CHSH Inequalities Leads to Different Conclusions Depending on the Description Used
Abstract
1. Introduction
2. A Short Review of Kolmogorov Axioms
2.1. The Probability Space
2.1.1. The Sample Space
2.1.2. The Event Space
- It must contain the sample space. Therefore, there is an event, the “total” event, that contains all the possible outputs of the experiment. Just as we explained above, for a dice, this event is .
- If an event belongs to the space, then its “complement” also belongs to the space. For instance, if the total event is in the space, then the null event must also be in the space. For the dice, if the event containing all the even outputs is in the event space, then the event , the one containing all odd outputs, must also be in the space.
- The space must be closed under countable unions and intersections. That is, if the space has the event and also has the event , then the event and the event must also be in the space. This can be interpreted as “the event where the output is even and is less than 5”.In this example, the word “and” refers to the intersection of subsets. In a similar way, the union of subsets is referred to with the word “or”, as in “the event where the output is even or less than 5”.
2.1.3. The Probability Measure
2.2. Kolmogorov Axioms
2.2.1. Conditional Probabilities
2.2.2. Probabilities and Relative Frequencies
2.2.3. Expected Values
3. Probabilities and Bell Inequalities
3.1. Bell-Type Experiment
3.2. The Probability Space 1
3.2.1. The Sample Space 1
3.2.2. The Event Space 1
3.2.3. The Probability Measure 1
3.3. The Probability Space 2
3.3.1. The Sample Space 2
3.3.2. The Event Space 2 and the Probability Measure 2
3.4. Events and Probabilities in the Analysis of the Bell Experiments
3.4.1. The Same Event in the Two Probability Spaces
3.4.2. The Same Probability in the Two Probability Spaces
3.4.3. Some Events Exist Only in One Probability Space
4. Two Bell-CHSH Inequalities
4.1. Bell Inequality in Probability Space 1
4.2. Bell Inequality in Probability Space 2
4.3. Bell Inequality in a Third Probability Space
4.4. Bell Inequalities without Probability
- The outputs have assigned values in all the runs, although only two of them are measured in each run.
- The observed product averages, , can be experimentally determined only for the subset of the results in which the angles were selected, while the theoretical average refers to the whole set of values. A version of the fair sampling assumption is required, to associate the observed and predicted values [26].
5. Interpretations of Inequality Violation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Derivation of the Numerical Inequality
References
- Einstein, A.; Podolsky, B.; Rosen, N. Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? Phys. Rev. 1935, 47, 777–780. [Google Scholar] [CrossRef]
- Pais, A. Einstein and the Quantum Theory. Rev. Mod. Phys. 1979, 51, 863–914. [Google Scholar] [CrossRef]
- Bell, J.S. On the Problem of Hidden Variables in Quantum Mechanics. Rev. Mod. Phys. 1966, 38, 447–452. [Google Scholar] [CrossRef]
- Aspect, A. Proposed Experiment to Test the Nonseparability of Quantum Mechanics. Phys. Rev. D 1976, 14, 1944–1951. [Google Scholar] [CrossRef]
- Santos, E. Mathematical and Physical Meaning of the Bell Inequalities. Eur. J. Phys. 2016, 37, 055402. [Google Scholar] [CrossRef]
- Collaboration, T.B.B.T. Challenging local realism with human choices. Nature 2018, 557, 212–216. [Google Scholar] [CrossRef]
- Bell, J.S. The Theory of Local Beables. In Speakable and Unspeakable in Quantum Mechanics: Collected Papers on Quantum Philosophy, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004; pp. 52–62. [Google Scholar] [CrossRef]
- Maudlin, T. What Bell Did. J. Phys. A Math. Theor. 2014, 47, 424010. [Google Scholar] [CrossRef]
- Nieuwenhuizen, T.M. Is the Contextuality Loophole Fatal for the Derivation of Bell Inequalities? Found. Phys. 2011, 41, 580–591. [Google Scholar] [CrossRef]
- Kwiat, P.G.; Eberhard, P.H.; Steinberg, A.M.; Chiao, R.Y. Proposal for a Loophole-Free Bell Inequality Experiment. Phys. Rev. A 1994, 49, 3209–3220. [Google Scholar] [CrossRef] [PubMed]
- Gisin, N.; Zbinden, H. Bell Inequality and the Locality Loophole: Active versus Passive Switches. Phys. Lett. A 1999, 264, 103–107. [Google Scholar] [CrossRef]
- Barrett, J.; Collins, D.; Hardy, L.; Kent, A.; Popescu, S. Quantum Nonlocality, Bell Inequalities, and the Memory Loophole. Phys. Rev. A 2002, 66, 042111. [Google Scholar] [CrossRef]
- Branciard, C. Detection Loophole in Bell Experiments: How Postselection Modifies the Requirements to Observe Nonlocality. Phys. Rev. A 2011, 83, 032123. [Google Scholar] [CrossRef]
- Hensen, B.; Bernien, H.; Dréau, A.E.; Reiserer, A.; Kalb, N.; Blok, M.S.; Ruitenberg, J.; Vermeulen, R.F.L.; Schouten, R.N.; Abellán, C.; et al. Loophole-Free Bell Inequality Violation Using Electron Spins Separated by 1.3 Kilometres. Nature 2015, 526, 682–686. [Google Scholar] [CrossRef] [PubMed]
- Shalm, L.K.; Meyer-Scott, E.; Christensen, B.G.; Bierhorst, P.; Wayne, M.A.; Stevens, M.J.; Gerrits, T.; Glancy, S.; Hamel, D.R.; Allman, M.S.; et al. Strong Loophole-Free Test of Local Realism. Phys. Rev. Lett. 2015, 115, 250402. [Google Scholar] [CrossRef]
- Giustina, M.; Versteegh, M.A.M.; Wengerowsky, S.; Handsteiner, J.; Hochrainer, A.; Phelan, K.; Steinlechner, F.; Kofler, J.; Larsson, J.A.; Abellán, C.; et al. Significant-Loophole-Free Test of Bell’s Theorem with Entangled Photons. Phys. Rev. Lett. 2015, 115, 250401. [Google Scholar] [CrossRef] [PubMed]
- Salavrakos, A.; Augusiak, R.; Tura, J.; Wittek, P.; Acín, A.; Pironio, S. Bell Inequalities Tailored to Maximally Entangled States. Phys. Rev. Lett. 2017, 119, 040402. [Google Scholar] [CrossRef]
- Zeilinger, A. The message of the quantum. Nature 2005, 438, 743. [Google Scholar] [CrossRef]
- Bera, M.N.; Acín, A.; Kuś, M.; Mitchell, M.W.; Lewenstein, M. Randomness in quantum mechanics: Philosophy, physics and technology. Rep. Prog. Phys. 2017, 80, 124001. [Google Scholar] [CrossRef]
- Grangier, P.; Auffèves, A. What is quantum in quantum randomness? Philos. Trans. A Math. Phys. Eng. Sci. 2018, 376. [Google Scholar] [CrossRef] [PubMed]
- Pironio, S.; Acín, A.; Massar, S.; de la Giroday, A.B.; Matsukevich, D.N.; Maunz, P.; Olmschenk, S.; Hayes, D.; Luo, L.; Manning, T.A.; et al. Random Numbers Certified by Bell’s Theorem. Nature 2010, 464, 1021–1024. [Google Scholar] [CrossRef]
- Colbeck, R.; Kent, A. Private Randomness Expansion with Untrusted Devices. J. Phys. A Math. Theor. 2011, 44, 095305. [Google Scholar] [CrossRef]
- Fehr, S.; Gelles, R.; Schaffner, C. Security and Composability of Randomness Expansion from Bell Inequalities. Phys. Rev. A 2013, 87, 012335. [Google Scholar] [CrossRef]
- Khrennikov, A.; Svozil, K. Quantum Probability and Randomness. Entropy 2019, 21, 35. [Google Scholar] [CrossRef]
- Pitowsky, I. Quantum Mechanics as a Theory of Probability. In Physical Theory and Its Interpretation: Essays in Honor of Jeffrey Bub; The Western Ontario Series in Philosophy of Science; Demopoulos, W., Pitowsky, I., Eds.; Springer: Dordrecht, The Netherlands, 2006; pp. 213–240. [Google Scholar] [CrossRef]
- Khrennikov, A. Nonlocality as well as rejection of realism are only sufficient (but non-necessary!) conditions for violation of Bell’s inequality. Inf. Sci. 2009, 179, 492–504. [Google Scholar] [CrossRef]
- Khrennikov, A. Two Faced Janus of Quantum Nonlocality. Entropy 2020, 22, 303. [Google Scholar] [CrossRef] [PubMed]
- De Muynck, W.M.; Abu-Zeid, O. On an Alternative Interpretation of the Bell Inequalities. Phys. Lett. A 1984, 100, 485–489. [Google Scholar] [CrossRef]
- Jarrett, J.P. On the Physical Significance of the Locality Conditions in the Bell Arguments. Noûs 1984, 18, 569–589. [Google Scholar] [CrossRef]
- Berkovitz, J. The World According to de Finetti: On de Finetti’s Theory of Probability and Its Application to Quantum Mechanics. In Probability in Physics; The Frontiers Collection; Ben-Menahem, Y., Hemmo, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 249–280. [Google Scholar] [CrossRef]
- Janotta, P.; Hinrichsen, H. Generalized probability theories: What determines the structure of quantum theory? J. Phys. A Math. Theor. 2014, 47, 323001. [Google Scholar] [CrossRef]
- Rosenthal, J.S. A First Look at Rigorous Probability Theory; World Scientific: Singapore, 2006. [Google Scholar]
- Kolmogorov, A.N.; Bharucha-Reid, A.T. Foundations of the Theory of Probability: Second English Edition; Courier Dover Publications: Mineola, NY, USA, 2018. [Google Scholar]
- Townsend, J.S. A Modern Approach to Quantum Mechanics; University Science Books: Herndon, VA, USA, 2000. [Google Scholar]
- Cohen-Tannoudji, C.; Diu, B.; Laloe, F. Quantum Mechanics; Wiley: Hoboken, NJ, USA, 1991; Volume 1. [Google Scholar]
- Sakurai, J.J.; Napolitano, J. Modern Quantum Mechanics; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information: 10th Anniversary Edition; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Gut, A. Probability: A Graduate Course; Springer Texts in Statistics; Springer: New York, NY, USA, 2005. [Google Scholar] [CrossRef]
- Chung, K.L.; Zhong, K. A Course in Probability Theory; Academic Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Gillies, D. Philosophical Theories of Probability; Psychology Press: Hove, UK, 2000. [Google Scholar]
- Ross, S.M. A First Course in Probability; Pearson: London, UK, 2018. [Google Scholar]
- Clauser, J.F.; Horne, M.A.; Shimony, A.; Holt, R.A. Proposed Experiment to Test Local Hidden-Variable Theories. Phys. Rev. Lett. 1969, 23, 880–884. [Google Scholar] [CrossRef]
- Genovese, M. Research on Hidden Variable Theories: A Review of Recent Progresses. Phys. Rep. 2005, 413, 319–396. [Google Scholar] [CrossRef]
- Bell, J.S. (Ed.) Introduction to the Hidden-Variable Question. In Speakable and Unspeakable in Quantum Mechanics: Collected Papers on Quantum Philosophy, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004; pp. 29–39. [Google Scholar] [CrossRef]
- Ciepielewski, G.S.; Okon, E.; Sudarsky, D. On Superdeterministic Rejections of Settings Independence. Br. Soc. Philos. Sci. 2020. [Google Scholar] [CrossRef]
- Eberhard, P.H. Bell’s Theorem without Hidden Variables. Il Nuovo Cimento B (1971–1996) 1977, 38, 75–80. [Google Scholar] [CrossRef]
- Redhead, M. Incompleteness, Non Locality and Realism. A Prolegomenon to the Philosophy of Quantum Mechanics. Revue Philosophique de la France Et de l’Etranger 1987, 180, 712–713. [Google Scholar]
- de Muynck, W.M. The Bell Inequalities and Their Irrelevance to the Problem of Locality in Quantum Mechanics. Phys. Lett. A 1986, 114, 65–67. [Google Scholar] [CrossRef]
- Larsson, J.A. Loopholes in Bell Inequality Tests of Local Realism. J. Phys. A Math. Theor. 2014, 47, 424003. [Google Scholar] [CrossRef]
- Valdenebro, A.G. Assumptions Underlying Bell s Inequalities. Eur. J. Phys. 2002, 23, 569–577. [Google Scholar] [CrossRef]
- Tittel, W.; Brendel, J.; Zbinden, H.; Gisin, N. Violation of Bell Inequalities by Photons More Than 10 Km Apart. Phys. Rev. Lett. 1998, 81, 3563–3566. [Google Scholar] [CrossRef]
- Handsteiner, J.; Friedman, A.S.; Rauch, D.; Gallicchio, J.; Liu, B.; Hosp, H.; Kofler, J.; Bricher, D.; Fink, M.; Leung, C.; et al. Cosmic Bell Test: Measurement Settings from Milky Way Stars. Phys. Rev. Lett. 2017, 118, 060401. [Google Scholar] [CrossRef] [PubMed]
- Rowe, M.A.; Kielpinski, D.; Meyer, V.; Sackett, C.A.; Itano, W.M.; Monroe, C.; Wineland, D.J. Experimental Violation of a Bell’s Inequality with Efficient Detection. Nature 2001, 409, 791–794. [Google Scholar] [CrossRef] [PubMed]
- Giustina, M.; Mech, A.; Ramelow, S.; Wittmann, B.; Kofler, J.; Beyer, J.; Lita, A.; Calkins, B.; Gerrits, T.; Nam, S.W.; et al. Bell Violation Using Entangled Photons without the Fair-Sampling Assumption. Nature 2013, 497, 227–230. [Google Scholar] [CrossRef] [PubMed]
- Hall, M.J.W. The Significance of Measurement Independence for Bell Inequalities and Locality. In At the Frontier of Spacetime: Scalar-Tensor Theory, Bells Inequality, Machs Principle, Exotic Smoothness; Fundamental Theories of Physics; Asselmeyer-Maluga, T., Ed.; Springer International Publishing: Cham, Switzerland, 2016; pp. 189–204. [Google Scholar] [CrossRef]
- Khrennikov, A. Can There Be Given Any Meaning to Contextuality Without Incompatibility? Int. J. Theor. Phys. 2021, 60, 106–114. [Google Scholar] [CrossRef]
- Eberhard, P.H. Bell’s Theorem and the Different Concepts of Locality. Il Nuovo Cimento B (1971–1996) 1978, 46, 392–419. [Google Scholar] [CrossRef]
- Fine, A. Correlations and Physical Locality. PSA Proc. Bienn. Meet. Philos. Sci. Assoc. 1980, 1980, 535–562. [Google Scholar] [CrossRef]
- Berkovitz, J. Aspects of Quantum Non-Locality I: Superluminal Signalling, Action-at-a-Distance, Non-Separability and Holism. Stud. Hist. Philos. Sci. Part B Stud. Hist. Philos. Mod. Phys. 1998, 29, 183–222. [Google Scholar] [CrossRef]
- Bohm, D. A Suggested Interpretation of the Quantum Theory in Terms of “Hidden” Variables. I. Phys. Rev. 1952, 85, 166–179. [Google Scholar] [CrossRef]
- Bohm, D. Reply to a Criticism of a Causal Re-Interpretation of the Quantum Theory. Phys. Rev. 1952, 87, 389–390. [Google Scholar] [CrossRef]
- Murdoch, D.R. Niels Bohr’s Philosophy of Physics; Cambridge University Press: Cambridge, UK, 1987. [Google Scholar] [CrossRef]
- Peres, A. Unperformed Experiments Have No Results. Am. J. Phys. 1978, 46, 745–747. [Google Scholar] [CrossRef]
- Fine, A. Hidden Variables, Joint Probability, and the Bell Inequalities. Phys. Rev. Lett. 1982, 48, 291–295. [Google Scholar] [CrossRef]
- Fine, A. Joint Distributions, Quantum Correlations, and Commuting Observables. J. Math. Phys. 1982, 23, 1306–1310. [Google Scholar] [CrossRef]
- Müller, T.; Placek, T. Against a Minimalist Reading of Bell’s Theorem: Lessons from Fine. Synthese 2001, 128, 343–379. [Google Scholar] [CrossRef]
- Khrennikov, A. Bell’s Inequality: Physics Meets Probability. arXiv 2007, arXiv:0709.3909. [Google Scholar]
- de la Peña, L.; Cetto, A.M.; Brody, T.A. On Hidden-Variable Theories and Bell’s Inequality. Lettere al Nuovo Cimento (1971–1985) 1972, 5, 177–181. [Google Scholar] [CrossRef]
- Pitowsky, I. Resolution of the Einstein-Podolsky-Rosen and Bell Paradoxes. Phys. Rev. Lett. 1982, 48, 1299–1302. [Google Scholar] [CrossRef]
- Wigner, E. On the Quantum Correction For Thermodynamic Equilibrium. Phys. Rev. 1932, 40, 749–759. [Google Scholar] [CrossRef]
- Spekkens, R.W. Negativity and Contextuality Are Equivalent Notions of Nonclassicality. Phys. Rev. Lett. 2008, 101, 020401. [Google Scholar] [CrossRef]
- de Barros, J.A.; Kujala, J.V.; Oas, G. Negative Probabilities and Contextuality. J. Math. Psychol. 2016, 74, 34–45. [Google Scholar] [CrossRef]
- Hacking, E.U.P.I. The Emergence of Probability: A Philosophical Study of Early Ideas about Probability, Induction and Statistical Inference; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Daston, L. Classical Probability in the Enlightenment; Princeton University Press: Princeton, NJ, USA, 1988. [Google Scholar]
- Svetlichny, G.; Redhead, M.; Brown, H.; Butterfield, J. Do the Bell Inequalities Require the Existence of Joint Probability Distributions? Philos. Sci. 1988, 55, 387–401. [Google Scholar] [CrossRef]
- Khrennikov, A. Frequency Analysis of the EPR-Bell Argumentation. Found. Phys. 2002, 32, 1159–1174. [Google Scholar] [CrossRef]

| Space 1 | Space 2 | ||||
|---|---|---|---|---|---|
| Run | Run | ||||
| 1 | 1 | 1 | 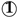 | 0 | |
| 2 | 1 | 2 | 0 | ① | |
| 3 | 1 | 3 | 1 | ① | |
| 4 | 1 | 4 | 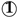 | 0 | |
| 5 | 0 | 5 | ⓪ | 1 | |
| 6 | 1 | 6 | 1 | ① | |
| ⋮ | ⋮ | ||||
| To Prove | Inequality 1 | Inequality 2 | Inequality 3 |
|---|---|---|---|
| Sample space | |||
| Kolmogorov Axioms | Kolmogorov Axioms | Kolmogorov Axioms | |
| Locality | Locality | ||
| -independence | -independence |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Solis-Labastida, A.F.G.; Gastelum, M.; Hirsch, J.G. The Violation of Bell-CHSH Inequalities Leads to Different Conclusions Depending on the Description Used. Entropy 2021, 23, 872. https://doi.org/10.3390/e23070872
Solis-Labastida AFG, Gastelum M, Hirsch JG. The Violation of Bell-CHSH Inequalities Leads to Different Conclusions Depending on the Description Used. Entropy. 2021; 23(7):872. https://doi.org/10.3390/e23070872
Chicago/Turabian StyleSolis-Labastida, Aldo F. G., Melina Gastelum, and Jorge G. Hirsch. 2021. "The Violation of Bell-CHSH Inequalities Leads to Different Conclusions Depending on the Description Used" Entropy 23, no. 7: 872. https://doi.org/10.3390/e23070872
APA StyleSolis-Labastida, A. F. G., Gastelum, M., & Hirsch, J. G. (2021). The Violation of Bell-CHSH Inequalities Leads to Different Conclusions Depending on the Description Used. Entropy, 23(7), 872. https://doi.org/10.3390/e23070872






