Quasi-Static Variation of Power-Law and Log-Normal Distributions of Urban Population
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data
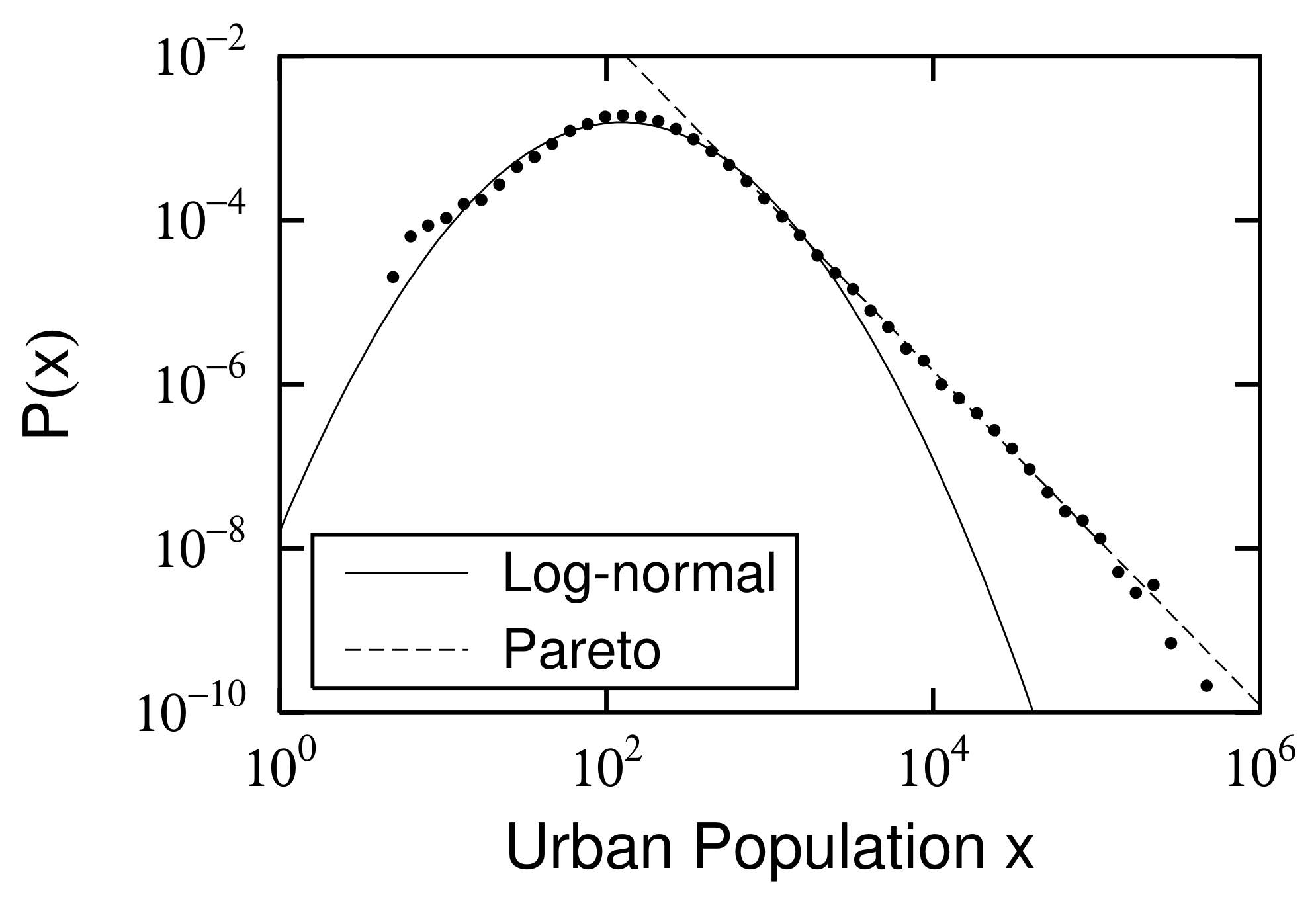
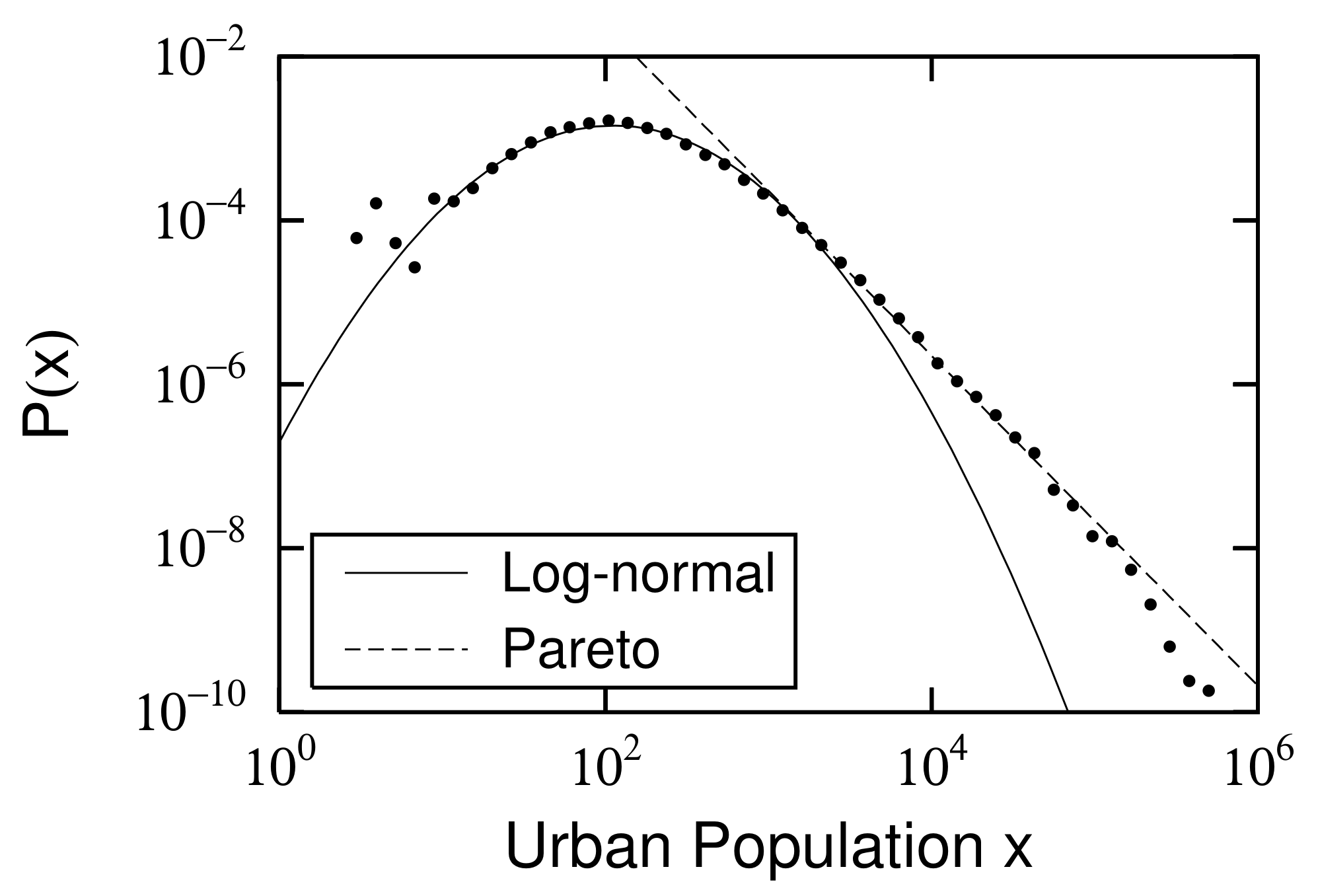
2.2. Power and Log-Normal Distributions and Their Changes
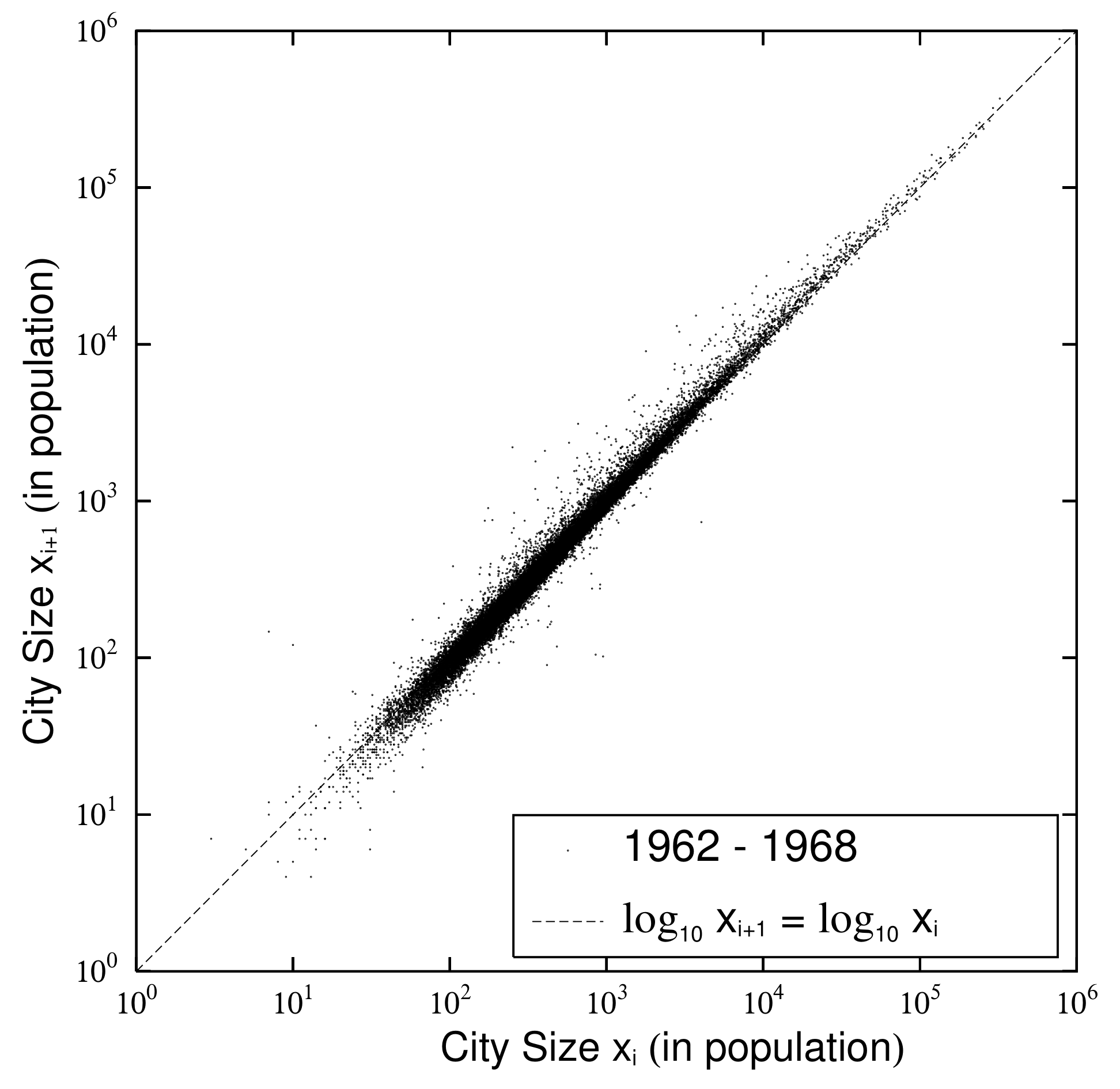
2.3. Quasi-Time-Reversal and Changes
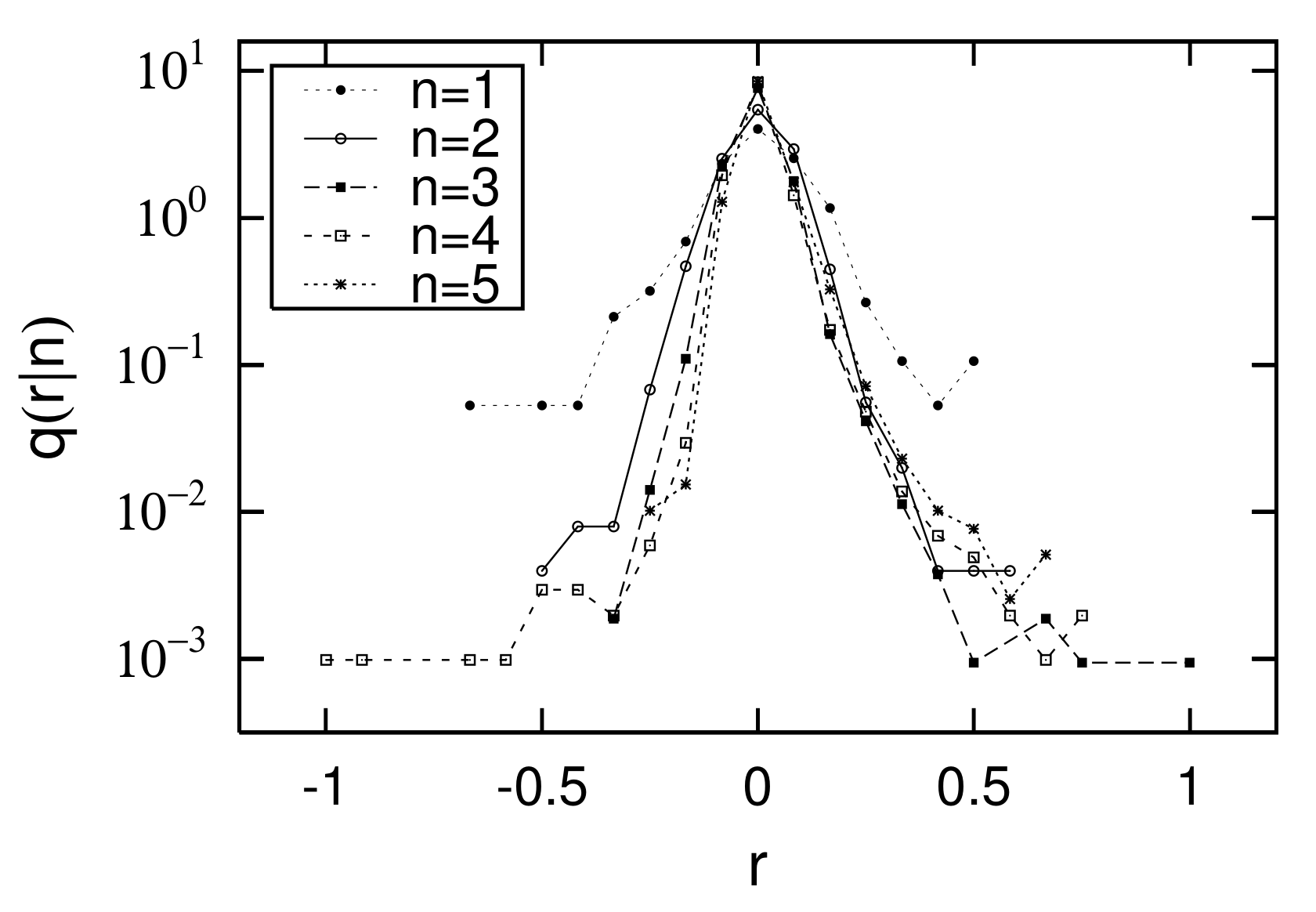
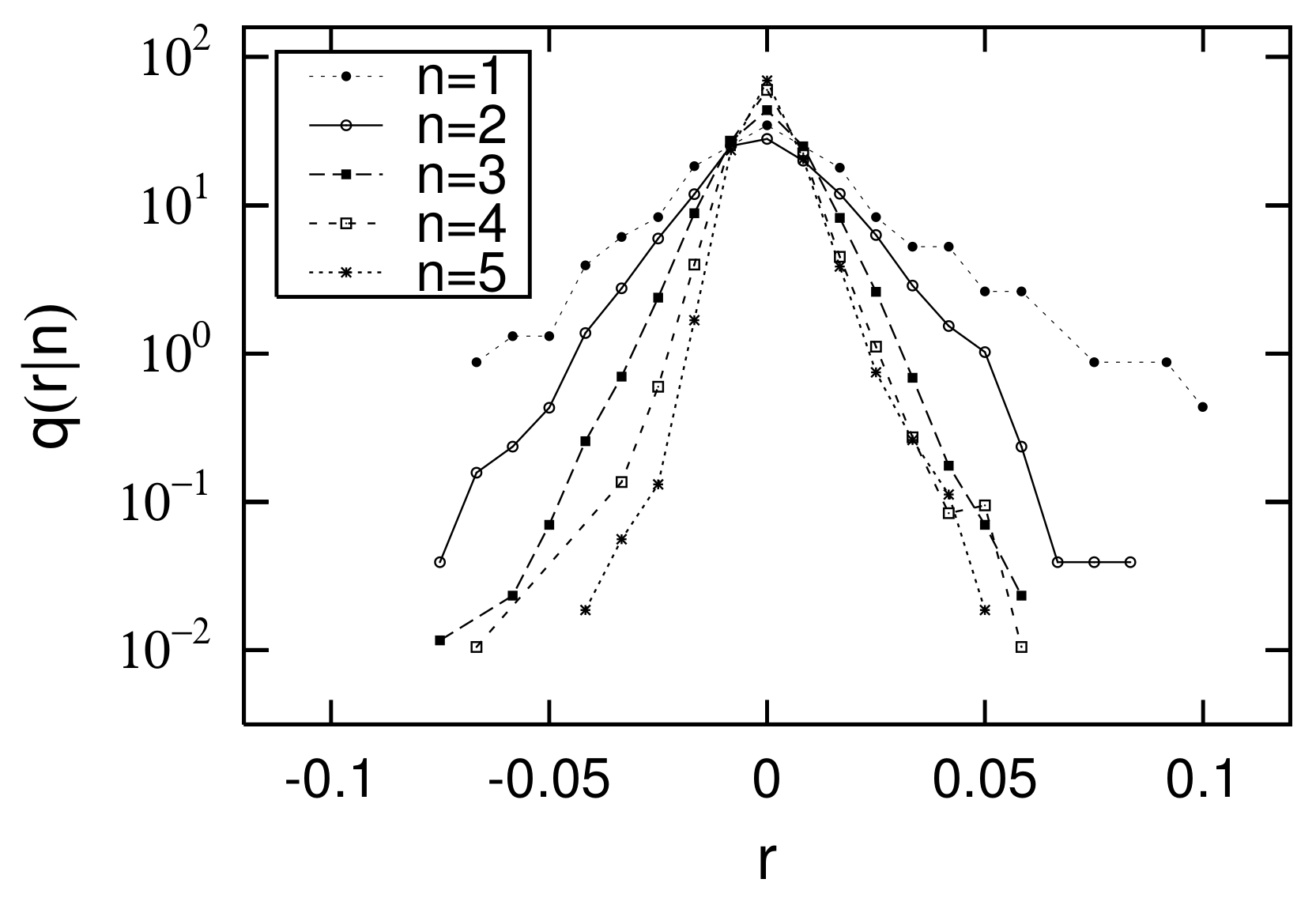
2.4. Gibrat’s Law and Non-Gibrat’s Property
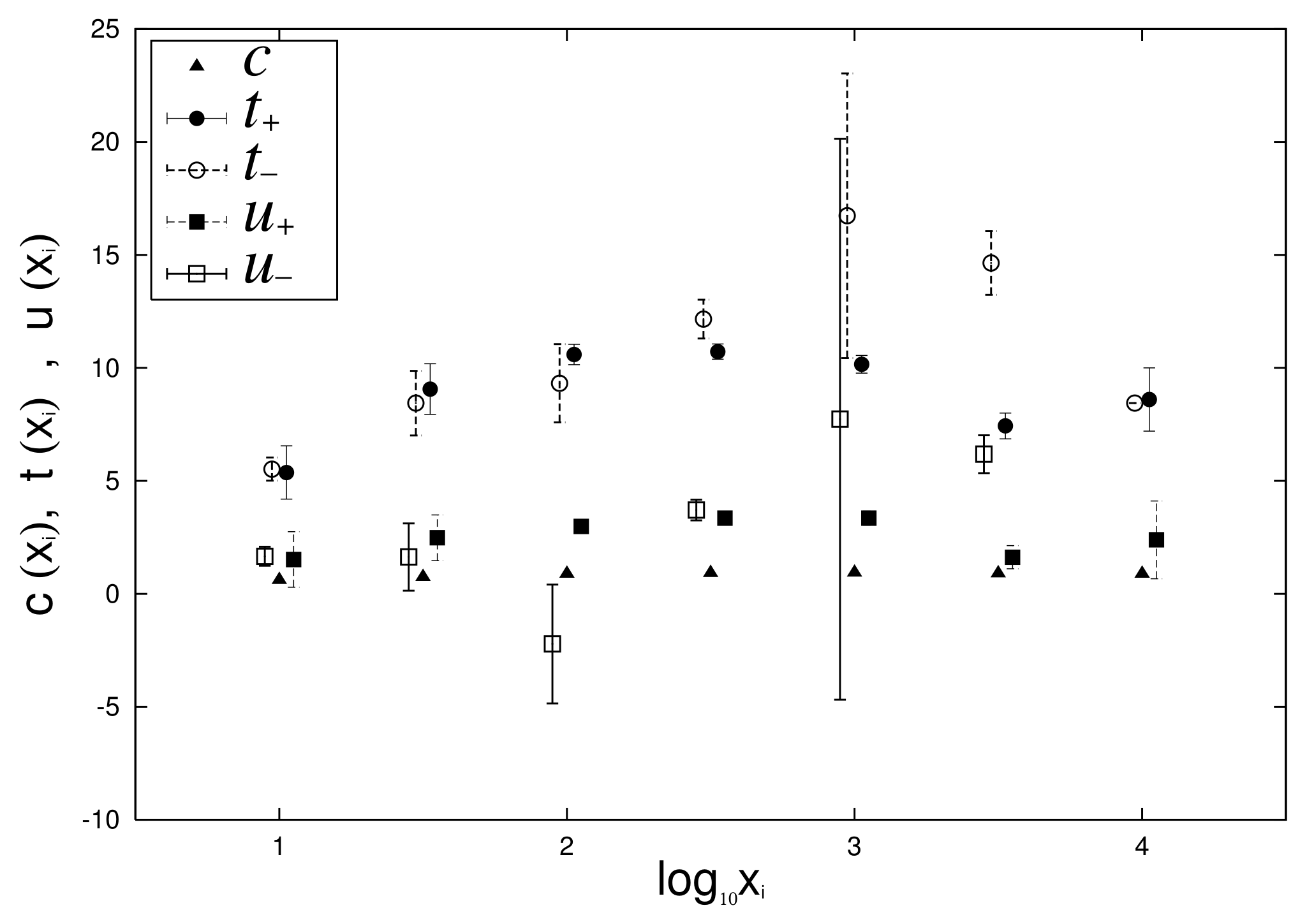
2.5. Quasi-Static Change of Power-Law Distribution
2.6. Quasi-Static Change of Log-Normal Distribution
3. Results
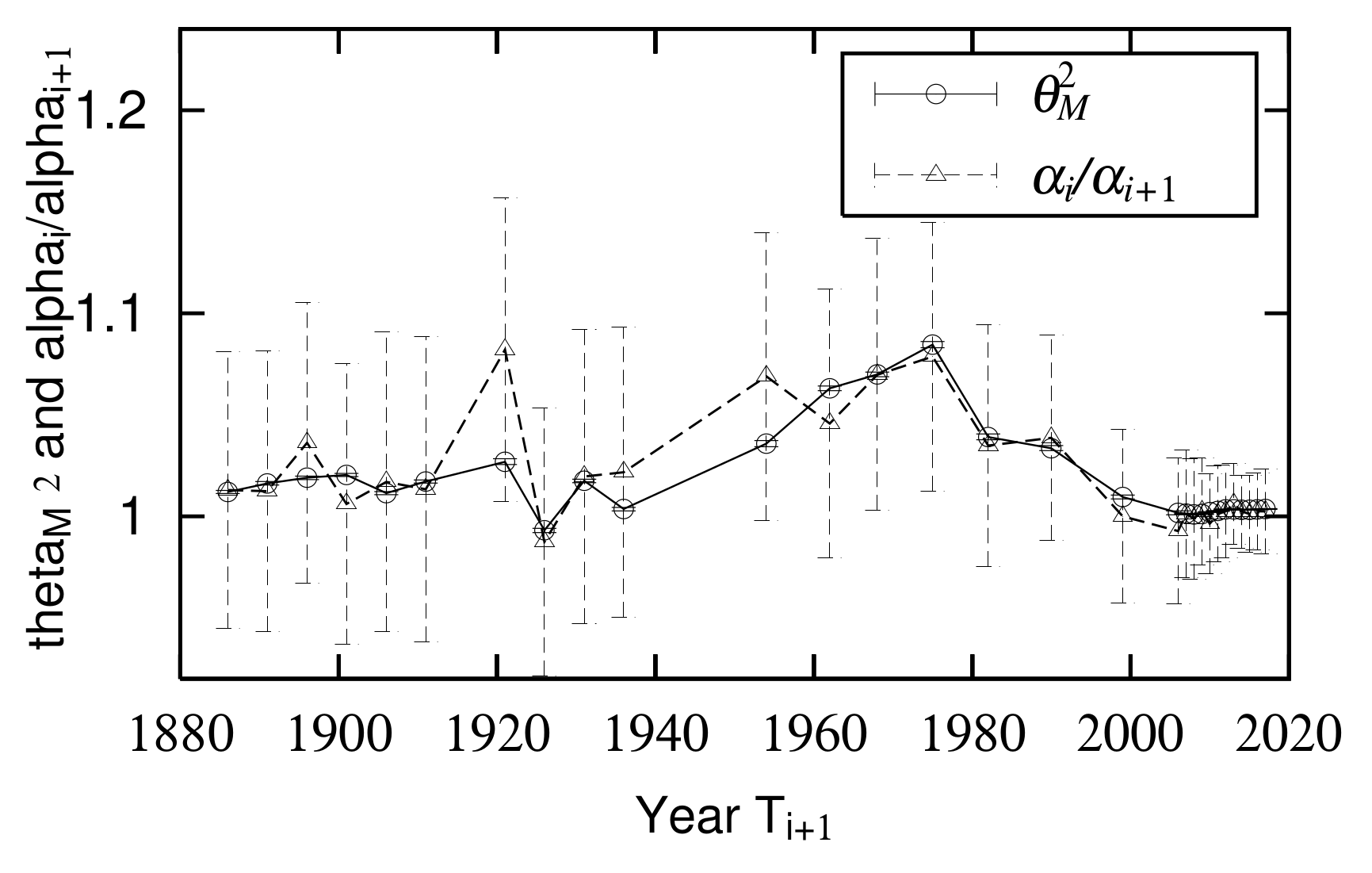
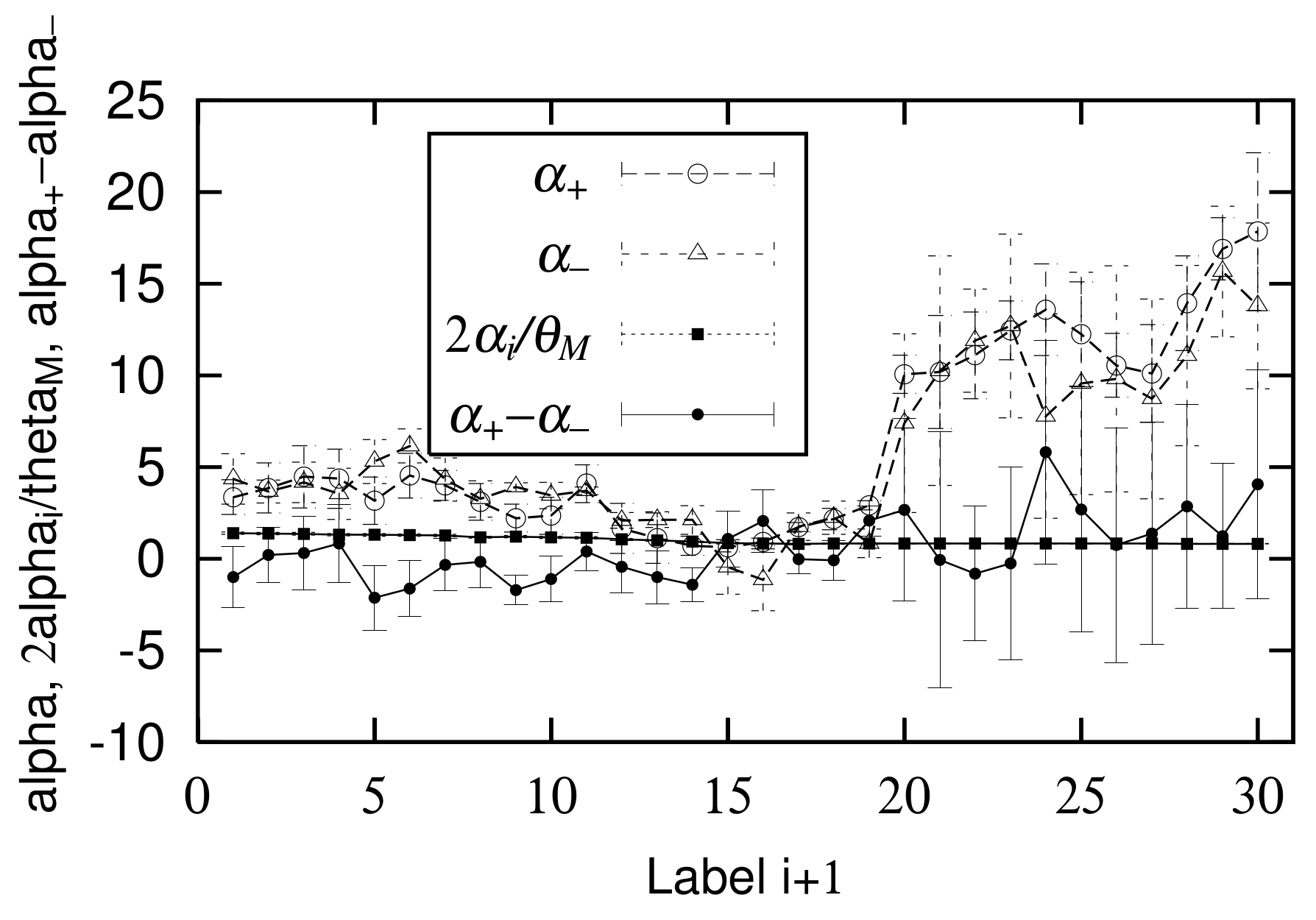
3.1. Consistency between Quasi-Time-Reversal Symmetry and Changes of Power-Law Index
3.2. Consistency of Quasi-Time-Reversal Symmetry and Changes in Logarithmic Standard Deviation
3.3. Consistency between Non-Gibrat’s Property and Log-Normal Distribution
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Stanley, H.E. Introduction to Phase Transitions and Critical Phenomena; Oxford University Press: Oxford, UK, 1987. [Google Scholar]
- Saichev, A.I.; Malevergne, Y.; Sornette, D. Theory of Zip’s Law and Beyond; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Mizuno, T.; Katori, M.; Takayasu, H.; Takayasu, M. Statistical and Stochastic Laws in the Income of Japanese Companies. In Empirical Science of Financial Fluctuations—The Advent of Econophysics; Takayasu, H., Ed.; Springer: Tokyo, Japan, 2002; pp. 321–330. [Google Scholar]
- Ishikawa, A. Annual change of Pareto index dynamically deduced from the law of detailed quasi-balance. Physica 2006, A371, 525–535. [Google Scholar] [CrossRef] [Green Version]
- Ishikawa, A. Quasi-statically varying Pareto-law and log-normal distributions in the large and the middle scale regions of Japanese land prices. Prog. Theor. Phys. Suppl. 2009, 179, 103–113. [Google Scholar] [CrossRef] [Green Version]
- Gibrat, R. Les Inégalités Économique; Sirey: Paris, France, 1932. [Google Scholar]
- Sutton, J. Gibrat’s Legacy. J. Econ. Lit. 1997, 35, 40–59. [Google Scholar]
- Ishikawa, A.; Fujimoto, S.; Mizuno, T. Why does production function take the Cobb-Douglas form? Direct observation of production function using empirical data. Evol. Inst. Econ. Rev. 2020, 18, 79–102. [Google Scholar] [CrossRef]
- Cobb, C.W.; Douglas, P.H. A Theory of Production. Am. Econ. Rev. 1928, 18, 139–165. [Google Scholar]
- Ishikawa, A.; Fujimoto, S.; Ramos, A.; Mizuno, T. Initial value dependence of urban population’s growth-rate distribution and long-term growth. Front. Phys. 2020, 8, 32. [Google Scholar] [CrossRef]
- The National Institute of Statistics and Economic Studies. Available online: https://www.insee.fr/en/accueil (accessed on 1 January 2020).
- Pareto, V. Cours d’Économie Politique; Macmillan: London, UK, 1897. [Google Scholar]
- Zipf, G.K. Human Behavior and the Principle of Least Effort; Addison-Wesley: Cambridge, MA, USA, 1949. [Google Scholar]
- Newman, M.E.J. Power laws, Pareto distributions and Zipf’s law. Contemp. Phys. 2005, 46, 323–351. [Google Scholar] [CrossRef] [Green Version]
- Clauset, A.; Shalizi, C.R.; Newman, M.E.J. Power-law distributions in empirical data. SIAM Rev. 2009, 51, 661–703. [Google Scholar] [CrossRef] [Green Version]
- Badger, W.W. An entropy-utility model for the size distribution of income. In Mathematical Models as a Tool for the Social Science; West, B.J., Ed.; Gordon and Breach: New York, NY, USA, 1980; pp. 87–120. [Google Scholar]
- Montroll, E.W.; Shlesinger, M.F. Maximum entropy formalism, fractals, scaling phenomena, and 1/f noise: A tale of tails. J. Stat. Phys. 1983, 32, 209–230. [Google Scholar] [CrossRef]
- Fujiwara, Y.; Souma, W.; Aoyama, H.; Kaizoji, T.; Aoki, M. Growth and fluctuations of personal income. Physica 2003, A321, 598–604. [Google Scholar] [CrossRef] [Green Version]
- Fujiwara, Y.; Guilmi, C.D.; Aoyama, H.; Gallegati, M.; Souma, W. Do Pareto-Zipf and Gibrat laws hold true? An analysis with European firms. Physica 2004, A335, 197–216. [Google Scholar] [CrossRef] [Green Version]
- Yokoyama, R.; Sirasawa, M.; Kikuchi, Y. Representation of topographical features by opennesses. J. Jpn. Soc. Photogramm. Remote Sens. 1999, 38, 26–34, (In Japanese with English abstract). [Google Scholar]
- Yokoyama, R.; Sirasawa, M.; Pike, R. Visualizing Topography by Openness: A New Application of Image Processing to Digital Elevation Models. Photogramm. Eng. Remote Sens. 2002, 68, 257–265. [Google Scholar]
- Prima, O.D.A.; Echigo, A.; Yokoyama, R.; Yoshida, T. Supervised landform classification of Northeast Honshu from DEM-derived thematic maps. Geomorphology 2006, 78, 373–386. [Google Scholar] [CrossRef]
- Ishikawa, A.; Fujimoto, S.; Mizuno, T.; Watanabe, T. Analytical derivation of power laws in firm size variables from Gibrat’s law and quasi-inversion symmetry: A geomorphological approach. J. Phys. Soc. Jpn. 2014, 83, 034802. [Google Scholar] [CrossRef]
- Ishikawa, A. Derivation of the distribution from extended Gibrat’s law. J. Phys. 2006, A367, 425–434. [Google Scholar] [CrossRef] [Green Version]
- Ishikawa, A. The uniqueness of firm size distribution function from tent-shaped growth rate distribution. J. Phys. 2007, A383, 79–84. [Google Scholar] [CrossRef] [Green Version]
- Tomoyose, M.; Fujimoto, S.; Ishikawa, A. Non-Gibrat’s law in the middle scale region. Prog. Theor. Phys. Suppl. 2009, 179, 114–122. [Google Scholar] [CrossRef] [Green Version]
- Ishikawa, A.; Fujimoto, S.; Mizuno, T. Shape of Growth Rate Distribution Determines the Type of Non-Gibrat’s Property. Physica 2011, A390, 4273–4285. [Google Scholar] [CrossRef] [Green Version]
- Canning, D.; Amaral, L.A.N.; Lee, Y.; Meyer, M.; Stanley, H.E. Scaling the volatility of GDP growth rates. Econ. Lett. 1998, 60, 335–341. [Google Scholar] [CrossRef]
- Ishikawa, A. Statistical Properties in Firms’ Large-Scale Data; Springer: Tokyo, Japan, 2021; in press. [Google Scholar]





| Mark | Year | Communes | Population |
|---|---|---|---|
| 0 | 1876 | 34,500 | 38,173,561 |
| 1 | 1881 | 34,500 | 38,969,724 |
| 2 | 1886 | 34,500 | 39,508,491 |
| 3 | 1891 | 34,500 | 39,660,067 |
| 4 | 1896 | 34,500 | 39,871,028 |
| 5 | 1901 | 34,500 | 40,390,113 |
| 6 | 1906 | 34,500 | 40,780,507 |
| 7 | 1911 | 34,500 | 41,147,539 |
| 8 | 1921 | 34,500 | 38,932,989 |
| 9 | 1926 | 34,500 | 40,458,773 |
| 10 | 1931 | 34,500 | 41,541,494 |
| 11 | 1936 | 34,860 | 41,813,397 |
| 12 | 1954 | 34,946 | 43,394,688 |
| 13 | 1962 | 34,972 | 47,376,787 |
| 14 | 1968 | 34,972 | 50,798,112 |
| 15 | 1975 | 34,972 | 53,764,064 |
| 16 | 1982 | 34,972 | 55,569,542 |
| 17 | 1990 | 34,972 | 58,040,659 |
| 18 | 1999 | 34,972 | 60,149,901 |
| 19 | 2006 | 34,972 | 63,186,117 |
| 20 | 2007 | 34,972 | 63,600,690 |
| 21 | 2008 | 34,972 | 63,961,859 |
| 22 | 2009 | 34,972 | 64,304,500 |
| 23 | 2010 | 34,972 | 64,612,939 |
| 24 | 2011 | 34,972 | 64,933,400 |
| 25 | 2012 | 34,972 | 65,241,241 |
| 26 | 2013 | 34,972 | 65,564,756 |
| 27 | 2014 | 34,972 | 65,907,160 |
| 28 | 2015 | 34,972 | 66,190,280 |
| 29 | 2016 | 34,972 | 66,361,658 |
| 30 | 2017 | 34,972 | 66,524,339 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ishikawa, A.; Fujimoto, S.; Ramos, A.; Mizuno, T. Quasi-Static Variation of Power-Law and Log-Normal Distributions of Urban Population. Entropy 2021, 23, 908. https://doi.org/10.3390/e23070908
Ishikawa A, Fujimoto S, Ramos A, Mizuno T. Quasi-Static Variation of Power-Law and Log-Normal Distributions of Urban Population. Entropy. 2021; 23(7):908. https://doi.org/10.3390/e23070908
Chicago/Turabian StyleIshikawa, Atushi, Shouji Fujimoto, Arturo Ramos, and Takayuki Mizuno. 2021. "Quasi-Static Variation of Power-Law and Log-Normal Distributions of Urban Population" Entropy 23, no. 7: 908. https://doi.org/10.3390/e23070908






