Stabilization and Synchronization of a Complex Hidden Attractor Chaotic System by Backstepping Technique
Abstract
:1. Introduction
2. Related Work
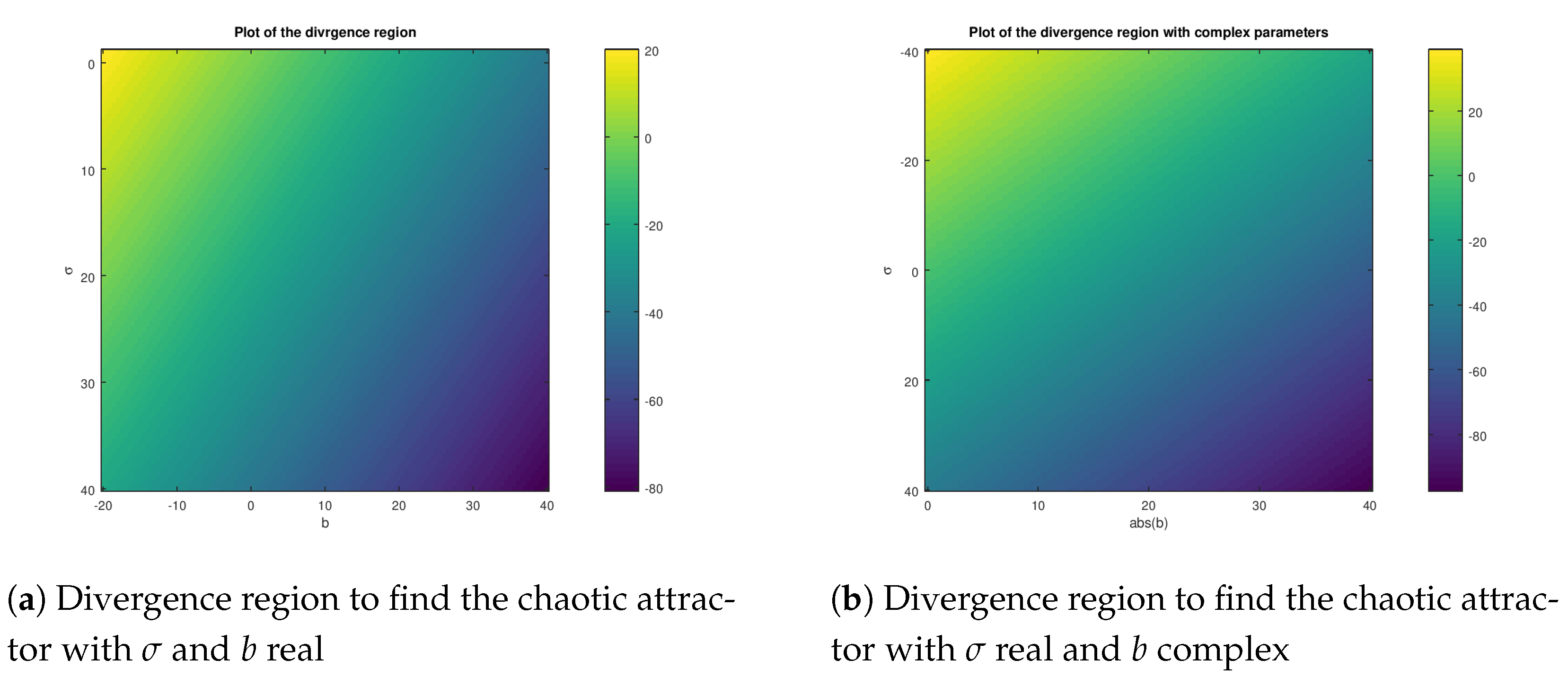
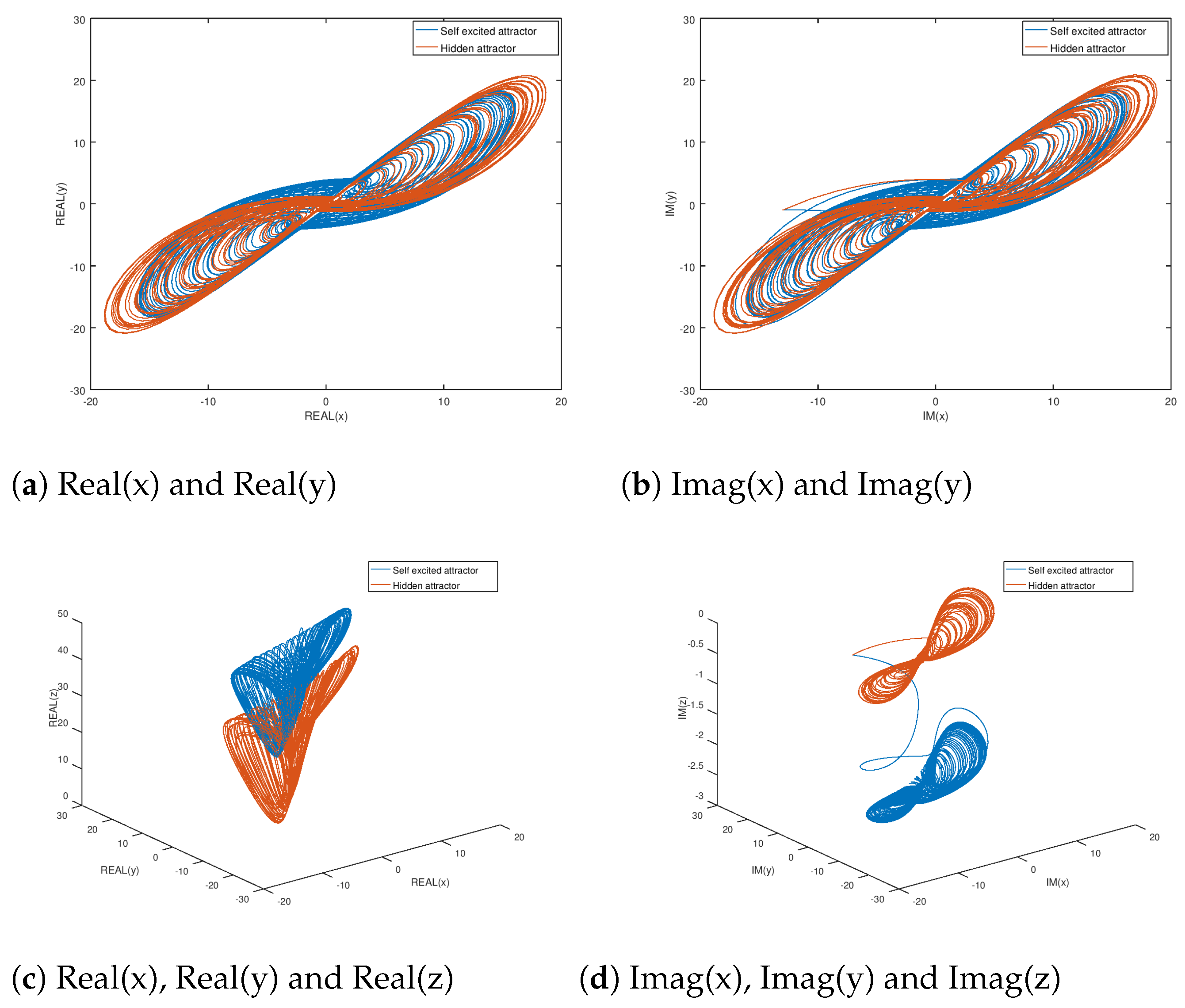
3. Problem Formulation: Complex Hidden Attractor
4. Control and Synchronization of the Hidden Attractor
4.1. Stabilization of the Complex Hidden Attractor
4.2. Synchronization of the Complex Hidden Attractor
5. Numerical Experiments
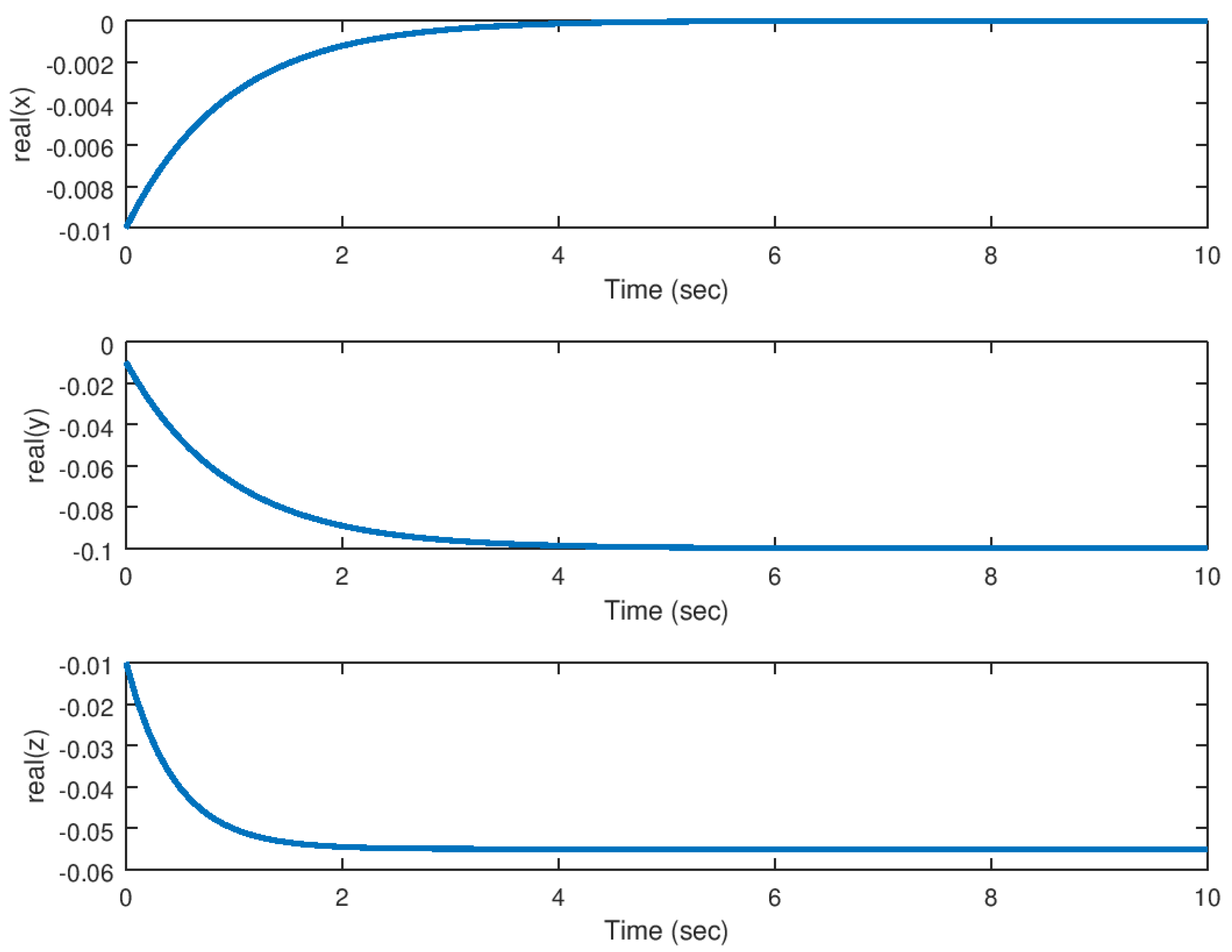
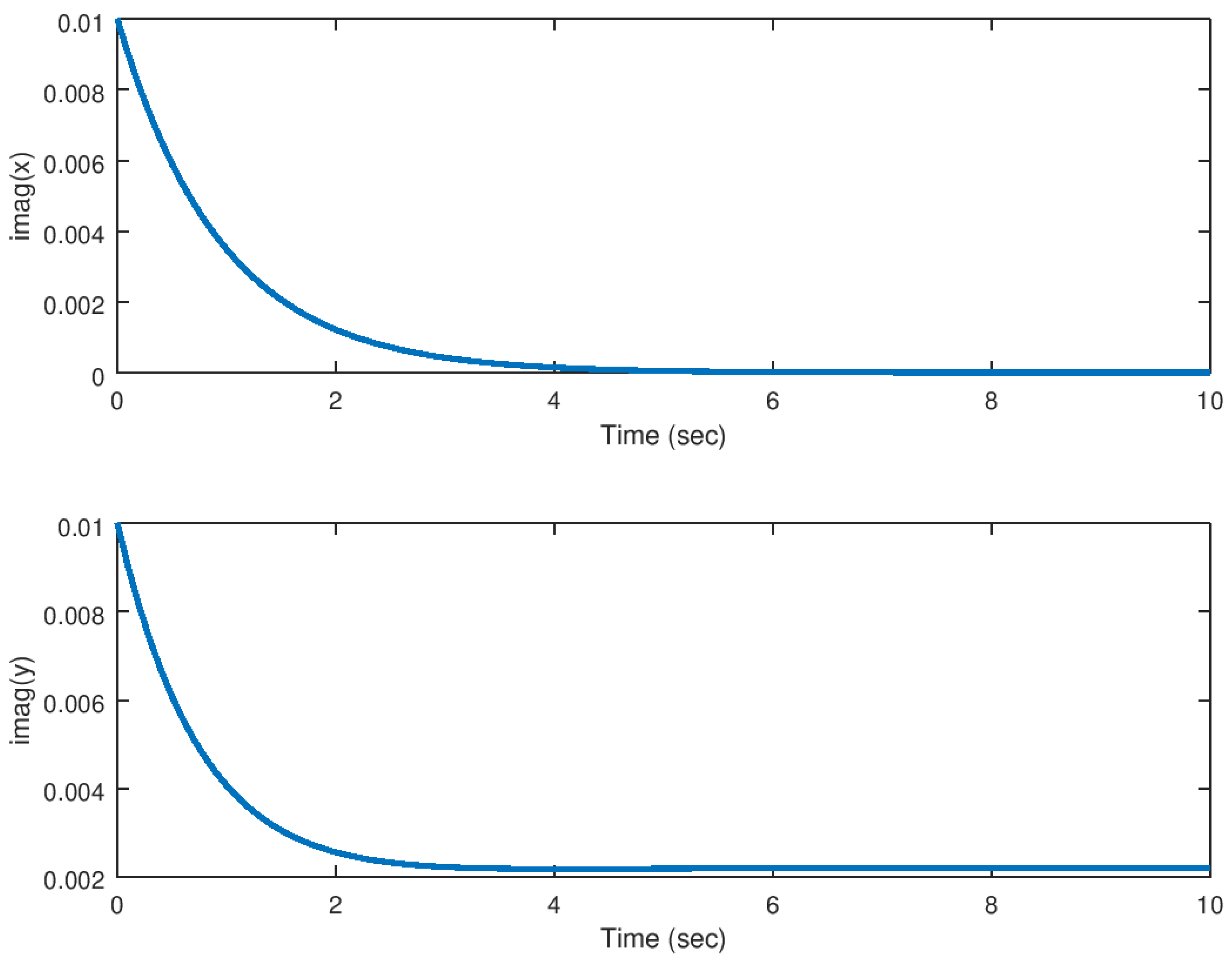
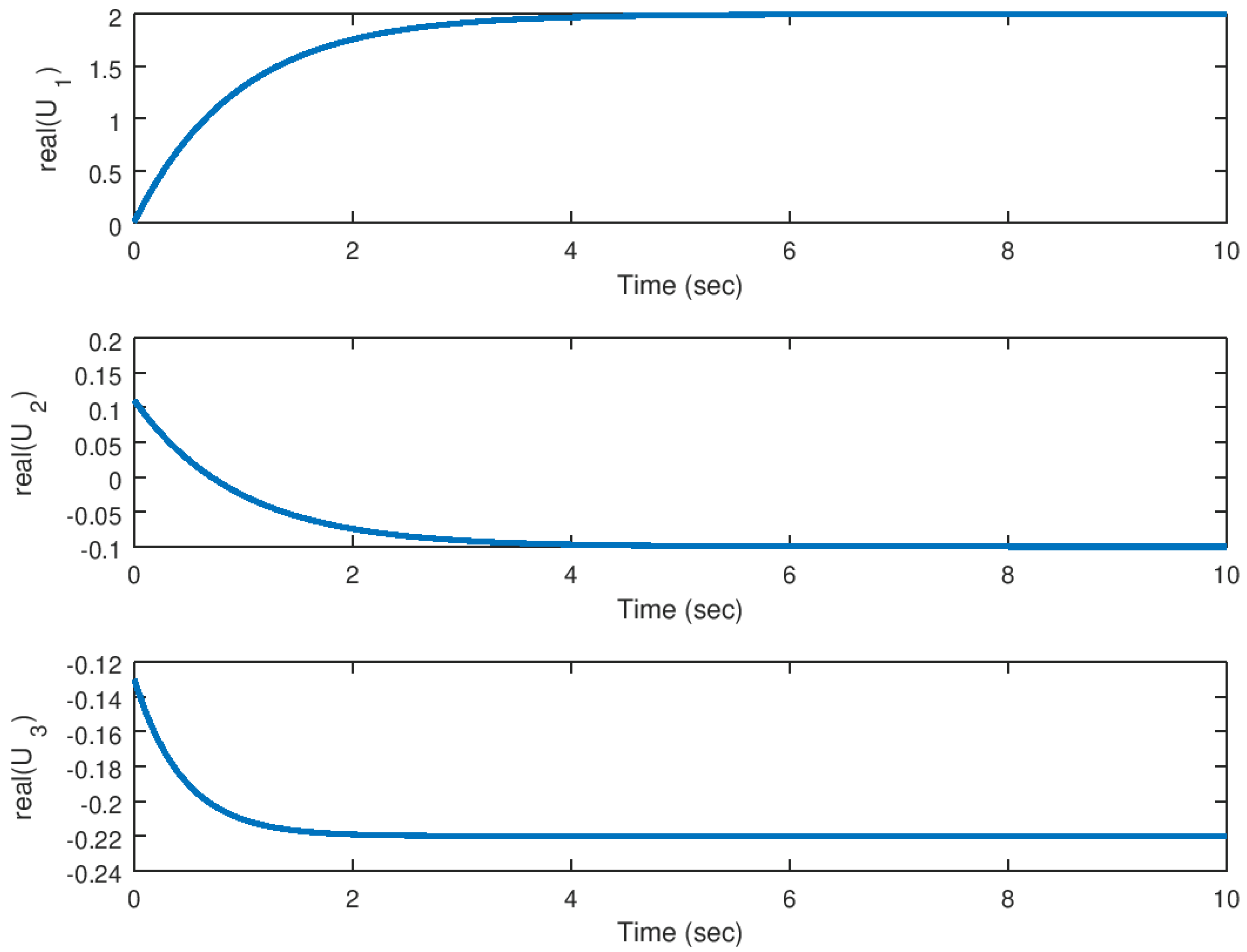
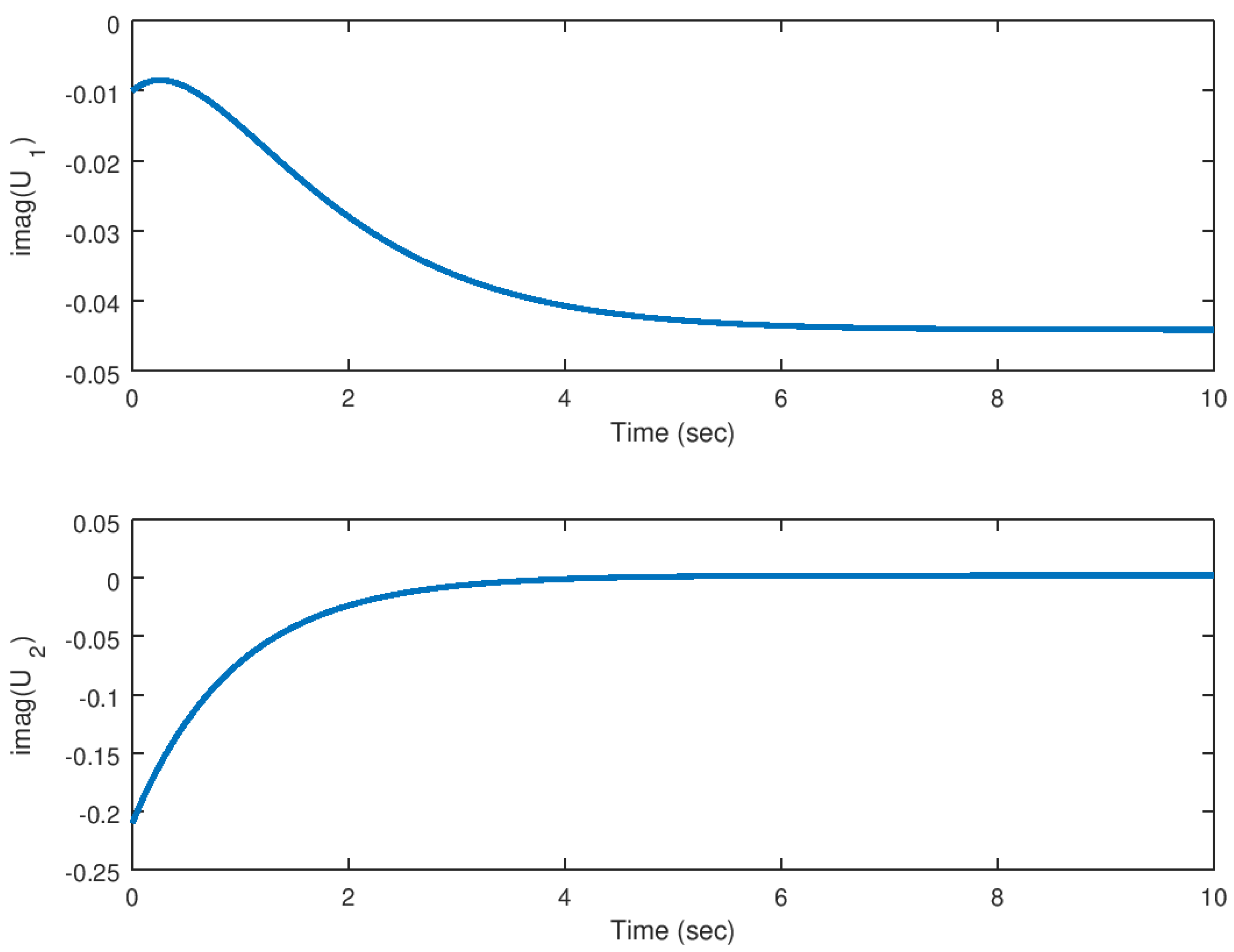
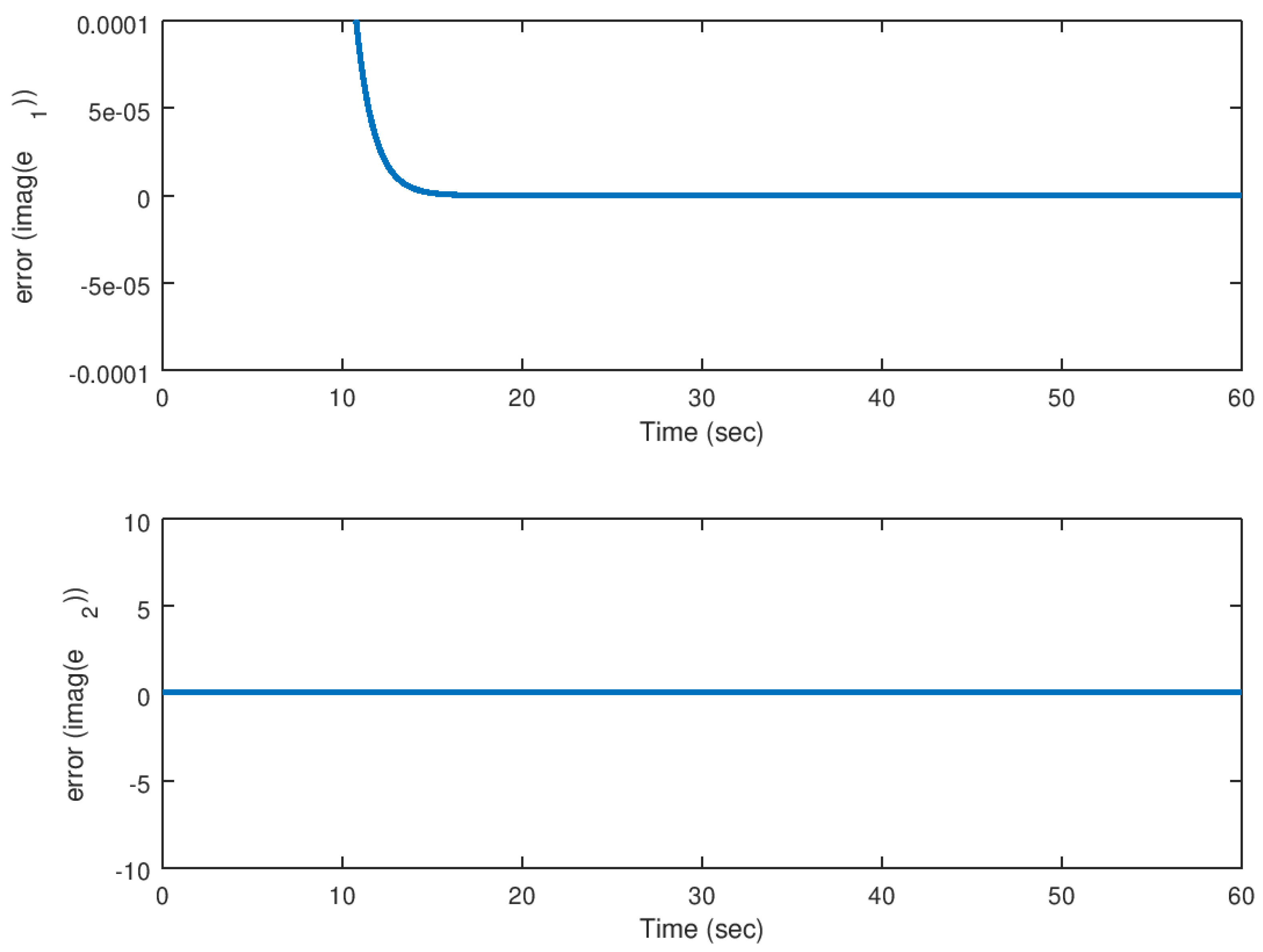
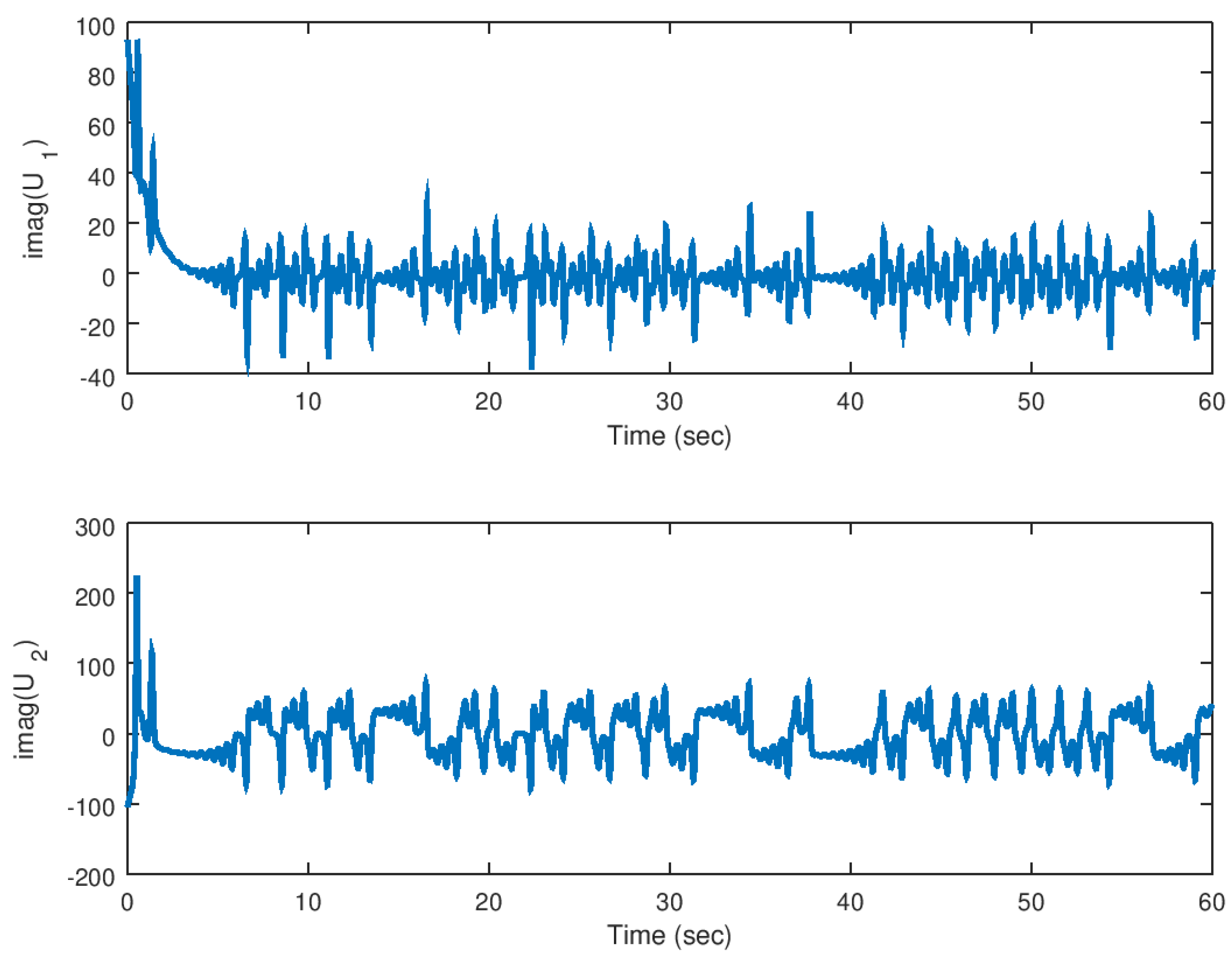
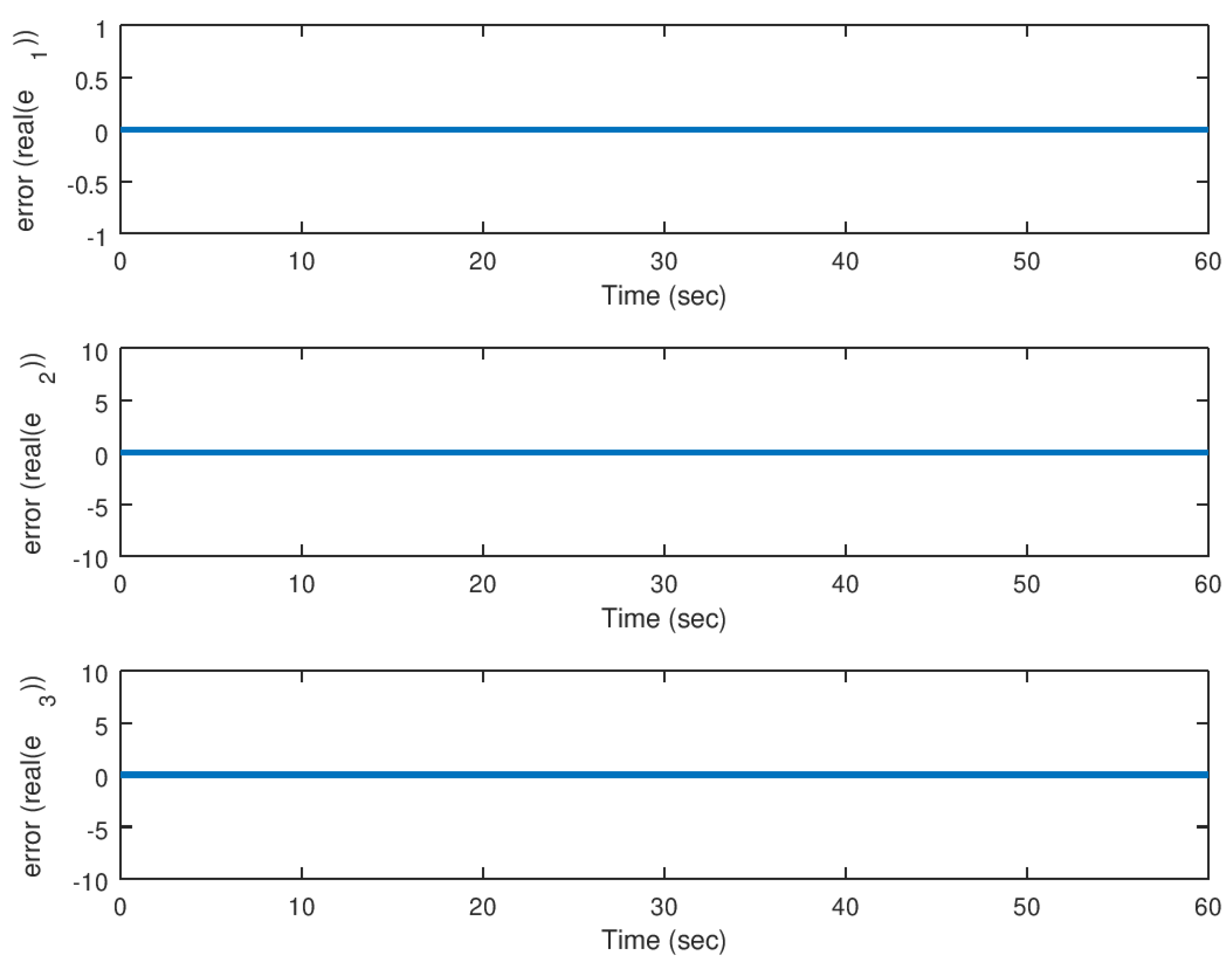
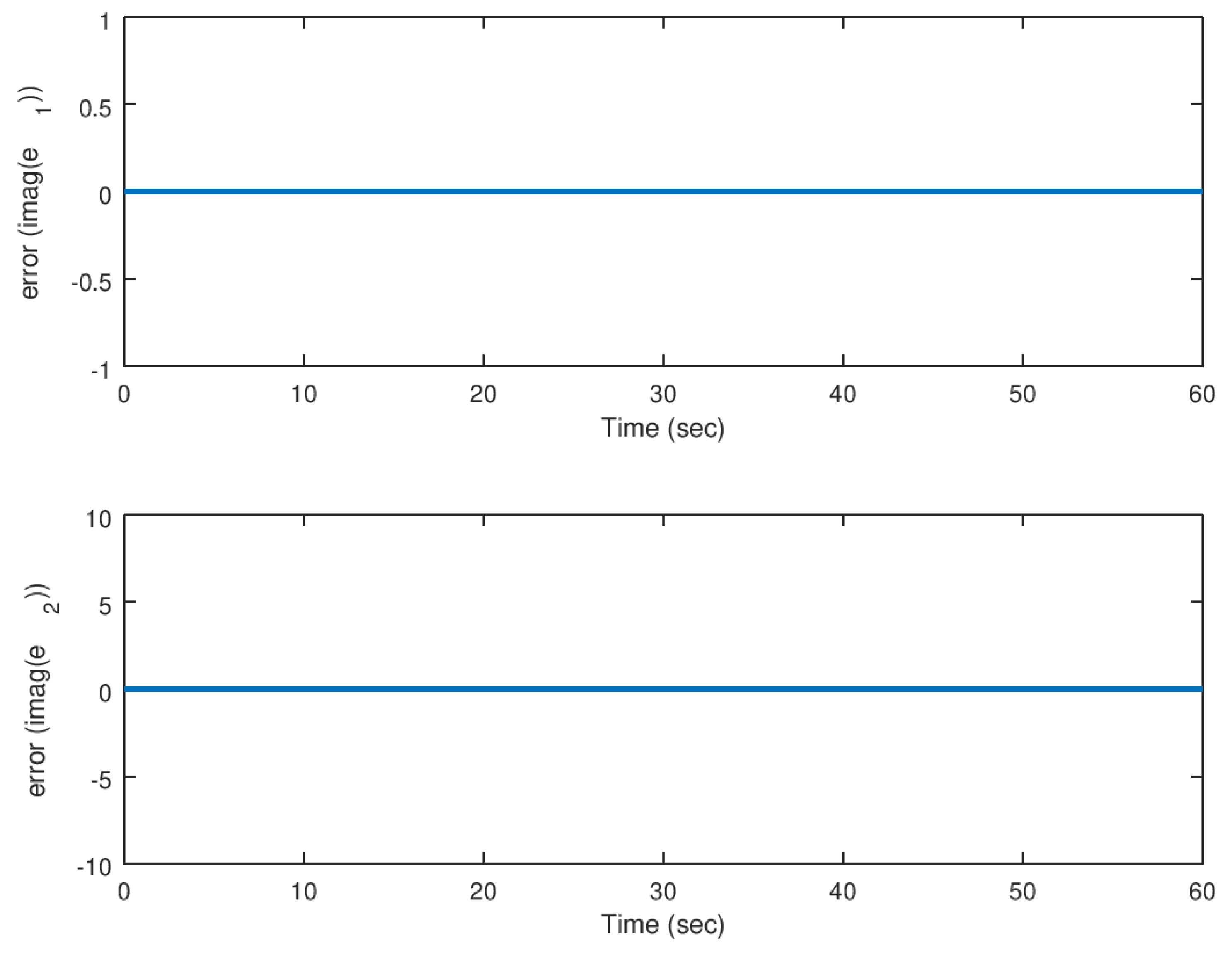
5.1. Experiment 1: Stabilization of the Hidden Attractor
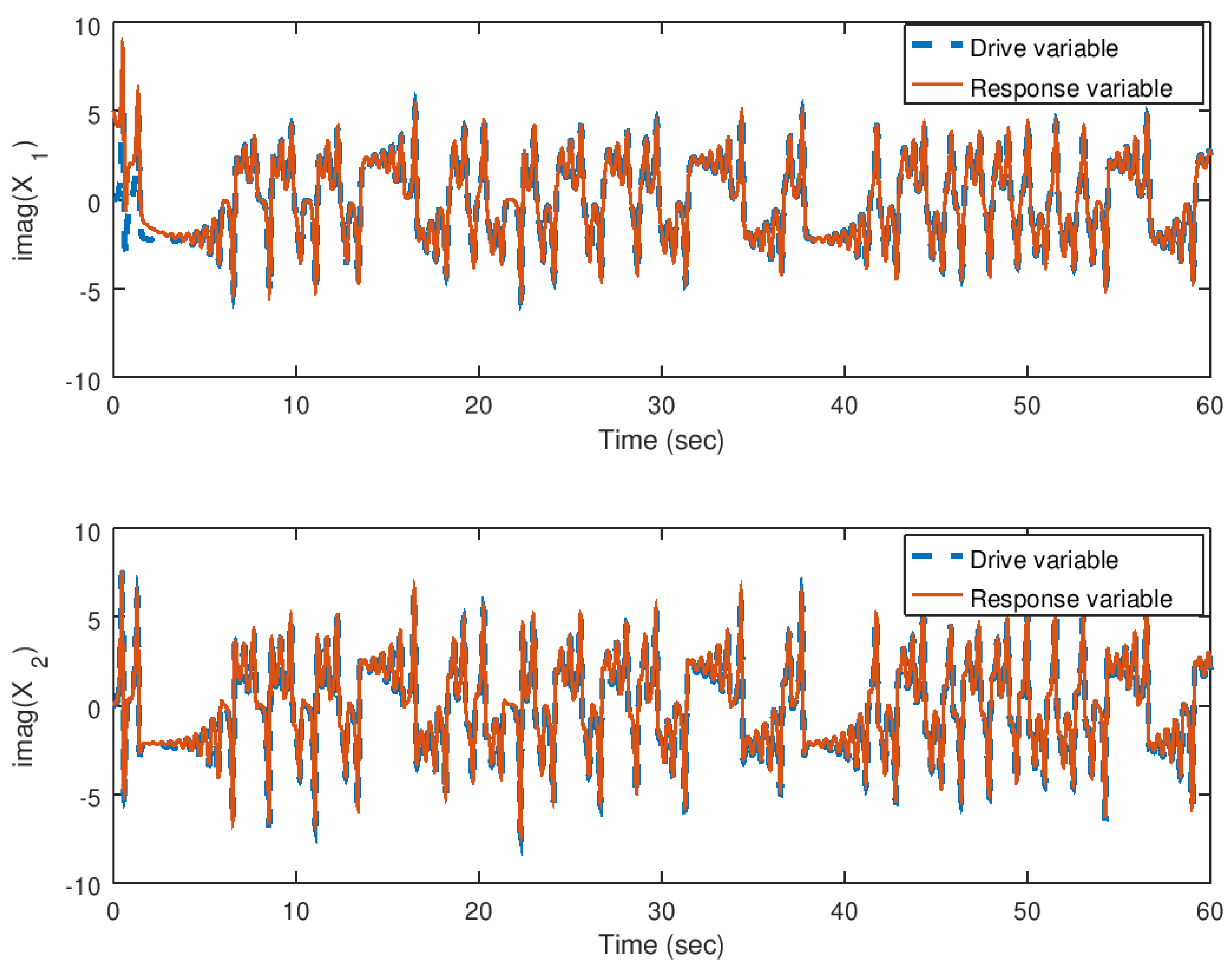
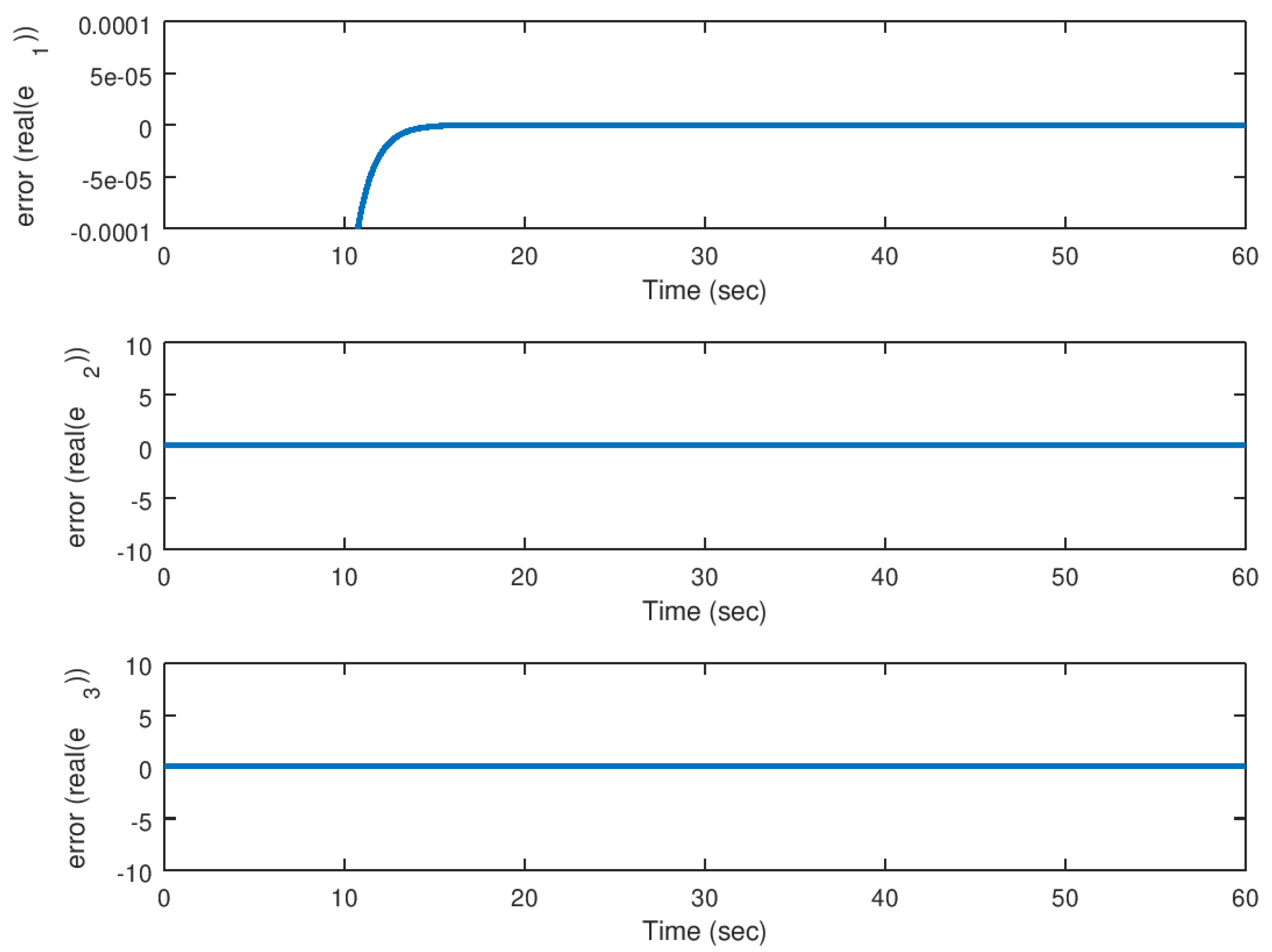
5.2. Experiment 2: Synchronization of the Hidden Attractor with Real Parameter
5.3. Experiment 3: Synchronization of the Hidden Attractor with Complex Value Parameter
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ning, C.Z.; Haken, H. Detuned lasers and the complex Lorenz equations: Subcritical and supercritical Hopf bifurcations. Phys. Rev. A 1990, 41, 3826–3837. [Google Scholar] [CrossRef]
- Fowler, A.; Gibbon, J.; McGuinness, M. The real and complex Lorenz equations and their relevance to physical systems. Phys. D Nonlinear Phenom. 1983, 7, 126–134. [Google Scholar] [CrossRef]
- Clerc, M.; Coullet, P.; Tirapegui, E. The Maxwell-Bloch description of 1/1 resonances. Opt. Commun. 1999, 167, 159–164. [Google Scholar] [CrossRef]
- Cang, S.; Li, Y.; Xue, W.; Chen, Z. Conservative chaos and invariant tori in the modified Sprott A system. Nonlinear Dyn. 2020, 99, 1699–1708. [Google Scholar] [CrossRef]
- Qi, G.; Hu, J.; Wang, Z. Modeling of a Hamiltonian conservative chaotic system and its mechanism routes from periodic to quasiperiodic, chaos and strong chaos. Appl. Math. Model. 2020, 78, 350–365. [Google Scholar] [CrossRef]
- Ning, C.Z.; Haken, H. Geometrical phase and amplitude accumulations in dissipative systems with cyclic attractors. Phys. Rev. Lett. 1992, 68, 2109–2112. [Google Scholar] [CrossRef]
- Clerc, M.; Coullet, P.; Tirapegui, E. Lorenz Bifurcation: Instabilities in Quasireversible Systems. Phys. Rev. Lett. 1999, 83, 3820–3823. [Google Scholar] [CrossRef] [Green Version]
- Zheng, S. Stability of uncertain impulsive complex-variable chaotic systems with time-varying delays. ISA Trans. 2015, 58, 20–26. [Google Scholar]
- Yadav, V.K.; Kumar, R.; Leung, A.; Das, S. Dual phase and dual anti-phase synchronization of fractional order chaotic systems in real and complex variables with uncertainties. Chin. J. Phys. 2019, 57, 282–308. [Google Scholar]
- Zheng, S. Synchronization analysis of time delay complex-variable chaotic systems with discontinuous coupling. J. Frankl. Inst. 2016, 353, 1460–1477. [Google Scholar]
- Sun, J.; Deng, W.; Cui, G.; Wang, Y. Real combination synchronization of three fractional-order complex-variable chaotic systems. Optik 2016, 127, 11460–11468. [Google Scholar] [CrossRef]
- Yadav, V.K.; Shukla, V.K.; Das, S. Exponential synchronization of fractional-order complex chaotic systems and its application. Chaos Solitons Fractals 2021, 147, 110937. [Google Scholar] [CrossRef]
- Cui, L.; Luo, W.; Ou, Q. Analysis of basins of attraction of new coupled hidden attractor system. Chaos Solitons Fractals 2021, 146, 110913. [Google Scholar] [CrossRef]
- Wu, Q.; Hong, Q.; Liu, X.; Wang, X.; Zeng, Z. A novel amplitude control method for constructing nested hidden multi-butterfly and multiscroll chaotic attractors. Chaos Solitons Fractals 2020, 134, 109727. [Google Scholar] [CrossRef]
- Wang, N.; Zhang, G.; Kuznetsov, N.; Bao, H. Hidden attractors and multistability in a modified Chua’s circuit. Commun. Nonlinear Sci. Numer. Simul. 2021, 92, 105494. [Google Scholar] [CrossRef]
- Liu, T.; Yan, H.; Banerjee, S.; Mou, J. A fractional-order chaotic system with hidden attractor and self-excited attractor and its DSP implementation. Chaos Solitons Fractals 2021, 145, 110791. [Google Scholar] [CrossRef]
- Danca, M.F.; Lampart, M. Hidden and self-excited attractors in a heterogeneous Cournot oligopoly model. Chaos Solitons Fractals 2021, 142, 110371. [Google Scholar] [CrossRef]
- Jahanshahi, H.; Yousefpour, A.; Munoz-Pacheco, J.M.; Moroz, I.; Wei, Z.; Castillo, O. A new multi-stable fractional-order four-dimensional system with self-excited and hidden chaotic attractors: Dynamic analysis and adaptive synchronization using a novel fuzzy adaptive sliding mode control method. Appl. Soft Comput. 2020, 87, 105943. [Google Scholar] [CrossRef]
- Vaidyanathan, S.; Sambas, A.; Azar, A.T.; Singh, S. Chapter 9—A new multistable plasma torch chaotic jerk system, its dynamical analysis, active backstepping control, and circuit design. In Backstepping Control of Nonlinear Dynamical Systems; Advances in Nonlinear Dynamics and Chaos (ANDC); Vaidyanathan, S., Azar, A.T., Eds.; Academic Press: Cambridge, MA, USA, 2021; pp. 191–214. [Google Scholar]
- Vaidyanathan, S.; Sambas, A.; Azar, A.T.; Serrano, F.E.; Fekik, A. Chapter 8—A new thermally excited chaotic jerk system, its dynamical analysis, adaptive backstepping control, and circuit simulation. In Backstepping Control of Nonlinear Dynamical Systems; Advances in Nonlinear Dynamics and Chaos (ANDC); Vaidyanathan, S., Azar, A.T., Eds.; Academic Press: Cambridge, MA, USA, 2021; pp. 165–189. [Google Scholar]
- Mondal, J.; Chatterjee, S. Controlling self-excited vibration of a nonlinear beam by nonlinear resonant velocity feedback with time-delay. Int. J. Non-Linear Mech. 2021, 131, 103684. [Google Scholar] [CrossRef]
- Yu, C.; Jiang, J.; Zhen, Z.; Bhatia, A.K.; Wang, S. Adaptive backstepping control for air-breathing hypersonic vehicle subject to mismatched uncertainties. Aerosp. Sci. Technol. 2020, 107, 106244. [Google Scholar] [CrossRef]
- Deng, W.; Yao, J.; Wang, Y.; Yang, X.; Chen, J. Output feedback backstepping control of hydraulic actuators with valve dynamics compensation. Mech. Syst. Signal Process. 2021, 158, 107769. [Google Scholar] [CrossRef]
- Huang, J.; Lv, Z.; Sun, J.Q. Optimal full-state feedback observer integrated backstepping control of chemical processes with unknown internal dynamics. ISA Trans. 2021, in press. [Google Scholar] [CrossRef] [PubMed]
- Kharabian, B.; Mirinejad, H. Synchronization of Rossler chaotic systems via hybrid adaptive backstepping/sliding mode control. Results Control. Optim. 2021, 4, 100020. [Google Scholar] [CrossRef]
- Zheng, K.; Zhang, Q.; Hu, Y.; Wu, B. Design of fuzzy system-fuzzy neural network-backstepping control for complex robot system. Inf. Sci. 2021, 546, 1230–1255. [Google Scholar] [CrossRef]
- Liu, J.; Liu, S. Complex modified function projective synchronization of complex chaotic systems with known and unknown complex parameters. Appl. Math. Model. 2017, 48, 440–450. [Google Scholar] [CrossRef]
- Sun, B.; Li, M.; Zhang, F.; Wang, H.; Liu, J. The characteristics and self-time-delay synchronization of two-time-delay complex Lorenz system. J. Frankl. Inst. 2019, 356, 334–350. [Google Scholar] [CrossRef]
- Leonov, G.; Kuznetsov, N.; Mokaev, T. Hidden attractor and homoclinic orbit in Lorenz-like system describing convective fluid motion in rotating cavity. Commun. Nonlinear Sci. Numer. Simul. 2015, 28, 166–174. [Google Scholar] [CrossRef] [Green Version]
- Mohanty, N.P.; Dey, R.; Roy, B.K. A New 3-D Memristive Time-delay Chaotic System with Multi-scroll and Hidden Attractors. IFAC-PapersOnLine 2018, 51, 580–585. [Google Scholar]
- Yu, H.; Wang, J.; Deng, B.; Wei, X.; Che, Y.; Wong, Y.; Chan, W.; Tsang, K. Adaptive backstepping sliding mode control for chaos synchronization of two coupled neurons in the external electrical stimulation. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 1344–1354. [Google Scholar] [CrossRef]
- Alimi, M.; Rhif, A.; Rebai, A.; Vaidyanathan, S.; Azar, A.T. Chapter 13—Optimal adaptive backstepping control for chaos synchronization of nonlinear dynamical systems. In Backstepping Control of Nonlinear Dynamical Systems; Advances in Nonlinear Dynamics and Chaos (ANDC); Vaidyanathan, S., Azar, A.T., Eds.; Academic Press: Cambridge, MA, USA, 2021; pp. 291–345. [Google Scholar]
- Njah, A.; Sunday, O. Generalization on the chaos control of 4-D chaotic systems using recursive backstepping nonlinear controller. Chaos Solitons Fractals 2009, 41, 2371–2376. [Google Scholar] [CrossRef]
- Zambrano-Serrano, E.; Anzo-Hernández, A. A novel antimonotic hyperjerk system: Analysis, synchronization and circuit design. Phys. D Nonlinear Phenom. 2021, 424, 132927. [Google Scholar] [CrossRef]
- Azar, A.T.; Serrano, F.E.; Vaidyanathan, S.; Kamal, N.A. Chapter 16—Backstepping control and synchronization of chaotic time delayed systems. In Backstepping Control of Nonlinear Dynamical Systems; Advances in Nonlinear Dynamics and Chaos (ANDC); Vaidyanathan, S., Azar, A.T., Eds.; Academic Press: Cambridge, MA, USA, 2021; pp. 407–424. [Google Scholar]
- Singh, S.; Mathpal, S.; Azar, A.T.; Vaidyanathan, S.; Kamal, N.A. Chapter 17—Multi-switching synchronization of nonlinear hyperchaotic systems via backstepping control. In Backstepping Controlof Nonlinear Dynamical Systems; Advances in Nonlinear Dynamics and Chaos (ANDC); Vaidyanathan, S., Azar, A.T., Eds.; Academic Press: Cambridge, MA, USA, 2021; pp. 425–447. [Google Scholar]
- Shukla, M.K.; Sharma, B. Backstepping based stabilization and synchronization of a class of fractional order chaotic systems. Chaos Solitons Fractals 2017, 102, 274–284. [Google Scholar] [CrossRef]
- Yu, J.; Shi, P.; Liu, J.; Lin, C. Neuroadaptive Finite-Time Control for Nonlinear MIMO Systems with Input Constraint. IEEE Trans. Cybern. 2020, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Fu, C.; Wang, Q.G.; Yu, J.; Lin, C. Neural Network-Based Finite-Time Command Filtering Control for Switched Nonlinear Systems With Backlash-Like Hysteresis. IEEE Trans. Neural Netw. Learn. Syst. 2020, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Patra, A.; Altshuler, B.L.; Yuzbashyan, E.A. Driven-dissipative dynamics of atomic ensembles in a resonant cavity: Quasiperiodic route to chaos and chaotic synchronization. Ann. Phys. 2020, 417, 168106. [Google Scholar] [CrossRef] [Green Version]
- Korneev, I.; Semenov, V.; Slepnev, A.; Vadivasova, T. Complete synchronization of chaos in systems with nonlinear inertial coupling. Chaos Solitons Fractals 2021, 142, 110459. [Google Scholar] [CrossRef]
- Mahmoud, E.E.; Trikha, P.; Jahanzaib, L.S.; Eshmawi, A.A.; Matoog, R. Chaos control and Penta-compound combination anti-synchronization on a novel fractional chaotic system with analysis and application. Results Phys. 2021, 24, 104130. [Google Scholar] [CrossRef]
- Tai, W.; Teng, Q.; Zhou, Y.; Zhou, J.; Wang, Z. Chaos synchronization of stochastic reaction-diffusion time-delay neural networks via non-fragile output-feedback control. Appl. Math. Comput. 2019, 354, 115–127. [Google Scholar] [CrossRef]
- Tang, Y.; Li, Q.; Dong, W.; Hu, M.; Zeng, R. Optical chaotic communication using correlation demodulation between two synchronized chaos lasers. Opt. Commun. 2021, 127232. [Google Scholar] [CrossRef]
- Al Bayati, B.M.; Ahmad, A.K.; Al Naimee, K.A. Effect of control parameters on chaos synchronization by means of optical feedback. Opt. Commun. 2020, 472, 126032. [Google Scholar] [CrossRef]
- Deepika, D. Hyperbolic uncertainty estimator based fractional order sliding mode control framework for uncertain fractional order chaos stabilization and synchronization. ISA Trans. 2021. [Google Scholar] [CrossRef]
- Pillai, N.; Craig, M.; Dokoumetzidis, A.; Schwartz, S.L.; Bies, R.; Freedman, I. Chaos synchronization and Nelder-Mead search for parameter estimation in nonlinear pharmacological systems: Estimating tumor antigenicity in a model of immunotherapy. Prog. Biophys. Mol. Biol. 2018, 139, 23–30. [Google Scholar] [CrossRef] [PubMed]
- Haddad, W.; Chellaboina, V. Nonlinear Dynamical Systems and Control, a Lyapunov Based Approach; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Munmuangsaen, B.; Srisuchinwong, B. A hidden chaotic attractor in the classical Lorenz system. Chaos Solitons Fractals 2018, 107, 61–66. [Google Scholar] [CrossRef]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Munoz-Pacheco, J.M.; Volos, C.; Serrano, F.E.; Jafari, S.; Kengne, J.; Rajagopal, K. Stabilization and Synchronization of a Complex Hidden Attractor Chaotic System by Backstepping Technique. Entropy 2021, 23, 921. https://doi.org/10.3390/e23070921
Munoz-Pacheco JM, Volos C, Serrano FE, Jafari S, Kengne J, Rajagopal K. Stabilization and Synchronization of a Complex Hidden Attractor Chaotic System by Backstepping Technique. Entropy. 2021; 23(7):921. https://doi.org/10.3390/e23070921
Chicago/Turabian StyleMunoz-Pacheco, Jesus M., Christos Volos, Fernando E. Serrano, Sajad Jafari, Jacques Kengne, and Karthikeyan Rajagopal. 2021. "Stabilization and Synchronization of a Complex Hidden Attractor Chaotic System by Backstepping Technique" Entropy 23, no. 7: 921. https://doi.org/10.3390/e23070921
APA StyleMunoz-Pacheco, J. M., Volos, C., Serrano, F. E., Jafari, S., Kengne, J., & Rajagopal, K. (2021). Stabilization and Synchronization of a Complex Hidden Attractor Chaotic System by Backstepping Technique. Entropy, 23(7), 921. https://doi.org/10.3390/e23070921







