An Overview of Geometrical Optics Restricted Quantum Key Distribution
Abstract
:1. Introduction
2. Quantum Key Distribution (QKD)
2.1. BB84
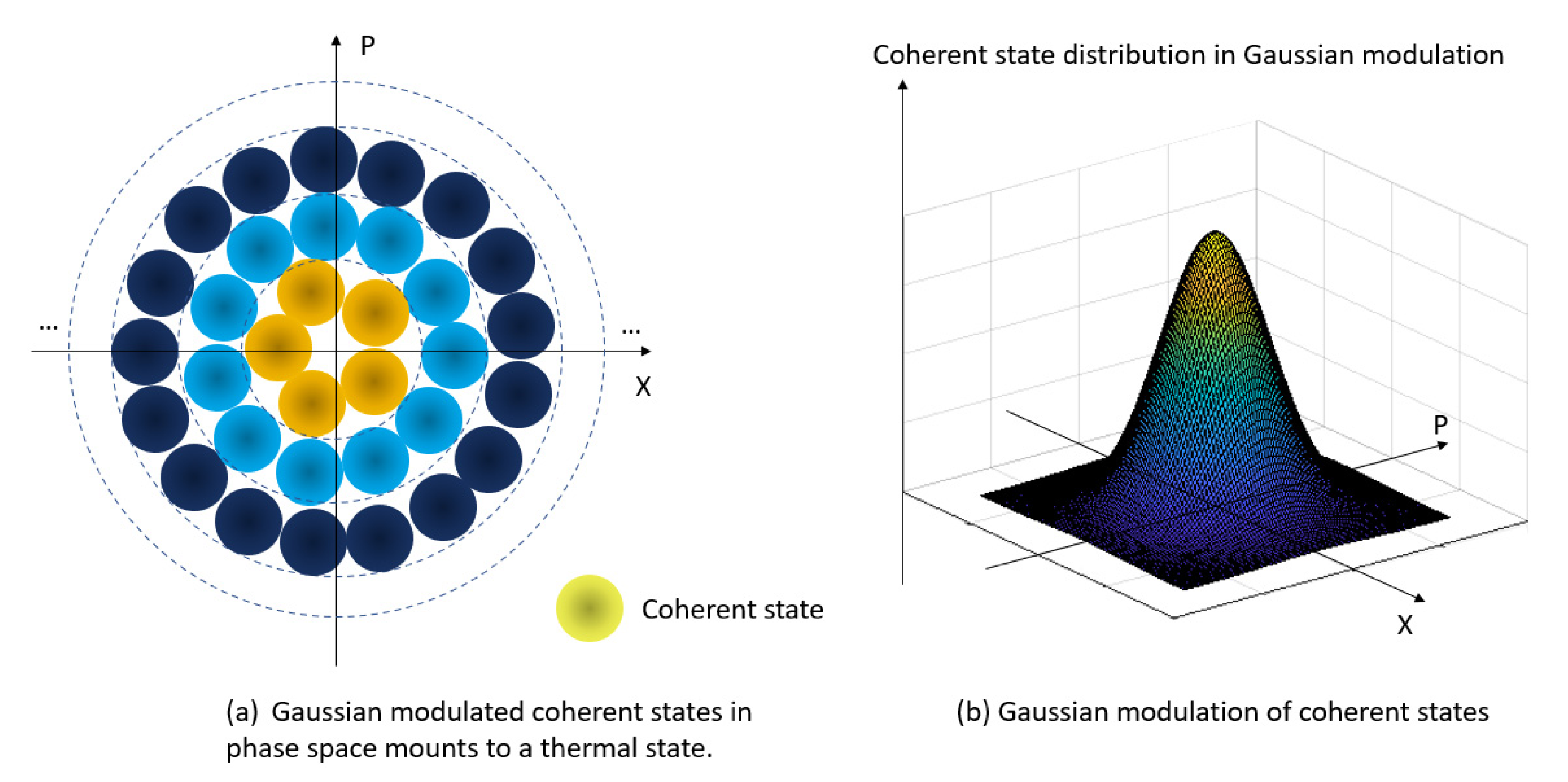
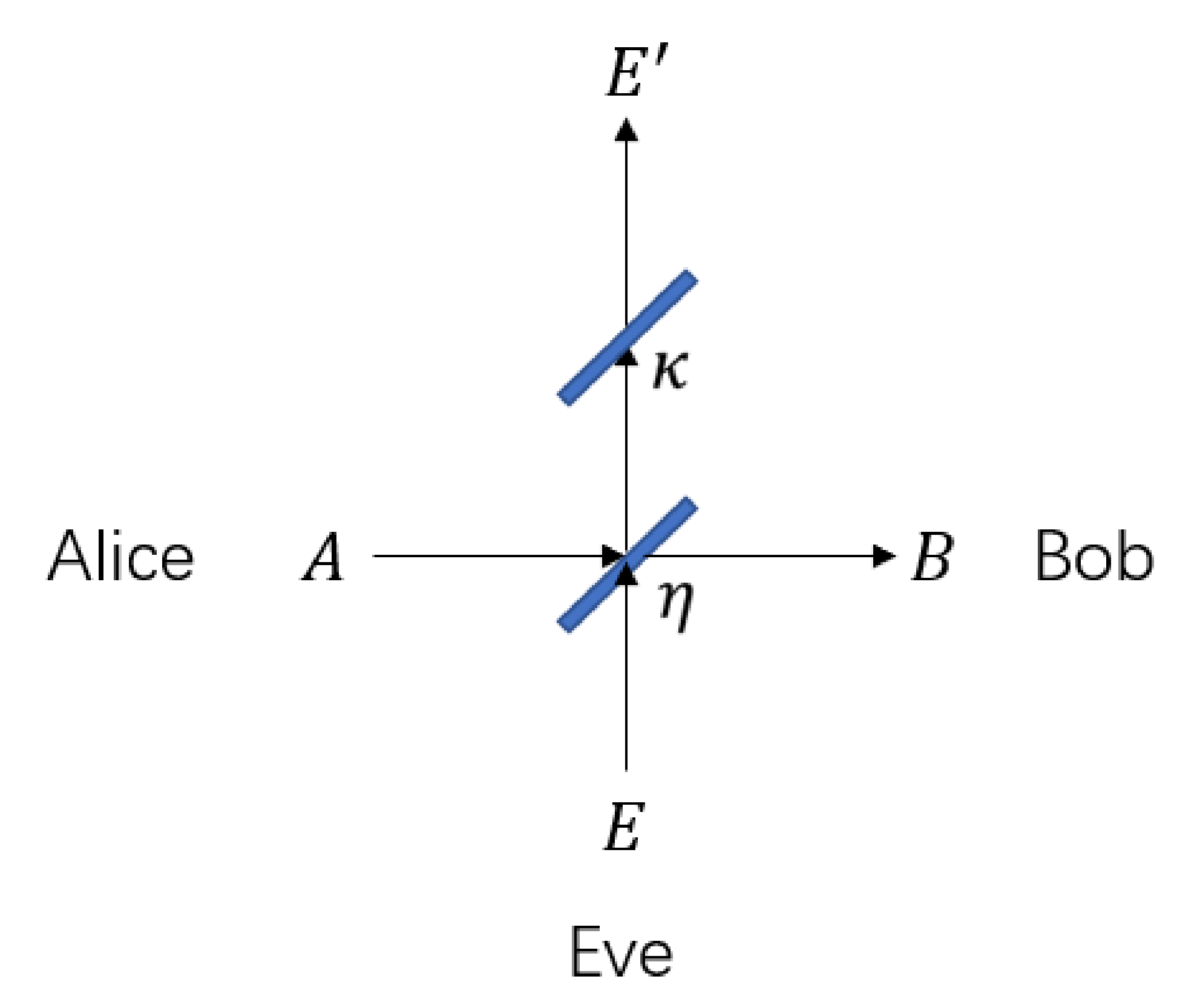
2.2. GG02
3. Geometrical Optics Restricted Model
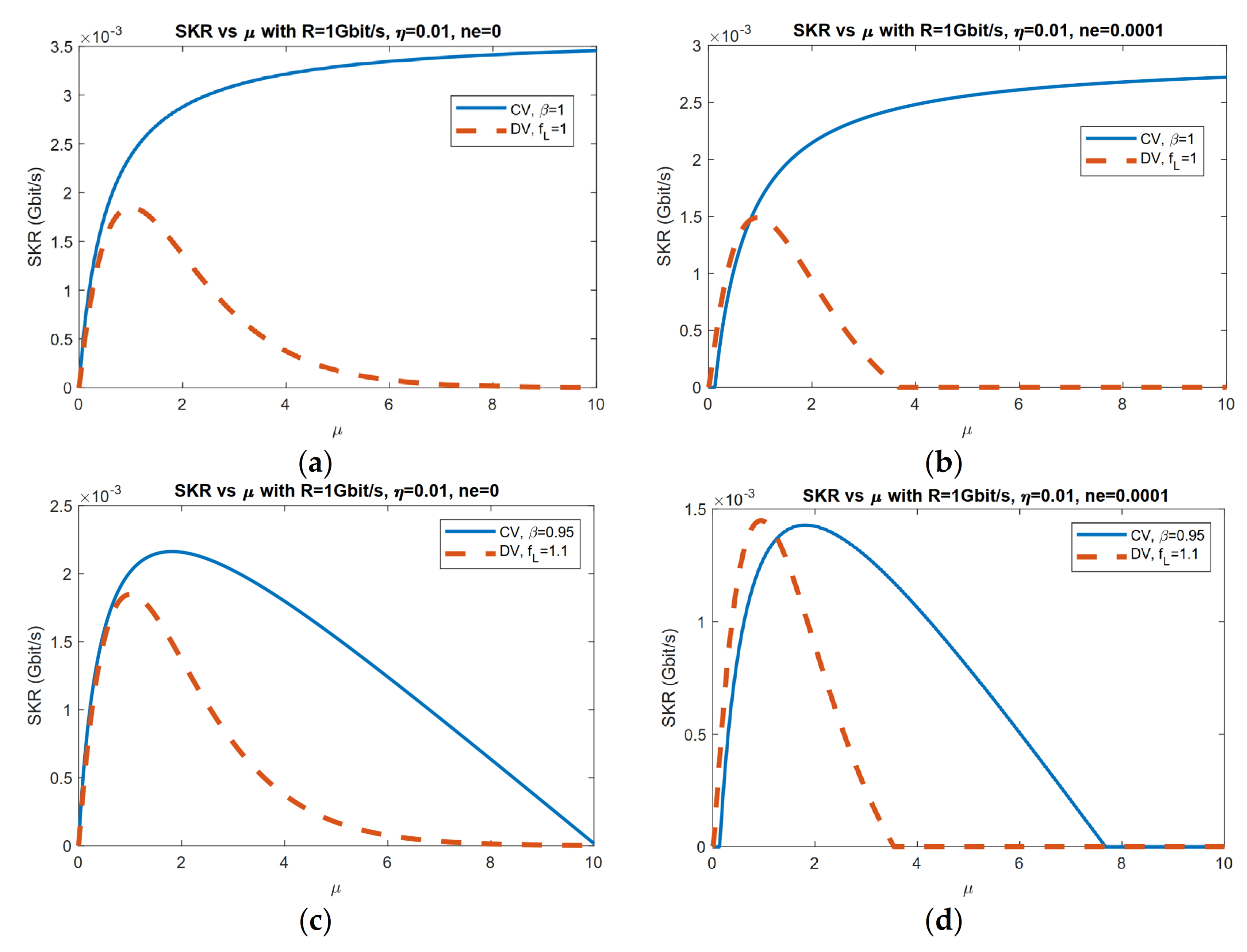
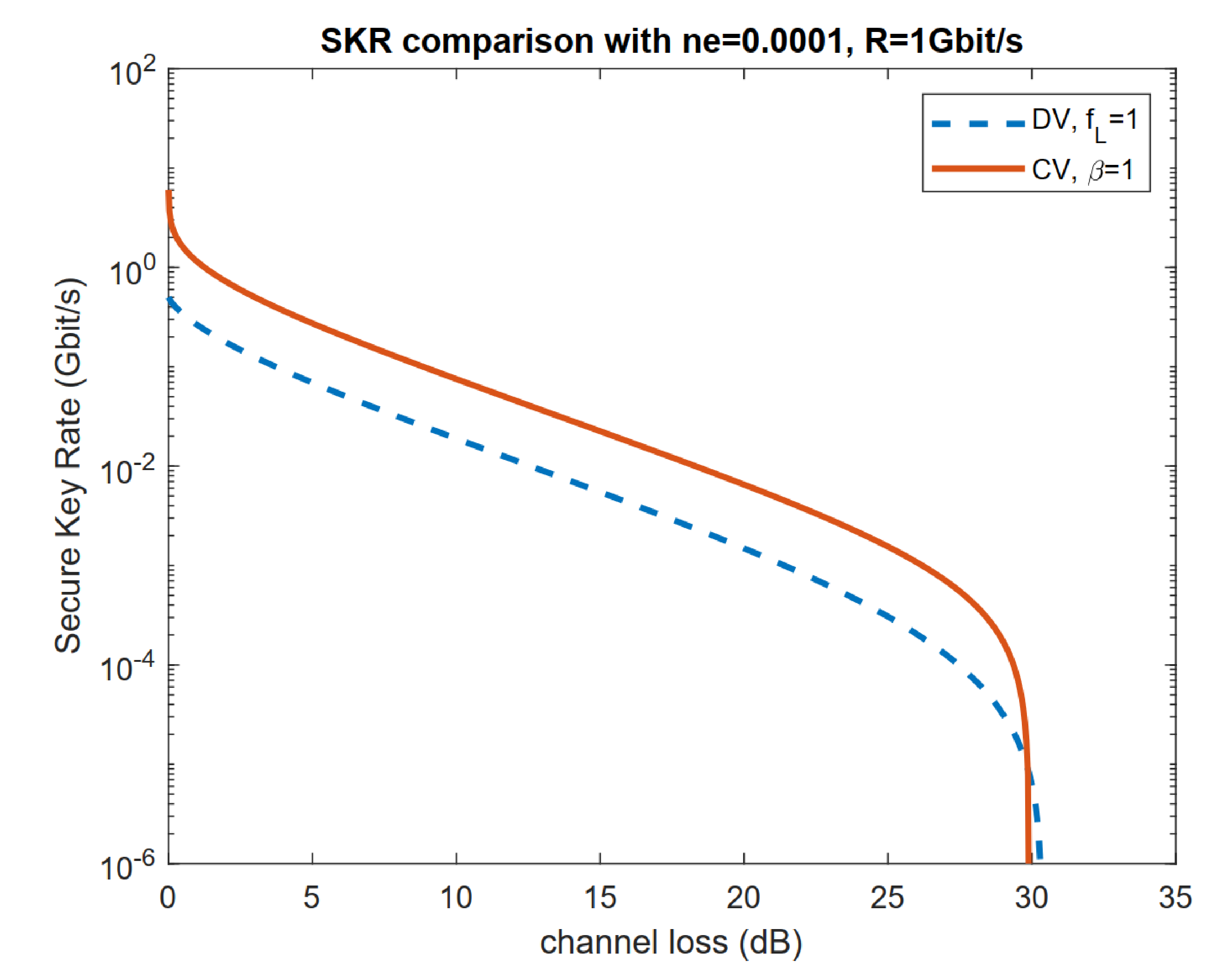
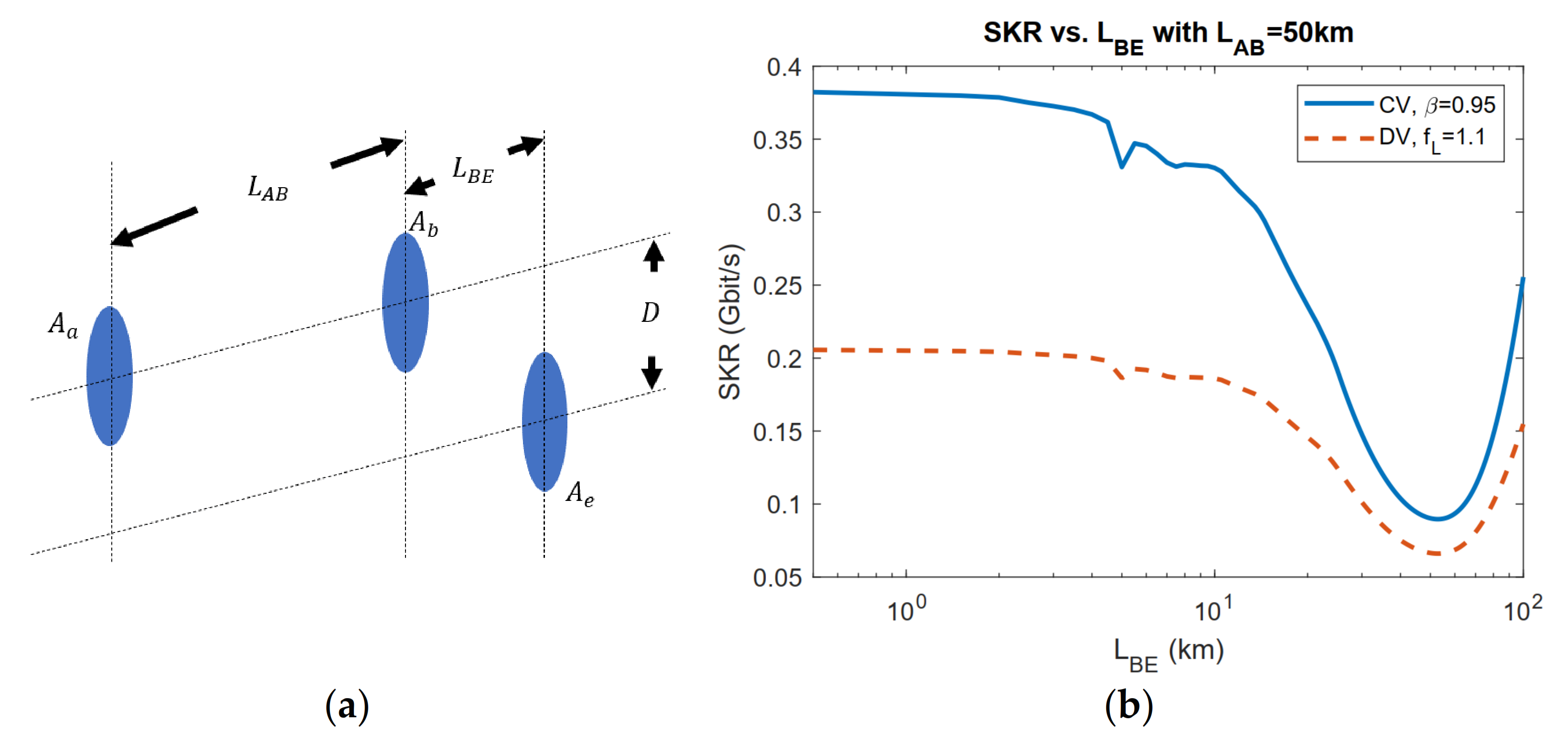
3.1. Application of Geometrical Optics Restricted Model: Limited Aperture Size Analysis
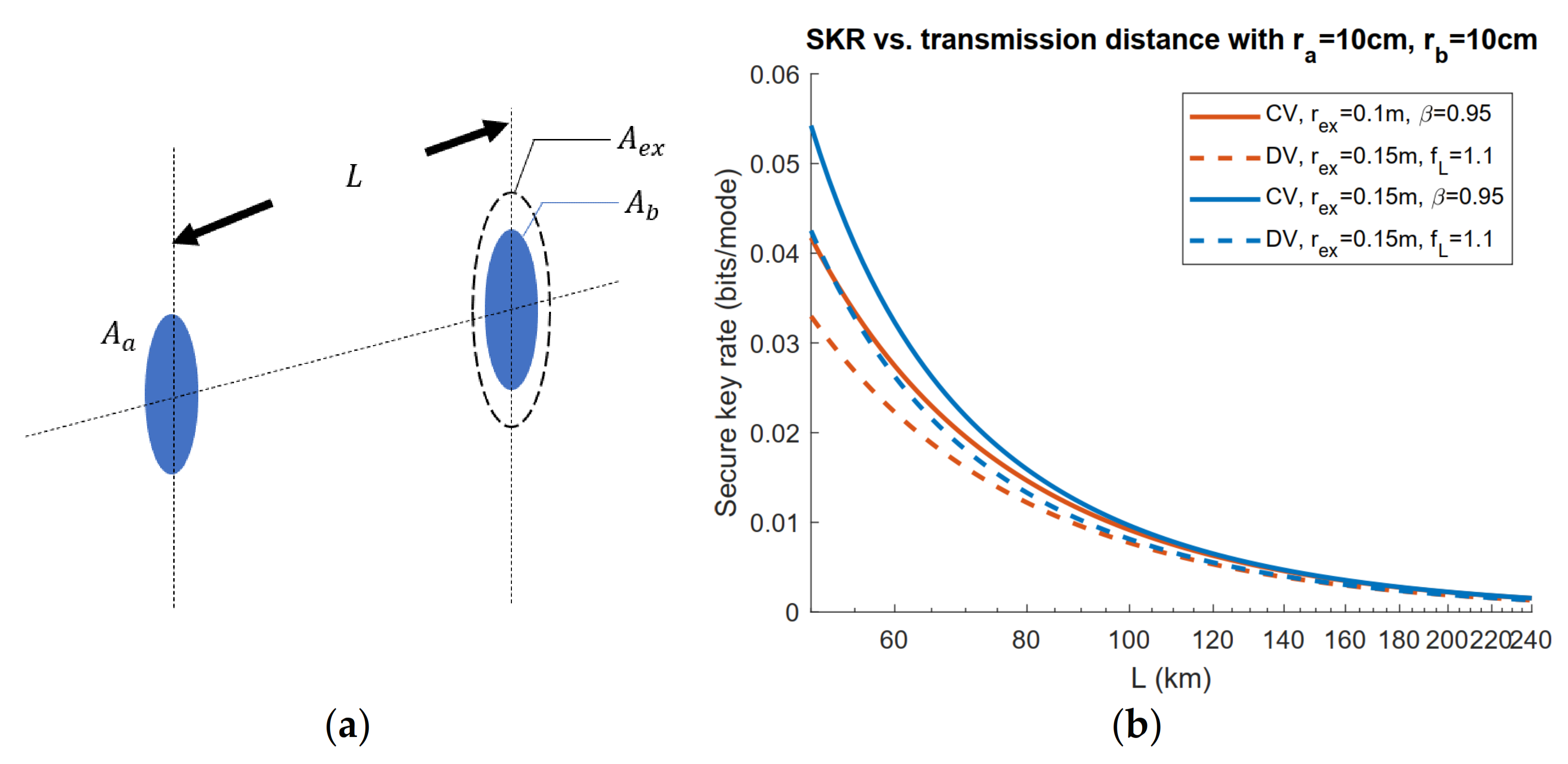
3.2. Application of Geometrical Optics Restricted Model: Exclusion Zone Analysis
4. Discussion
Funding
Acknowledgments
Conflicts of Interest
References
- Shannon, C.E. Communication theory of secrecy systems. Bell Syst. Tech. J. 1949, 28, 656–715. [Google Scholar] [CrossRef]
- Bennett, C.H.; Gilles, B. Quantum cryptography: Public key distribution and coin tossing. Comput. Sci. 2014, 560, 7–11. [Google Scholar] [CrossRef]
- Bennett, C.H. Quantum cryptography using any two nonorthogonal states. Phys. Rev. Lett. 1992, 21, 3121. [Google Scholar] [CrossRef] [PubMed]
- Bennett, C.H.; Gilles, B.; Mermin, N.D. Quantum cryptography without Bell’s theorem. Phys. Rev. Lett. 1992, 68, 557. [Google Scholar] [CrossRef] [PubMed]
- Ekert, A.K. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 1991, 67, 661. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mayers, D.; Yao, A. Quantum Cryptography with Imperfect Apparatus. In Proceedings of the 39th Annual Symposium on Foundations of Computer Science (Cat. No. 98CB36280), Palo Alto, CA, USA, 8–11 November 1998. [Google Scholar]
- Katz, J.; Yehuda, L. Introduction to Modern Cryptography; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Nyquist, H. Regeneration theory. Bell Syst. Tech. J. 1932, 11, 126–147. [Google Scholar] [CrossRef]
- Nyquist, H. Certain factors affecting telegraph speed. Bell Syst. Tech. J. 1924, 3, 324–346. [Google Scholar] [CrossRef]
- Nyquist, H. Certain topics in telegraph transmission theory. Trans. AIEE 1928, 47, 617–644, Reprint as classic paper in Proc. IEEE 2002, 90, 280–305. [Google Scholar] [CrossRef]
- Hartley, R.V.L. Relations of Carrier and Side-Bands in Radio Transmission. Proc. IRE 1923, 11, 34–56. [Google Scholar] [CrossRef]
- Hartley, R.V.L. Transmission of Information. Bell Syst. Tech. J. 1928, 7, 535–563. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef] [Green Version]
- Data Encryption Standard. Available online: https://telluur.com/utwente/master/SyS%20-%20System%20Security/2018/Aanvullende%20docs/Data_Encryption_Standard.pdf (accessed on 28 July 2021).
- Advanced Encryption Standard. Available online: https://telluur.com/utwente/master/SyS%20-%20System%20Security/2018/Aanvullende%20docs/AES.pdf (accessed on 28 July 2021).
- Rivest, R.L.; Shamir, A.; Adleman, L. A Method for Obtaining Digital Signatures and Public-Key Cryptosystems. Commun. ACM. 1978, 21, 120–126. [Google Scholar] [CrossRef]
- Diffie, W.; Hellman, M. New Directions in Cryptography (PDF). IEEE Trans. Inf. Theory 1976, 6, 644–654. [Google Scholar] [CrossRef] [Green Version]
- Preskill, J. Quantum Computing in the NISQ era and beyond. Quantum 2018, 2, 79. [Google Scholar] [CrossRef]
- Mavroeidis, V.; Kamer, V.; Mateusz, D.Z.; Audun, J. The impact of quantum computing on present cryptography. Int. J. Adv. Comput. Sci. Appl. 2018, 9, 405–414. [Google Scholar] [CrossRef] [Green Version]
- Shor, P.W. Algorithms for quantum computation: Discrete logarithms and factoring. In Proceedings of the 35th Annual Symposium on Foundations of Computer Science, Washington, DC, USA, 20–22 November 1994. [Google Scholar]
- Grover, L.K. A fast quantum mechanical algorithm for database search. In Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing, Philadelphia, PA, USA, 22–24 May 1996; pp. 212–219. [Google Scholar]
- Barrett, J.; Hardy, L.L.; Kent, A.A. No Signaling and Quantum Key Distribution. Phys. Rev. Lett. 2005, 95, 010503. [Google Scholar] [CrossRef] [Green Version]
- Pironio, S.; Acín, A.; Brunner, N.; Gisin, N.; Massar, S.; Scarani, V. Device-independent quantum key distribution secure against collective attacks. New J. Phys. 2009, 11, 045021. [Google Scholar] [CrossRef]
- McKague, M. Device independent quantum key distribution secure against coherent attacks with memoryless meas-urement devices. New J. Phys. 2009, 11, 103037. [Google Scholar] [CrossRef]
- Cerf, N.J.; Lévy, M.; Van Assche, G. Quantum distribution of Gaussian keys using squeezed states. Phys. Rev. A 2001, 63, 052311. [Google Scholar] [CrossRef] [Green Version]
- Grosshans, F.; Grangier, P. Continuous Variable Quantum Cryptography Using Coherent States. Phys. Rev. Lett. 2002, 88, 057902. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.-B. Decoy-state protocol for quantum cryptography with four different intensities of coherent light. Phys. Rev. A 2005, 72, 012322. [Google Scholar] [CrossRef] [Green Version]
- Lo, H.-K.; Ma, X.; Chen, K. Decoy State Quantum Key Distribution. Phys. Rev. Lett. 2005, 94, 230504. [Google Scholar] [CrossRef] [Green Version]
- Ma, X.; Qi, B.; Zhao, Y.; Lo, H.-K. Practical decoy state for quantum key distribution. Phys. Rev. A 2005, 72, 012326. [Google Scholar] [CrossRef] [Green Version]
- Mafu, M.; Dudley, A.; Goyal, S.; Giovannini, D.; McLaren, M.; Padgett, M.; Konrad, T.; Petruccione, F.; Lutkenhaus, N.; Forbes, A. Higher-dimensional orbital-angular-momentum-based quantum key distribution with mutually unbiased bases. Phys. Rev. A 2013, 88, 032305. [Google Scholar] [CrossRef] [Green Version]
- Pan, Z.; Cai, J.; Wang, C. Quantum Key Distribution with High Order Fibonacci-like Orbital Angular Momentum States. Int. J. Theor. Phys. 2017, 56, 2622–2634. [Google Scholar] [CrossRef] [Green Version]
- Djordjevic, I.B. Deep-space and near-Earth optical communications by coded orbital angular momentum (OAM) modulation. Opt. Express 2015, 19, 14277–14289. [Google Scholar] [CrossRef]
- Pan, Z.; Seshadreesan, K.P.; Clark, W.; Adcock, M.R.; Djordjevic, I.B.; Shapiro, J.H.; Guha, S. Secret-Key Distillation across a Quantum Wiretap Channel under Restricted Eavesdropping. Phys. Rev. Appl. 2020, 14, 024044. [Google Scholar] [CrossRef]
- Pan, Z.; Seshadreesan, K.P.; Clark, W.; Adcock, M.R.; Djordjevic, I.B.; Shapiro, J.H.; Guha, S. Secret key distillation over a pure loss quantum wiretap channel under restricted eavesdropping. In Proceedings of the 2019 IEEE International Symposium on Information Theory (ISIT), Paris, France, 7–12 July 2019; pp. 3032–3036. [Google Scholar] [CrossRef]
- Pan, Z.; Djordjevic, I.B. Security of Satellite-Based CV-QKD under Realistic Assumptions. In Proceedings of the 2020 22nd International Conference on Transparent Optical Networks (ICTON), Bari, Italy, 19–23 July 2020; pp. 1–4. [Google Scholar]
- Pan, Z.; Gariano, J.; Djordjevic, I.B. Secret Key Distillation over Satellite-to-satellite Free-space Channel with Eavesdropper Dynamic Positioning. In OSA Advanced Photonics Congress (AP) 2020 (IPR, NP, NOMA, Networks, PVLED, PSC, SPPCom, SOF); The Optical Society: Washington, DC, USA, 2020; p. SpTu3I.4. [Google Scholar]
- Pan, Z.; Djordjevic, I.B. Secret key distillation over satellite-to-satellite free-space optics channel with a lim-ited-sized aperture eavesdropper in the same plane of the legitimate receiver. Opt. Express 2020, 28, 37129–37148. [Google Scholar] [CrossRef] [PubMed]
- Pan, Z.; Gariano, J.; Clark, W.; Djordjevic, I.B. Secret key distillation over realistic satellite-to-satellite free-space channel. In Proceedings of the OSA Quantum 2.0 Conference, Washington, DC, USA, 14–17 September 2020; p. QTh7B.15. [Google Scholar]
- Pan, Z.; Djordjevic, I.B. Secret key distillation over realistic satellite-to-satellite free-space channel: Exclusion zone analysis. arXiv 2020, arXiv:2009.05929. [Google Scholar]
- Pan, Z.; Djordjevic, I.B. Secret Key Distillation over Satellite-to-satellite Free-space Optics Channel with Eaves-dropper Dynamic Positioning. arXiv 2020, arXiv:2012.13865. [Google Scholar]
- Fröhlich, B.; Dynes, J.F.; Lucamarini, M.; Sharpe, A.W.; Yuan, Z.; Shields, A.J. A quantum access network. Nat. Cell Biol. 2013, 501, 69–72. [Google Scholar] [CrossRef] [Green Version]
- Kimble, H.J. The quantum internet. Nat. Cell Biol. 2008, 453, 1023–1030. [Google Scholar] [CrossRef]
- Vallone, G.; Bacco, D.; Dequal, D.; Gaiarin, S.; Luceri, V.; Bianco, G.; Villoresi, P. Experimental Satellite Quantum Communications. Phys. Rev. Lett. 2015, 115, 040502. [Google Scholar] [CrossRef]
- Jian-Yu, S.; Yang, B.; Sheng-Kai, L.; Zhang, L.; Shen, Q.; Xiao-Fang, H.; Jin-Cai, W. Direct and full-scale experimental verifications towards ground–satellite quantum key distribution. Nat. Photonics 2013, 7, 387–393. [Google Scholar]
- Liao, S.-K.; Cai, W.-Q.; Liu, W.-Y.; Zhang, L.; Li, Y.; Ren, J.-G.; Yin, J.; Shen, Q.; Cao, Y.; Li, Z.-P.; et al. Satellite-to-ground quantum key distribution. Nat. Cell Biol. 2017, 549, 43–47. [Google Scholar] [CrossRef] [Green Version]
- Bedington, R.; Arrazola, J.M.; Ling, A. Progress in satellite quantum key distribution. Quantum Inf. 2017, 3, 30. [Google Scholar] [CrossRef]
- Ecker, S.; Liu, B.; Handsteiner, J.; Fink, M.; Rauch, D.; Steinlechner, F.; Scheidl, T.; Zeilinger, A.; Ursin, R. Strategies for achieving high key rates in satellite-based QKD. Npj Quantum Inf. 2021, 7, 1–7. [Google Scholar] [CrossRef]
- Pironio, S.; Acín, A.; Massar, S.; Boyer de La Giroday, A.; Matsukevich, N.D.; Maunz, P.; Olmschenk, S. Random numbers certified by Bell’s theorem. Nature 2010, 464, 1021–1024. [Google Scholar] [CrossRef] [Green Version]
- Masanes, L.; Pironio, S.; Acín, A. Secure device-independent quantum key distribution with causally in-dependent measurement devices. Nat. Commun. 2011, 2, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Pironio, S.; Masanes, L.; Leverrier, A.; Acín, A. Security of Device-Independent Quantum Key Distribution in the Bounded-Quantum-Storage Model. Phys. Rev. X 2013, 3, 031007. [Google Scholar] [CrossRef] [Green Version]
- Vazirani, U.; Vidick, T. Fully Device Independent Quantum Key Distribution. Phys. Rev. Lett. 2014, 62, 133. [Google Scholar] [CrossRef] [Green Version]
- Pusey, M.F. Verifying the quantumness of a channel with an untrusted device. J. Opt. Soc. Am. B 2015, 32, A56–A63. [Google Scholar] [CrossRef] [Green Version]
- Braunstein, S.L.; Van Loock, P. Quantum information with continuous variables. Rev. Mod. Phys. 2005, 77, 513–577. [Google Scholar] [CrossRef] [Green Version]
- Schmitt-Manderbach, T.; Weier, H.; Fürst, M.; Ursin, R.; Tiefenbacher, F.; Scheidl, T.; Perdigues, J. Experimental demonstration of free-space decoy-state quantum key distribution over 144 km. Phys. Rev. Lett. 2007, 98, 010504. [Google Scholar] [CrossRef]
- Lutkenhaus, N. Security against individual attacks for realistic quantum key distribution. Phys. Rev. A 2000, 61, 052304. [Google Scholar] [CrossRef] [Green Version]
- Scarani, V.; Renato, R. Quantum cryptography with finite resources: Unconditional security bound for discrete-variable protocols with one-way postprocessing. Phys. Rev. Lett. 2008, 100, 200501. [Google Scholar] [CrossRef] [Green Version]
- Lo, H.-K.; Curty, M.; Qi, B. Measurement-Device-Independent Quantum Key Distribution. Phys. Rev. Lett. 2012, 108, 130503. [Google Scholar] [CrossRef] [Green Version]
- Tittel, W.; Brendel, J.; Zbinden, H.; Gisin, N. Quantum Cryptography Using Entangled Photons in Energy-Time Bell States. Phys. Rev. Lett. 2000, 84, 4737–4740. [Google Scholar] [CrossRef] [Green Version]
- Qi, B. Single-photon continuous-variable quantum key distribution based on the energy-time uncertainty relation. Opt. Lett. 2006, 31, 2795–2797. [Google Scholar] [CrossRef]
- Pirandola, S.; Laurenza, R.; Ottaviani, C.; Banchi, L. Fundamental limits of repeaterless quantum communications. Nat. Commun. 2017, 8, 15043. [Google Scholar] [CrossRef] [Green Version]
- Takeoka, M.; Seshadreesan, K.P.; Wilde, M.M. Unconstrained distillation capacities of a pure-loss bosonic broadcast channel. In Proceedings of the 2016 IEEE International Symposium on Information Theory (ISIT), Barcelona, Spain, 10–15 July 2016; pp. 2484–2488. [Google Scholar] [CrossRef] [Green Version]
- Takeoka, M.; Seshadreesan, K.P.; Wilde, M.M. Unconstrained Capacities of Quantum Key Distribution and Entanglement Distillation for Pure-Loss Bosonic Broadcast Channels. Phys. Rev. Lett. 2017, 119, 150501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Devetak, I.; Winter, A. Distillation of secret key and entanglement from quantum states. Proc. R. Soc. A Math. Phys. Eng. Sci. 2005, 461, 207–235. [Google Scholar] [CrossRef] [Green Version]
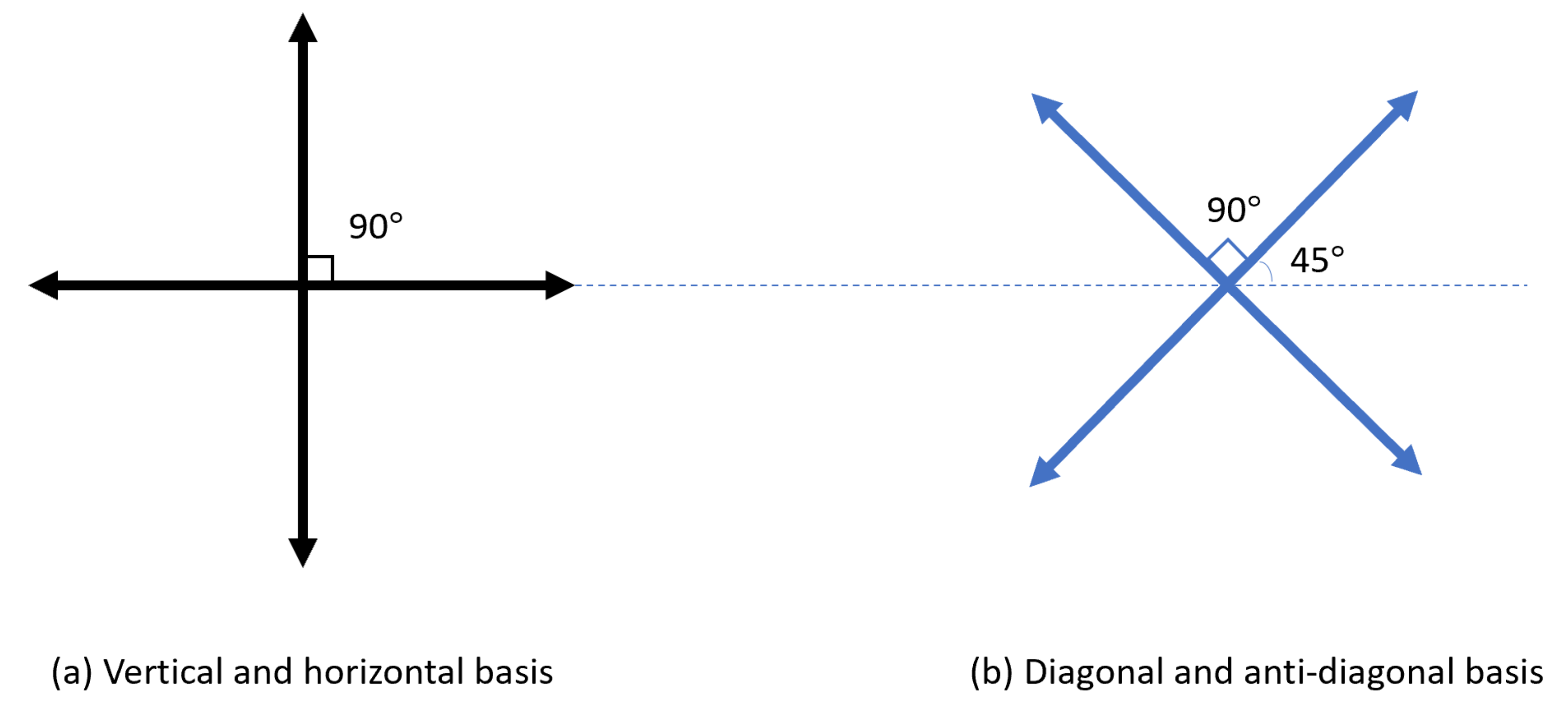


| Random Bits | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 |
|---|---|---|---|---|---|---|---|---|---|
| Alice basis | a | a | b | a | b | a | b | b | a |
| Polarization state sent |  |  |  |  |  | 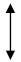 |  |  | 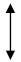 |
| Bob basis | b | a | a | b | b | a | b | a | b |
| Bob measurement results | random | 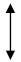 | random | random |  | 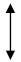 |  | random | random |
| Sifted keys | 1 | 1 | 1 | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, Z.; Djordjevic, I.B. An Overview of Geometrical Optics Restricted Quantum Key Distribution. Entropy 2021, 23, 1003. https://doi.org/10.3390/e23081003
Pan Z, Djordjevic IB. An Overview of Geometrical Optics Restricted Quantum Key Distribution. Entropy. 2021; 23(8):1003. https://doi.org/10.3390/e23081003
Chicago/Turabian StylePan, Ziwen, and Ivan B. Djordjevic. 2021. "An Overview of Geometrical Optics Restricted Quantum Key Distribution" Entropy 23, no. 8: 1003. https://doi.org/10.3390/e23081003






