Thermal Robustness of Entanglement in a Dissipative Two-Dimensional Spin System in an Inhomogeneous Magnetic Field
Abstract
1. Introduction
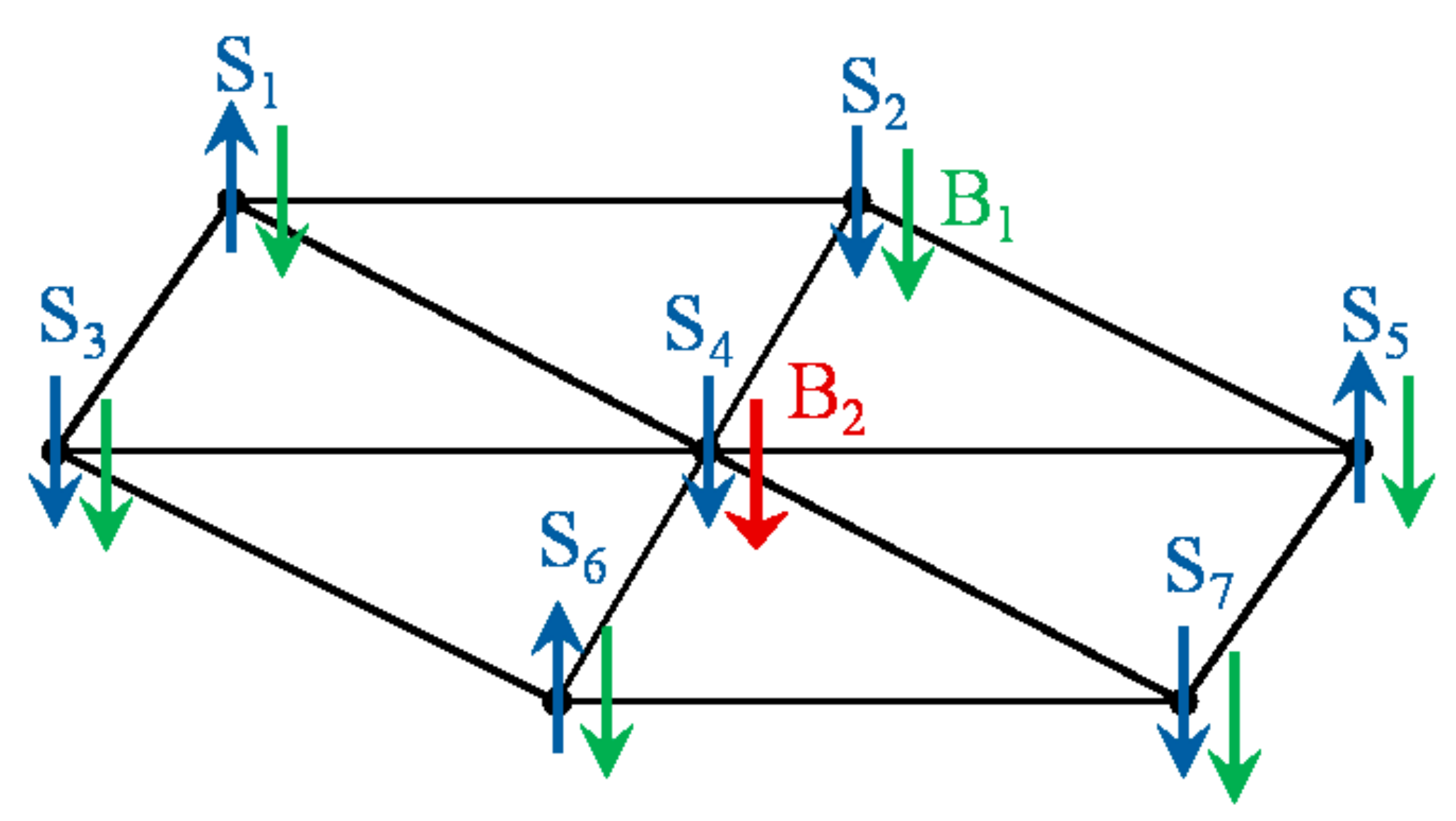
2. The Model
3. Dynamics of Entanglement
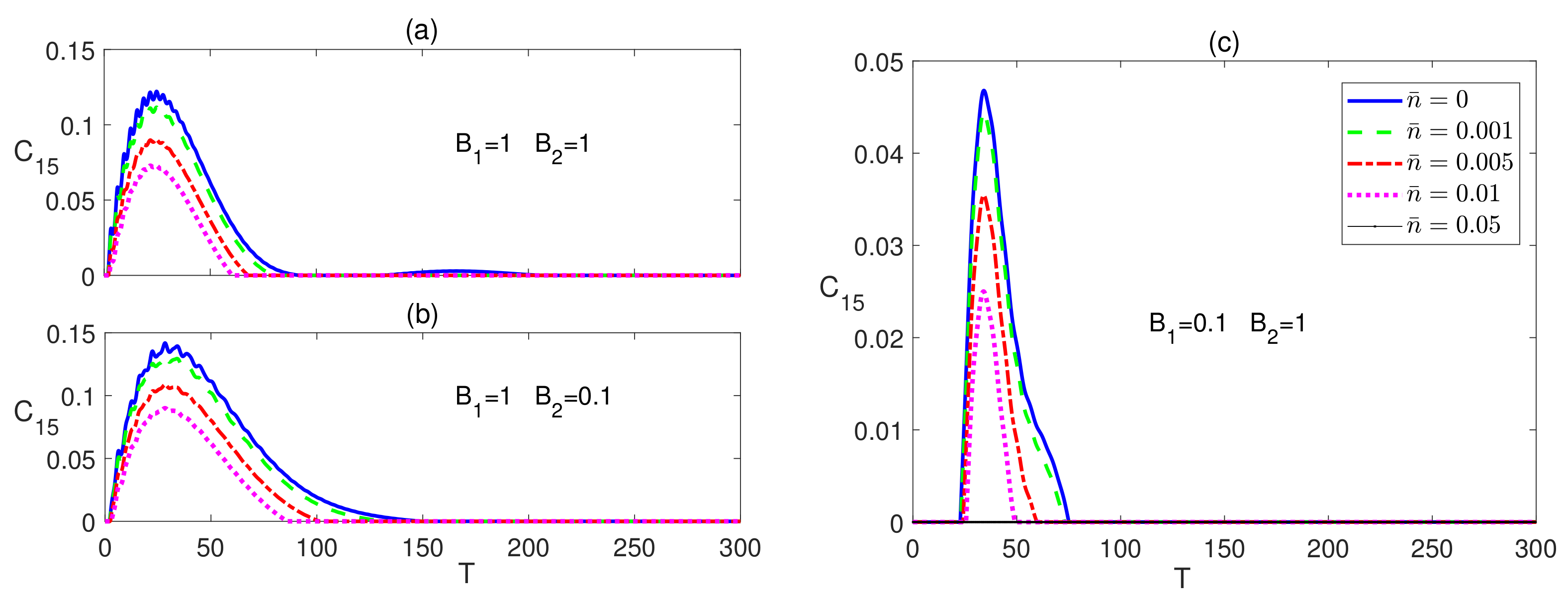
3.1. Anisotropic Spin System (Ising Model)
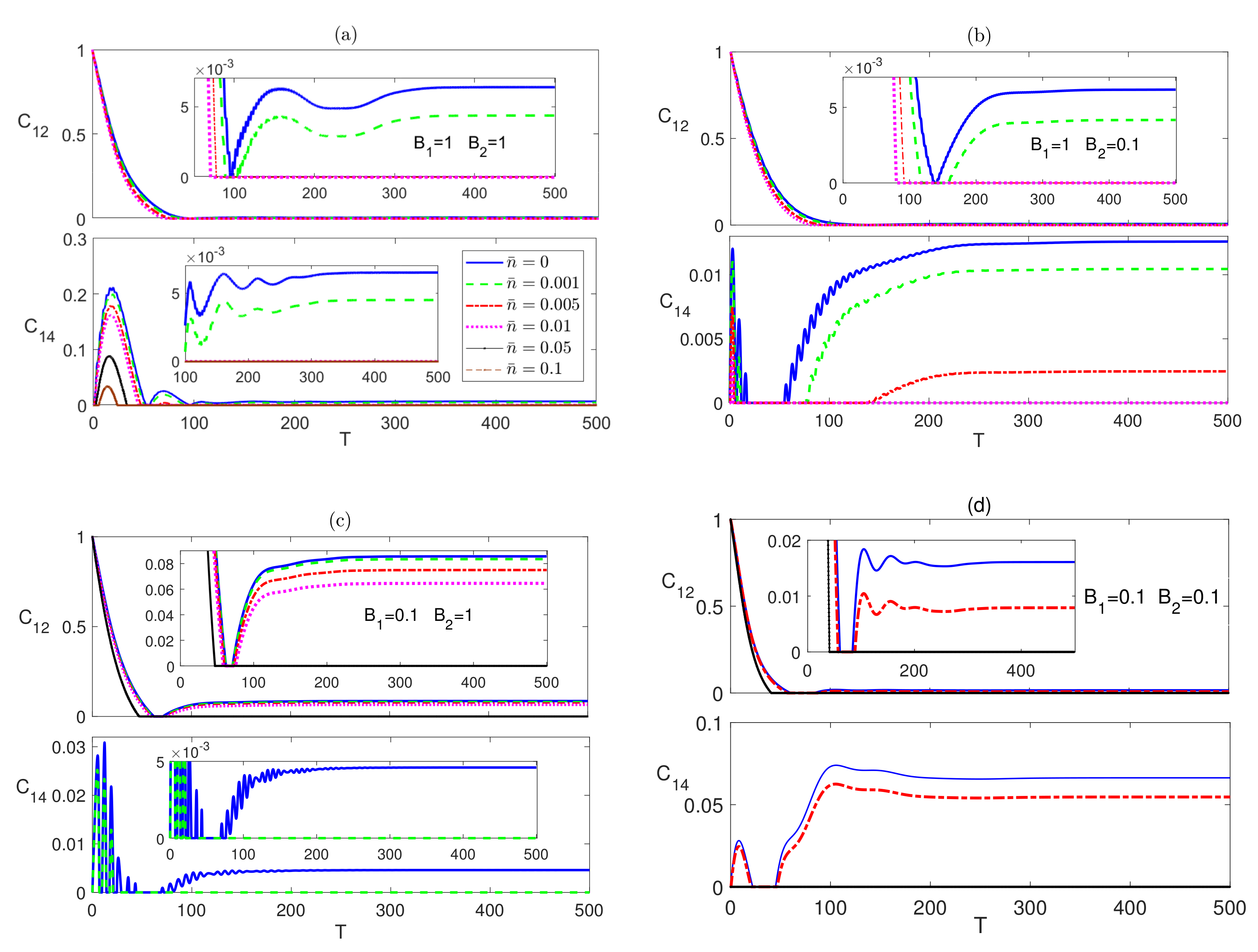
3.2. Partially Anisotropic System (XYZ Model)
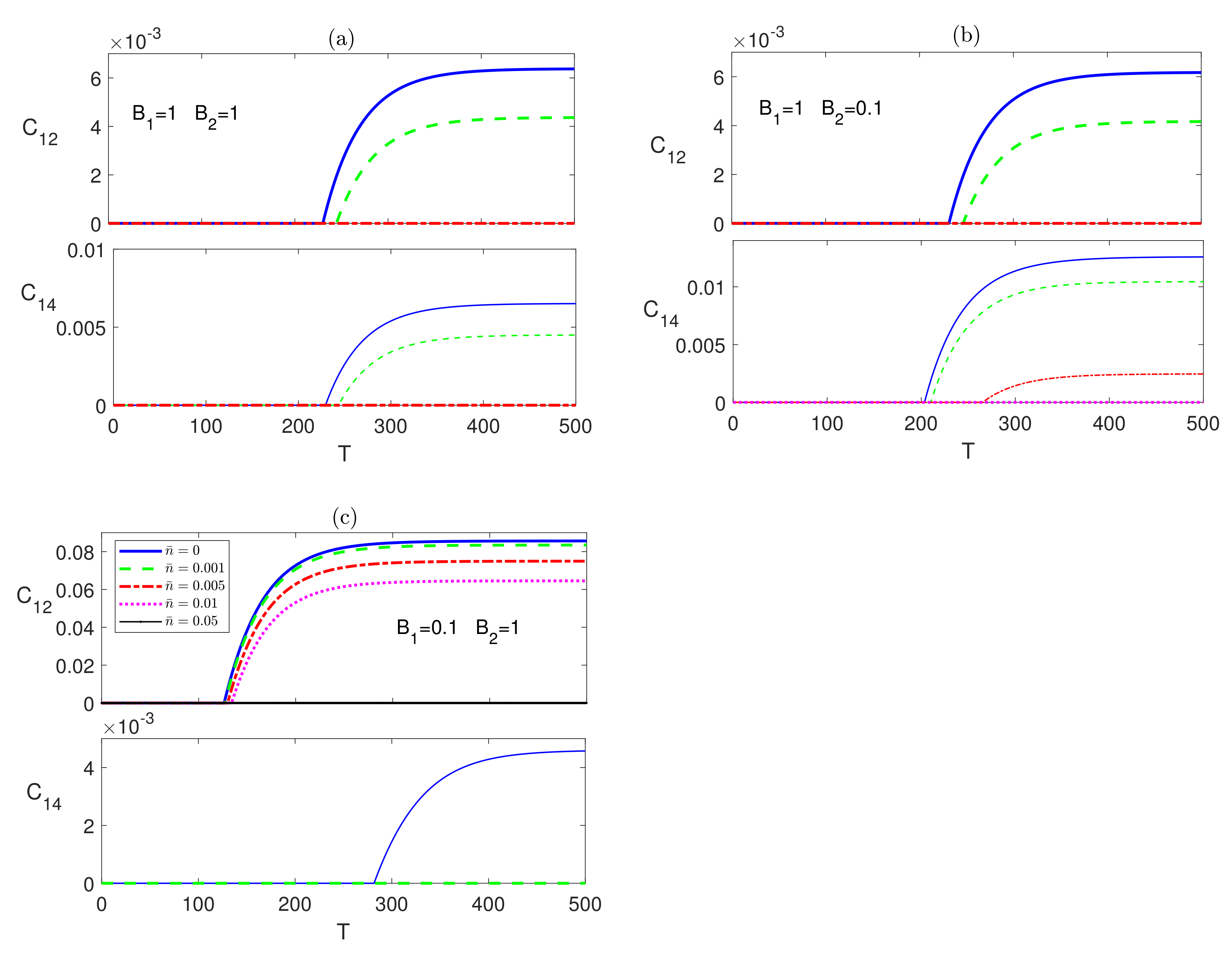
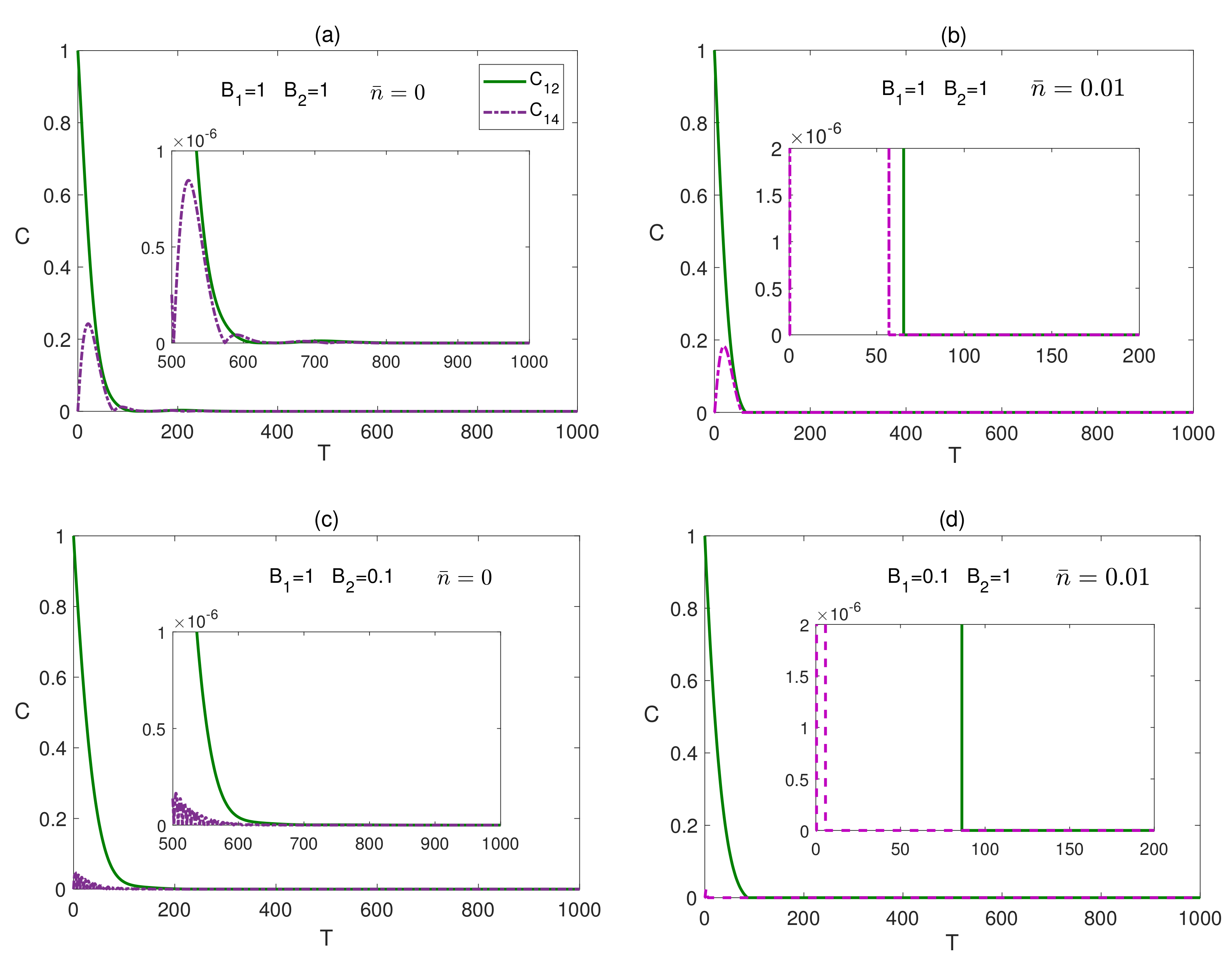
3.3. Isotropic System (XXX Model)
4. Spin Relaxation
4.1. Ising System
4.2. XYZ System
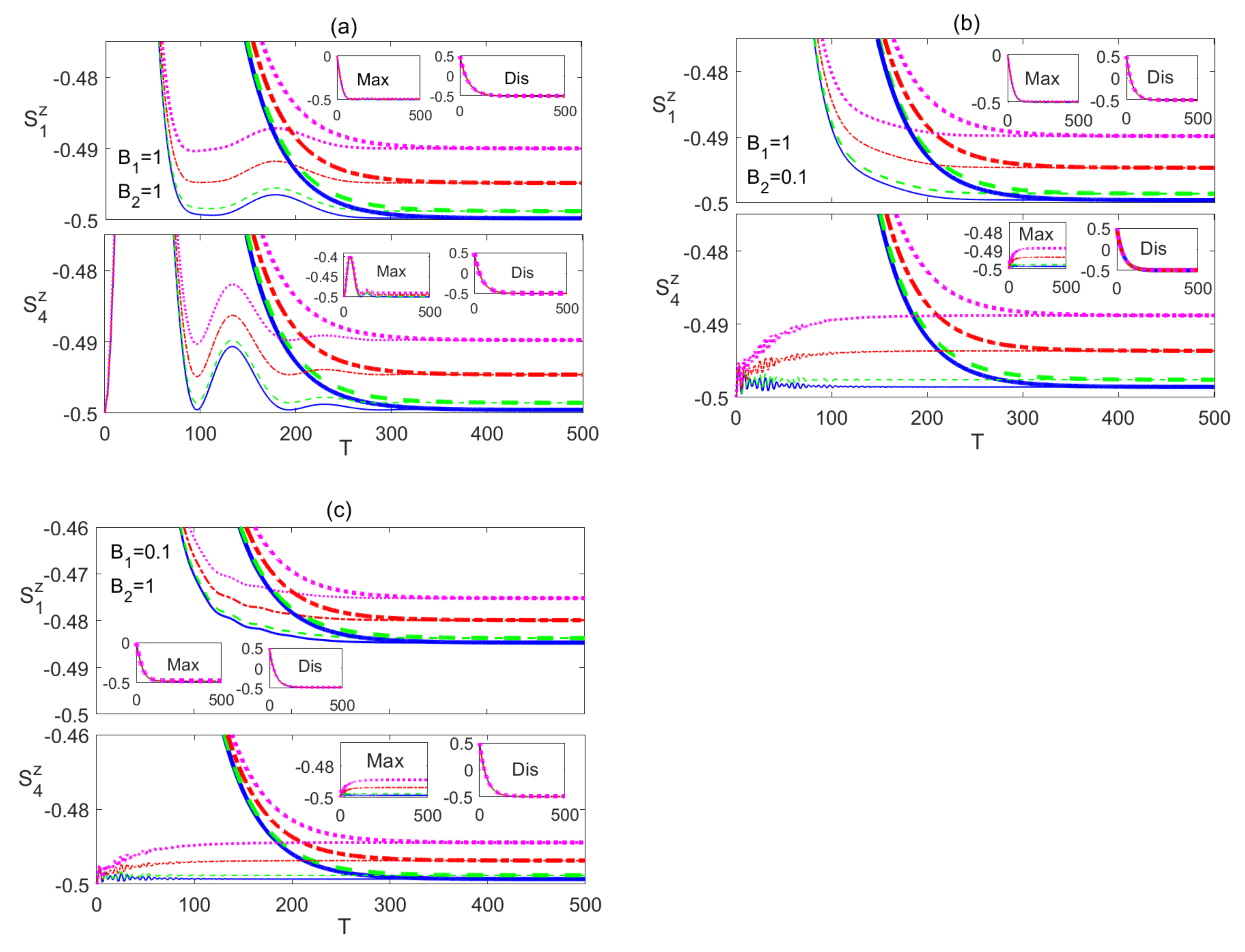
4.3. XXX System
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Peres, A. Quantum Theory: Concepts and Methods; Springer: Dordrecht, The Netherlands, 1993. [Google Scholar]
- Sachdev, S. Quantum Phase Transitions 2001; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Nielsen, M.; Chuang, I. Quantum Computation and Quantum Communication; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Zurek, W. Decoherence and the transition from quantum to classical. Phys. Today 1991, 44, 36–44. [Google Scholar] [CrossRef]
- Bacon, D.; Kempe, J.; Lidar, D.A.; Whaley, K.B. Universal fault-tolerant quantum computation on decoherence-free subspaces. Phys. Rev. Lett. 2000, 85, 1758. [Google Scholar] [CrossRef] [PubMed]
- Diehl, S.; Tomadin, A.; Micheli, A.; Fazio, R.; Zoller, P. Dynamical phase transitions and instabilities in open atomic man-body systems. Phys. Rev. Lett. 2010, 105, 015702. [Google Scholar] [CrossRef] [PubMed]
- Torre, E.G.D.; Demler, E.; Giamarchi, T.; Altman, E. Quantum critical states and phase transitions in the presence of non-equilibrium noise. Nat. Phys. 2010, 6, 806–810. [Google Scholar] [CrossRef]
- Ritsch, H.; Domokos, P.; Brennecke, F.; Esslinger, T. Cold atoms in cavity-generated dynamical optical potentials. Rev. Mod. Phys. 2013, 85, 553–601. [Google Scholar] [CrossRef]
- Carusotto, I.; Ciuti, C. Quantum fluids of light. Rev. Mod. Phys. 2013, 85, 299–366. [Google Scholar] [CrossRef]
- Markus, M.; Sebastian, D.; Guido, P.; Peter, Z. Engineered Open Systems and Quantum Simulations with Atoms and Ions. Adv. At. Mol. Opt. Phys. 2012, 61, 1–80. [Google Scholar]
- Heule, R.; Bruder, C.; Burgarth, D.; Stojanovic, V.M. Controlling qubit arrays with anisotropic XXZ Heisenberg interaction by acting on a single qubit. Eur. Phys. J. D 2011, 63, 41–46. [Google Scholar] [CrossRef]
- Houck, A.A.; Tureci, H.E.; Koch, J. On-chip quantum simulation with superconducting circuits. Nat. Phys. 2012, 8, 292. [Google Scholar] [CrossRef]
- Fitzpatrick, M.; Sundaresan, N.M.; Li, A.C.Y.; Koch, J.; Houck, A.A. Observation of a dissipative phase transition in a one-dimensional circuit QED lattice. Phys. Rev. X 2017, 7, 011016. [Google Scholar] [CrossRef]
- Sadiek, G.; Alkurtass, B.; Aldossary, O. Entanglement in a time-dependent coupled XY spin chain in an external magnetic field. Phys. Rev. A 2010, 82, 052337. [Google Scholar] [CrossRef]
- Barouch, E.; McCoy, B.M.; Dresden, M. Statistical mechanics of the XY model. I. Phys. Rev. A 1970, 2, 1075–1092. [Google Scholar] [CrossRef]
- Sadiek, G.; Huang, Z.; Aldossary, O.; Kais, S. Nuclear-induced time evolution of entanglement of two-electron spins in anisotropically coupled quantum dot. Mol. Phys. 2008, 106, 1777. [Google Scholar] [CrossRef]
- De Sen, A.; Sen, U.; Lewenstein, M. Nonergodicity of entanglement and its complementary behavior to magnetization in an infinite spin chain. Phys. Rev. A 2004, 70, 060304. [Google Scholar]
- Huang, Z.; Kais, D. Entanglement evolution of one-dimensional spin systems in external magnetic fields. Phys. Rev. A 2006, 73, 022339. [Google Scholar] [CrossRef]
- Lieb, E.; Schultz, T.; Mattis, D. Two soluble models of an antiferromagnetic chain. Ann. Phys. 1961, 16, 407–466. [Google Scholar] [CrossRef]
- Lashin, E.; Sadiek, G.; Abdalla, M.S.; Aldufeery, E. Two driven coupled qubits in a time varying magnetic field: Exact approximate solutions. Appl. Math. Inf. Sci. 2014, 8, 1071. [Google Scholar] [CrossRef][Green Version]
- Xu, Q.; Kais, S.; Naumov, M.; Sameh, A. Exact calculation of entanglement in a 19-site two-dimensional spin system. Phys. Rev. A 2010, 81, 022324. [Google Scholar] [CrossRef]
- Xu, Q.; Sadiek, G.; Kais, S. Dynamics of entanglement in a two-dimensional spin system. Phys. Rev. A 2011, 83, 062312. [Google Scholar] [CrossRef]
- Sadiek, G.; Kais, S. Persistence of entanglement in thermal states spin systems. J. Phys. B 2013, 46, 245501. [Google Scholar] [CrossRef]
- Sadiek, G.; Al-Drees, W.; Sebaweh, A.S. Manipulating entanglement sudden death in two coupled two-level atoms interacting off-resonance with a radiation field: An exact treatment. Opt. Express 2019, 27, 33799. [Google Scholar] [CrossRef]
- Wang, J.; Batelaan, H.; Podany, J.; Starace, A.F. Entanglement evolution in the presence of decoherence. J. Phys. B At. Mol. Opt. Phys. 2006, 39, 4343. [Google Scholar] [CrossRef]
- Abliz, A.; Gao, H.J.; Xie, X.C.; Wu, Y.S.; Liu, W.M. Entanglement control in an anisotropic two-qubit Heisenberg XYZ model with external magnetic fields. Phys. Rev. A 2006, 74, 052105. [Google Scholar] [CrossRef]
- Dubi, Y.; Di Ventra, M. Relaxation times in an open interacting two-qubit system. Phys. Rev. A 2009, 79, 012328. [Google Scholar] [CrossRef]
- Hein, M.; Dür, W.; Briegel, H.J. Entanglement properties of multipartite entangled states under the influence of decoherence. Phys. Rev. A 2005, 71, 032350. [Google Scholar] [CrossRef]
- Tsomokos, D.I.; Hartmann, M.J.; Huelga, S.F.; Plenio, M.B. Entanglement dynamics in chains of qubits with noise and disorder. New J. Phys. 2007, 9, 79. [Google Scholar] [CrossRef]
- Buric, N. Influence of the thermal environment on entanglement dynamics in small rings of qubits. Phys. Rev. A 2008, 77, 012321. [Google Scholar] [CrossRef]
- Hu, M.L.; Xi, X.Q. Impurity-assisted enhancement of entanglement in dissipative environments. Opt. Commun. 2009, 282, 4819. [Google Scholar] [CrossRef]
- Hu, M.L.; Xi, X.Q.; Lian, H.L. Thermal and phase decoherence effects on entanglement dynamics of the quantum spin systems. Phys. B Condens. Matter 2009, 404, 3499. [Google Scholar] [CrossRef]
- Buric, N.; Linden, B.L. Entanglement in quantum integrable and chaotic systems with Markov dynamics. Phys. Lett. A 2009, 373, 1531. [Google Scholar] [CrossRef]
- Pumulo, N.; Sinayskiy, I.; Petruccione, F. Non-equilibrium thermal entanglement for a three spin chain. Phys. Lett. A 2011, 375, 3157–3166. [Google Scholar] [CrossRef]
- Zhang, X.X.; Zhang, A.P.; Zhang, J.; Wang, J.X. Geometric Phase of Spin Chain System in the Nonequilibrium Thermal Environments. Mod. Phys. Lett. B 2013, 27, 1350078. [Google Scholar] [CrossRef]
- Lakshminarayan, A. Entangling power of quantized chaotic systems. Phys. Rev. E 2001, 64, 036207. [Google Scholar] [CrossRef] [PubMed]
- Sadiek, G.; Almalki, S. Entanglement dynamics in Heisenberg spin chains coupled to a dissipative environment at finite temperature. Phys. Rev. A 2016, 94, 012341. [Google Scholar] [CrossRef]
- Lee, T.E.; Gopalakrishnan, S.; Lukin, M.D. Unconventional Magnetism via Optical Pumping of Interacting Spin Systems. Phys. Rev. Lett. 2013, 110, 257204. [Google Scholar] [CrossRef]
- Rios, E.; Rossignoli, R.; Canosa, N. Entanglement and coherence in a spin-s XXZ system under non-uniform fields. J. Phys. B At. Mol. Opt. Phys. 2017, 50, 095501. [Google Scholar] [CrossRef]
- Sun, Y.; Chen, Y.; Chen, H. Thermal entanglement in the two-qubit Heisenberg XY model under a nonuniform external magnetic field. Phys. Rev. A 2003, 68, 044301. [Google Scholar] [CrossRef]
- Asoudeh, M.; Karimipour, V. Thermal entanglement of spins in an inhomogeneous magnetic field. Phys. Rev. A 2005, 71, 022308. [Google Scholar] [CrossRef]
- Zhang, G.F.; Li, S.S. Thermal entanglement in a two-qubit Heisenberg XXZ spin chain under an inhomogeneous magnetic field. Phys. Rev. A 2005, 72, 034302. [Google Scholar] [CrossRef]
- Hu, Z.N.; Yi, K.S.; Park, K.S. Thermal entanglement of a three-qubit system in inhomogeneous magnetic fields. J. Phys. A Math. Theor. 2007, 40, 7283. [Google Scholar] [CrossRef]
- Hassan, A.S.M.; Lari, B.; Joag, P.S. Thermal quantum and classical correlations in a two-qubit XX model in a nonuniform external magnetic field. J. Phys. A Math. Theor. 2010, 43, 485302. [Google Scholar] [CrossRef]
- Guo, J.L.; Mi, Y.J.; Zhang, J.; Song, H.S. Thermal quantum discord of spins in an inhomogeneous magnetic field. Phys. B At. Mol. Opt. Phys. 2011, 44, 065504. [Google Scholar] [CrossRef]
- Zhang, G.F.; Fan, H.; Ji, A.L.; Jiang, Z.T.; Abliz, A.; Liu, W.M. Quantum correlations in spin models. Ann. Phys. N. Y. 2011, 326, 2694–2701. [Google Scholar] [CrossRef][Green Version]
- Albayrak, E. Thermal entanglement in two-qubit spin-1 anisotropic Heisenberg model with inhomogeneous magnetic field. Chin. Phys. B 2010, 19, 090319. [Google Scholar] [CrossRef]
- Guo, K.T.; Liang, M.C.; Xu, H.Y.; Zhu, C.B. Entanglement in a two-spin (1/2,3/2) mixed-spin Heisenberg XXZ chain with an inhomogeneous external magnetic field. J. Phys. A Math. Theor. 2010, 43, 505301. [Google Scholar] [CrossRef]
- Hu, L.; Li, D.-C.; Wang, X.-P.; Yang, M.; Cao, Z.-L. Thermal Entanglement in the Spin-S Heisenberg XYZ Model. Chem. Phys. Lett. 2014, 31, 040301. [Google Scholar]
- Cerezo, M.; Rossignoli, R.; Canosa, N.; Ríos, E. Factorization and Criticality in Finite XXZ Systems of Arbitrary Spin. Phys. Rev. Lett. 2017, 119, 220605. [Google Scholar] [CrossRef]
- Rota, R.; Storme, F.; Bartolo, N.; Fazio, R.; Ciuti, C. Critical behavior of dissipative two-dimensional spin lattices. Phys. Rev. B 2017, 95, 134431. [Google Scholar] [CrossRef]
- Finazzi, S.; Le Boite, A.; Storme, A.; Baksic, A.; Ciuti, C. Corner-Space Renormalization Method for Driven-Dissipative Two-Dimensional Correlated Systems. Phys. Rev. Lett. 2015, 115, 080604. [Google Scholar] [CrossRef]
- Cerezo, M.; Rossignoli, R.; Canosa, N.; Lamas, C.A.O. Inducing critical phenomena in spin chains through sparse alternating fields. Phys. Rev. B 2019, 99, 014409. [Google Scholar] [CrossRef]
- Chalker, J.T.; Lacroix, C.; Mendels, P. (Eds.) Introduction to Frustrated Magnetism: Materials, Experiments, Theory; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Struck, J.; Olschlager, C.; Targat, R.L.; Soltan-Panahi, R.; Eckardt, A.; Lewenstein, M.; Windpassinger, P.; Sengstock, K. Quantum simulation of frustrated classical magnetism in triangular optical lattice. Science 2011, 333, 996. [Google Scholar] [CrossRef]
- Kim, K.; Chang, M.-S.; Korenblit, S.; Islam, R.; Edwards, E.E.; Freericks, J.K.; Lin, G.-D.; Duan, L.-M.; Monroe, C. Quantum simulation of frustrated Ising spins with trapped ions. Nature 2010, 465, 474. [Google Scholar] [CrossRef]
- Pip, P.; Glavic, A.; Skjærvo, S.H.; Weber, A.; Smerald, A.; Zhernenkov, K.; Leo, N.; Mila, F.; Philippei, L.; Heyderman, L.J. Direct observation of spin correlations in an artificial triangular lattice Ising spin system with grazing-incidence small-angle neutron scattering. Nanoscale Horiz. 2021, 6, 474. [Google Scholar] [CrossRef]
- Cai, J.; Retzker, A.; Jelezko, F.; Plenio, M.B. A large-scale quantum simulator on a diamond surface at room temperature. Nat. Phys. 2014, 9, 168. [Google Scholar] [CrossRef]
- Lindblad, G. On the generators of quantum dynamical semigroups. Comm. Math. Phys. 1976, 48, 119–130. [Google Scholar] [CrossRef]
- Breuer, H.P.; Petruccione, F. The Theory of Open Quantum Systems; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Mintert, F.; Carvalho, A.R.R.; Kus, M.; Buchleitner, A. Measures and dynamics of entangled states. Phys. Rep. 2005, 415, 207–259. [Google Scholar] [CrossRef]
- Wootters, K. Entanglement of formation of an arbitrary state of two qubits. Phys. Rev. Lett. 1998, 80, 2245–2248. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sadiek, G.; Almalki, S. Thermal Robustness of Entanglement in a Dissipative Two-Dimensional Spin System in an Inhomogeneous Magnetic Field. Entropy 2021, 23, 1066. https://doi.org/10.3390/e23081066
Sadiek G, Almalki S. Thermal Robustness of Entanglement in a Dissipative Two-Dimensional Spin System in an Inhomogeneous Magnetic Field. Entropy. 2021; 23(8):1066. https://doi.org/10.3390/e23081066
Chicago/Turabian StyleSadiek, Gehad, and Samaher Almalki. 2021. "Thermal Robustness of Entanglement in a Dissipative Two-Dimensional Spin System in an Inhomogeneous Magnetic Field" Entropy 23, no. 8: 1066. https://doi.org/10.3390/e23081066
APA StyleSadiek, G., & Almalki, S. (2021). Thermal Robustness of Entanglement in a Dissipative Two-Dimensional Spin System in an Inhomogeneous Magnetic Field. Entropy, 23(8), 1066. https://doi.org/10.3390/e23081066





