Interfacial Area Transport Equation for Bubble Coalescence and Breakup: Developments and Comparisons
Abstract
:1. Introduction
2. Transition of Bubbly to Churn-Turbulent Flows
2.1. Bubbly to Slug Transition
2.2. Slug to Churn Transition
2.3. Slug/Churn to Anular Flow Transition
3. Interfacial Area Transport Equation (IATE) for Bubble Coalescence and Breakup
3.1. One-group IATE for Bubble Coalescence and Breakup
3.2. Two-Group IATE for Bubble Coalescence and Breakup
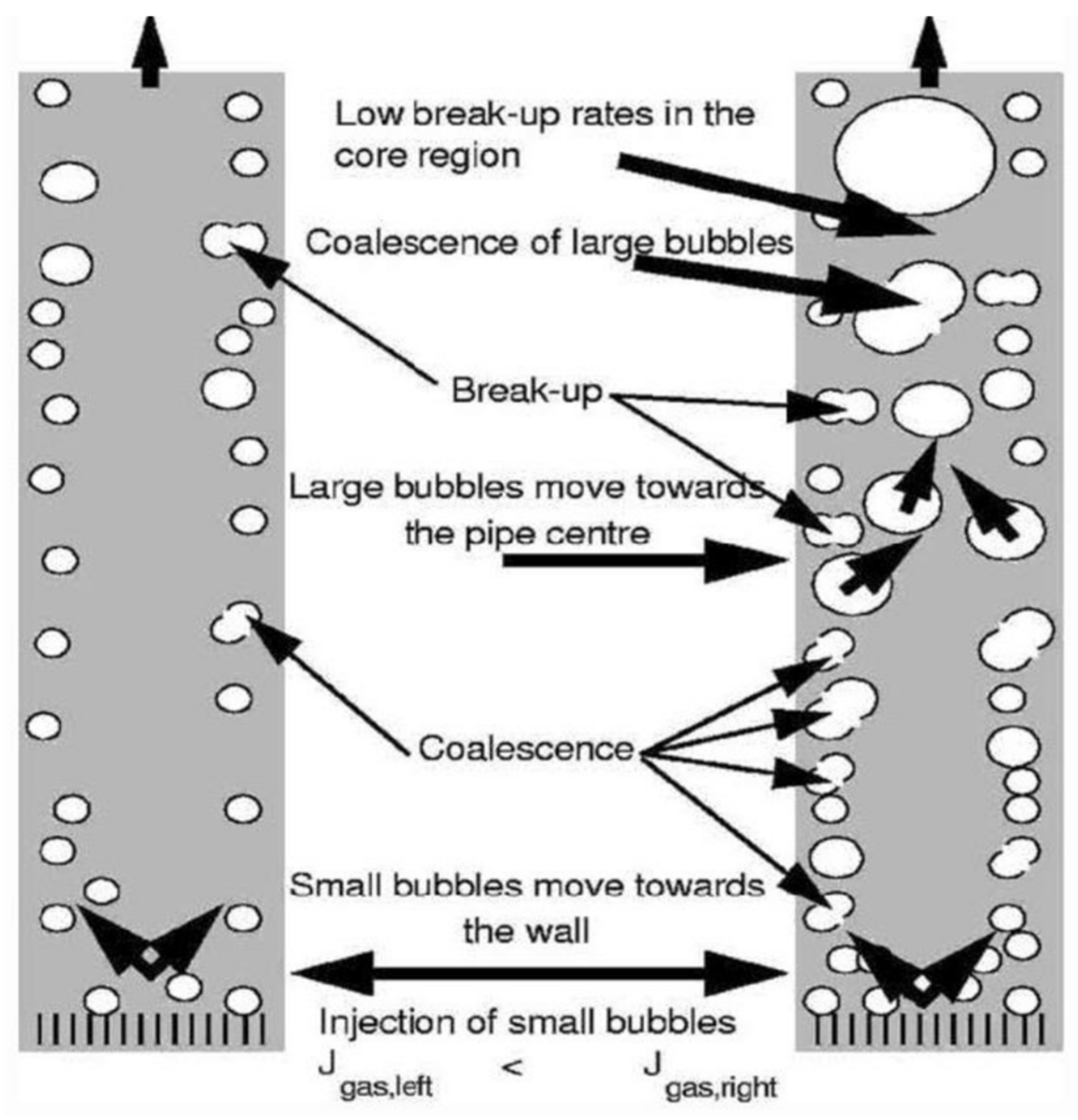
4. Identification of Bubble Coalescence and Breakup Interaction Mechanisms
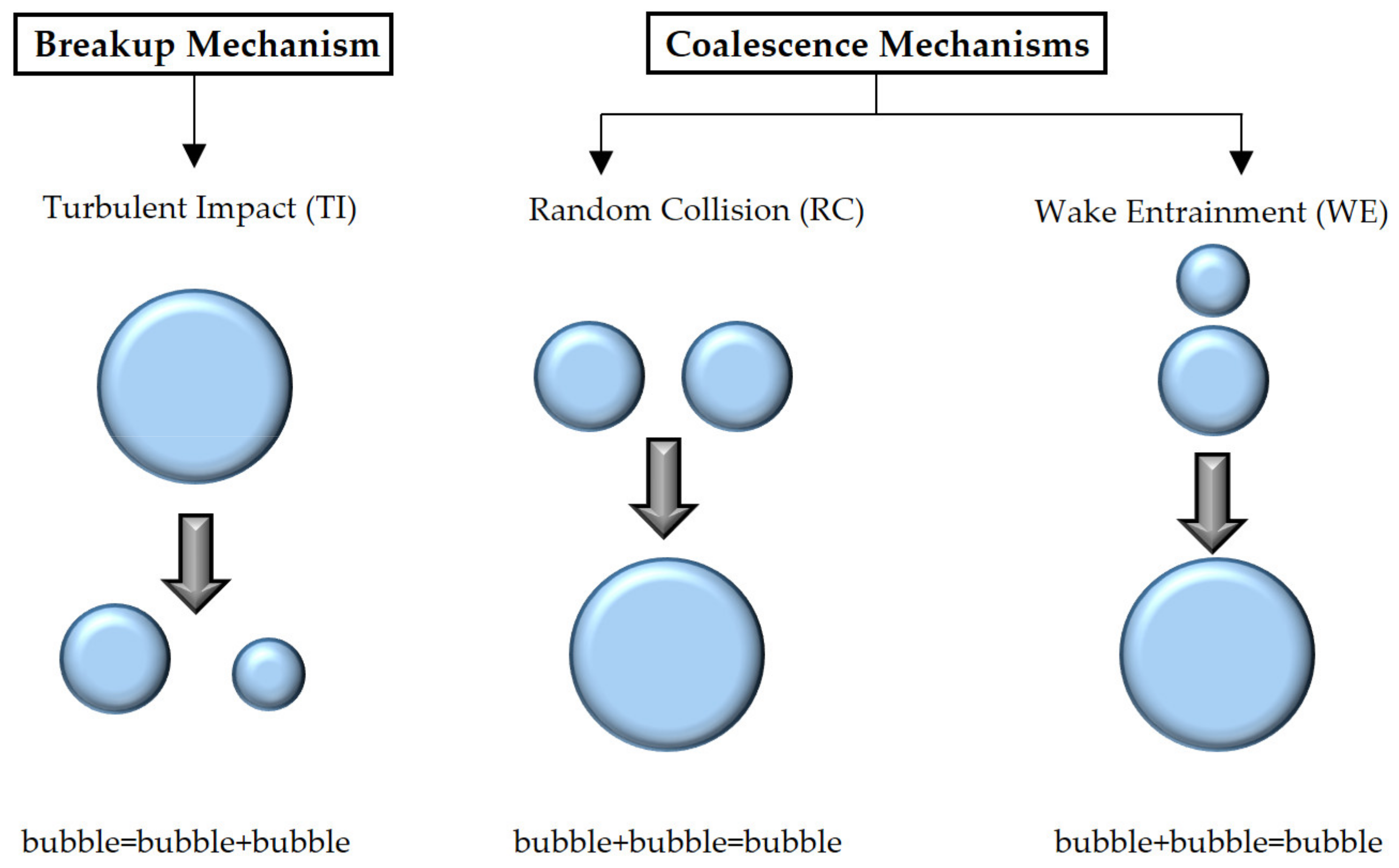
4.1. Bubble Coalescence Mechanisms
4.2. Bubble Breakup Mechanisms
4.2.1. Breakup due to Turbulent Impact
4.2.2. Breakup due to Shearing-Off
4.2.3. Breakup due to Viscous Shear Forces
4.2.4. Breakup due to Surface Instability
5. Evaluation of Frequency Models and Constitutive Models for Bubble Coalescence and Breakup
5.1. Frequency Models
5.1.1. Breakup Frequency Models
5.1.2. Coalescence Frequency Models
5.2. Constitutive Models for the One-Group IATE
- Flow orientation and channel size:
- 2.
- Pressure and liquid type:
- 3.
- Simulation of developing and transient flow [65]:
- 4.
- Bubble coalescence and breakup:
5.2.1. Bubble Coalescence due to RC
5.2.2. Bubble Breakup due to TI
5.3. Constitutive Models for the Two-Group IATE
6. Conclusions and Outlook
- Models for bubble coalescence and breakup processes of interfacial area density transport equation are based on the kinetic theory of gases. (1) The breakup frequency models are inconsistent and different models show completely different behaviors, where closure parameters change the conditions, such as integration limits, can have to be set. (2) In coalescence frequency models, the main difference in the models present results from the calculation of and modification factors , Π which need further study to obtain collision frequency. Wang et al. gave a small collision frequency for small bubbles due to the larger mean distance between small bubbles than big ones in the case of the same bubble number [47,48].
- Some important limitations of constitutive models for one-group IATE general applicability, such as flow orientation, channel size, pressure, liquid type, simulation of developing, and transient flow and bubble coalescence and breakup are summarized. Based on the summary and evaluation of the constitutive models for the one-group IATE in the literature, the best model for bubble coalescence due to RC is , and the best one for bubble breakup due to TI is so far.
- Constitutive models for two-group IATE in a three-type channel (i.e., narrow confined channel, round pipe, and relatively larger pipe) are reviewed, including five bubble interaction mechanisms, and their corresponding experimental conditions are summarized. Although great progress in extending the IATE beyond churn-turbulent flow to churn-annual flow was made, there is still some trouble in their modeling and experiments due to the highly distorted interface measurement.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | area, |
| interfacial area concentration (IAC), 1/m | |
| C | coefficient |
| drag coefficient | |
| inter-group transfer coefficient | |
| Ca | Capillary number |
| - | adjustable parameters |
| D | bubble size, m |
| critical diameter for transition between bubble groups, m | |
| bubble critical size due to phase change, m | |
| hydraulic diameter of the flow channel, m | |
| an arbitrarily defined minimum eddy size, m | |
| surface equivalent diameter, m | |
| Sauter mean diameter, m | |
| diameter of bubble 1, m | |
| diameter of bubble 2, m | |
| d | parent bubble diameter, m |
| daughter bubble diameter, m | |
| eddy size, m | |
| E | kinetic energy, kg |
| F(α) | turbulence damping factor due to the presence of the gas phase |
| f | frequency, 1/s |
| volume fraction, | |
| G | gap in a rectangular/annular channel, m |
| g | gravitational acceleration, m/ |
| I | turbulent intensity |
| j | superficial velocity, m/s |
| K | constant |
| k | the ratio of the average turbulent eddy size to the bubble Sauter mean diameter |
| average distance between bubbles, m | |
| N | average number of eddies arrive at the surface of a drop in unit time |
| n | number density of bubbles or eddies, 1/ |
| R | source/sink rates per unit mixture volume, 1/ |
| radius of the tube, m | |
| r | bubble radius, m |
| S | source/sink rates per unit mixture volume, 1/ |
| t | time, s |
| relative velocity between bubbles, m/s | |
| wake velocity of Group II bubbles, m/s | |
| wake velocity of Group I bubbles, m/s | |
| V | volume, |
| v | velocity, m/s |
| volume influenced by a wake, | |
| interfacial velocity, m/s | |
| the average local particle velocity, m/s | |
| We Weber number | |
| Greek symbols | |
| volume fraction, packing limit | |
| factor considering the effect of the size ratio between bubbles and eddies | |
| shear rate, 1/s | |
| factor considering the effect of the bubble that reduces the free space for bubble movement and causes an increase in the collision frequency. | |
| energy dissipation rate, / | |
| η | efficiency |
| rate of volume source per unit mixture volume, 1/s | |
| mass generation rate, kg/s | |
| IAC source/sink rate, 1/ms | |
| liquid viscosity, Pa·s | |
| ν | kinetic viscosity, / |
| ρ | density, kg/ |
| Π | factor considering the ratio of the mean bubble distance to the turbulent path length |
| surface tension, N/m | |
| surface tension forces, N | |
| viscous stress, N | |
| factor depending on bubble shape | |
| inter-group transfer coefficient | |
| Subscripts | |
| 1 | Group I |
| 2 | Group II |
| b | breakup |
| c | coalescence |
| coll | collision |
| cr | critical value |
| D | drag force |
| d | dispersed |
| e | eddy |
| f | liquid phase |
| g | gas phase |
| i | i-th component |
| j | j-th component |
| kin | kinetic |
| m | mixture value |
| max | maximum |
| max2 | maximum in Group II |
| min | minimum |
| nuc | nucleation |
| ph | phase change |
| RC | random collision mechanism |
| SO | shearing-off mechanism |
| TI | turbulent impact mechanism |
| WE | wake entrainment mechanism |
| SI | surface instability mechanism |
| Superscripts | |
| * non-dimensional value | |
| (1) | interactions within Group I bubbles |
| (11, 2) | coalescence of a Group I bubble with another Group I bubble to generate a Group II bubble |
| (12, 2) | coalescence of a Group I bubble with a Group II bubble to generate a new Group II bubble |
| (2) | interactions within Group II bubbles |
| (2, 1) | Group I bubbles generated from breakup of a Group II bubble |
| (2, 2) | Group II bubbles generated from breakup of a Group II bubble |
| (2, 11) | breakup of a Group II bubble to generate two Group I bubbles |
| (2, 12) | breakup of a Group II bubble to generate a (or multiple) Group I bubble(s) and a Group II bubble |
References
- Atamanchuk, D.; Koelling, J.; Send, U.; Wallace, D.W.R. Rapid transfer of oxygen to the deep ocean mediated by bubbles. Nat. Geosci. 2020, 13, 232–237. [Google Scholar] [CrossRef]
- Tikhomirov, D.A.; Kopylov, S.I. An Energy-Efficient Electric Plant for Hot Steam and Water Supply of Agricultural Enterprises. Russ. Electr. Eng. 2018, 89, 437–440. [Google Scholar] [CrossRef]
- Wu, Y.; Jiang, Z.; Lin, Z.; Liang, Y.; Wang, H. Direct electrosynthesis of methylamine from carbon dioxide and nitrate. Nat. Sustain. 2021, 4, 725–730. [Google Scholar] [CrossRef]
- Vignes, A. Oxygen Steelmaking. In Extractive Metallurgy 2: Metallurgical Reaction Processes; Wiley: Hoboken, NJ, USA, 2013; pp. 221–254. [Google Scholar]
- Feng, J.; Roché, M.; Vigolo, D.; Arnaudov, L.N.; Stoyanov, S.D.; Gurkov, T.D.; Tsutsumanova, G.G.; Stone, H.A. Nanoemulsions obtained via bubble-bursting at a compound interface. Nat. Phys. 2014, 10, 606–612. [Google Scholar] [CrossRef] [Green Version]
- Jin, K.; Kumar, P.; Vanka, S.P.; Thomas, B.G. Rise of an argon bubble in liquid steel in the presence of a transverse magnetic field. Phys. Fluids 2016, 28, 093301. [Google Scholar] [CrossRef]
- Wang, Q.L.; Zhu, D.D.; Liu, X.B.; Chen, B.Z.; Guo, X.D. Microneedles with Controlled Bubble Sizes and Drug Distributions for Efficient Transdermal Drug Delivery. Sci. Rep. 2016, 6, 38755. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Walls, P.L.L.; McRae, O.; Natarajan, V.; Johnson, C.; Antoniou, C.; Bird, J.C. Quantifying the potential for bursting bubbles to damage suspended cells. Sci. Rep. 2017, 7, 15102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kocamustafaogullari, G.; Ishii, M. Foundation of the interfacial area transport equation and its closure relations. Int. J. Heat Mass Tran. 1995, 38, 481–493. [Google Scholar] [CrossRef]
- Krepper, E.; Lucas, D.; Prasser, H.M. On the modelling of bubbly flow in vertical pipes. Nucl. Eng. Des. 2005, 235, 597–611. [Google Scholar] [CrossRef]
- Taitel, Y.; Bornea, D.; Dukler, A.E. Modelling flow pattern transitions for steady upward gas-liquid flow in vertical tubes. AIChE J. 1980, 26, 345–354. [Google Scholar] [CrossRef]
- Ishii, M.; Kim, S. Development of One-Group and Two-Group Interfacial Area Transport Equation. Nucl. Sci. Eng. 2004, 146, 257–273. [Google Scholar] [CrossRef]
- Wu, Q.; Kim, S.; Ishii, M.; Beus, S.G. One-group interfacial area transport in vertical bubbly flow. Int. J. Heat Mass Tran. 1998, 41, 1103–1112. [Google Scholar] [CrossRef]
- Ishii, M.; Hibiki, T. Thermo-Fluid Dynamics of Two-Phase Flow; Springer: New York, NY, USA, 2006. [Google Scholar]
- Wu, Q.; Ishii, M.; Uhle, J. Framework of two-group model for interfacial area transport in vertical two-phase flows. Trans. ANS 1998, 79, 351–352. [Google Scholar]
- Ishii, M.; Kim, S. Micro four-sensor probe measurement of interfacial area transport for bubbly flow in round pipes. Nucl. Eng. Des. 2001, 205, 123–131. [Google Scholar] [CrossRef]
- Hibiki, T.; Ishii, M. Development of one-group interfacial area transport equation in bubbly flow systems. Int. J. Heat Mass Tran. 2002, 45, 2351–2372. [Google Scholar] [CrossRef]
- Yao, W.; Morel, C. Volumetric interfacial area prediction in upward bubbly two-phase flow. Int. J. Heat Mass Tran. 2004, 47, 307–328. [Google Scholar] [CrossRef]
- Nguyen, V.T.; Song, C.-H.; Bae, B.-U.; Euh, D.-J. Modeling of bubble coalescence and break-up considering turbulent suppression phenomena in bubbly two-phase flow. Int. J. Multiphas Flow 2013, 54, 31–42. [Google Scholar] [CrossRef]
- Ishii, M.; Mi, Y.; Assad, A. Development and Evaluation of One Group Interfacial Area Transport Equation; Purdue University: West Lafayette, IN, USA, 1999. [Google Scholar]
- Kim, S. Interfacial Area Transport Equation and Measurement of Local Interfacial Characteristics; Purdue University: West Lafayette, IN, USA, 1999. [Google Scholar]
- Ishii, M.; Zuber, N. Drag coefficient and relative velocity in bubbly, droplet or particulate flows. AIChE J. 1979, 25, 843–855. [Google Scholar] [CrossRef]
- Worosz, T.S. Interfacial Area Transport Equation for Bubbly to Cap-Bubbly Transition Flows. Ph.D. Thesis, The Pennsylvania State University, Ann Arbor, MI, USA, 2015. [Google Scholar]
- Wang, G.; Zhu, Q.; Dang, Z.; Yang, X.; Ishii, M. Prediction of interfacial area concentration in a small diameter round pipe. Int. J. Heat Mass Tran. 2019, 130, 252–265. [Google Scholar] [CrossRef]
- Wang, T.F.; Wang, J.F.; Jin, Y. A novel theoretical breakup kernel function for bubbles/droplets in a turbulent flow. Chem. Eng. Sci. 2003, 58, 4629–4637. [Google Scholar] [CrossRef]
- Zhao, H.; Ge, W. A theoretical bubble breakup model for slurry beds or three-phase fluidized beds under high pressure. Chem. Eng. Sci. 2007, 62, 109–115. [Google Scholar] [CrossRef]
- Liao, Y.X.; Lucas, D. A literature review of theoretical models for drop and bubble breakup in turbulent dispersions. Chem. Eng. Sci. 2009, 64, 3389–3406. [Google Scholar] [CrossRef]
- Coulaloglou, C.A.; Tavlarides, L.L. Description of interaction processes in agitated liquid-liquid dispersions. Chem. Eng. Sci. 1977, 32, 1289–1297. [Google Scholar] [CrossRef]
- Chatzi, E.; Gavrielides, A.; Kiparissides, C. Generalized model for prediction of the steady-state drop size distribution in batch stirred vessel. Ind. Eng. Chem. Res. 1989, 28, 1704–1711. [Google Scholar] [CrossRef]
- Narsimhan, G.; Gupta, J.P.; Ramkrishna, D. A model for transitional breakage probability of droplets in agitated lean liquid-liquid dispersions. Chem. Eng. Sci. 1979, 34, 257–265. [Google Scholar] [CrossRef]
- Alopaeus, V.; Koskinen, J.; Keskinen, K.I.; Majander, J. Simulation of the population balances for liquid–liquid systems in a nonideal stirred tank. Part 2—parameter fitting and the use of the multiblock model for dense dispersions. Chem. Eng. Sci. 2002, 57, 1815–1825. [Google Scholar] [CrossRef]
- Lee, C.-H.; Erickson, L.; Glasgow, L.A. Dynamics of bubble size distribution in turbulent gas-liquid dispersions. Chem. Eng. Commun. 1987, 61, 181–195. [Google Scholar] [CrossRef]
- Lee, C.-H.; Erickson, L.; Glasgow, L.A. Bubble breakup and coalescence in turbulent gas–liquid dispersion. Chem. Eng. Commun. 1987, 59, 65–84. [Google Scholar] [CrossRef]
- Prince, M.J.; Blanch, H.W. Bubble coalescence and break-up in air-sparged bubble columns. AIChE J. 1990, 36, 1485–1499. [Google Scholar] [CrossRef]
- Tsouris, C.; Tavlarides, L.L. Breakage and coalescence models for drops in turbulent dispersions. AIChE J. 1994, 40, 395–406. [Google Scholar] [CrossRef]
- Luo, H.; Svendsen, H.F. Theoretical model for drop and bubble breakup in turbulent dispersions. AIChE J. 1996, 42, 1225–1233. [Google Scholar] [CrossRef]
- Martinez-Bazan, C.; Montanes, J.L.; Lasheras, J.C. On the breakup of an air bubble injected into a fully developed turbulent flow. Part 1. Breakup frequency. J. Fluid Mech. 1999, 401, 157–182. [Google Scholar] [CrossRef] [Green Version]
- Lehr, F.; Mewes, D. A transport equation for the interfacial area density in two-phase flow. In Proceedings of the Second European Congress of Chemical Engineering, Montpellier, France, 5–7 October 1999. [Google Scholar]
- Lehr, F.; Millies, M.; Mewes, D. Bubble-size distributions and flow fields in bubble columns. AIChE J. 2002, 48, 2426–2443. [Google Scholar] [CrossRef]
- Fu, X.Y.; Ishii, M. Two-group interfacial area transport in vertical air–water flow: I. Mechanistic model. Nucl. Eng. Des. 2003, 219, 143–168. [Google Scholar] [CrossRef]
- Renardy, Y.Y.; Cristini, V. Scalings for fragments produced from drop breakup in shear flow with inertia. Phys. Fluids 2001, 13, 2161–2164. [Google Scholar] [CrossRef] [Green Version]
- Renardy, Y.Y.; Cristini, V. Effect of inertia on drop breakup under shear. Phys. Fluids 2001, 13, 7–13. [Google Scholar] [CrossRef] [Green Version]
- Sun, X.; Kim, S.; Ishii, M.; Beus, S.G. Modeling of bubble coalescence and disintegration in confined upward two-phase flow. Nucl. Eng. Des. 2004, 230, 3–26. [Google Scholar] [CrossRef]
- Lasheras, J.C.; Eastwood, C.; Martíánez-Bazán, C.; Montañés, J.L. A review of statistical models for the break-up of an immiscible fluid immersed into a fully developed turbulent flow. Int. J. Multiphas Flow 2002, 28, 247–278. [Google Scholar] [CrossRef] [Green Version]
- Kennard, E. Kinetic Theory of Gases; McGraw-Hill: New York, NY, USA, 1938; pp. 328–329. [Google Scholar]
- Chesters, A.K. The modeling of coalescence processes in fluid-liquid dispersions: A review of current understanding. Chem. Eng. Res. Des. 1991, 69, 259–270. [Google Scholar]
- Wang, T.; Wang, J.; Jin, Y. Population Balance Model for Gas−Liquid Flows: Influence of Bubble Coalescence and Breakup Models. Ind. Eng. Chem. Res. 2005, 44, 7540–7549. [Google Scholar] [CrossRef]
- Wang, T.; Wang, J.; Jin, Y. Theoretical prediction of flow regime transition in bubble columns by the population balance model. Chem. Eng. Sci. 2005, 60, 6199–6209. [Google Scholar] [CrossRef]
- Hibiki, T.; Ishii, M. One-group interfacial area transport of bubbly flows in vertical round tubes. Int. J. Heat Mass Tran. 2000, 43, 2711–2726. [Google Scholar] [CrossRef]
- Nguyen, V.-T.; Bae, B.-U.; Euh, D.-J.; Song, C.-H.; Yun, B.-J. The effect of bubble-induced turbulence on the interfacial area transport in gas-liquid Two-phase slow. J. Comput. Multiph. Flows 2012, 4, 327–340. [Google Scholar] [CrossRef]
- Wang, X. Simulations of Two-Phase Flows Using Interfacial Area Transport Equation. Ph.D. Thesis, The Ohio State University, Columbus, OH, USA, 2010. [Google Scholar]
- Talley, J.D. Interfacial Area Transportation Equation for Vertical and Horizontal Bubbly Flows and Its Application to the Trace Code. Ph.D. Thesis, The Pennsylvania State University, State College, PA, USA, 2012. [Google Scholar]
- Talley, J.D.; Worosz, T.; Kim, S.; Buchanan, J.R. Characterization of horizontal air–water two-phase flow in a round pipe part I: Flow visualization. Int. J. Multiphas Flow 2015, 76, 212–222. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.; Ishii, M.; Kong, R.; Wang, G. Progress in two-phase flow modeling: Interfacial area transport. Nucl. Eng. Des. 2021, 373, 111019. [Google Scholar] [CrossRef]
- Pistorius, P.C. Chapter 2.3-Bubbles in Process Metallurgy. In Treatise on Process Metallurgy; Seetharaman, S., Ed.; Elsevier: Boston, MA, USA, 2014; pp. 179–196. [Google Scholar]
- Yadav, M.S.; Kim, S.; Tien, K.; Bajorek, S.M. Experiments on geometric effects of 90-degree vertical-upward elbow in air water two-phase flow. Int. J. Multiphas Flow 2014, 65, 98–107. [Google Scholar] [CrossRef]
- Yadav, M.S.; Worosz, T.; Kim, S.; Tien, K.; Bajorek, S.M. Characterization of the dissipation of elbow effects in bubbly two-phase flows. Int. J. Multiphas Flow 2014, 66, 101–109. [Google Scholar] [CrossRef]
- Qiao, S. Characterization of Geometric Effects Induced by 90° Vertical Elbows in Air-Water Two-Phase Flow. Ph.D. Thesis, The Pennsylvania State University, State College, PA, USA, 2017. [Google Scholar]
- Qiao, S.; Kim, S. Air-water two-phase bubbly flow across 90° vertical elbows. Part I: Experiment. Int. J. Heat Mass Tran. 2018, 123, 1221–1237. [Google Scholar] [CrossRef]
- Qiao, S.; Kim, S. Interfacial area transport across a 90° vertical-upward elbow in air–water bubbly two-phase flow. Int. J. Multiphas Flow 2016, 85, 110–122. [Google Scholar] [CrossRef]
- Qiao, S.; Kong, R.; Kim, S. Air-water two-phase bubbly flow across 90° vertical elbows Part II: Modeling. Int. J. Heat Mass Tran. 2018, 123, 1238–1252. [Google Scholar] [CrossRef]
- Kong, R.; Qiao, S.; Kim, S.; Bajorek, S.; Tien, K.; Hoxie, C. Interfacial area transport models for horizontal air-water bubbly flow in different pipe sizes. Int. J. Multiphas Flow 2018, 106, 46–59. [Google Scholar] [CrossRef]
- Kong, R. Characterization of Horizontal Air-Water Two-Phase Flow in Different Pipe Sizes. Ph.D. Thesis, Purdue University, Ann Arbor, MI, USA, 2018. [Google Scholar]
- Chuang, T.-J.; Hibiki, T. Vertical upward two-phase flow CFD using interfacial area transport equation. Prog. Nucl. Energy 2015, 85, 415–427. [Google Scholar] [CrossRef]
- Liu, H.; Hibiki, T. Bubble breakup and coalescence models for bubbly flow simulation using interfacial area transport equation. Int. J. Heat Mass Tran. 2018, 126, 128–146. [Google Scholar] [CrossRef]
- Ozar, B.; Brooks, C.S.; Hibiki, T.; Ishii, M. Interfacial area transport of vertical upward steam–water two-phase flow in an annular channel at elevated pressures. Int. J. Heat Mass Tran. 2013, 57, 504–518. [Google Scholar] [CrossRef]
- Liu, T.J.; Bankoff, S.G. Structure of air-water bubbly flow in a vertical pipe—II. Void fraction, bubble velocity and bubble size distribution. Int. J. Heat Mass Tran. 1993, 36, 1061–1072. [Google Scholar] [CrossRef]
- Miller, J.W.; Ishii, M.; Revankar, S.T. An Experimental Analysis of Larger Spherical Cap Bubbles Rising in an Extended Liquid; Purdue University Report, PU-NE-93-5; Purdue University: West Lafayette, IN, USA, 1993. [Google Scholar]
- Sun, X. Two-Group Interfacial Area Transport Equation for a Confined Test Section. Ph.D. Thesis, Purdue University, Ann Arbor, MI, USA, 2001. [Google Scholar]
- Ozar, B.; Brooks, C.S.; Euh, D.J.; Hibiki, T.; Ishii, M. Investigation of one-dimensional interfacial area transport for vertical upward air–water two-phase flow in an annular channel at elevated pressures. Nucl. Eng. Des. 2013, 263, 362–379. [Google Scholar] [CrossRef]
- Yang, X.; Schlegel, J.P.; Liu, Y.; Paranjape, S.; Hibiki, T.; Ishii, M.; Bajorek, S.; Ireland, A. Prediction of interfacial area transport in a scaled 8×8 BWR rod bundle. Nucl. Eng. Des. 2016, 310, 638–647. [Google Scholar] [CrossRef]
- Fu, X.Y. Interfacial Area Measurement and Transport Modeling in Air -Water Two-Phase Flow. Ph.D. Thesis, Purdue University, Ann Arbor, MI, USA, 2001. [Google Scholar]
- Smith, T.R. Two-Group Interfacial Area Transport Equation in Large Diameter Pipes. Ph.D. Thesis, Purdue University, Ann Arbor, MI, USA, 2002. [Google Scholar]
- Smith, T.R.; Schlegel, J.P.; Hibiki, T.; Ishii, M. Two-phase flow structure in large diameter pipes. Int. J. Heat Fluid Flow 2012, 33, 156–167. [Google Scholar] [CrossRef]
- Smith, T.R.; Schlegel, J.P.; Hibiki, T.; Ishii, M. Mechanistic modeling of interfacial area transport in large diameter pipes. Int. J. Multiphas Flow 2012, 47, 1–16. [Google Scholar] [CrossRef]
- Schlegel, J.P.; Hibiki, T.; Ishii, M. Two-group modeling of interfacial area transport in large diameter channels. Nucl. Eng. Des. 2015, 293, 75–86. [Google Scholar] [CrossRef]
- Sun, X.; Kim, S.; Ishii, M.; Beus, S.G. Model evaluation of two-group interfacial area transport equation for confined upward flow. Nucl. Eng. Des. 2004, 230, 27–47. [Google Scholar] [CrossRef]
- Doup, B.C. Methodology Development of a Gas-Liquid Dynamic Flow Regime Transition Model. Ph.D. Thesis, The Ohio State University, Columbus, OH, USA, 2014. [Google Scholar]
- Isao, K.; Mamoru, I. Drift flux model for large diameter pipe and new correlation for pool void fraction. Int. J. Heat Mass Tran. 1987, 30, 1927–1939. [Google Scholar] [CrossRef]













| Criterion | Authors |
|---|---|
| Coulaloglou and Tavlaride [28] |
| Chatzi et al. [29] | |
| Narsimhan and Ghupta [30] |
| Alopaeus et al. [31] | |
| Lee et al. [32,33] |
| Prince and Blanch [34] | |
| Tsouris and Tavlarides [35] | |
| Luo and Svendsen [36] | |
| Martinez Bazan et al. [37] | |
| Lehr and Mewes [38] |
| Lehr et al. [39] | |
| Wang et al. [25] |
| Zhao and Ge [26] |
| Mechanism | Interaction | ||
|---|---|---|---|
| RC | (1)+(1)→(1) | Sink in 1 | |
| (1)+(1)→(2) | Sink in 1; source in 2 | ||
| (1)+(2)→(2) | Sink in 1; source in 2 (no number change) | ||
| (2)+(2)→(2) | Sink in 2 | ||
| WE | (1)+(1)→(1) | Sink in 1 | |
| (1)+(1)→(2) | Sink in 1; source in 2 | ||
| (1)+(2)→(2) | Sink in 1; source in 2 (no number change) | ||
| (2)+(2)→(2) | Sink in 2 | ||
| TI | (1)→(1)+(1) | Source in 1 | |
| (2)→(1)+(1) | Source in 1; sink in 2 | ||
| (2)→(2)+(1) | Source in 1; sink in 2 (no number change) | ||
| (2)→(2)+(2) | Source in 2 | ||
| SO | (2)→(2)+n(1) | Source in 1 (multiple number); sink in 2 (no number change) | |
| SI | (2)→(2)+(2) | Source in 2 |
| Modification Factor | Definition |
|---|---|
| The effect of the size ratio between bubbles and eddies. | |
| The effect of the bubble that reduces the free space for bubble movement and causes an increase in the collision frequency. | |
| Π | The ratio of the mean distance between bubbles to their average relative turbulent path length. |
| Investigators | Flow Orientation | Dimensions | Channel Size (mm) | Pressure (MPa) | System | Bubble Coalescence | Bubble Breakup | ||
|---|---|---|---|---|---|---|---|---|---|
| Collision Frequency | Efficiency | Collision Frequency | Efficiency | ||||||
| Wu et al. (1998) [13] | Upward | 1D | 50.8 | 0.1 | Air-water | ||||
| Ishii and Kim (2001) [16] | Upward | 1D | 25.4/50.8/101.6 | 0.1 | Air-water | ||||
| Hibiki and Ishii (2002) [17] | Upward | 1D | 25.4/50.8 | 0.1 | Air-water | ) | |||
| Yao and Morel (2004) [18] | Upward | 3D | 19.2 | 1.46–26.17 | Air-dichlorodifluoromethane | ||||
| Nguyen et al. (2013) [19] | Upward | 3D | 80 | 0.2 | Air-water | ||||
| Channel Type | Investigators | Channel Size [mm] | Flow Conditions | Bubble Coalescence | Bubble Breakup | |||
|---|---|---|---|---|---|---|---|---|
| RC | WE | TI | SO | SI/Pressure Change | ||||
| Narrow confined channel | Sun et al. (2004) [43,69] | 10 200 | 0.1 MPa | |||||
| Ozar et al. (2013) [70] | Annular: 19.1 (inner)/38 (outer) | 0.58 MPa, = 0.23~3.31 m/s, = 0.04~3.06 m/s | ||||||
| Yang et al. (2016) [71] | 10.3 | 0.1~0.3 MPa | ||||||
| Round channel | Fu (2001) [72], Fu & Ishii (2003) [40] | 25~100 | 0.1 MPa | where | where , , | for , otherwise . | where | where , |
| Woroz (2015) [23] | 50.8 | 0.1 MPa | ||||||
| Wang et al. (2019) [24] | 25.4 | 0.1 MPa | ||||||
| Relatively larger channel (>2) | Smith (2002) [73] | 101.6/152.4 | 0.1 MPa | |||||
| Smith et al. (2012) [74,75] | 102~152 | 0.5 MPa, = 0.05~1 m/s, = 0.05~8 m/s | ||||||
| Schlegel et al. (2015) [76] | 304 | 0.1~0.3 MPa, = 2 m/s, = 11 m/s | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.; Wei, S.; Ding, W.; Wei, H.; Li, L.; Saxén, H.; Long, H.; Yu, Y. Interfacial Area Transport Equation for Bubble Coalescence and Breakup: Developments and Comparisons. Entropy 2021, 23, 1106. https://doi.org/10.3390/e23091106
Chen H, Wei S, Ding W, Wei H, Li L, Saxén H, Long H, Yu Y. Interfacial Area Transport Equation for Bubble Coalescence and Breakup: Developments and Comparisons. Entropy. 2021; 23(9):1106. https://doi.org/10.3390/e23091106
Chicago/Turabian StyleChen, Huiting, Shiyu Wei, Weitian Ding, Han Wei, Liang Li, Henrik Saxén, Hongming Long, and Yaowei Yu. 2021. "Interfacial Area Transport Equation for Bubble Coalescence and Breakup: Developments and Comparisons" Entropy 23, no. 9: 1106. https://doi.org/10.3390/e23091106
APA StyleChen, H., Wei, S., Ding, W., Wei, H., Li, L., Saxén, H., Long, H., & Yu, Y. (2021). Interfacial Area Transport Equation for Bubble Coalescence and Breakup: Developments and Comparisons. Entropy, 23(9), 1106. https://doi.org/10.3390/e23091106








