Extension of Operational Matrix Technique for the Solution of Nonlinear System of Caputo Fractional Differential Equations Subjected to Integral Type Boundary Constrains
Abstract
:1. Introduction
2. Preliminaries
The Shifted Legendre Polynomials (LP)
3. Operational Matrices (OP)
4. Application of Operational Matrices
4.1. Linear FDEs with Variable Coefficients
4.2. Nonlinear FDEs
- Approximate the initial solution, the solution of the linear part, by the method presented in previous section and name it and
- Linearize the nonlinear part at and . This will convert the system of nonlinear FDEs into a system of linear FDEs that is easily solvable with the method devolved. Solve it and name the solution as and .
- Repeat step 1.
5. Error Bound of the Approximate Solution and Convergence
5.1. Error Bound for Single Differential Equation
5.2. Error Bound for Coupled System of Fractional Differential Equations
6. Test Problems
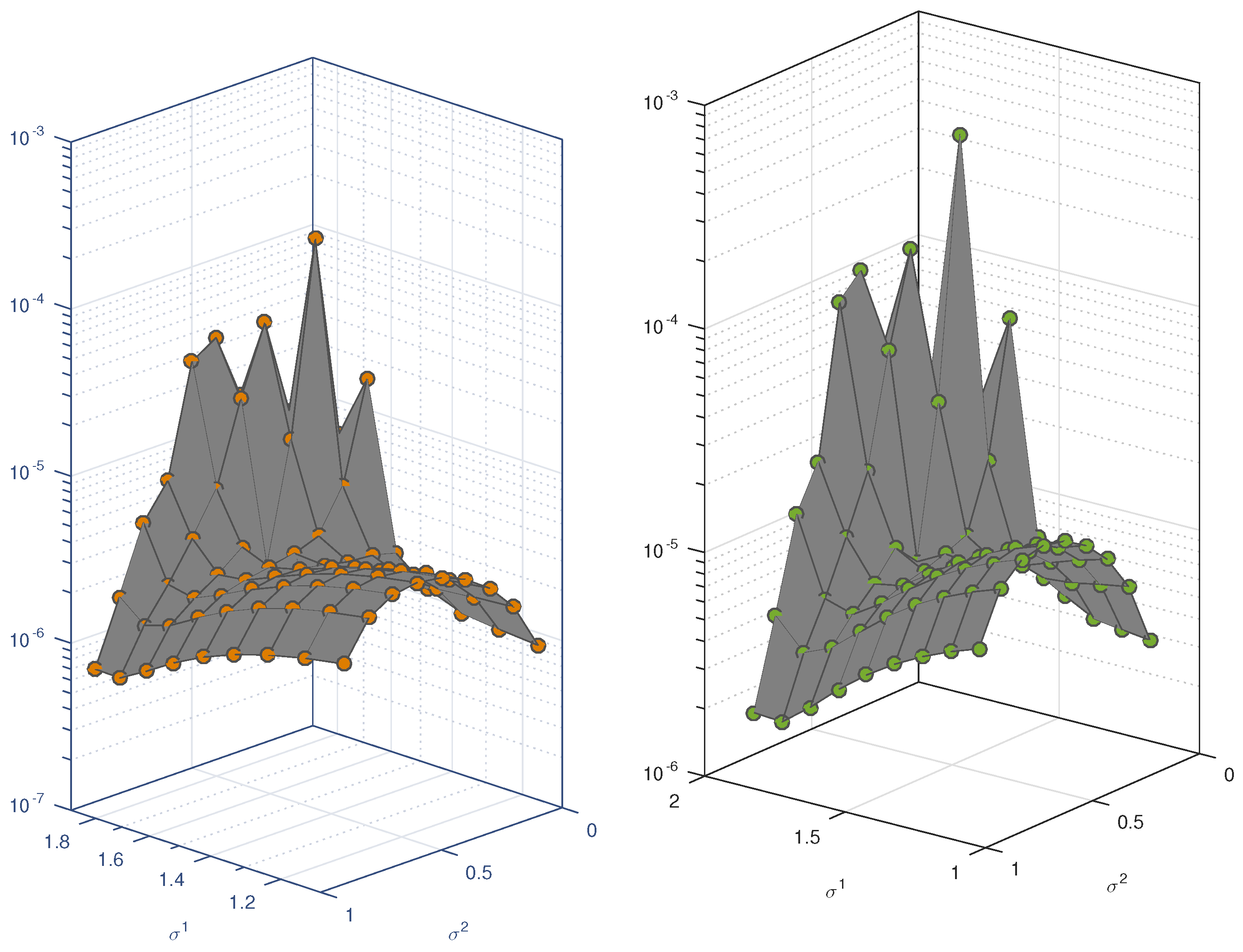
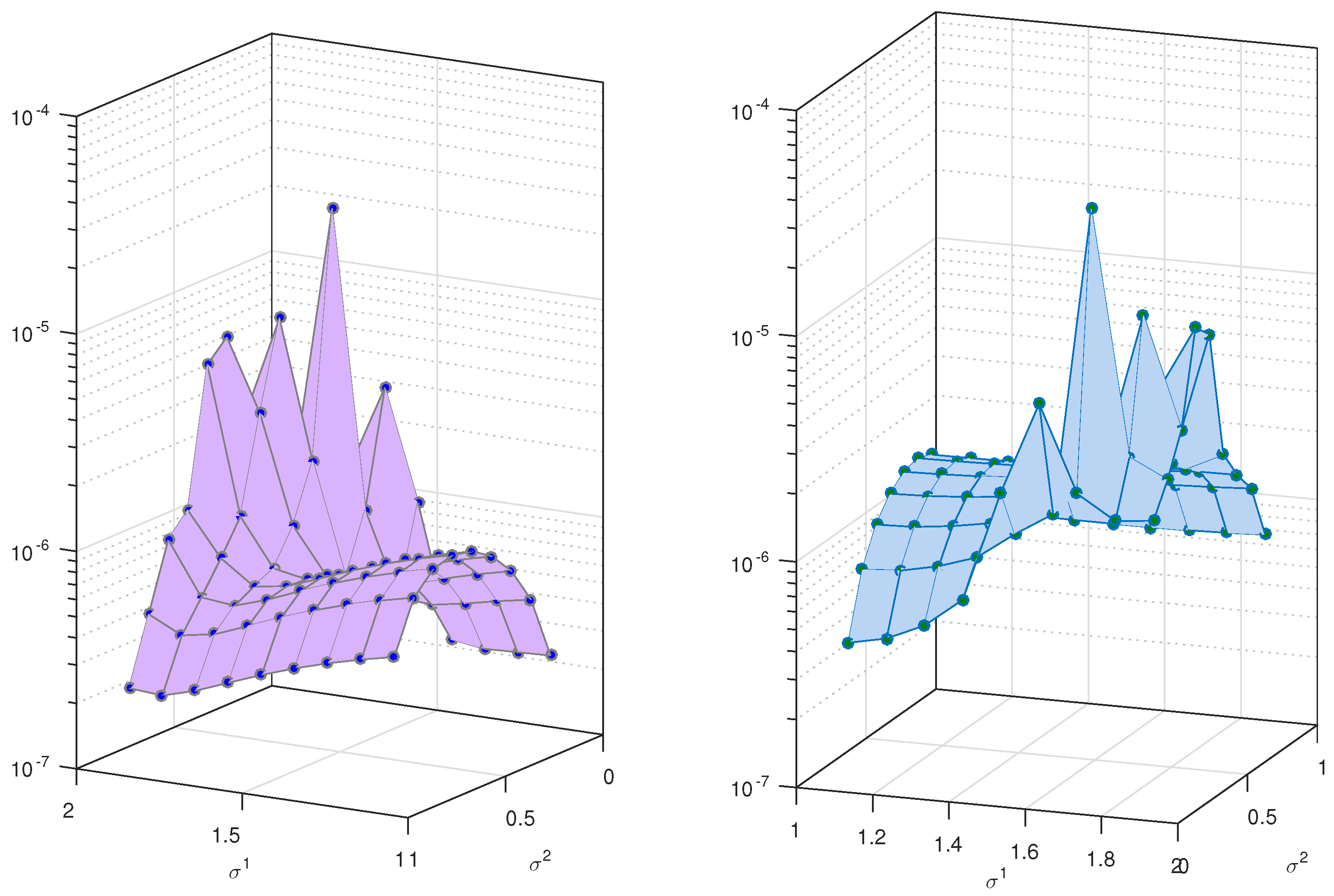
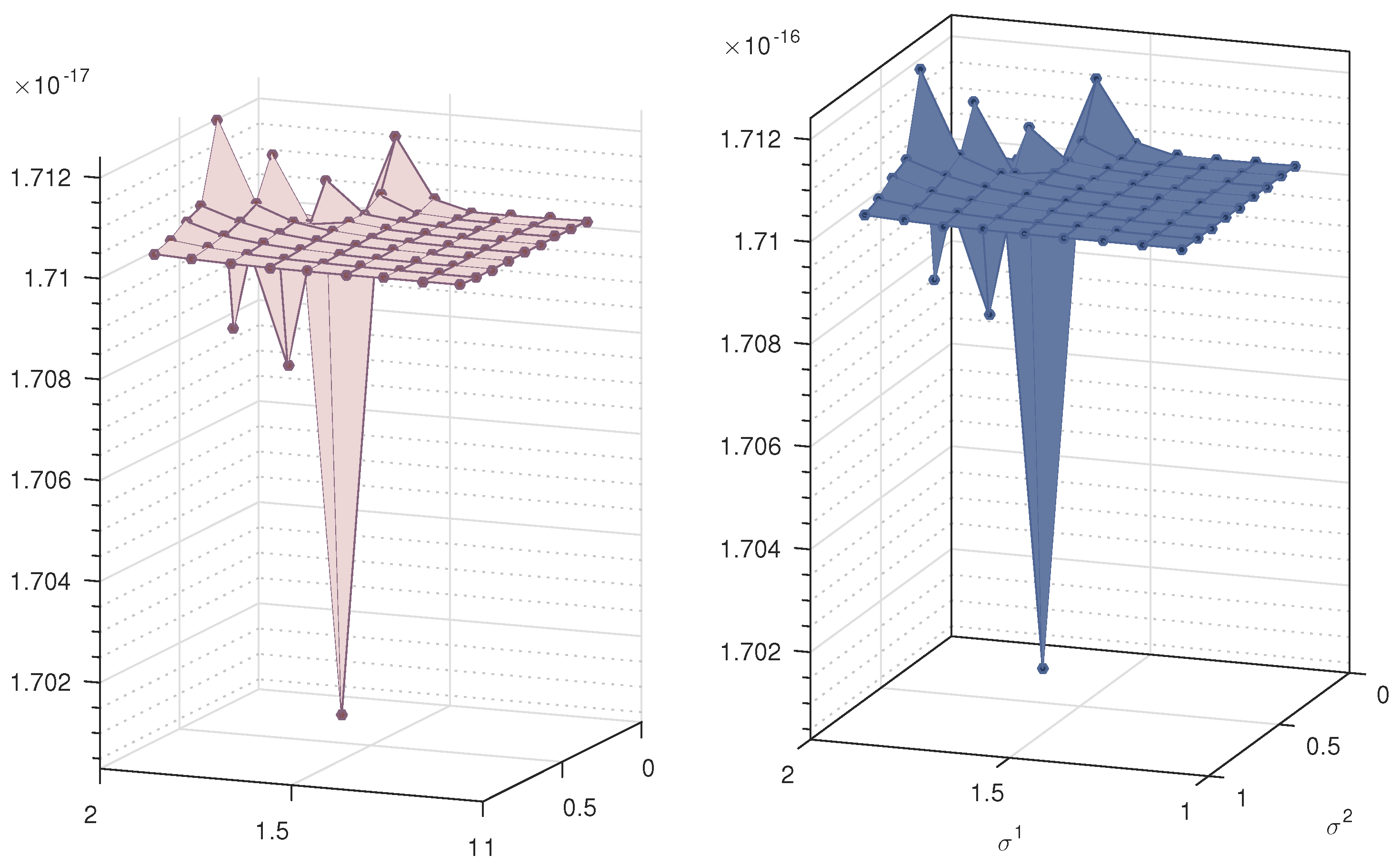
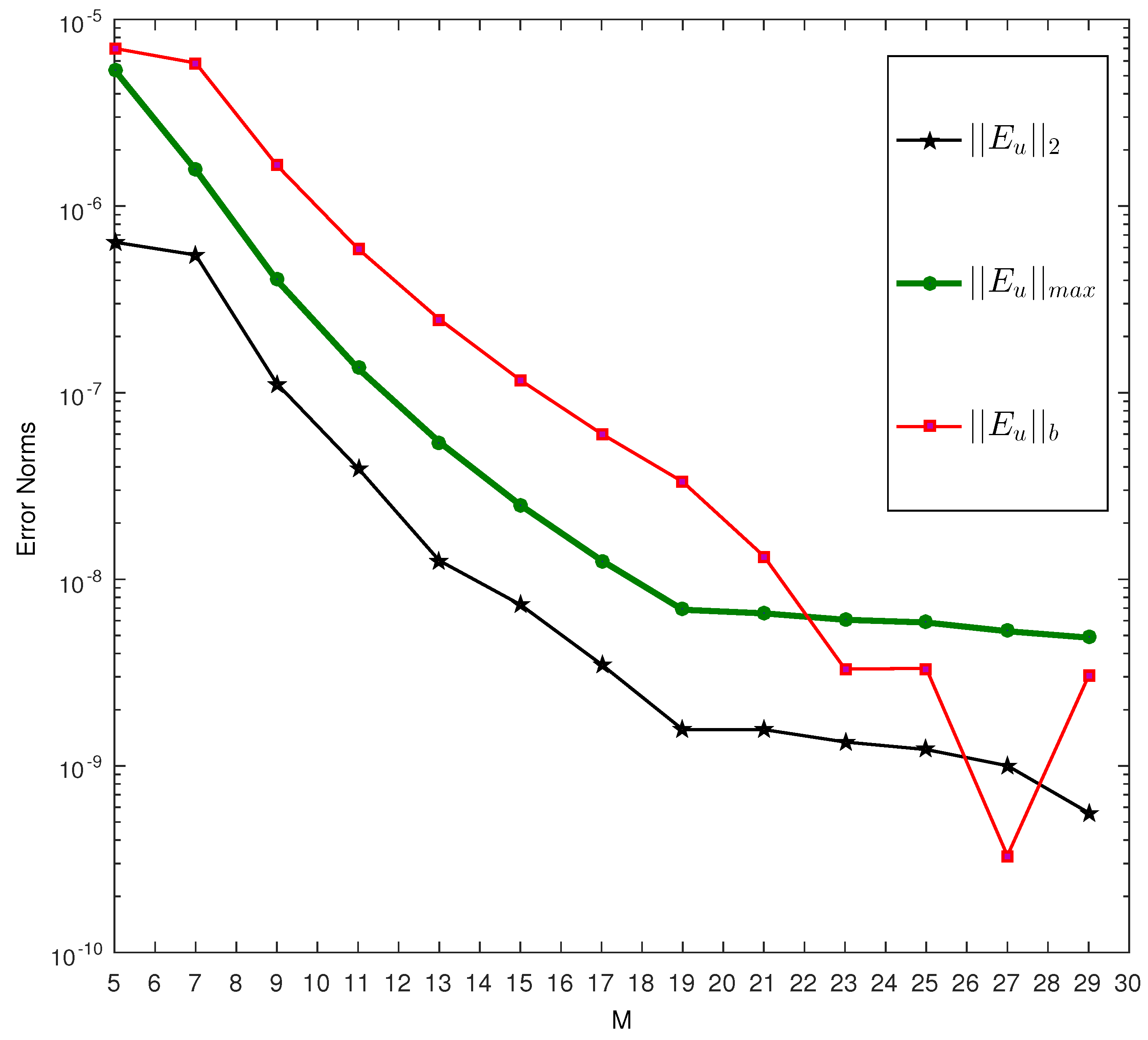
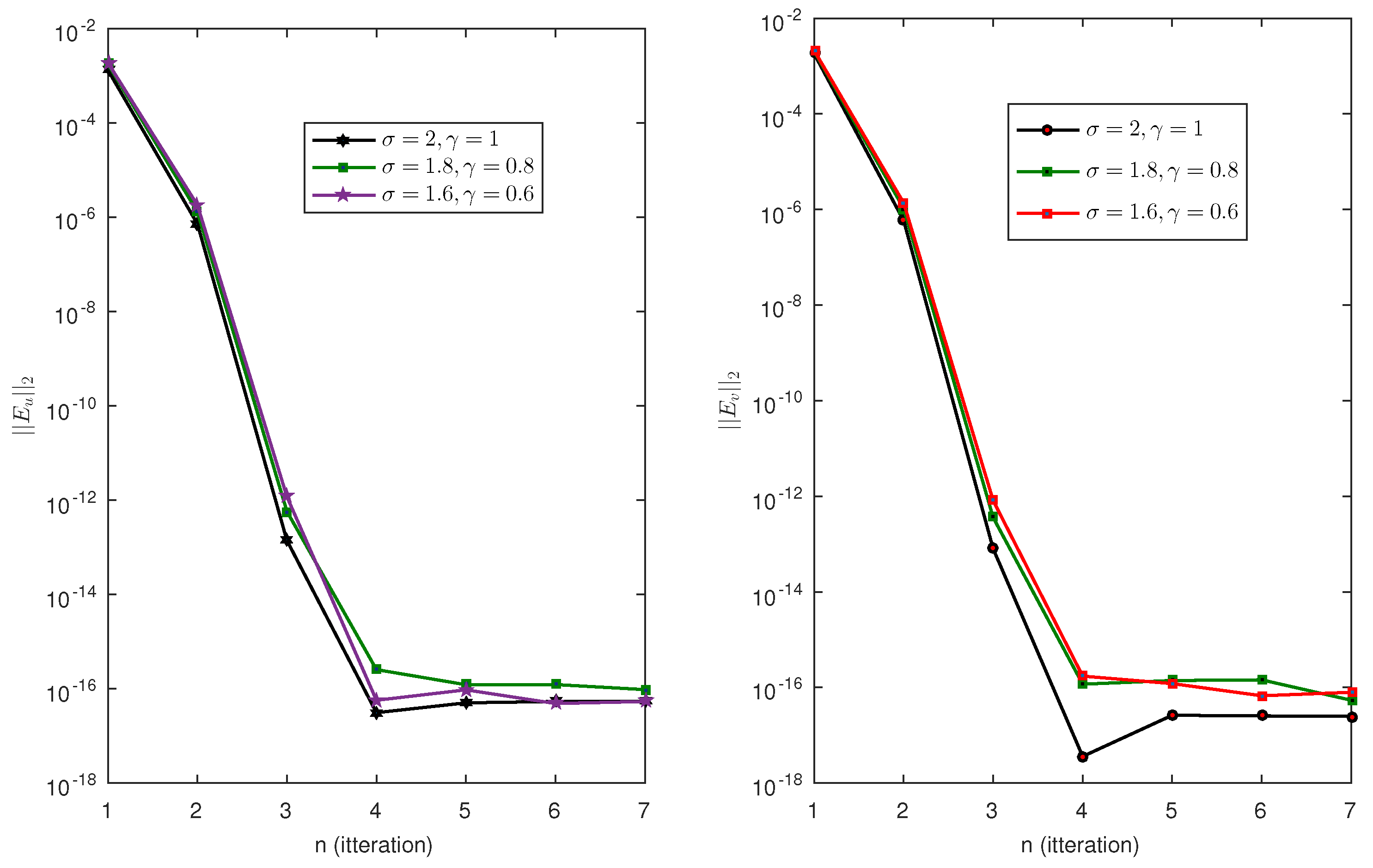
7. Results and Discussion
8. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Aytac, A.; Ozkol, I. Solution of fractional differential equations by using differential transform method. Chaos Solitons Fractals 2007, 34, 1473–1481. [Google Scholar]
- Muhammet, K.; Bayram, M. Approximate analytical solution for the fractional modified KdV by differential transform method. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 1777–1782. [Google Scholar]
- Che, H.C.H.; Kilicman, A. On the solution of fractional order nonlinear boundary value problems by using differential transformation method. Eur. J. Pure Appl. Math. 2011, 4, 174–185. [Google Scholar]
- Shaher, M.; Odibat, Z. Homotopy perturbation method for nonlinear partial differential equations of fractional order. Phys. Lett. A 2007, 365, 345–350. [Google Scholar]
- Zaid, O.; Momani, S. Modified homotopy perturbation method: Application to quadratic Riccati differential equation of fractional order. Chaos Solitons Fractals 2008, 36, 167–174. [Google Scholar]
- Mehdi, D.; Manafian, J.; Saadatmandi, A. Solving nonlinear fractional partial differential equations using the homotopy analysis method. Numer. Methods Partial Differ. Equ. Int. J. 2010, 26, 448–479. [Google Scholar]
- Saha, R.S.; Bera, R.K. An approximate solution of a nonlinear fractional differential equation by Adomian decomposition method. Appl. Math. Comput. 2005, 167, 561–571. [Google Scholar] [CrossRef]
- Varsha, D.-G.; Jafari, H. Solving a multi-order fractional differential equation using Adomian decomposition. Appl. Math. Comput. 2007, 189, 541–548. [Google Scholar]
- Shaher, M.; Odibat, Z. Numerical approach to differential equations of fractional order. J. Comput. Appl. Math. 2007, 207, 96–110. [Google Scholar]
- Bhrawy, A.H.; Alofi, A.S.; Ezz-Eldien, S.Z. A quadrature tau method for variable coefficients fractional differential equations. Appl. Math. Lett. 2011, 24, 2146–2152. [Google Scholar] [CrossRef] [Green Version]
- Bhrawy, A.H.; Alofi, A.S. A Jacobi–Gauss collocation method for solving nonlinear Lane-Emden type equations. Commun. Non. Sci. Numer. Simul. 2012, 17, 62–70. [Google Scholar] [CrossRef]
- Bhrawy, A.H. A shifted Legendre spectral method for fractional-order multi-point boundary value problems. Adv. Differ. Equ. 2012, 8, 2012. [Google Scholar] [CrossRef] [Green Version]
- Canuto, C.; Hussaini, M.Y.; Quarteroni, A.; Zang, T.A. Spectral Methods in Fluid Dynamics; Springer: New York, NY, USA, 1988. [Google Scholar]
- Canuto, C.; Hussaini, M.Y.; Quarteroni, A.; Zang, T.A. Spectral Methods: Fundamentals in Single Domains; Springer: New York, NY, USA, 2006. [Google Scholar]
- Doha, E.H.; Bhrawy, A.H.; Hafez, R.M. A Jacobi-Jacobi dual-Petrov-Galerkin method for third- and fifth-order differential equations. Math. Comput. Model. 2011, 53, 1820–1832. [Google Scholar] [CrossRef]
- Doha, E.H.; Bhrawy, A.H.; Saker, M.A. Integrals of Bernstein polynomials: An application for the solution of high even-order differential equations. Appl. Math. Lett. 2011, 24, 559–565. [Google Scholar] [CrossRef] [Green Version]
- Doha, E.H.; Bhrawy, A.H.; Saker, M.A. On the Derivatives of Bernstein Polynomials: An application for the solution of higher even-order differential equations. Bound. Value Probl. 2011, 16, 2011. [Google Scholar] [CrossRef] [Green Version]
- Doha, E.H.; Bhrawy, A.H.; Ezz-Eldien, S.S. Efficient Chebyshev spectral methods for solving multi-term fractional orders differential equations. Appl. Math. Model. 2011, 35, 5662–5672. [Google Scholar] [CrossRef]
- Doha, E.H.; Bhrawy, A.H.; Ezz-Eldien, S.S. A Chebyshev spectral method based on operational matrix for initial and boundary value problems of fractional order. Comput. Math. Appl. 2011, 62, 2364–2373. [Google Scholar] [CrossRef] [Green Version]
- Doha, E.H.; Bhrawy, A.H.; Hafez, R.M. A Jacobi dual-Petrov-Galerkin method for solving some odd-order ordinary differential equations. Abstr. Appl. Anal. 2011, 2011, 947230. [Google Scholar] [CrossRef] [Green Version]
- Khalil, H.; Khan, R.A. A new method based on Legendre polynomials for solutions of the fractional two-dimensional heat conduction equation. Comput. Math. Appl. 2014, 67, 1938–1953. [Google Scholar] [CrossRef]
- Khalil, H.; Khan, R.A. New operational matrix of integration and coupled system of fredholm integral equations. Chin. J. Math. 2014, 2014, 146013. [Google Scholar] [CrossRef]
- Khalil, H.; Khan, R.A. A new method based on legender polynomials for solution of system of fractional order partial differential equation. Int. J. Comput. Math. 2014, 91, 2554–2567. [Google Scholar] [CrossRef]
- Khalil, H.; Khan, R.A. The use of Jacobi polynomials in the numerical solution of coupled system of fractional differential equations. Int. J. Comput. Math. 2014, 92, 1452–1472. [Google Scholar] [CrossRef]
- Khalil, H.; Khan, R.A. New Operational Matrix For Shifted Legendre Polynomials and Fractional Differential Equations with Variable Coefficients. J. Math. 2020, 47, 81–103. [Google Scholar]
- Saadatmandi, A.; Deghan, M. A new operational matrix for solving fractional-order differential equation. Comput. Math. Appl. 2010, 59, 1326–1336. [Google Scholar] [CrossRef] [Green Version]
- Almomani, R.; Almefleh, H. On Heat Conduction Problem with Integral Boundary Condition. J. Em. T. Eng. Sci. 2012, 3, 977–979. [Google Scholar]
- Ma, R. A survey on nonlocal boundary value problems. Appl. Math. E-Notes 2007, 7, 257–279. [Google Scholar]
- Eziani, D.G.; Shvili, G.A. Investigation of the nonlocal initial boundary value problems for some hyperbolic equations. Hiroshima Math. J. 2001, 31, 345–366. [Google Scholar]
- Berikelashvili, G.; Khomeriki, N. On a numerical solution of one nonlocal boundary-value problem with mixed Dirichlet–Neumann conditions. Lith. Math. J. 2013, 53, 367–380. [Google Scholar] [CrossRef]
- Sajavicius, S. Radial basis function method for a multidimensional linear elliptic equation with nonlocal boundary conditions. Comput. Math. Appl. 2014, 67, 1407–1420. [Google Scholar] [CrossRef]
- Vaqueroa, J.M.; Aguiar, J. On the numerical solution of the heat conduction equations subject to nonlocal conditions. Appl. Numer. Math. 2009, 59, 2507–2514. [Google Scholar] [CrossRef]
- Siddique, M. Smoothing of cranknicolson scheme for the two-dimensional diffusion with an integral condition. Appl. Math. Comput. 2009, 214, 512–522. [Google Scholar]
- Yang, A.M.; Zhang, Y.Z.; Cattani, C.; Xie, G.N.; Rashidi, M.M.; Zhou, Y.J.; Yang, X.J. Application of Local Fractional Series Expansion Method to Solve Klein-Gordon Equations on Cantor Sets. Abstr. Appl. Anal. 2014, 2014, 372741. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, D.; Abbasbandy, S.; Rashidi, M.M. Analytical solution of fractional Navier–Stokes equation by using modified Laplace decomposition method. Ain Shams Eng. J. 2014, 5, 569–574. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y. Numerical solution of the heat equation with nonlocal boundary condition. J. Comput. Appl. Math. 1999, 110, 115–127. [Google Scholar] [CrossRef] [Green Version]
- Ang, W. A method of solution for the one-dimensional heat equation subject to nonlocal condition. Southeast Asian Bull. Math. 2002, 26, 185–191. [Google Scholar] [CrossRef]
- Dehghan, M. The one-dimensional heat equation subject to a boundary integral specification. Chaos Solitons Fractals 2007, 32, 661–675. [Google Scholar] [CrossRef]
- Noye, K.H.B.J. Explicit two-level finite difference methods for the two-dimensional diffusion equation. Int. J. Comput. Math. 1992, 42, 223–236. [Google Scholar] [CrossRef]
- Avalishvili, G.; Avalishvili, M.; Gordeziani, D. On integral nonlocal boundary value problems for some partial differential equations. Bull. Georgian Natl. Acad. Sci. 2011, 5, 31–37. [Google Scholar]
- Petras, I. A note on the fractional-order Chuas system. Chaos Solitons Fractals 2008, 38, 140–147. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations. In Mathematics in Science and Engineering; Academic Press Inc.: San Diego, CA, USA, 1999; Volume 198. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives: Theory and Applications; Gordon and Breach: Yverdon, Switzerland, 1993. [Google Scholar]
- Ma, R. Multiple positive solutions for nonlinear m-point boundary value problems. Appl. Math. Comput. 2004, 148, 249–262. [Google Scholar] [CrossRef]
- Ahmad, B. Approximation of solutions of the forced Duffing equation with m-point boundary conditions. Commun. Appl. Anal. 2009, 13, 11–20. [Google Scholar]
- Agarwal, R.P.; Chow, Y.M. Iterative methods for a fourth order boundary value problem. J. Comput. Appl. Math. 1984, 10, 203–217. [Google Scholar] [CrossRef] [Green Version]
- AkyuzDascioglu, A.; Isler, N. Bernstein collocation method for solving nonlinear differential equations. Math. Comput. Appl. 2013, 18, 293–300. [Google Scholar]
- Bellman, R.E.; Kalaba, R.E. Quasilinearization and Non-Linear Boundary Value Problems; Elsevier: New York, NY, USA, 1965. [Google Scholar]
- Charles, A.; Baird, J. Modified quasilinearization technique for the solution of boundary-value problems for ordinary differential equations. J. Optim. Theory Appl. 1969, 3, 227–242. [Google Scholar]
- Mandelzweig, V.B.; Tabakin, F. Quasilinearization approach to nonlinear problems in physics with application to nonlinear ODEs. Comput. Phys. Commun. 2001, 141, 268–281. [Google Scholar] [CrossRef] [Green Version]
- Gupta, C.P. Solvability of a three-point nonlinear boundary value problem for a second order ordinary differential equation. J. Math. Anal. Appl. 1992, 168, 540–551. [Google Scholar] [CrossRef] [Green Version]
- Saeed, U.; ur Rehman, M. Wavelet-Galerkin Quasilinearization Method for Nonlinear Boundary Value Problems. Abstr. Appl. Ana. 2014, 2014, 868934. [Google Scholar] [CrossRef] [Green Version]
- Stanley, E.L. Quasilinearization and Invariant Imbedding; Academic Press: New York, NY, USA, 1968. [Google Scholar]


| M | |||
|---|---|---|---|
| 5 | |||
| 6 | |||
| 7 | |||
| 8 | |||
| 9 | |||
| 10 | |||
| 11 | |||
| 12 | |||
| 13 |
| M | ||||||
|---|---|---|---|---|---|---|
| 5 | ||||||
| 6 | ||||||
| 7 | ||||||
| 8 | ||||||
| 9 | ||||||
| 10 | ||||||
| 11 | ||||||
| 12 | ||||||
| 13 |
| N | ||||||
|---|---|---|---|---|---|---|
| 5 | ||||||
| 6 | ||||||
| 7 | ||||||
| 8 | ||||||
| 9 | ||||||
| 10 | ||||||
| 11 | ||||||
| 12 | ||||||
| 13 |
| N | ||||||
|---|---|---|---|---|---|---|
| 5 | ||||||
| 6 | ||||||
| 7 | ||||||
| 8 | 9.6413 × | |||||
| 9 | ||||||
| 10 | ||||||
| 11 | ||||||
| 12 | ||||||
| 13 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khalil, H.; Khalil, M.; Hashim, I.; Agarwal, P. Extension of Operational Matrix Technique for the Solution of Nonlinear System of Caputo Fractional Differential Equations Subjected to Integral Type Boundary Constrains. Entropy 2021, 23, 1154. https://doi.org/10.3390/e23091154
Khalil H, Khalil M, Hashim I, Agarwal P. Extension of Operational Matrix Technique for the Solution of Nonlinear System of Caputo Fractional Differential Equations Subjected to Integral Type Boundary Constrains. Entropy. 2021; 23(9):1154. https://doi.org/10.3390/e23091154
Chicago/Turabian StyleKhalil, Hammad, Murad Khalil, Ishak Hashim, and Praveen Agarwal. 2021. "Extension of Operational Matrix Technique for the Solution of Nonlinear System of Caputo Fractional Differential Equations Subjected to Integral Type Boundary Constrains" Entropy 23, no. 9: 1154. https://doi.org/10.3390/e23091154








