Localization, Disorder, and Entropy in a Coarse-Grained Model of the Amorphous Solid
Abstract
:1. Introduction
2. Entropy of Delocalization
2.1. The Coarse Grained Model
2.2. Microscopic Description
2.2.1. Debye Distribution
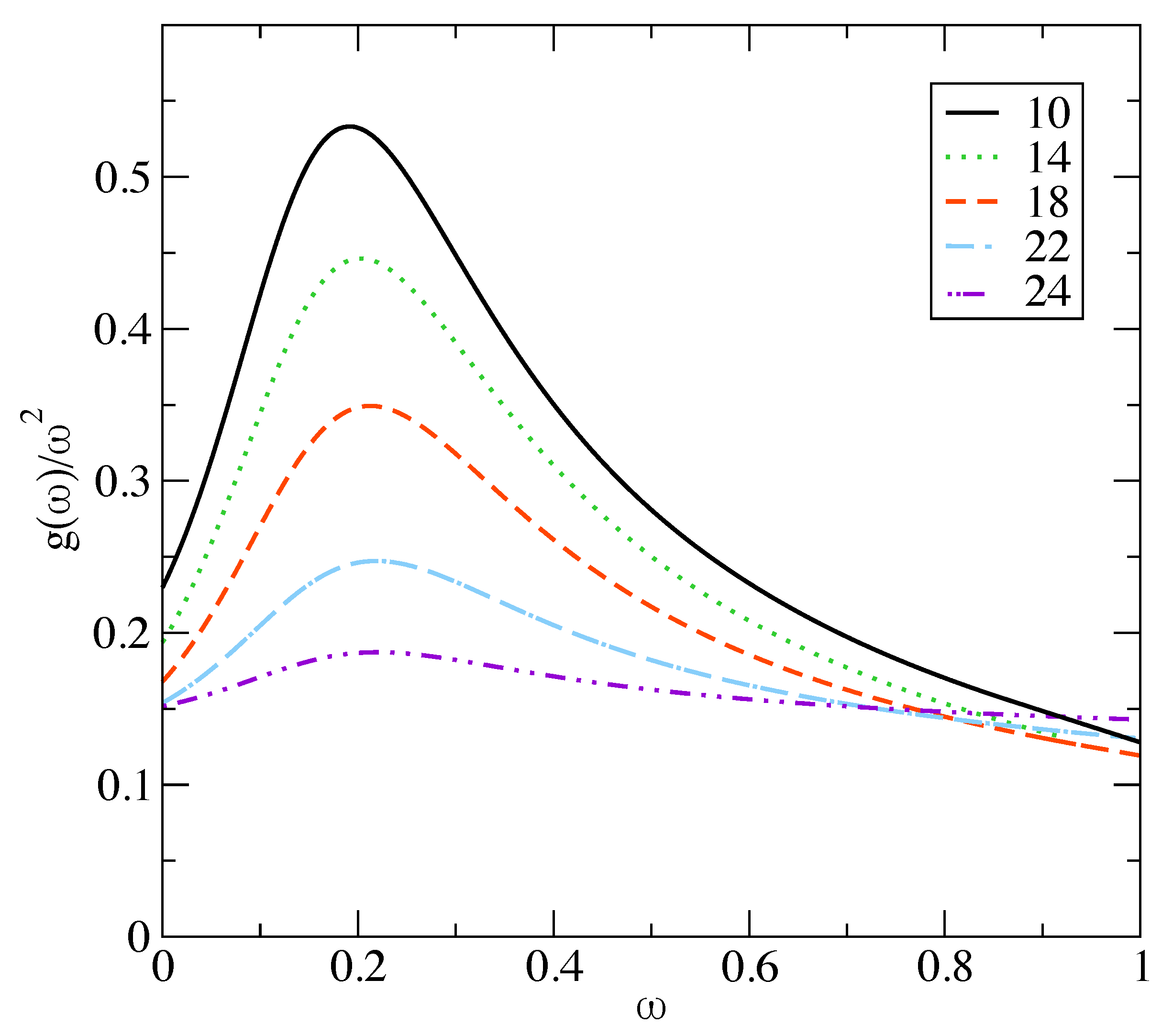
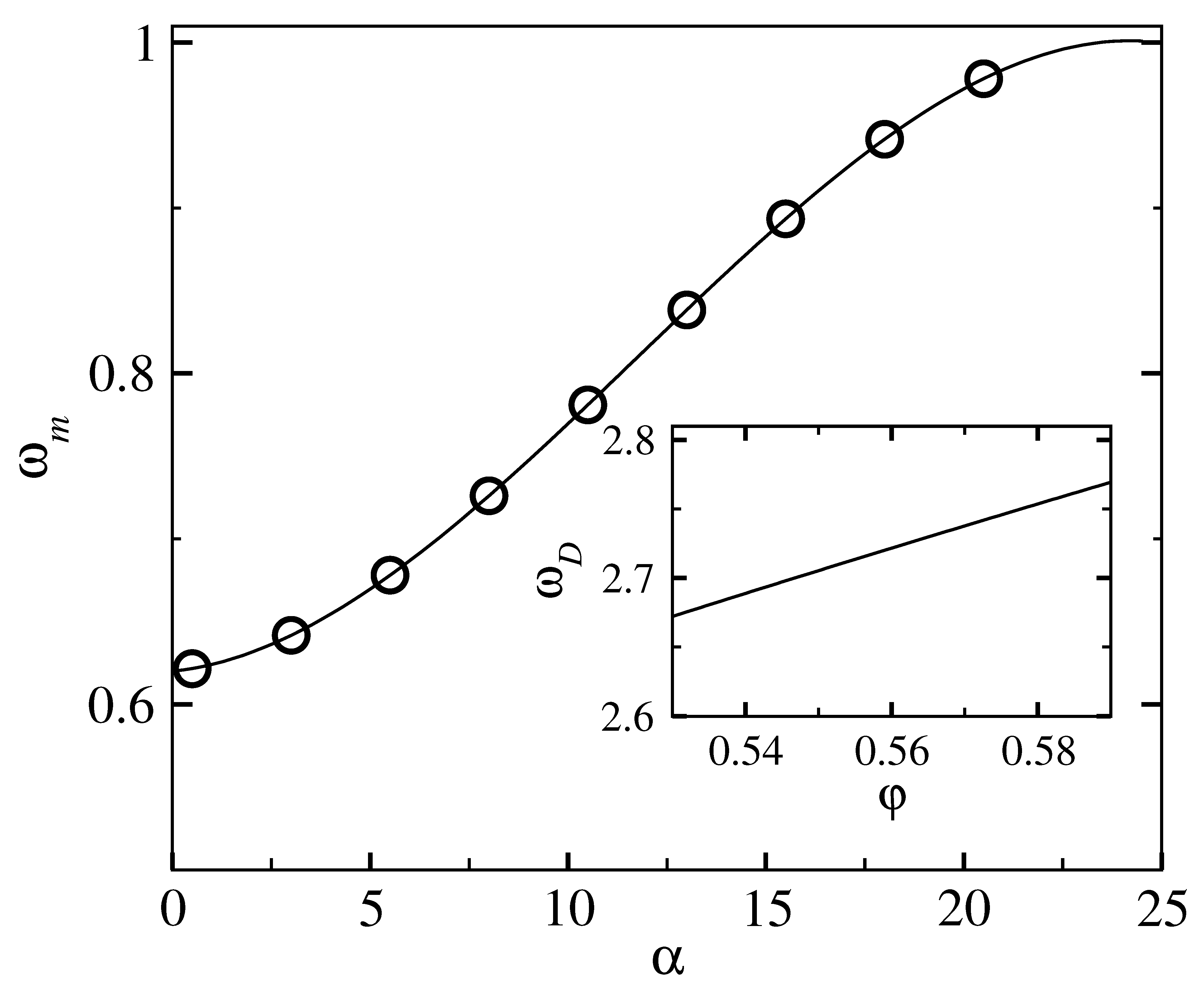
2.2.2. Excess Density of States
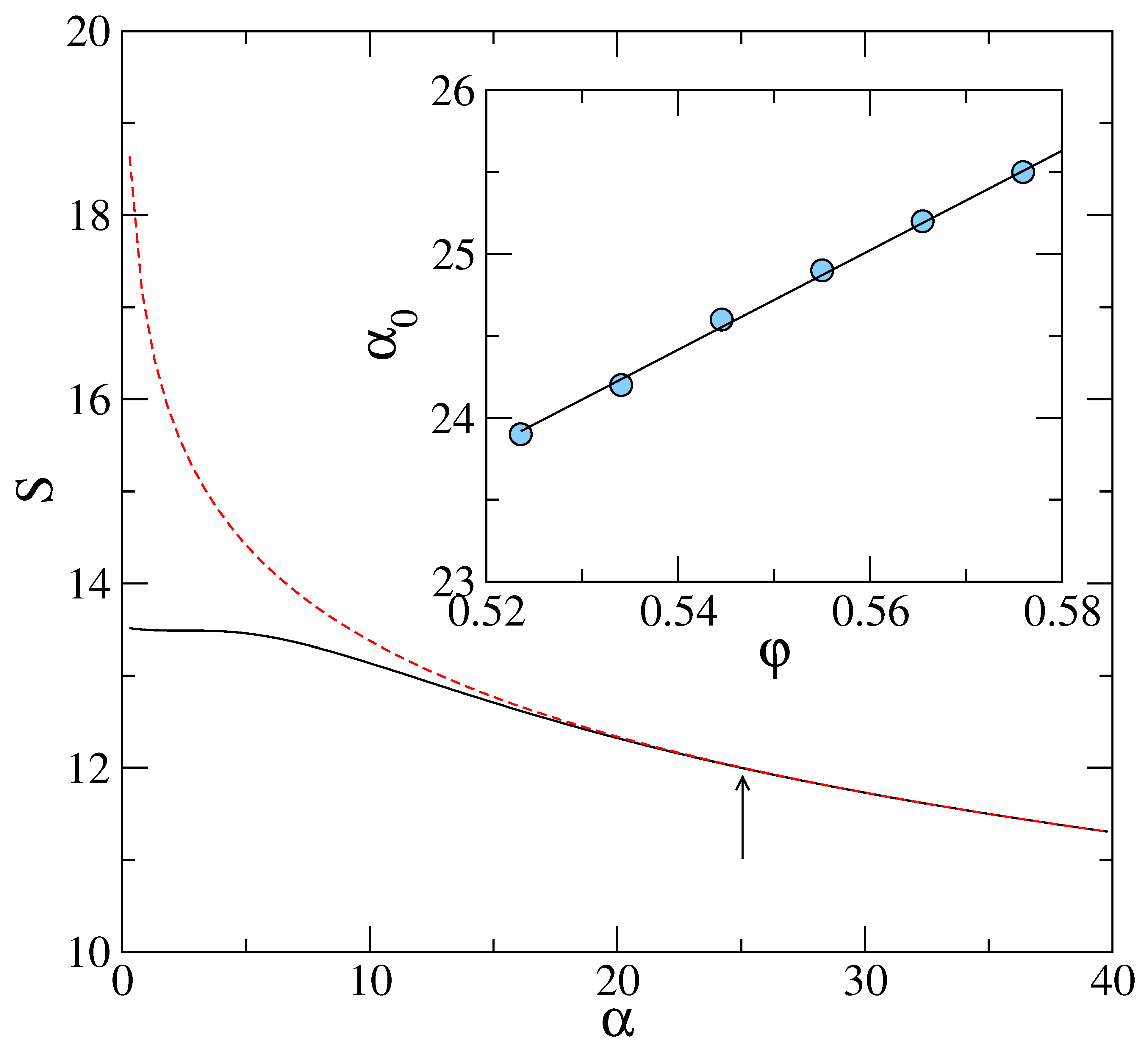
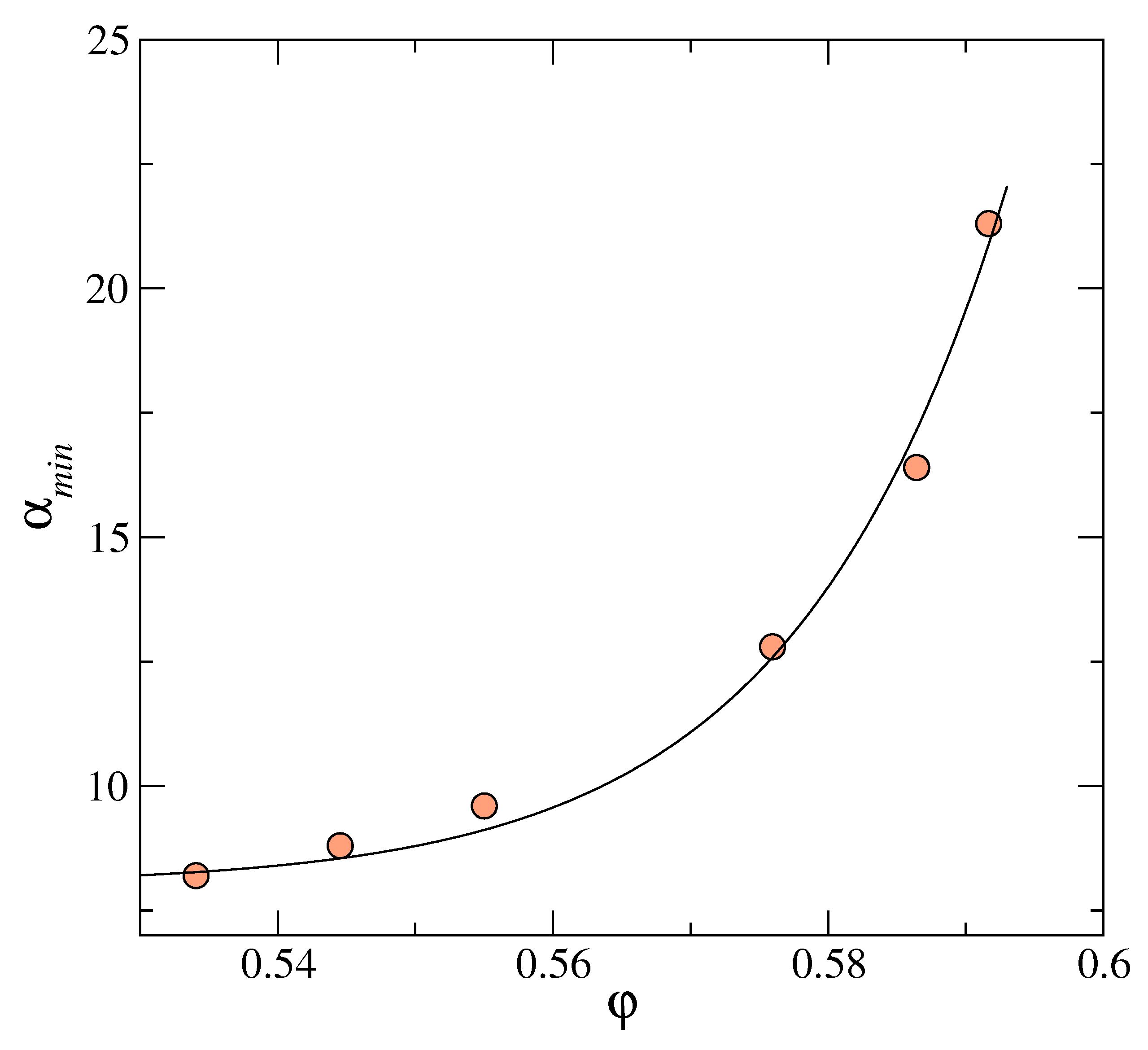
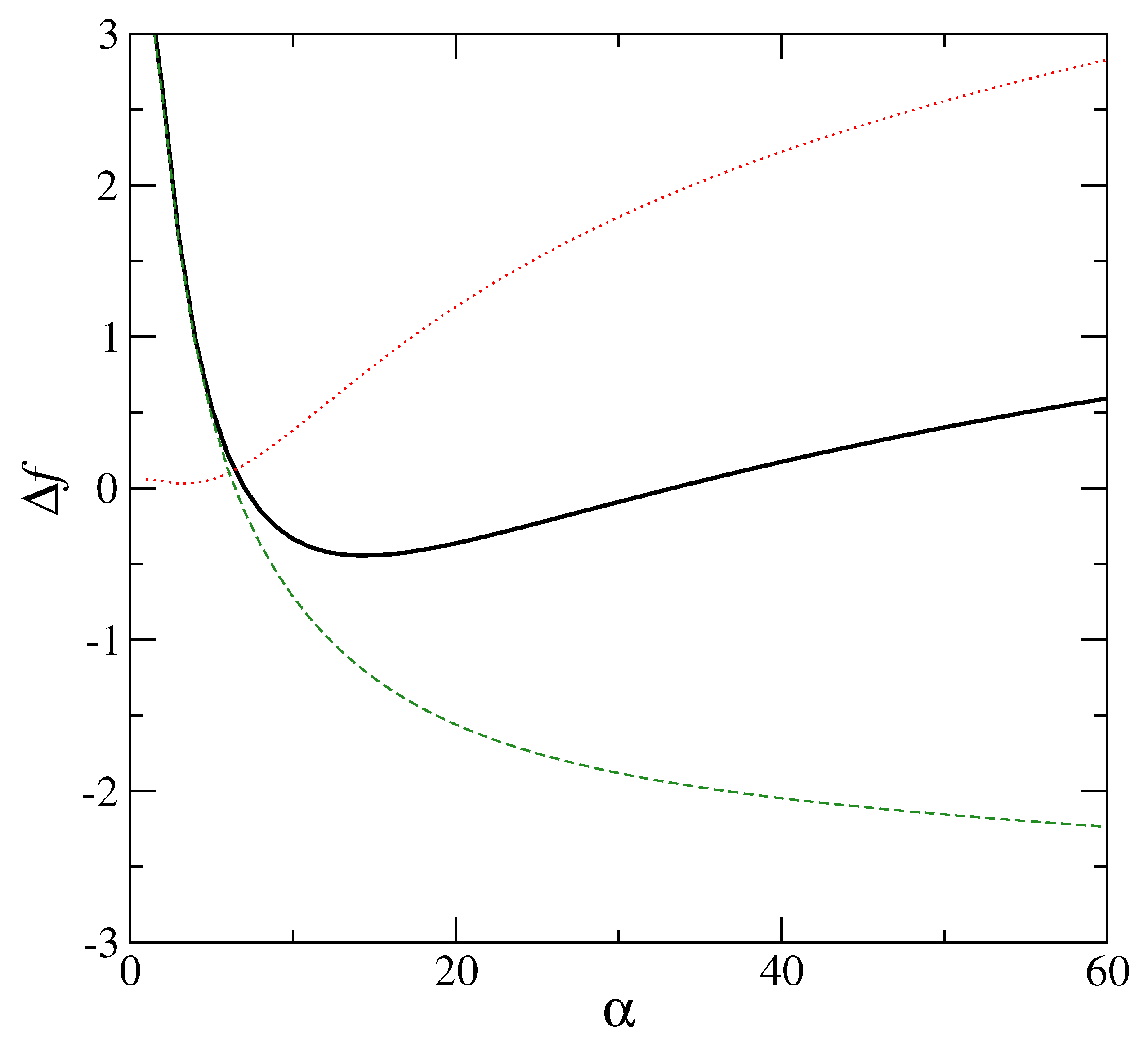
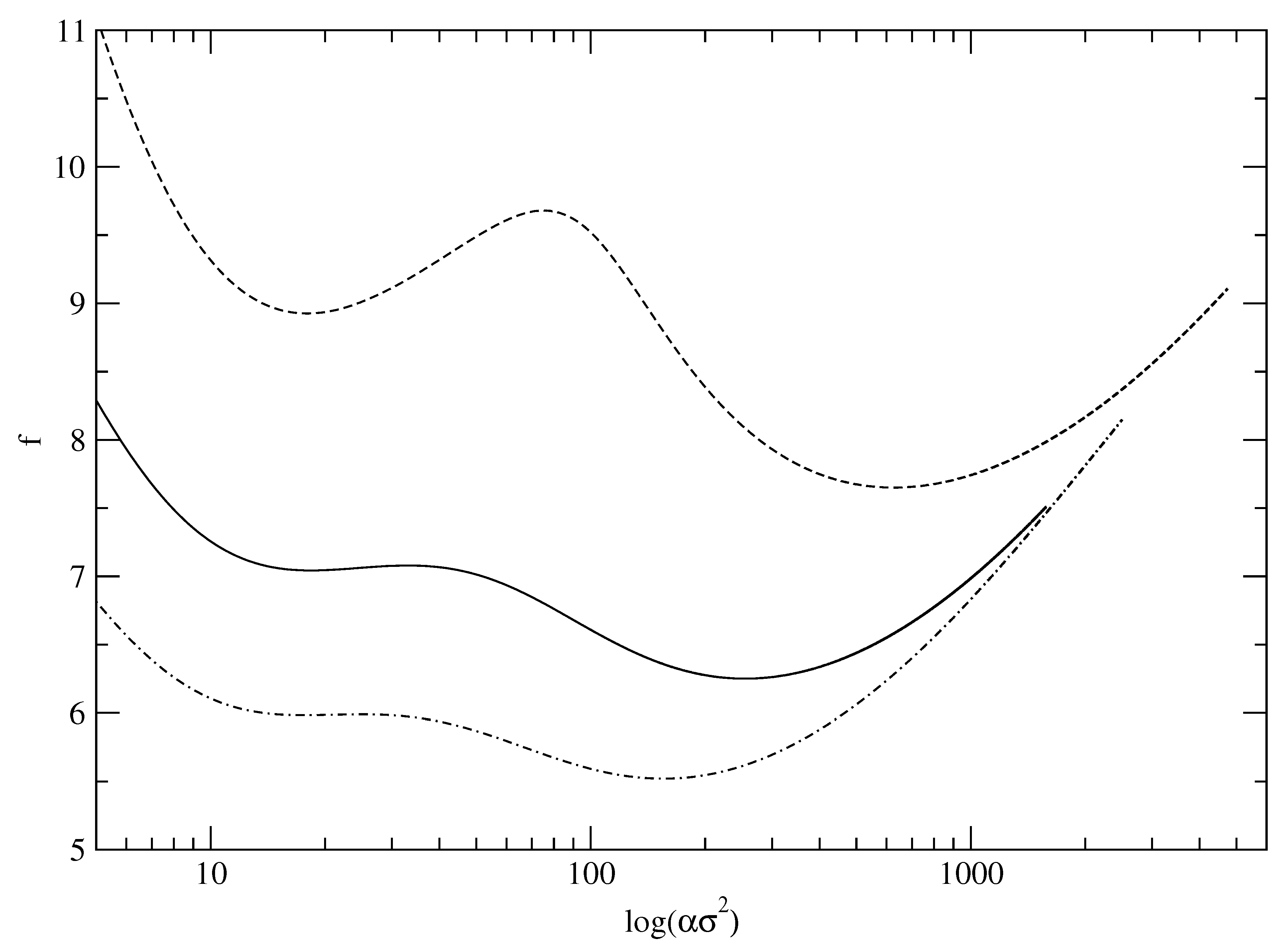
3. The Free Energy Landscape
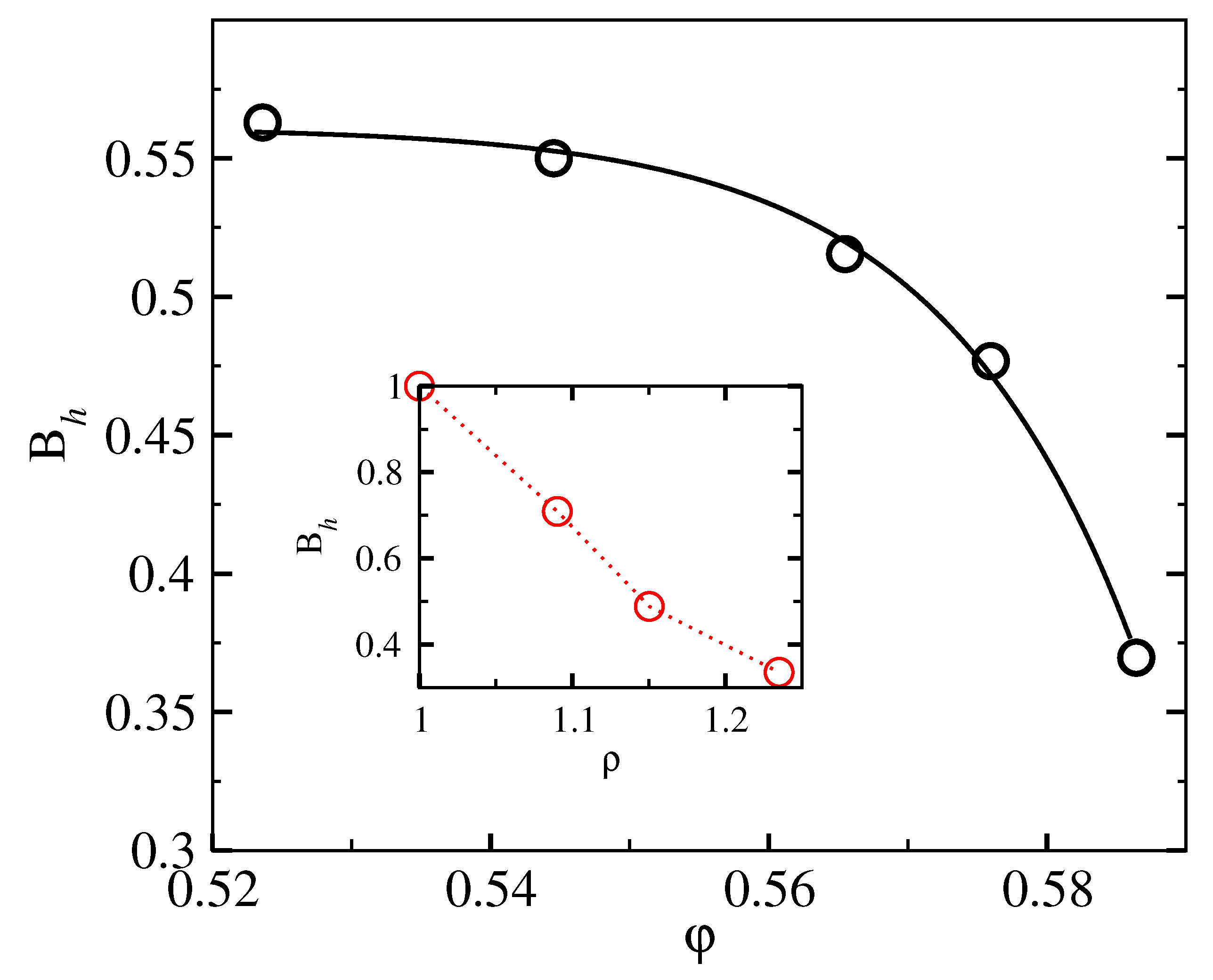
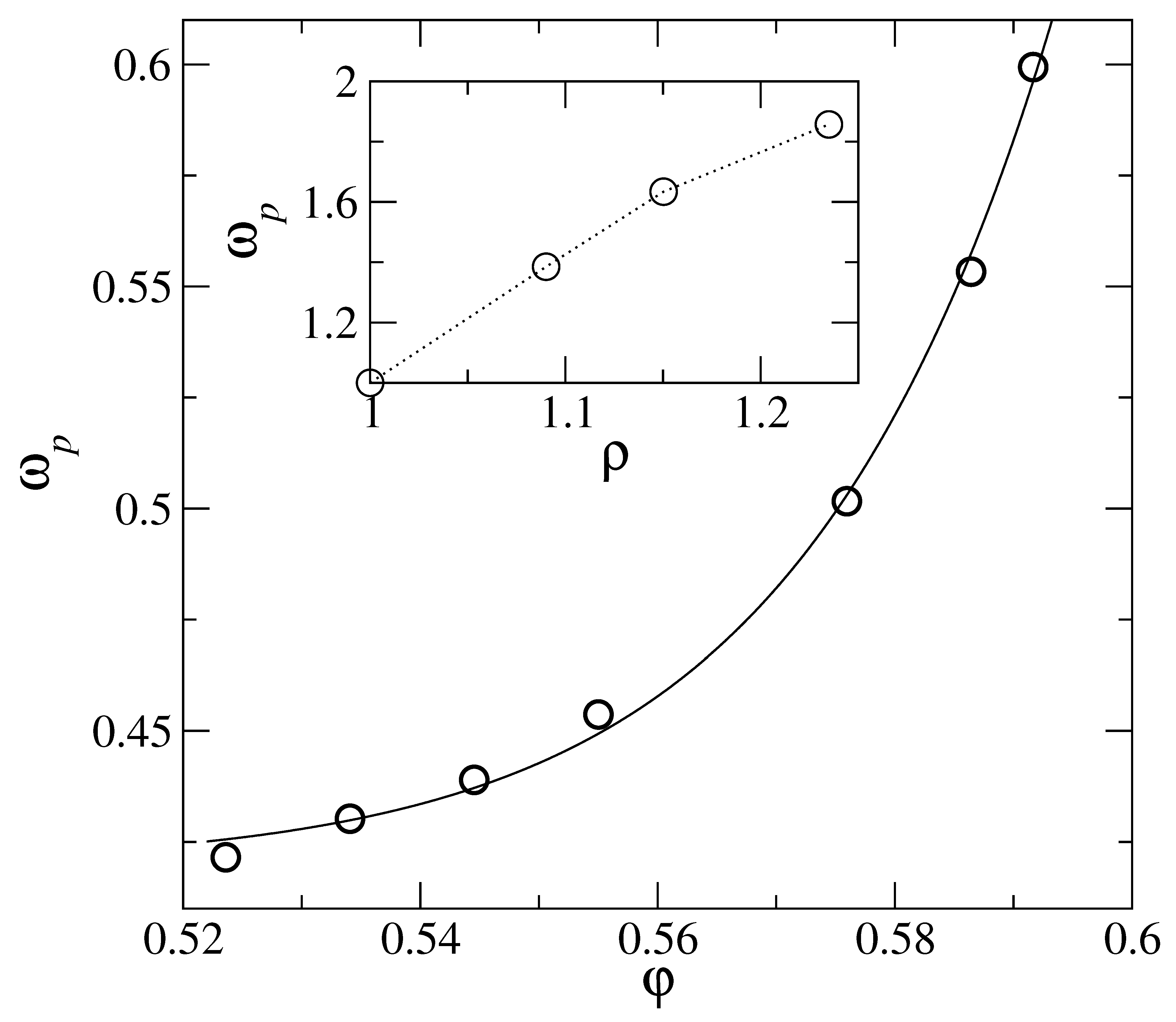
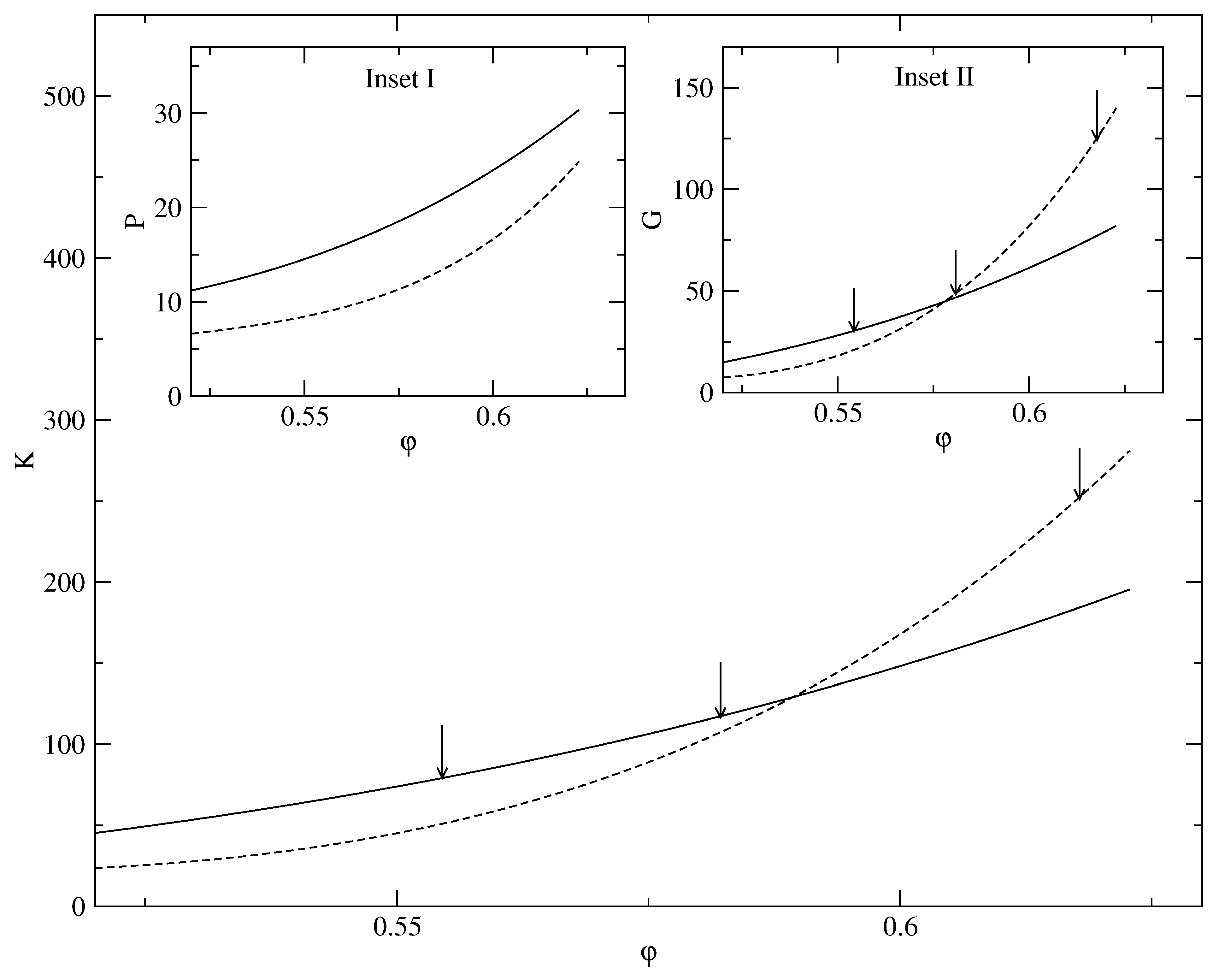
4. Elasticity of the Localized State
5. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Alder, B.J.; Wainright, T.E. Decay of the velocity autocorrelation function. Phys. Rev. A 1970, 1, 18. [Google Scholar] [CrossRef]
- Ramakrishnan, T.V.; Yussouff, M. First-principles order-parameter theory of freezing. Phys. Rev. B 1979, 19, 2775. [Google Scholar] [CrossRef]
- Das, S.P. Statistical Physics of Liquids at Freezing and Beyond; Cambridge University Press: NewYork, NY, USA, 2011. [Google Scholar]
- Tarazona, P. A density functional theory of melting. Mol. Phys. 1984, 52, 871. [Google Scholar] [CrossRef]
- Singh, Y.; Stoessel, J.P.; Wolynes, P.G. Hard-sphere glass and the density-functional theory of aperiodic crystals. Phys. Rev. Lett. 1985, 54, 1059. [Google Scholar] [CrossRef]
- Dasgupta, C. Glass transition in the density functional theory of freezing. Europhys. Lett. 1992, 20, 131. [Google Scholar] [CrossRef]
- Kaur, C.; Das, S.P. Heterogeneities in supercooled liquids: A density-functional study. Phys. Rev. Lett. 2001, 86, 2062. [Google Scholar] [CrossRef] [Green Version]
- Goldstone, J. Field theories with «Superconductor» solutions. Nuovo C 1961, 19, 15. [Google Scholar] [CrossRef]
- Zeller, R.C.; Pohl, R.O. Thermal conductivity and specific heat of noncrystalline solids. Phys. Rev. B 1971, 4, 2029. [Google Scholar] [CrossRef]
- Monaco, A.; Chumakov, A.I.; Monaco, G.; Crichton, W.A.; Meyer, A.; Comez, L.; Fioretto, D.; Korecki, J.; Rüffer, R. Effect of densification on the density of vibrational states of glasses. Phys. Rev. Lett. 2006, 97, 135501. [Google Scholar] [CrossRef] [PubMed]
- Grigera, T.S.; Martin-Mayor, V.; Parisi, G.; Verrocchio, P. Phonon interpretation of the ‘boson peak’ in supercooled liquids. Nature 2003, 422, 289. [Google Scholar] [CrossRef] [PubMed]
- Duval, E.; Boukenter, A.; Achibat, T. Vibrational dynamics and the structure of glasses. J. Phys. Cond. Matt. 1990, 2, 0227. [Google Scholar] [CrossRef]
- Das, S.P. Model of defect diffusion and development of the boson peak in an amorphous solid. Phys. Rev. E 1999, 59, 3870. [Google Scholar] [CrossRef]
- Parshin, D.A.; Schober, H.R.; Gurevich, V.L. Vibrational instability, two-level systems, and the boson peak in glasses. Phys. Rev. B 2007, 76, 064206. [Google Scholar] [CrossRef] [Green Version]
- Lubchenko, V.; Wolynes, P.G. Theory of structural glasses and supercooled liquids. Proc. Natl. Acad. Sci. USA 2003, 100, 1515. [Google Scholar] [CrossRef] [Green Version]
- Schirmacher, W.; Diezemann, G.; Ganter, C. Harmonic vibrational excitations in disordered solids and the “boson peak”. Phys. Rev. Lett. 1998, 81, 136. [Google Scholar] [CrossRef] [Green Version]
- Sokolov, A.P. Vibrations at the boson peak: Random-and coherent-phase contributions. J. Phys. Condens. Matter 1999, 11, A213. [Google Scholar] [CrossRef]
- Schirmacher, W.; Ruocco, G.; Scopigno, T. Acoustic attenuation in glasses and its relation with the boson peak. Phys. Rev. Lett. 2007, 98, 025501. [Google Scholar] [CrossRef] [Green Version]
- Dove, M.T.; Harris, M.J.; Hannon, A.C.; Parker, J.M.; Swainson, I.; Gambhir, M. Floppy modes in crystalline and amorphous silicates. Phys. Rev. Lett. 1997, 78, 1070. [Google Scholar] [CrossRef] [Green Version]
- Zorn, R. Boson peak in confined disordered systems. Phys. Rev. B 2010, 81, 054208. [Google Scholar] [CrossRef] [Green Version]
- Shen, Y.C.; Oxtoby, D.W. Nucleation of Lennard-Jones fluids: A density functional approach. J. Chem. Phys. 1996, 105, 6517. [Google Scholar] [CrossRef]
- Bernal, J.D. The Bakerian lecture, 1962. The structure of liquids. Proc. R. Soc. Lond. Ser. A 1964, 280, 299. [Google Scholar]
- Bennett, C. Serially deposited amorphous aggregates of hard spheres. J. Appl. Phys. 1972, 43, 2727. [Google Scholar] [CrossRef]
- Lőwen, H. Elastic constants of the hard-sphere glass: A density functional approach. J. Phys. C 1990, 2, 8477. [Google Scholar] [CrossRef] [Green Version]
- Kim, K.; Munakata, T. Glass transition of hard sphere systems: Molecular dynamics and density functional theory. Phys. Rev. E 2003, 68, 021502. [Google Scholar] [CrossRef] [Green Version]
- Chaudhary, P.; Karmakar, S.; Dasgupta, C.; Krishnamurthy, H.R.; Sood, A.K. Equilibrium glassy phase in a polydisperse hard-sphere system. Phys. Rev. Lett. 2005, 95, 248301. [Google Scholar] [CrossRef] [Green Version]
- Kaur, C.; Das, S.P. Metastable structures with modified weighted density-functional theory. Phys. Rev. E 2002, 65, 026123. [Google Scholar] [CrossRef] [PubMed]
- Singh, S.P.; Das, S.P. Characteristic temperatures of glassy behaviour in a simple liquid. J. Phys. Cond. Matt. 2007, 19, 246107. [Google Scholar] [CrossRef] [PubMed]
- Mondal, A.; Das, S.P. A classical density functional theory model for fragility in the hard-sphere limit. Prog. Theor. Exp. Phys. 2020, 2020, 073102. [Google Scholar]
- Ahmad, F.; Das, S.P. Density Functional model for a Hertzian Liquid. Unpublished work.
- Percus, J.K.; Yevick, G.J. Analysis of classical statistical mechanics by means of collective coordinates. Phys. Rev. 1958, 1, 1103. [Google Scholar] [CrossRef]
- Odagaki, T. Non-equilibrium statistical mechanics based on the free energy landscape and its application to glassy systems. J. Phys. Soc. Jpn. 2017, 86, 082001. [Google Scholar] [CrossRef]
- Orsingher, L.; Fontana, A.; Gilioli, E.; Carnini, G., Jr.; Carini, G.; Unruh, T.; Buchenau, U. Vibrational dynamics of permanently densified glasses: Densification-induced changes in the boson peak. J. Chem. Phys. 2010, 132, 124508. [Google Scholar] [CrossRef]
- Denton, A.R.; Ashcroft, N.W. Modified weighted-density-functional theory of nonuniform classical liquids. Phys. Rev. A 1989, 39, 4701. [Google Scholar] [CrossRef] [PubMed]
- Evans, R. The nature of the liquid-vapour interface and other topics in the statistical mechanics of non-uniform, classical fluids. Adv. Phys. 1979, 28, 143. [Google Scholar] [CrossRef]
- Singh, Y. Density-functional theory of freezing and properties of the ordered phase. Phys. Rep. 1991, 207, 351. [Google Scholar] [CrossRef]
- Löwen, H. Melting, freezing and colloidal suspensions. Phys. Rep. 1994, B 237, 249–324. [Google Scholar] [CrossRef]
- Ashcroft, N.W. Density functional descriptions of classical inhomogeneous fluids. Aust. J. Phys. 1996, 49, 3. [Google Scholar] [CrossRef]
- Hansen, J.-P.; McDonald, I.R. Theory of Simple Liquids, 3rd ed.; Elsevier Aca. Pr.: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Henderson, D.; Grundke, E.W. Direct correlation function: Hard sphere fluid. J. Chem. Phys. 1975, 63, 601. [Google Scholar] [CrossRef]
- Boon, J.; Yip, S. Molecular Hydrodynamics; Dover: New York, NY, USA, 1991. [Google Scholar]
- Zwanzig, R.; Mountain, R.D. High-frequency elastic moduli of simple fluids. J. Chem. Phys. 1965, 43, 4464. [Google Scholar] [CrossRef]
- Schofield, P. Wavelength-dependent fluctuations in classical fluids: I. The long wavelength limit. Proc. Phys. Soc. 1966, 88, 149. [Google Scholar] [CrossRef]
- Miller, B.N. Elastic Moduli of a Fluid of Rigid Spheres. Chem. Phys. 1969, 50, 2733. [Google Scholar] [CrossRef]
- Green, H.S. The Molecular Theory of Fluids; North-Holland Publ. Co.: Amsterdam, The Netherlands, 1952. [Google Scholar]
- Kharpak, S. Elastic properties of dense hard-sphere fluids. Phys. Rev. E 2019, 100, 032138. [Google Scholar] [CrossRef] [Green Version]
- ASokolov, P.; Calemczuk, R.; Salce, B.; Kisliuk, A.; Quitmann, D.; Duval, E. Low-temperature anomalies in strong and fragile glass formers. Phys. Rev. Lett. 1997, 78, 2405. [Google Scholar] [CrossRef]
- Angell, C.A. Formation of glasses from liquids and biopolymers. Science 1995, 267, 1924. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kirkpatrick, T.R.; Wolynes, P.G. Connections between some kinetic and equilibrium theories of the glass transition. Phys. Rev. A 1987, 35, 3072. [Google Scholar] [CrossRef] [PubMed]
- Premkumar, L.; Bidhoodi, N.; Das, S.P. Linking density functional and mode coupling models for supercooled liquids. J. Chem. Phys. 2016, 144, 124511. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Curtin, W.A.; Ashcroft, N.W. Density-functional theory and freezing of simple liquids. Phys. Rev. Lett. 1986, 56, 2775. [Google Scholar] [CrossRef] [Green Version]
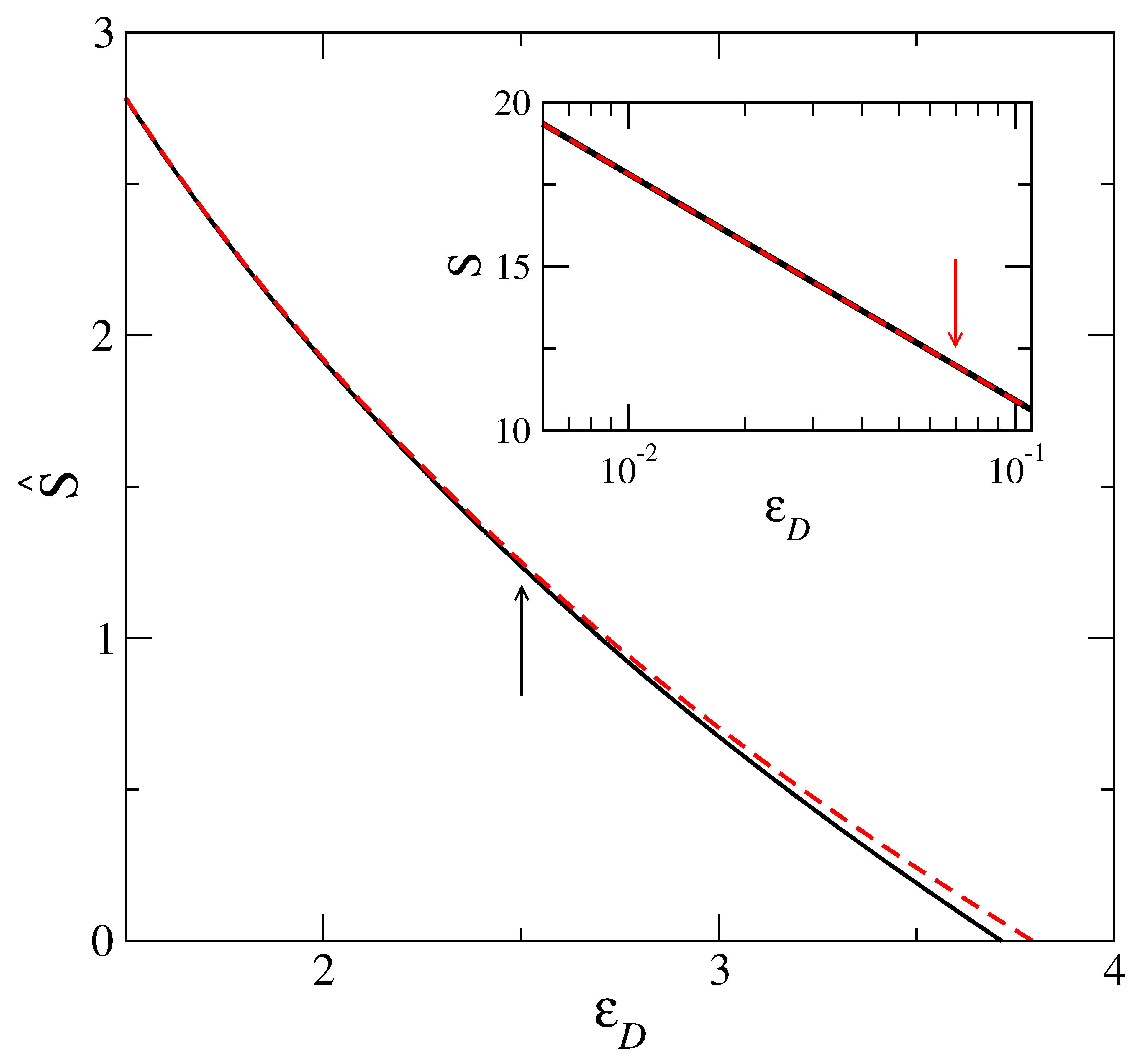

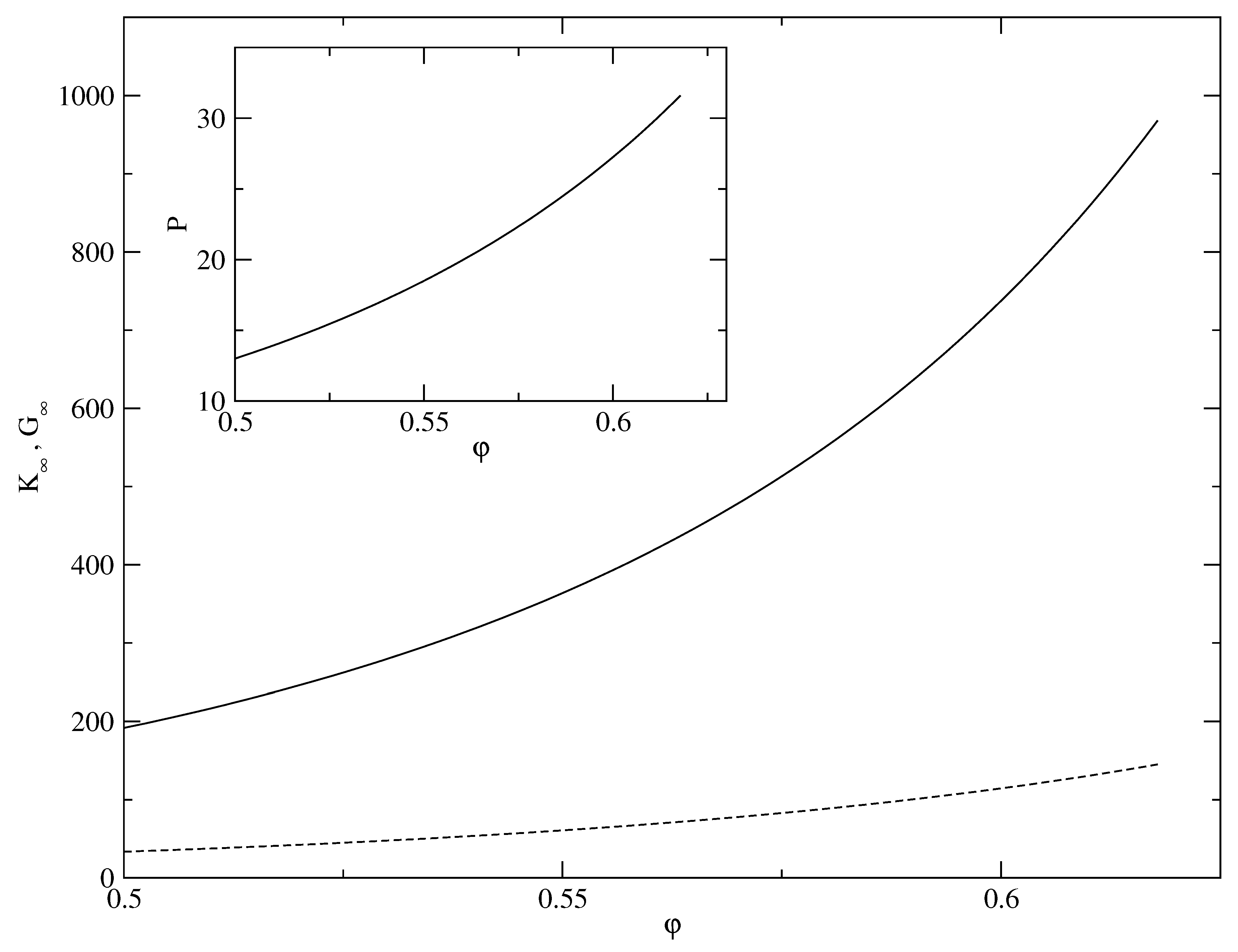
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leishangthem, P.; Ahmad, F.; Das, S.P. Localization, Disorder, and Entropy in a Coarse-Grained Model of the Amorphous Solid. Entropy 2021, 23, 1171. https://doi.org/10.3390/e23091171
Leishangthem P, Ahmad F, Das SP. Localization, Disorder, and Entropy in a Coarse-Grained Model of the Amorphous Solid. Entropy. 2021; 23(9):1171. https://doi.org/10.3390/e23091171
Chicago/Turabian StyleLeishangthem, Premkumar, Faizyab Ahmad, and Shankar P. Das. 2021. "Localization, Disorder, and Entropy in a Coarse-Grained Model of the Amorphous Solid" Entropy 23, no. 9: 1171. https://doi.org/10.3390/e23091171





