Heat Modulation on Target Thermal Bath via Coherent Auxiliary Bath
Abstract
:1. Introduction
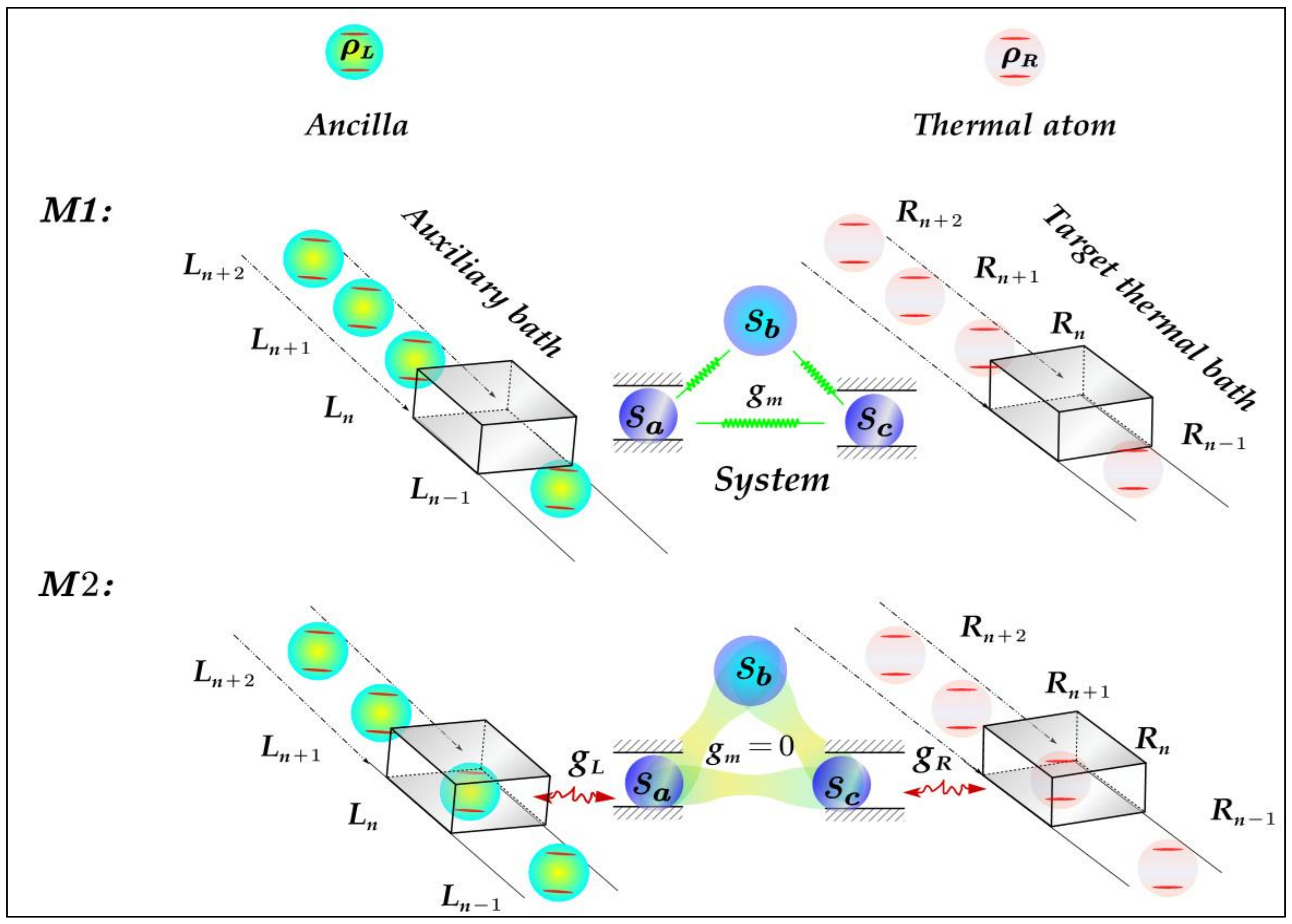
2. Model
3. Modulation of Heat Current via Auxiliary Bath
3.1. Initial States of System and Baths
3.2. Thermal Modulation with Thermal Auxiliary Bath
3.3. Thermal Modulation with CAB
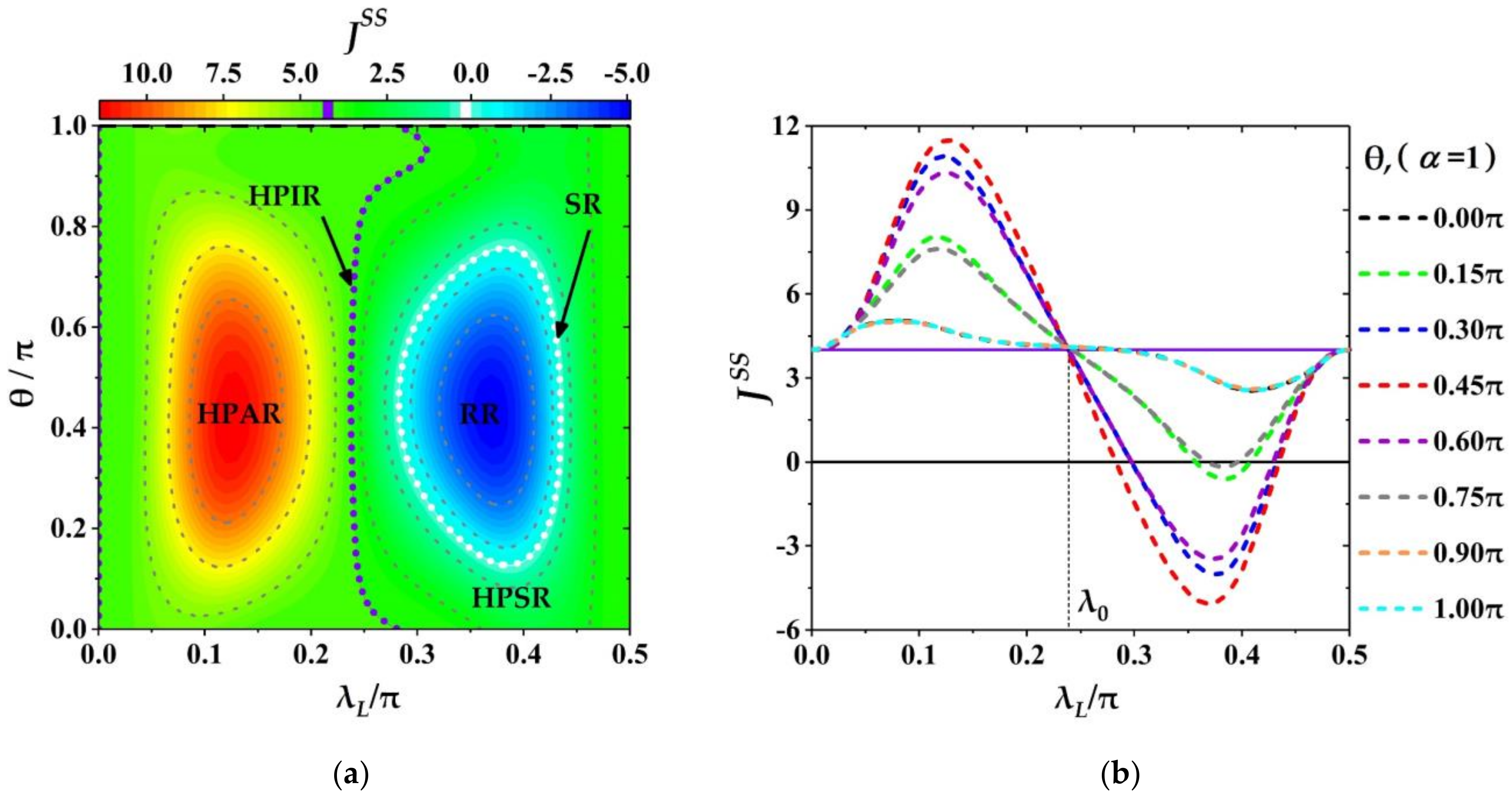
3.3.1. Effects of Relative Phase on THC
3.3.2. Effects of Coherence Magnitude on THC
3.3.3. Maximum and Minimum of THC and Modulation Width
3.3.4. Effect of Temperature on THC
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Brandner, K.; Seifert, U. Periodic thermodynamics of open quantum systems. Phys. Rev. E 2016, 93, 062134. [Google Scholar] [CrossRef] [Green Version]
- Brandão, F.; Horodecki, M.; Ng, N.; Oppenheim, J.; Wehner, S. The second laws of quantum thermodynamics. Proc. Natl. Acad. Sci. USA 2015, 112, 3275–3279. [Google Scholar] [CrossRef] [Green Version]
- Kosloff, R. Quantum Thermodynamics: A Dynamical Viewpoint. Entropy 2013, 15, 2100–2128. [Google Scholar] [CrossRef] [Green Version]
- Millen, J.; Xuereb, A. Perspective on quantum thermodynamics. New J. Phys. 2016, 18, 011002. [Google Scholar] [CrossRef]
- Winter, A.; Yang, D. Operational Resource Theory of Coherence. Phys. Rev. Lett. 2016, 116, 120404. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Streltsov, A.; Adesso, G.; Plenio, M.B. Colloquium: Quantum coherence as a resource. Rev. Mod. Phys. 2017, 89, 041003. [Google Scholar] [CrossRef] [Green Version]
- De Vicente, J.I.; Streltsov, A. Genuine quantum coherence. J. Phys. A Math. Theor. 2017, 50, 045301. [Google Scholar] [CrossRef] [Green Version]
- Lostaglio, M.; Korzekwa, K.; Jennings, D.; Rudolph, T. Quantum Coherence, Time-Translation Symmetry, and Thermodynamics. Phys. Rev. X 2015, 5, 021001. [Google Scholar] [CrossRef] [Green Version]
- Misra, A.; Singh, U.; Bhattacharya, S.; Pati, A.K. Energy cost of creating quantum coherence. Phys. Rev. A 2016, 93, 052335. [Google Scholar] [CrossRef] [Green Version]
- Manzano, G.; Plastina, F.; Zambrini, R. Optimal Work Extraction and Thermodynamics of Quantum Measurements and Correlations. Phys. Rev. Lett. 2018, 121, 120602. [Google Scholar] [CrossRef] [Green Version]
- Vedral, V.; Plenio, M.B.; Rippin, M.A.; Knight, P.L. Quantifying Entanglement. Phys. Rev. Lett. 1997, 78, 2275. [Google Scholar] [CrossRef] [Green Version]
- Bruß, D. Characterizing entanglement. J. Math. Phys. 2002, 43, 4237. [Google Scholar] [CrossRef] [Green Version]
- Roßnagel, J.; Abah, O.; Schmidt-Kaler, F.; Singer, K.; Lutz, E. Nanoscale Heat Engine Beyond the Carnot Limit. Phys. Rev. Lett. 2014, 112, 030602. [Google Scholar] [CrossRef] [PubMed]
- Levy, A.; Kosloff, R. The local approach to quantum transport may violate the second law of thermodynamics. EPL 2014, 107, 20004. [Google Scholar] [CrossRef] [Green Version]
- Evans, D.J.; Cohen, E.G.D.; Morriss, G.P. Probability of Second Law Violations in Shearing Steady States. Phys. Rev. Lett. 1993, 71, 2401. [Google Scholar] [CrossRef] [Green Version]
- Ćwikliński, P.; Studziński, M.; Horodecki, M.; Oppenheim, J. Limitations on the Evolution of Quantum Coherences: Towards Fully Quantum Second Laws of Thermodynamics. Phys. Rev. Lett. 2015, 115, 210403. [Google Scholar] [CrossRef] [Green Version]
- Roßnagel, J.; Dawkins, S.T.; Tolazzi, K.N.; Abah, O.; Lutz, E.; Schmidt-Kaler, F.; Singer, K. A single-atom heat engine. Science 2016, 352, 325–329. [Google Scholar] [CrossRef] [Green Version]
- Quan, H.T.; Liu, Y.; Sun, C.P.; Nori, F. Quantum thermodynamic cycles and quantum heat engines. Phys. Rev. E 2007, 76, 031105. [Google Scholar] [CrossRef] [Green Version]
- Haack, G.; Giazotto, F. Efficient and tunable Aharonov-Bohm quantum heat engine. Phys. Rev. B 2019, 100, 235442. [Google Scholar] [CrossRef] [Green Version]
- Du, J.; Shen, W.; Su, S.; Chen, J. Quantum thermal management devices based on strong coupling qubits. Phys. Rev. E 2019, 99, 062123. [Google Scholar] [CrossRef]
- Xu, X.; Choo, K.; Balachandran, V.; Poletti, D. Transport and Energetic Properties of a Ring of Interacting Spins Coupled to Heat Baths. Entropy 2019, 21, 228. [Google Scholar] [CrossRef] [Green Version]
- Werlang, T.; Rigolin, G. Thermal and magnetic quantum discord in Heisenberg models. Phys. Rev. A 2010, 81, 044101. [Google Scholar] [CrossRef] [Green Version]
- Lidar, D.A.; Chuang, I.L.; Whaley, K.B. Decoherence Free Subspaces for Quantum Computation. Phys. Rev. Lett. 1997, 81, 2594–2597. [Google Scholar] [CrossRef] [Green Version]
- Fanchini, F.F.; Castelano, L.K.; Caldeira, A.O. Entanglement versus quantum discord in two coupled double quantum dots. New J. Phys. 2010, 12, 073009. [Google Scholar] [CrossRef]
- Mukherjee, S.; De, B.; Muralidharan, B. Three-terminal vibron-coupled hybrid quantum dot thermoelectric refrigeration. J. Appl. Phy. 2020, 128, 234303. [Google Scholar] [CrossRef]
- Daré, A.M. Comparative study of heat-driven and power-driven refrigerators with Coulomb-coupled quantum dots. Phys. Rev. B 2019, 100, 195427. [Google Scholar] [CrossRef] [Green Version]
- Mitchison, M.T.; Huber, M.; Prior, J.; Woods, M.P.; Plenio, M.B. Realising a quantum absorption refrigerator with an atom-cavity system. Quantum Sci. Technol. 2016, 1, 015001. [Google Scholar] [CrossRef]
- Quan, H.T.; Zhang, P.; Sun, C.P. Quantum heat engine with multilevel quantum systems. Phys. Rev. E 2005, 72, 056110. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.S.; Li, C.F.; Zhang, C.J.; Xu, X.Y.; Zhang, Y.S.; Guo, G.C. Experimental investigation of the non-Markovian dynamics of classical and quantum correlations. Phys. Rev. A 2010, 82, 042328. [Google Scholar] [CrossRef] [Green Version]
- Ashrafi, S.M.; Malekfar, R.; Bahrampour, A.R.; Feist, J. Optomechanical heat transfer between molecules in a nanoplasmonic cavity. Phys. Rev. A 2019, 100, 013826. [Google Scholar] [CrossRef] [Green Version]
- Pereira, E. Heat, work, and energy currents in the boundary-driven XXZ spin chain. Phys. Rev. E 2018, 97, 022115. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Reis, L.H.; Silva, S.; Pereira, E. Beyond the Lindblad master equation: Heat, work, and energy currents in boundary-driven spin chains. Phys. Rev. E 2020, 101, 062107. [Google Scholar] [CrossRef]
- Esposito, M.; Ochoa, M.A.; Galperin, M. Nature of heat in strongly coupled open quantum systems. Phys. Rev. B 2015, 92, 235440. [Google Scholar] [CrossRef] [Green Version]
- Dorfman, K.E.; Xu, D.; Cao, J. Efficiency at maximum power of a laser quantum heat engine enhanced by noise-induced coherence. Phys. Rev. E 2018, 97, 042120. [Google Scholar] [CrossRef] [Green Version]
- Rodrigues, F.L.S.; Chiara, G.D.; Paternostro, M.; Landi, G.T. Thermodynamics of Weakly Coherent Collisional Models. Phys. Rev. Lett. 2019, 123, 140601. [Google Scholar] [CrossRef] [Green Version]
- Abdallah, P.B.; Biehs, S.A. Near-Field Thermal Transistor. Phys. Rev. Lett. 2014, 112, 044301. [Google Scholar] [CrossRef] [Green Version]
- Landi, G.T.; Novais, E.; de Oliveira, M.J.; Karevski, D. Flux rectification in the quantum XXZ chain. Phys. Rev. E 2014, 90, 042142. [Google Scholar] [CrossRef] [Green Version]
- Schuab, L.; Pereira, E.; Landi, G.T. Energy rectification in quantum graded spin chains: Analysis of the XXZ Model. Phys. Rev. E 2016, 94, 042122. [Google Scholar] [CrossRef] [Green Version]
- Joulain, K.; Drevillon, J.; Ezzahri, Y.; Ordonez-Miranda, J. Quantum Thermal Transistor. Phys. Rev. Lett. 2016, 116, 200601. [Google Scholar] [CrossRef] [Green Version]
- Mascarenhas, E.; Santos, M.F.; Auffèves, A.; Gerace, D. Quantum rectifier in a one-dimensional photonic channel. Phys. Rev. A 2016, 93, 043821. [Google Scholar] [CrossRef] [Green Version]
- Giazotto, F.; Martínez-Pérez, M.J. The Josephson heat interferometer. Nature 2012, 492, 401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ronzani, A.; Karimi, B.; Senior, J.; Chang, Y.; Peltonen, J.T.; Chen, C.; Pekola, J.P. Tunable photonic heat transport in a quantum heat valve. Nat. Phys. 2018, 14, 991–995. [Google Scholar] [CrossRef] [Green Version]
- Wijesekara, R.T.; Gunapala, S.D.; Stockman, M.I.; Premaratne, M. Optically controlled quantum thermal gate. Phys. Rev. B 2020, 101, 245402. [Google Scholar] [CrossRef]
- Scovil, H.E.D.; Schulz-DuBois, E.O. Three-Level Masers as Heat Engines. Phys. Rev. Lett. 1995, 2, 262–263. [Google Scholar] [CrossRef]
- Kosloff, R.; Levy, A. Quantum Heat Engines and Refrigerators: Continuous Devices. Annu. Rev. Phys. Chem. 2014, 65, 365–393. [Google Scholar] [CrossRef] [Green Version]
- Brunner, N.; Huber, M.; Linden, N.; Popescu, S.; Silva, R.; Skrzypczyk, P. Entanglement enhances cooling in microscopic quantum refrigerators. Phys. Rev. E 2014, 89, 032115. [Google Scholar] [CrossRef] [Green Version]
- Balachandran, V.; Benenti, G.; Pereira, E.; Casati, G.; Poletti, D. Perfect Diode in Quantum Spin Chains. Phys. Rev. Lett. 2018, 120, 200603. [Google Scholar] [CrossRef] [Green Version]
- Guo, B.; Liu, T.; Yu, C. Quantum thermal transistor based on qubit-qutrit coupling. Phys. Rev. E 2018, 98, 022118. [Google Scholar] [CrossRef] [Green Version]
- Majland, M.; Christensen, K.S.; Zinner, N.T. Quantum thermal transistor in superconducting circuits. Phys. Rev. B 2020, 101, 184510. [Google Scholar] [CrossRef]
- Yang, J.; Elouard, C.; Splettstoesser, J.; Sothmann, B.; Sánchez, R.; Jordan, A.N. Thermal transistor and thermometer based on Coulomb-coupled conductors. Phys. Rev. B 2019, 100, 045418. [Google Scholar] [CrossRef] [Green Version]
- Correa, L.A.; Mehboudi, M.; Adesso, G.; Sanpera, A. Individual quantum probes for optimal thermometry. Phys. Rev. Lett. 2015, 114, 220405. [Google Scholar] [CrossRef] [Green Version]
- Banerjee, S.; Singha, A. A realistic non-local electrical thermometer based on Coulomb coupled systems. J. Appl. Phys. 2021, 129, 114901. [Google Scholar] [CrossRef]
- Hofer, P.P.; Brask, J.B.; Perarnau-Llobet, M.; Brunner, N. Quantum Thermal Machine as a Thermometer. Phys. Rev. Lett. 2017, 119, 090603. [Google Scholar] [CrossRef] [Green Version]
- Lee, M.H.; Dunietz, B.D. Active control of thermal transport in molecular spin valves. Phys. Rev. B 2013, 88, 045421. [Google Scholar] [CrossRef]
- Huangfu, Y.; Qi, S.; Jing, J. A multifunctional quantum thermal device: With and without inner coupling. Phys. Lett. A 2021, 393, 127172. [Google Scholar] [CrossRef]
- Zhong, W.R.; Zheng, D.Q.; Hu, B. Thermal control in graphene nanoribbons: Thermal valve, thermal switch and thermal amplifier. Nanoscale 2012, 4, 5217. [Google Scholar] [CrossRef]
- Manzano, G.; Sánchez, R.; Silva, R.; Haack, G.; Brask, J.; Brunner, N. Hybrid thermal machines: Generalized thermodynamic resources for multitasking. Phys. Rev. Res. 2020, 2, 043302. [Google Scholar] [CrossRef]
- Wang, C.; Xu, D.; Liu, H.; Gao, X. Thermal rectification and heat amplification in a nonequilibrium V-type three-level system. Phys. Rev. E 2019, 99, 042102. [Google Scholar] [CrossRef] [Green Version]
- Guo, B.; Liu, T.; Yu, C. Multifunctional quantum thermal device utilizing three qubits. Phys. Rev. E 2019, 99, 032112. [Google Scholar] [CrossRef] [Green Version]
- Pereira, E.; Lemos, H.C.F. Symmetry of heat conductivity in inhomogeneous quantum chains. J. Phys. A Math. Theor. 2009, 42, 225006. [Google Scholar] [CrossRef]
- Werlang, T.; Marchiori, M.A.; Cornelio, M.F.; Valente, D. Optimal rectification in the ultrastrong coupling regime. Phys. Rev. E 2014, 89, 062109. [Google Scholar] [CrossRef] [Green Version]
- Chen, T.; Wang, X.B. Thermal rectification in the nonequilibrium quantum-dots-system. Phys. E Low-Dimens. Syst. Nanostruct. 2015, 72, 58–62. [Google Scholar] [CrossRef]
- Ordonez-Miranda, J.; Ezzahri, Y.; Joulain, K. Quantum thermal diode based on two interacting spinlike systems under different excitations. Phys. Rev. E 2017, 95, 022128. [Google Scholar] [CrossRef]
- Karimi, B.; Pekola, J.P.; Campisi, M.; Fazio, R. Coupled qubits as a quantum heat switch. Quantum Sci. Technol. 2017, 2, 044007. [Google Scholar] [CrossRef] [Green Version]
- Pereira, E. Perfect thermal rectification in a many-body quantum Ising model. Phys. Rev. E 2019, 99, 032116. [Google Scholar] [CrossRef] [Green Version]
- Naseem, M.T.; Misra, A.; Müstecaplioglu, Ö.E.; Kurizki, G. Minimal quantum heat manager boosted by bath spectral filtering. Phys. Rev. E 2020, 2, 033285. [Google Scholar]
- Tian, F.; Zou, J.; Li, L.; Li, H.; Shao, B. Effect of Inter-System Coupling on Heat Transport in a Microscopic Collision Model. Entropy 2021, 230, 471. [Google Scholar] [CrossRef]
- Skrzypczyk, P.; Short, A.J.; Popescu, S. Work extraction and thermodynamics for individual quantum systems. Nat. Commun. 2014, 5, 5185. [Google Scholar] [CrossRef] [Green Version]
- Ivan, H.; Serra, R.M. Role of quantum coherence in the thermodynamics of energy transfer. Phys. Rev. E 2018, 97, 062105. [Google Scholar]
- Ghosh, A.; Latune, C.L.; Davidovich, L.; Kurizki, G. Catalysis of heat-to-work conversion in quantum machines. Proc. Natl. Acad. Sci. USA 2017, 114, 12156–12161. [Google Scholar] [CrossRef] [Green Version]
- Ghosh, A.; Gelbwaser-Klimovsky, D.; Niedenzu, W.; Lvovsky, A.I.; Mazets, I.; Scully, M.O.; Kurizki, G. Two-level masers as heat-to-work converters. Proc. Natl. Acad. Sci. USA 2018, 115, 9941–9944. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Zou, J.; Li, H.; Xu, B.M.; Wang, Y.M.; Shao, B. Effect of coherence of nonthermal reservoirs on heat transport in a microscopic collision model. Phys. Rev. E 2018, 97, 022111. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Li, X.; Jin, J. Information scrambling in a collision model. Phys. Rev. A 2020, 101, 042324. [Google Scholar] [CrossRef] [Green Version]
- Campbell, S.; Vacchini, B. Collision models in open system dynamics: A versatile tool for deeper insights? EPL 2021, 133, 60001. [Google Scholar] [CrossRef]
- Bernardes, N.K.; Carvalho, A.; Monken, C.H.; Santos, M.F. Environmental correlations and Markovian to non-Markovian transitions in collisional models. Phys. Rev. A 2014, 90, 032111. [Google Scholar] [CrossRef] [Green Version]
- Guarnieri, G.; Morrone, D.; Çakmak, B.; Plastina, F.; Campbell, S. Non-equilibrium steady-states of memoryless quantum collision models. Phys. Lett. A 2020, 384, 126576. [Google Scholar] [CrossRef]
- Stable, A.L.L.; Noa, C.E.F.; Oropesa, W.G.C.; Fiore, C.E. Thermodynamics of collisional models for Brownian particles: General properties and efficiency. Phys. Rev. Res. 2020, 2, 043016. [Google Scholar] [CrossRef]
- Strasberg, P.; Schaller, G.; Brandes, T.; Esposito, M. Quantum and Information Thermodynamics: A unifying Framework Based on Repeated Interactions. Phys. Rev. X 2017, 7, 021003. [Google Scholar] [CrossRef] [Green Version]
- Cattaneo, M.; Chiara, G.D.; Maniscalco, S.; Zambrini, R.; Giorgi, G.L. Collision models can efficiently simulate any multipartite markovian quantum dynamics. Phys. Rev. Lett. 2021, 126, 130403. [Google Scholar] [CrossRef]
- Seah, S.; Nimmrichter, S.; Scarani, V. Nonequilibrium dynamics with finite-time repeated interactions. Phys. Rev. E 2019, 99, 042103. [Google Scholar] [CrossRef] [Green Version]
- García-Pérez, G.; Rossi, M.A.C.; Maniscalco, S. IBM Q experience as a versatile experimental testbed for simulating open quantum systems. NPJ Quantum Inf. 2020, 6, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Seah, S.; Nimmrichter, S.; Scarani, V. Refrigeration beyond weak internal coupling. Phys. Rev. E 2018, 98, 012131. [Google Scholar] [CrossRef] [Green Version]
- Pachos, J.K.; Plenio, M.B. Three-Spin Interactions in Optical Lattices and Criticality in Cluster Hamiltonians. Phys. Rev. Lett. 2004, 93, 056402. [Google Scholar] [CrossRef] [Green Version]
- Bermudez, A.; Porras, D.; Martin-Delgado, M.A. Competing many-body interactions in systems of trapped ions. Phys. Rev. A 2009, 79, 060303. [Google Scholar] [CrossRef]
- Reiss, T.O.; Khaneja, N.; Glaser, S.J. Broadband geodesic pulses for three spin systems: Time-optimal realization of effective trilinear coupling terms and indirect SWAP gates. J. Magn. Reson. 2003, 165, 95–101. [Google Scholar] [CrossRef] [Green Version]
- Linden, N.; Popescu, S.; Skrzypczyk, P. How Small Can Thermal Machines Be? The Smallest Possible Refrigerator. Phys. Rev. Lett. 2010, 105, 130401. [Google Scholar] [CrossRef]
- Skrzypczyk, P.; Brunner, N.; Linden, N.; Popescu, S. The smallest refrigerators can reach maximal efficiency. J. Phys. A Math. Theor. 2011, 44, 492002. [Google Scholar] [CrossRef]
- Wax, N. Selected Papers on Noise and Stochastic Processes; Dover: New York, NY, USA, 1954. [Google Scholar]
- Karevski, D.; Platini, T. Quantum Nonequilibrium Steady States Induced by Repeated Interactions. Phys. Rev. Lett. 2009, 102, 207207. [Google Scholar] [CrossRef] [Green Version]
- Scarani, V.; Ziman, M.; Štelmachovič, P.; Gisin, N.; Bužek, V. Thermalizing Quantum Machines: Dissipation and Entanglement. Phys. Rev. Lett. 2002, 88, 097905. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lorenzo, S.; McCloskey, R.; Ciccarello, F.; Paternostro, M.; Palma, G. M. Landauer’s Principle in Multipartite Open Quantum System Dynamics. Phys. Rev. Lett. 2015, 115, 120403. [Google Scholar] [CrossRef] [PubMed]
- Gardas, B.; Deffner, S. Thermodynamic universality of quantum Carnot engines. Phys. Rev. E 2015, 92, 042126. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Misra, A.; Singh, U.; Bera, M.N.; Rajagopal, A.K. Quantum Renyi relative entropies affirm universality of thermodynamics. Phys. Rev. E 2015, 92, 042161. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liao, J.Q.; Dong, H.; Sun, C.P. Single-particle machine for quantum thermalization. Phys. Rev. A 2010, 81, 052121. [Google Scholar] [CrossRef] [Green Version]
- Scully, M.O.; Zubairy, M.S.; Agarwal, G.S.; Walther, H. Extracting Work from a Single Heat Bath via Vanishing Quantum Coherence. Science 2003, 299, 862–864. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Zou, J.; Yu, W.L.; Xu, B.M.; Li, J.G.; Shao, B. Quantum coherence rather than quantum correlations reflect the effects of a reservoir on a system’s work capability. Phys. Rev. E 2014, 89, 052132. [Google Scholar] [CrossRef] [Green Version]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, W.-L.; Li, T.; Li, H.; Zhang, Y.; Zou, J.; Wang, Y.-D. Heat Modulation on Target Thermal Bath via Coherent Auxiliary Bath. Entropy 2021, 23, 1183. https://doi.org/10.3390/e23091183
Yu W-L, Li T, Li H, Zhang Y, Zou J, Wang Y-D. Heat Modulation on Target Thermal Bath via Coherent Auxiliary Bath. Entropy. 2021; 23(9):1183. https://doi.org/10.3390/e23091183
Chicago/Turabian StyleYu, Wen-Li, Tao Li, Hai Li, Yun Zhang, Jian Zou, and Ying-Dan Wang. 2021. "Heat Modulation on Target Thermal Bath via Coherent Auxiliary Bath" Entropy 23, no. 9: 1183. https://doi.org/10.3390/e23091183





