Common Environmental Effects on Quantum Thermal Transistor
Abstract
:1. Introduction
2. The Model of the Thermal Transistor
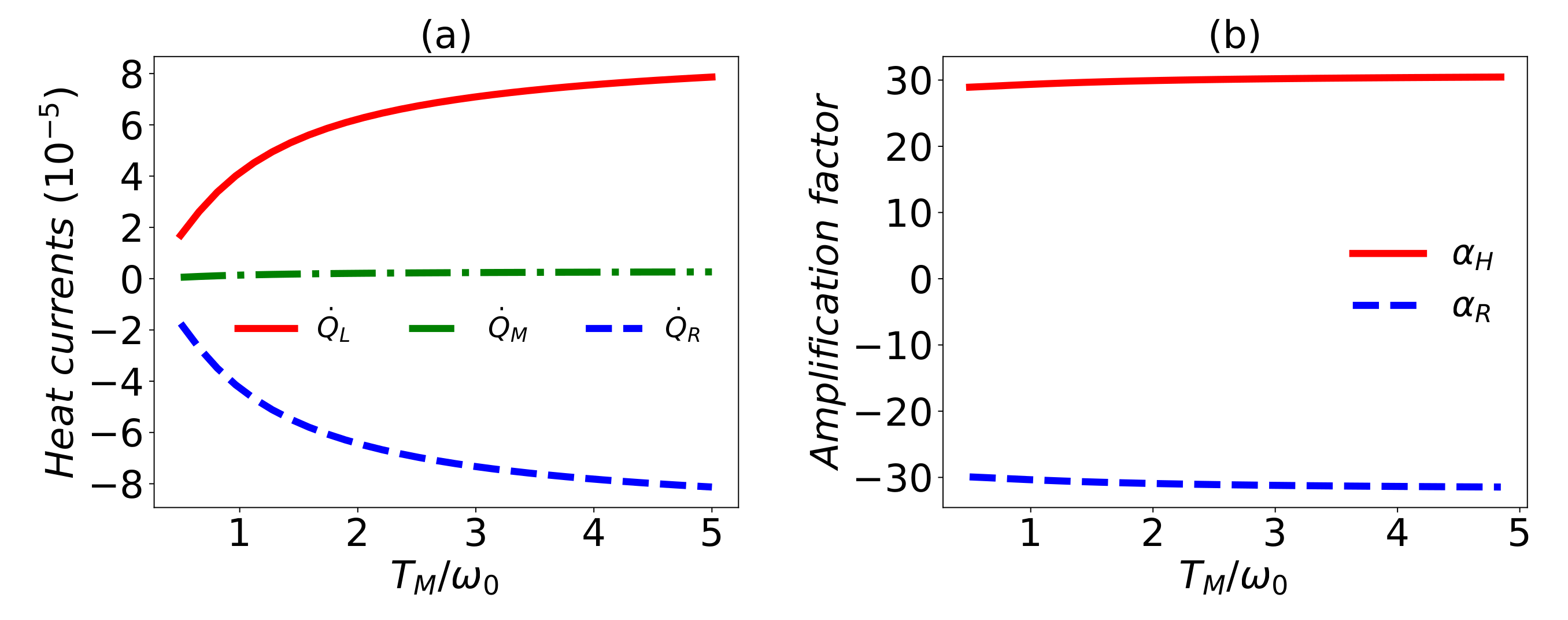
3. Dynamics of the System and the Thermal Transistor
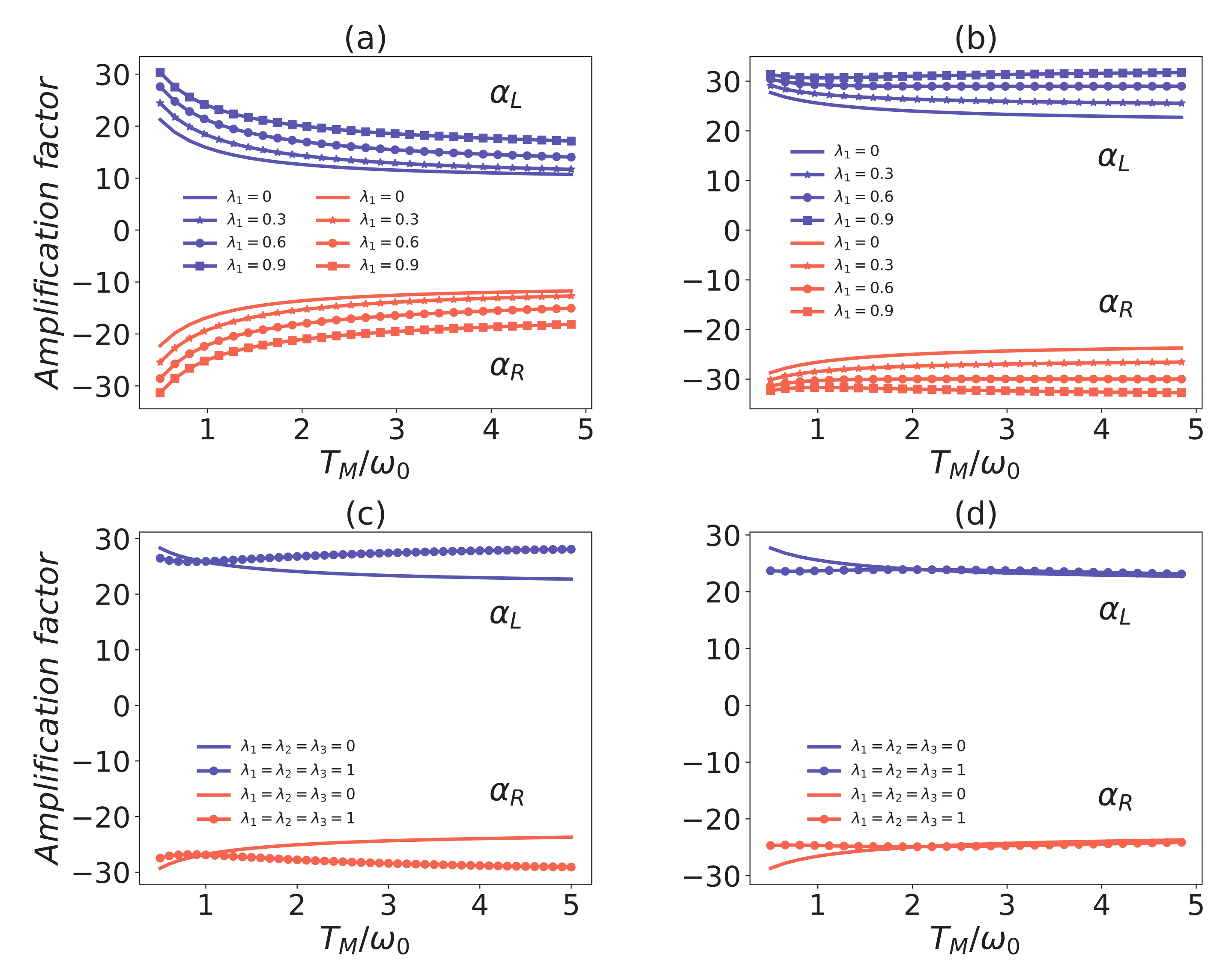
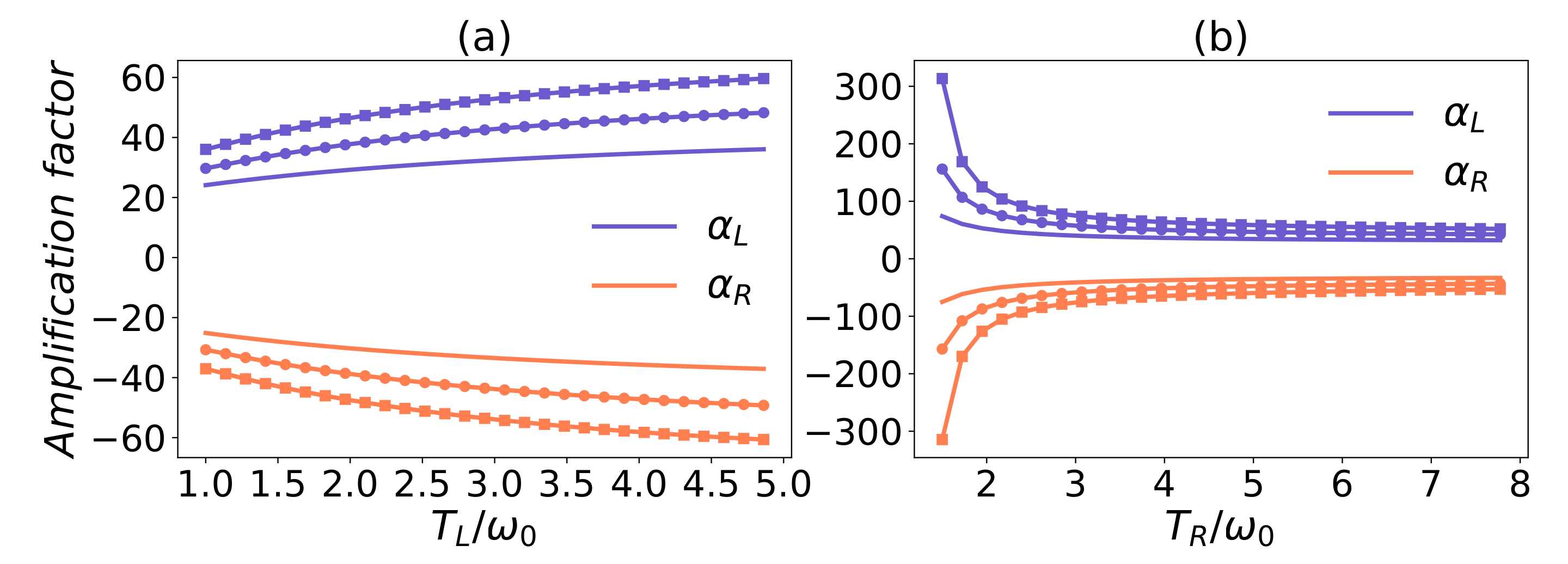
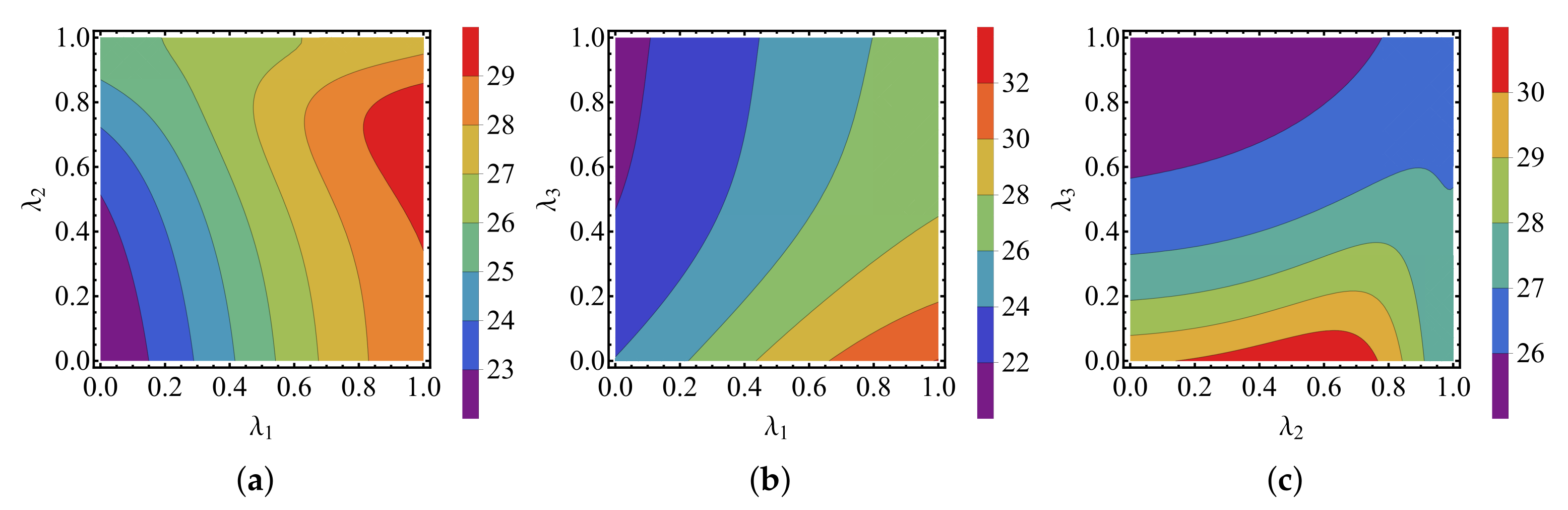
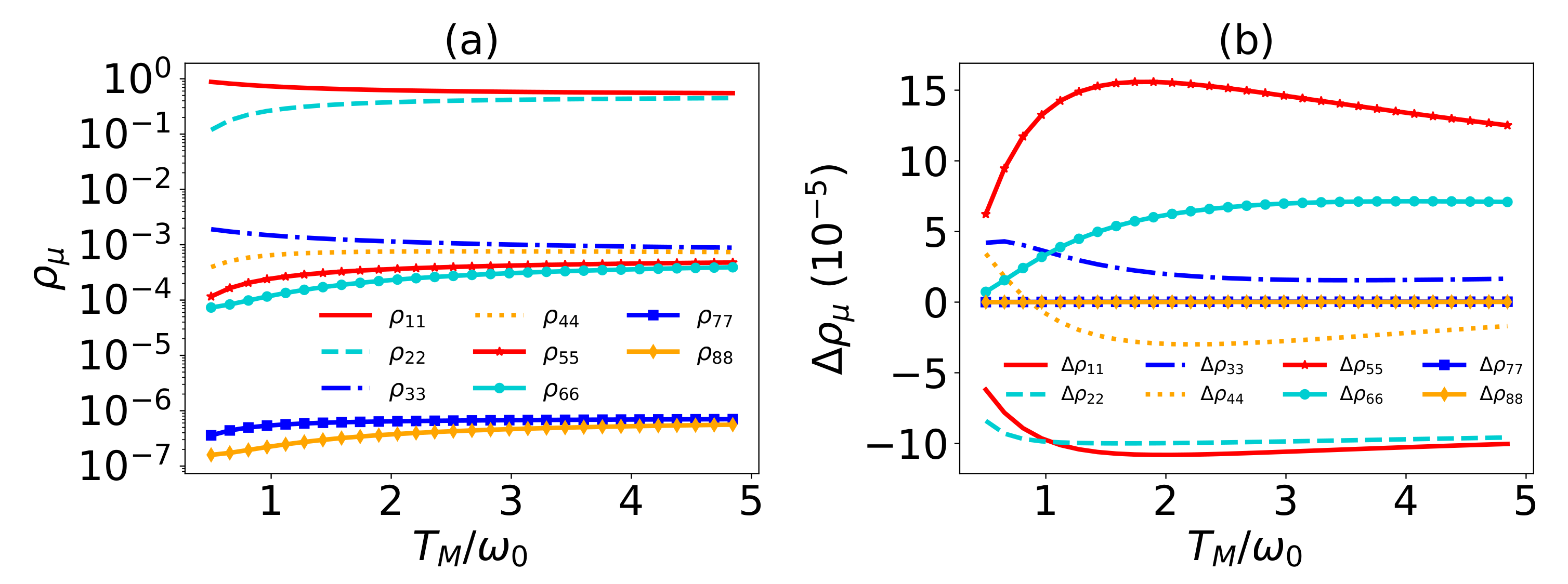
4. The Common Environmental Effects
5. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. The Eigenstate and Its Corresponding Eigenvalue
Appendix B. The Lindblad Operators
Appendix C. The Expression of Heat Currents
Appendix D. Dependence on the Decay Rates

References
- Binder, F.; Correa, L.A.; Gogolin, C.; Anders, J.; Adesso, G. Thermodynamics in the quantum regime. Fundam. Theor. Phys. 2018, 195, 1–2. [Google Scholar]
- Millen, J.; Xuereb, A. Perspective on quantum thermodynamics. New J. Phys. 2016, 18, 011002. [Google Scholar] [CrossRef]
- Vinjanampathy, S.; Anders, J. Quantum thermodynamics. Contemp. Phys. 2016, 57, 545–579. [Google Scholar] [CrossRef] [Green Version]
- Wilming, H.; Gallego, R. Third Law of Thermodynamics as a Single Inequality. Phys. Rev. X 2017, 7, 041033. [Google Scholar] [CrossRef] [Green Version]
- Klatzow, J.; Becker, J.N.; Ledingham, P.M.; Weinzetl, C.; Kaczmarek, K.T.; Saunders, D.J.; Nunn, J.; Walmsley, I.A.; Uzdin, R.; Poem, E. Experimental Demonstration of Quantum Effects in the Operation of Microscopic Heat Engines. Phys. Rev. Lett. 2019, 122, 110601. [Google Scholar] [CrossRef] [Green Version]
- Seifert, U. First and Second Law of Thermodynamics at Strong Coupling. Phys. Rev. Lett. 2016, 116, 020601. [Google Scholar] [CrossRef] [Green Version]
- Gemmer, J.; Otte, A.; Mahler, G. Quantum Approach to a Derivation of the Second Law of Thermodynamics. Phys. Rev. Lett. 2001, 86, 1927–1930. [Google Scholar] [CrossRef] [Green Version]
- Niedenzu, W.; Mukherjee, V.; Ghosh, A.; Kofman, A.G.; Kurizki, G. Quantum engine efficiency bound beyond the second law of thermodynamics. Nat. Commun. 2018, 9, 165. [Google Scholar] [CrossRef] [Green Version]
- Majland, M.; Christensen, K.S.; Zinner, N.T. Quantum thermal transistor in superconducting circuits. Phys. Rev. B 2020, 101, 184510. [Google Scholar] [CrossRef]
- Kosloff, R. A quantum mechanical open system as a model of a heat engine. J. Chem. Phys. 1984, 80, 1625–1631. [Google Scholar] [CrossRef]
- Rossnagel, J.; Dawkins, S.; Tolazzi, K.N.; Abah, O.; Lutz, E.; Schmidt-Kaler, F.; Singer, K. A single-atom heat engine. Science 2016, 352, 325–329. [Google Scholar] [CrossRef] [Green Version]
- He, J.; Chen, J.; Hua, B. Quantum refrigeration cycles using spin- systems as the working substance. Phys. Rev. E 2002, 65, 036145. [Google Scholar] [CrossRef]
- Chen, Y.X.; Li, S.W. Quantum refrigerator driven by current noise. EPL (Europhys. Lett.) 2012, 97, 40003. [Google Scholar] [CrossRef] [Green Version]
- Venturelli, D.; Fazio, R.; Giovannetti, V. Minimal Self-Contained Quantum Refrigeration Machine Based on Four Quantum Dots. Phys. Rev. Lett. 2013, 110, 256801. [Google Scholar] [CrossRef] [Green Version]
- Scovil, H.E.D.; Schulz-DuBois, E.O. Three-Level Masers as Heat Engines. Phys. Rev. Lett. 1959, 2, 262–263. [Google Scholar] [CrossRef]
- Geusic, J.E.; Schulz-DuBios, E.O.; Scovil, H.E.D. Quantum Equivalent of the Carnot Cycle. Phys. Rev. 1967, 156, 343–351. [Google Scholar] [CrossRef]
- Alicki, R. The quantum open system as a model of the heat engine. J. Phys. A: Math. Gen. 1979, 12, L103–L107. [Google Scholar] [CrossRef]
- Quan, H.T.; Zhang, P.; Sun, C.P. Quantum heat engine with multilevel quantum systems. Phys. Rev. E 2005, 72, 056110. [Google Scholar] [CrossRef] [Green Version]
- Senior, J.; Gubaydullin, A.; Karimi, B.; Peltonen, J.; Ankerhold, J.; Pekola, J. Heat rectification via a superconducting artificial atom. Commun. Phys. 2019, 3, 1–5. [Google Scholar] [CrossRef]
- Naseem, M.T.; Misra, A.; Müstecaplioğlu, O.E.; Kurizki, G. Minimal quantum heat manager boosted by bath spectral filtering. Phys. Rev. Res. 2020, 2, 033285. [Google Scholar] [CrossRef]
- Balachandran, V.; Benenti, G.; Pereira, E.; Casati, G.; Poletti, D. Perfect Diode in Quantum Spin Chains. Phys. Rev. Lett. 2018, 120, 200603. [Google Scholar] [CrossRef] [Green Version]
- Lin, B.; Chen, J. Performance analysis of an irreversible quantum heat engine working with harmonic oscillators. Phys. Rev. E 2003, 67, 046105. [Google Scholar] [CrossRef]
- Dong, Y.; Zhang, K.; Bariani, F.; Meystre, P. Work measurement in an optomechanical quantum heat engine. Phys. Rev. A 2015, 92, 033854. [Google Scholar] [CrossRef] [Green Version]
- Joulain, K.; Drevillon, J.; Ezzahri, Y.; Ordonez-Miranda, J. Quantum Thermal Transistor. Phys. Rev. Lett. 2016, 116, 200601. [Google Scholar] [CrossRef] [Green Version]
- Kosloff, R.; Levy, A. Quantum Heat Engines and Refrigerators: Continuous Devices. Annu. Rev. Phys. Chem. 2014, 65, 365–393. [Google Scholar] [CrossRef] [Green Version]
- Silva, R.; Manzano, G.; Skrzypczyk, P.; Brunner, N. Performance of autonomous quantum thermal machines: Hilbert space dimension as a thermodynamical resource. Phys. Rev. E 2016, 94, 032120. [Google Scholar] [CrossRef] [Green Version]
- Levy, A.; Alicki, R.; Kosloff, R. Quantum refrigerators and the third law of thermodynamics. Phys. Rev. E 2012, 85, 061126. [Google Scholar] [CrossRef] [Green Version]
- Man, Z.X.; Xia, Y.J. Smallest quantum thermal machine: The effect of strong coupling and distributed thermal tasks. Phys. Rev. E 2017, 96, 012122. [Google Scholar] [CrossRef]
- Skrzypczyk, P.; Brunner, N.; Linden, N.; Popescu, S. The smallest refrigerators can reach maximal efficiency. J. Phys. A: Math. Theor. 2011, 44, 492002. [Google Scholar] [CrossRef]
- Levy, A.; Kosloff, R. Quantum Absorption Refrigerator. Phys. Rev. Lett. 2012, 108, 070604. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hofer, P.P.; Perarnau-Llobet, M.; Brask, J.B.; Silva, R.; Huber, M.; Brunner, N. Autonomous quantum refrigerator in a circuit QED architecture based on a Josephson junction. Phys. Rev. B 2016, 94, 235420. [Google Scholar] [CrossRef] [Green Version]
- Correa, L.A.; Palao, J.P.; Adesso, G.; Alonso, D. Performance bound for quantum absorption refrigerators. Phys. Rev. E 2013, 87, 042131. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Maslennikov, G.; Ding, S.; Hablutzel, R.; Gan, J.; Roulet, A.; Nimmrichter, S.; Dai, J.; Scarani, V.; Matsukevich, D.N. Quantum absorption refrigerator with trapped ions. Nature Communications 2019, 10, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Linden, N.; Popescu, S.; Skrzypczyk, P. How Small Can Thermal Machines Be? The Smallest Possible Refrigerator. Phys. Rev. Lett. 2010, 105, 130401. [Google Scholar] [CrossRef]
- Brunner, N.; Linden, N.; Popescu, S.; Skrzypczyk, P. Virtual qubits, virtual temperatures, and the foundations of thermodynamics. Phys. Rev. E 2012, 85, 051117. [Google Scholar] [CrossRef] [Green Version]
- Mitchison, M.T.; Huber, M.; Prior, J.; Woods, M.P.; Plenio, M.B. Realising a quantum absorption refrigerator with an atom-cavity system. Quantum Sci. Technol 2016, 1, 015001. [Google Scholar] [CrossRef]
- Manzano, G.; Giorgi, G.L.; Fazio, R.; Zambrini, R. Boosting the performance of small autonomous refrigerators via common environmental effects. New J. Phys. 2019, 21, 123026. [Google Scholar] [CrossRef]
- Brunner, N.; Huber, M.; Linden, N.; Popescu, S.; Silva, R.; Skrzypczyk, P. Entanglement enhances cooling in microscopic quantum refrigerators. Phys. Rev. E 2014, 89, 032115. [Google Scholar] [CrossRef] [Green Version]
- Brask, J.B.; Haack, G.; Brunner, N.; Huber, M. Autonomous quantum thermal machine for generating steady-state entanglement. New J. Phys. 2015, 17, 113029. [Google Scholar] [CrossRef]
- Kilgour, M.; Segal, D. Coherence and decoherence in quantum absorption refrigerators. Phys. Rev. E 2018, 98, 012117. [Google Scholar] [CrossRef] [Green Version]
- Mitchison, M.T.; Woods, M.P.; Prior, J.; Huber, M. Coherence-assisted single-shot cooling by quantum absorption refrigerators. New J. Phys. 2015, 17, 115013. [Google Scholar] [CrossRef] [Green Version]
- Yu, C.S.; Zhu, Q.Y. Re-examining the self-contained quantum refrigerator in the strong-coupling regime. Phys. Rev. E 2014, 90, 052142. [Google Scholar] [CrossRef] [Green Version]
- He, Z.C.; Huang, X.Y.; Yu, C.S. Enabling the self-contained refrigerator to work beyond its limits by filtering the reservoirs. Phys. Rev. E 2017, 96, 052126. [Google Scholar] [CrossRef] [Green Version]
- Seah, S.; Nimmrichter, S.; Scarani, V. Refrigeration beyond weak internal coupling. Phys. Rev. E 2018, 98, 012131. [Google Scholar] [CrossRef] [Green Version]
- Yu, C.S.; Guo, B.Q.; Liu, T. Quantum self-contained refrigerator in terms of the cavity quantum electrodynamics in the weak internal-coupling regime. Opt. Express 2019, 27, 6863–6877. [Google Scholar] [CrossRef]
- Lörch, N.; Bruder, C.; Brunner, N.; Hofer, P.P. Optimal work extraction from quantum states by photo-assisted Cooper pair tunneling. Quantum Sci. Technol 2018, 3, 035014. [Google Scholar] [CrossRef] [Green Version]
- Seah, S.; Nimmrichter, S.; Scarani, V. Work production of quantum rotor engines. New J. Phys. 2018, 20, 043045. [Google Scholar] [CrossRef]
- Guo, B.Q.; Liu, T.; Yu, C.S. Quantum thermal transistor based on qubit-qutrit coupling. Phys. Rev. E 2018, 98, 022118. [Google Scholar] [CrossRef] [Green Version]
- Guo, B.Q.; Liu, T.; Yu, C.S. Multifunctional quantum thermal device utilizing three qubits. Phys. Rev. E 2019, 99, 032112. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Chen, X.M.; Sun, K.W.; Ren, J. Heat amplification and negative differential thermal conductance in a strongly coupled nonequilibrium spin-boson system. Phys. Rev. A 2018, 97, 052112. [Google Scholar] [CrossRef] [Green Version]
- Wijesekara, R.T.; Gunapala, S.D.; Stockman, M.I.; Premaratne, M. Optically controlled quantum thermal gate. Phys. Rev. B 2020, 101, 245402. [Google Scholar] [CrossRef]
- Ghosh, R.; Ghoshal, A.; Sen, U. Quantum thermal transistors: Operation characteristics in steady state vs transient regimes. Phys. Rev. A 2020. [Google Scholar] [CrossRef]
- Lu, J.; Wang, R.; Wang, C.; Jiang, J.H. Brownian thermal transistors and refrigerators in mesoscopic systems. Phys. Rev. B 2020, 102, 125405. [Google Scholar] [CrossRef]
- Lu, J.; Wang, R.; Ren, J.; Kulkarni, M.; Jiang, J.H. Quantum-dot circuit-QED thermoelectric diodes and transistors. Phys. Rev. B 2019, 99, 035129. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Xu, D.; Liu, H.; Gao, X. Thermal rectification and heat amplification in a nonequilibrium V-type three-level system. Phys. Rev. E 2019, 99, 042102. [Google Scholar] [CrossRef] [Green Version]
- Balachandran, V.; Benenti, G.; Pereira, E.; Casati, G.; Poletti, D. Heat current rectification in segmented XXZ chains. Phys. Rev. E 2019, 99, 032136. [Google Scholar] [CrossRef] [Green Version]
- Kargı, C.; Naseem, M.T.; Opatrný, T.C.V.; Müstecaplıoğlu, O.E.; Kurizki, G. Quantum optical two-atom thermal diode. Phys. Rev. E 2019, 99, 042121. [Google Scholar] [CrossRef] [Green Version]
- Ordonez-Miranda, J.; Ezzahri, Y.; Joulain, K. Quantum thermal diode based on two interacting spinlike systems under different excitations. Phys. Rev. E 2017, 95, 022128. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Yan, Y.; Wu, C.Q.; Wang, J.S.; Li, B. Reversal of thermal rectification in quantum systems. Phys. Rev. B 2009, 80, 172301. [Google Scholar] [CrossRef] [Green Version]
- Silva, S.H.S.; Landi, G.T.; Drumond, R.C.; Pereira, E. Heat rectitication on the XX chain. Phys. Rev. E 2020. [Google Scholar] [CrossRef] [PubMed]
- Barra, F. Dissipative Charging of a Quantum Battery. Phys. Rev. Lett. 2019, 122, 210601. [Google Scholar] [CrossRef] [Green Version]
- Campaioli, F.; Pollock, F.A.; Binder, F.C.; Céleri, L.; Goold, J.; Vinjanampathy, S.; Modi, K. Enhancing the Charging Power of Quantum Batteries. Phys. Rev. Lett. 2017, 118, 150601. [Google Scholar] [CrossRef] [Green Version]
- Santos, A.C.; Saguia, A.; Sarandy, M.S. Stable and charge-switchable quantum batteries. Phys. Rev. E 2020, 101, 062114. [Google Scholar] [CrossRef]
- Hofer, P.P.; Brask, J.B.; Perarnau-Llobet, M.; Brunner, N. Quantum Thermal Machine as a Thermometer. Phys. Rev. Lett. 2017, 119, 090603. [Google Scholar] [CrossRef] [Green Version]
- Jevtic, S.; Newman, D.; Rudolph, T.; Stace, T.M. Single-qubit thermometry. Phys. Rev. A 2015, 91, 012331. [Google Scholar] [CrossRef] [Green Version]
- Mancino, L.; Genoni, M.G.; Barbieri, M.; Paternostro, M. Nonequilibrium readiness and precision of Gaussian quantum thermometers. Phys. Rev. Res. 2020, 2, 033498. [Google Scholar] [CrossRef]
- Chand, S.; Biswas, A. Critical-point behavior of a measurement-based quantum heat engine. Phys. Rev. E 2018, 98, 052147. [Google Scholar] [CrossRef] [Green Version]
- Streltsov, A.; Adesso, G.; Plenio, M.B. Colloquium: Quantum coherence as a resource. Rev. Mod. Phys. 2017, 89, 041003. [Google Scholar] [CrossRef] [Green Version]
- Latune, C.L.; Sinayskiy, I.; Petruccione, F. Apparent temperature: Demystifying the relation between quantum coherence, correlations, and heat flows. Q. Sci. Technol. 2019, 4, 025005. [Google Scholar] [CrossRef] [Green Version]
- Camati, P.A.; Santos, J.F.G.; Serra, R.M. Coherence effects in the performance of the quantum Otto heat engine. Phys. Rev. A 2019, 99, 062103. [Google Scholar] [CrossRef] [Green Version]
- Latune, C.L.; Sinayskiy, I.; Petruccione, F. Roles of quantum coherences in thermal machines. Eur. Phys. J. Spec. Top. 2021, 230, 841–850. [Google Scholar] [CrossRef]
- Karar, S.; Datta, S.; Ghosh, S.; Majumdar, A.S. Anharmonicity can enhance the performance of quantum refrigerators. arXiv 2020, arXiv:1902.10616. [Google Scholar]
- Camati, P.A.; Santos, J.F.G.; Serra, R.M. Employing non-Markovian effects to improve the performance of a quantum Otto refrigerator. Phys. Rev. A 2020, 102, 012217. [Google Scholar] [CrossRef]
- Braun, D. Creation of Entanglement by Interaction with a Common Heat Bath. Phys. Rev. Lett. 2002, 89, 277901. [Google Scholar] [CrossRef] [Green Version]
- Karimi, B.; Pekola, J.P. Correlated versus uncorrelated noise acting on a quantum refrigerator. Phys. Rev. B 2017, 96, 115408. [Google Scholar] [CrossRef] [Green Version]
- Contreras-Pulido, L.D.; Aguado, R. Entanglement between charge qubits induced by a common dissipative environment. Phys. Rev. B 2008, 77, 155420. [Google Scholar] [CrossRef] [Green Version]
- Paz, J.P.; Roncaglia, A.J. Dynamics of the Entanglement between Two Oscillators in the Same Environment. Phys. Rev. Lett. 2008, 100, 220401. [Google Scholar] [CrossRef] [Green Version]
- Galve, F.; Mandarino, A.; Paris, M.G.A.; Benedetti, C.; Zambrini, R. Microscopic description for the emergence of collective dissipation in extended quantum systems. Sci. Rep. 2017, 7. [Google Scholar] [CrossRef]
- Man, Z.X.; Tavakoli, A.; Brask, J.B.; Xia, Y.J. Improving autonomous thermal entanglement generation using a common reservoir. Phys. Scr. 2019, 94, 075101. [Google Scholar] [CrossRef] [Green Version]
- Ren, W.; Liu, W.; Song, C.; Li, H.; Guo, Q.; Wang, Z.; Zheng, D.; Agarwal, G.S.; Scully, M.O.; Zhu, S.Y.; et al. Simultaneous Excitation of Two Noninteracting Atoms with Time-Frequency Correlated Photon Pairs in a Superconducting Circuit. Phys. Rev. Lett. 2020, 125, 133601. [Google Scholar] [CrossRef]
- Garziano, L.; Macrì, V.; Stassi, R.; Di Stefano, O.; Nori, F.; Savasta, S. One Photon Can Simultaneously Excite Two or More Atoms. Phys. Rev. Lett. 2016, 117, 043601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Breuer, H.P.; Petruccione, F. The Theory of Open Quantum Systems; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Weiss, U. Quantum Dissipative Systems; World Scientific: Jerusalem, Israel, 2012; Volume 13. [Google Scholar]
- Schaller, G. Open Quantum Systems Far from Equilibrium; Springer: Berlin, Germany, 2014; Volume 881. [Google Scholar]
- Johansson, J.; Nation, P.; Nori, F. QuTiP 2: A Python framework for the dynamics of open quantum systems. Comput. Phys. Commun. 2013, 184, 1234–1240. [Google Scholar] [CrossRef] [Green Version]
- Li, B.; Wang, L.; Casati, G. Negative differential thermal resistance and thermal transistor. Appl. Phys. Lett. 2006, 88, 143501. [Google Scholar] [CrossRef] [Green Version]
- Liao, J.Q.; Huang, J.F.; Kuang, L.M. Quantum thermalization of two coupled two-level systems in eigenstate and bare-state representations. Phys. Rev. A 2011, 83, 052110. [Google Scholar] [CrossRef] [Green Version]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.-Q.; Yu, D.-H.; Yu, C.-S. Common Environmental Effects on Quantum Thermal Transistor. Entropy 2022, 24, 32. https://doi.org/10.3390/e24010032
Liu Y-Q, Yu D-H, Yu C-S. Common Environmental Effects on Quantum Thermal Transistor. Entropy. 2022; 24(1):32. https://doi.org/10.3390/e24010032
Chicago/Turabian StyleLiu, Yu-Qiang, Deng-Hui Yu, and Chang-Shui Yu. 2022. "Common Environmental Effects on Quantum Thermal Transistor" Entropy 24, no. 1: 32. https://doi.org/10.3390/e24010032
APA StyleLiu, Y.-Q., Yu, D.-H., & Yu, C.-S. (2022). Common Environmental Effects on Quantum Thermal Transistor. Entropy, 24(1), 32. https://doi.org/10.3390/e24010032





