A Concise Method to Predict the Mean Dynamic Pressure on a Plunge Pool Slab
Abstract
:1. Introduction
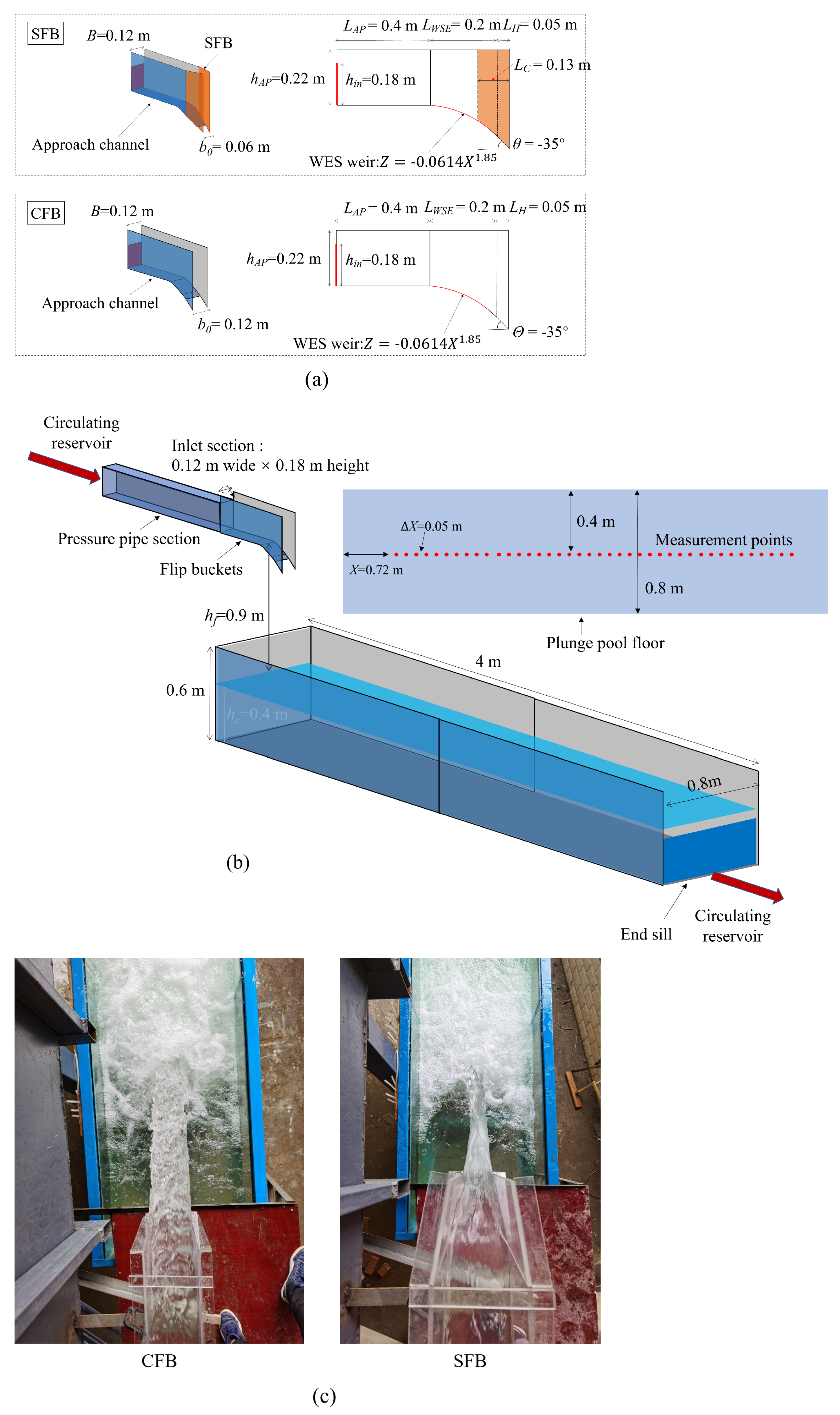
2. Experimental Setup
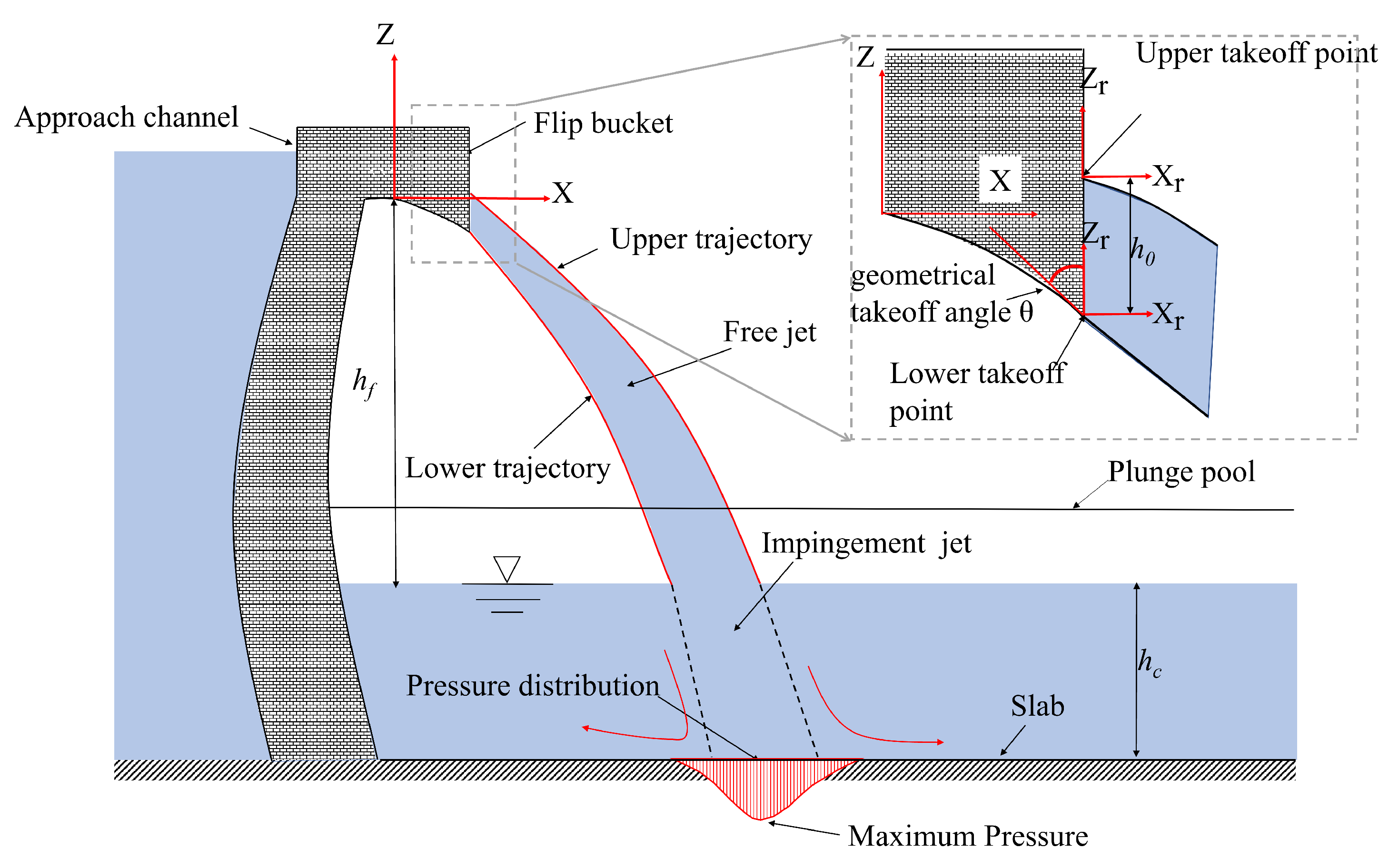
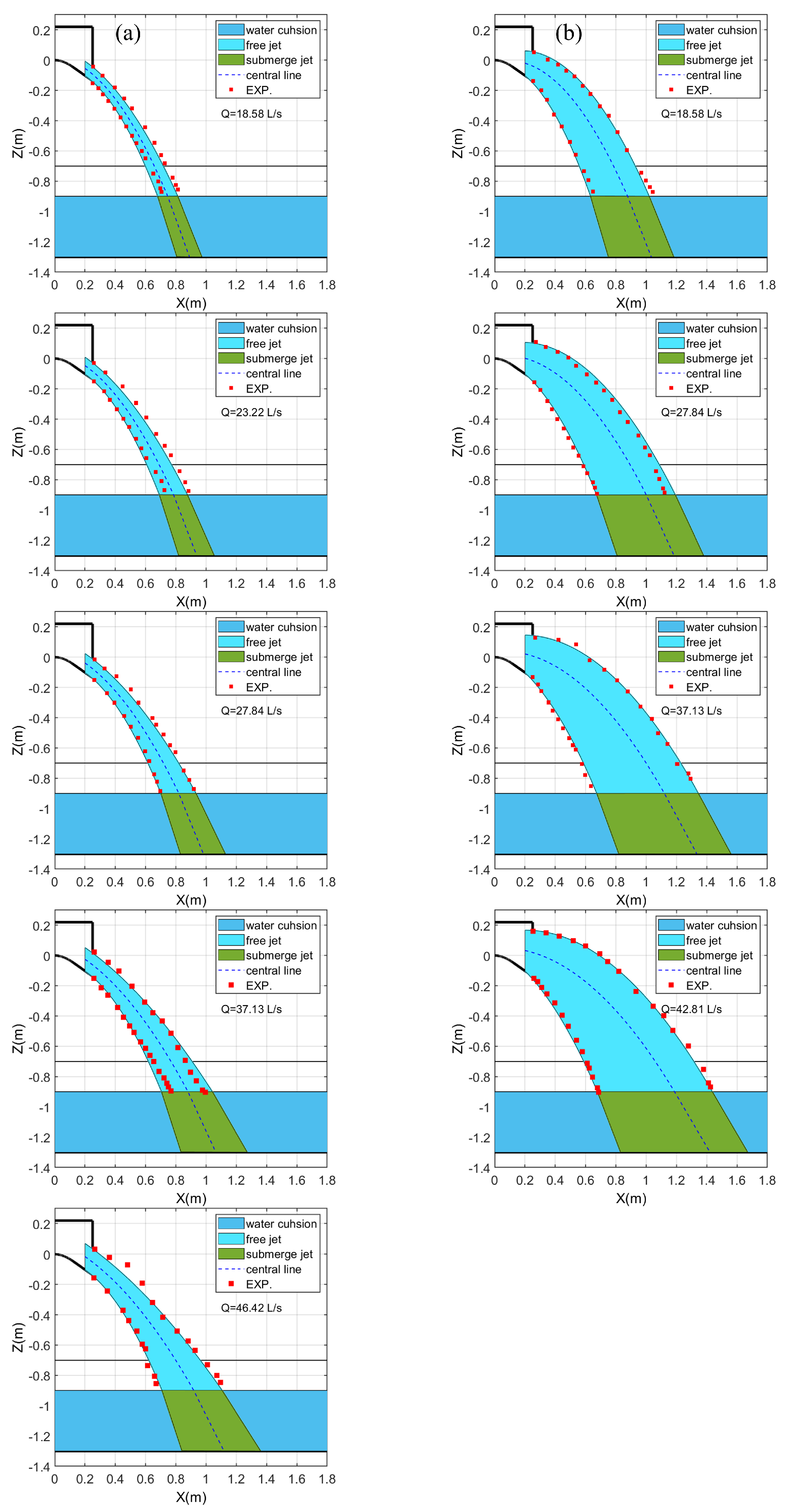
3. Calculating the Trajectory of the Free Jet
3.1. General Equation
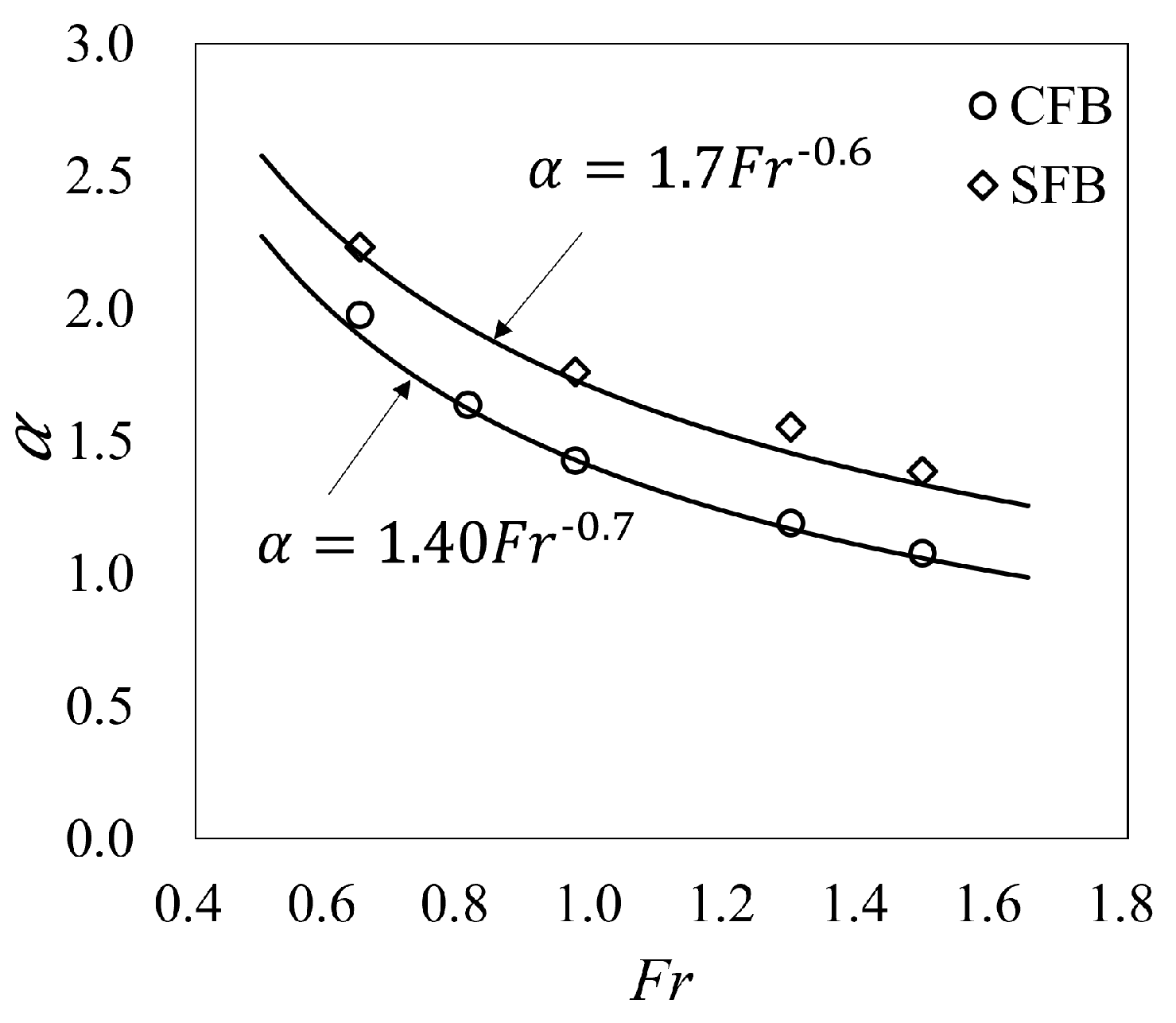
3.2. Mean Velocity Coefficients
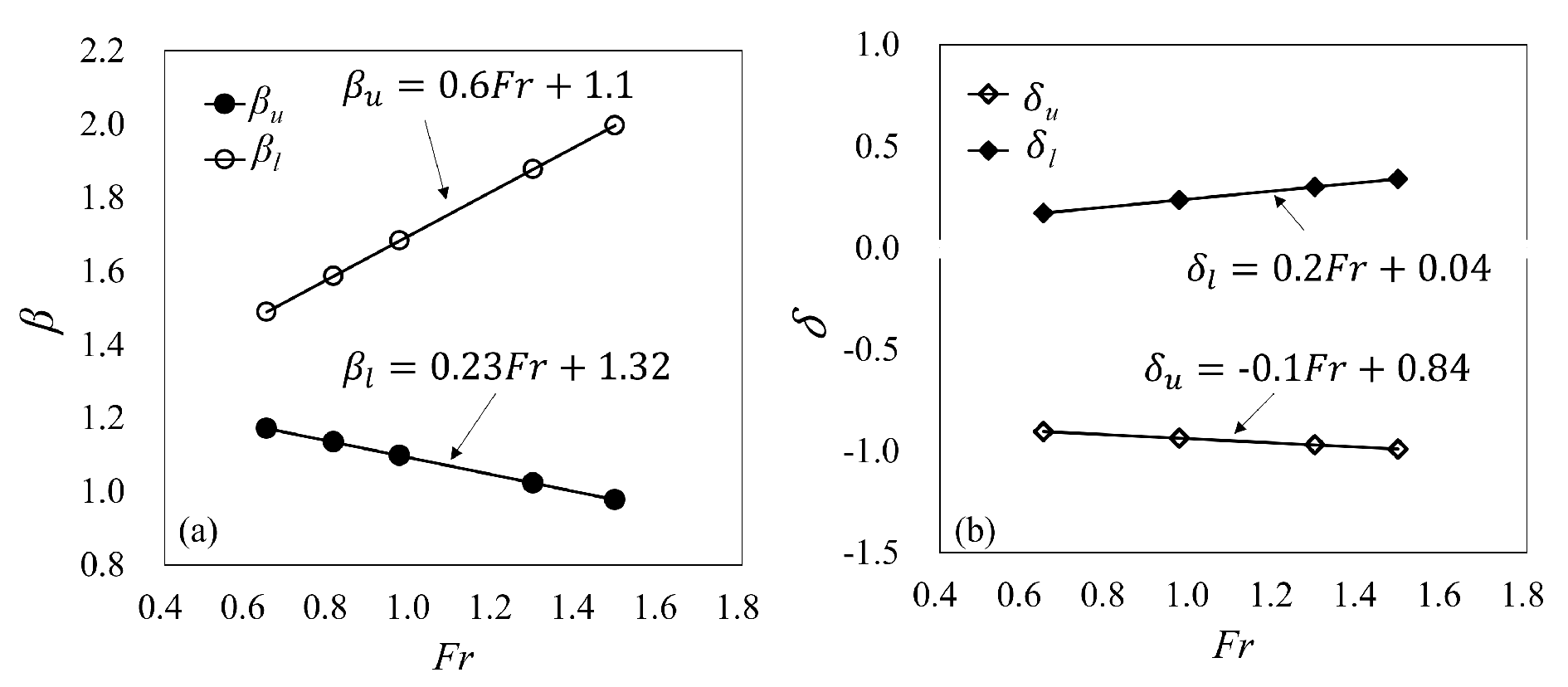
3.3. Takeoff Velocity Coefficients
3.4. Takeoff Angle Coefficients
4. Predicting the Dynamic Pressure
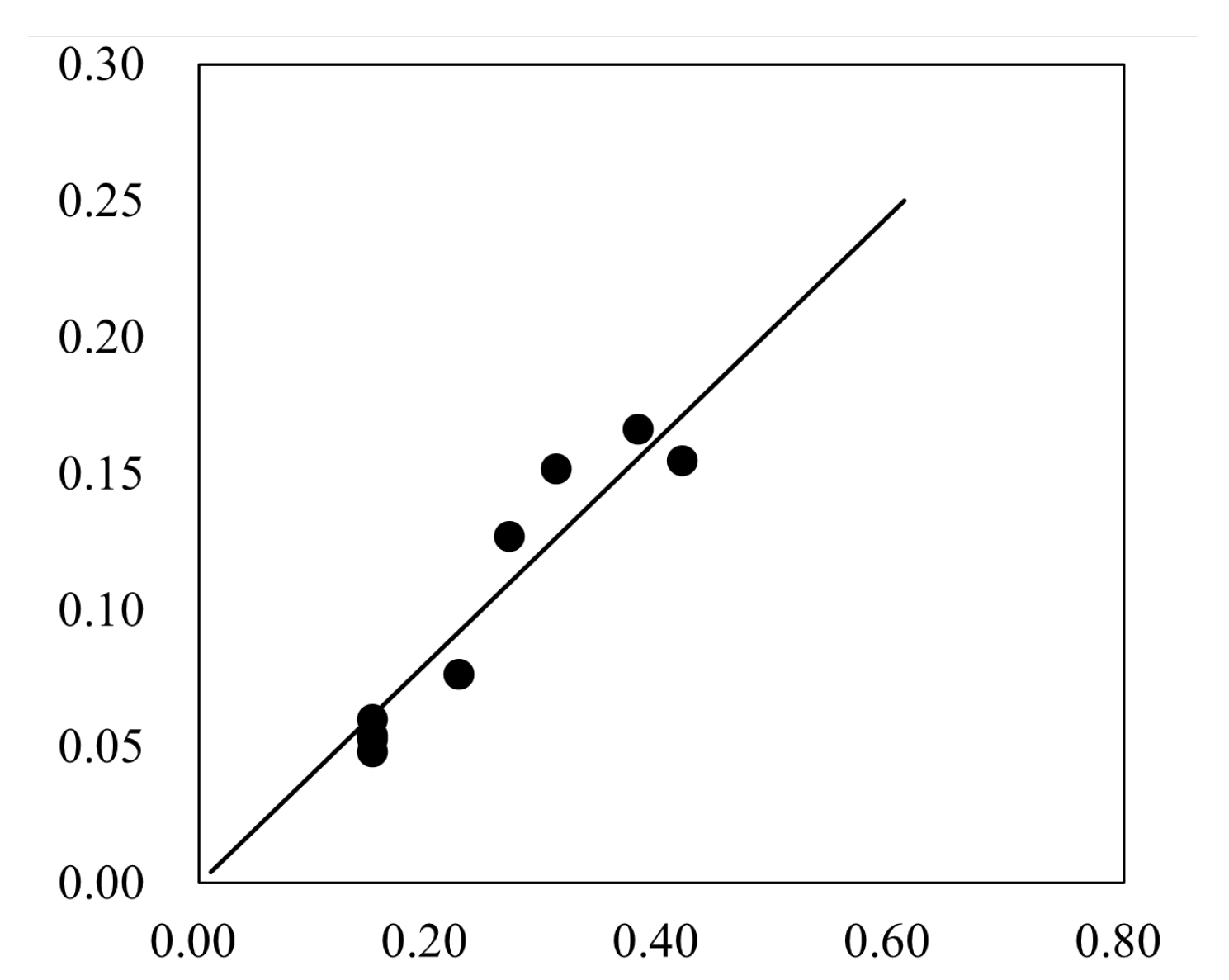
4.1. Location of the Stagnation Point
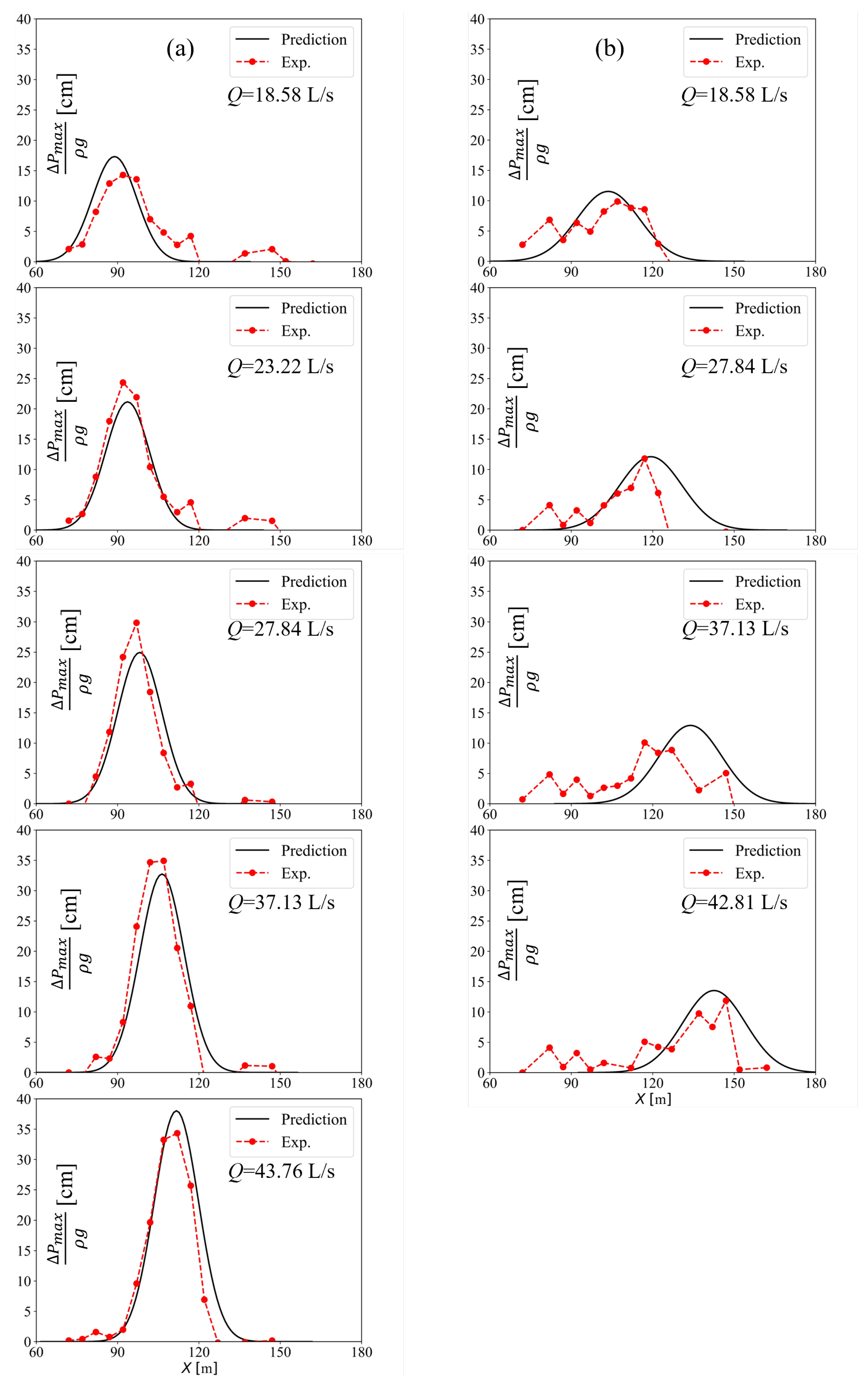
4.2. Maximum Mean Dynamic Pressure
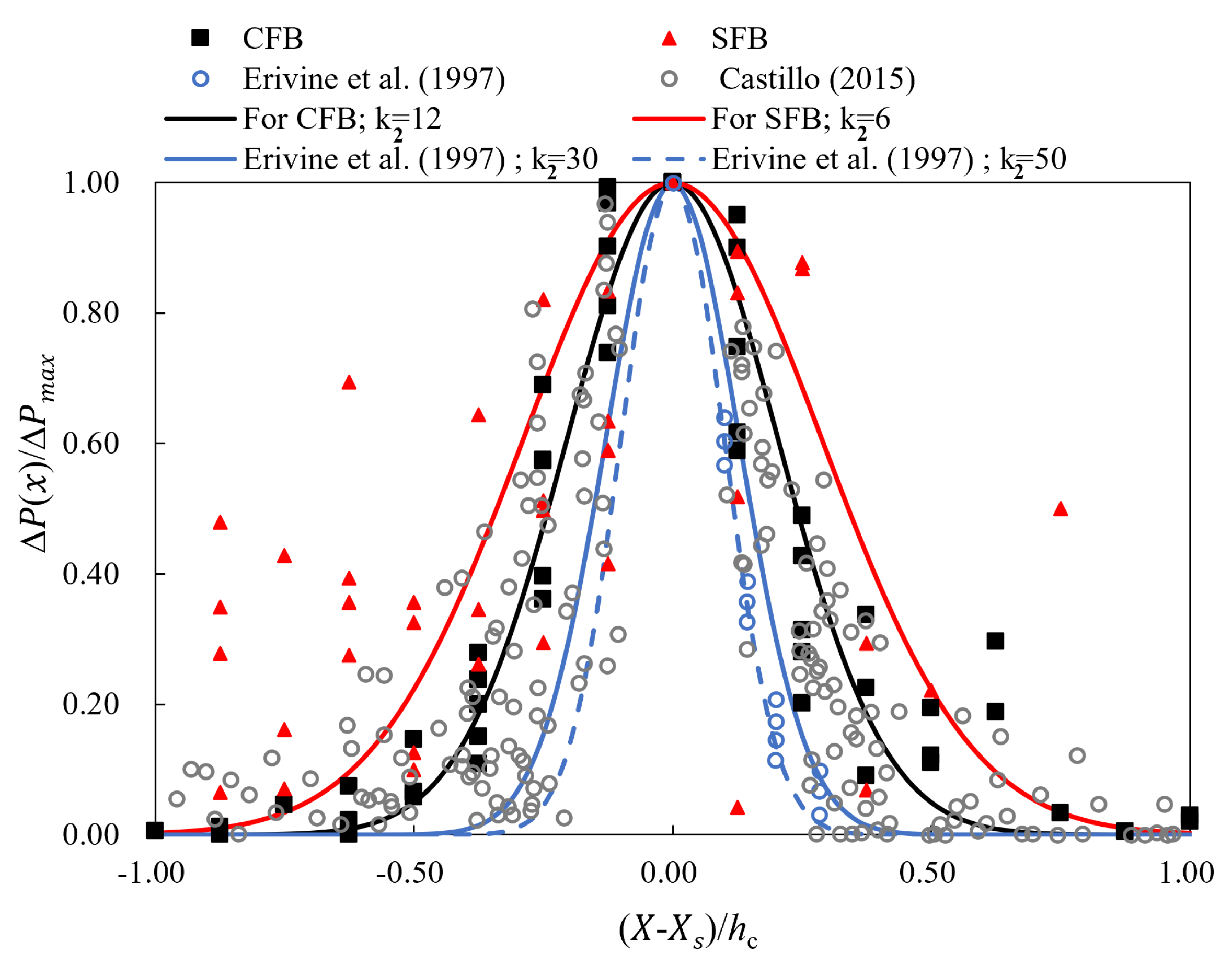
4.3. Distribution of the Mean Dynamic Pressure
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Q | Flow rate |
| Takeoff bulk velocity | |
| U | Inlet velocity |
| Takeoff velocity | |
| Takeoff velocity at the upper takeoff point | |
| Takeoff velocity at the lower takeoff point | |
| Froude number | |
| Position of the stagnation point | |
| Height of the free jet at the takeoff cross-section | |
| Width of the flip bucket | |
| Depth of water cushion | |
| Height difference between approach channel bottom and water cushion | |
| Characteristic width of free jets | |
| Geometrical takeoff angle of the flip bucket | |
| Effective takeoff angle | |
| Effective takeoff angle at the upper takeoff point | |
| Effective takeoff angle at the lower takeoff | |
| Mean velocity coefficient | |
| Upper takeoff velocity coefficients | |
| Lower takeoff velocity coefficients | |
| takeoff angle coefficient at the upper takeoff point | |
| Mean dynamic pressure | |
| Maximum mean dynamic pressure |
References
- Robertson, R.A.; Ball, J.W. Model Study of Power Intake Gate of Mossyrock Dam. J. Hydraul. Div. 1971, 97, 889–906. [Google Scholar] [CrossRef]
- Wu, S.Y.; Cao, W.; Zheng, J. Analysis of working behavior of Jinping-I Arch Dam during initial impoundment. Water Sci. Eng. 2016, 9, 240–248. [Google Scholar] [CrossRef]
- Deng, J.; Yang, Z.L.; Tian, Z.; Zhang, F.X.; Wei, W.R.; You, X.; Xu, W.L. A new type of leak-floor flip bucket. Sci. China Technol. Sci. 2016, 59, 565–572. [Google Scholar] [CrossRef]
- Teng, P.; Yang, J. Modeling and Prototype Testing of Flows over Flip-Bucket Aerators. J. Hydraul. Eng. 2018, 144, 04018069. [Google Scholar] [CrossRef]
- Melo, J.F.; Pinheiro, A.N.; Ramos, C.M. Forces on Plunge Pool Slabs: Influence of Joints Location and Width. J. Hydraul. Eng. 2006, 132, 49–60. [Google Scholar] [CrossRef]
- Wahl, T.L.; Frizell, K.H.; Cohen, E.A. Computing the Trajectory of Free Jets. J. Hydraul. Eng. 2008, 134, 49–60. [Google Scholar] [CrossRef] [Green Version]
- Juon, R.; Hager, W.H. Flip Bucket without and with Deflectors. J. Hydraul. Eng. 2000, 126. [Google Scholar] [CrossRef]
- Toombes, L.; Chanson, H. Free-surface aeration and momentum exchange at a bottom outlet. J. Hydraul. Res. 2007, 45, 100–110. [Google Scholar] [CrossRef]
- Pfister, M.; Hager, W.H.; Boes, R.M. Trajectories and air flow features of ski jump-generated jets. J. Hydraul. Res. 2014, 52, 336–346. [Google Scholar] [CrossRef]
- Deng, J.; Wei, W.; Tian, Z.; Zhang, F.; Yang, Z. Analysis of Pressure Differences and Water Transverse Movement in a Partial-Flip Bucket. J. Hydraul. Eng. 2020, 146, 04020063. [Google Scholar] [CrossRef]
- US Department of the Interior, Bureau of Reclamation. Design of Small Dams; United States Government Printing Office: Washington, DC, USA, 1987.
- Zhang, Y.; Wu, W. Experimental researches on the flow profile and the nappe trajectory distance for slit-type bucket. Shuili Xuebao 1989, 20, 14–21. (In Chinese) [Google Scholar]
- Zhu, Y. Study on the Hydraulic Characteristics for Tongue-Shaped Flip Bucket. Ph.D. Thesis, Sichuan University, Chengdu, China, 2004. (In Chinese). [Google Scholar]
- Heller, V.; Hager, W.H.; Minor, H.E. Ski Jump Hydraulics. J. Hydraul. Eng. 2005, 131, 347–355. [Google Scholar] [CrossRef]
- Wu, J.; Ruan, S. Cavity length below chute aerators. Sci. China Ser. E Technol. Sci. 2008, 51, 170–178. [Google Scholar] [CrossRef]
- Wu, J.H.; Xu, Z.; Yao, L.; Ma, F. Ski-jump trajectory based on take-off velocity. J. Hydrodyn. 2016, 28, 166–169. [Google Scholar] [CrossRef]
- Cui, G.T.; Lin, J.Y.; Liang, X.R. Research on the force and influence of the overflow water tongue of the arch dam on the river bed. Shuili Xuebao 1985, 8, 58–63. (In Chinese) [Google Scholar]
- Puertas, J.; Dolz, J. Plunge Pool Pressures Due to a Falling Rectangular Jet. J. Hydraul. Eng. 2005, 131, 404–407. [Google Scholar] [CrossRef]
- Cola, R. Energy dissipation of a high-velocity vertical jet entering a basin. In Proceedings of the 11th IAHR Congress, Leningrad, Russia; 1965; Volume 1. [Google Scholar]
- Guo, Y. Numerical Simulation of the Spreading of Aerated and Nonaerated Turbulent Water Jet in a Tank with Finite Water Depth. J. Hydraul. Eng. 2014, 140, 04014034. [Google Scholar] [CrossRef] [Green Version]
- Lin, J.; Lian, J. Calculation of the point area wall fluctuating pressure amplitude by two-dimensional jets. In Proceedings of the Internernational Symposium on Hydraulics for High Dams, Beijing, China, 15–18 November 1988; pp. 375–382. [Google Scholar]
- Manso, P.A.; Bollaert, E.F.R.; Schleiss, A.J. Impact pressures of turbulent high-velocity jets plunging in pools with flat bottom. Exp. Fluids 2007, 42, 49–60. [Google Scholar] [CrossRef] [Green Version]
- Manso, P.F.; Bollaert, E.F.; Schleiss, A.J. Evaluation of high-velocity pluning jet-issuing characteristics as a basis for plunge pool analysis. J. Hydraul. Res. 2008, 46, 147–157. [Google Scholar] [CrossRef]
- Tu, C.V.; Wood, D.H. Wall pressure and shear stress measurements beneath an impinging jet. Exp. Therm. Fluid Sci. 1996, 13, 364–373. [Google Scholar] [CrossRef]
- Ervine, D.A.; Falvey, H.T.; Withers, W. Pressure fluctuations on plunge pool floors. J. Hydraul. Res. 1997, 35, 257–279. [Google Scholar] [CrossRef]
- Bollaert, E.; Schleiss, A. Scour of rock due to the impact of plunging high velocity jets Part I: A state-of-the-art review. J. Hydraul. Res. 2003, 41, 451–464. [Google Scholar] [CrossRef]
- Borghei, S.M.; Zarnani, P. Jet impact geometry and plunge pool dimensions effects on dynamic pressures at pool sidewalls. Can. J. Civ. Eng. 2008, 35, 408–417. [Google Scholar] [CrossRef]
- Wang, Y.; Hu, Y.; Gu, J.; Peng, Y.; Xue, Y. Impact pressure distribution of inverted arch plunge pool for large discharge. Water Sci. Technol. Water Supply 2020, 20. [Google Scholar] [CrossRef]
- Wei, W.; Xu, W.; Deng, J.; Liu, B. Experimental Study of Impact Pressures on Deep Plunge Pool Floors Generated by Submerged Inclined Jets with Controlled Aeration. J. Hydraul. Eng. 2020, 146, 04020021. [Google Scholar] [CrossRef]
- Smith, S.H.; Mungal, M.G. Mixing, structure and scaling of the jet in crossflow. J. Fluid Mech. 1998, 357, 83–122. [Google Scholar] [CrossRef]
- Lai, H.; Naughton, J.W.; Lindberg, W.R. An Experimental Investigation of Starting Impinging Jets. J. Fluids Eng. 2003, 125, 275–282. [Google Scholar] [CrossRef]
- Chanson, H. Turbulent air–water flows in hydraulic structures: Dynamic similarity and scale effects. Environ. Fluid Mech. 2009, 9, 125–142. [Google Scholar] [CrossRef] [Green Version]
- Heller, V. Scale effects in physical hydraulic engineering models. J. Hydraul. Res. 2011, 49, 293–306. [Google Scholar] [CrossRef]
- Li, N.; Deng, J.; Guo, W.; Li, L. Jet geometry effects on the velocity decay of an oblique submerged jet in a plunge pool. Deep. Rock Mech. Res. Eng. 2018, 571–584. [Google Scholar] [CrossRef]
- Li, X.; Zhou, M.; Zhang, J.; Xu, W. Numerical study of the velocity decay of offset jet in a narrow and deep pool. Water 2018, 11, 59. [Google Scholar] [CrossRef] [Green Version]
- Castillo, L.G.; Carrillo, J.M.; Blázquez, A. Plunge pool dynamic pressures: A temporal analysis in the nappe flow case. J. Hydraul. Res. 2015, 53, 101–118. [Google Scholar] [CrossRef]
- Ma, Y.; David, Z.; Rajarathnam, N.; Camina, G. Experimental Study of the Breakup of a Free-Falling Turbulent Water Jet in Air, 2016. J. Hydraul. Eng. 2016, 142, 06016014. [Google Scholar] [CrossRef]
- Ma, F.; Zhang, X.; Wu, J. Trajectories and air flow features of ski jump generated jets, 2016. J. Hydraul. Res. 2016, 54, 245–247. [Google Scholar] [CrossRef]
| Test Number | Discharge Q (L/S) | Inlet Velocity U (m/s) | Type of the Flip Bucket |
|---|---|---|---|
| 1 | 18.58 | 0.86 | CFB |
| 2 | 23.22 | 1.08 | CFB |
| 3 | 27.84 | 1.29 | CFB |
| 4 | 37.13 | 1.72 | CFB |
| 5 | 43.76 | 2.03 | CFB |
| 6 | 18.58 | 0.86 | SFB |
| 7 | 23.22 | 1.08 | SFB |
| 8 | 27.84 | 1.29 | SFB |
| 9 | 43.76 | 1.98 | SFB |
| Type | Q (L/S) | (m) | (m) | (m) |
|---|---|---|---|---|
| CFB | 18.58 | 0.090 | 0.120 | 0.090 |
| CFB | 23.22 | 0.108 | 0.120 | 0.108 |
| CFB | 27.84 | 0.124 | 0.120 | 0.124 |
| CFB | 37.13 | 0.152 | 0.120 | 0.152 |
| CFB | 43.76 | 0.167 | 0.120 | 0.167 |
| SFB | 18.58 | 0.090 | 0.060 | 0.060 |
| SFB | 23.22 | 0.108 | 0.060 | 0.060 |
| SFB | 27.84 | 0.124 | 0.060 | 0.060 |
| SFB | 42.81 | 0.167 | 0.060 | 0.060 |
| Step | Goal and Approach | Requisite Steps (Rs.) and Parameters (Rp.) |
|---|---|---|
| 1 | Goal: obtain the takeoff velocity ( ) at takeoff cross-section; Approaches: Equations (4)–(6). | Rs.: None Rp.: U, , |
| 2 | Goal: obtain takeoff velocities at upper and lower takeoff points and ; Approaches: Equations (7) and (8). | Rs.: None Rp.: , , |
| 3 | Goal: obtain effective takeoff angle at lower takeoff points ( and ); Approach: Equation (12). | Rs.: None Rp.: , , |
| 4 | Goal: obtain the location of the stagnation point (); Approaches: calculate the central line by Equations (3), (16) and (17), and the end point of central line is the stagnation point. | Rs.: step 1, 2, and 3 Rp.: , , |
| 5 | Goal: calculate the maximum mean dynamic pressure ; Approach: Equation (24). | Rs.: None Rp.: , , U, , |
| 6 | Goal: obtain the distribution of the dynamic pressure ; Approach: Equation (25). | Rs.: step 4 and 5 Rp.: , , , |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, M.; Li, X.; Zhang, J.; Xu, W. A Concise Method to Predict the Mean Dynamic Pressure on a Plunge Pool Slab. Entropy 2022, 24, 45. https://doi.org/10.3390/e24010045
Zhou M, Li X, Zhang J, Xu W. A Concise Method to Predict the Mean Dynamic Pressure on a Plunge Pool Slab. Entropy. 2022; 24(1):45. https://doi.org/10.3390/e24010045
Chicago/Turabian StyleZhou, Maolin, Xin Li, Jianmin Zhang, and Weilin Xu. 2022. "A Concise Method to Predict the Mean Dynamic Pressure on a Plunge Pool Slab" Entropy 24, no. 1: 45. https://doi.org/10.3390/e24010045
APA StyleZhou, M., Li, X., Zhang, J., & Xu, W. (2022). A Concise Method to Predict the Mean Dynamic Pressure on a Plunge Pool Slab. Entropy, 24(1), 45. https://doi.org/10.3390/e24010045






