Regularity Normalization: Neuroscience-Inspired Unsupervised Attention across Neural Network Layers †
Abstract
:1. Introduction
2. Related Work
2.1. Neuroscience Inspirations
2.2. Normalization Methods in Neural Networks
2.3. Description Length in Neural Networks
2.4. Attention Maps
3. Background
3.1. Minimum Description Length
3.2. Normalized Maximum Likelihood
4. Neural Networks as Model Selection
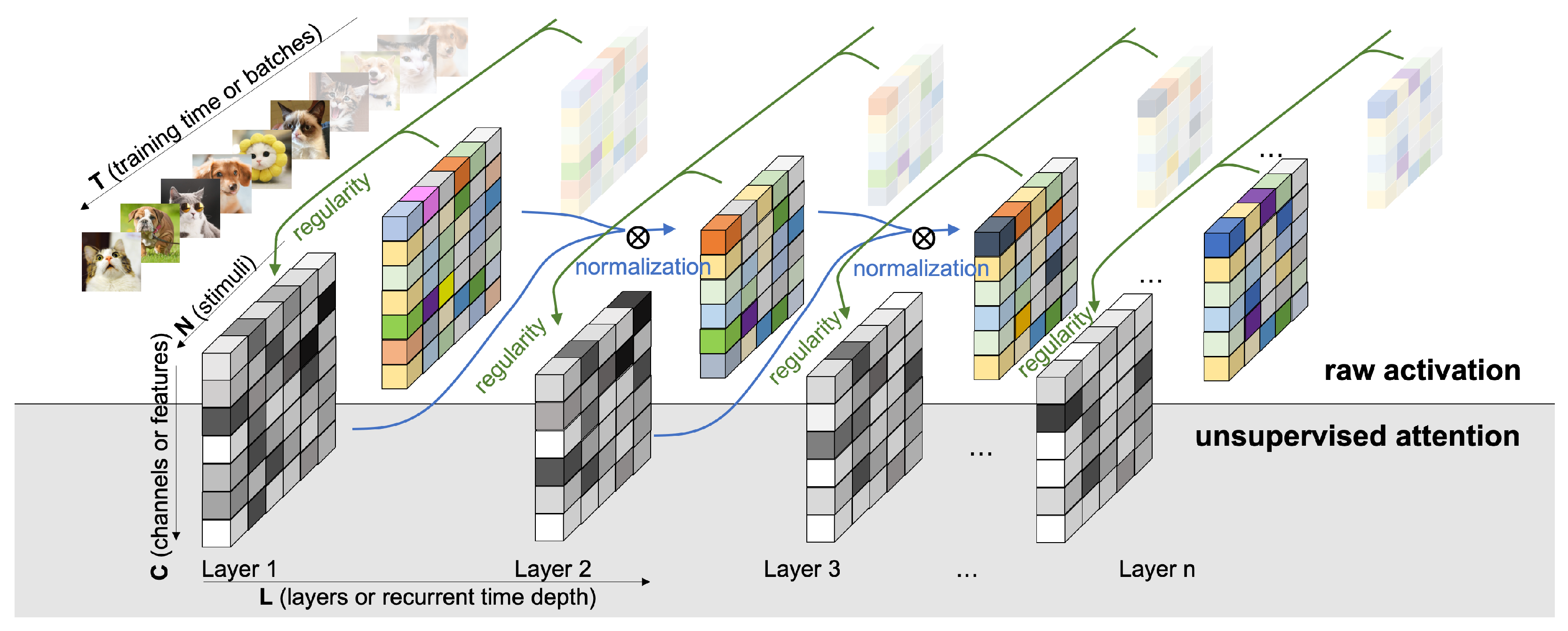
5. The Unsupervised Attention Mechanism
5.1. Standard Case: Regularity Normalization
| Algorithm 1 Regularity Normalization (RN) |
|
5.2. Variant: Saliency Normalization
5.3. Variant: Beyond Elementwise Normalization
6. Demonstration: The Unsupervised Attention Mechanism as a Probing Tool
6.1. Over Different Layers in the Feedforward Neural Networks (FFNN)
6.2. Over Recurrent Time Steps in the Recurrent Neural Networks (RNN)
7. Empirical Results
7.1. The Imbalanced MNIST Problem with Feedforward Neural Network
7.2. The Classic Control Problem in OpenAI Gym with Deep Q Networks (DQN)
7.3. The Generative Modeling Problem with Deep Recurrent Attentive Writer (DRAW)
7.4. The Dialogue Modeling Problem in bAbI with Gated Graph Neural Networks (GGNN)
7.5. Procedurally-Generated Reinforcement Learning in MiniGrid with Proximal Policy Optimization (PPO)
8. Discussion
9. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Further Discussions
Appendix A.1. More Analytics
Appendix A.2. Gaussian and Beyond
Appendix B. More details on the Imbalanced MNIST Tasks
Appendix B.1. Neural Network Settings
Appendix B.2. Supplementary Figures

Appendix C. More Details on the OpenAI Gym Tasks
Appendix C.1. Neural Network Settings
Appendix C.2. Game Settings
Appendix C.3. Supplementary Figures









Appendix D. More Details on the bAbI Tasks
Appendix D.1. Neural Network Settings
Appendix D.2. Game Settings
Appendix E. More Details on the MiniGrid Tasks
Appendix E.1. Neural Network Settings
Appendix E.2. Game Settings
Appendix E.3. Reproducibility and Code Availability
References
- Rissanen, J. Modeling by shortest data description. Automatica 1978, 14, 465–471. [Google Scholar] [CrossRef]
- Grünwald, P.D. The Minimum Description Length Principle; MIT press: Cambridge, MA, USA, 2007. [Google Scholar]
- Rissanen, J. Stochastic Complexity in Statistical Inquiry; World Scientific: Singapore, 1989. [Google Scholar]
- Zemel, R.S.; Hinton, G.E. Learning Population Coes by Minimizing Description Length; Unsupervised learning; Bradford Company: Brighton, MI, USA, 1999; pp. 261–276. [Google Scholar]
- Lin, B. Neural Networks as Model Selection with Incremental MDL Normalization. In Proceedings of the International Workshop on Human Brain and Artificial Intelligence, Macao, China, 12 August 2019; Springer: Berlin/Heidelberg, Germany, 2019; pp. 195–208. [Google Scholar]
- Ding, S.; Cueva, C.J.; Tsodyks, M.; Qian, N. Visual perception as retrospective Bayesian decoding from high-to low-level features. Proc. Natl. Acad. Sci. USA 2017, 114, E9115–E9124. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Blakemore, C.; Campbell, F.W. Adaptation to spatial stimuli. J. Physiol. 1969, 200, 11P–13P. [Google Scholar] [PubMed]
- Dragoi, V.; Sharma, J.; Sur, M. Adaptation-induced plasticity of orientation tuning in adult visual cortex. Neuron 2000, 28, 287–298. [Google Scholar] [CrossRef] [Green Version]
- Qian, N.; Zhang, J. Neuronal Firing Rate As Code Length: A Hypothesis. Comput. Brain Behav. 2020, 3, 34–53. [Google Scholar] [CrossRef]
- Marblestone, A.H.; Wayne, G.; Kording, K.P. Toward an integration of deep learning and neuroscience. Front. Comput. Neurosci. 2016, 10, 94. [Google Scholar] [CrossRef]
- Glaser, J.I.; Benjamin, A.S.; Farhoodi, R.; Kording, K.P. The roles of supervised machine learning in systems neuroscience. Prog. Neurobiol. 2019, 175, 126–137. [Google Scholar] [CrossRef] [Green Version]
- Botvinick, M.; Wang, J.X.; Dabney, W.; Miller, K.J.; Kurth-Nelson, Z. Deep reinforcement learning and its neuroscientific implications. Neuron 2020, 107, 603–616. [Google Scholar] [CrossRef]
- Lin, B.; Cecchi, G.; Bouneffouf, D.; Reinen, J.; Rish, I. A Story of Two Streams: Reinforcement Learning Models from Human Behavior and Neuropsychiatry. In Proceedings of the Nineteenth International Conference on Autonomous Agents and Multi-Agent Systems, AAMAS-20, Auckland, New Zealand, 9–13 May 2020; 2020; pp. 744–752. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. arXiv 2015, arXiv:1502.03167. [Google Scholar]
- Ba, J.L.; Kiros, J.R.; Hinton, G.E. Layer normalization. arXiv 2016, arXiv:1607.06450. [Google Scholar]
- Salimans, T.; Kingma, D.P. Weight normalization: A simple reparameterization to accelerate training of deep neural networks. In Proceedings of the 30th Conference on Neural Information Processing Systems (NIPS 2016), Barcelona, Spain, 5–10 December 2016; pp. 901–909. [Google Scholar]
- Hinton, G.; Van Camp, D. Keeping neural networks simple by minimizing the description length of the weights. In Proceedings of the sixth annual conference on Computational learning theory, Santa Cruz, CA, USA, 26–28 July 1993. [Google Scholar]
- Blier, L.; Ollivier, Y. The description length of deep learning models. arXiv 2018, arXiv:1802.07044. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is All You Need. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; pp. 5998–6008.
- Frankle, J.; Carbin, M. The lottery ticket hypothesis: Finding sparse, trainable neural networks. arXiv 2018, arXiv:1803.03635. [Google Scholar]
- Han, S.; Pool, J.; Tran, J.; Dally, W. Learning both weights and connections for efficient neural network. In Proceedings of the Advances in Neural Information Processing Systems 28 (NIPS 2015), Montreal, QC, Canada, 7–12 December 2015; pp. 1135–1143. [Google Scholar]
- Wang, F.; Jiang, M.; Qian, C.; Yang, S.; Li, C.; Zhang, H.; Wang, X.; Tang, X. Residual attention network for image classification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 3156–3164. [Google Scholar]
- Fu, J.; Liu, J.; Tian, H.; Li, Y.; Bao, Y.; Fang, Z.; Lu, H. Dual attention network for scene segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 3146–3154. [Google Scholar]
- Tang, J.; Shu, X.; Yan, R.; Zhang, L. Coherence constrained graph LSTM for group activity recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2019. [Google Scholar] [CrossRef]
- Shu, X.; Zhang, L.; Sun, Y.; Tang, J. Host–Parasite: Graph LSTM-in-LSTM for Group Activity Recognition. IEEE Trans. Neural Networks Learn. Syst. 2020, 32, 663–674. [Google Scholar] [CrossRef]
- Shu, X.; Zhang, L.; Qi, G.J.; Liu, W.; Tang, J. Spatiotemporal co-attention recurrent neural networks for human-skeleton motion prediction. IEEE Trans. Pattern Anal. Mach. Intell. 2021. [Google Scholar] [CrossRef]
- Rissanen, J. Strong optimality of the normalized ML models as universal codes and information in data. IEEE Trans. Inf. Theory 2001, 47, 1712–1717. [Google Scholar] [CrossRef] [Green Version]
- Myung, J.I.; Navarro, D.J.; Pitt, M.A. Model selection by normalized maximum likelihood. J. Math. Psychol. 2006, 50, 167–179. [Google Scholar] [CrossRef] [Green Version]
- Shtarkov, Y.M. Universal sequential coding of single messages. Probl. Peredachi Informatsii 1987, 23, 3–17. [Google Scholar]
- Calafiore, G.C.; El Ghaoui, L. Optimization Models; Cambridge university press: Cambridge, UK, 2014. [Google Scholar]
- Zhang, J. Model Selection with Informative Normalized Maximum Likelihood: Data Prior and Model Prior. In Descriptive and Normative Approaches to Human Behavior; World Scientific: Singapore, 2012; pp. 303–319. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Graves, A.; Antonoglou, I.; Wierstra, D.; Riedmiller, M. Playing atari with deep reinforcement learning. arXiv 2013, arXiv:1312.5602. [Google Scholar]
- Brockman, G.; Cheung, V.; Pettersson, L.; Schneider, J.; Schulman, J.; Tang, J.; Zaremba, W. Openai gym. arXiv 2016, arXiv:1606.01540. [Google Scholar]
- Gregor, K.; Danihelka, I.; Graves, A.; Rezende, D.J.; Wierstra, D. Draw: A recurrent neural network for image generation. arXiv 2015, arXiv:1502.04623. [Google Scholar]
- Weston, J.; Bordes, A.; Chopra, S.; Rush, A.M.; van Merriënboer, B.; Joulin, A.; Mikolov, T. Towards ai-complete question answering: A set of prerequisite toy tasks. arXiv 2015, arXiv:1502.05698. [Google Scholar]
- Li, Y.; Tarlow, D.; Brockschmidt, M.; Zemel, R. Gated graph sequence neural networks. arXiv 2015, arXiv:1511.05493. [Google Scholar]
- Chevalier-Boisvert, M.; Willems, L.; Pal, S. Minimalistic gridworld environment for openai gym. GitHub Repos. 2018. Available online: https://github.com/maximecb/gym-minigrid (accessed on 17 November 2021).
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Shwartz-Ziv, R.; Tishby, N. Opening the black box of deep neural networks via information. arXiv 2017, arXiv:1703.00810. [Google Scholar]
- Paninski, L. Estimation of entropy and mutual information. Neural Comput. 2003, 15, 1191–1253. [Google Scholar] [CrossRef] [Green Version]
- Belghazi, M.I.; Baratin, A.; Rajeswar, S.; Ozair, S.; Bengio, Y.; Courville, A.; Hjelm, R.D. Mine: Mutual information neural estimation. arXiv 2018, arXiv:1801.04062. [Google Scholar]
- Saxe, A.M.; Bansal, Y.; Dapello, J.; Advani, M.; Kolchinsky, A.; Tracey, B.D.; Cox, D.D. On the information bottleneck theory of deep learning. J. Stat. Mech. Theory Exp. 2019, 2019, 124020. [Google Scholar] [CrossRef]
- Vapnik, V.N.; Chervonenkis, A.Y. On the uniform convergence of relative frequencies of events to their probabilities. In Measures of Complexity; Springer: Berlin/Heidelberg, Germany, 2015; pp. 11–30. [Google Scholar]
- Mohri, M.; Rostamizadeh, A. Rademacher complexity bounds for non-iid processes. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: New York, NY, USA, 2009; pp. 1097–1104. [Google Scholar]
- Nakkiran, P.; Kaplun, G.; Bansal, Y.; Yang, T.; Barak, B.; Sutsk, I. Deep double descent: Where bigger models and more data hurt. arXiv 2019, arXiv:1912.02292. [Google Scholar]
- Zhang, C.; Bengio, S.; Hardt, M.; Recht, B.; Vinyals, O. Understanding deep learning requires rethinking generalization. arXiv 2016, arXiv:1611.03530. [Google Scholar] [CrossRef]
- Mehrabi, N.; Morstatter, F.; Saxena, N.; Lerman, K.; Galstyan, A. A survey on bias and fairness in machine learning. arXiv 2019, arXiv:1908.09635. [Google Scholar] [CrossRef]
- Suresh, H.; Guttag, J.V. A framework for understanding unintended consequences of machine learning. arXiv 2019, arXiv:1901.10002. [Google Scholar]
- Samadi, S.; Tantipongpipat, U.; Morgenstern, J.H.; Singh, M.; Vempala, S. The Price of Fair pca: One Extra Dimension. arXiv 2018, arXiv:1811.00103. [Google Scholar]
- Cox, D.D.; Dean, T. Neural networks and neuroscience-inspired computer vision. Curr. Biol. 2014, 24, R921–R929. [Google Scholar] [CrossRef] [Green Version]
- Lake, B.; Salakhutdinov, R.; Gross, J.; Tenenbaum, J. One shot learning of simple visual concepts. Proc. Annu. Meet. Cogn. Sci. Soc. 2011, 33, 2568–2573. [Google Scholar]
- Torralba, A.; Efros, A.A. Unbiased look at dataset bias. In Proceedings of the Computer Vision and Pattern Recognition (CVPR), Colorado Springs, CO, USA, 20–25 June 2011; pp. 1521–1528. [Google Scholar]
- Szegedy, C.; Zaremba, W.; Sutskever, I.; Bruna, J.; Erhan, D.; Goodfellow, I.; Fergus, R. Intriguing properties of neural networks. arXiv 2013, arXiv:1312.6199. [Google Scholar]
- Reddy, M.V.; Banburski, A.; Pant, N.; Poggio, T. Biologically Inspired Mechanisms for Adversarial Robustness. arXiv 2020, arXiv:2006.16427. [Google Scholar]
- Lin, B.; Bouneffouf, D.; Cecchi, G. Split Q Learning: Reinforcement Learning with Two-Stream Rewards. In Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence, Macao, China, 10–16 August 2019; pp. 6448–6449. [Google Scholar]
- Lin, B.; Cecchi, G.; Bouneffouf, D.; Reinen, J.; Rish, I. Models of Human Behavioral Agents in Bandits, Contextual Bandits and RL. In Proceedings of the Human Brain and Artificial Intelligence: Second International Workshop, HBAI 2020, Held in Conjunction with IJCAI-PRICAI 2020, Yokohama, Japan, 7 January 2021; Revised Selected Papers 2. Springer: Berlin/Heidelberg, Germany, 2021; pp. 14–33. [Google Scholar]
- Liao, Q.; Poggio, T. Bridging the gaps between residual learning, recurrent neural networks and visual cortex. arXiv 2016, arXiv:1604.03640. [Google Scholar]
- Hassabis, D.; Kumaran, D.; Summerfield, C.; Botvinick, M. Neuroscience-inspired artificial intelligence. Neuron 2017, 95, 245–258. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lin, B.; Bouneffouf, D.; Cecchi, G.A.; Rish, I. Contextual bandit with adaptive feature extraction. In Proceedings of the 2018 IEEE International Conference on Data Mining Workshops (ICDMW), Singapore, 17–20 November 2018; pp. 937–944. [Google Scholar]
- Lin, L.J. Self-improving reactive agents based on reinforcement learning, planning and teaching. Mach. Learn. 1992, 8, 293–321. [Google Scholar] [CrossRef]
- Konda, V.R.; Tsitsiklis, J.N. Actor-critic algorithms. Adv. Neural Inf. Process. Syst. 2000, 1008–1014. Available online: https://proceedings.neurips.cc/paper/1999/file/6449f44a102fde848669bdd9eb6b76fa-Paper.pdf (accessed on 17 November 2021).
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Pineda, F.J. Generalization of back-propagation to recurrent neural networks. Phys. Rev. Lett. 1987, 59, 2229. [Google Scholar] [CrossRef] [PubMed]
- Levesque, H.; Davis, E.; Morgenstern, L. The winograd schema challenge. In Proceedings of the Thirteenth International Conference on the Principles of Knowledge Representation and Reasoning, Rome, Italy, 10–14 June 2012. [Google Scholar]
- Chen, D.L.; Mooney, R.J. Learning to interpret natural language navigation instructions from observations. In Proceedings of the Twenty-Fifth AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 7–11 August 2011. [Google Scholar]






| “Balanced” | “Rare Minority” | “Highly Imbalanced” | “Dominant Oligarchy” | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| baseline | ||||||||||
| BN | ||||||||||
| LN | ||||||||||
| WN | ||||||||||
| RN | ||||||||||
| RLN | ||||||||||
| LN+RN | ||||||||||
| SN | ||||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, B. Regularity Normalization: Neuroscience-Inspired Unsupervised Attention across Neural Network Layers. Entropy 2022, 24, 59. https://doi.org/10.3390/e24010059
Lin B. Regularity Normalization: Neuroscience-Inspired Unsupervised Attention across Neural Network Layers. Entropy. 2022; 24(1):59. https://doi.org/10.3390/e24010059
Chicago/Turabian StyleLin, Baihan. 2022. "Regularity Normalization: Neuroscience-Inspired Unsupervised Attention across Neural Network Layers" Entropy 24, no. 1: 59. https://doi.org/10.3390/e24010059
APA StyleLin, B. (2022). Regularity Normalization: Neuroscience-Inspired Unsupervised Attention across Neural Network Layers. Entropy, 24(1), 59. https://doi.org/10.3390/e24010059






