An External Circular Crack in an Infinite Solid under Axisymmetric Heat Flux Loading in the Framework of Fractional Thermoelasticity
Abstract
:1. Introduction
2. Formulation of the Problem
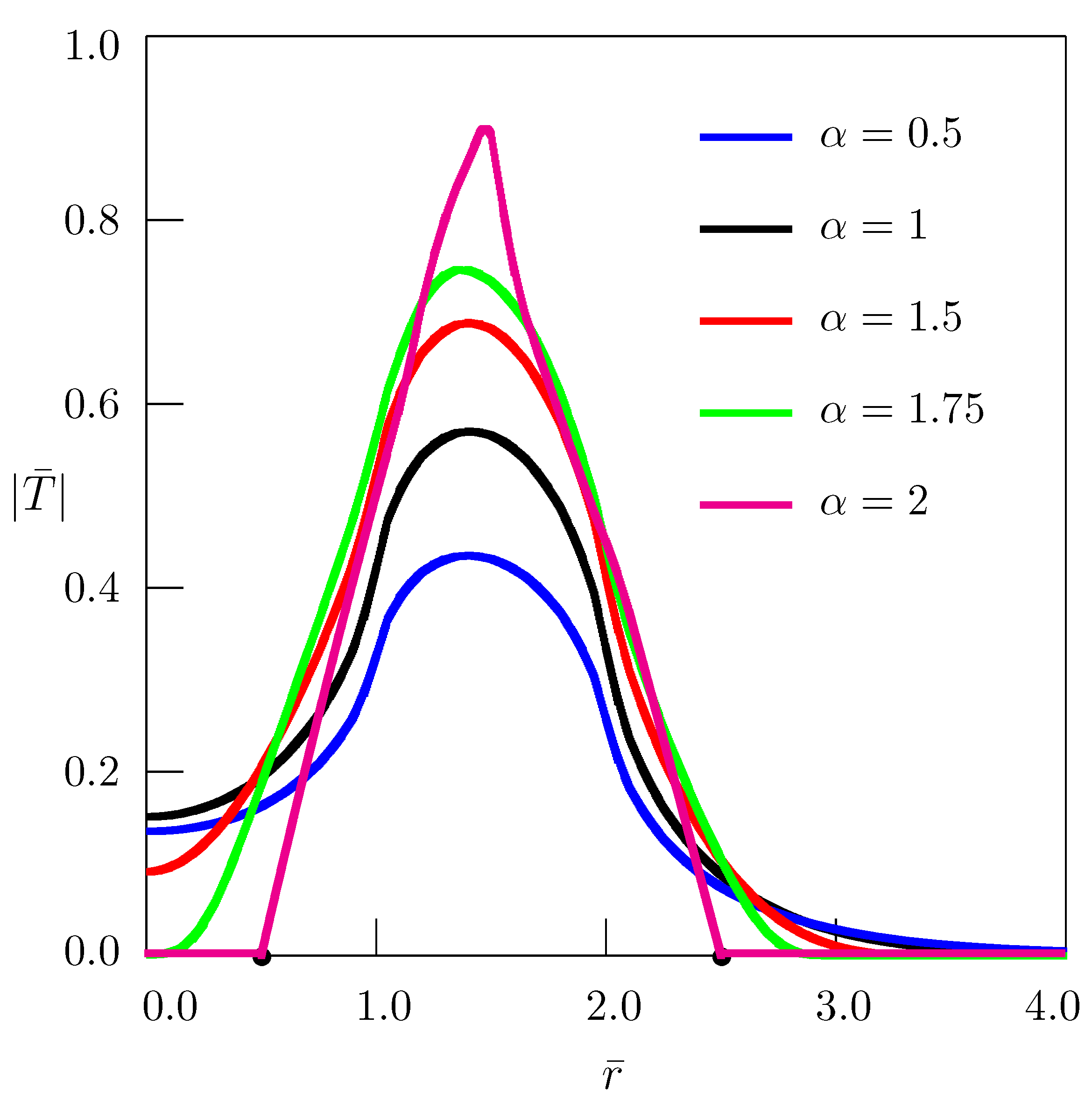
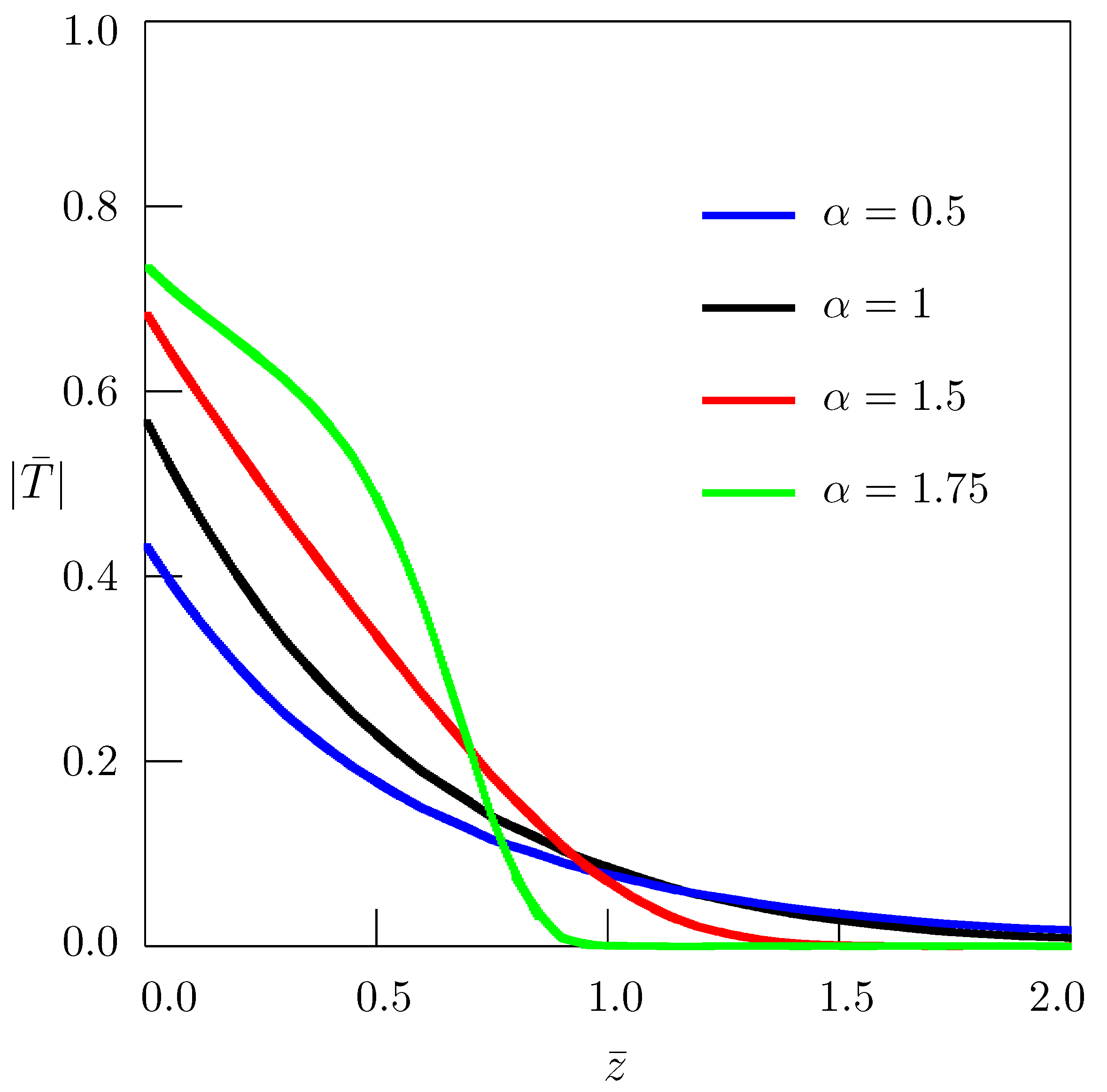
3. The Temperature Field
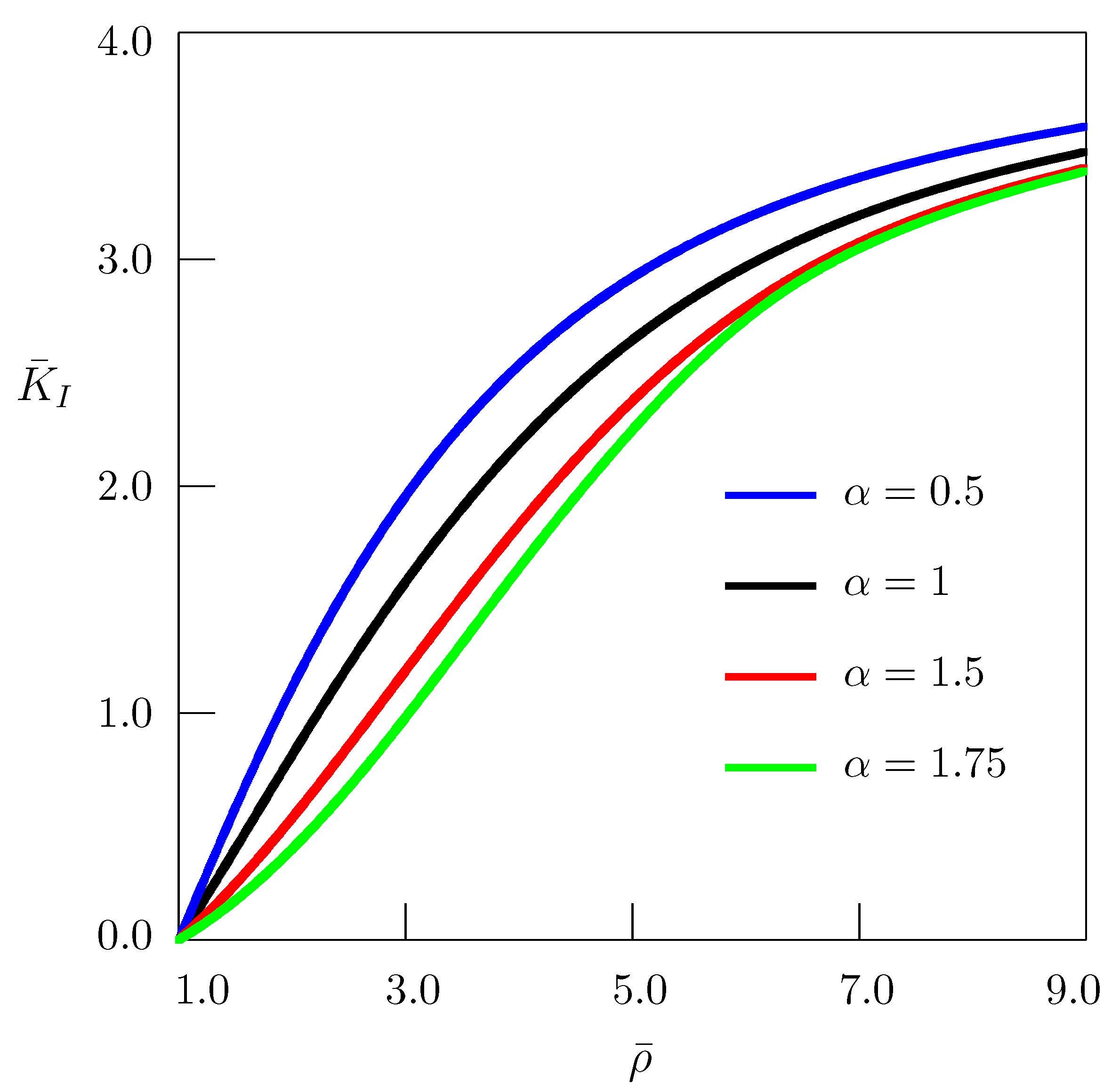
4. The Stress Intensity Factor
5. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Uflyand, Y.S. Elastic equilibrium in an infinite body weakened by an external circular crack. J. Appl. Math. Mech. 1959, 23, 134–144. [Google Scholar] [CrossRef]
- Uflyand, Y.S. Integral Transforms in Problem of the Theory of Elasticity; Nauka: Leningrad, Russia, 1967. (In Russian) [Google Scholar]
- Dhaliwal, R.S.; Singh, B.M. Formation of external circular crack by normal impact or by sudden twisting. Eng. Fracture Mech. 1984, 20, 93–101. [Google Scholar] [CrossRef]
- Fabrikant, V.I. Mixed Boundary Value Problems of Potential Theory and Their Applications in Engineering; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1991. [Google Scholar]
- Parihar, K.S.; Krishna Rao, J.V.S. Axisymmetric stress distribution in the vicinity of an external crack under general surface loadings. Int. J. Solids Strurt. 1993, 30, 2567–2586. [Google Scholar] [CrossRef]
- Fabrikant, V.I.; Rubin, B.S.; Karapetian, E.N. External circular crack under normal load: A complete solution. J. Appl. Mech. 1994, 61, 809–814. [Google Scholar] [CrossRef]
- Fabrikant, V.I. External circular crack under arbitrary shear loading. Z. Angew. Math. Phys. 1996, 47, 717–729. [Google Scholar] [CrossRef]
- Fabrikant, V.I. Complete solution to the problem of an external circular crack in a transversely isotropic body subjected to arbitrary shear loading. Int. J. Solids Structures 1996, 33, 167–191. [Google Scholar] [CrossRef]
- Chen, W.; Shioya, T. Green’s functions of an external circular crack in a transversely isotropic piezoelectric medium. JSME Int. J. Ser. A 1999, 42, 73–79. [Google Scholar] [CrossRef] [Green Version]
- Selvadurai, A.P.S. The bridged external circular crack. In Damage & Fracture Mechanics, V.I., Brebbia, C.A., Selvadurai, A.P.S., Eds.; WIT Press: Ashurst Lodge, UK, 2000; pp. 15–22. [Google Scholar]
- Mavrothanasis, F.I.; Pavlou, D.G. Green’s function for KI determination of axisymmetric elastic solids containing external circular crack. Eng. Fracture Mech. 2008, 75, 1891–1905. [Google Scholar] [CrossRef]
- Fabrikant, V.I. Contact and Crack Problems in Linear Theory of Elasticity; Bentham Science Publishers: Sharjah, United Arab Emirates, 2010. [Google Scholar]
- Li, X.-F.; Tang, G.-J.; Shen, Z.-B.; Lee, K.Y. Stress intensify factors for an external circular crack at the interface of a bi-material in shear–compression. Int. J. Solids Struct. 2015, 64–65, 221–231. [Google Scholar] [CrossRef]
- Olesiak, Z.; Sneddon, I.N. The distribution of thermal stress in an infinite elastic solid containing a penny-shaped crack. Arch. Rational. Mech. Anal. 1959, 4, 238–254. [Google Scholar] [CrossRef]
- Sih, G.C. On the singular character of thermal stresses near a crack tip. J. Appl. Mech. 1962, 29, 587–589. [Google Scholar] [CrossRef]
- Kassir, M.K.; Sih, G.C. Thermal stresses in a solid weakened by an external circular crack. Int. J. Solids Struct. 1969, 5, 351–367. [Google Scholar] [CrossRef]
- Das, B.R. Some axially symmetric thermal stress distributions in elastic solids containing cracks—I An external crack in an infinite solid. Int. J. Eng. Sci. 1971, 9, 469–478. [Google Scholar] [CrossRef]
- Singh, B.M.; Danyluk, H.T.; Selvadurai, A.P.S. Thermal stresses in a transversely isotropic elastic solid weakened by an external circular crack. Int. J. Solids Struct. 1981, 23, 403–412. [Google Scholar] [CrossRef]
- Noda, N.; Matsunaga, Y.; Nyuko, H. Stress intensity factor for transient thermal stresses in an infinite elastic body with an external crack. J. Thermal Stress. 1986, 9, 119–131. [Google Scholar] [CrossRef]
- Noda, N.; Ashida, F. Stress intensity factor for transient thermal stresses in a transversely isotropic infinite body with an external circular crack. Acta Mech. 1987, 66, 217–231. [Google Scholar] [CrossRef]
- Noda, N.; Ashida, F.; Matsunaga, Y. Stress intensity factors for external and penny-shaped cracks in transversely isotropic cylinders subjected to thermal shock. Arch. Appl. Mech. 1994, 64, 383–394. [Google Scholar]
- Krishna Rao, J.V.S.; Hasebe, N. Axially symmetric thermal stress of an external circular crack under general thermal conditions. Arch. Appl. Mech. 1995, 65, 374–389. [Google Scholar] [CrossRef]
- Bhowmick, R.; Das, R.B. An axisymmetric steady-state thermoelastic problem of an external circular crack in an isotropic thick plate. Proc. Indian Acad. Sci. (Math. Sci.) 1995, 105, 445–459. [Google Scholar] [CrossRef]
- Cattaneo, C. Sulla conduzione del calore. Atti Sem. Mat. Fis. Univ. Modena 1948, 3, 83–101. [Google Scholar]
- Gurtin, M.E.; Pipkin, A.C. A general theory of heat conduction with finite wave speeds. Arch. Ration. Mech. Anal. 1968, 31, 113–126. [Google Scholar] [CrossRef]
- Nigmatullin, R.R. To the theoretical explanation of the “universal response”. Phys. Status Solidi 1984, 123, 739–745. [Google Scholar] [CrossRef]
- Nigmatullin, R.R. On the theory of relaxation with remnant temperature. Phys. Status Solidi 1984, 124, 389–393. [Google Scholar] [CrossRef]
- Joseph, D.D.; Preziosi, L. Heat waves. Rev. Mod. Phys. 1989, 61, 41–73. [Google Scholar] [CrossRef]
- Tamma, K.K.; Zhou, X. Macroscale and microscale thermal transport and thermo-mechanical interactions: Some noteworthy perspectives. J. Thermal Stress. 1998, 21, 405–449. [Google Scholar] [CrossRef]
- Selitto, A.; Tibullo, V.; Dong, Y. Nonlinear heat-transport equation beyond Fourier law: Application to heat-wave propagation in isotropic thin layers. Contin. Mech. Thermodyn. 2017, 29, 411–428. [Google Scholar] [CrossRef]
- Berezovski, A. Internal variables representation of generalized heat equations. Contin. Mech. Thermodyn. 2019, 31, 1733–1741. [Google Scholar] [CrossRef]
- Day, W. The Thermodynamics of Simple Materials with Fading Memory; Springer: Berlin/Heidelberg, Germany, 1972. [Google Scholar]
- Rabotnov, Y.N. Elements of Hereditary Solid Mechanics; Mir Publishers: Moscow, Russia, 1980. [Google Scholar]
- Ignaczak, J.; Ostoja-Starzewski, M. Thermoelasticity with Finite Wave Speeds; Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity: An Introduction to Mathematical Models; Imperial College Press: London, UK, 2010. [Google Scholar]
- Tarasov, V.E. Fractional Dynamics: Applications of Fractional Calculus to Dynamics of Particles, Fields and Media; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Fabrizio, M.; Giorgi, C.; Pata, V. A new approach to equations with memory. Arch. Rational Mech. Anal. 2010, 198, 189–232. [Google Scholar] [CrossRef] [Green Version]
- Amendola, G.; Fabrizio, M.; Golden, J.M. Thermodynamics of Materials with Memory. Theory and Applications; Springer: New York, NY, USA, 2012. [Google Scholar]
- Povstenko, Y. Fractional Thermoelasticity; Springer: New York, NY, USA, 2015. [Google Scholar]
- Tarasov, V.E. (Ed.) Handbook of Fractional Calculus with Applications, Vol. 4: Applications in Physics, Part A; De Gruyter: Berlin, Germany, 2019. [Google Scholar]
- Tarasov, V.E. (Ed.) Handbook of Fractional Calculus with Applications, Vol. 5: Applications in Physics, Part B; De Gruyter: Berlin, Germany, 2019. [Google Scholar]
- Tarasov, V.E.; Tarasova, V.V. Economic Dynamics with Memory. Fractional Calculus Approach; De Gruyter: Berlin, Germany, 2021. [Google Scholar]
- Green, A.E.; Naghdi, P.M. Thermoelasticity without energy dissipation. J. Elast. 1993, 31, 189–208. [Google Scholar] [CrossRef]
- Lord, H.W.; Shulman, Y. A generalized dynamic theory of thermoelasticity. J. Mech. Phys. Solids 1967, 15, 299–309. [Google Scholar] [CrossRef]
- Green, A.E.; Lindsay, K.A. Thermoelasticity. J. Elast. 1972, 2, 1–8. [Google Scholar] [CrossRef]
- Gorenflo, R.; Mainardi, F. Fractional calculus: Integral and differential equations of fractional order. In Fractals and Fractional Calculus in Continuum Mechanics; Carpinteri, A., Mainardi, F., Eds.; Springer: Wien, Austria, 1997; pp. 223–276. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Magin, R.L. Fractional Calculus in Bioengineering; Begell House Publishers, Inc.: Redding, CA, USA, 2006. [Google Scholar]
- Uchaikin, V.V. Fractional Derivatives for Physicists and Engineers; Springer: Berlin, Germany, 2013. [Google Scholar]
- Atanacković, T.M.; Pilipović, S.; Stanković, B.; Zorica, D. Fractional Calculus with Applications in Mechanics: Vibrations and Diffusion Processes; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Herrmann, R. Fractional Calculus: An Introduction for Physicists, 2nd ed.; World Scientific: Singapore, 2014. [Google Scholar]
- Povstenko, Y. Linear Fractional Diffusion-Wave Equation for Scientists and Engineers; Birkhäuser: New York, NY, USA, 2015. [Google Scholar]
- Su, N. Fractional Calculus for Hydrology, Soil Scirnce and Geomechanics; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar]
- Povstenko, Y. Fractional heat conduction equation and associated thermal stresses. J. Thermal Stress. 2005, 28, 83–102. [Google Scholar] [CrossRef]
- Povstenko, Y. Thermoelasticity which uses fractional heat conduction equation. J. Math. Sci. 2009, 162, 296–305. [Google Scholar] [CrossRef]
- Povstenko, Y. Non-axisymmetric solutions to time-fractional diffusion-wave equation in an infinite cylinder. Fract. Calc. Appl. Anal. 2011, 14, 418–435. [Google Scholar] [CrossRef]
- Povstenko, Y. Fractional thermoelasticity. In Encyclopedia of Thermal Stresses; Hetnarski, R.B., Ed.; Springer: Dordrecht, The Netherlands, 2014; pp. 1778–1787. [Google Scholar]
- Povstenko, Y. Fractional calculus in thermoelasticity. In Encyclopedia of Continuum Mechanics; Altenbach, H., Öchsner, A., Eds.; Springer: Berlin, Germany, 2020; pp. 953–961. [Google Scholar]
- Povstenko, Y. Fractional Cattaneo-type equations and generalized thermoelasticity. J. Thermal Stress. 2011, 34, 97–114. [Google Scholar] [CrossRef]
- Povstenko, Y. Theories of thermal stresses based on space-time-fractional telegraph equations. Comput. Math. Appl. 2012, 64, 3321–3328. [Google Scholar] [CrossRef] [Green Version]
- Hosseini-Tehrani, P.; Eslami, M.R.; Azari, S. Analysis of thermoelastic crack problems using Green—Lindsay theory. J. Thermal Stress. 2006, 29, 317–330. [Google Scholar] [CrossRef]
- Bagri, A.; Eslami, M.R. Generalized coupled thermoelasticity of functionally graded annular disk considering the Lord—Shulman theory. Compos. Struct. 2008, 83, 168–179. [Google Scholar] [CrossRef]
- Mallik, S.H.; Kanoria, M. A unified generalized thermoelasticity formulation: Application to penny-shaped crack analysis. J. Thermal Stress. 2009, 32, 943–965. [Google Scholar] [CrossRef]
- Zamani, A.; Hetnarski, R.B.; Eslami, M.R. Second sound in a cracked layer based on Lord–Shulman theory. J. Thermal Stress. 2011, 34, 181–200. [Google Scholar] [CrossRef]
- Zamani, A.; Hetnarski, R.B.; Eslami, M.R. Generalized thermoelasticity of a crack problem considering Lord -Shulman theory. In Encyclopedia of Thermal Stresses; Hetnarski, R.B., Ed.; Springer: Dordrecht, The Netherlands, 2014; pp. 1966–1974. [Google Scholar]
- Fu, J.W.; Chen, Z.T.; Qian, L.F.; Xu, Y.D. Thermal fracture of cracked cylinders associated with nonclassical heat conduction: The effect of material property. J. Thermal Stress. 2016, 39, 1119–1137. [Google Scholar] [CrossRef]
- Povstenko, Y.; Kyrylych, T. Fractional thermoelasticity problem for a plane with a line crack under heat flux loading. J. Thermal Stress. 2018, 41, 1313–1328. [Google Scholar] [CrossRef]
- Povstenko, Y.; Kyrylych, T. Time-fractional heat conduction in an infinite plane containing an external crack under heat flux loading. Comp. Math. Appl. 2019, 78, 1386–1395. [Google Scholar] [CrossRef]
- Povstenko, Y.; Kyrylych, T. Time-fractional heat conduction in a plane with two external half-infinite line slits under heat flux loading. Symmetry 2019, 11, 689. [Google Scholar] [CrossRef] [Green Version]
- Povstenko, Y.; Kyrylych, T. Fractional thermoelasticity problem for an infinite solid with a penny-shaped crack under prescribed heat flux across its surfaces. Phil. Trans. R. Soc. A 2020, 378, 20190289. [Google Scholar] [CrossRef]
- Parkus, H. Instationäre Wärmespannungen; Springer: Wien, Austria, 1959. (In German) [Google Scholar]
- Nowacki, W. Thermoelasticity; Polish Scientific Publishers: Warsaw, Poland, 1986. [Google Scholar]
- Gorenflo, R.; Loutchko, J.; Luchko, Y. Computation of the Mittag-Leffler function and its derivatives. Fract. Calc. Appl. Anal. 2002, 5, 491–518. [Google Scholar]
- Erdélyi, A.; Magnus, W.; Oberhettinger, F.; Tricomi, F. Tables of Integral Transforms; McGraw-Hill: New York, NY, USA, 1954; Volume 1. [Google Scholar]
- Erdélyi, A.; Magnus, W.; Oberhettinger, F.; Tricomi, F. Tables of Integral Transforms; McGraw-Hill: New York, NY, USA, 1954; Volume 2. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Povstenko, Y.; Kyrylych, T.; Woźna-Szcześniak, B.; Kawa, R.; Yatsko, A. An External Circular Crack in an Infinite Solid under Axisymmetric Heat Flux Loading in the Framework of Fractional Thermoelasticity. Entropy 2022, 24, 70. https://doi.org/10.3390/e24010070
Povstenko Y, Kyrylych T, Woźna-Szcześniak B, Kawa R, Yatsko A. An External Circular Crack in an Infinite Solid under Axisymmetric Heat Flux Loading in the Framework of Fractional Thermoelasticity. Entropy. 2022; 24(1):70. https://doi.org/10.3390/e24010070
Chicago/Turabian StylePovstenko, Yuriy, Tamara Kyrylych, Bożena Woźna-Szcześniak, Renata Kawa, and Andrzej Yatsko. 2022. "An External Circular Crack in an Infinite Solid under Axisymmetric Heat Flux Loading in the Framework of Fractional Thermoelasticity" Entropy 24, no. 1: 70. https://doi.org/10.3390/e24010070
APA StylePovstenko, Y., Kyrylych, T., Woźna-Szcześniak, B., Kawa, R., & Yatsko, A. (2022). An External Circular Crack in an Infinite Solid under Axisymmetric Heat Flux Loading in the Framework of Fractional Thermoelasticity. Entropy, 24(1), 70. https://doi.org/10.3390/e24010070





