Analysis of Energy Dissipation of Interval-Pooled Stepped Spillways
Abstract
:1. Introduction
2. Numerical Simulation
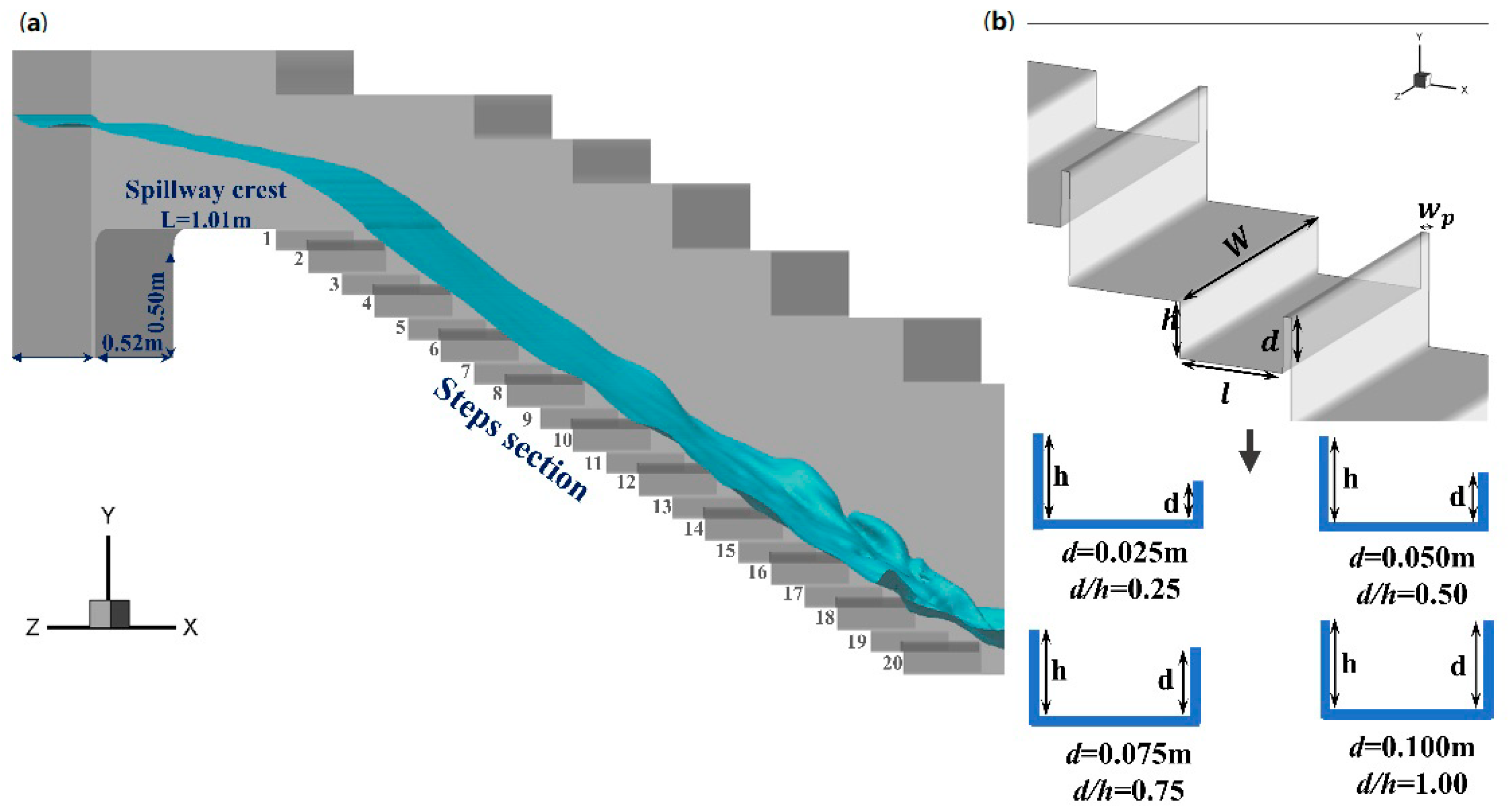
2.1. Computational Domain
2.2. Boundary Conditions
2.3. Mesh and Model Validation
3. Results and Discussion
3.1. Energy Dissipation Performance
3.2. Energy Dissipation Analysis Using the Omega Vortex Identification Method
3.3. Formation of a “Pseudo-Weir”
3.4. Quantifying Vortex Strength
4. Conclusions
- The interval-stepped spillway allowed the flow to perform sufficient energy dissipation by longitudinal abrupt expansion and contraction, creating a robust vortex zone in the step cavity. The overall energy dissipation rate had an exponential decay with and was generally better than conventional spillways and pooled, stepped spillways.
- After ≥ 0.50, each step without a pool formed a “pseudo-weir”, which formed a “pseudo-continuous weir” with an increasing pool, increasing the strength of the vortex on the one hand, and on the other hand, the stagnant water body also increased, resulting in an interval-pooled stepped spillway efficiency effect that did not change significantly with the change in pool height.
- A comprehensive analysis of the step spillway vortex structure was conducted. Three parameters were defined to quantify the variation in vortices within the step, whose could represent the dissipation rate approximately. This shows that the average intensity of the vortex was closely related to the dissipation effect.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Boes, R.M.; Hager, W.H. Hydraulic Design of Stepped Spillways. J. Hydraul. Eng. 2003, 129, 671–679. [Google Scholar] [CrossRef] [Green Version]
- Chanson, H. Hydraulics of Skimming Flows over Stepped Channels and Spillways. J. Hydraul. Res. 1994, 32, 445–460. [Google Scholar] [CrossRef] [Green Version]
- Chanson, H. Energy Dissipation in Hydraulic Structures; CRC Press: Boca Raton, FL, USA, 2015; ISBN 978-1-315-68029-3. [Google Scholar]
- Felder, S.; Fromm, C.; Chanson, H. Air Entrainment and Energy Dissipation on a 8.9 Slope Stepped Spillway with Flat and Pooled Steps; Department of Civil Engineering, University of Queensland: Brisbane, Australia, 2012; ISBN 978-1-74272-053-1. [Google Scholar]
- Chinnarasri, C.; Wongwises, S. Flow Patterns and Energy Dissipation over Various Stepped Chutes. J. Irrig. Drain. Eng. 2006, 132, 70–76. [Google Scholar] [CrossRef]
- Felder, S.; Chanson, H. Energy Dissipation down a Stepped Spillway with Nonuniform Step Heights. J. Hydraul. Eng. 2011, 137, 1543–1548. [Google Scholar] [CrossRef] [Green Version]
- Thorwarth, J. Hydraulisches Verhalten von Treppengerinnen Mit Eingetieften Stufen: Selbstinduzierte Abflussinstationaritäten Und Energiedissipation; University of Aachen: Aachen, Germany, 2009. [Google Scholar]
- Felder, S.; Chanson, H. Aeration, Flow Instabilities, and Residual Energy on Pooled Stepped Spillways of Embankment Dams. J. Irrig. Drain. Eng. 2013, 139, 880–887. [Google Scholar] [CrossRef] [Green Version]
- André, S.; Schleiss, A. High Velocity Aerated Flows on Stepped Chutes with Macro-Roughness Elements; Ecole Polytechnique Federale de Lausanne, Laboratoire de Constructions Hydrauliques: Lausanne, Switzerland, 2004. [Google Scholar]
- Kökpinar, M.A. Flow over a Stepped Chute with and without Macro-Roughness Elements. Can. J. Civ. Eng. 2004, 31, 880–891. [Google Scholar] [CrossRef]
- Felder, S.; Chanson, H. Air–Water Flow Measurements in a Flat Slope Pooled Stepped Waterway. Can. J. Civ. Eng. 2013, 40, 361–372. [Google Scholar] [CrossRef] [Green Version]
- Morovati, K.; Eghbalzadeh, A.; Javan, M. Numerical Investigation of the Configuration of the Pools on the Flow Pattern Passing over Pooled Stepped Spillway in Skimming Flow Regime. Acta Mech. 2016, 227, 353–366. [Google Scholar] [CrossRef]
- Gualtieri, C.; Chanson, H. Physical and Numerical Modelling of Air-Water Flows: An Introductory Overview. Environ. Model. Softw. 2021, 143, 105109. [Google Scholar] [CrossRef]
- Meireles, I.C.; Bombardelli, F.A.; Matos, J. Air Entrainment Onset in Skimming Flows on Steep Stepped Spillways: An Analysis. J. Hydraul. Res. 2014, 52, 375–385. [Google Scholar] [CrossRef]
- Valero, D.; Bung, D.B.; Crookston, B.M. Energy Dissipation of a Type III Basin under Design and Adverse Conditions for Stepped and Smooth Spillways. J. Hydraul. Eng. 2018, 144, 04018036. [Google Scholar] [CrossRef]
- Wan, H.; Li, R.; Gualtieri, C.; Yang, H.; Feng, J. Numerical Simulation of Hydrodynamics and Reaeration over a Stepped Spillway by the SPH Method. Water 2017, 9, 565. [Google Scholar] [CrossRef] [Green Version]
- JCR, H.; Wray, A.; Moin, P. Eddies, Stream, and Convergence Zones in Turbulent Flows. Stud. Turbul. Using Numer. Simul. Databases-I1 1988, 193–207. Available online: https://ntrs.nasa.gov/api/citations/19890015184/downloads/19890015184.pdf (accessed on 28 November 2021).
- Liu, C.; Gao, Y.; Tian, S.; Dong, X. Rortex—A New Vortex Vector Definition and Vorticity Tensor and Vector Decompositions. Phys. Fluids 2018, 30, 035103. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.; Wang, Y.; Yang, Y.; Duan, Z. New Omega Vortex Identification Method. Sci. China Phys. Mech. Astron. 2016, 59, 684711. [Google Scholar] [CrossRef]
- Jeong, J.; Hussain, F. On the Identification of a Vortex. J. Fluid Mech. 1995, 285, 69–94. [Google Scholar] [CrossRef]
- Wang, C.; Liu, Y.; Chen, J.; Zhang, F.; Huang, B.; Wang, G. Cavitation Vortex Dynamics of Unsteady Sheet/Cloud Cavitating Flows with Shock Wave Using Different Vortex Identification Methods. J. Hydrodyn 2019, 31, 475–494. [Google Scholar] [CrossRef]
- Li, S.; Yang, J.; Liu, W. Estimation of Aerator Air Demand by an Embedded Multi-Gene Genetic Programming. J. Hydroinformatics 2021, 23, 1000–1013. [Google Scholar] [CrossRef]
- Nóbrega, J.D.; Matos, J.; Schulz, H.E.; Canelas, R.B. Smooth and Stepped Spillway Modeling Using the SPH Method. J. Hydraul. Eng. 2020, 146, 04020054. [Google Scholar] [CrossRef]
- Li, S.; Xie, Q.; Yang, J. Daily Suspended Sediment Forecast by an Integrated Dynamic Neural Network. J. Hydrol. 2022, 604, 127258. [Google Scholar] [CrossRef]
- Felder, S.; Guenther, P.; Chanson, H. Air-Water Flow Properties and Energy Dissipation on Stepped Spillways: A Physical Study of Several Pooled Stepped Configurations; School of Civil Engineering: Brisbane, Australia, 2012. [Google Scholar]
- Blocken, B.; Gualtieri, C. Ten Iterative Steps for Model Development and Evaluation Applied to Computational Fluid Dynamics for Environmental Fluid Mechanics. Environ. Model. Softw. 2012, 33, 1–22. [Google Scholar] [CrossRef]
- Roache, P.J. Perspective: Validation—What Does It Mean? J. Fluids Eng. 2009, 131, 034503-3. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of Fluid (VOF) Method for the Dynamics of Free Boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Morovati, K.; Eghbalzadeh, A. Study of Inception Point, Void Fraction and Pressure over Pooled Stepped Spillways Using Flow-3D. Int. J. Numer. Methods Heat Fluid Flow 2018, 28, 982–998. [Google Scholar] [CrossRef]
- Bayon, A.; Toro, J.P.; Bombardelli, F.A.; Matos, J.; López-Jiménez, P.A. Influence of VOF Technique, Turbulence Model and Discretization Scheme on the Numerical Simulation of the Non-Aerated, Skimming Flow in Stepped Spillways. J. Hydro-Environ. Res. 2018, 19, 137–149. [Google Scholar] [CrossRef] [Green Version]
- Bombardelli, F.A.; Meireles, I.; Matos, J. Laboratory Measurements and Multi-Block Numerical Simulations of the Mean Flow and Turbulence in the Non-Aerated Skimming Flow Region of Steep Stepped Spillways. Environ. Fluid Mech 2011, 11, 263–288. [Google Scholar] [CrossRef] [Green Version]
- Yakhot, V.; Orszag, S.A. Renormalization Group Analysis of Turbulence. I. Basic Theory. J. Sci. Comput. 1986, 1, 3–51. [Google Scholar] [CrossRef]
- Celik, I.B.; Ghia, U.; Roache, P.J.; Freitas, C.J. Procedure for Estimation and Reporting of Uncertainty Due to Discretization in CFD Applications. J. Fluids Eng.-Trans. ASME 2008, 130, 078001. [Google Scholar]
- Eça, L.; Hoekstra, M.; Roache, P. Verification of Calculations: An Overview of the 2nd Lisbon Workshop. In Proceedings of the 18th AIAA Computational Fluid Dynamics Conference, Miami, FL, USA, 25–28 June 2007; American Institute of Aeronautics and Astronautics: Reston, VA, USA. [Google Scholar]









| Reference | (°) | Step Geometry | Comment | Flow Regime | Methodology |
|---|---|---|---|---|---|
| Kökpinar (2004) | 30 | = 6 cm, = 10.4 cm, = 3 cm | = 0.5 m, 64 steps, = 2.6 cm | NA/TRA/SK | physical model experiment |
| André and Schleiss (2004) | 18.6/30 | = 6 cm, = 17.8 cm, = 3 cm, = 6 cm, = 10.4 cm, = 3 cm | = 0.5 m, 42/64 steps, = 2.6 cm | NA/TRA/SK | physical model experiment |
| Felder and Chanson (2013) | 8.9 | = 5 cm, = 5 cm, = 31.9 cm | = 0.5 m, 21 steps, = 1.5 cm | NA/TRA | physical model experiment |
| Q (m3/s) | dc/h | Flat | Pooled | d = 0.25 h | d = 0.50 h | d = 0.75 h | d = 1.00 h |
|---|---|---|---|---|---|---|---|
| Q1 = 0.123 | 1.79 | √ | √ | √ | |||
| Q2 = 0.135 | 1.90 | √ | √ | √ | √ | √ | √ |
| Q3 = 0.148 | 2.02 | √ | √ | √ | √ | ||
| Q4 = 0.160 | 2.13 | √ | √ | √ | √ | √ | √ |
| Q5 = 0.188 | 2.37 | √ | √ | ||||
| Q6 = 0.216 | 2.60 | √ | √ | ||||
| Q7 = 0.244 | 2.82 | √ | √ | √ | √ | √ | |
| Q8 = 0.272 | 3.03 | √ | √ | √ | |||
| Q9 = 0.300 | 3.24 | √ | √ | √ | √ | √ | √ |
| Flat | Pooled | d/h = 0.25 | d/h = 0.50 | d/h = 0.75 | d/h = 1.00 |
|---|---|---|---|---|---|
| 0.68 | 0.72 | 0.76 | 0.82 | 0.86 | 0.95 |
| d/h = 0.25 | d/h = 0.50 | d/h = 0.75 | d/h = 1.00 | Flat (d/h = 0.00) | Pooled (d/h = 0.31) | |
|---|---|---|---|---|---|---|
| 0.34 | 0.44 | 0.43 | 0.39 | 0.49 | 0.41 | |
| 0.58 | 0.58 | 0.59 | 0.60 | 0.54 | 0.54 | |
| 0.20 | 0.26 | 0.25 | 0.24 | 0.27 | 0.22 | |
| 0.46 | 0.42 | 0.41 | 0.42 | 0.39 | 0.38 |
| d/h = 0.25 | d/h = 0.50 | d/h = 0.75 | d/h = 1.00 | Flat (d/h = 0.00) | Pooled (d/h = 0.31) | |
|---|---|---|---|---|---|---|
| 0.38 | 0.41 | 0.39 | 0.36 | 0.43 | 0.39 | |
| 0.57 | 0.58 | 0.59 | 0.60 | 0.54 | 0.55 | |
| 0.22 | 0.24 | 0.23 | 0.21 | 0.23 | 0.22 | |
| 0.46 | 0.42 | 0.41 | 0.42 | 0.39 | 0.38 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, X.; Zhang, J.; Hu, Y. Analysis of Energy Dissipation of Interval-Pooled Stepped Spillways. Entropy 2022, 24, 85. https://doi.org/10.3390/e24010085
Ma X, Zhang J, Hu Y. Analysis of Energy Dissipation of Interval-Pooled Stepped Spillways. Entropy. 2022; 24(1):85. https://doi.org/10.3390/e24010085
Chicago/Turabian StyleMa, Xin, Jianmin Zhang, and Yaan Hu. 2022. "Analysis of Energy Dissipation of Interval-Pooled Stepped Spillways" Entropy 24, no. 1: 85. https://doi.org/10.3390/e24010085
APA StyleMa, X., Zhang, J., & Hu, Y. (2022). Analysis of Energy Dissipation of Interval-Pooled Stepped Spillways. Entropy, 24(1), 85. https://doi.org/10.3390/e24010085






