Machine-Learned Free Energy Surfaces for Capillary Condensation and Evaporation in Mesopores
Abstract
:1. Introduction
2. Simulation Method and Models
2.1. Force Fields
2.2. Simulations
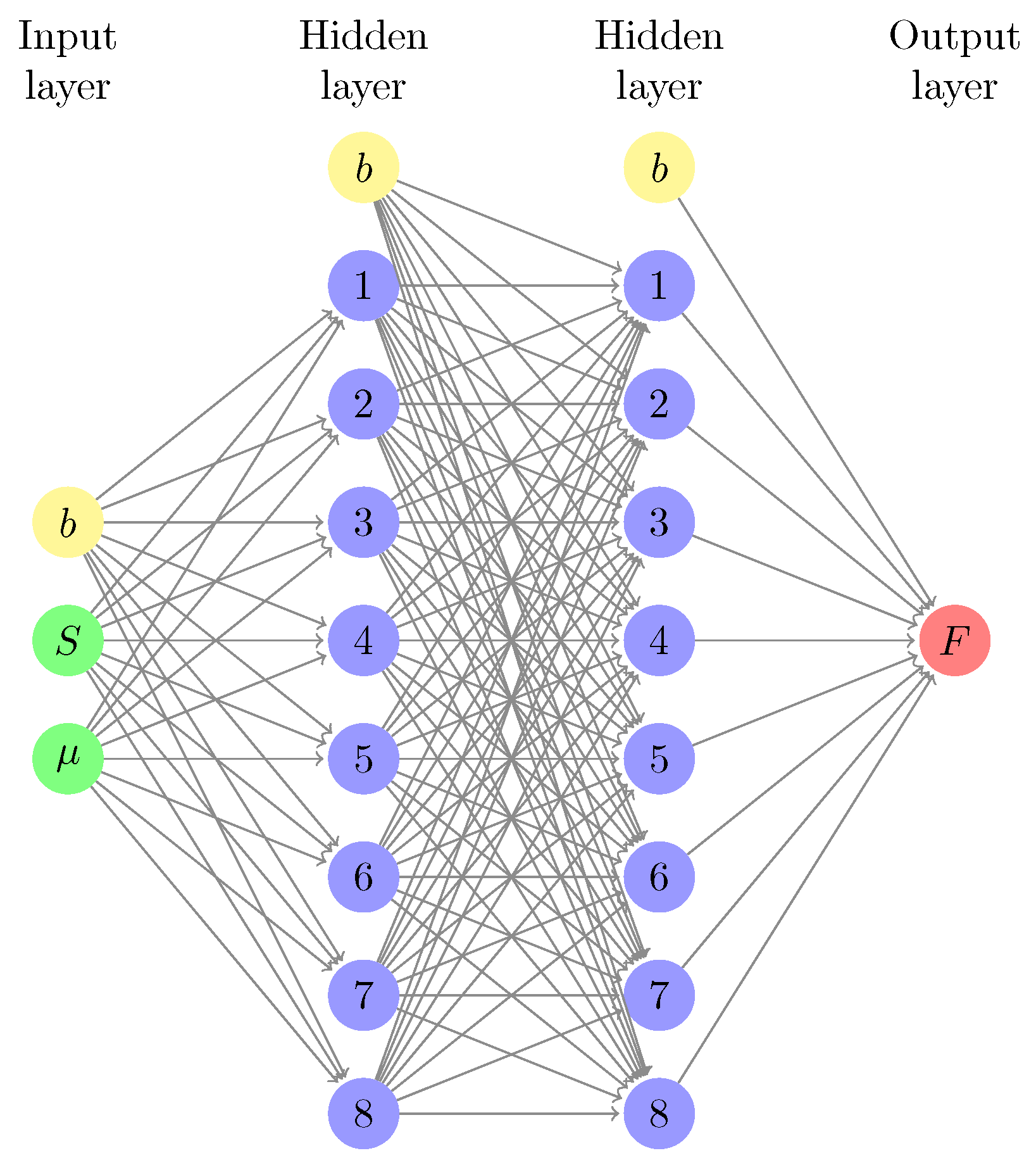
2.3. Machine-Learned Free Energy Surfaces
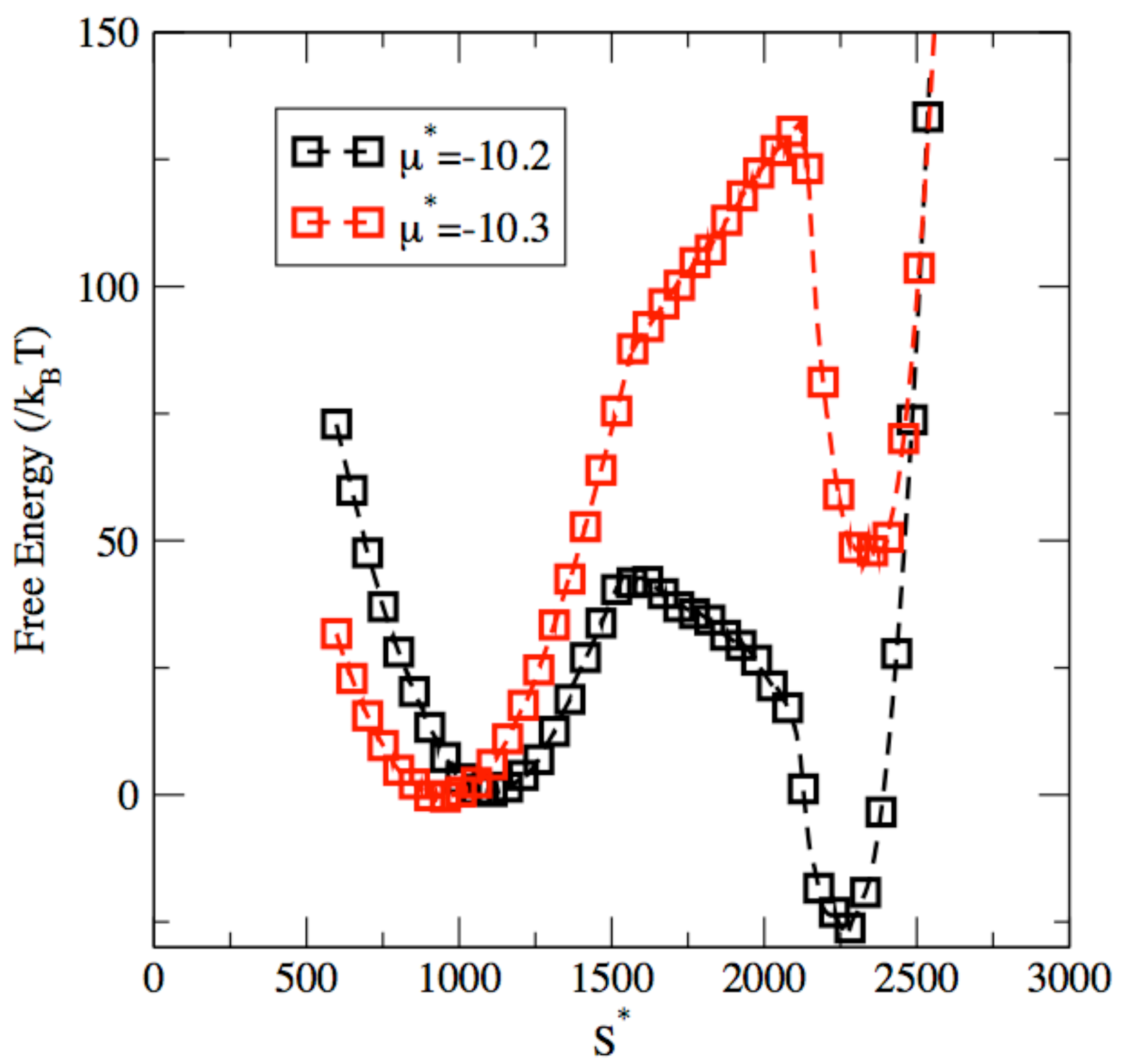
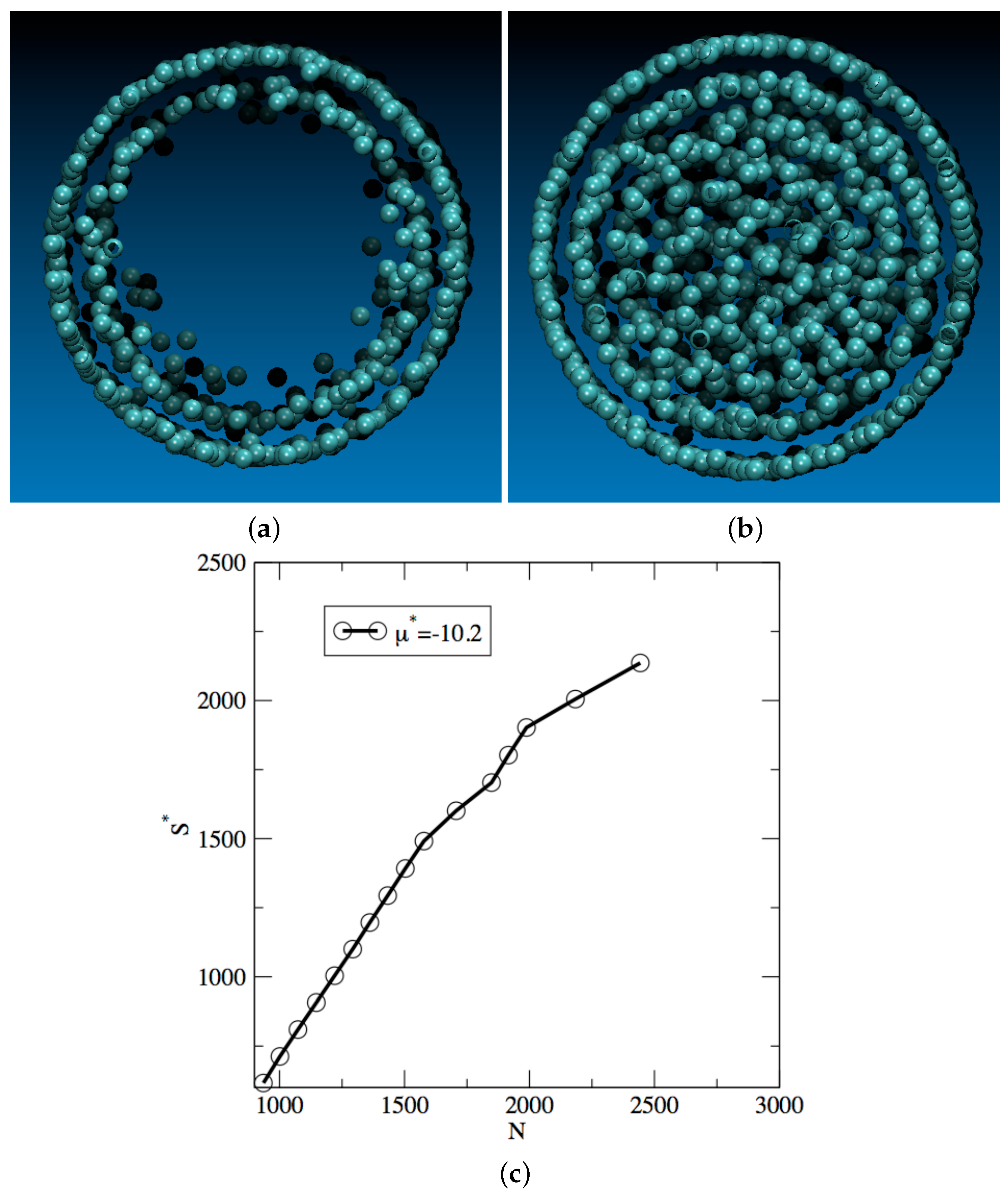
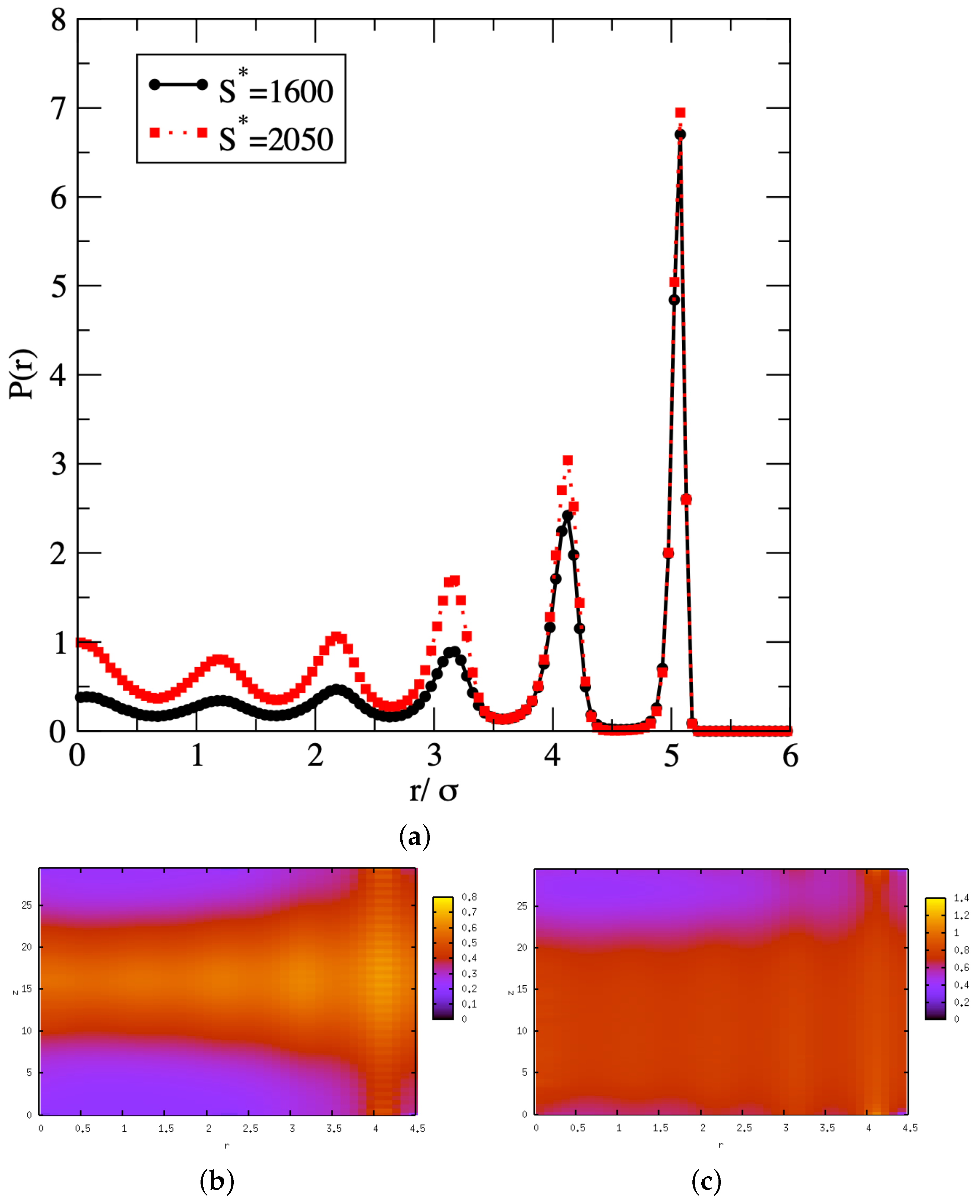
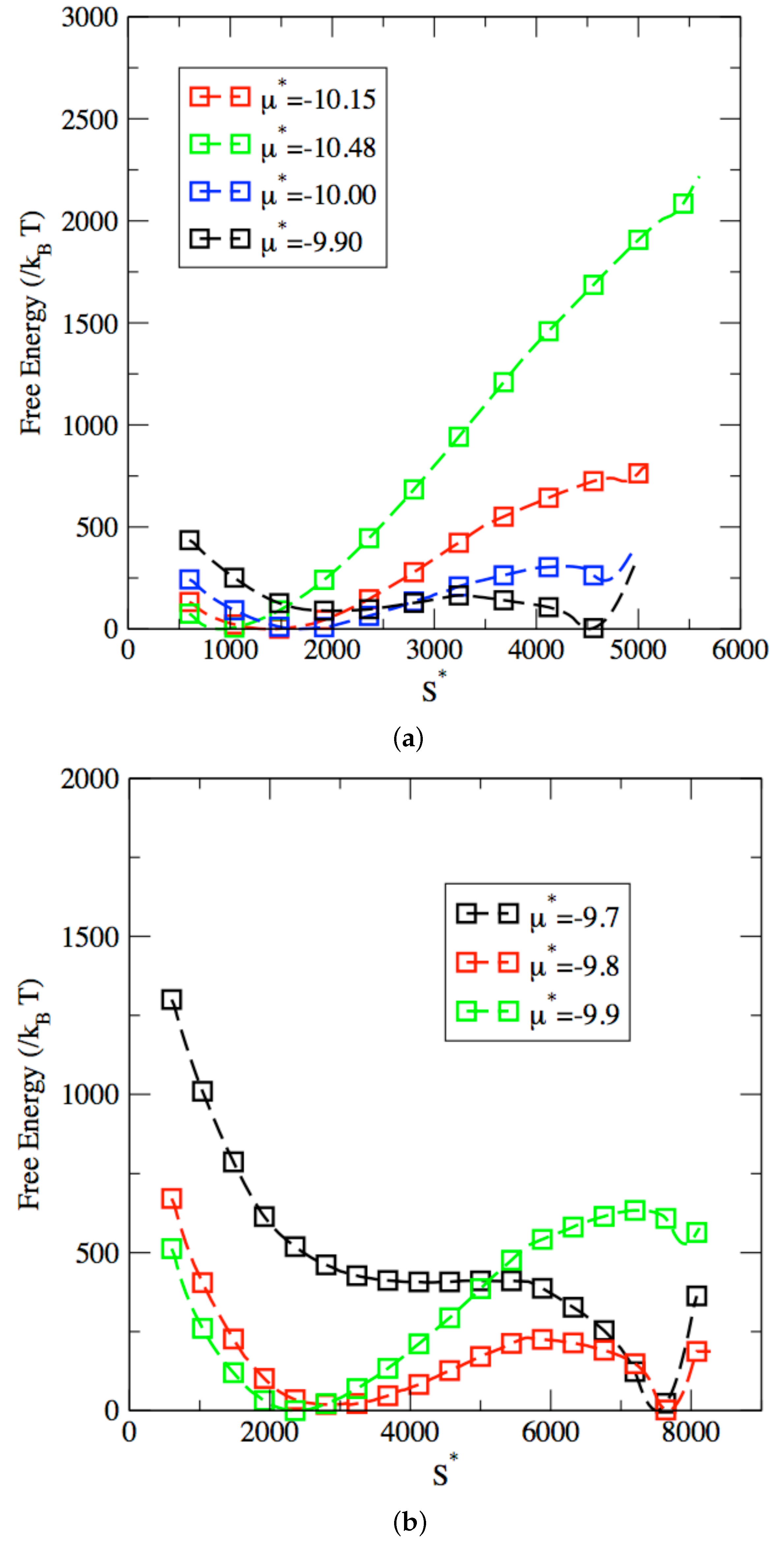
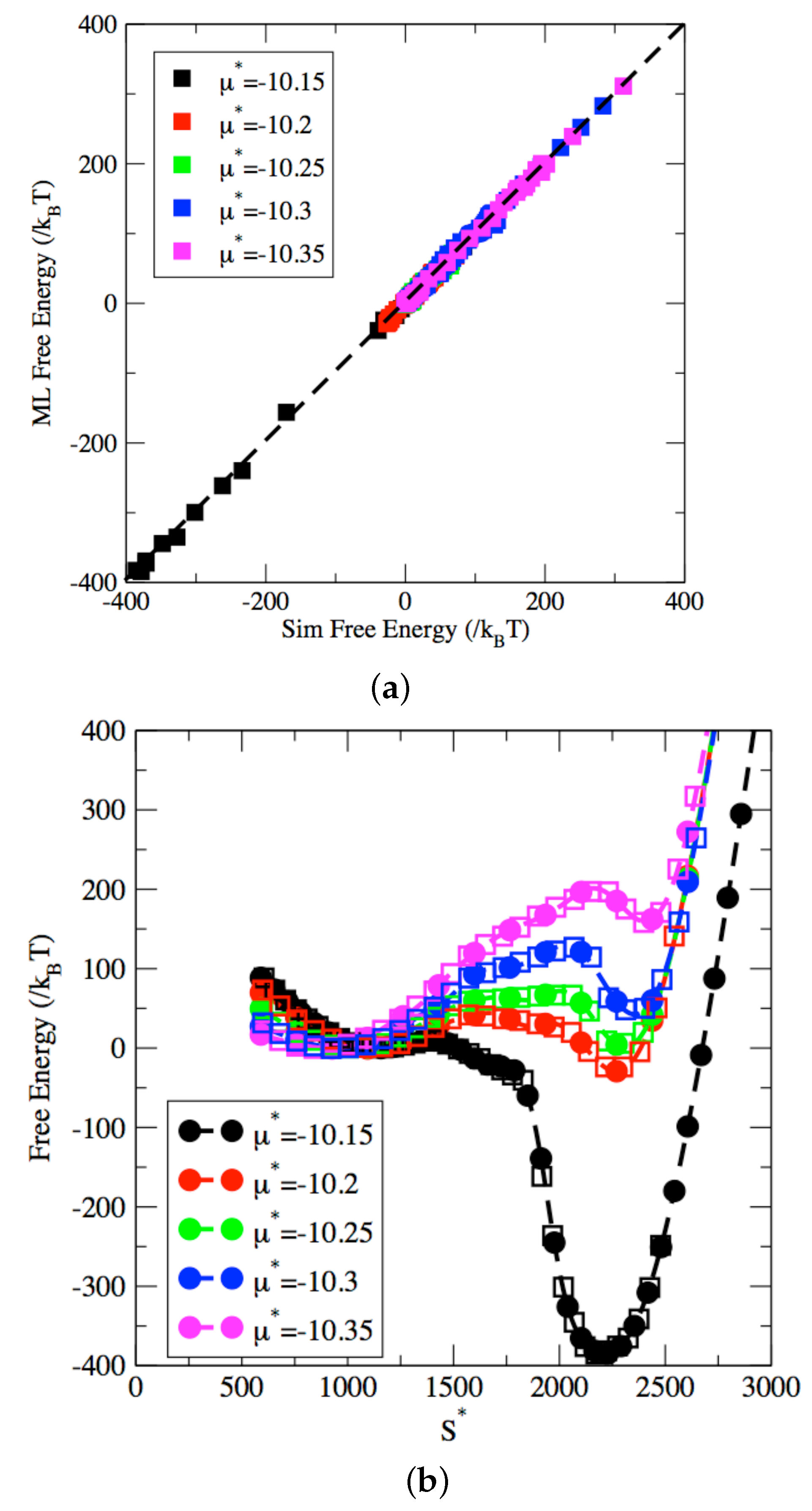
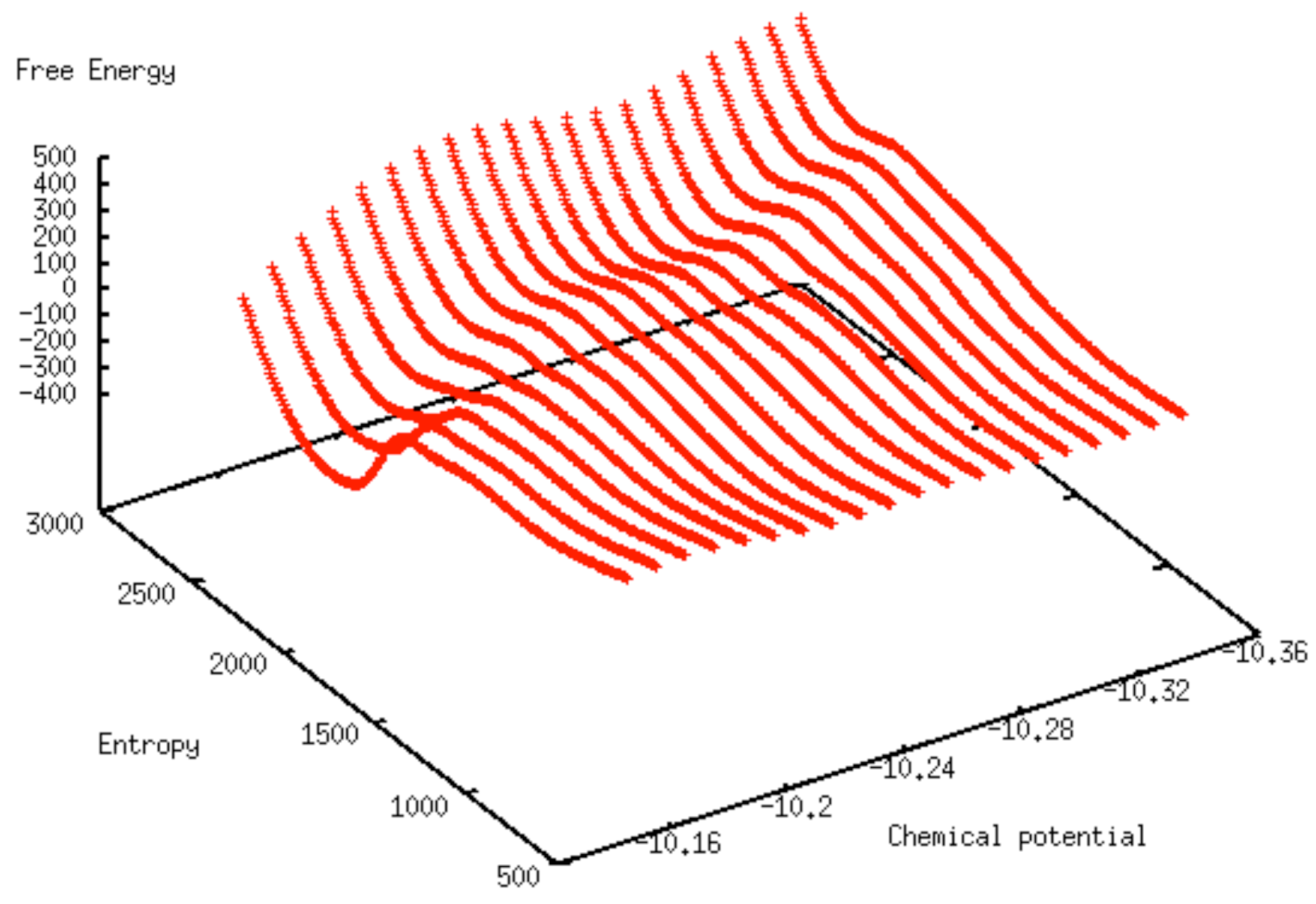
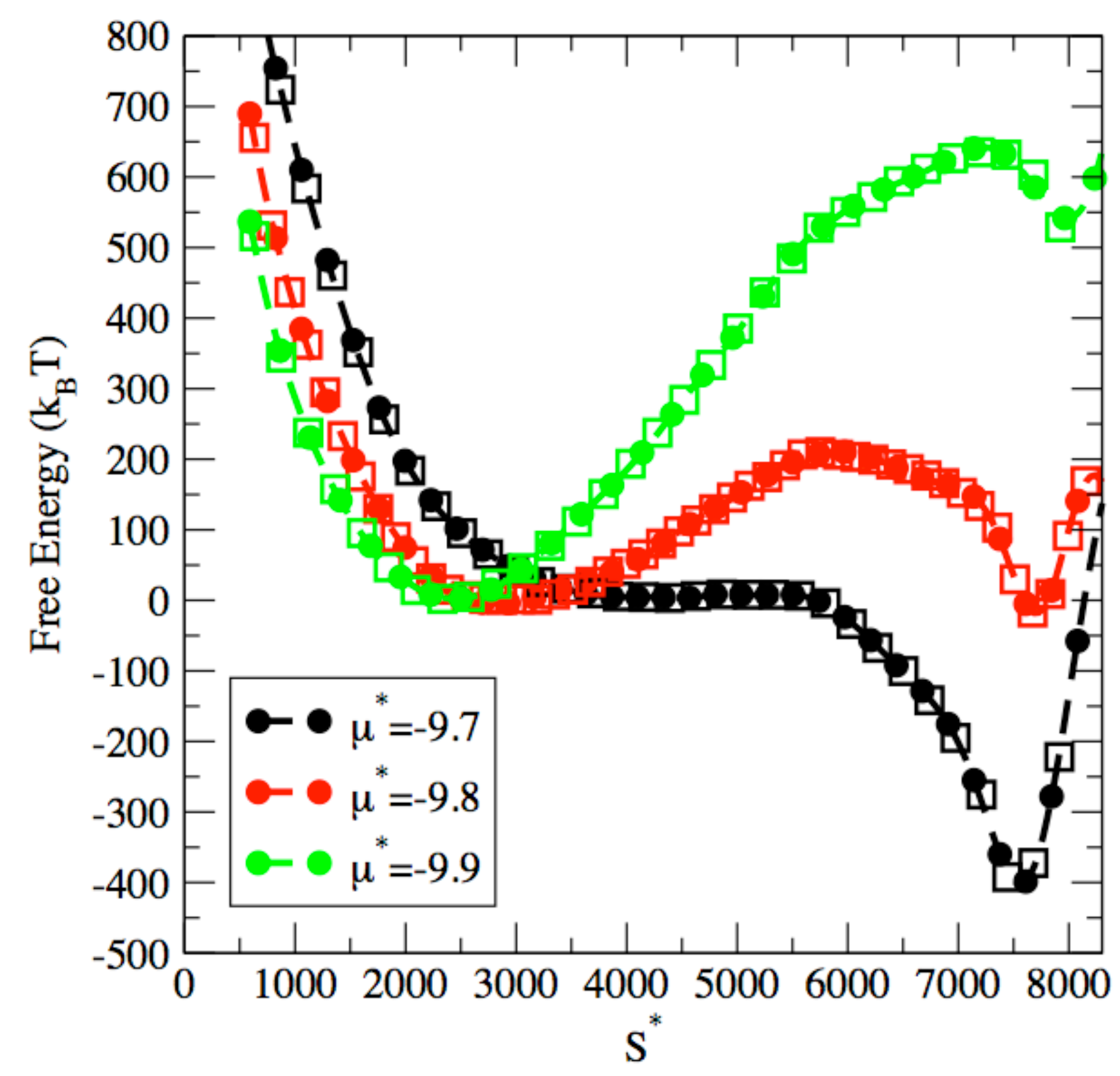
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANN | Artificial Neural Network |
| COF | Covalent Organic Framework |
| MC | Monte Carlo |
| MCM-41 pore | silica mesoporous molecular sieve |
| ML | Machine Learning |
| MOF | Metal-Organic Framework |
| PT-S | enhanced sampling simulations in the grand-canonical (VT) |
| ensemble using entropy (S) as reaction coordinate | |
| NPT-S | enhanced sampling simulations in the isothermal-isobaric (NPT) ensemble using |
| entropy (S) as reaction coordinate |
References
- Derjaguin, B. A theory of capillary condensation in the pores of sorbents and of other capillary phenomena taking into account the disjoining action of polymolecular liquid films. Prog. Surf. Sci. 1992, 40, 46–61. [Google Scholar] [CrossRef]
- Coasne, B.; Pellenq, R.M. A grand canonical Monte Carlo study of capillary condensation in mesoporous media: Effect of the pore morphology and topology. J. Chem. Phys. 2004, 21, 149–160. [Google Scholar] [CrossRef] [PubMed]
- Saugey, A.; Bocquet, L.; Barrat, J. Nucleation in hydrophobic cylindrical pores: A lattice model. J. Phys. Chem. B 2005, 109, 6520–6526. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Major, R.; Houston, J.; McGrath, M.; Siepmann, J.; Zhu, X.Y. Viscous water meniscus under nanoconfinement. Phys. Rev. Lett. 2006, 96, 177803. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Casanova, F.; Chiang, C.E.; Li, C.P.; Schuller, I.K. Direct observation of cooperative effects in capillary condensation: The hysteretic origin. Appl. Phys. Lett. 2007, 91, 243103. [Google Scholar] [CrossRef] [Green Version]
- Puibasset, J. Monte-Carlo multiscale simulation study of argon adsorption/desorption hysteresis in mesoporous heterogeneous tubular pores like MCM-41 or oxidized porous silicon. Langmuir 2008, 25, 903–911. [Google Scholar] [CrossRef] [PubMed]
- Edison, J.R.; Monson, P.A. Dynamics of capillary condensation in lattice gas models of confined fluids: A comparison of dynamic mean field theory with dynamic Monte Carlo simulations. J. Chem. Phys. 2013, 138, 234709. [Google Scholar] [CrossRef]
- Lin, M.; Sinha, S.; Drake, J.; Wu, X.L.; Thiyagarajan, P.; Stanley, H. Study of phase separation of a binary fluid mixture in confined geometry. Phys. Rev. Lett. 1994, 72, 2207. [Google Scholar] [CrossRef]
- Willett, C.D.; Adams, M.J.; Johnson, S.A.; Seville, J.P. Capillary bridges between two spherical bodies. Langmuir 2000, 16, 9396–9405. [Google Scholar] [CrossRef]
- Gogotsi, Y.; Libera, J.A.; Güvenç-Yazicioglu, A.; Megaridis, C.M. In situ multiphase fluid experiments in hydrothermal carbon nanotubes. Appl. Phys. Lett. 2001, 79, 1021–1023. [Google Scholar] [CrossRef]
- He, M.; Szuchmacher Blum, A.; Aston, D.E.; Buenviaje, C.; Overney, R.M.; Luginbühl, R. Critical phenomena of water bridges in nanoasperity contacts. J. Chem. Phys. 2001, 114, 1355–1360. [Google Scholar] [CrossRef] [Green Version]
- Heuberger, M.; Zäch, M.; Spencer, N. Density fluctuations under confinement: When is a fluid not a fluid? Science 2001, 292, 905–908. [Google Scholar] [CrossRef]
- Patel, N.M.; Dodge, M.R.; Alexander, J.I.D.; Slobozhanin, L.A.; Taylor, P.; Rosenblatt, C. Stability of connected cylindrical liquid bridges. Phys. Rev. E 2002, 65, 026306. [Google Scholar] [CrossRef] [PubMed]
- Maeda, N.; Israelachvili, J.N. Nanoscale mechanisms of evaporation, condensation and nucleation in confined geometries. J. Phys. Chem. B 2002, 106, 3534–3537. [Google Scholar] [CrossRef]
- Jang, J.; Schatz, G.C.; Ratner, M.A. Capillary force on a nanoscale tip in dip-pen nanolithography. Phys. Rev. Lett. 2003, 90, 156104. [Google Scholar] [CrossRef]
- Weeks, B.L.; Vaughn, M.W.; DeYoreo, J.J. Direct imaging of meniscus formation in atomic force microscopy using environmental scanning electron microscopy. Langmuir 2005, 21, 8096–8098. [Google Scholar] [CrossRef]
- Berim, G.O.; Ruckenstein, E. Nanodrop on a nanorough solid surface: Density functional theory considerations. J. Chem. Phys. 2008, 129, 014708. [Google Scholar] [CrossRef]
- Restagno, F.; Bocquet, L.; Biben, T. Metastability and nucleation in capillary condensation. Phys. Rev. Lett. 2000, 84, 2433. [Google Scholar] [CrossRef]
- Talanquer, V.; Oxtoby, D. Nucleation in a slit pore. J. Chem. Phys. 2001, 114, 2793–2801. [Google Scholar] [CrossRef] [Green Version]
- Ustinov, E.; Do, D. Modeling of adsorption and nucleation in infinite cylindrical pores by two-dimensional density functional theory. J. Phys. Chem. B 2005, 109, 11653–11660. [Google Scholar] [CrossRef]
- Men, Y.; Yan, Q.; Jiang, G.; Zhang, X.; Wang, W. Nucleation and hysteresis of vapor-liquid phase transitions in confined spaces: Effects of fluid-wall interaction. Phys. Rev. E 2009, 79, 051602. [Google Scholar] [CrossRef] [PubMed]
- Liu, A.J.; Grest, G.S. Wetting in a confined geometry: A Monte Carlo study. Phys. Rev. A 1991, 44, R7894. [Google Scholar] [CrossRef] [PubMed]
- Gac, W.; Patrykiejew, A.; Sokołowski, S. Influence of surface energetical heterogeneity on capillary condensation in slit-like pores: A Monte Carlo study. Surf. Sci. 1994, 306, 434–446. [Google Scholar] [CrossRef]
- Gelb, L.D.; Gubbins, K.; Radhakrishnan, R.; Sliwinska-Bartkowiak, M. Phase separation in confined systems. Rep. Prog. Phys. 1999, 62, 1573. [Google Scholar] [CrossRef] [Green Version]
- Bock, H.; Schoen, M. Phase behavior of a simple fluid confined between chemically corrugated substrates. Phys. Rev. E 1999, 59, 4122. [Google Scholar] [CrossRef]
- Bolhuis, P.G.; Chandler, D. Transition path sampling of cavitation between molecular scale solvophobic surfaces. J. Chem. Phys. 2000, 113, 8154–8160. [Google Scholar] [CrossRef] [Green Version]
- Stroud, W.J.; Curry, J.E.; Cushman, J.H. Capillary condensation and snap-off in nanoscale contacts. Langmuir 2001, 17, 688–698. [Google Scholar] [CrossRef]
- Liu, J.C.; Monson, P. Monte Carlo simulation study of water adsorption in activated carbon. Ind. Eng. Chem. Res. 2006, 45, 5649–5656. [Google Scholar] [CrossRef]
- Mota, J.P.; Esteves, I.A. Simplified gauge-cell method and its application to the study of capillary phase transition of propane in carbon nanotubes. Adsorption 2007, 13, 21–32. [Google Scholar] [CrossRef]
- Winkler, A.; Wilms, D.; Virnau, P.; Binder, K. Capillary condensation in cylindrical pores: Monte Carlo study of the interplay of surface and finite size effects. J. Chem. Phys. 2010, 133, 164702. [Google Scholar] [CrossRef]
- Gor, G.Y.; Rasmussen, C.J.; Neimark, A.V. Capillary condensation hysteresis in overlapping spherical pores: A Monte Carlo simulation study. Langmuir 2012, 28, 12100–12107. [Google Scholar] [CrossRef]
- Siderius, D.W.; Shen, V.K. Use of the grand canonical transition-matrix Monte Carlo method to model gas adsorption in porous materials. J. Phys. Chem. C 2013, 117, 5861–5872. [Google Scholar] [CrossRef]
- Hiratsuka, T.; Tanaka, H.; Miyahara, M.T. Mechanism of Kinetically Controlled Capillary Condensation in Nanopores: A Combined Experimental and Monte Carlo Approach. ACS Nano 2017, 11, 269–276. [Google Scholar] [CrossRef]
- Desgranges, C.; Delhommelle, J. Nucleation of Capillary Bridges and Bubbles in Nanoconfined CO2. Langmuir 2019, 35, 15401–15409. [Google Scholar] [CrossRef]
- Rasmussen, C.J.; Vishnyakov, A.; Thommes, M.; Smarsly, B.M.; Kleitz, F.; Neimark, A.V. Cavitation in Metastable Liquid Nitrogen Confined to Nanoscale Pores. Langmuir 2010, 26, 10147–10157. [Google Scholar] [CrossRef]
- Kornev, K.G.; Shingareva, I.K.; Neimark, A.V. Capillary condensation as a morphological transition. Adv. Colloid Interface Sci. 2002, 96, 143–167. [Google Scholar] [CrossRef]
- Neimark, A.V.; Ravikovitch, P.I.; Vishnyakov, A. Bridging scales from molecular simulations to classical thermodynamics: Density functional theory of capillary condensation in nanopores. J. Phys. Condens. Matter 2003, 15, 347. [Google Scholar] [CrossRef]
- Vishnyakov, A.; Neimark, A.V. Monte Carlo simulation test of pore blocking effects. Langmuir 2003, 19, 3240–3247. [Google Scholar] [CrossRef]
- Vishnyakov, A.; Neimark, A.V. Nucleation of liquid bridges and bubbles in nanoscale capillaries. J. Chem. Phys. 2003, 119, 9755–9764. [Google Scholar] [CrossRef] [Green Version]
- Neimark, A.V.; Vishnyakov, A. Monte Carlo simulation study of droplet nucleation. J. Chem. Phys. 2005, 122, 174508. [Google Scholar] [CrossRef]
- Neimark, A.V.; Vishnyakov, A. The birth of a bubble: A molecular simulation study. J. Chem. Phys. 2005, 122, 054707. [Google Scholar] [CrossRef]
- Neimark, A.V.; Vishnyakov, A. Vapor-to-droplet transition in a Lennard-Jones fluid: Simulation study of nucleation barriers using the ghost field method. J. Phys. Chem. B 2005, 109, 5962–5976. [Google Scholar] [CrossRef] [Green Version]
- Horikawa, T.; Do, D.; Nicholson, D. Capillary condensation of adsorbates in porous materials. Adv. Colloid Interface Sci. 2011, 169, 40–58. [Google Scholar] [CrossRef]
- Kierlik, E.; Monson, P.; Rosinberg, M.; Sarkisov, L.; Tarjus, G. Capillary Condensation in Disordered Porous Materials: Hysteresis versus Equilibrium Behavior. Phys. Rev. Lett. 2001, 87, 055701. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Desgranges, C.; Delhommelle, J. Free energy calculations along entropic pathways. III. Nucleation of capillary bridges and bubbles. J. Chem. Phys. 2017, 146, 184104. [Google Scholar] [CrossRef]
- Everett, D.; Haynes, J. Model studies of capillary condensation. I. Cylindrical pore model with zero contact angle. J. Colloid Interface Sci. 1972, 38, 125–137. [Google Scholar] [CrossRef]
- Behler, J. Perspective: Machine Learning Potentials for Atomistic Simulations. J. Chem. Phys. 2016, 145, 170901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Butler, K.T.; Davies, D.W.; Cartwright, H.; Isayev, O.; Walsh, A. Machine learning for molecular and materials science. Nature 2018, 559, 547–555. [Google Scholar] [CrossRef]
- Hachmann, J.; Afzal, M.A.F.; Haghighatlari, M.; Pal, Y. Building and Deploying a Cyberinfrastructure for the Data-Driven Design of Chemical Systems and the Exploration of Chemical Space. Mol. Simul. 2018, 44, 921–929. [Google Scholar] [CrossRef]
- Ceriotti, M. Unsupervised Machine Learning in Atomistic Simulations, between Predictions and Understanding. J. Chem. Phys. 2019, 150, 150901. [Google Scholar] [CrossRef] [Green Version]
- Handley, C.M.; Popelier, P.L. Potential Energy Surfaces Fitted by Artificial Neural Networks. J. Phys. Chem. A 2010, 114, 3371–3383. [Google Scholar] [CrossRef]
- Behler, J. Neural Network Potential-Energy Surfaces in Chemistry: A Tool for Large-Scale Simulations. Phys. Chem. Chem. Phys. 2011, 13, 17930–17955. [Google Scholar] [CrossRef] [PubMed]
- Behler, J. Representing Potential Energy Surfaces by High-Dimensional Neural Network Potentials. J. Phys. Condens. Matter 2014, 26, 183001. [Google Scholar] [CrossRef]
- Jiang, B.; Li, J.; Guo, H. Potential Energy Surfaces from High Fidelity Fitting of Ab Initio Points: The Permutation Invariant Polynomial-Neural Network Approach. Int. Rev. Phys. Chem. 2016, 35, 479–506. [Google Scholar] [CrossRef]
- Smith, J.S.; Isayev, O.; Roitberg, A.E. ANI-1: An Extensible Neural Network Potential with DFT Accuracy at Force Field Computational Cost. Chem. Sci. 2017, 8, 3192–3203. [Google Scholar] [CrossRef] [Green Version]
- Nüske, F.; Boninsegna, L.; Clementi, C. Coarse-Graining Molecular Systems by Spectral Matching. J. Chem. Phys. 2019, 151, 044116. [Google Scholar] [CrossRef] [PubMed]
- Ballard, A.J.; Das, R.; Martiniani, S.; Mehta, D.; Sagun, L.; Stevenson, J.D.; Wales, D.J. Energy Landscapes for Machine Learning. Phys. Chem. Chem. Phys. 2017, 19, 12585–12603. [Google Scholar] [CrossRef] [Green Version]
- Sauceda, H.E.; Chmiela, S.; Poltavsky, I.; Müller, K.R.; Tkatchenko, A. Molecular Force Fields with Gradient-Domain Machine Learning: Construction and Application to Dynamics of Small Molecules with Coupled Cluster Forces. J. Chem. Phys. 2019, 150, 114102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brockherde, F.; Vogt, L.; Li, L.; Tuckerman, M.E.; Burke, K.; Müller, K.R. Bypassing the Kohn-Sham equations with machine learning. Nat. Commun. 2017, 8, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Olsson, S.; Wehmeyer, C.; Pérez, A.; Charron, N.E.; De Fabritiis, G.; Noé, F.; Clementi, C. Machine Learning of Coarse-Grained Molecular Dynamics force fields. ACS Cent. Sci. 2019, 5, 755–767. [Google Scholar] [CrossRef] [Green Version]
- Long, A.W.; Zhang, J.; Granick, S.; Ferguson, A.L. Machine Learning Assembly Landscapes from Particle Tracking Data. Soft Matter 2015, 11, 8141–8153. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jiang, B.; Yang, M.; Xie, D.; Guo, H. Quantum Dynamics of Polyatomic Dissociative Chemisorption on Transition Metal Surfaces: Mode Specificity and Bond Selectivity. Chem. Soc. Rev. 2016, 45, 3621–3640. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mansbach, R.A.; Ferguson, A.L. Machine learning of single molecule free energy surfaces and the impact of chemistry and environment upon structure and dynamics. J. Chem. Phys. 2015, 142, 03B607_1. [Google Scholar] [CrossRef]
- Mones, L.; Bernstein, N.; Csányi, G. Exploration, Sampling, and reconstruction of free energy surfaces with Gaussian process regression. J. Chem. Theory Comput. 2016, 12, 5100–5110. [Google Scholar] [CrossRef] [PubMed]
- Schneider, E.; Dai, L.; Topper, R.Q.; Drechsel-Grau, C.; Tuckerman, M.E. Stochastic neural network approach for learning high-dimensional free energy surfaces. Phys. Rev. Lett. 2017, 119, 150601. [Google Scholar] [CrossRef] [Green Version]
- Desgranges, C.; Delhommelle, J. Crystal nucleation along an entropic pathway: Teaching liquids how to transition. Phys. Rev. E 2018, 98, 063307. [Google Scholar] [CrossRef] [Green Version]
- Noé, F.; Olsson, S.; Köhler, J.; Wu, H. Boltzmann Generators: Sampling Equilibrium States of Many-Body systems with Deep Learning. Science 2019, 365, eaaw1147. [Google Scholar] [CrossRef] [Green Version]
- Desgranges, C.; Delhommelle, J. Ensemble Learning of Partition Functions for the Prediction of Thermodynamic Properties of Adsorption in Metal-Organic and Covalent Organic Frameworks. J. Phys. Chem. C 2020, 124, 1907–1917. [Google Scholar] [CrossRef]
- Desgranges, C.; Delhommelle, J. Towards a machine learned thermodynamics: Exploration of free energy landscapes in molecular fluids, biological systems and for gas storage and separation in metal–organic frameworks. Mol. Syst. Des. Eng. 2021, 6, 52–65. [Google Scholar] [CrossRef]
- Jäger, M.O.; Morooka, E.V.; Canova, F.F.; Himanen, L.; Foster, A.S. Machine learning hydrogen adsorption on nanoclusters through structural descriptors. npj Comput. Mater. 2018, 4, 1–8. [Google Scholar] [CrossRef]
- Pardakhti, M.; Moharreri, E.; Wanik, D.; Suib, S.L.; Srivastava, R. Machine learning using combined structural and chemical descriptors for prediction of methane adsorption performance of metal organic frameworks (MOFs). ACS Comb. Sci. 2017, 19, 640–645. [Google Scholar] [CrossRef]
- Ahmed, A.; Seth, S.; Purewal, J.; Wong-Foy, A.G.; Veenstra, M.; Matzger, A.J.; Siegel, D.J. Exceptional Hydrogen Storage Achieved by Screening Nearly Half a Million Metal-Organic Frameworks. Nat. Commun. 2019, 10, 1568. [Google Scholar] [CrossRef] [Green Version]
- Anderson, G.; Schweitzer, B.; Anderson, R.; Gomez-Gualdron, D.A. Attainable Volumetric Targets for Adsorption-Based Hydrogen Storage in Porous Crystals: Molecular Simulation and Machine Learning. J. Phys. Chem. C 2018, 123, 120–130. [Google Scholar] [CrossRef]
- Wu, X.; Xiang, S.; Su, J.; Cai, W. Understanding Quantitative Relationship between Methane Storage Capacities and Characteristic Properties of Metal–Organic Frameworks Based on Machine Learning. J. Phys. Chem. C 2019, 123, 8550–8559. [Google Scholar] [CrossRef]
- Bobbitt, N.S.; Snurr, R.Q. Molecular Modelling and Machine Learning for High-Throughput Screening of Metal-Organic Frameworks for Hydrogen Storage. Mol. Simul. 2019, 45, 1069–1081. [Google Scholar] [CrossRef]
- Anderson, R.; Biong, A.; Gómez-Gualdrón, D.A. Adsorption Isotherm Predictions for Multiple Molecules in MOFs using the Same Deep Learning Model. J. Chem. Theory Comput. 2020, 16, 1271–1283. [Google Scholar] [CrossRef]
- Toyao, T.; Suzuki, K.; Kikuchi, S.; Takakusagi, S.; Shimizu, K.i.; Takigawa, I. Toward Effective Utilization of Methane: Machine Learning Prediction of Adsorption Energies on Metal Alloys. J. Phys. Chem. C 2018, 122, 8315–8326. [Google Scholar] [CrossRef]
- Zhang, Z.; Schott, J.A.; Liu, M.; Chen, H.; Lu, X.; Sumpter, B.G.; Fu, J.; Dai, S. Prediction of Carbon Dioxide Adsorption via Deep Learning. Angew. Chem. Int. Ed. 2019, 58, 259–263. [Google Scholar] [CrossRef]
- Jablonka, K.M.; Ongari, D.; Moosavi, S.M.; Smit, B. Big-Data Science in Porous Materials: Materials Genomics and Machine Learning. Chem. Rev. 2020, in press. [Google Scholar] [CrossRef]
- Hiratsuka, T.; Tanaka, H.; Miyahara, M.T. Critical Energy Barrier for Capillary Condensation in Mesopores: Hysteresis and Reversibility. J. Chem. Phys. 2016, 144, 164705. [Google Scholar] [CrossRef]
- Neimark, A.V.; Vishnyakov, A. Gauge cell method for simulation studies of phase transitions in confined systems. Phys. Rev. E 2000, 62, 4611. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Desgranges, C.; Delhommelle, J. Evaluation of the grand-canonical partition function using expanded Wang-Landau simulations. II. Adsorption of atomic and molecular fluids in a porous material. J. Chem. Phys. 2012, 136, 184108. [Google Scholar] [CrossRef] [PubMed]
- Dantas, S.; Struckhoff, K.C.; Thommes, M.; Neimark, A.V. Phase Behavior and Capillary Condensation Hysteresis of Carbon Dioxide in Mesopores. Langmuir 2019, 35, 11291–11298. [Google Scholar] [CrossRef] [PubMed]
- Desgranges, C.; Delhommelle, J. Stabilization of Nanobubbles under Hydrophobic Confinement. J. Phys. Chem. C 2019, 123, 11707–11713. [Google Scholar] [CrossRef] [Green Version]
- Hofmann, T.; Wallacher, D.; Perlich, J.; Koyiloth Vayalil, S.; Huber, P. Formation of Periodically Arranged Nanobubbles in Mesopores: Capillary Bridge Formation and Cavitation during Sorption and Solidification in an Hierarchical Porous SBA-15 Matrix. Langmuir 2016, 32, 2928–2936. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Kim, D.; Kim, J.; An, S.; Jhe, W. Direct Evidence for Curvature-Dependent Surface Tension in Capillary Condensation: Kelvin Equation at Molecular Scale. Phys. Rev. X 2018, 8, 041046. [Google Scholar] [CrossRef] [Green Version]
- Barsotti, E.; Tan, S.P.; Piri, M.; Chen, J.H. Phenomenological Study of Confined Criticality: Insights from the Capillary Condensation of Propane, n-Butane, and n-Pentane in Nanopores. Langmuir 2018, 34, 4473–4483. [Google Scholar] [CrossRef]
- Desgranges, C.; Delhommelle, J. Free energy calculations along entropic pathways. I. Homogeneous vapor-liquid nucleation for atomic and molecular systems. J. Chem. Phys. 2016, 145, 204112. [Google Scholar] [CrossRef]
- Desgranges, C.; Delhommelle, J. Free energy calculations along entropic pathways. II. Droplet nucleation in binary mixtures. J. Chem. Phys. 2016, 145, 234505. [Google Scholar] [CrossRef]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Clarendon Press: Oxford, UK, 1987. [Google Scholar]
- Ravikovitch, P.; Wei, D.; Chueh, W.; Haller, G.; Neimark, A. Evaluation of pore structure parameters of MCM-41 catalyst supports and catalysts by means of nitrogen and argon adsorption. J. Phys. Chem. B 1997, 101, 3671–3679. [Google Scholar] [CrossRef]
- Torrie, G.M.; Valleau, J.P. Nonphysical sampling distributions in Monte Carlo free-energy estimation: Umbrella sampling. J. Comput. Phys. 1977, 23, 187–199. [Google Scholar] [CrossRef]
- Ten Wolde, P.R.; Ruiz-Montero, M.J.; Frenkel, D. Numerical evidence for bcc ordering at the surface of a critical fcc nucleus. Phys. Rev. Lett. 1995, 75, 2714. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schrader, M.; Virnau, P.; Binder, K. Simulation of vapor-liquid coexistence in finite volumes: A method to compute the surface free energy of droplets. Phys. Rev. E 2009, 79, 061104. [Google Scholar] [CrossRef] [PubMed]
- Remsing, R.C.; Xi, E.; Vembanur, S.; Sharma, S.; Debenedetti, P.G.; Garde, S.; Patel, A.J. Pathways to dewetting in hydrophobic confinement. Proc. Natl. Acad. Sci. USA 2015, 112, 8181. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Desgranges, C.; Delhommelle, J. Controlling polymorphism during the crystallization of an atomic fluid. Phys. Rev. Lett. 2007, 98, 235502. [Google Scholar] [CrossRef] [PubMed]
- Punnathanam, S.; Monson, P. Crystal nucleation in binary hard sphere mixtures: A Monte Carlo simulation study. J. Chem. Phys. 2006, 125, 024508. [Google Scholar] [CrossRef] [PubMed]
- Desgranges, C.; Delhommelle, J. Unraveling the Coupling between Demixing and Crystallization in Mixtures. J. Am. Chem. Soc. 2014, 136, 8145–8148. [Google Scholar] [CrossRef]
- Desgranges, C.; Delhommelle, J. Role of liquid polymorphism during the crystallization of Silicon. J. Am. Chem. Soc. 2011, 133, 2872–2874. [Google Scholar] [CrossRef]
- Desgranges, C.; Delhommelle, J. Unusual Crystallization Behavior Close to the Glass Transition. Phys. Rev. Lett. 2018, 120, 115701. [Google Scholar] [CrossRef] [Green Version]
- Desgranges, C.; Delhommelle, J. Can ordered precursors promote the nucleation of solid solutions? Phys. Rev. Lett. 2019, 123, 195701. [Google Scholar] [CrossRef]
- Waghe, A.; Rasaiah, J.C.; Hummer, G. Entropy of single-file water in (6, 6) carbon nanotubes. J. Chem. Phys. 2012, 137, 044709. [Google Scholar] [CrossRef]
- Wolde Pieter-Reináten, M.J.R.M.; Frenkel, D. Simulation of homogeneous crystal nucleation close to coexistence. Faraday Discuss. 1996, 104, 93–110. [Google Scholar] [CrossRef] [Green Version]
- Piaggi, P.M.; Valsson, O.; Parrinello, M. Enhancing entropy and enthalpy fluctuations to drive crystallization in atomistic simulations. Phys. Rev. Lett. 2017, 119, 015701. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Piaggi, P.M.; Parrinello, M. Predicting polymorphism in molecular crystals using orientational entropy. Proc. Natl. Acad. Sci. USA 2018, 115, 10251–10256. [Google Scholar] [CrossRef] [Green Version]
- Ravikovitch, P.; Domhnaill, S.Ó.; Neimark, A.; Schüth, F.; Unger, K. Capillary hysteresis in nanopores: Theoretical and experimental studies of nitrogen adsorption on MCM-41. Langmuir 1995, 11, 4765–4772. [Google Scholar] [CrossRef]
- LeCun, Y.; Boser, B.; Denker, J.; Henderson, D.; Howard, R.; Hubbard, W.; Jackel, L. Handwritten digit recognition with a back-propagation network. Adv. Neural Inf. Process. Syst. 1989, 2, 396–404. [Google Scholar]
- Desgranges, C.; Delhommelle, J. A new approach for the prediction of partition functions using machine learning techniques. J. Chem. Phys. 2018, 149, 044118. [Google Scholar] [CrossRef]
- Desgranges, C.; Delhommelle, J. Determination of mixture properties via a combined Expanded Wang-Landau simulations-Machine Learning approach. Chem. Phys. Lett. 2019, 715, 1–6. [Google Scholar] [CrossRef]
- Towns, J.; Cockerill, T.; Dahan, M.; Foster, I.; Gaither, K.; Grimshaw, A.; Hazlewood, V.; Lathrop, S.; Lifka, D.; Peterson, G.D.; et al. XSEDE: Accelerating Scientific Discovery. Comput. Sci. Eng. 2014, 16, 62–74. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Desgranges, C.; Delhommelle, J. Machine-Learned Free Energy Surfaces for Capillary Condensation and Evaporation in Mesopores. Entropy 2022, 24, 97. https://doi.org/10.3390/e24010097
Desgranges C, Delhommelle J. Machine-Learned Free Energy Surfaces for Capillary Condensation and Evaporation in Mesopores. Entropy. 2022; 24(1):97. https://doi.org/10.3390/e24010097
Chicago/Turabian StyleDesgranges, Caroline, and Jerome Delhommelle. 2022. "Machine-Learned Free Energy Surfaces for Capillary Condensation and Evaporation in Mesopores" Entropy 24, no. 1: 97. https://doi.org/10.3390/e24010097
APA StyleDesgranges, C., & Delhommelle, J. (2022). Machine-Learned Free Energy Surfaces for Capillary Condensation and Evaporation in Mesopores. Entropy, 24(1), 97. https://doi.org/10.3390/e24010097





