On the Zero-Outage Secrecy-Capacity of Dependent Fading Wiretap Channels
Abstract
:1. Introduction
- First, we consider a basic wiretap channel where there are two paths to a single legitimate receiver and one single path to a single eavesdropper. The channel gains are correlated slow fading and perfectly known at the receiver and eavesdropper, but unknown to the transmitter.
- Based on copulas, we derive an analytical solution for the ZOSR when Rayleigh fading is considered. In particular, the positive ZOSR is achieved by counter-monotonically distributed channel gains between the transmitter and the legitimate receiver. In contrast, the sum of the above two channel gains is co-monotonically distributed with respect to Eve’s channel gain.
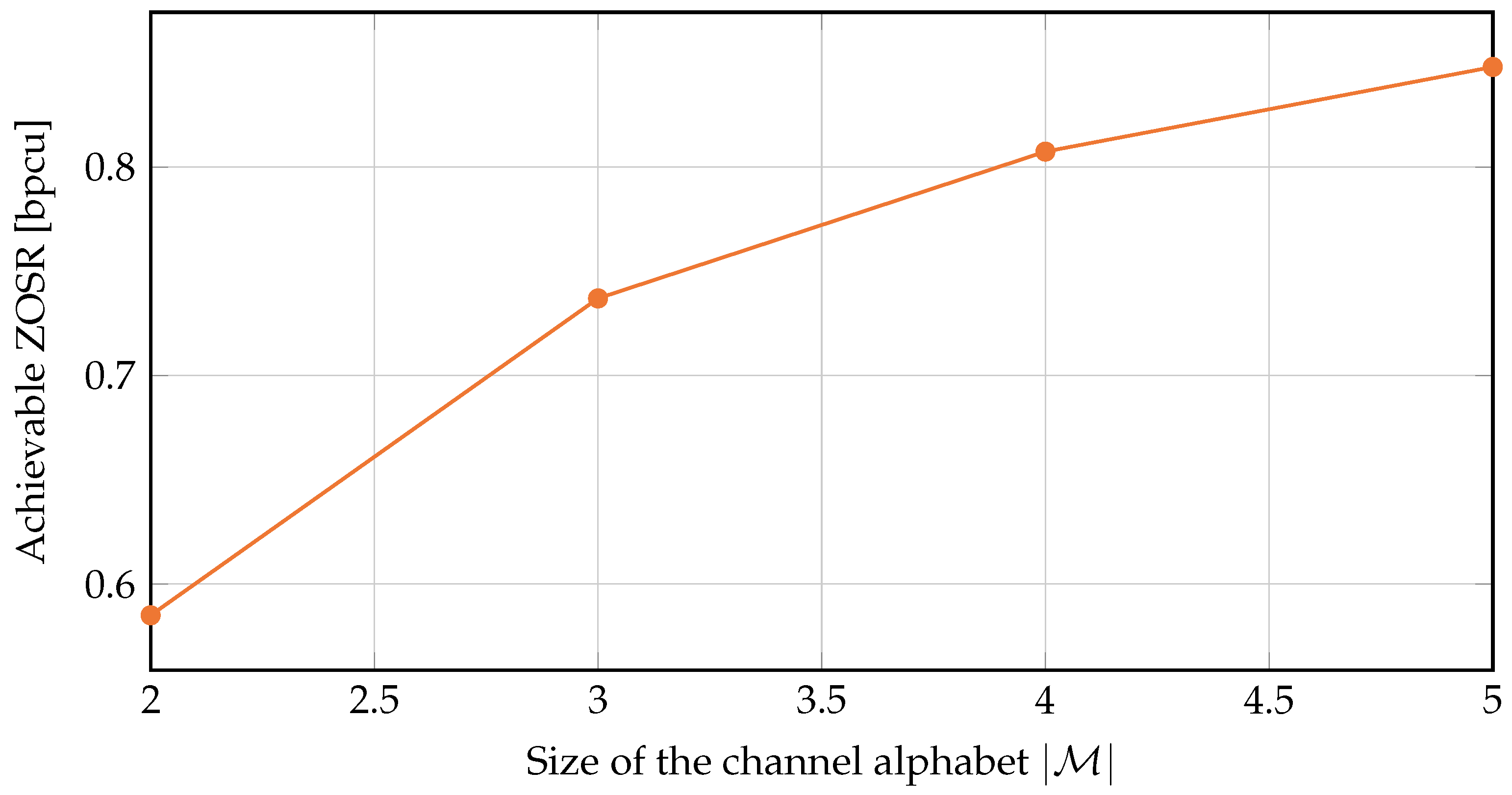
- To gain a better understanding of the optimality of the dependency structure, we further transform the original ZOSC maximization problem into an equivalent form. Using the equivalent form, we propose an algorithm which efficiently solves the case where the channel gains are from finite alphabets. Interestingly, numerical results show that the optimal joint distribution of channel gains does not follow the aforementioned counter- and co-monotonicity relation.
- Then, we consider the generalization of the wiretap setup to multiple observations at Bob and Eve. We provide an algorithm to compute an achievable ZOSR and apply the rearrangement algorithm (RA) to solve the ZOSR problem for fading gains with continuous alphabets for a general number of observations.
2. System Model and Preliminaries
2.1. System Model
2.2. Problem Formulation
2.3. Mathematical Background
3. Achievable ZOSC for the [2,1]-Wiretap Channel
4. An Equivalent Outage Problem Formulation for the [2,1]-Wiretap Channel
Discrete Alphabets
- : .
- : .
- : .
- : .
| Algorithm 1 Solve globally optimal ZOSC with channel gains from finite alphabet |
| 0. Initialize the marginal distributions and define . |
| 1. Construct the -ary expansion matrix , where each row of is a tuple (the 1st row is (0,0,0) and the proceedings follow an increasing order with respect to the -ary expansion). |
| 2. Construct , where , if by the j-th row of , and is not used in calculating the marginal probability , where is the i-row of , , . Define . |
| 3. Reorder and as and , respectively, such that are in an increasing manner. |
| repeat |
| 4. Update : set columns of as a zero vectors, where the indices of those columns correspond to the rows of having the smallest rates. |
| 5. Solve , , , , by CVX. |
| 6. Set L = L + 1. |
| until is feasible, |
| 7. ZOSC = , where |
| . |
5. Positive ZOSR for [,]-Wiretap Channels
- First, we find the joint distribution between Bob’s channels that maximizes the ZOC. The simple reason behind this first step is that we cannot find a positive ZOSC, if we do not have a positive ZOC to the legitimate receiver. In fact, the ZOSC is upper bounded by the ZOC to Bob.
- Next, we find the same dependency structure for Eve’s channels that maximizes the ZOC. It may seem counter-intuitive to choose a joint distribution for which is always greater than a positive constant. However, the reasoning behind this particular choice is to balance the realizations of Eve’s channels such that only little probability mass is placed on high realizations of . Otherwise, there could be a positive probability that , which would result in a ZOSC of zero. It should be emphasized that this is a particular choice for this scheme and might not be the optimal dependency for the general case.
- Finally, we set and as co-monotonic in order to maximize the ZOSR for fixed and as shown in Lemma 1.
Example: Rayleigh Fading
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AWGN | additive white Gaussian noise |
| CDF | cumulative distribution function |
| CSI | channel-state information |
| CSI-T | channel-state information at the transmitter |
| probability density function | |
| PMF | probability mass function |
| RA | rearrangement algorithm |
| RIS | reconfigurable intelligent surface |
| SISO | single-input single-output |
| SNR | signal-to-noise ratio |
| SOP | secrecy outage probability |
| ZOC | zero-outage capacity |
| ZOSC | zero-outage secrecy capacity |
| ZOSR | zero-outage secrecy rate |
References
- Saad, W.; Bennis, M.; Chen, M. A Vision of 6G Wireless Systems: Applications, Trends, Technologies, and Open Research Problems. IEEE Netw. 2019, 34, 134–142. [Google Scholar] [CrossRef] [Green Version]
- Bloch, M.; Barros, J. Physical-Layer Security; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar] [CrossRef]
- Gidney, C.; Ekerå, M. How to factor 2048 bit RSA integers in 8 h using 20 million noisy qubits. Quantum 2021, 5, 433. [Google Scholar] [CrossRef]
- Gungor, O.; Tan, J.; Koksal, C.E.; El-Gamal, H.; Shroff, N.B. Secrecy Outage Capacity of Fading Channels. IEEE Trans. Inf. Theory 2013, 59, 5379–5397. [Google Scholar] [CrossRef] [Green Version]
- Bloch, M.; Barros, J.; Rodrigues, M.R.D.; McLaughlin, S.W. Wireless Information-Theoretic Security. IEEE Trans. Inf. Theory 2008, 54, 2515–2534. [Google Scholar] [CrossRef]
- Gopala, P.K.; Lai, L.; El Gamal, H. On the Secrecy Capacity of Fading Channels. IEEE Trans. Inf. Theory 2008, 54, 4687–4698. [Google Scholar] [CrossRef] [Green Version]
- Zhao, H.; Liu, Y.; Sultan-Salem, A.; Alouini, M.S. A Simple Evaluation for the Secrecy Outage Probability Over Generalized-K Fading Channels. IEEE Commun. Lett. 2019, 23, 1479–1483. [Google Scholar] [CrossRef] [Green Version]
- Biglieri, E.; Lai, I.W. The impact of independence assumptions on wireless communication analysis. In Proceedings of the 2016 IEEE International Symposium on Information Theory (ISIT), Barcelona, Spain, 10–15 July 2016; pp. 2184–2188. [Google Scholar] [CrossRef]
- Liang, Y.; Poor, H.V.; (Shitz), S.S. Information Theoretic Security. Found. Trends Commun. Inf. Theory 2009, 5, 355–580. [Google Scholar] [CrossRef]
- Peters, G.W.; Myrvoll, T.A.; Matsui, T.; Nevat, I.; Septier, F. Communications meets copula modeling: Non-standard dependence features in wireless fading channels. In Proceedings of the 2014 IEEE Global Conference on Signal and Information Processing (GlobalSIP), Atlanta, GA, USA, 3–5 December 2014; pp. 1224–1228. [Google Scholar] [CrossRef]
- Lee, W.Y. Effects on correlation between two mobile radio base-station antennas. IEEE Trans. Veh. Technol. 1973, 22, 130–140. [Google Scholar] [CrossRef]
- Jeon, H.; Kim, N.; Choi, J.; Lee, H.; Ha, J. Bounds on Secrecy Capacity Over Correlated Ergodic Fading Channels at High SNR. IEEE Trans. Inf. Theory 2011, 57, 1975–1983. [Google Scholar] [CrossRef]
- Sun, X.; Wang, J.; Xu, W.; Zhao, C. Performance of Secure Communications Over Correlated Fading Channels. IEEE Signal Process. Lett. 2012, 19, 479–482. [Google Scholar] [CrossRef]
- Liu, X. Outage Probability of Secrecy Capacity over Correlated Log-Normal Fading Channels. IEEE Commun. Lett. 2013, 17, 289–292. [Google Scholar] [CrossRef]
- Alexandropoulos, G.C.; Peppas, K.P. Secrecy Outage Analysis Over Correlated Composite Nakagami-m/Gamma Fading Channels. IEEE Commun. Lett. 2018, 22, 77–80. [Google Scholar] [CrossRef]
- Ghadi, F.R.; Hodtani, G.A. Copula-Based Analysis of Physical Layer Security Performances Over Correlated Rayleigh Fading Channels. IEEE Trans. Inf. Forensics Secur. 2021, 16, 431–440. [Google Scholar] [CrossRef]
- Besser, K.L.; Jorswieck, E.A. Bounds on the Secrecy Outage Probability for Dependent Fading Channels. IEEE Trans. Commun. 2021, 69, 443–456. [Google Scholar] [CrossRef]
- Besser, K.L.; Lin, P.H.; Jorswieck, E.A. On Fading Channel Dependency Structures with a Positive Zero-Outage Capacity. IEEE Trans. Commun. 2021, 69, 6561–6574. [Google Scholar] [CrossRef]
- Besser, K.L.; Jorswieck, E.A. Reliability Bounds for Dependent Fading Wireless Channels. IEEE Trans. Wirel. Commun. 2020, 19, 5833–5845. [Google Scholar] [CrossRef]
- Mucchi, L.; Jayousi, S.; Caputo, S.; Panayirci, E.; Shahabuddin, S.; Bechtold, J.; Morales, I.; Stoica, R.A.; Abreu, G.; Haas, H. Physical-Layer Security in 6G Networks. IEEE Open J. Commun. Soc. 2021, 2, 1901–1914. [Google Scholar] [CrossRef]
- Basar, E.; Poor, H.V. Present and Future of Reconfigurable Intelligent Surface-Empowered Communications [Perspectives]. IEEE Signal Process. Mag. 2021, 38, 146–152. [Google Scholar] [CrossRef]
- Khisti, A.; Wornell, G.W. Secure Transmission With Multiple Antennas—Part II: The MIMOME Wiretap Channel. IEEE Trans. Inf. Theory 2010, 56, 5515–5532. [Google Scholar] [CrossRef] [Green Version]
- Nelsen, R.B. An Introduction to Copulas, 2nd ed.; Springer Series in Statistics; Springer: New York, NY, USA, 2006. [Google Scholar] [CrossRef]
- Jorswieck, E.; Lin, P.H. Ultra-Reliable Multi-Connectivity with Negatively Dependent Fading Channels. In Proceedings of the 2019 16th International Symposium on Wireless Communication Systems (ISWCS), Oulu, Finland, 27–30 August 2019; pp. 373–378. [Google Scholar] [CrossRef]
- Frank, M.J.; Nelsen, R.B.; Schweizer, B. Best-possible Bounds for the Distribution of a Sum—A Problem of Kolmogorov. Probab. Theory Relat. Fields 1987, 74, 199–211. [Google Scholar] [CrossRef]
- Embrechts, P.; Puccetti, G.; Rüschendorf, L. Model uncertainty and VaR aggregation. J. Bank. Financ. 2013, 37, 2750–2764. [Google Scholar] [CrossRef]
- Puccetti, G.; Wang, R. Extremal Dependence Concepts. Stat. Sci. 2015, 30, 485–517. [Google Scholar] [CrossRef]
- Puccetti, G.; Rüschendorf, L. Computation of sharp bounds on the distribution of a function of dependent risks. J. Comput. Appl. Math. 2012, 236, 1833–1840. [Google Scholar] [CrossRef] [Green Version]
- Besser, K.L.; Jorswieck, E.A. Calculation of Bounds on the Ergodic Capacity for Fading Channels with Dependency Uncertainty. In Proceedings of the ICC 2021—2021 IEEE International Conference on Communications (ICC), Montreal, QC, Canada, 14–23 June 2021. [Google Scholar]
- Besser, K.L.; Lin, P.H. Zero-Outage Secrecy-Capacity of Dependent Fading Wiretap Channels—Supplementary Material. Available online: https://gitlab.com/klb2/zero-outage-secrecy-capacity (accessed on 16 November 2021).
- Besser, K.L. Rearrangement Algorithm: Python Implementation. Version 0.1.1. Available online: https://pypi.org/project/rearrangement-algorithm/ (accessed on 28 October 2021).
- Hofert, M. Implementing the Rearrangement Algorithm: An Example from Computational Risk Management. Risks 2020, 8, 47. [Google Scholar] [CrossRef]
- Wang, B.; Wang, R. Joint Mixability. Math. Oper. Res. 2016, 41, 808–826. [Google Scholar] [CrossRef] [Green Version]
- Di Renzo, M.; Debbah, M.; Phan-Huy, D.T.; Zappone, A.; Alouini, M.S.; Yuen, C.; Sciancalepore, V.; Alexandropoulos, G.C.; Hoydis, J.; Gacanin, H.; et al. Smart radio environments empowered by reconfigurable AI meta-surfaces: An idea whose time has come. EURASIP J. Wirel. Commun. Netw. 2019, 2019, 129. [Google Scholar] [CrossRef] [Green Version]


| Y | Secrecy Capacity | |||
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 1 | a |
| 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | b |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | c | |
| 1 | 1 | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jorswieck, E.; Lin, P.-H.; Besser, K.-L. On the Zero-Outage Secrecy-Capacity of Dependent Fading Wiretap Channels. Entropy 2022, 24, 99. https://doi.org/10.3390/e24010099
Jorswieck E, Lin P-H, Besser K-L. On the Zero-Outage Secrecy-Capacity of Dependent Fading Wiretap Channels. Entropy. 2022; 24(1):99. https://doi.org/10.3390/e24010099
Chicago/Turabian StyleJorswieck, Eduard, Pin-Hsun Lin, and Karl-Ludwig Besser. 2022. "On the Zero-Outage Secrecy-Capacity of Dependent Fading Wiretap Channels" Entropy 24, no. 1: 99. https://doi.org/10.3390/e24010099
APA StyleJorswieck, E., Lin, P.-H., & Besser, K.-L. (2022). On the Zero-Outage Secrecy-Capacity of Dependent Fading Wiretap Channels. Entropy, 24(1), 99. https://doi.org/10.3390/e24010099







