An Application of Inverse Reinforcement Learning to Estimate Interference in Drone Swarms
Abstract
:1. Introduction
2. Materials and Methods
2.1. Double Transition Model (DTM)
2.2. Inverse Reinforcement Learning (IRL)
2.3. Entropy and Interference
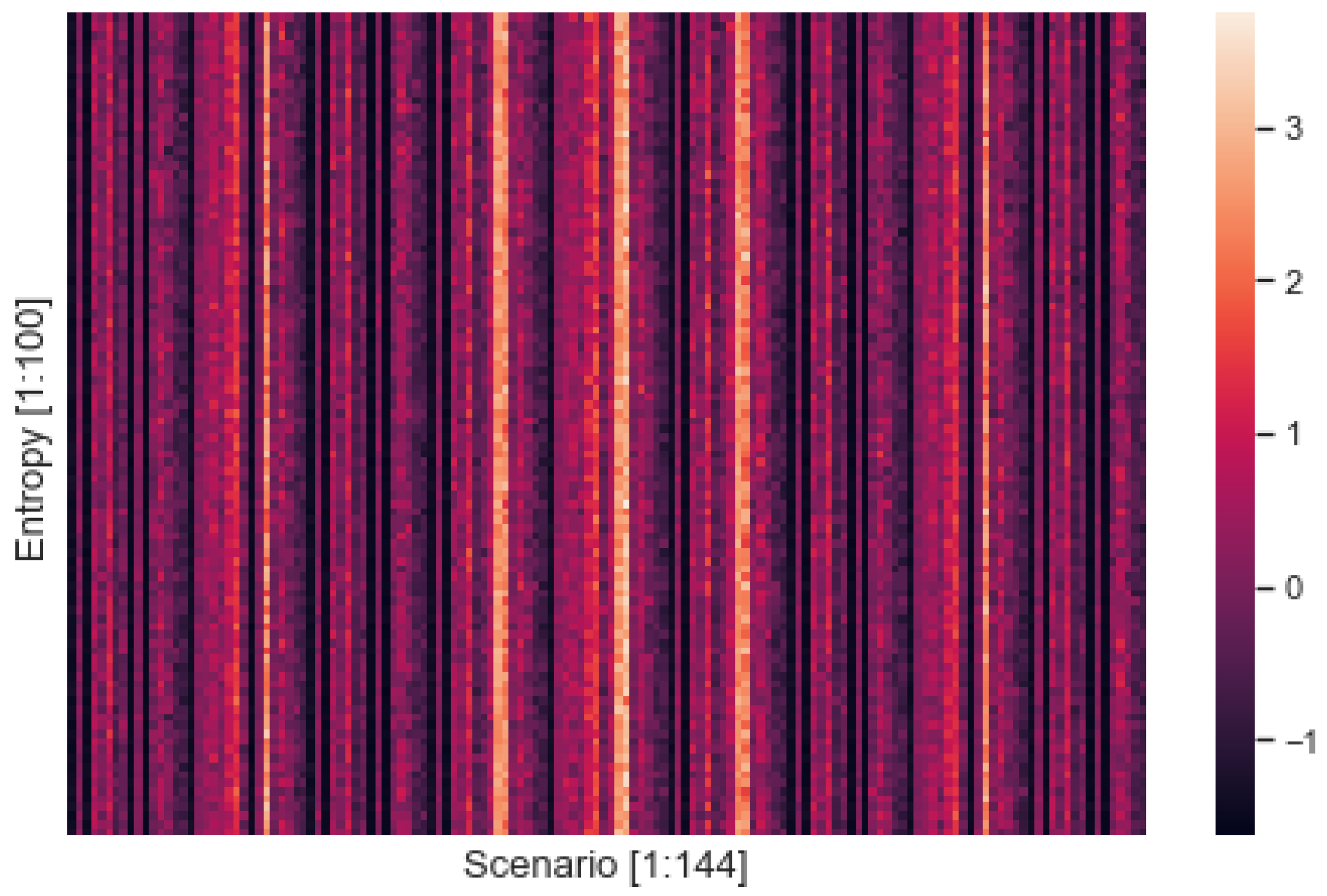
2.3.1. Entropy
2.3.2. Interference
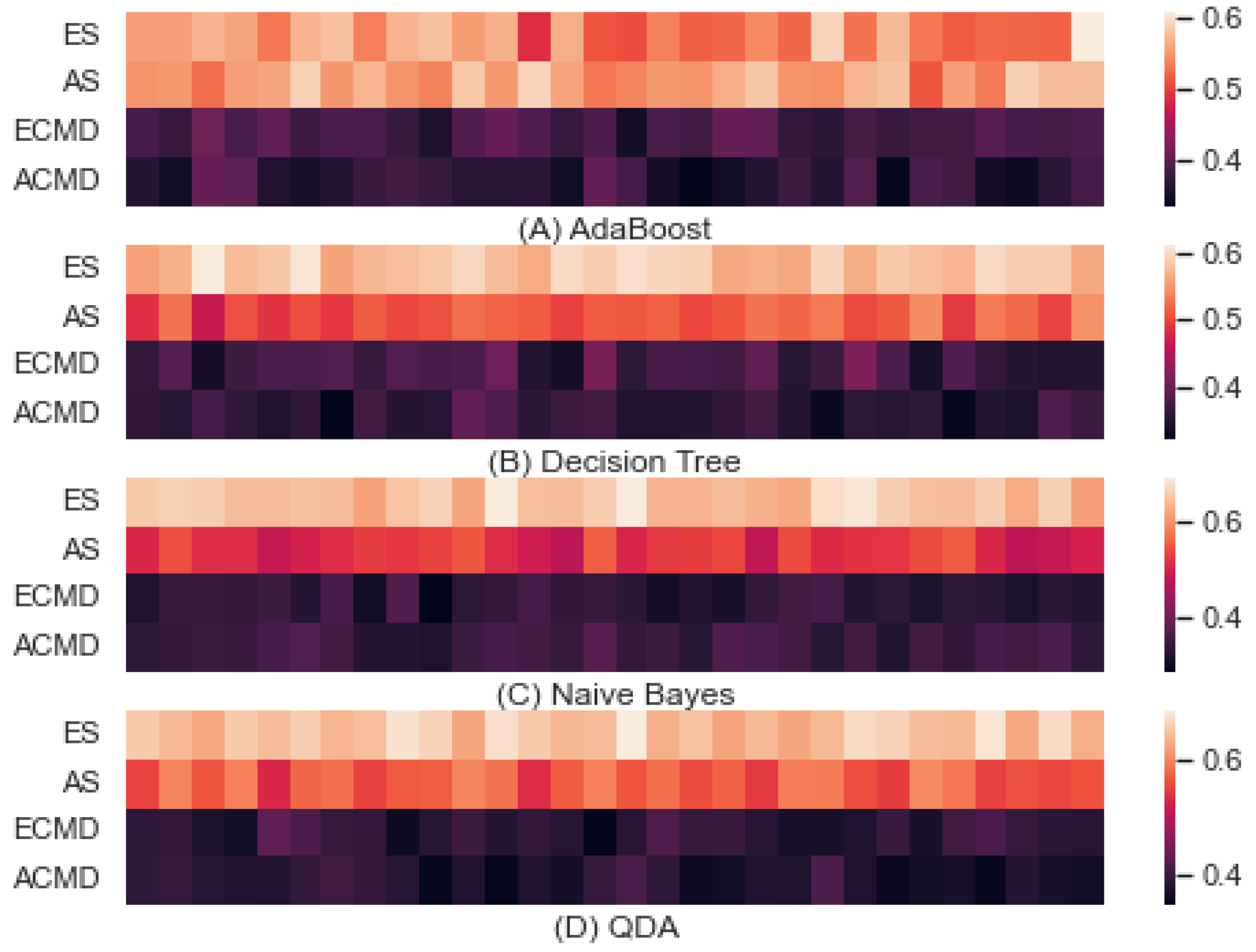
- ACMD is an ally side cognitive style of commander
- ECMD is an enemy side cognitive style of commander
- AS is an ally side combat strategy
- ES is an enemy side combat strategy
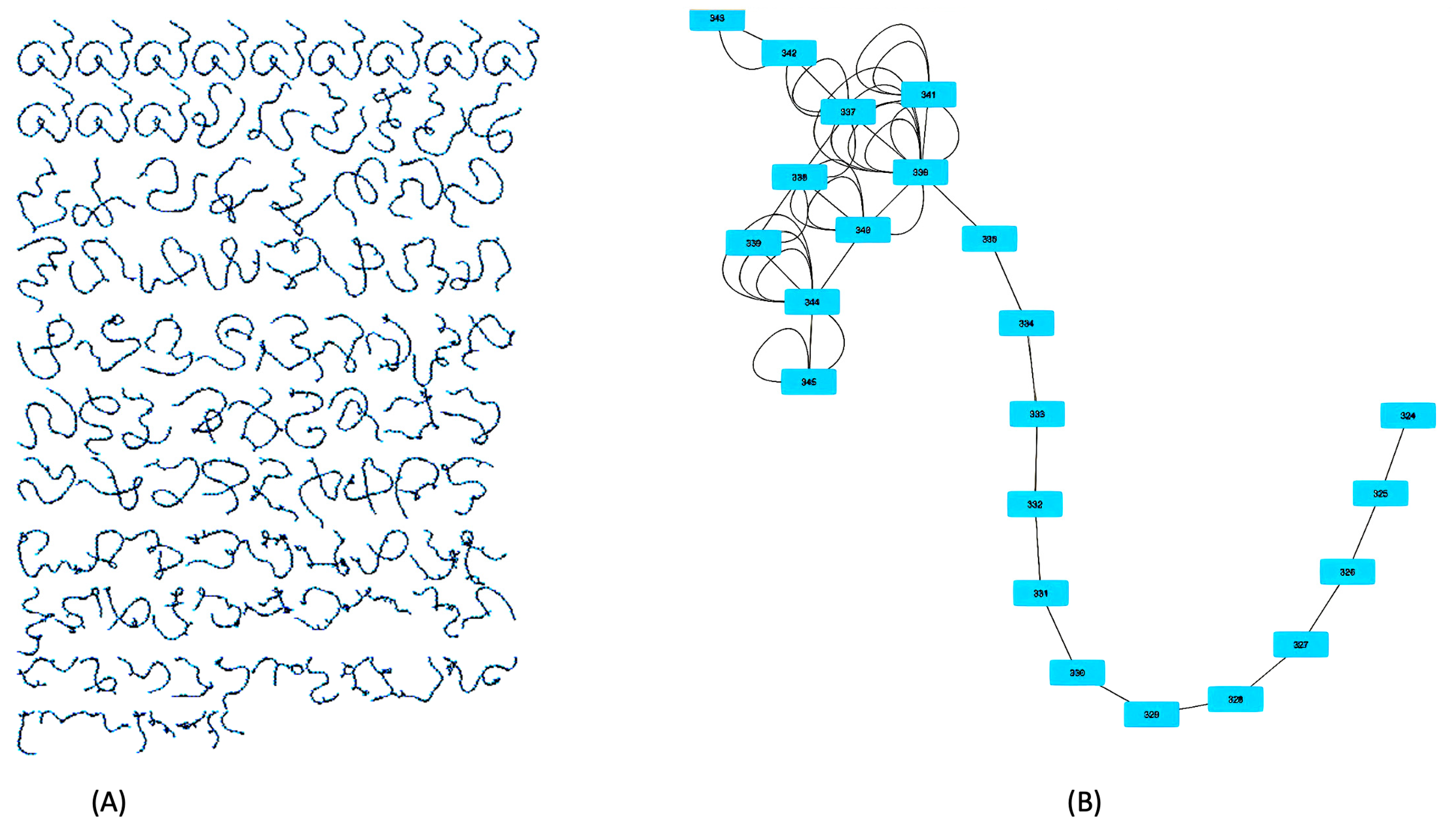
2.4. Drone Swarm Simulation
3. Results
3.1. Performance
3.2. Entropy
3.3. Interference
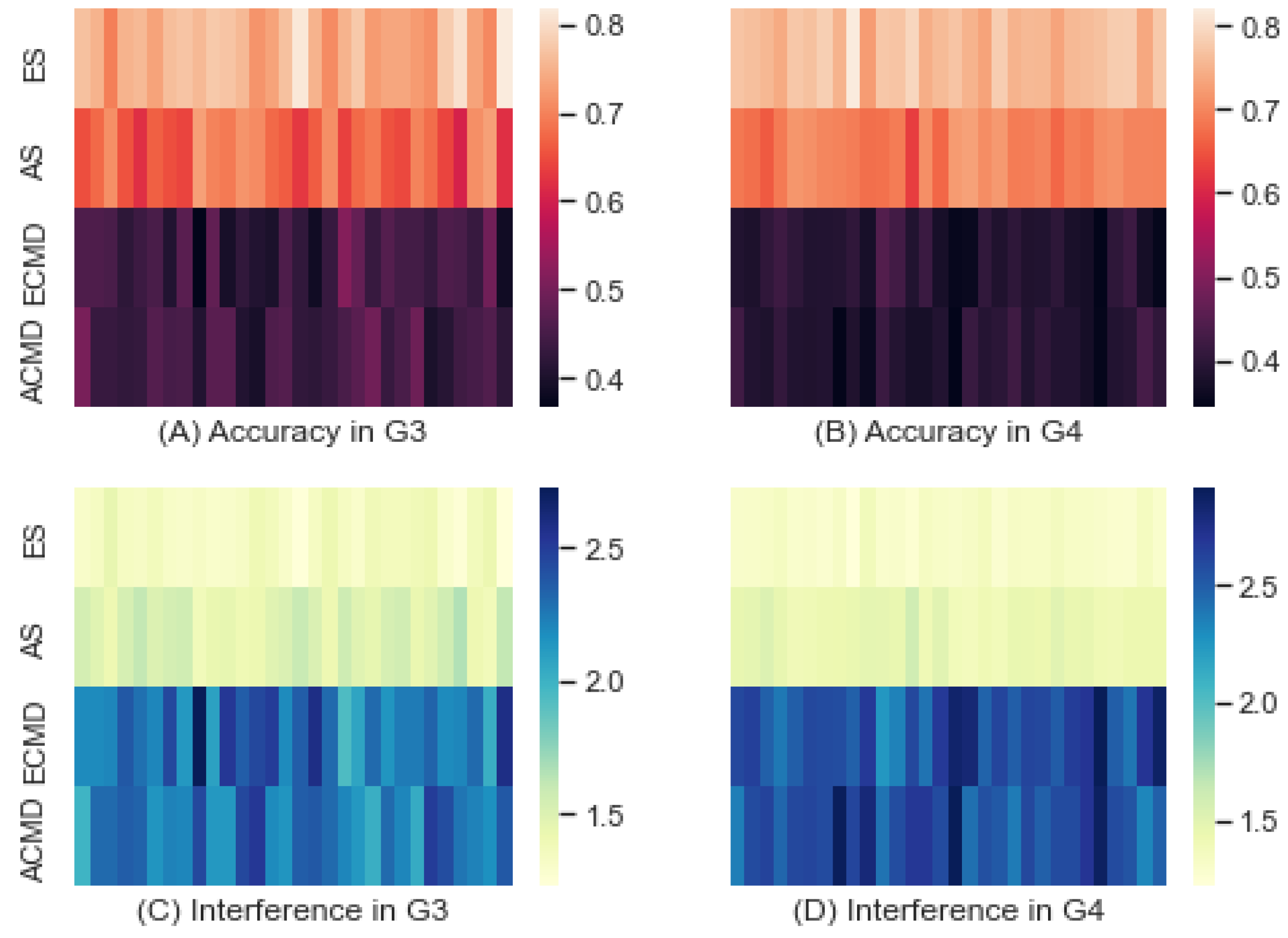
3.3.1. Variations by Learning Method
Machine Learning
Deep Learning
3.3.2. From Predictive Accuracy to Interference
3.4. Homogeneity vs. Interference
3.4.1. Homogeneity in Combat Strategy
3.4.2. Homogeneity in Command Style
3.5. Scenarios by Homogeneity
3.5.1. Performance
3.5.2. Entropy
3.5.3. Interference
3.6. Correlation Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhao, J.; Sun, J.; Cai, Z.; Wang, Y.; Wu, K. Distributed Coordinated Control Scheme of UAV Swarm Based on Heterogeneous Roles. Chin. J. Aeronaut. 2022, 35, 81–97. [Google Scholar] [CrossRef]
- Floreano, D.; Wood, R.J. Science, Technology and the Future of Small Autonomous Drones. Nature 2015, 521, 460–466. [Google Scholar] [CrossRef] [PubMed]
- Rahbari, D.; Mahtab Alam, M.; Le Moullec, Y.; Jenihhin, M. Edge-to-Fog Collaborative Computing in a Swarm of Drones. In Advances in Model and Data Engineering in the Digitalization Era; Bellatreche, L., Chernishev, G., Corral, A., Ouchani, S., Vain, J., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 78–87. [Google Scholar]
- Pyke, L.M.; Stark, C.R. Dynamic Pathfinding for a Swarm Intelligence Based UAV Control Model Using Particle Swarm Optimisation. Front. Appl. Math. Stat. 2021, 7, 744955. [Google Scholar] [CrossRef]
- Horvath, D.; Gazda, J.; Slapak, E.; Maksymyuk, T. Modeling and Analysis of Self-Organizing UAV-Assisted Mobile Networks with Dynamic On-Demand Deployment. Entropy 2019, 21, 1077. [Google Scholar] [CrossRef]
- Wen, X.; Wu, G. Heterogeneous Multi-Drone Routing Problem for Parcel Delivery. Transp. Res. Part C Emerg. Technol. 2022, 141, 103763. [Google Scholar] [CrossRef]
- Walker, O.; Vanegas, F.; Gonzalez, F. A Framework for Multi-Agent UAV Exploration and Target-Finding in GPS-Denied and Partially Observable Environments. Sensors 2020, 20, 4739. [Google Scholar] [CrossRef]
- Sukhbaatar, S.; Szlam, A.; Fergus, R. Learning Multiagent Communication with Backpropagation. arXiv 2016, arXiv:1605.07736. [Google Scholar] [CrossRef]
- Yu, F.; Santos, E. On Modeling the Interplay Between Opinion Change and Formation. In Proceedings of the Twenty-Ninth International Florida Artificial Intelligence Research Society Conference, FLAIRS 2016, Key Largo, FL, USA, 16–18 May 2016; Markov, Z., Russell, I., Eds.; AAAI Press: California, CA, USA, 2016; pp. 140–145. [Google Scholar]
- Alagoz, O.; Hsu, H.; Schaefer, A.J.; Roberts, M.S. Markov Decision Processes: A Tool for Sequential Decision Making under Uncertainty. Med. Decis. Making 2010, 30, 474–483. [Google Scholar] [CrossRef]
- Santos, E.; Nguyen, H.; Kim, K.J.; Hyde, G.; Nyanhongo, C. Validation of Double Transition Model by Analyzing Reward Distributions. In Proceedings of the 2020 IEEE/WIC/ACM International Joint Conference on Web Intelligence and Intelligent Agent Technology (WI-IAT), Melbourne, Australia, 14–17 December 2020; pp. 586–591. [Google Scholar] [CrossRef]
- Lawless, W.F.; Mittu, R.; Sofge, D.A.; Shortell, T.; McDermott, T.A. (Eds.) Systems Engineering and Artificial Intelligence; Springer International Publishing: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]
- Namdari, A.; Li, Z. (Steven). A Review of Entropy Measures for Uncertainty Quantification of Stochastic Processes. Adv. Mech. Eng. 2019, 11, 168781401985735. [Google Scholar] [CrossRef]
- Kim, N.V.; Mikhailov, N.A. Drone Searches for Objects on the Ground: An Entropy-Based Approach. Russ. Eng. Res. 2020, 40, 164–167. [Google Scholar] [CrossRef]
- Cofta, P.; Ledziński, D.; Śmigiel, S.; Gackowska, M. Cross-Entropy as a Metric for the Robustness of Drone Swarms. Entropy 2020, 22, 597. [Google Scholar] [CrossRef] [PubMed]
- Chinthi-Reddy, S.R.; Lim, S.; Choi, G.S.; Chae, J.; Pu, C. DarkSky: Privacy-Preserving Target Tracking Strategies Using a Flying Drone. Veh. Commun. 2022, 35, 100459. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Tate, J.; Ward, G. Interferences in Immunoassay. Clin. Biochem. Rev. 2004, 25, 105–120. [Google Scholar]
- Candell, R.; Montgomery, K.; Kashef, M.; Liu, Y.; Foufou, S. Wireless Interference Estimation Using Machine Learning in a Robotic Force-Seeking Scenario. In Proceedings of the 2019 IEEE 28th International Symposium on Industrial Electronics (ISIE), Vancouver, BC, Canada, 12–14 June 2019; pp. 1334–1341. [Google Scholar] [CrossRef]
- Kumar, A.; Augusto de Jesus Pacheco, D.; Kaushik, K.; Rodrigues, J.J.P.C. Futuristic View of the Internet of Quantum Drones: Review, Challenges and Research Agenda. Veh. Commun. 2022, 36, 100487. [Google Scholar] [CrossRef]
- Li, X.; Kim, J.H. Managing Disruptive Technologies: Exploring the Patterns of Local Drone Policy Adoption in California. Cities 2022, 126, 103736. [Google Scholar] [CrossRef]
- Uddin, Z.; Altaf, M.; Bilal, M.; Nkenyereye, L.; Bashir, A.K. Amateur Drones Detection: A Machine Learning Approach Utilizing the Acoustic Signals in the Presence of Strong Interference. Comput. Commun. 2020, 154, 236–245. [Google Scholar] [CrossRef]
- Lin, S.; Cheng, R.; Wright, F.A. Genetic Crossover Interference in the Human Genome. Ann. Hum. Genet. 2001, 65, 79–93. [Google Scholar] [CrossRef] [Green Version]
- Dou, L.-Y.; Cao, D.-Z.; Xu, D.-Q.; Zhang, A.-N.; Song, X.-B. Observation of Positive–Negative Sub-Wavelength Interference without Intensity Correlation Calculation. Sci. Rep. 2021, 11, 2477. [Google Scholar] [CrossRef]
- Ran, M.; Chen, J. An Information Dissemination Model Based on Positive and Negative Interference in Social Networks. Phys. Stat. Mech. Its Appl. 2021, 572, 125915. [Google Scholar] [CrossRef]
- Ng, A.Y.; Russell, S. Algorithms for Inverse Reinforcement Learning. In Proceedings of the 17th International Conference on Machine Learning, San Francisco, CA, USA, 29 June–2 July 2000; Morgan Kaufmann: San Francisco, CA, USA, 2000; pp. 663–670. [Google Scholar]
- Arora, S.; Doshi, P. A Survey of Inverse Reinforcement Learning: Challenges, Methods and Progress. Artif. Intell. 2021, 297, 103500. [Google Scholar] [CrossRef]
- Koul, A. Ma-Gym: Collection of Multi-Agent Environments Based on OpenAI Gym. GitHub Repos. 2019. Available online: https://github.com/cjm715/mgym (accessed on 30 July 2022).
- Brockman, G.; Cheung, V.; Pettersson, L.; Schneider, J.; Schulman, J.; Tang, J.; Zaremba, W. OpenAI Gym. 2016. Available online: https://github.com/openai/gym (accessed on 30 July 2022).
- Breiman, L. [No Title Found]. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Chang, C.-C.; Lin, C.-J. LIBSVM: A Library for Support Vector Machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 1–27. [Google Scholar] [CrossRef]
- Zhang, L.; Tan, J.; Han, D.; Zhu, H. From Machine Learning to Deep Learning: Progress in Machine Intelligence for Rational Drug Discovery. Drug Discov. Today 2017, 22, 1680–1685. [Google Scholar] [CrossRef]
- Hastie, T.; Rosset, S.; Zhu, J.; Zou, H. Multi-Class AdaBoost. Stat. Interface 2009, 2, 349–360. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer series in statistics; Springer: New York, NY, USA, 2009. [Google Scholar]
- Zhang, H. The Optimality of Naive Bayes. In Proceedings of the 17th International Florida Artificial Intelligence Research Society Conference, Menlo Park, CA, USA, 12–14 May 2004; pp. 562–567. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference for Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Kumar, A.; Sarkar, S.; Pradhan, C. Malaria Disease Detection Using CNN Technique with SGD, RMSprop and ADAM Optimizers. In Deep Learning Techniques for Biomedical and Health Informatics; Dash, S., Acharya, B.R., Mittal, M., Abraham, A., Kelemen, A., Eds.; Studies in Big Data; Springer International Publishing: Cham, Switzerland, 2020; Volume 68, pp. 211–230. [Google Scholar] [CrossRef]
- Dozat, T. Incorporating Nesterov Momentum into Adam. In Proceedings of the 4th International Conference on Learning Representations, San Juan, Puerto Rico, 2–4 May 2016; pp. 1–4. [Google Scholar]
- McMahan, H.B.; Holt, G.; Sculley, D.; Young, M.; Ebner, D.; Grady, J.; Nie, L.; Phillips, T.; Davydov, E.; Golovin, D.; et al. Ad Click Prediction: A View from the Trenches. In Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Chicago, IL, USA, 11–14 August 2013; pp. 1222–1230. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-Learn: Machine Learning in Python. Mach. Learn. PYTHON 6. Available online: https://scikit-learn.org/stable/ (accessed on 30 July 2022).
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems. arXiv 2015, arXiv:1603.04467. [Google Scholar]
- Rizwan, M.; Nadeem, A.; Sindhu, M.A. Analyses of Classifier’s Performance Measures Used in Software Fault Prediction Studies. IEEE Access 2019, 7, 82764–82775. [Google Scholar] [CrossRef]




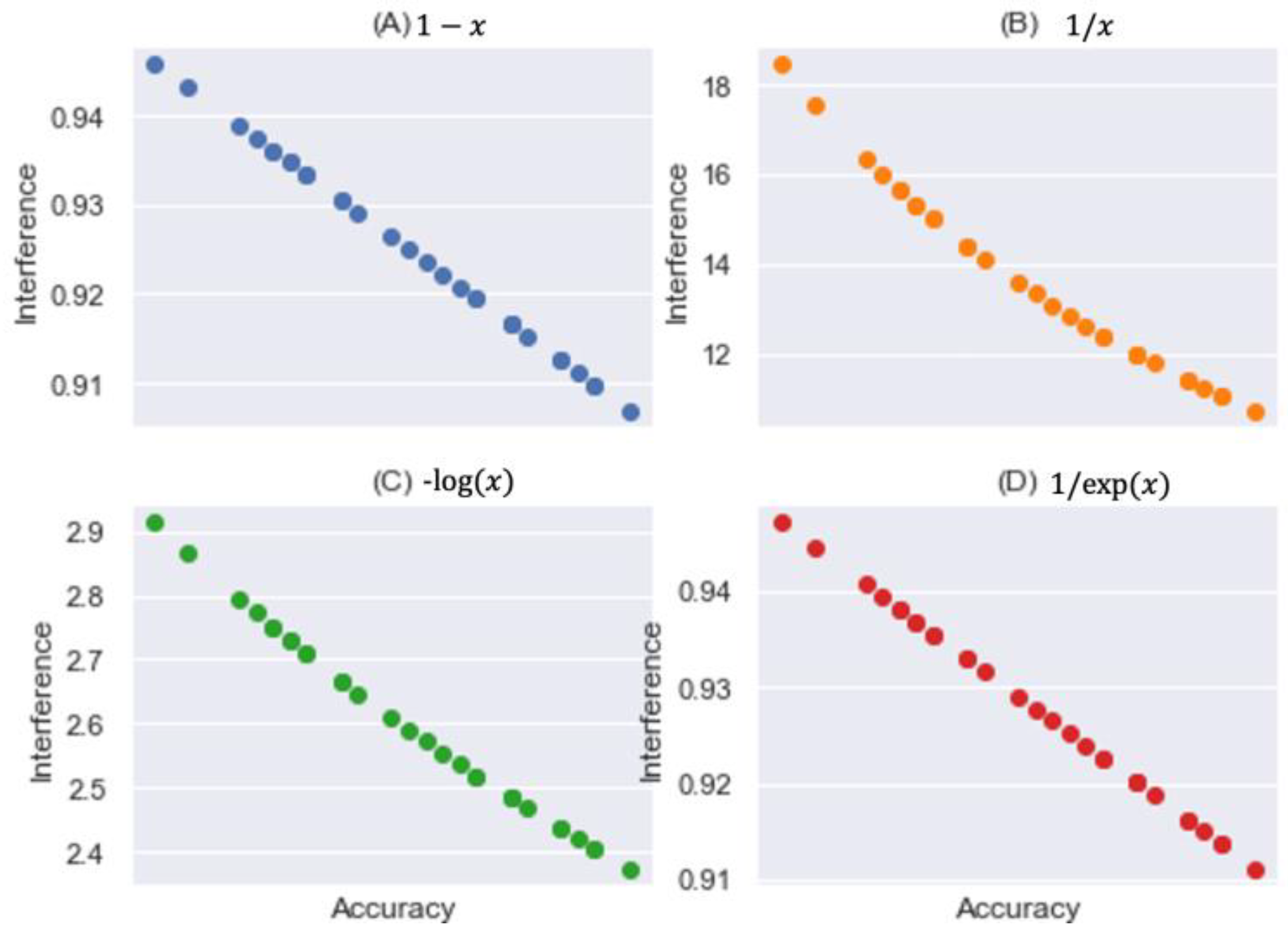




| Formula | Range | Mean | STD | |
|---|---|---|---|---|
| A | [0.907: 0.946] | 0.925 | 0.011 | |
| B | [10.746: 18.461] | 13.613 | 2.032 | |
| C | [2.375: 2.916] | 2.600 | 0.146 | |
| D | [0.911: 0.947] | 0.928 | 0.011 |
| H | Metric1 | Metric2 | Correlation | p-Value | # Positive | H | Metric1 | Metric2 | Correlation | p-Value | # Negative |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | PERF | ENTR | 0.236 | 0.702 | 5 | 1 | PERF | ENTR | 0.936 | 0.002 | 7 |
| 1 | PERF | INTF | 0.704 | 0.185 | 5 | 1 | PERF | INTF | −0.884 | 0.008 | 7 |
| 1 | ENTR | INTF | −0.407 | 0.496 | 5 | 1 | ENTR | INTF | −0.743 | 0.056 | 7 |
| 2 | PERF | ENTR | −0.113 | 0.726 | 12 | 2 | PERF | ENTR | 0.934 | <0.001 | 12 |
| 2 | PERF | INTF | 0.745 | 0.005 | 12 | 2 | PERF | INTF | −0.567 | 0.055 | 12 |
| 2 | ENTR | INTF | −0.144 | 0.655 | 12 | 2 | ENTR | INTF | −0.352 | 0.261 | 12 |
| 3 | PERF | ENTR | 0.439 | 0.068 | 18 | 3 | PERF | ENTR | 0.485 | 0.042 | 18 |
| 3 | PERF | INTF | 0.514 | 0.029 | 18 | 3 | PERF | INTF | −0.744 | <0.001 | 18 |
| 3 | ENTR | INTF | 0.195 | 0.439 | 18 | 3 | ENTR | INTF | −0.351 | 0.153 | 18 |
| 4 | PERF | ENTR | 0.402 | 0.011 | 39 | 4 | PERF | ENTR | 0.576 | <0.001 | 33 |
| 4 | PERF | INTF | 0.527 | 0.001 | 39 | 4 | PERF | INTF | −0.538 | 0.001 | 33 |
| 4 | ENTR | INTF | 0.213 | 0.194 | 39 | 4 | ENTR | INTF | −0.172 | 0.339 | 33 |
| Positive Correlations | Negative Correlations | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| H | st1 | St2 | Style1 | Style2 | H | St1 | St2 | Style1 | Style2 |
| 1 | BF | BF | SPONT | SPONT | 1 | CS | CS | INT: RATNL: SPONT | INT: RATNL: SPONT |
| 1 | FF | FF | INT: RATNL: SPONT | INT: RATNL: SPONT | 1 | BF | BF | INT: RATNL | INT: RATNL |
| 1 | AN | AN | RATNL | RATNL | 1 | AN | AN | INT: SPONT | INT: SPONT |
| 2 | CS | CS | INT: RATNL: SPONT | RATNL: SPONT | 2 | CS | CS | INT: RATNL: SPONT | SPONT: INT |
| 2 | BF | BF | RATNL | INT | 2 | BF | BF | INT: RATNL: SPONT | RATNL: SPONT: INT |
| 2 | FF | FF | INT: RATNL: SPONT | RATNL: SPONT: INT | 2 | AN | AN | INT: RATNL: SPONT | RATNL: SPONT: INT |
| 2 | AN | AN | RATNL: SPONT | INT: RATNL | 3 | CS | AN: BF | INT: SPONT | INT: SPONT |
| 3 | CS | BF: FF: AN | INT: RATNL: SPONT | INT: RATNL: SPONT | 3 | BF | CS: FF: AN | INT: RATNL: SPONT | INT: RATNL: SPONT |
| 3 | BF | FF | RATNL | RATNL | 3 | FF | AN: CS: BF | INT: RATNL: SPONT | INT: RATNL: SPONT |
| 3 | FF | CS: BF: AN | INT: SPONT | INT: SPONT | 3 | AN | FF: BF | INT: RATNL | INT: RATNL |
| 3 | AN | CS: BF: FF | INT: RATNL: SPONT | INT: RATNL: SPONT | 4 | CS | AN | RATNL | RATNL |
| 4 | CS | BF: FF: AN | INT: RATNL: SPONT | RATNL: SPONT: INT | 4 | BF | CS: AN: FF | INT: RATNL: SPONT | RATNL: SPONT: INT |
| 4 | BF | FF: AN: CS | INT: RATNL: SPONT | RATNL: INT: SPONT | 4 | FF | AN: CS: BF | INT: RATNL: SPONT | SPONT: INT: RATNL |
| 4 | FF | CS: BF: AN | INT: SPONT | RATNL: SPONT: INT | 4 | AN | CS: BF: FF | INT: RATNL: SPONT | SPONT: INT: RATNL |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, K.J.; Santos, E., Jr.; Nguyen, H.; Pieper, S. An Application of Inverse Reinforcement Learning to Estimate Interference in Drone Swarms. Entropy 2022, 24, 1364. https://doi.org/10.3390/e24101364
Kim KJ, Santos E Jr., Nguyen H, Pieper S. An Application of Inverse Reinforcement Learning to Estimate Interference in Drone Swarms. Entropy. 2022; 24(10):1364. https://doi.org/10.3390/e24101364
Chicago/Turabian StyleKim, Keum Joo, Eugene Santos, Jr., Hien Nguyen, and Shawn Pieper. 2022. "An Application of Inverse Reinforcement Learning to Estimate Interference in Drone Swarms" Entropy 24, no. 10: 1364. https://doi.org/10.3390/e24101364
APA StyleKim, K. J., Santos, E., Jr., Nguyen, H., & Pieper, S. (2022). An Application of Inverse Reinforcement Learning to Estimate Interference in Drone Swarms. Entropy, 24(10), 1364. https://doi.org/10.3390/e24101364







