Fuzzy Reasoning Numerical Spiking Neural P Systems for Induction Motor Fault Diagnosis
Abstract
:1. Introduction
- The NSN P system, as a combination of the SNP system and the NP system, is applied to motor fault diagnosis for the first time. In order to prove its ability to deal with induction motor fault diagnosis, the NSN P system is used to solve the SAT problem first. The results show that the NSN P system can successfully solve the SAT problem in six steps;
- The IVTFNs are applied to the NSN P system, and the FRNSN P system is proposed to deal with the incompleteness and uncertainty of motor fault information. The FRNSN P system can successfully model the fault fuzzy production rules of induction motors;
- A FRNSN P reasoning algorithm is designed by using the operating mechanism of FRNSN P systems, making the motor fault diagnosis intelligent;
- The relative preference relationship is used to estimate the severity of multiple faults when they occur, so as to diagnose the faults in a timely manner and to prevent the deterioration of the faults.
2. Preliminaries
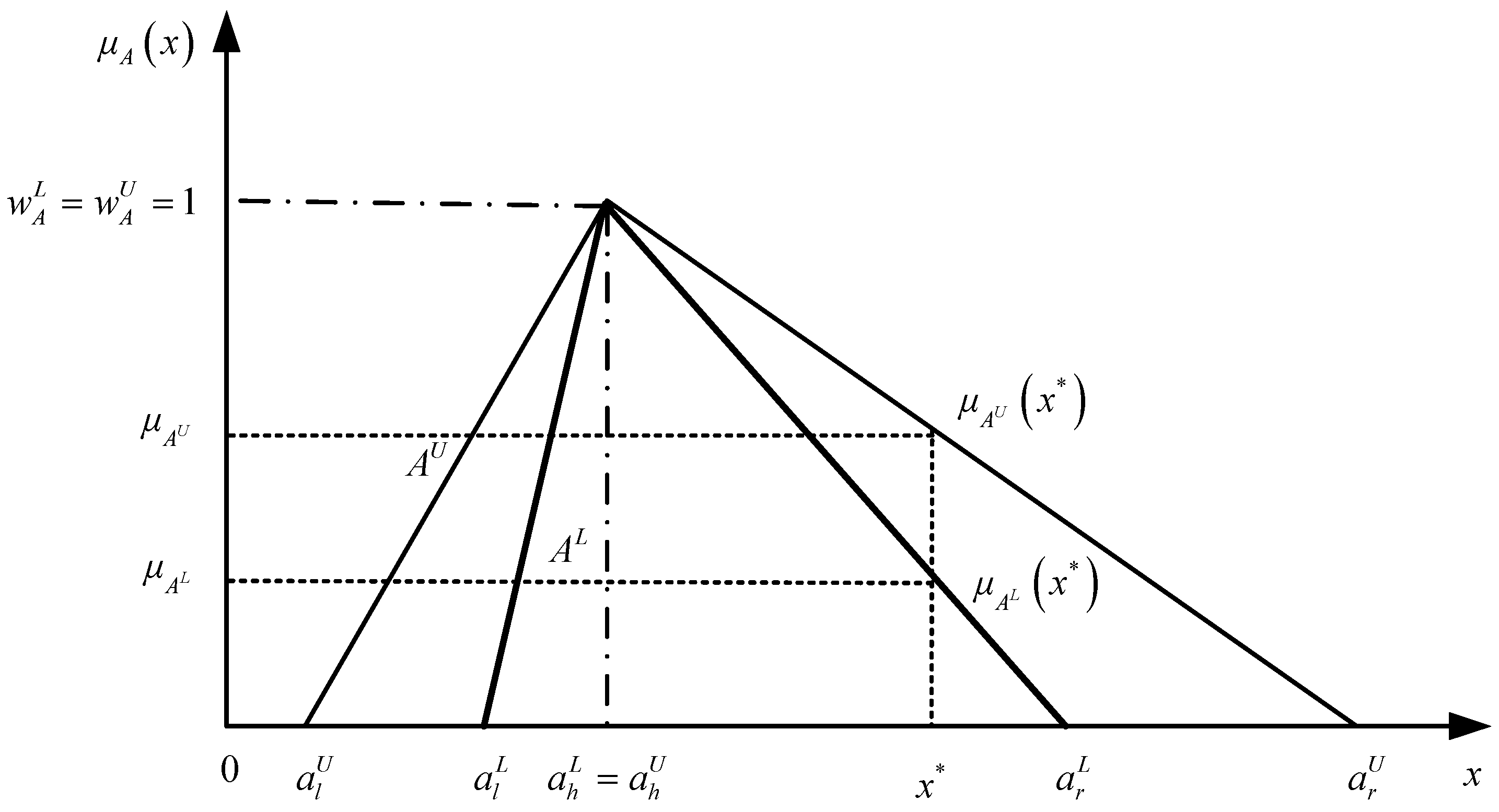
2.1. The Interval-Valued Triangular Fuzzy Number
2.2. The Relative Preference Relation
3. The NSN P System and Its Extension to the FRNSN P System
3.1. The NSN P System
- (1)
- represent l neurons with the form , for , where
- (a)
- is the threshold of neuron ;
- (b)
- is a set of variables in neuron , where hk is the number of variables in ;
- (c)
- refers to the set of initial values of the variables in the set ;
- (d)
- is a set of programs, where is called a production function in neuron , where is the number of programs in .
- (2)
- is the set of synapses.
- (3)
- and correspond to the input neuron and the output neuron , respectively.
3.2. An Application to the SAT Problem
- 2
- if , but and do not appear in ,
- 3
- if , but and do not appear in ,
- 3
- if , but appears and does not appear in ,
- 4
- if , but appears and does not appear in ,
- 4
- if , but appears and does not appear in ,
- 5
- if , but appears and does not appear in .
3.3. Definition of the FRNSN P System
- (1)
- (a)
- is the firing threshold of neuron , for ;
- (b)
- indicates the confidence factor of neuron , for .
- (c)
- is the variable of neuron , for ;
- (d)
- is the initial fuzzy value of variable , for .
- (e)
- , is a set of programs, where is called the production function, for .
- (2)
- with is the set of synapses.
- (3)
- and correspond to the input neuron and the output neuron , respectively.
- (1)
- : , where ;
- (2)
- : , where ;
- (3)
- If , then .
4. The FRNSN P Reasoning Algorithm
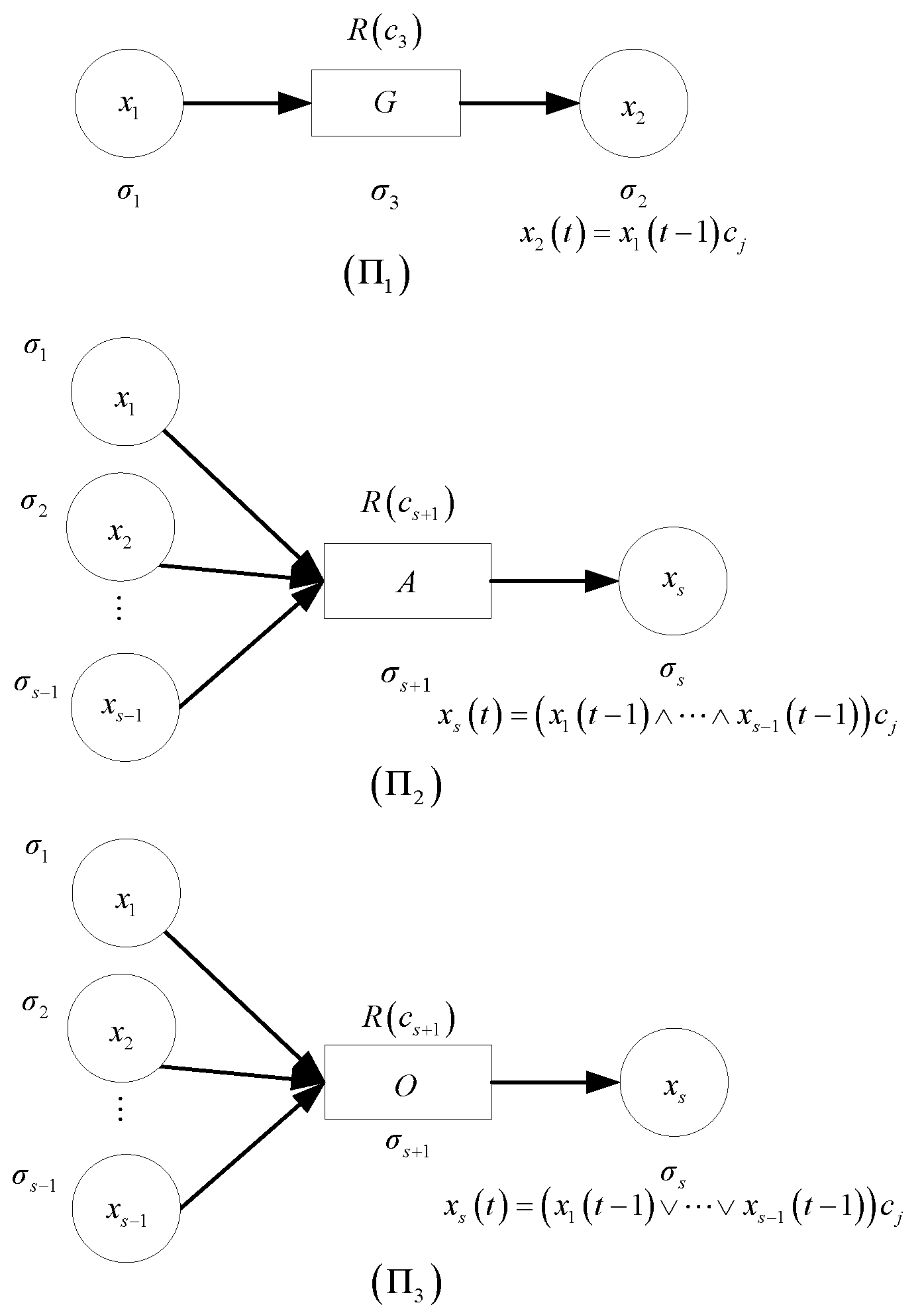
4.1. Modeling and Fuzzy Reasoning
- General rule: IF , THEN ;
- And rule: IF AND AND AND , THEN ;
- Or rule: IF OR OR OR , THEN ;
- (1)
- is a proposition neuron representing fuzzy propositions for ;
- (2)
- is a G-rule neuron;
- (3)
- is the set of synapses;
- (4)
- and are the input and output proposition neurons.
- (1)
- is a proposition neuron representing fuzzy proposition for ;
- (2)
- is an A-rule neuron;
- (3)
- is the set of synapses;
- (4)
- and are the set of input neurons and the output neuron.
- (1)
- is a proposition neuron representing fuzzy proposition for ;
- (2)
- is the O-rule neuron;
- (3)
- is the set of synapses;
- (4)
- and are the set of input neurons and the output neuron.
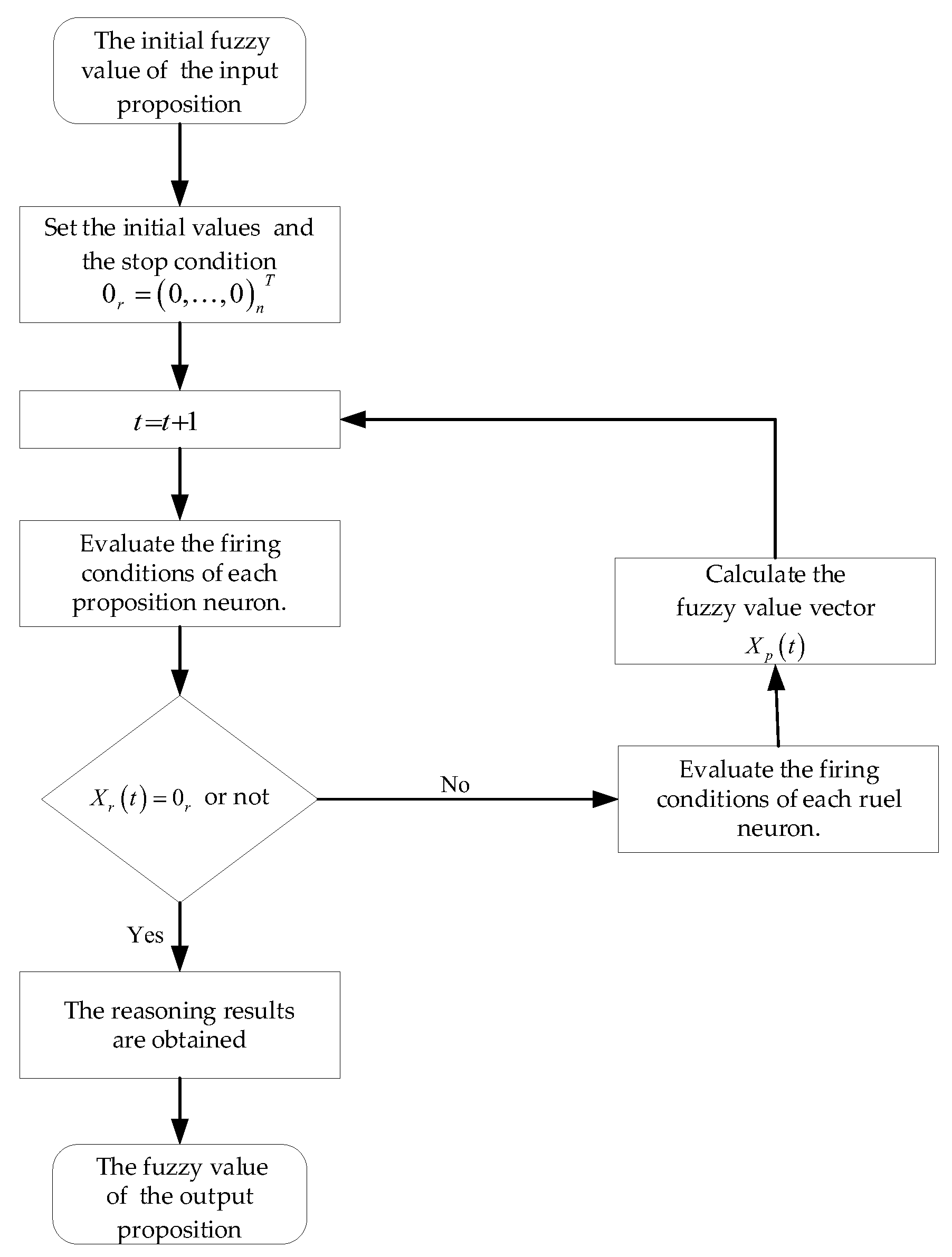
4.2. The FRNSN P Reasoning Algorithm
- (1)
- is a vector consisting of the fuzzy values of the variables contained in the proposition neurons, where is an NIVTFN, for ;
- (2)
- is a vector consisting of the fuzzy values of the variables contained in the rule neurons, where is an NIVTFN, for ;
- (3)
- is a vector consisting of the firing thresholds of the neurons, where is an NIVTFN, for ;
- (4)
- is a diagonal matrix consisting of the confidence factors of the rule neurons, where , for , is the confidence factor of neuron , an NIVTFN, representing the credibility of the fuzzy production rule ;
- (5)
- is a matrix representing the synaptic connections from proposition neurons to neurons, such that if a synapse exists from proposition neuron to neuron , and otherwise, for and ;
- (6)
- is a matrix representing the synaptic connections from proposition neurons to neurons, such that if a synapse exists from proposition neuron to neuron , and otherwise, for and ;
- (7)
- is a matrix representing the synaptic connections from proposition neurons to neurons such that if a synapse exists from proposition neuron to neuron , and otherwise, for and ;
- (8)
- is a matrix representing the synaptic connections from rule neurons to proposition neurons such that if a synapse exists from rule neuron to proposition neuron , and otherwise, for and ;
- (9)
- is a vector consisting of the values passed by proposition neuron to the postsynaptic rule neuron variable. If neuron does not have a postsynaptic neuron, then this value is passed to the environment as the output value. In particular, , for ;
- (10)
- is a vector consisting of the values passed by rule neuron to the postsynaptic proposition neuron variable. In particular, for .
- (1)
- . Similarly, , where , for ;
- (2)
- , where , for ;
- (3)
- , where , for .
| Algorithm 1: The FRNSN P reasoning algorithm |
| Input: , , , , , , , |
|
| Output: The fuzzy values of the output proposition neurons. |
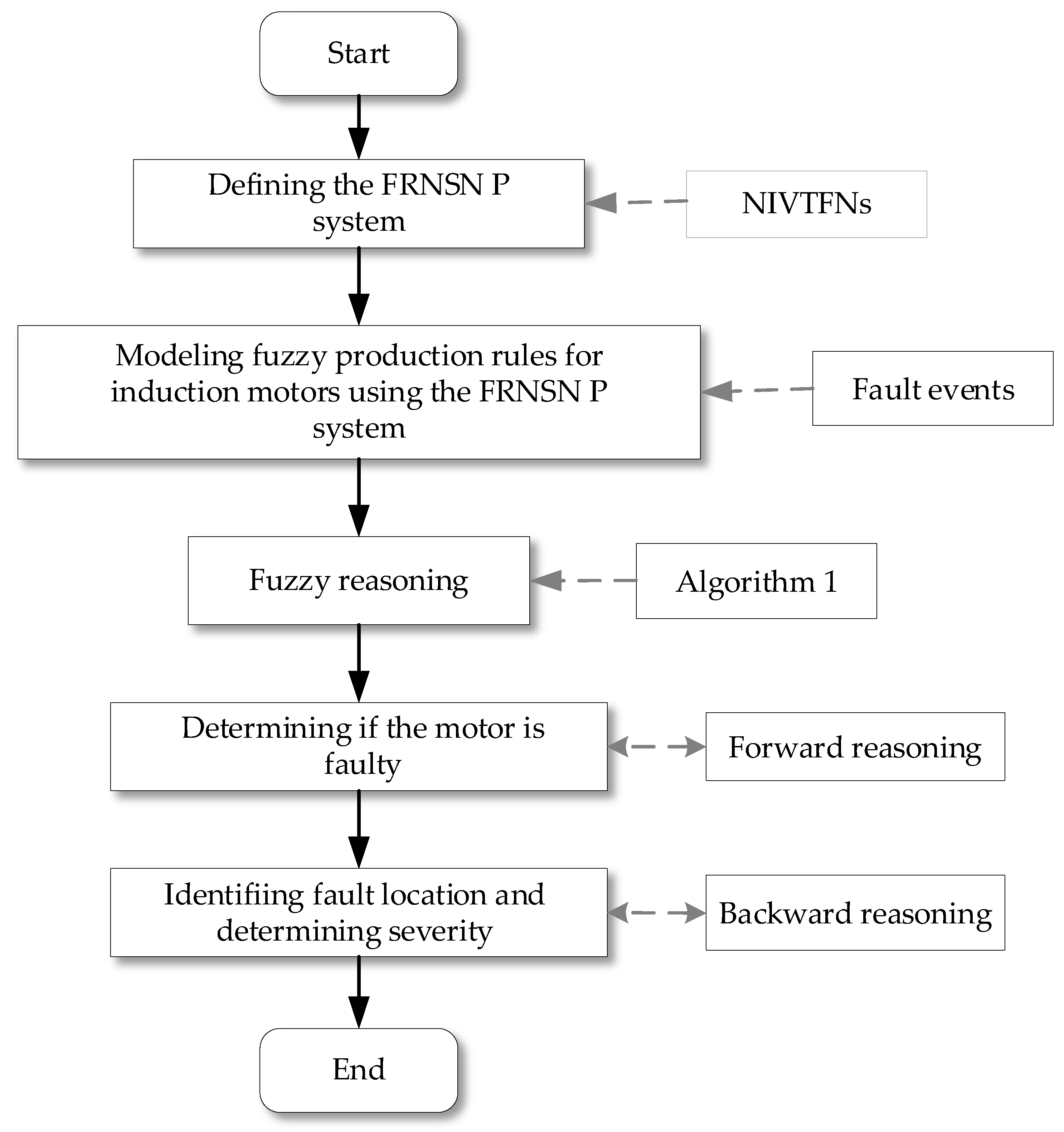
5. Fault Diagnosis of Induction Motors Using the FRNSN P Reasoning Algorithm
5.1. Fuzzy Production Rules for Induction Motors
5.2. Parameter Settings
5.3. Case Studies
5.3.1. Forward Reasoning
5.3.2. Backward Reasoning
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, X.; Wang, T.; Ying, R.; Cao, Z. A Fault Diagnosis Method Considering Meteorological Factors for Transmission Networks Based on P Systems. Entropy 2021, 23, 1008. [Google Scholar] [CrossRef]
- Li, X.; Zhang, W.; Ding, Q.; Sun, J.-Q. Intelligent rotating machinery fault diagnosis based on deep learning using data augmentation. J. Intell. Manuf. 2018, 31, 433–452. [Google Scholar] [CrossRef]
- Xiong, G.; Shi, D.; Zhu, L.; Duan, X. A New Approach to Fault Diagnosis of Power Systems Using Fuzzy Reasoning Spiking Neural P Systems. Math. Probl. Eng. 2013, 2013, 815352. [Google Scholar] [CrossRef]
- Wang, T.; Liu, W.; Zhao, J.; Guo, X.; Terzija, V. A rough set-based bio-inspired fault diagnosis method for electrical substations. Int. J. Electr. Power Energy Syst. 2020, 119, 105961. [Google Scholar] [CrossRef]
- Zhao, J.; Hu, T.; Zheng, R.; Ba, P.; Mei, C.; Zhang, Q. Defect Recognition in Concrete Ultrasonic Detection Based on Wavelet Packet Transform and Stochastic Configuration Networks. IEEE Access 2021, 9, 9284–9295. [Google Scholar] [CrossRef]
- Kumar, P.; Hati, A.S. Dilated convolutional neural network based model for bearing faults and broken rotor bar detection in squirrel cage induction motors. Expert Syst. Appl. 2022, 191, 116290. [Google Scholar] [CrossRef]
- Shao, H.; Xia, M.; Han, G.; Zhang, Y.; Wan, J. Intelligent fault diagnosis of rotor-bearing system under varying working conditions with modified transfer CNN and thermal images. IEEE Trans. Ind. Inform. 2020, 17, 3488–3496. [Google Scholar] [CrossRef]
- Toma, R.N.; Piltan, F.; Kim, J.M. A deep autoencoder-based convolution neural network framework for bearing fault classification in induction motors. Sensors 2021, 21, 8453. [Google Scholar] [CrossRef]
- Defdaf, M.; Berrabah, F.; Chebabhi, A.; Cherif, B.D.E. A new transform discrete wavelet technique based on artificial neural network for induction motor broken rotor bar faults diagnosis. Int. Trans. Electr. Energy Syst. 2021, 31, e12807. [Google Scholar] [CrossRef]
- Ibrahim, M.; Saeed, T.; El-Shorbagy, M.A.; Nofal, T.A.; Aamir, N. Implementation of the artificial neural network to predict the effectiveness of the solar system using Cu/water-ethylene nanofluid to save energy. Eng. Anal. Bound. Elem. 2022, 138, 30–41. [Google Scholar] [CrossRef]
- Deng, W.; Zhang, S.; Zhao, H.; Yang, X. A Novel Fault Diagnosis Method Based on Integrating Empirical Wavelet Transform and Fuzzy Entropy for Motor Bearing. IEEE Access 2018, 6, 35042–35056. [Google Scholar] [CrossRef]
- Mejia-Barron, A.; Tapia-Tinoco, G.; Razo-Hernandez, J.R.; Valtierra-Rodriguez, M.; Granados-Lieberman, D. A neural network-based model for MCSA of inter-turn short-circuit faults in induction motors and its power hardware in the loop simulation. Comput. Electr. Eng. 2021, 93, 107234. [Google Scholar] [CrossRef]
- Zhou, N.; Wang, A. Fault diagnosis of transmission circuit based on triangular interval valued fuzzy spike neural network P system. Energy Rep. 2022, 8, 776–784. [Google Scholar] [CrossRef]
- Pang, S.C.; Wang, M.; Qiao, S.B.; Wang, X.; Chen, H.Q. Fault Diagnosis for Service Composition by Spiking Neural P Systems with Colored Spikes. Chin. J. Electron. 2019, 28, 1033–1040. [Google Scholar] [CrossRef]
- Peng, H.; Wang, J.; Ming, J.; Shi, P.; Perez-Jimenez, M.J.; Yu, W.P.; Tao, C.Y. Fault Diagnosis of Power Systems Using Intuitionistic Fuzzy Spiking Neural P Systems. IEEE Trans. Smart Grid 2018, 9, 4777–4784. [Google Scholar] [CrossRef]
- Peng, H.; Wang, J.; Perez-Jimenez, M.J.; Wang, H.; Shao, J.; Wang, T. Fuzzy reasoning spiking neural P system for fault diagnosis. Inf. Sci. 2013, 235, 106–116. [Google Scholar] [CrossRef]
- Sheng, N.; Zhang, D.; Zhang, Q. Fuzzy Command Filtered Backstepping Control for Nonlinear System with Nonlinear Faults. IEEE Access 2021, 9, 60409–60418. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, G.X.; Zhao, J.B.; He, Z.Y.; Wang, J.; Perez-Jimenez, M.J. Fault Diagnosis of Electric Power Systems Based on Fuzzy Reasoning Spiking Neural P Systems. IEEE Trans. Power Syst. 2015, 30, 1182–1194. [Google Scholar] [CrossRef]
- Huang, K.; Wang, T.; He, Y.; Zhang, G.; Pérez-Jiménez, M.J. Temporal Fuzzy Reasoning Spiking Neural P Systems with Real Numbers for Power System Fault Diagnosis. J. Comput. Theor. Nanosci. 2016, 13, 3804–3814. [Google Scholar] [CrossRef]
- Rong, H.; Yi, K.; Zhang, G.; Dong, J.; Paul, P.; Huang, Z. Automatic Implementation of Fuzzy Reasoning Spiking Neural P Systems for Diagnosing Faults in Complex Power Systems. Complexity 2019, 2019, 2635714. [Google Scholar] [CrossRef]
- Wang, T.; Wei, X.; Wang, J.; Huang, T.; Peng, H.; Song, X.; Cabrera, L.V.; Pérez-Jiménez, M.J. A weighted corrective fuzzy reasoning spiking neural P system for fault diagnosis in power systems with variable topologies. Eng. Appl. Artif. Intell. 2020, 92, 103680. [Google Scholar] [CrossRef]
- Ionescu, M.; Pǎun, G.; Yokomori, T. Spiking neural P systems. Fundam. Inform. 2006, 71, 279–308. [Google Scholar]
- Tang, X.; Zhang, Q.; Dai, X.; Zou, Y. Neural Membrane Mutual Coupling Characterisation Using Entropy-Based Iterative Learning Identification. IEEE Access 2020, 8, 205231–205243. [Google Scholar] [CrossRef]
- Ionescu, M.; Sburlan, D. Some Applications of Spiking Neural P Systems. Comput. Inform. 2008, 27, 515–528. [Google Scholar]
- Dong, J.; Zhang, G.; Luo, B.; Yang, Q.; Guo, D.; Rong, H.; Zhu, M.; Zhou, K. A distributed adaptive optimization spiking neural P system for approximately solving combinatorial optimization problems. Inf. Sci. 2022, 596, 1–14. [Google Scholar] [CrossRef]
- Song, T.; Pang, S.; Hao, S.; Rodríguez-Patón, A.; Zheng, P. A Parallel Image Skeletonizing Method Using Spiking Neural P Systems with Weights. Neural Process. Lett. 2018, 50, 1485–1502. [Google Scholar] [CrossRef]
- Gou, X.; Liu, Q.; Rong, H.; Hu, M.; Paul, P.; Zhang, X.; Yu, Z. A Novel Spiking Neural P System for Image Recognition. Int. J. Unconv. Comput. 2021, 16, 121–139. [Google Scholar]
- Ma, T.; Hao, S.; Wang, X.; Rodriguez-Paton, A.A.; Wang, S.; Song, T. Double Layers Self-Organized Spiking Neural P Systems with Anti-Spikes for Fingerprint Recognition. IEEE Access 2019, 7, 177562–177570. [Google Scholar] [CrossRef]
- Wang, T.; Wei, X.; Huang, T.; Wang, J.; Peng, H.; Perez-Jimenez, M.J.; Valencia-Cabrera, L. Modeling Fault Propagation Paths in Power Systems: A New Framework Based on Event SNP Systems with Neurotransmitter Concentration. IEEE Access 2019, 7, 12798–12808. [Google Scholar] [CrossRef]
- Wu, T.; Pan, L.; Yu, Q.; Tan, K.C. Numerical Spiking Neural P Systems. IEEE Trans. Neural Netw Learn. Syst. 2021, 32, 2443–2457. [Google Scholar] [CrossRef]
- Wang, Y.-J. Interval-valued fuzzy multi-criteria decision-making based on simple additive weighting and relative preference relation. Inf. Sci. 2019, 503, 319–335. [Google Scholar] [CrossRef]
- Wang, Y.-J. Combining technique for order preference by similarity to ideal solution with relative preference relation for interval-valued fuzzy multi-criteria decision-making. Soft Comput. 2019, 24, 11347–11364. [Google Scholar] [CrossRef]
- Yin, X.; Liu, X.; Sun, M.; Ren, Q. Novel Numerical Spiking Neural P Systems with a Variable Consumption Strategy. Processes 2021, 9, 549. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, X.; Wang, W. Spiking Neural P Systems with Neuron Division and Dissolution. PLoS ONE 2016, 11, e0162882. [Google Scholar] [CrossRef]
- Wang, J.; Hoogeboom, H.J.; Pan, L.; Paun, G.; Perez-Jimenez, M.J. Spiking neural P systems with weights. Neural Comput. 2010, 22, 2615–2646. [Google Scholar] [CrossRef]
- Pan, L.; Pǎun, G.; Pérez-Jiménez, M.J. Spiking neural P systems with neuron division and budding. Sci. China Inf. Sci. 2011, 54, 1596–1607. [Google Scholar] [CrossRef]
- Cheng, X.; Wang, C.; Yu, Y.; Yi, L.; Chen, Q. An approach for three-phase asynchronous motor failure analysis based on fuzzy fault petri net. Trans. China Electrotech. Soc. 2015, 30, 132–139. [Google Scholar] [CrossRef]
- Cheng, X.; Wang, C.; Li, J.; Bai, X. Adaptive fault diagnosis of motors using comprehensive learning particle swarm optimizer with fuzzy petri net. Comput. Inform. 2020, 39, 246–263. [Google Scholar] [CrossRef]
- Yang, B.-S.; Jeong, S.K.; Oh, Y.-M.; Tan, A.C.C. Case-based reasoning system with Petri nets for induction motor fault diagnosis. Expert Syst. Appl. 2004, 27, 301–311. [Google Scholar] [CrossRef]
- Huang, Z.; Wang, T.; Liu, W.; Valencia-Cabrera, L.; Pérez-Jiménez, M.J.; Li, P.; Geem, Z.W. A Fault Analysis Method for Three-Phase Induction Motors Based on Spiking Neural P Systems. Complexity 2021, 2021, 2087027. [Google Scholar] [CrossRef]
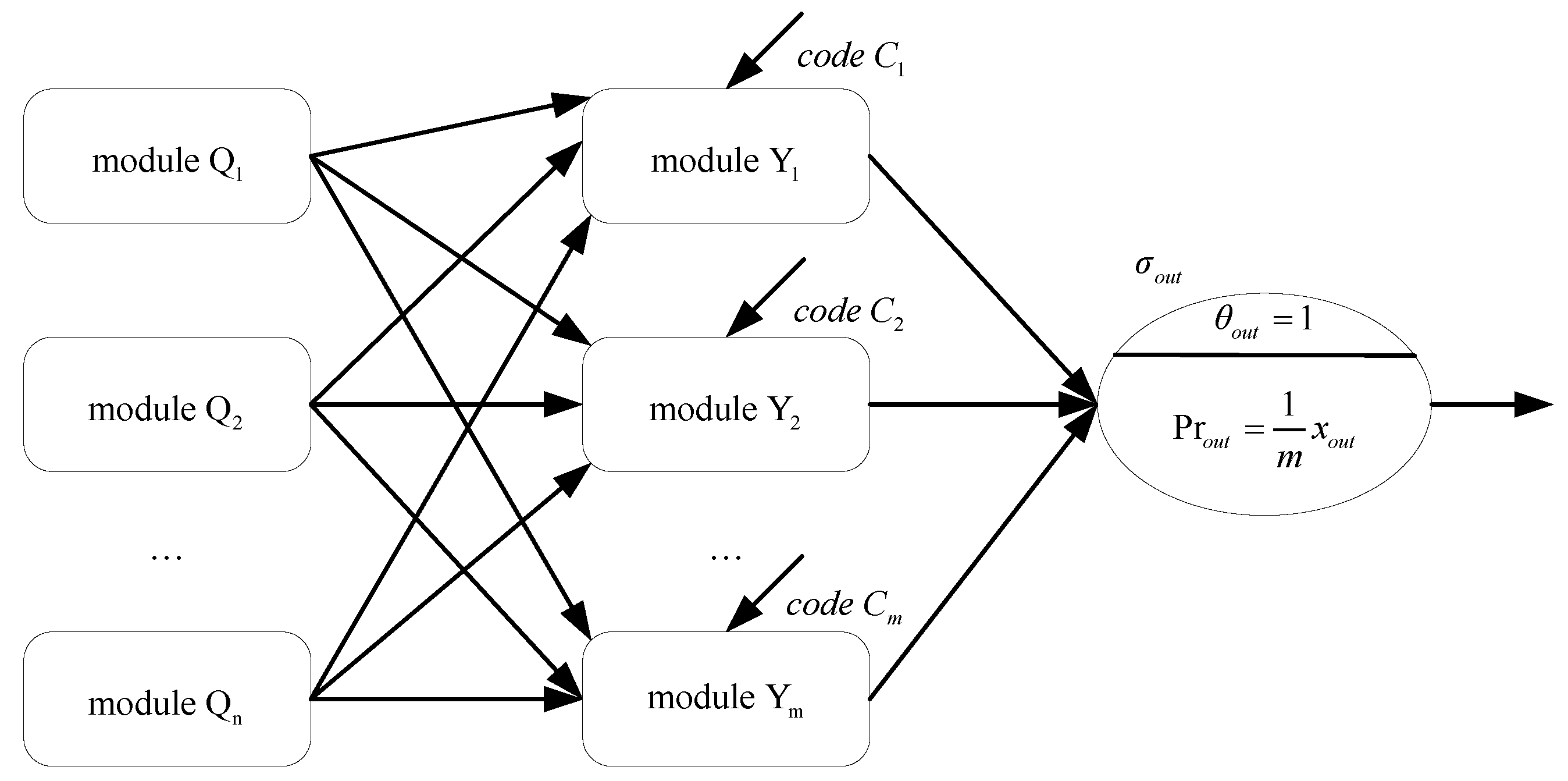

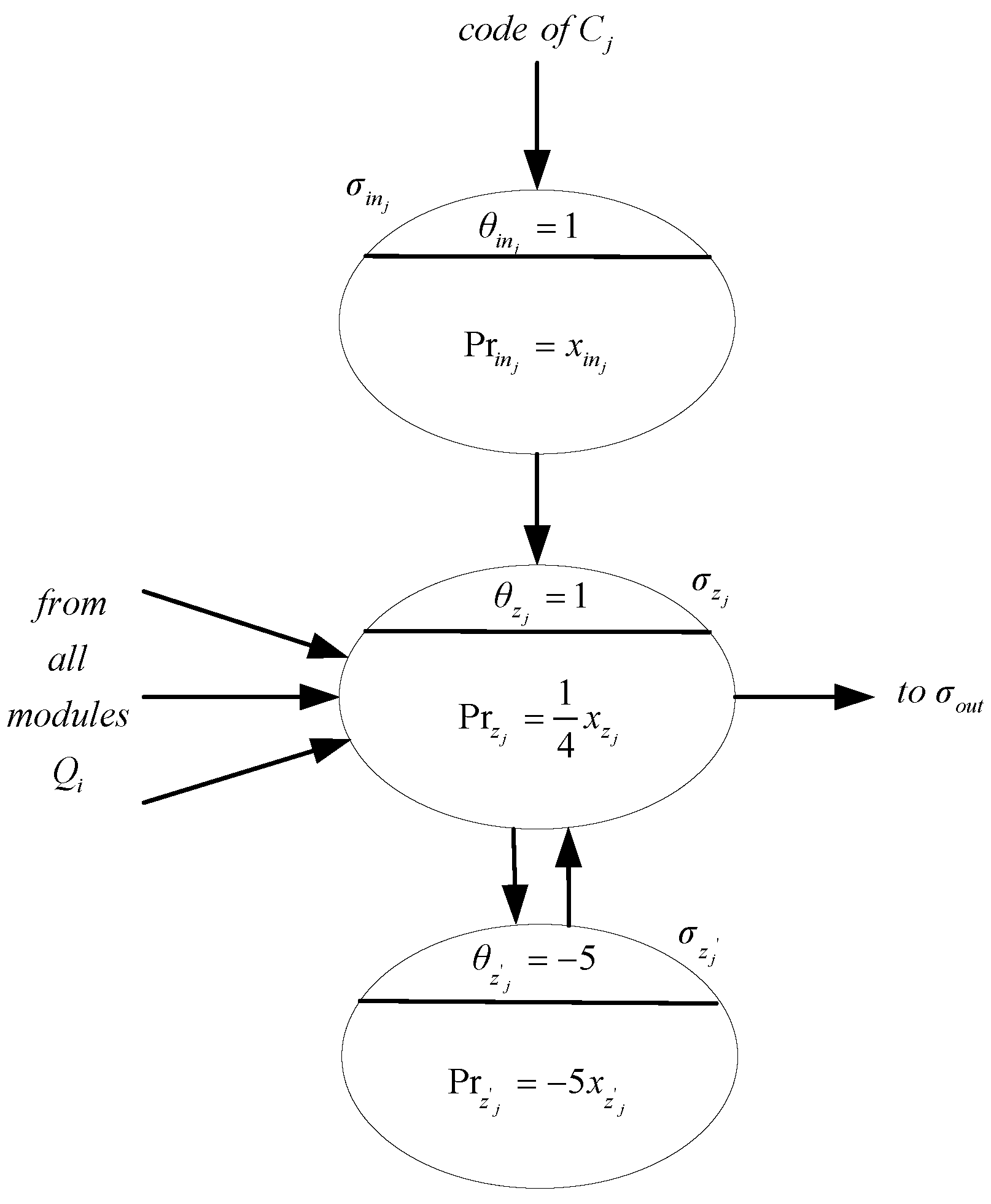
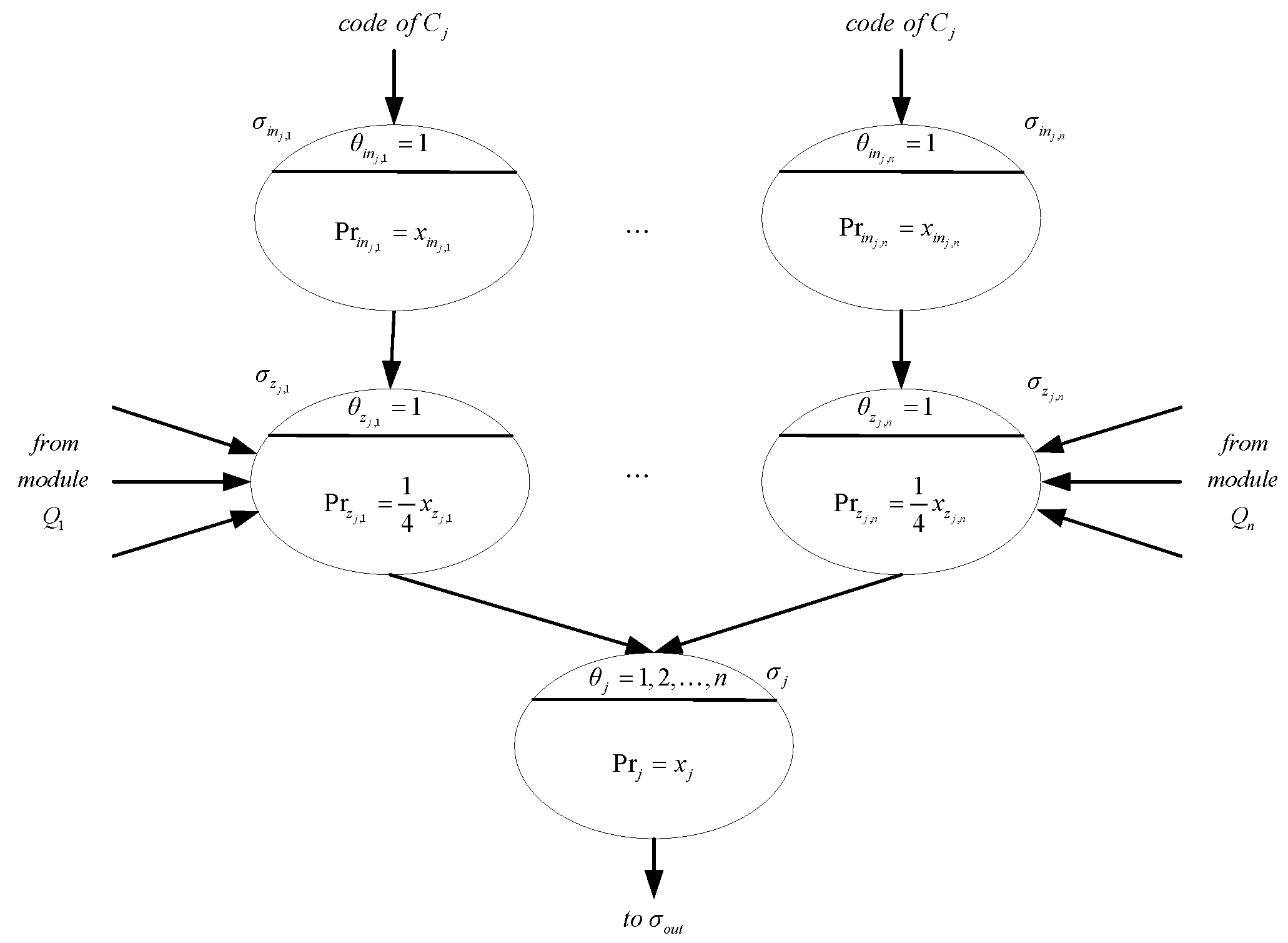
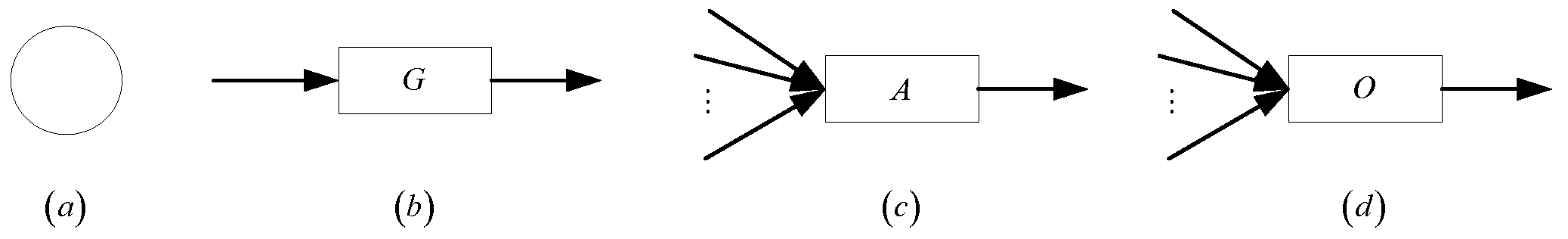

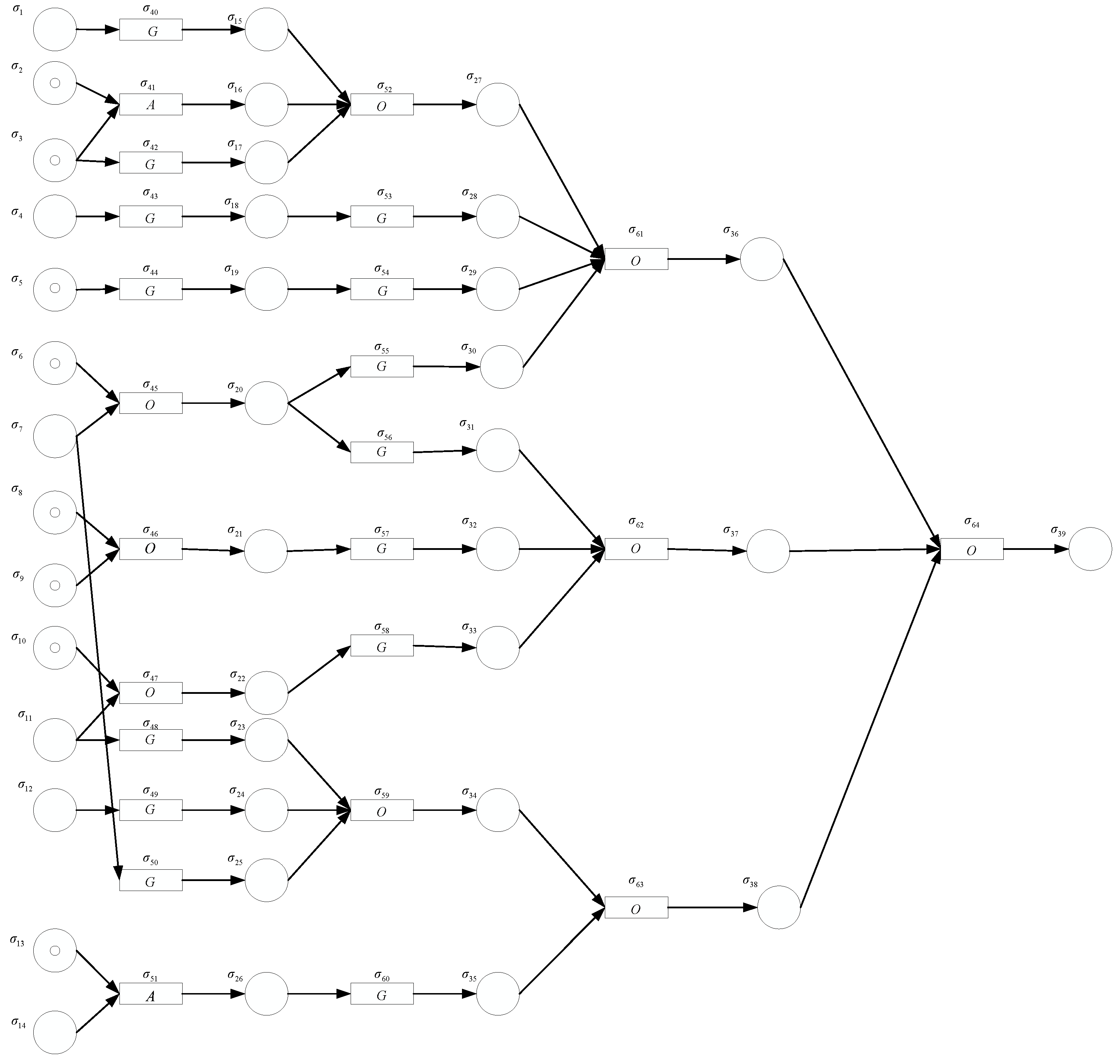
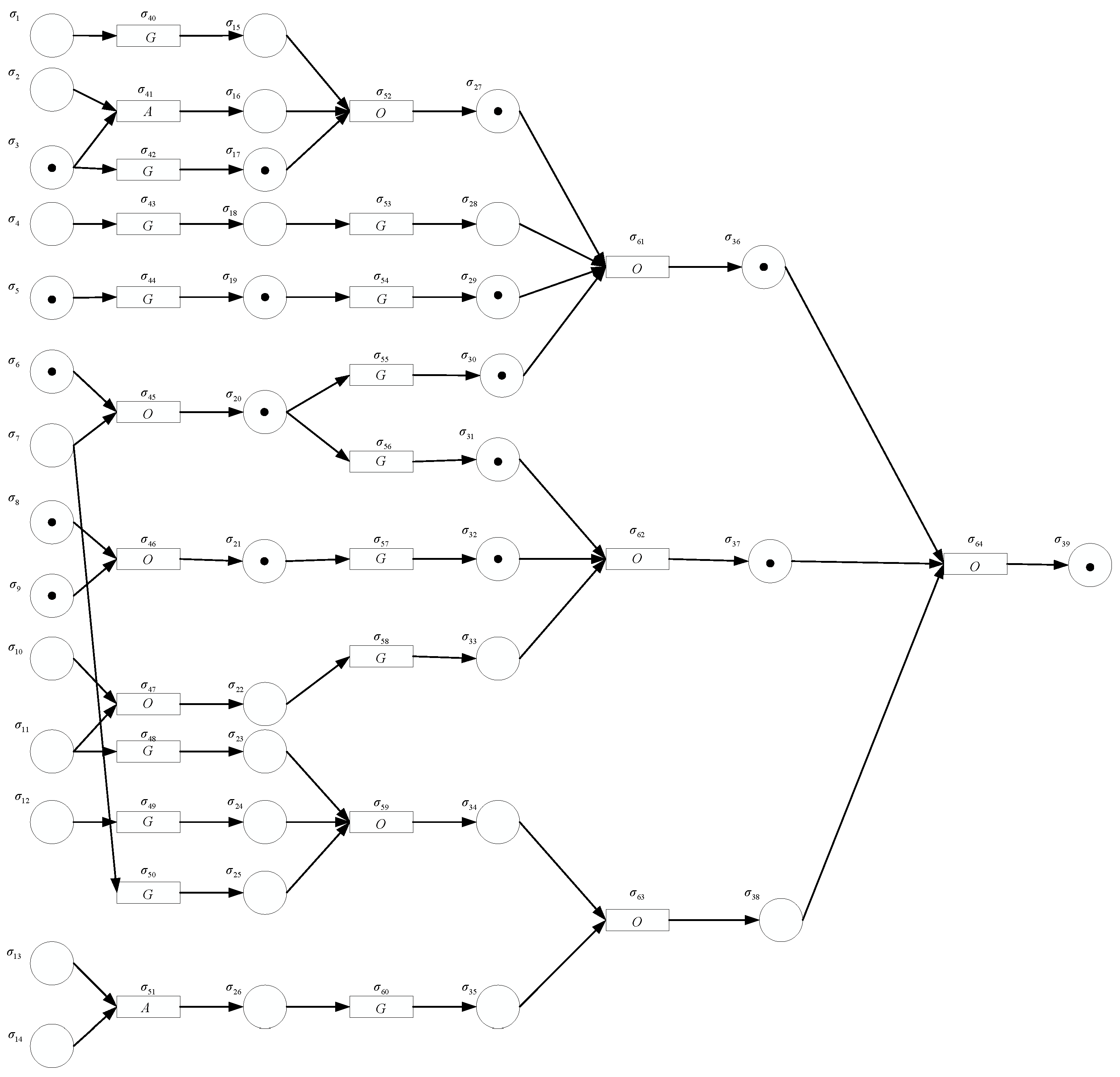
| Modules | Time Steps |
|---|---|
| NSN P systems | 6 |
| DDSN P systems [34] | |
| WSN P systems [35] | |
| SN P systems with neuron division and budding [36] |
| Linguistic Terms | NIVTFNs |
|---|---|
| Extremely Low (EL) | |
| Very Low (VL) | |
| Low (L) | |
| Fairly Low (FL) | |
| Medium (M) | |
| Fairly High (FH) | |
| High (H) | |
| Very High (VH) | |
| Extremely High (EH) |
| Preset | Methods | Result | ||||||
|---|---|---|---|---|---|---|---|---|
| Cases | Fault Locations | Fault Symptoms | Fault Cases | Fault Events | Fault Sources | Fault Cases | ||
| 1 | Broken rotor bar | FFPN [37] | ||||||
| CLPSO-FPN [38] | ||||||||
| rMFRSNPs [40] | ||||||||
| FRNSN P | ||||||||
| 2 | Winding insulation burnt | FFPN [37] | ||||||
| CLPSO-FPN [38] | ||||||||
| rMFRSNPs [40] | ||||||||
| FRNSN P | ||||||||
| 3 | Bearing damage | FFPN [37] | ||||||
| CLPSO-FPN [38] | ||||||||
| rMFRSNPs [40] | ||||||||
| FRNSN P | ||||||||
| 4 | Bearing damage and broken rotor bar | FFPN [37] | ||||||
| CLPSO-FPN [38] | ||||||||
| rMFRSNPs [40] | ||||||||
| FRNSN P | ||||||||
| 5 | Winding insulation burnt and bearing damage | FFPN [37] | ||||||
| CLPSO-FPN [38] | ||||||||
| rMFRSNPs [40] | ||||||||
| FRNSN P | ||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, X.; Liu, X.; Sun, M.; Dong, J.; Zhang, G. Fuzzy Reasoning Numerical Spiking Neural P Systems for Induction Motor Fault Diagnosis. Entropy 2022, 24, 1385. https://doi.org/10.3390/e24101385
Yin X, Liu X, Sun M, Dong J, Zhang G. Fuzzy Reasoning Numerical Spiking Neural P Systems for Induction Motor Fault Diagnosis. Entropy. 2022; 24(10):1385. https://doi.org/10.3390/e24101385
Chicago/Turabian StyleYin, Xiu, Xiyu Liu, Minghe Sun, Jianping Dong, and Gexiang Zhang. 2022. "Fuzzy Reasoning Numerical Spiking Neural P Systems for Induction Motor Fault Diagnosis" Entropy 24, no. 10: 1385. https://doi.org/10.3390/e24101385
APA StyleYin, X., Liu, X., Sun, M., Dong, J., & Zhang, G. (2022). Fuzzy Reasoning Numerical Spiking Neural P Systems for Induction Motor Fault Diagnosis. Entropy, 24(10), 1385. https://doi.org/10.3390/e24101385









