A Supervised Link Prediction Method Using Optimized Vertex Collocation Profile
Abstract
1. Introduction
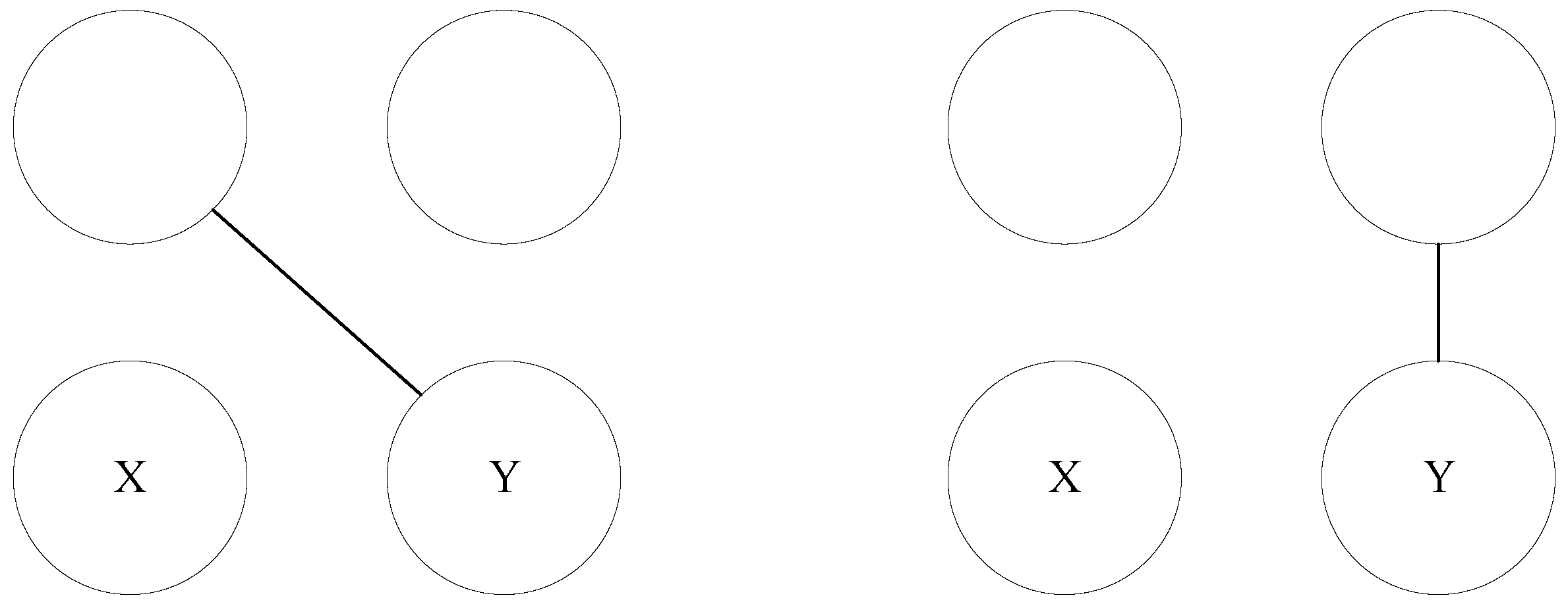
- We propose a method, OVCP, to represent topological context between vertexes in networks. We consider paths as topological structure. According to the “three degrees of influence rule” [19] and the “six degrees of separation” [20], we assume that two vertexes will not connect to each other if the path length between them is longer than 6. Therefore, we ignore the paths longer than 6. For a path between and , we complete the links between any two vertexes on the path. Therefore, we can obtain a topology context with more information. The length of the path in any topological structure is shorter than or equal to 6, and we can store it by a graph with seven vertexes, which is called 7-subgraph;
- We propose a supervised link prediction method based on OVCP. OVCP provides a way to convert a 7-subgraph to a unique address. For a 7-subgraph, we can calculate its address and treat it as a feature. We set a feature vector for each vertex pair and . The value of a feature represents the number of occurrences of a 7-subgraph on the path. If two vertexes connect to each other in a time interval, we will set the vector of them as a true sample. Otherwise, we will set it as a false sample. Then, we use the vectors and their labels to train the supervised learning model for link prediction;
- We propose a vertex pairs selection method based on overlapping community detection algorithm [21]. The complexity of finding vertex pairs that will be likely to link to each other is . In this paper, we use fast unfolding community detection algorithm [22,23] and overlapping community detection algorithm to split the original networks. These two algorithms can split the network into several small communities. We assume that only the vertexes in the same community will connect to each other, which can reduce the complexity. However, the fast unfolding community detection algorithm will ignore some possible links between vertexes in different communities, but the overlapping community detection algorithm will not;
- The experimental results on the DBLP dataset, Facebook Friendship dataset and Facebook Wall dataset demonstrate that our method achieves excellent link prediction performance, which outperforms the traditional link prediction methods based on topology.
2. Related Work
2.1. Link Prediction Methods Based on Vertex Attributes
2.2. Link Prediction Methods Based on Topological Structure
2.2.1. Methods Based on Common Neighbors
2.2.2. Methods Based on Paths
2.2.3. Methods Based on Random Walk
2.3. Link Prediction Methods Based on Learning
2.3.1. Feature-Based Classification Methods
2.3.2. Probabilistic Graph Models
2.3.3. Matrix Decomposition Methods
2.3.4. Network Embedding Methods
2.3.5. Graph Neural Networks Methods
2.4. Link Prediction Methods Based on Social Theory
2.5. The Study of Topological Structure
3. Problem Statement
- (1)
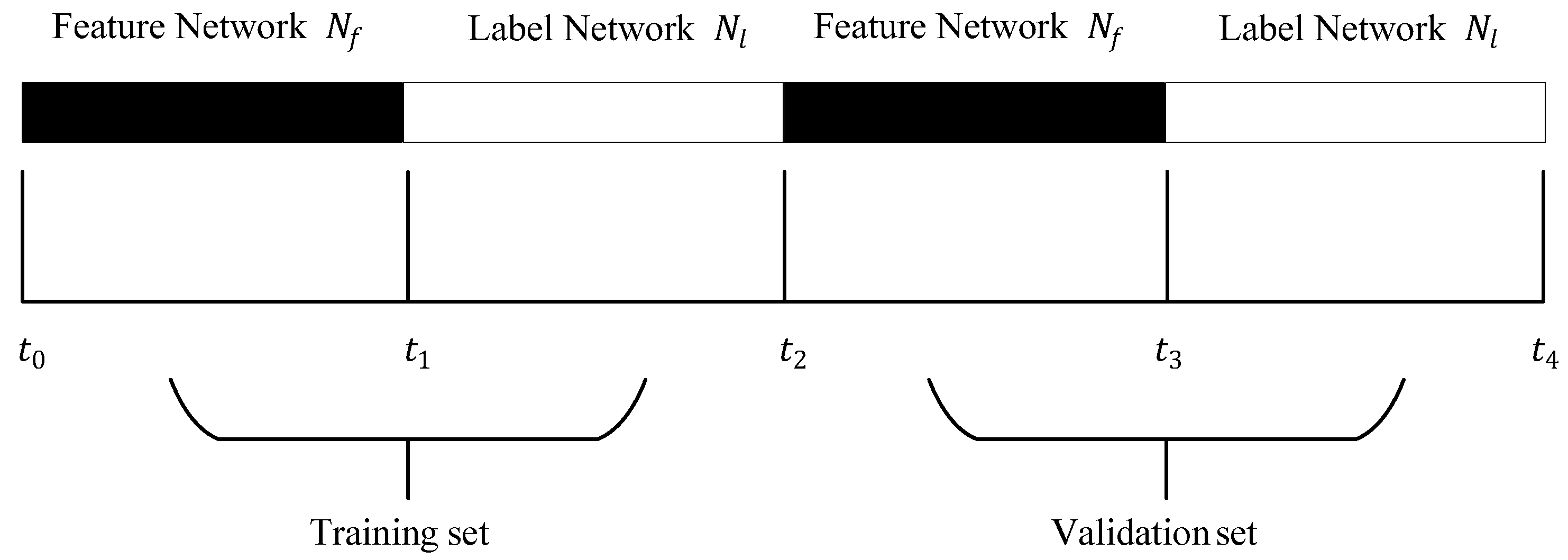
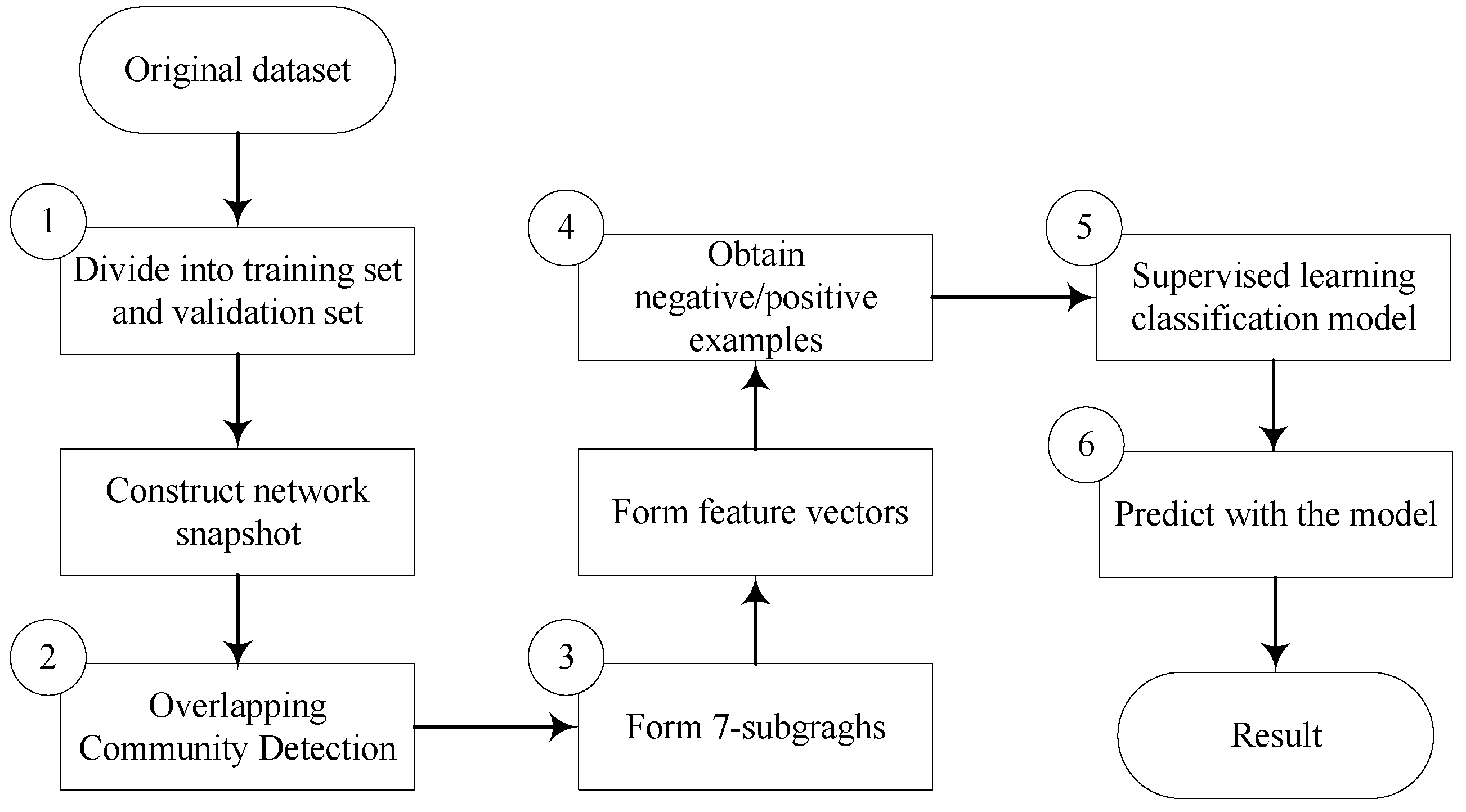
- The training set and validation set are selected from the original dataset, and the network snapshot is constructed according to the edge information of the training set and validation set;
- (2)
- The overlapping community detection algorithms are applied to divide the network into multiple communities;
- (3)
- For unconnected vertex pairs in each community, we find all paths with length less than or equal to 6 between two vertexes and record the transition vertexes on the paths. Then we complete the paths between vertexes to form 7-subgraghs. For each 7-subgraph, its address is calculated, and the number of occurrences of each 7-subgraph is counted to form the feature vector;
- (4)
- For each vertex pair obetained in step (3), if it appears in the Label Network then denoting as 1, otherwise denoting as −1. Then a positive sample or a negative sample can be obtained by combining the feature vector of this vertex pair obtained in step (3) and its label;
- (5)
- The positive and negative samples sets obtained in step (4) will be fed to the supervised learning classification model as training data;
- (6)
- Validate performance on validation set with the trained model obtained in step (5).
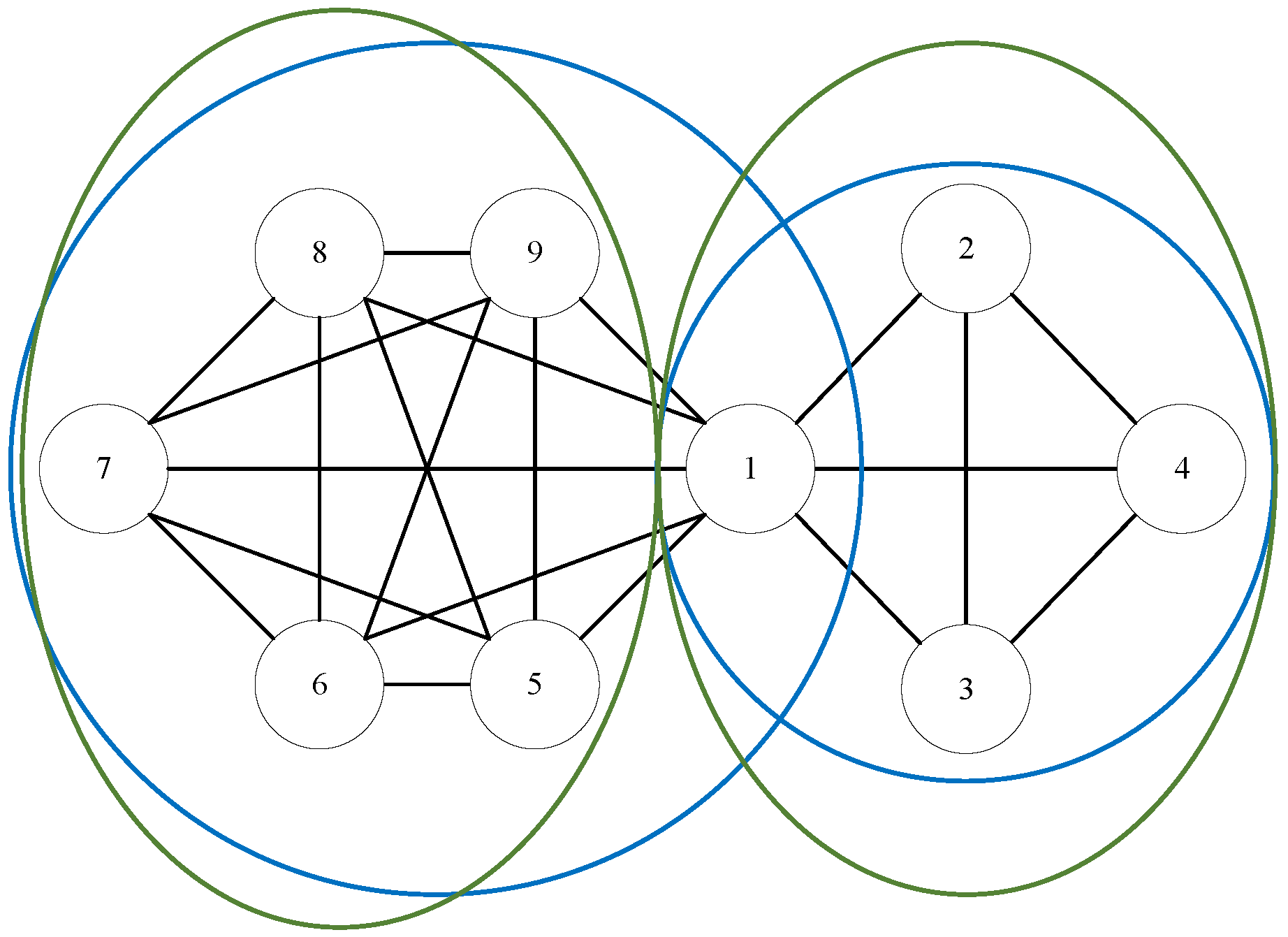
4. OVCP Feature Extraction
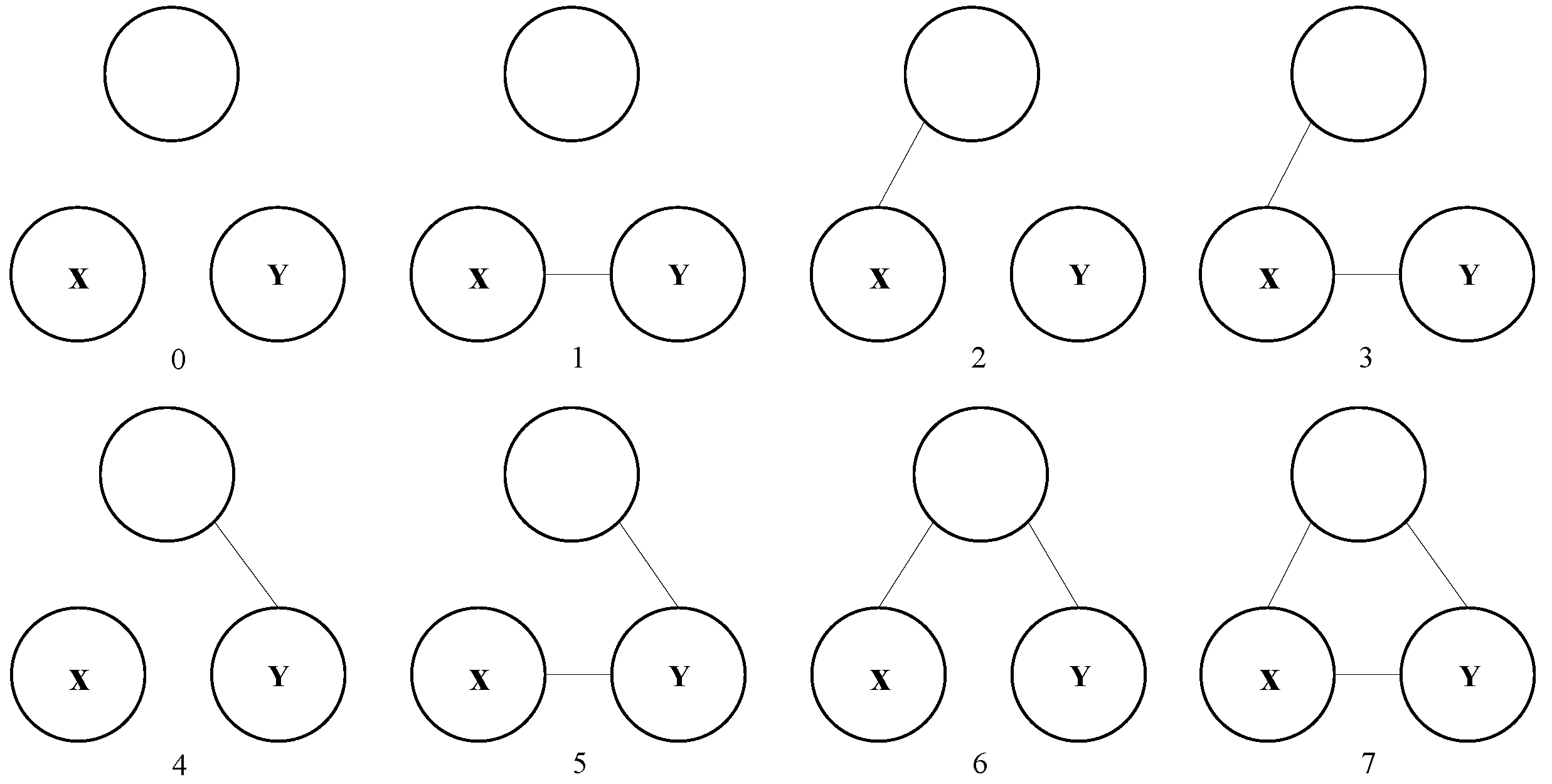
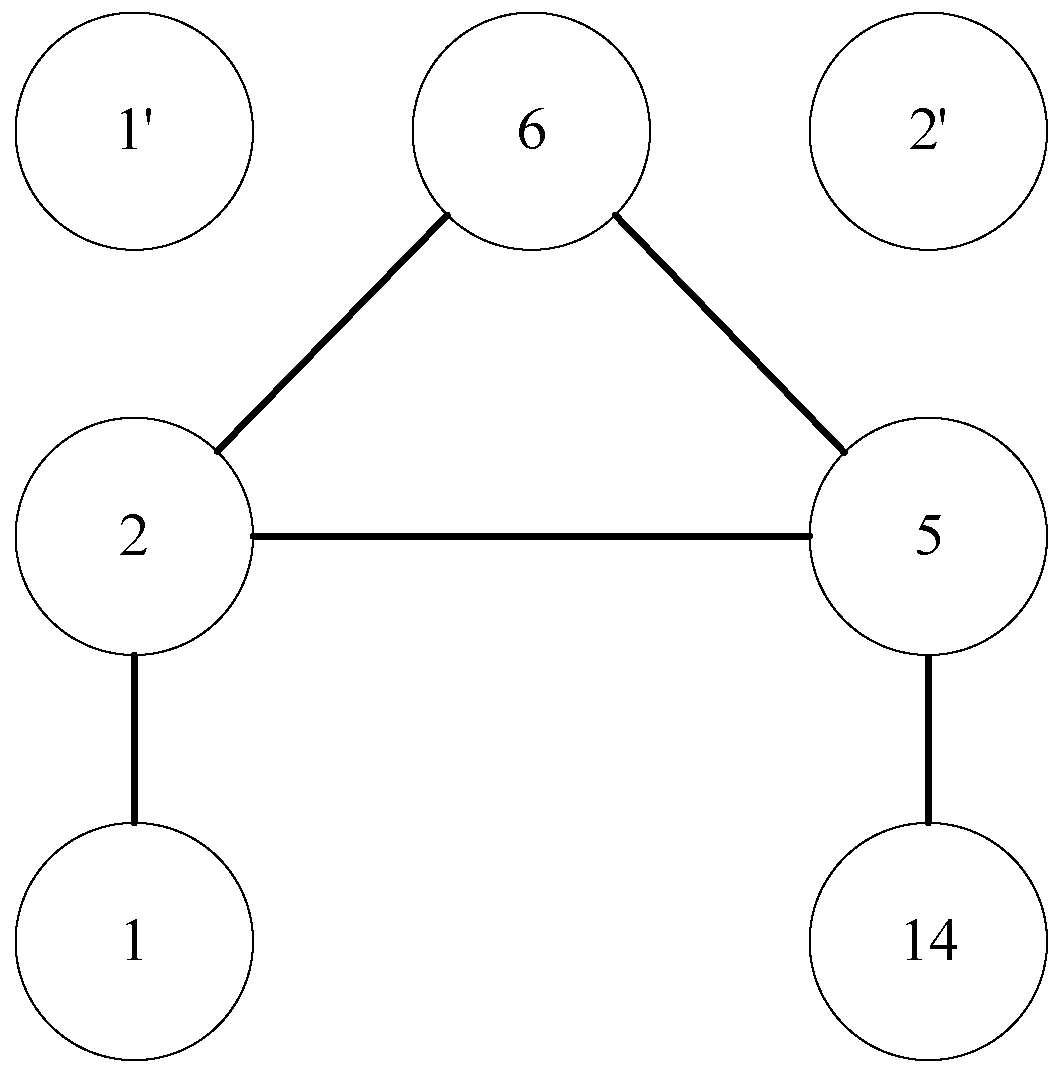
4.1. VCP
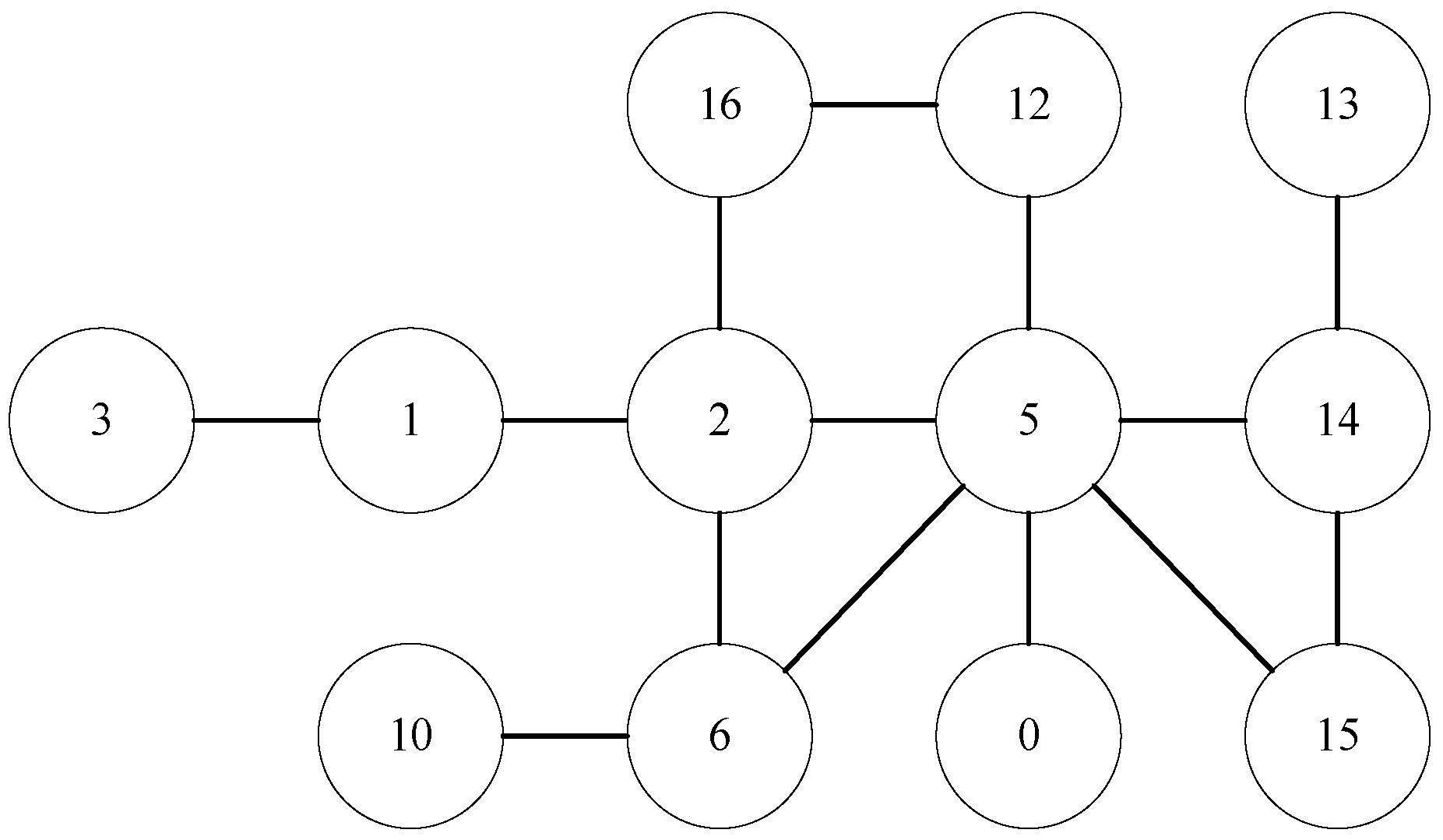
4.2. OVCP
- (1)
- 1-2-5-14
- (2)
- 1-2-6-5-14
- (3)
- 1-2-5-15-14
- (4)
- 1-2-6-5-15-14
- (5)
- 1-2-16-12-5-14
- (6)
- 1-2-16-12-5-15-14
4.3. Complexity Analysis
5. Community Detection
5.1. Fast Unfolding Community Detection
5.2. Overlapping Community Detection
6. Learning-Based Link Prediction Model
7. Experiments
7.1. Datasets
7.2. Results
7.2.1. Parameter Selection of Overlapping Community Detection
7.2.2. Effect of Selecting Vertex Pairs
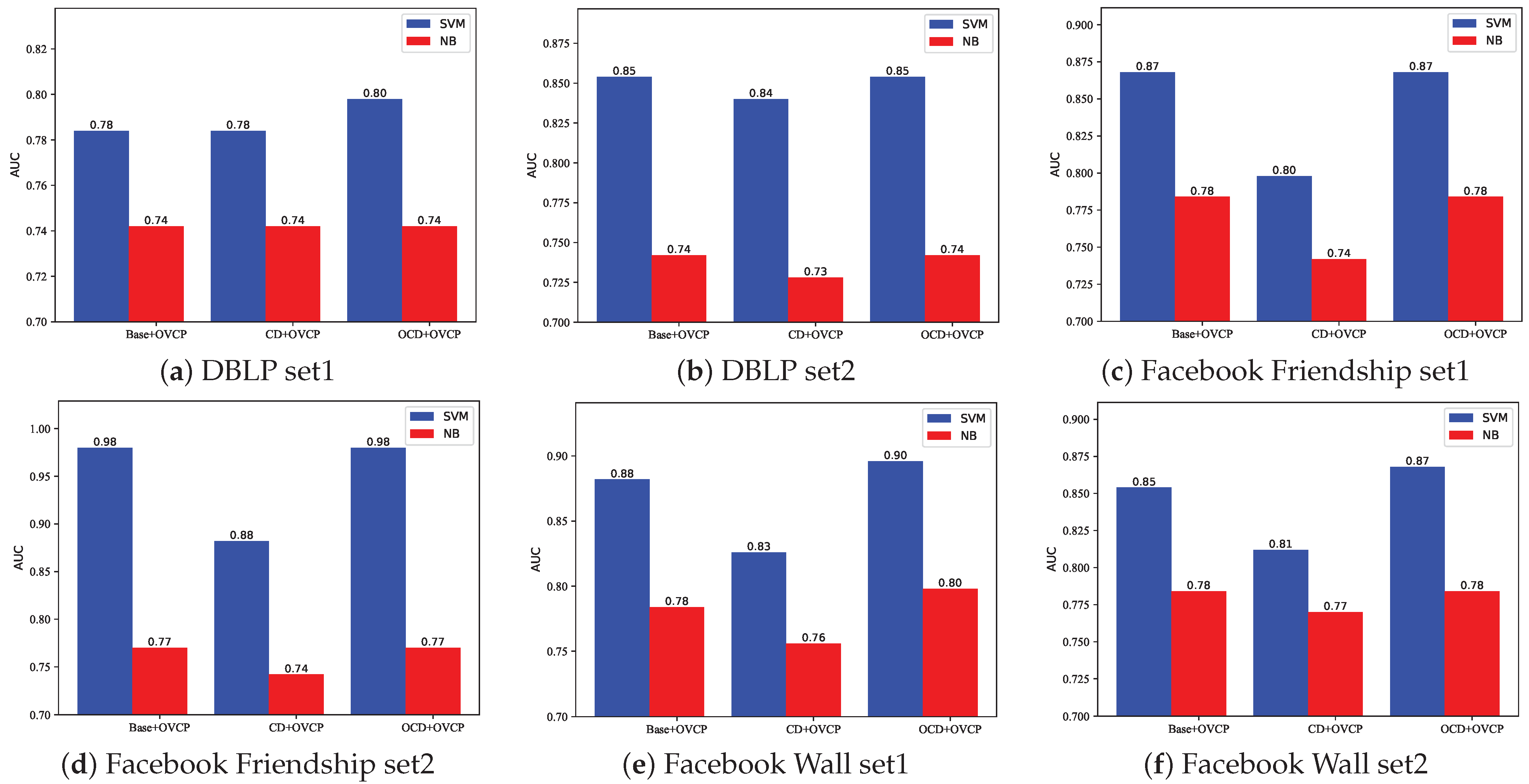
7.2.3. Comparison Experiments
7.2.4. Efficiency Experiment
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, P.; Xu, B.; Wu, Y.; Zhou, X. Link prediction in social networks: The state-of-the-art. Sci. China Inf. Sci. 2015, 58, 1–38. [Google Scholar] [CrossRef]
- Liben-Nowell, D.; Kleinberg, J. The link-prediction problem for social networks. J. Am. Soc. Inf. Sci. Technol. 2003, 556–559. [Google Scholar] [CrossRef]
- Lü, L.; Zhou, T. Link prediction in complex networks: A survey. Phys. A Stat. Mech. Its Appl. 2011, 1150–1170. [Google Scholar] [CrossRef]
- Haghani, S.; Keyvanpour, M.R. A systemic analysis of link prediction in social network. Artif. Intell. Rev. 2019, 52, 1961–1995. [Google Scholar] [CrossRef]
- Hall, P.A.; Dowling, G.R. Approximate string matching. ACM Comput. Surv. 1980, 12, 381–402. [Google Scholar] [CrossRef]
- Navarro, G. A guided tour to approximate string matching. ACM Comput. Surv. 2001, 33, 31–88. [Google Scholar] [CrossRef]
- Huang, Z. Link prediction based on graph topology: The predictive value of generalized clustering coefficient. Soc. Sci. Res. Netw. 2010. [Google Scholar] [CrossRef][Green Version]
- Mallick, K.; Bandyopadhyay, S.; Chakraborty, S.; Choudhuri, R.; Bose, S. Topo2vec: A novel node embedding generation based on network topology for link prediction. IEEE Trans. Comput. Soc. Syst. 2019, 6, 1306–1317. [Google Scholar] [CrossRef]
- Daud, N.N.; Ab Hamid, S.H.; Saadoon, M.; Sahran, F.; Anuar, N.B. Applications of link prediction in social networks: A review. J. Netw. Comput. Appl. 2020, 166, 102716. [Google Scholar] [CrossRef]
- Ouyang, B.; Jiang, L.; Teng, Z. A noise-filtering method for link prediction in complex networks. PLoS ONE 2016, 11, e0146925. [Google Scholar] [CrossRef][Green Version]
- Katz, L. A new status index derived from sociometric analysis. Psychometrika 1953, 39–43. [Google Scholar] [CrossRef]
- Newman, M.E. Clustering and preferential attachment in growing networks. Phys. Rev. E 2001, 025102. [Google Scholar] [CrossRef]
- Kumar, A.; Singh, S.S.; Singh, K.; Biswas, B. Link prediction techniques, applications, and performance: A survey. Phys. A Stat. Mech. Its Appl. 2020, 553, 124289. [Google Scholar] [CrossRef]
- Tang, J.; Qu, M.; Wang, M.; Zhang, M.; Yan, J.; Mei, Q. Line: Large-scale information network embedding. In Proceedings of the 24th International Conference on World Wide Web, Florence, Italy, 18–22 May 2015; pp. 1067–1077. [Google Scholar]
- Grover, A.; Leskovec, J. Node2vec: Scalable feature learning for networks. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 855–864. [Google Scholar]
- Xue, G.; Zhong, M.; Li, J.; Chen, J.; Zhai, C.; Kong, R. Dynamic network embedding survey. Neurocomputing 2022, 472, 212–223. [Google Scholar] [CrossRef]
- Lichtenwalter, R.N.; Chawla, N.V. Vertex collocation profiles: Subgraph counting for link analysis and prediction. In Proceedings of the 21st International Conference on World Wide Web, Lyon, France, 16–20 April 2012; pp. 1019–1028. [Google Scholar]
- Lichtenwalter, R.N.; Chawla, N.V. Vertex collocation profiles: Theory, computation, and results. SpringerPlus 2014, 3, 1–27. [Google Scholar] [CrossRef][Green Version]
- Christakis, N.A.; Fowler, J.H. Connected: The Surprising Power of Our Social Networks and How they Shape Our Lives; Brown Spark: Little, UK, 2009. [Google Scholar]
- Guare, J. Six degrees of separation. In The Contemporary Monologue Men; Routledge: London, UK, 2016; pp. 89–93. [Google Scholar]
- Xie, J.; Kelley, S.; Szymanski, B.K. Overlapping community detection in networks: The state-of-the-art and comparative study. ACM Comput. Surv. 2013, 45, 1–35. [Google Scholar] [CrossRef]
- Blondel, V.D.; Guillaume, J.L.; Lambiotte, R.; Lefebvre, E. Fast unfolding of communities in large networks. J. Stat. Mech. Theory Exp. 2008, 2008, P10008. [Google Scholar] [CrossRef]
- Traag, V.A. Faster unfolding of communities: Speeding up the Louvain algorithm. Phys. Rev. E 2015, 92, 032801. [Google Scholar] [CrossRef]
- Anderson, A.; Huttenlocher, D.; Kleinberg, J.; Leskovec, J. Effects of user similarity in social media. In Proceedings of the 5th ACM International Conference on Web Search and Data Mining, Seattle, CA, USA, 8–12 February 2012; pp. 703–712. [Google Scholar]
- Bhattacharyya, P.; Garg, A.; Wu, S.F. Analysis of user keyword similarity in online social networks. Soc. Netw. Anal. Min. 2011, 1, 143–158. [Google Scholar] [CrossRef]
- Akcora, C.G.; Carminati, B.; Ferrari, E. User similarities on social networks. Soc. Netw. Anal. Min. 2013, 3, 475–495. [Google Scholar] [CrossRef]
- Adamic, L.A.; Adar, E. Friends and neighbors on the web. Soc. Netw. 2003, 25, 211–230. [Google Scholar] [CrossRef]
- Zhou, T.; Lü, L.; Zhang, Y.C. Predicting missing links via local information. Eur. Phys. J. B 2009, 71, 623–630. [Google Scholar] [CrossRef]
- Lü, L.; Jin, C.H.; Zhou, T. Similarity index based on local paths for link prediction of complex networks. Phys. Rev. E 2009, 80, 046122. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.H.; Gou, L.; Zhang, X.; Giles, C.L. Discovering missing links in networks using vertex similarity measures. In Proceedings of the 27th Annual ACM Symposium on Applied Computing, Trento, Italy, 26–30 March 2012; pp. 138–143. [Google Scholar]
- Papadimitriou, A.; Symeonidis, P.; Manolopoulos, Y. Fast and accurate link prediction in social networking systems. J. Syst. Softw. 2012, 85, 2119–2132. [Google Scholar] [CrossRef]
- Fouss, F.; Pirotte, A.; Renders, J.M.; Saerens, M. Random-walk computation of similarities between nodes of a graph with application to collaborative recommendation. IEEE Trans. Knowl. Data Eng. 2007, 19, 355–369. [Google Scholar] [CrossRef]
- Jeh, G.; Widom, J. Simrank: A measure of structural-context similarity. In Proceedings of the 8th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Edmonton, AB, Canada, 23–26 July 2002; pp. 538–543. [Google Scholar]
- Li, X.; Chen, H. Recommendation as link prediction in bipartite graphs: A graph kernel-based machine learning approach. Decis. Support Syst. 2013, 54, 880–890. [Google Scholar] [CrossRef]
- Pujari, M.; Kanawati, R. Link prediction in complex networks by supervised rank aggregation. In Proceedings of the 2012 IEEE 24th International Conference on Tools with Artificial Intelligence, Athens, Greece, 7–9 November 2012; pp. 782–789. [Google Scholar]
- Hahn, F. General equilibrium theory. Public Interest 1980, 123. [Google Scholar]
- Chiang, K.Y.; Natarajan, N.; Tewari, A.; Dhillon, I.S. Exploiting longer cycles for link prediction in signed networks. In Proceedings of the 20th ACM International Conference on Information and Knowledge Management, Glasgow, UK, 24–28 October 2011; pp. 1157–1162. [Google Scholar]
- Wu, S.; Sun, J.; Tang, J. Patent partner recommendation in enterprise social networks. In Proceedings of the 6th ACM International Conference on Web Search and Data Mining, Rome, Italy, 4–8 February 2013; pp. 43–52. [Google Scholar]
- Clauset, A.; Moore, C.; Newman, M.E. Hierarchical structure and the prediction of missing links in networks. Nature 2008, 453, 98–101. [Google Scholar] [CrossRef]
- Guimerà, R.; Sales-Pardo, M. Missing and spurious interactions and the reconstruction of complex networks. Proc. Natl. Acad. Sci. USA 2009, 106, 22073–22078. [Google Scholar] [CrossRef]
- Kashima, H.; Abe, N. A parameterized probabilistic model of network evolution for supervised link prediction. In Proceedings of the 6th International Conference on Data Mining, Hong Kong, 18–22 December 2006; pp. 340–349. [Google Scholar]
- Menon, A.K.; Elkan, C. Link prediction via matrix factorization. In Proceedings of the 2011 European Conference on Machine Learning and Knowledge Discovery in Databases-Volume Part II, Athens, Greece, 5–9 September 2011; pp. 437–452. [Google Scholar]
- Perozzi, B.; Al-Rfou, R.; Skiena, S. Deepwalk: Online learning of social representations. In Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 24–27 August 2014; pp. 701–710. [Google Scholar]
- Zhang, M.; Chen, Y. Link prediction based on graph neural networks. Adv. Neural Inf. Process. Syst. 2018, 31. [Google Scholar]
- Islam, M.K.; Aridhi, S.; Smail-Tabbone, M. A comparative study of similarity-based and GNN-based link prediction approaches. arXiv 2020, arXiv:2008.08879. [Google Scholar]
- Valverde-Rebaza, J.; de Andrade Lopes, A. Exploiting behaviors of communities of twitter users for link prediction. Soc. Netw. Anal. Min. 2013, 3, 1063–1074. [Google Scholar] [CrossRef]
- Liu, H.; Hu, Z.; Haddadi, H.; Tian, H. Hidden link prediction based on node centrality and weak ties. Europhys. Lett. 2013, 101, 18004. [Google Scholar] [CrossRef]
- Li, R.H.; Yu, J.X.; Liu, J. Link prediction: The power of maximal entropy random walk. In Proceedings of the 20th ACM International Conference on Information and Knowledge Management, Glasgow, UK, 24–28 October 2011; pp. 1147–1156. [Google Scholar]
- Anderson, L.R.; Holt, C.A. Information cascade experiments. Handb. Exp. Econ. Results 2008, 1, 335–343. [Google Scholar]
- Qiu, B.; Ivanova, K.; Yen, J.; Liu, P. Behavior evolution and event-driven growth dynamics in social networks. In Proceedings of the 2010 IEEE Second International Conference on Social Computing, Minneapolis, MI, USA, 20–22 August 2010; pp. 217–224. [Google Scholar]
- Kashima, H.; Kato, T.; Yamanishi, Y.; Sugiyama, M.; Tsuda, K. Link propagation: A fast semi-supervised learning algorithm for link prediction. In Proceedings of the 2009 SIAM International Conference on Data Mining, Sparks, NV, USA, 30 April–2 May 2009; pp. 1100–1111. [Google Scholar]
- Ma, H.; Lu, Z.; Li, D.; Zhu, Y.; Fan, L.; Wu, W. Mining hidden links in social networks to achieve equilibrium. Theor. Comput. Sci. 2014, 556, 13–24. [Google Scholar] [CrossRef]
- Chandrasekhar, A.G.; Jackson, M.O. Tractable and Consistent Random Graph Models; National Bureau of Economic Research: Cambridge, MA, USA, 2014. [Google Scholar]
- Juszczyszyn, K.; Musial, K.; Budka, M. Link prediction based on subgraph evolution in dynamic social networks. In Proceedings of the 2011 IEEE International Conference on Social Computing, Dalian, China, 19–22 October 2011; pp. 27–34. [Google Scholar]
- Juszczyszyn, K.; Musiał, K.; Kazienko, P.; Gabrys, B. Temporal changes in local topology of an email-based social network. Comput. Inform. 2009, 28, 763–779. [Google Scholar]
- Juszczyszyn, K.; Budka, M.; Musial, K. The dynamic structural patterns of social networks based on triad transitions. In Proceedings of the 2011 International Conference on Advances in Social Networks Analysis and Mining, Kaohsiung City, Taiwan, 25–27 July 2011; pp. 581–586. [Google Scholar]
- Chang, C.C.; Lin, C.J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 1–27. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Van Der Walt, S.; Colbert, S.C.; Varoquaux, G. The NumPy array: A structure for efficient numerical computation. Comput. Sci. Eng. 2011, 13, 22–30. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
- Hagberg, A.; Swart, P.; Chult, D.S. Exploring Network Structure, Dynamics, and Function Using NetworkX; Technical Report; Los Alamos National Lab: Los Alamos, NM, USA, 2008. [Google Scholar]
- Ling, C.X.; Huang, J.; Zhang, H. AUC: A statistically consistent and more discriminating measure than accuracy. Ijcai 2003, 3, 519–524. [Google Scholar]
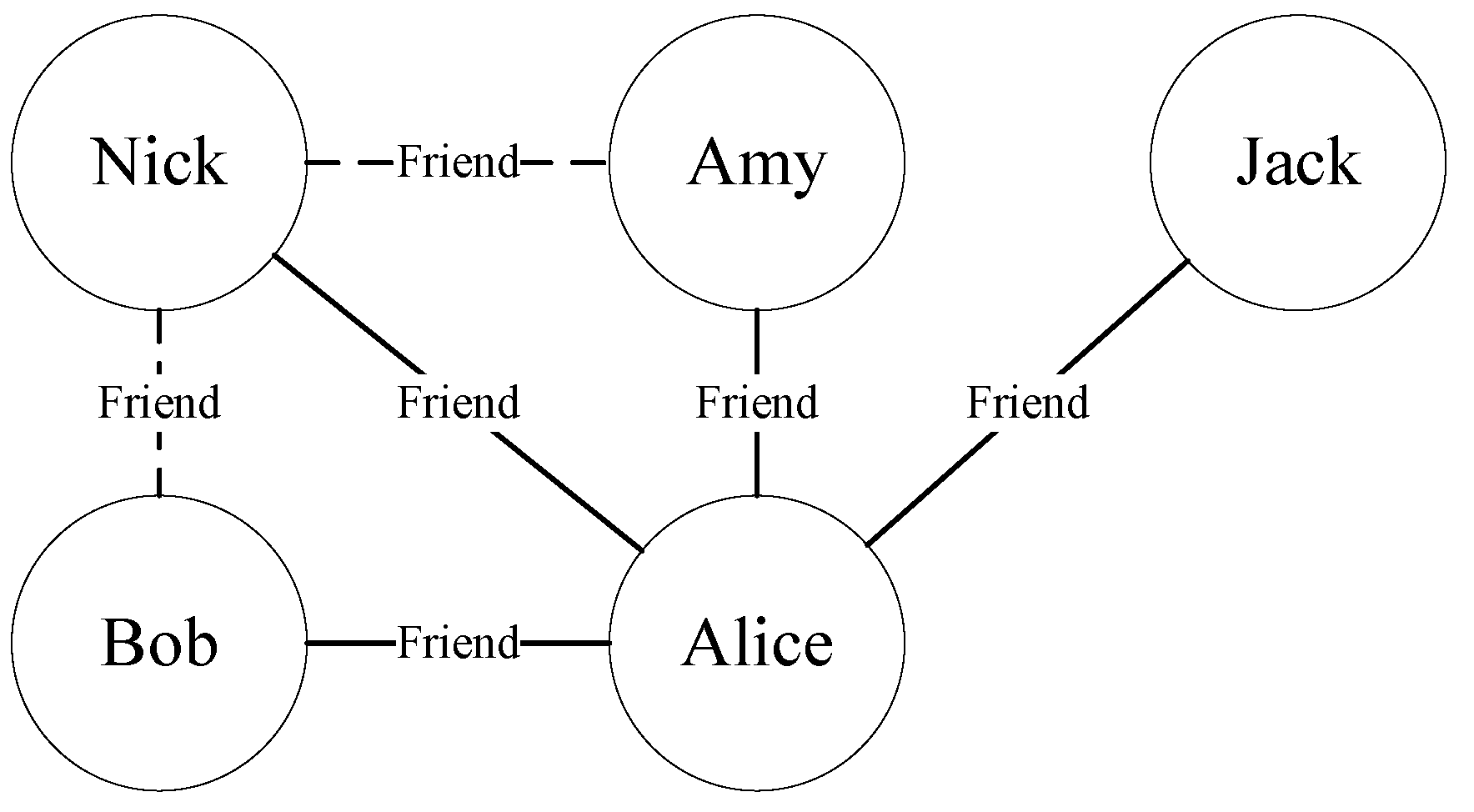



| Symbol | Description |
|---|---|
| vertex pair to be predicted | |
| V | set of vertexes |
| E | set of edges |
| graph with vertex set V and edge set E | |
| Feature Network | |
| Label Network | |
| set of unlinked edges | |
| set of nonexistent edges | |
| D | adjacency matrix |
| address of 7-subgraph | |
| minimal address of 7-subgraph | |
| union of the permutation of set {3,4,5,6,7} and set {1,2} | |
| relation vector |
| Vertexes | Edges | |
|---|---|---|
| DBLP set1 | 9393 | 22,468 |
| DBLP set2 | 27,710 | 80,632 |
| Facebook Friendship set1 | 12,715 | 31,882 |
| Facebook Friendship set2 | 17,336 | 62,454 |
| Facebook Wall set1 | 9787 | 24,232 |
| Facebook Wall set2 | 11,229 | 29,632 |
| Module | Time Cost |
|---|---|
| Base+OVCP+SVM | 10,970 s + 20 s |
| Base+OVCP+NB | 10,970 s + 5 s |
| CD+OVCP+SVM | 1086 s + 9 s |
| CD+OVCP+NB | 1086 s + 4 s |
| OCD+OVCP+SVM | 924 s + 3 s |
| OCD+OVCP+NB | 924 s + 2 s |
| VCP3 | 31 s |
| VCP4 | 42 s |
| Katz | 3126 s |
| AA | 51 s |
| RA | 46 s |
| CN | 48 s |
| Jaccard | 49 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, P.; Wu, C.; Huang, T.; Chen, Y. A Supervised Link Prediction Method Using Optimized Vertex Collocation Profile. Entropy 2022, 24, 1465. https://doi.org/10.3390/e24101465
Wang P, Wu C, Huang T, Chen Y. A Supervised Link Prediction Method Using Optimized Vertex Collocation Profile. Entropy. 2022; 24(10):1465. https://doi.org/10.3390/e24101465
Chicago/Turabian StyleWang, Peng, Chenxiao Wu, Teng Huang, and Yizhang Chen. 2022. "A Supervised Link Prediction Method Using Optimized Vertex Collocation Profile" Entropy 24, no. 10: 1465. https://doi.org/10.3390/e24101465
APA StyleWang, P., Wu, C., Huang, T., & Chen, Y. (2022). A Supervised Link Prediction Method Using Optimized Vertex Collocation Profile. Entropy, 24(10), 1465. https://doi.org/10.3390/e24101465





