Ray–Wave Correspondence in Microstar Cavities
Abstract
:1. Introduction
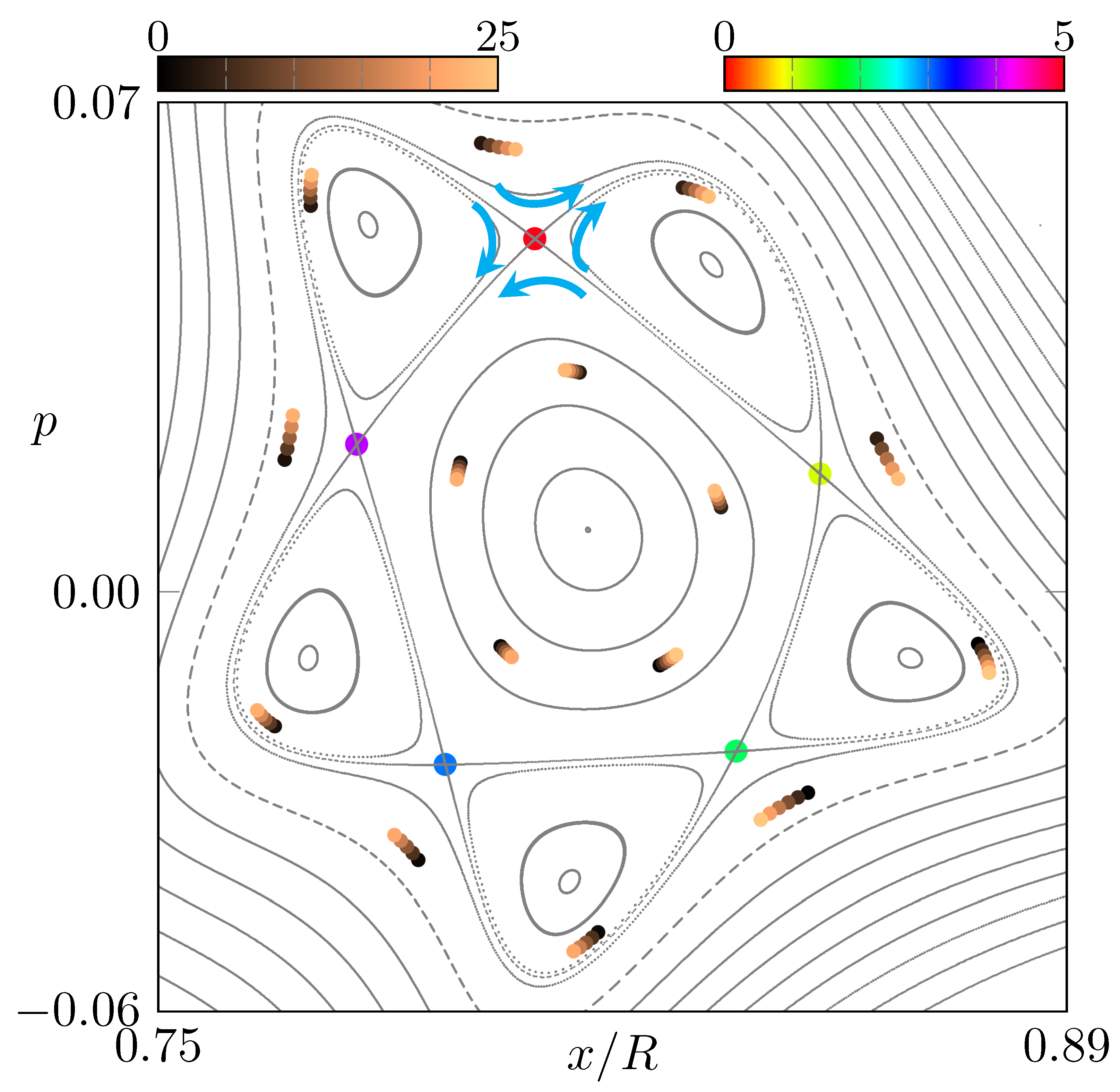
2. Ray Dynamics and Phase-Space Description for Microstar Cavities
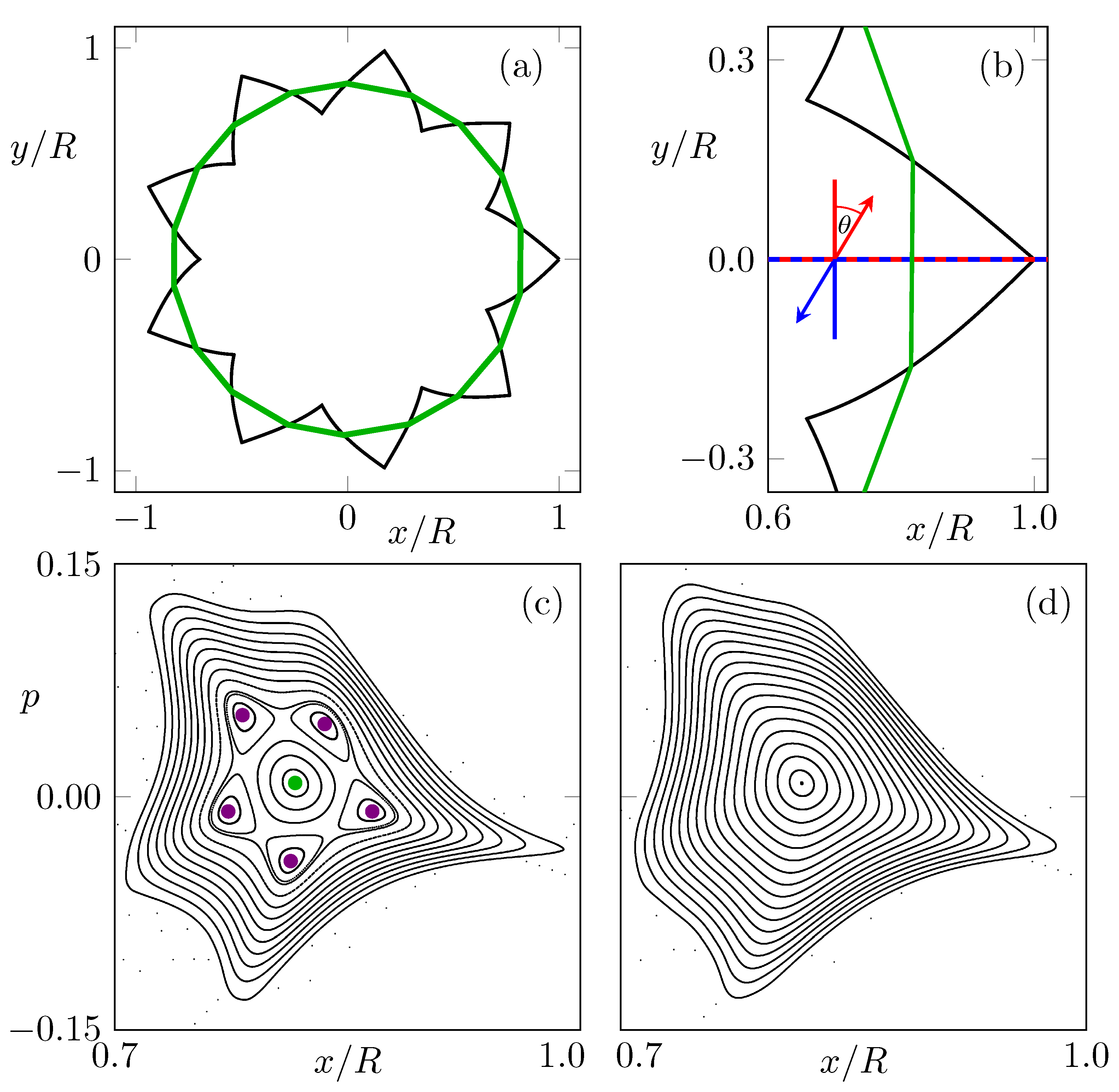
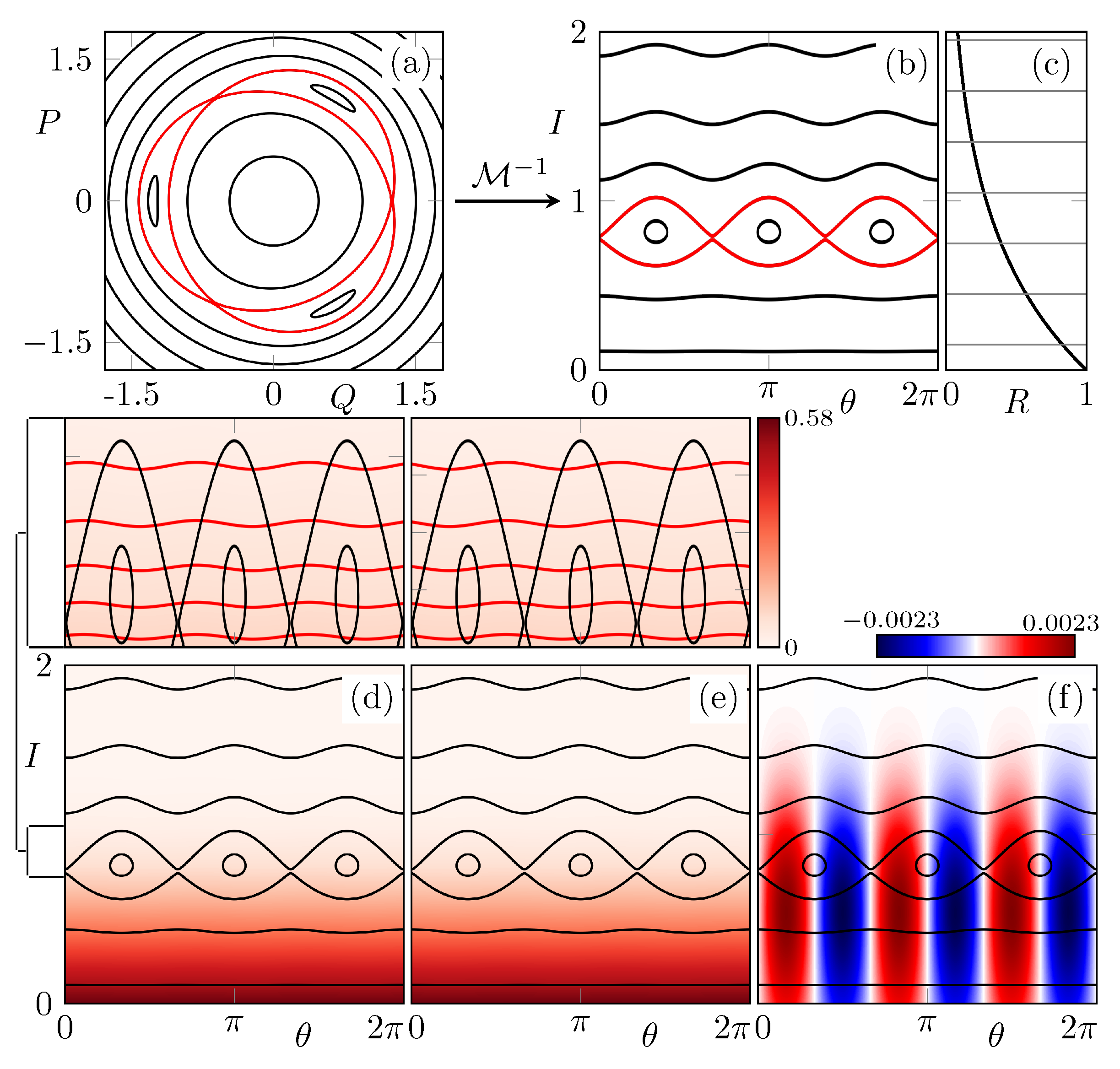
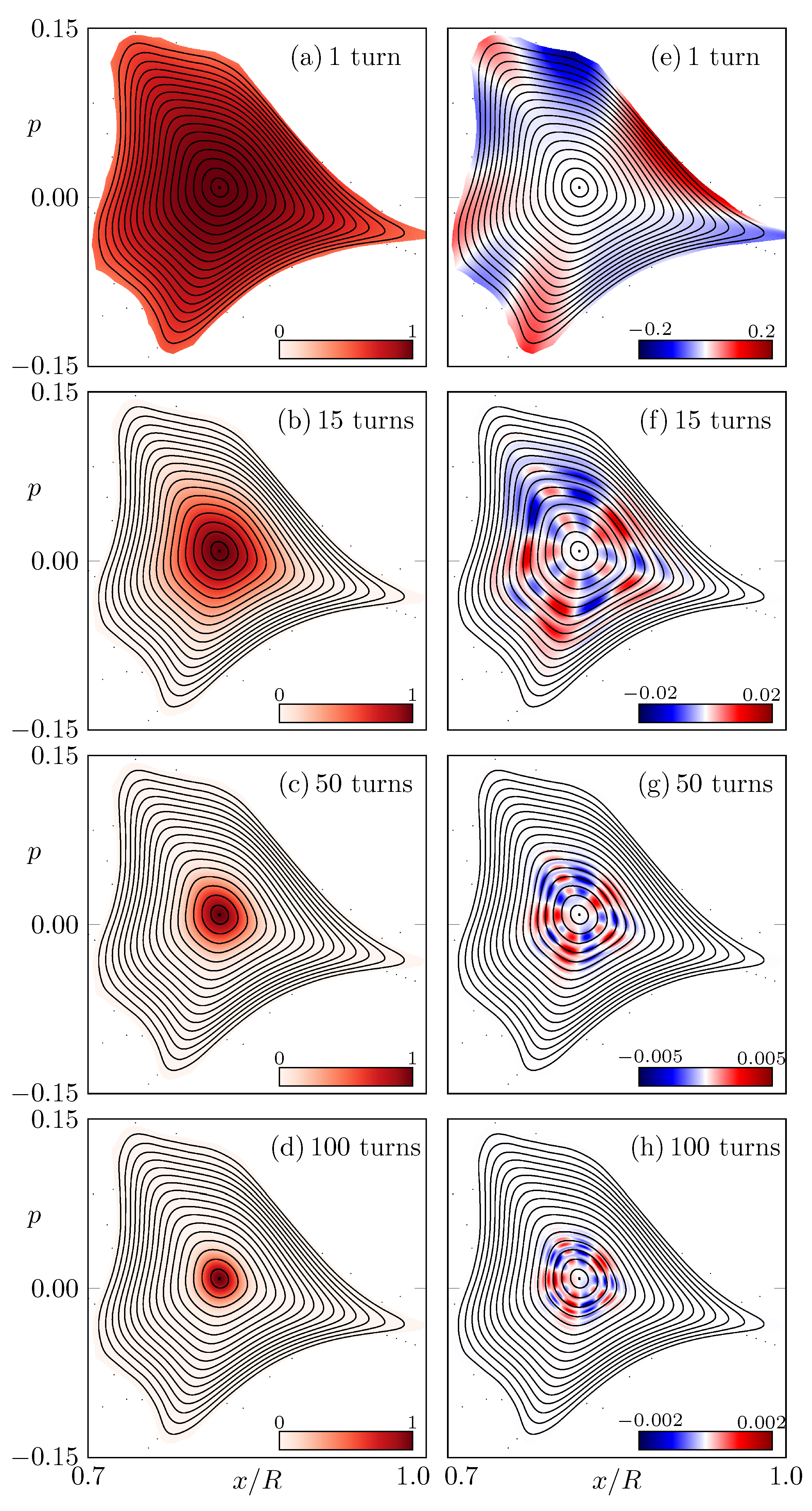
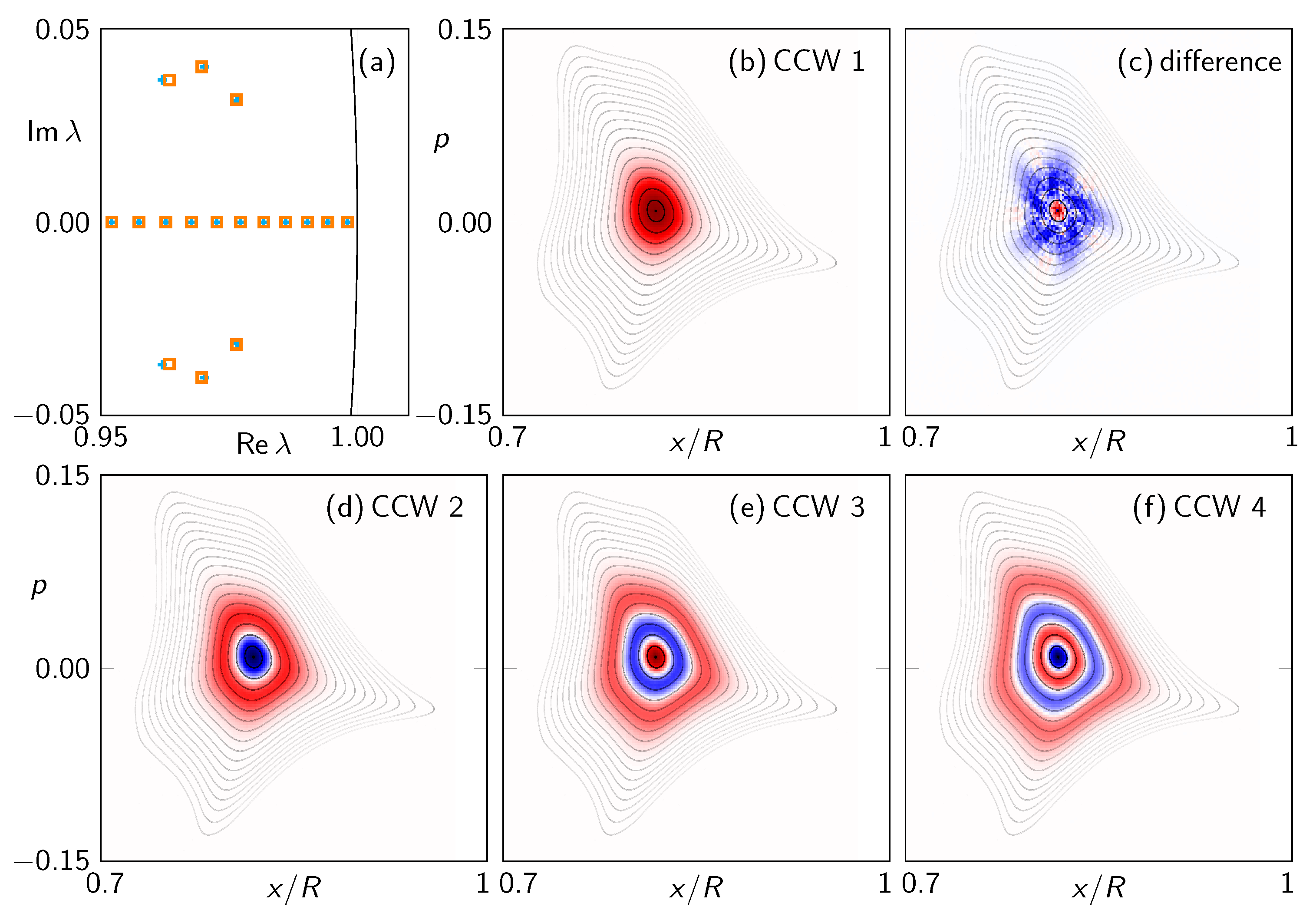
Frobenius–Perron Operator
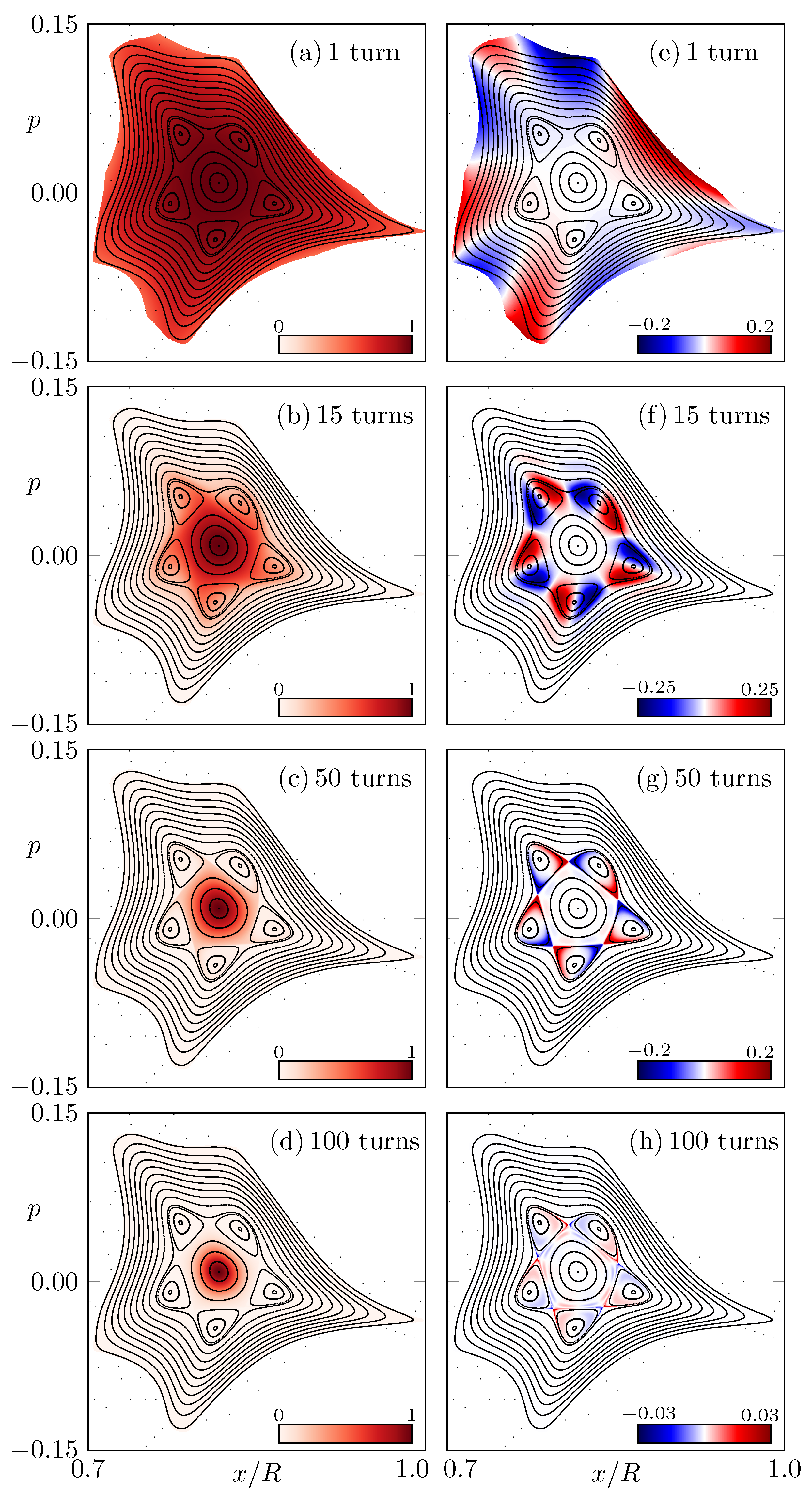
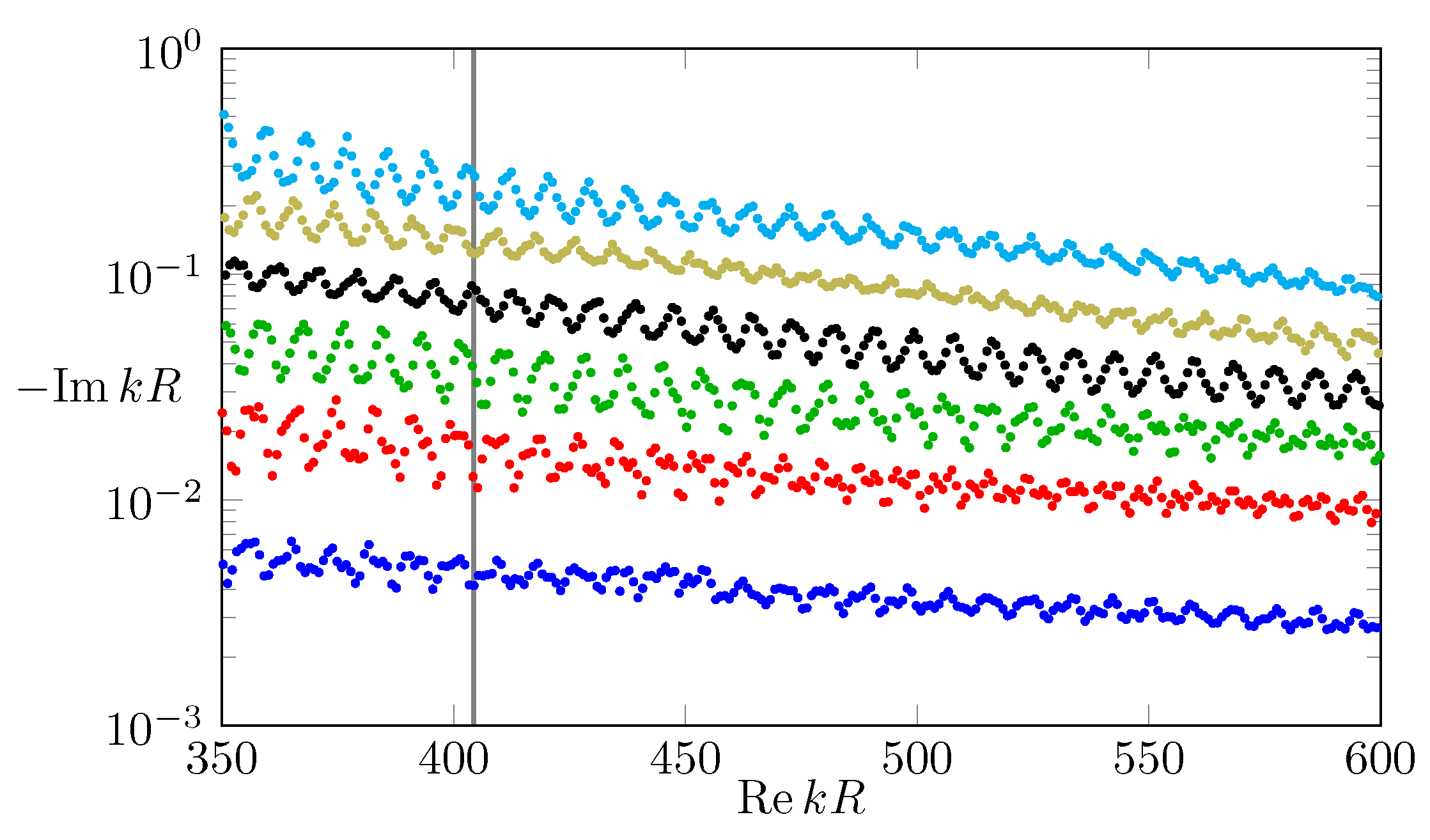
3. Wave Dynamics
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Difference in Forward and Backward Dynamics in a Generalized Pendulum Model
References
- Vahala, K.J. Optical Microcavities; Advanced Series in Applied Physics; World Scientific: Singapore, 2004; Volume 5. [Google Scholar]
- Chang, R.K.; Campillo, A.J. Optical Processes in Microcavities; Advanced Series in Applied Physics; World Scientific: Singapore, 1996; Volume 3. [Google Scholar]
- Kippenberg, T.J.; Kalkman, J.; Polman, A.; Vahala, K.J. Demonstration of an erbium-doped microdisk laser on a silicon chip. Phys. Rev. A 2006, 74, 051802(R). [Google Scholar] [CrossRef] [Green Version]
- McCall, S.L.; Levi, A.F.J.; Slusher, R.E.; Pearton, S.J.; Logan, R.A. Whispering-gallery mode microdisk lasers. Appl. Phys. Lett. 1992, 60, 289–291. [Google Scholar] [CrossRef]
- Levi, A.F.J.; Slusher, R.E.; McCall, S.L.; Glass, J.L.; Pearton, S.J.; Logan, R.A. Directional light coupling from microdisk lasers. App. Phys. Lett. 1993, 62, 561–563. [Google Scholar] [CrossRef] [Green Version]
- Tamboli, A.C.; Haberer, E.D.; Sharma, R.; Lee, K.W.; Nakamura, S.; Hu, E.L. Room-temperature continuous-wave lasing in GaN/InGaN microdisks. Nat. Photonics 2007, 1, 61–64. [Google Scholar] [CrossRef]
- Ilchenko, V.S.; Gorodetsky, M.L.; Yao, X.S.; Maleki, L. Microtorus: A high-finesse microcavity with whispering-gallery modes. Opt. Lett. 2001, 26, 256–258. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Armani, D.K.; Kippenberg, T.J.; Spillane, S.M.; Vahala, K.J. Ultra-high-Q toroid microcavity on a chip. Nature 2003, 421, 925–928. [Google Scholar] [CrossRef]
- Zhang, X.; Choi, H.S.; Armani, A.M. Ultimate quality factor of silica microtoroid resonant cavities. Appl. Phys. Lett. 2010, 96, 153304. [Google Scholar] [CrossRef]
- Collot, L.; Lefevre-Seguin, V.; Brune, M.; Raimond, J.; Haroche, S. Very high-Q whispering-gallery modes observed on fused silica microspheres. Europhys. Lett. 1993, 23, 327–334. [Google Scholar] [CrossRef]
- Yang, J.; Moon, S.; Lee, S.B.; Lee, J.H.; An, K.; Shim, J.B.; Lee, H.W.; Kim, S.W. Development of a deformation-tunable quadrupolar microcavity. Rev. Sci. Instrum. 2006, 77, 083103. [Google Scholar] [CrossRef] [Green Version]
- Stöckmann, H.J. Quantum Chaos; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Cao, H.; Wiersig, J. Dielectric microcavities: Model systems for wave chaos and non-Hermitian physics. Rev. Mod. Phys. 2015, 87, 61–111. [Google Scholar] [CrossRef]
- Nöckel, J.U.; Stone, A.D. Ray and wave chaos in asymmetric resonant optical cavities. Nature 1997, 385, 45–47. [Google Scholar] [CrossRef] [Green Version]
- Sunada, S.; Shinohara, S.; Fukushima, T.; Harayama, T. Signature of Wave Chaos in Spectral Characteristics of Microcavity Lasers. Phys. Rev. Lett. 2016, 116, 203903. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Peng, B.; Özdemir, S.K.; Lei, F.; Monifi, F.; Gianfreda, M.; Long, G.L.; Fan, S.; Nori, F.; Bender, C.M.; Yang, L. Parity–time-symmetric whispering-gallery microcavities. Nat. Phys. 2014, 10, 394–398. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.B.; Yang, J.; Moon, S.; Lee, S.Y.; Shim, J.B.; Kim, S.W.; Lee, J.H.; An, K. Observation of an Exceptional Point in a Chaotic Optical Microcavity. Phys. Rev. Lett. 2009, 103, 134101. [Google Scholar] [CrossRef] [Green Version]
- Zhu, J.; Özdemir, Ş.K.; He, L.; Yang, L. Controlled manipulation of mode splitting in an optical microcavity by two Rayleigh scatterers. Opt. Express 2010, 18, 23535–23543. [Google Scholar] [CrossRef] [Green Version]
- Peng, B.; Özdemir, Ş.K.; Liertzer, M.; Chen, W.; Kramer, J.; Yilmaz, H.; Wiersig, J.; Rotter, S.; Yang, L. Chiral modes and directional lasing at exceptional points. Proc. Natl. Acad. Sci. USA 2016, 113, 6845. [Google Scholar] [CrossRef] [Green Version]
- Richter, S.; Zirnstein, H.G.; Zúñiga Pérez, J.; Krüger, E.; Deparis, C.; Trefflich, L.; Sturm, C.; Rosenow, B.; Grundmann, M.; Schmidt-Grund, R. Voigt Exceptional Points in an Anisotropic ZnO-Based Planar Microcavity: Square-Root Topology, Polarization Vortices, and Circularity. Phys. Rev. Lett. 2019, 123, 227401. [Google Scholar] [CrossRef]
- Kippenberg, T.J.; Holzwarth, R.; Diddams, S.A. Microresonator-Based Optical Frequency Combs. Science 2011, 332, 555–559. [Google Scholar] [CrossRef]
- Nöckel, J.U.; Stone, A.D.; Chen, G.; Grossman, H.L.; Chang, R.K. Directional emission from asymmetric resonant cavities. Opt. Lett. 1996, 21, 1609–1611. [Google Scholar] [CrossRef] [Green Version]
- Wiersig, J.; Hentschel, M. Combining directional light output and ultralow loss in deformed microdisks. Phys. Rev. Lett. 2008, 100, 033901. [Google Scholar] [CrossRef]
- Wang, Q.J.; Yan, C.; Yu, N.; Unterhinninghofen, J.; Wiersig, J.; Pflügl, C.; Diehl, L.; Edamura, T.; Yamanishi, M.; Kan, H.; et al. Whispering-gallery mode resonators for highly unidirectional laser action. Proc. Natl. Acad. Sci. USA 2010, 107, 22407. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Albert, F.; Hopfmann, C.; Eberspächer, A.; Arnold, F.; Emmerling, M.; Schneider, C.; Höfling, S.; Forchel, A.; Kamp, M.; Wiersig, J.; et al. Directional whispering gallery mode emission from Limaçon-shaped electrically pumped quantum dot micropillar lasers. Appl. Phys. Lett 2012, 101, 021116. [Google Scholar] [CrossRef]
- Armani, A.M.; Kulkarni, R.P.; Fraser, S.E.; Flagan, R.C.; Vahala, K.J. Label-Free, Single-Molecule Detection with Optical Microcavities. Science 2007, 317, 783–787. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vollmer, F.; Arnold, S. Whispering-gallery-mode biosensing: Label-free detection down to single molecules. Nat. Methods 2008, 5, 591. [Google Scholar] [CrossRef]
- Lu, T.; Lee, H.; Chen, T.; Herchak, S.; Kim, J.H.; Fraser, S.E.; Flagan, R.C.; Vahala, K. High sensitivity nanoparticle detection using optical microcavities. Proc. Nat. Acad. Sci. USA 2011, 108, 5976–5979. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sunada, S.; Harayama, T. Design of resonant microcavities: Application to optical gyroscopes. Opt. Express 2007, 15, 16245–16254. [Google Scholar] [CrossRef]
- Miao, P.; Zhang, Z.; Sun, J.; Walasik, W.; Longhi, S.; Litchinitser, N.M.; Feng, L. Orbital angular momentum microlaser. Science 2016, 353, 464–467. [Google Scholar] [CrossRef] [Green Version]
- Kullig, J.; Jiang, X.; Yang, L.; Wiersig, J. Microstar cavities: An alternative concept for the confinement of light. Phys. Rev. Res. 2020, 2, 012072. [Google Scholar] [CrossRef] [Green Version]
- Kullig, J.; Wiersig, J. Microdisk cavities with a Brewster notch. Phys. Rev. Res. 2021, 3, 023202. [Google Scholar] [CrossRef]
- Wiersig, J.; Kim, S.W.; Hentschel, M. Asymmetric scattering and nonorthogonal mode patterns in optical microspirals. Phys. Rev. A 2008, 78, 053809. [Google Scholar] [CrossRef]
- Wiersig, J.; Eberspächer, A.; Shim, J.B.; Ryu, J.W.; Shinohara, S.; Hentschel, M.; Schomerus, H. Nonorthogonal pairs of copropagating optical modes in deformed microdisk cavities. Phys. Rev. A 2011, 84, 023845. [Google Scholar] [CrossRef] [Green Version]
- Wiersig, J. Non-Hermitian Effects Due to Asymmetric Backscattering of Light in Whispering-Gallery Microcavities. In Parity-Time Symmetry and Its Applications; Christodoulides, D., Yang, J., Eds.; Springer: Singapore, 2018; pp. 155–184. [Google Scholar]
- Beck, C.; Schögl, F. Thermodynamics of Chaotic Systems: An Introduction; Cambridge Nonlinear Science Series; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Altmann, E.G.; Portela, J.S.E.; Tél, T. Leaking chaotic systems. Rev. Mod. Phys. 2013, 85, 869–918. [Google Scholar] [CrossRef] [Green Version]
- Frahm, K.M.; Shepelyansky, D.L. Ulam method for the Chirikov standard map. Eur. Phys. J. B 2010, 76, 57–68. [Google Scholar] [CrossRef]
- Weber, J.; Haake, F.; Šeba, P. Frobenius-Perron Resonances for Maps with a Mixed Phase Space. Phys. Rev. Lett. 2000, 85, 3620–3623. [Google Scholar] [CrossRef] [Green Version]
- Ermann, L.; Shepelyansky, D.L. Ulam method and fractal Weyl law for Perron-Frobenius operators. Eur. Phys. J. B 2010, 75, 299–304. [Google Scholar] [CrossRef]
- Carlo, G.G.; Rivas, A.M.F.; Spina, M.E. Classical to quantum correspondence in dissipative directed transport. Phys. Rev. E 2015, 92, 052907. [Google Scholar] [CrossRef] [Green Version]
- Kullig, J.; Wiersig, J. Frobenius–Perron eigenstates in deformed microdisk cavities: Non-Hermitian physics and asymmetric backscattering in ray dynamics. New J. Phys. 2016, 18, 015005. [Google Scholar] [CrossRef]
- Ulam, S.M. A Collection of Mathematical Problems; Interscience Publishers: New York, NY, USA, 1960. [Google Scholar]
- Weber, J.; Haake, F.; Braun, P.A.; Manderfeld, C.; Seba, P. Resonances of the Frobenius-Perron operator for a Hamiltonian map with a mixed phase space. J. Phys. A Math. Gen. 2001, 34, 7195–7211. [Google Scholar] [CrossRef]
- Jackson, J.D. Classical Electrodynamics; John Wiley and Sons: New York, NY, USA, 1962. [Google Scholar]
- Wiersig, J. Boundary element method for resonances in dielectric microcavities. J. Opt. A Pure Appl. Opt. 2003, 5, 53. [Google Scholar] [CrossRef]
- COMSOL Multiphysics® v. 6.0; COMSOL AB: Stockholm, Sweden, 2022; Available online: www.comsol.com (accessed on 2 November 2022).
- Hentschel, M.; Schomerus, H.; Schubert, R. Husimi functions at dielectric interfaces: Inside-outside duality for optical systems and beyond. Europhys. Lett. 2003, 62, 636–642. [Google Scholar] [CrossRef]
- Lebœuf, P.; Mouchet, A. Normal Forms and Complex Periodic Orbits in Semiclassical Expansions of Hamiltonian Systems. Ann. Phys. 1999, 275, 54–112. [Google Scholar] [CrossRef] [Green Version]
- Lichtenberg, A.J.; Liebermann, M.A. Regular and Stochastic Motion; Springer: New York, NY, USA, 1983. [Google Scholar]
- Keshavamurthy, S.; Schlagheck, P.E. Dynamical Tunneling: Theory and Experiment, 1st ed.; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Löck, S.; Bäcker, A.; Ketzmerick, R.; Schlagheck, P. Regular-to-Chaotic Tunneling Rates: From the Quantum to the Semiclassical Regime. Phys. Rev. Lett. 2010, 104, 114101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mertig, N.; Kullig, J.; Löbner, C.; Bäcker, A.; Ketzmerick, R. Perturbation-free prediction of resonance-assisted tunneling in mixed regular-chaotic systems. Phys. Rev. E 2016, 94, 062220. [Google Scholar] [CrossRef] [PubMed]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kullig, J.; Wiersig, J. Ray–Wave Correspondence in Microstar Cavities. Entropy 2022, 24, 1614. https://doi.org/10.3390/e24111614
Kullig J, Wiersig J. Ray–Wave Correspondence in Microstar Cavities. Entropy. 2022; 24(11):1614. https://doi.org/10.3390/e24111614
Chicago/Turabian StyleKullig, Julius, and Jan Wiersig. 2022. "Ray–Wave Correspondence in Microstar Cavities" Entropy 24, no. 11: 1614. https://doi.org/10.3390/e24111614




