Exploiting Dual-Attention Networks for Explainable Recommendation in Heterogeneous Information Networks
Abstract
1. Introduction
- In order to alleviate the problem of data sparseness, we extracted multiple kinds of meta-paths between users and items from the heterogeneous information networks and generated multiple similarity matrices, which were used as complements of the rating matrix. Then, we decomposed the similarity matrices by matrix decomposition to obtain the multiple representations of users and items corresponding to different meta-paths;
- We propose a novel dual-attention network for explainable recommendation in heterogeneous information networks (DANER). It leverages a local attention layer to learn the representations of users and items, and a global attention layer to learn the joint representations of user–item interactions, both of which integrate multiple groups of different meta-path information. An attention mechanism helps to improve the explainability of the recommendation;
- We demonstrate better rating prediction accuracy than the state-of-the-art methods by performing comprehensive experiments on two benchmark datasets. In addition, by providing a critical meta-path based on attention coefficient, we show a case study on the explainability of DANER.
2. Related Works
2.1. Recommendation
2.2. HIN in Recommendation
2.3. Attention Mechanism
3. Problem Statement
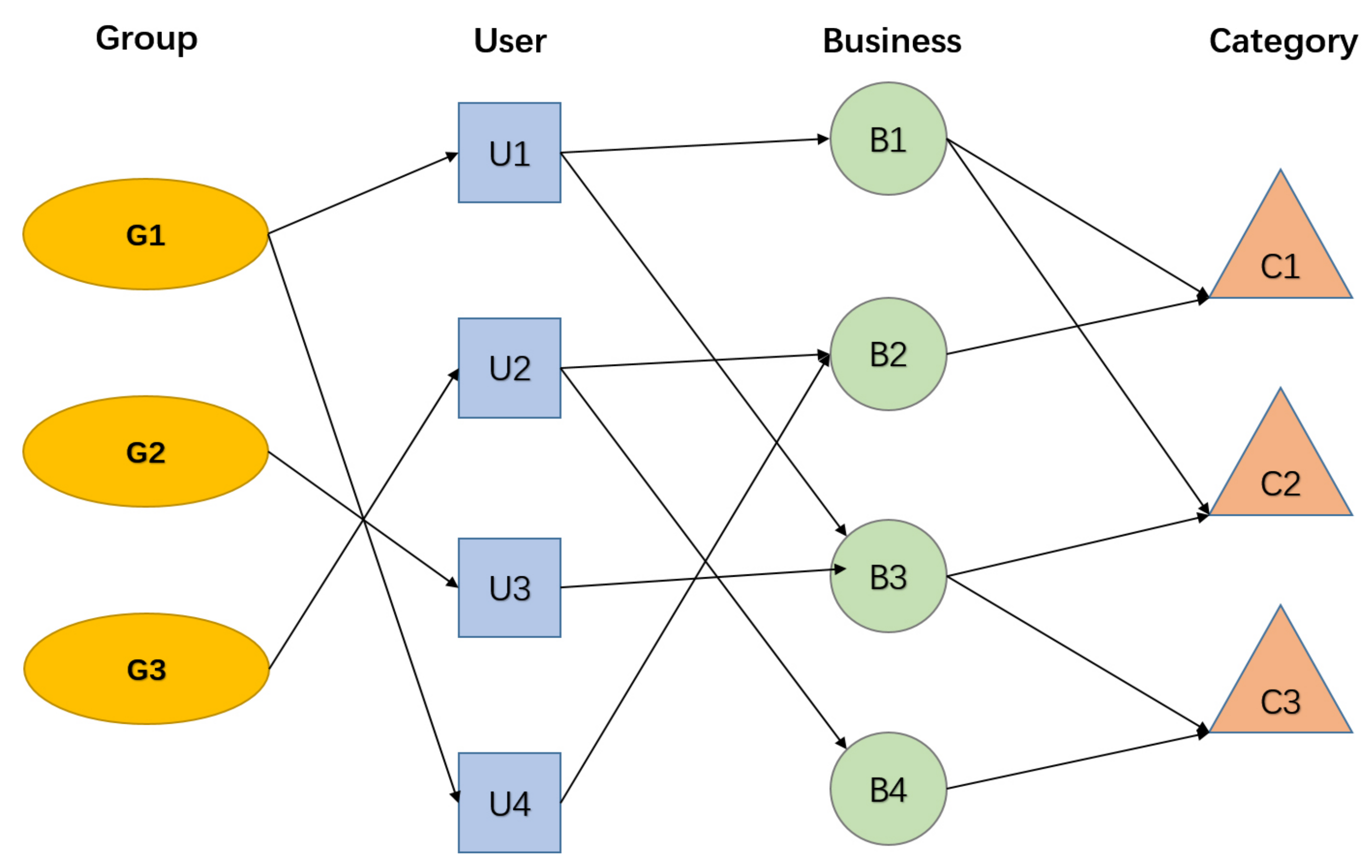
3.1. Definitions
3.2. Problem Statement
4. Framework
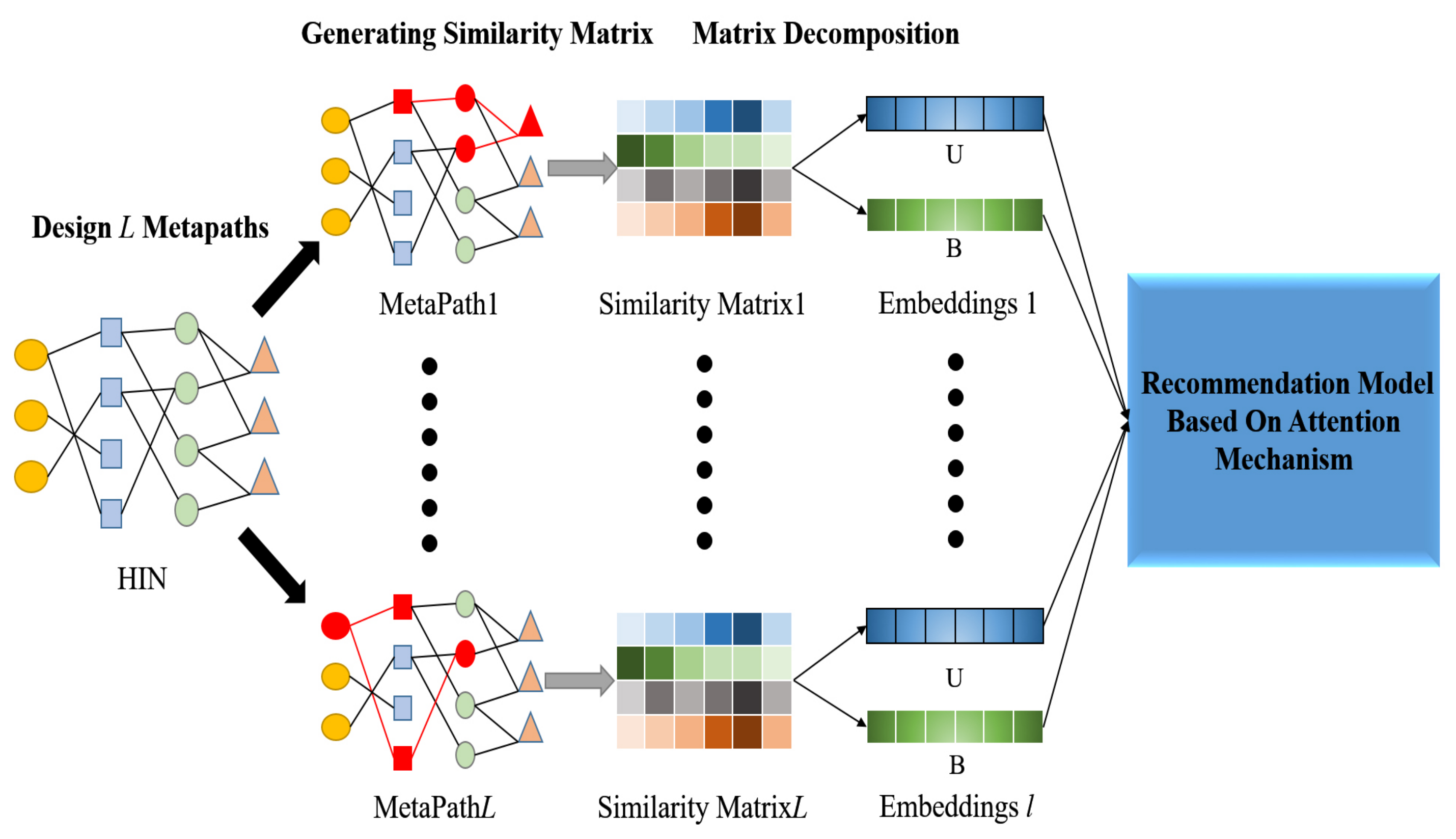
4.1. Similarity Matrix Based on Meta-Path
4.2. Latent Representation by Matrix Decomposition
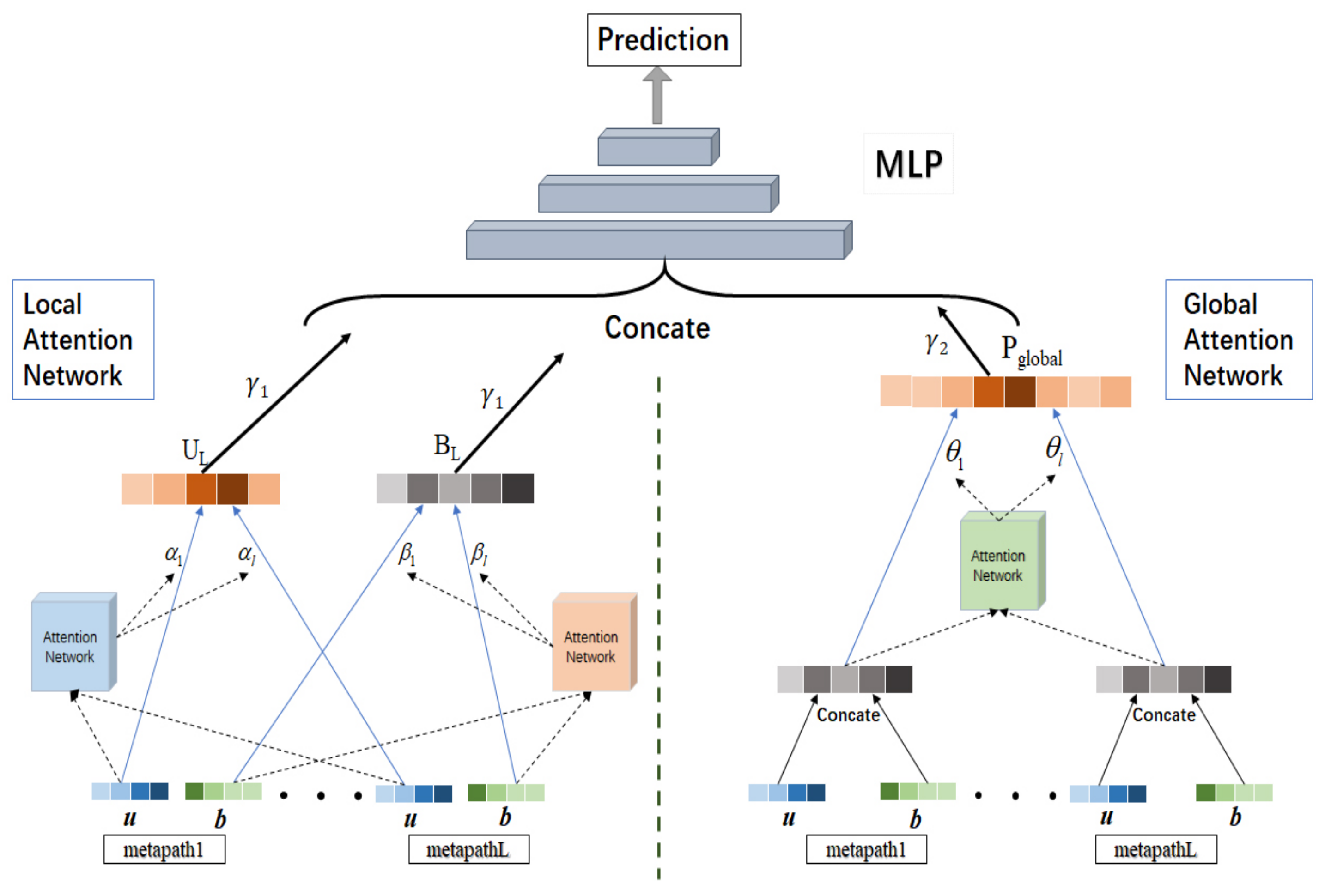
4.3. Recommendation Model Based on Attention Mechanism
4.3.1. Local Attention Network
4.3.2. Global Attention Network
4.3.3. Interaction Model
4.4. Model Optimization
5. Experiments
5.1. Datasets
5.2. Evaluation Metrics
5.3. Baselines
5.4. Experimental Performance
5.4.1. Experimental Settings
5.4.2. Model Variations Comparison Experiments
5.4.3. Baseline Methods Comparison Experiments
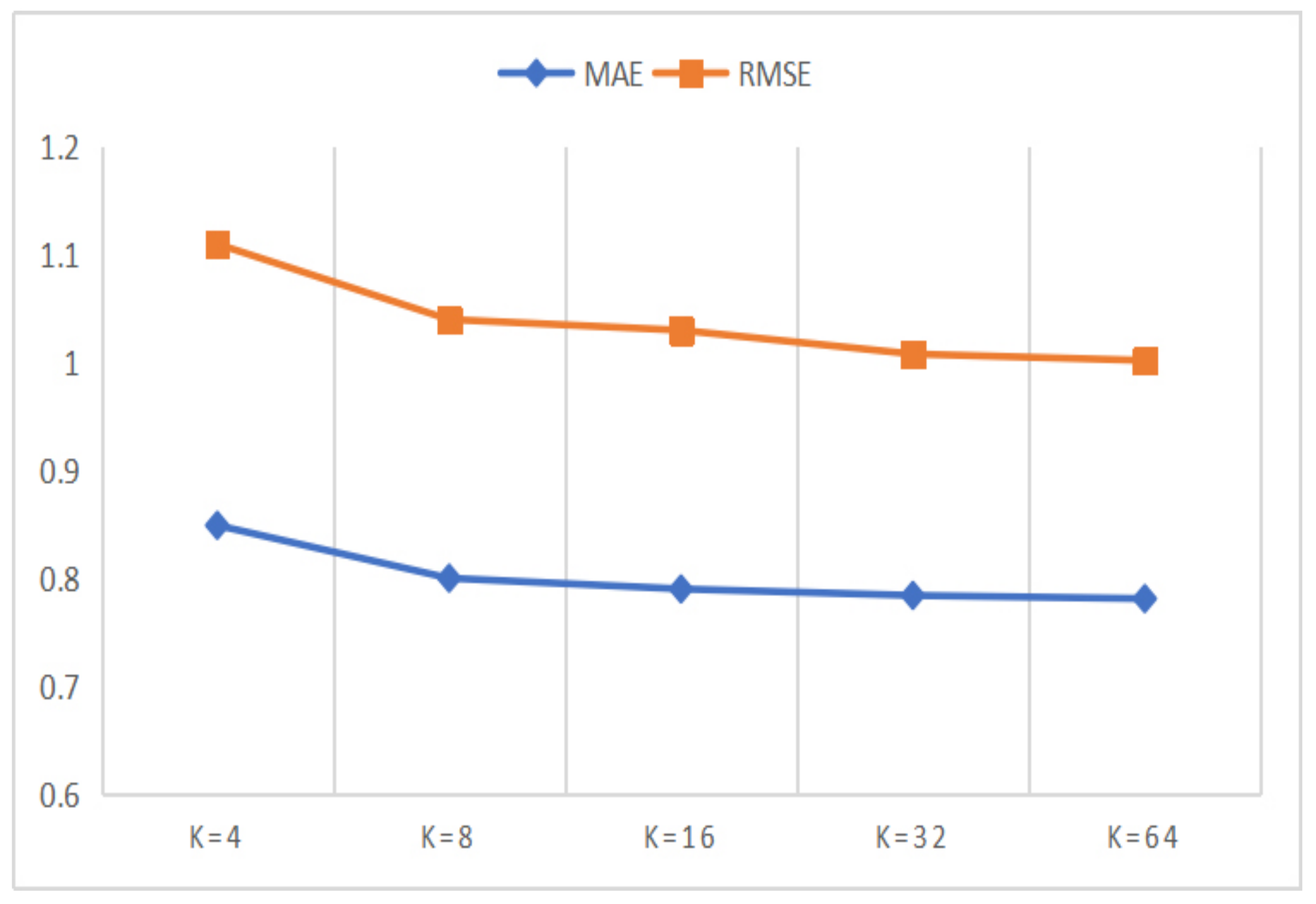
5.4.4. Parameter Comparison Experiments
5.4.5. Interpretability of Recommendation Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shao, B.; Li, X.; Bian, G. A survey of research hotspots and frontier trends of recommendation systems from the perspective of knowledge graph. Expert Syst. Appl. 2021, 165, 113764. [Google Scholar] [CrossRef]
- Wang, S.S.; Pan, Y.Y.; Yang, X. Research of Recommendation System Based on Deep Interest Network. J. Phys. Conf. Ser. 2021, 1732, 012015. [Google Scholar] [CrossRef]
- Wang, W.; Feng, F.; He, X.; Nie, L.; Chua, T.S. Denoising Implicit Feedback for Recommendation. In Proceedings of the 14th ACM International Conference on Web Search and Data Mining, Virtual, 8–12 March 2020. [Google Scholar] [CrossRef]
- Zhang, F.; Yuan, N.J.; Lian, D.; Xie, X.; Ma, W.Y. Collaborative knowledge base embedding for recommender systems. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar] [CrossRef]
- He, X.; Chua, T.S. Neural factorization machines for sparse predictive analytics. In Proceedings of the SIGIR 2017—The 40th International ACM SIGIR Conference on Research and Development in Information Retrieval, Tokyo, Japan, 7–11 August 2017. [Google Scholar] [CrossRef]
- Lu, W.; Altenbek, G. A recommendation algorithm based on fine-grained feature analysis. Expert Syst. Appl. 2021, 163, 113759. [Google Scholar] [CrossRef]
- F, S.Y.A.; B, H.W.; C, Y.L.; D, Y.Z.; E, L.H. Attention-aware Metapath-based Network Embedding for HIN based Recommendation. Expert Syst. Appl. 2021, 174, 114601. [Google Scholar]
- Ying, R.; He, R.; Chen, K.; Eksombatchai, P.; Hamilton, W.L.; Leskovec, J. Graph convolutional neural networks for web-scale recommender systems. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, London, UK, 19–23 August 2018. [Google Scholar] [CrossRef]
- Geng, S.; Fu, Z.; Tan, J.; Ge, Y.; de Melo, G.; Yongfeng, Z. Path Language Modeling over Knowledge Graphs for Explainable Recommendation. In Proceedings of the ACM Web Conference 2022, Lyon, France, 25–29 April 2022. [Google Scholar]
- Wang, P.; Cai, R.; Wang, H. Graph-based Extractive Explainer for Recommendations. arXiv 2022, arXiv:2202.09730. [Google Scholar]
- Zhang, J.; Yu, P.S.; Zhou, Z.H. Meta-path based multi-network collective link prediction. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 24–27 August 2014. [Google Scholar] [CrossRef]
- Sinha, B.B.; Dhanalakshmi, R. DNN-MF: Deep neural network matrix factorization approach for filtering information in multi-criteria recommender systems. Neural Comput. Appl. 2022, 34, 10807–10821. [Google Scholar] [CrossRef]
- Wang, X.; He, X.; Wang, M.; Feng, F.; Chua, T.S. Neural graph collaborative filtering. In Proceedings of the SIGIR 2019—The 42nd International ACM SIGIR Conference on Research and Development in Information Retrieval, Paris, France, 21–25 July 2019. [Google Scholar] [CrossRef]
- Chae, D.K.; Kim, S.W.; Kang, J.S.; Lee, J.T. CFGAN: A generic collaborative filtering framework based on generative adversarial networks. In Proceedings of the 27th ACM International Conference on Information and Knowledge Management, Torino, Italy, 22–26 October 2018. [Google Scholar] [CrossRef]
- Koren, Y.; Bell, R.; Volinsky, C. Matrix factorization techniques for recommender systems. Computer 2009, 42, 30–37. [Google Scholar] [CrossRef]
- Salakhutdinov, R.; Mnih, A. Probabilistic matrix factorization. In Advances in Neural Information Processing Systems 20; Neural Information Processing Systems Foundation: Vancouver, BC, Canada, 2009. [Google Scholar]
- Rendle, S.; Freudenthaler, C.; Gantner, Z.; Schmidt-Thieme, L. BPR: Bayesian personalized ranking from implicit feedback. In Proceedings of the 25th Conference on Uncertainty in Artificial Intelligence, UAI, Montreal, QC, Canada, 18–21 June 2009. [Google Scholar]
- Rendle, S. Factorization machines. In Proceedings of the IEEE International Conference on Data Mining, ICDM, Sydney, Australia, 13–17 December 2010. [Google Scholar] [CrossRef]
- Koren, Y. Factor in the neighbors: Scalable and accurate collaborative filtering. ACM Trans. Knowl. Discov. Data 2010, 4, 1–24. [Google Scholar] [CrossRef]
- Wu, S.; Tang, Y.; Zhu, Y.; Wang, L.; Xie, X.; Tan, T. Session-based recommendation with graph neural networks. In Proceedings of the AAAI Conference on Artificial Intelligence 2019, Atlanta, GA, USA, 8–12 October 2019. [Google Scholar] [CrossRef]
- Tran, D.H.; Sheng, Q.Z.; Zhang, W.E.; Aljubairy, A.; Zaib, M.; Hamad, S.A.; Tran, N.H.; Khoa, N.L.D. HeteGraph: Graph learning in recommender systems via graph convolutional networks. Neural Comput. Appl. 2021, 1–17. [Google Scholar] [CrossRef]
- Xiong, X.; Qiao, S.; Han, N.; Xiong, F.; Bu, Z.; Li, R.H.; Yue, K.; Yuan, G. Where to go: An effective point-of-interest recommendation framework for heterogeneous social networks. Neurocomputing 2020, 373, 56–69. [Google Scholar] [CrossRef]
- Fan, W.; Ma, Y.; Li, Q.; He, Y.; Zhao, E.; Tang, J.; Yin, D. Graph neural networks for social recommendation. In Proceedings of the World Wide Web Conference, San Francisco, CA, USA, 13 May 2019. [Google Scholar] [CrossRef]
- Cao, Y.; Wang, X.; He, X.; Hu, Z.; Chua, T.S. Unifying knowledge graph learning and recommendation: Towards a better understanding of user preferences. In Proceedings of the World Wide Web Conference, San Francisco, CA, USA, 13 May 2019. [Google Scholar] [CrossRef]
- Dong, Y.; Chawla, N.V.; Swami, A. Metapath2vec: Scalable representation learning for heterogeneous networks. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Halifax, NS, Canada, 13–17 August 2017. [Google Scholar] [CrossRef]
- Fu, T.Y.; Lee, W.C.; Lei, Z. HIN2Vec: Explore meta-paths in heterogeneous information networks for representation learning. In Proceedings of the International Conference on Information and Knowledge Management, Singapore, 6–10 November 2017. [Google Scholar] [CrossRef]
- Yu, X.; Ren, X.; Gu, Q.; Sun, Y.; Han, J. Collaborative Filtering with Entity Similarity Regularization in Heterogeneous Information Networks. In Proceedings of the IJCAI-13 HINA workshop (IJCAI-HINA’13), Beijing, China, 3–9 August 2013. [Google Scholar]
- Yu, X.; Ren, X.; Sun, Y.; Gu, Q.; Sturt, B.; Khandelwal, U.; Norick, B.; Han, J. Personalized entity recommendation: A heterogeneous information network approach. In Proceedings of the WSDM 2014—7th ACM International Conference on Web Search and Data Mining, New York, NY, USA, 24–28 February 2014. [Google Scholar] [CrossRef]
- Shi, C.; Zhang, Z.; Luo, P.; Yu, P.S.; Yue, Y.; Wu, B. Semantic path based personalized recommendation on weighted heterogeneous information networks. In Proceedings of the International Conference on Information and Knowledge Management, Melbourne, Australia, 18–23 October 2015. [Google Scholar] [CrossRef]
- Zhao, H.; Yao, Q.; Li, J.; Song, Y.; Lee, D.L. Meta-graph based recommendation fusion over heterogeneous information networks. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Halifax, NS, Canada, 13–17 August 2017. [Google Scholar] [CrossRef]
- Xie, J.; Zhu, F.; Li, X.; Huang, S.; Liu, S. Attentive Preference Personalized Recommendation with Sentence-level Explanations. Neurocomputing 2020, 426, 235–247. [Google Scholar] [CrossRef]
- Wang, H.; Wang, N.; Yeung, D.Y. Collaborative deep learning for recommender systems. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Sydney, NSW, Australia, 10–13 August 2015. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Song, W.; Duan, Z.; Xu, Y.; Shi, C.; Zhang, M.; Xiao, Z.; Tang, J. Autoint: Automatic feature interaction learning via self-attentive neural networks. In Proceedings of the International Conference on Information and Knowledge Management, Beijing, China, 3–7 November 2019. [Google Scholar] [CrossRef]
- Chen, L.; Zheng, Z.; Liu, Y.; Yu, P.S. Heterogeneous neural attentive factorization machine for rating prediction. In Proceedings of the International Conference on Information and Knowledge Management, Turin, Italy, 22–26 October 2018. [Google Scholar] [CrossRef]
- Chen, J.; Wang, X.; Zhao, S.; Qian, F.; Zhang, Y. Deep attention user-based collaborative filtering for recommendation. Neurocomputing 2020, 383, 57–68. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, H.; He, X.; Nie, L.; Liu, W.; Chua, T.S. Attentive collaborative filtering: Multimedia recommendation with item-And component-level attention. In Proceedings of the SIGIR 2017—The 40th International ACM SIGIR Conference on Research and Development in Information Retrieval, Tokyo, Japan, 7–11 August 2017. [Google Scholar] [CrossRef]
- Velicković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Liò, P.; Bengio, Y. Graph attention networks. STAT 2017, 1050, 20. [Google Scholar]
- Wang, X.; He, X.; Cao, Y.; Liu, M.; Chua, T.S. KGAT: Knowledge graph attention network for recommendation. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Paris, France, 28 June–1 July 2019. [Google Scholar] [CrossRef]
- Wang, X.; Ji, H.; Cui, P.; Yu, P.; Shi, C.; Wang, B.; Ye, Y. Heterogeneous graph attention network. In Proceedings of the The Web Conference 2019—The World Wide Web Conference, San Francisco, CA, USA, 13 May 2019. [Google Scholar] [CrossRef]
- Lu, R.; Hou, S. On semi-supervised multiple representation behavior learning. J. Comput. Sci. 2020, 46, 101111. [Google Scholar] [CrossRef]
- Juan, Y.; Zhuang, Y.; Chin, W.S.; Lin, C.J. Field-aware factorization machines for CTR prediction. In Proceedings of the RecSys 2016—10th ACM Conference on Recommender Systems, Boston, MA, USA, 17 September 2016. [Google Scholar] [CrossRef]
- Guo, H.; Tang, R.; Ye, Y.; Li, Z.; He, X. DeepFM: A factorization-machine based neural network for CTR prediction. In Proceedings of the IJCAI International Joint Conference on Artificial Intelligence, Melbourne, Australia, 19–25 August 2017. [Google Scholar] [CrossRef]
- Cheng, H.T.; Koc, L.; Harmsen, J.; Shaked, T.; Chandra, T.; Aradhye, H.; Anderson, G.; Corrado, G.; Chai, W.; Ispir, M.; et al. Wide & deep learning for recommender systems. In Proceedings of the ACM International Conference Proceeding Series, Indianapolis, IN, USA, 24–28 October 2016. [Google Scholar] [CrossRef]
- He, X.; Liao, L.; Zhang, H.; Nie, L.; Hu, X.; Chua, T.S. Neural collaborative filtering. In Proceedings of the 26th International World Wide Web Conference, Perth, Australia, 3–7 April 2007. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J.L. Adam: A method for stochastic optimization. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015—Conference Track Proceedings, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]




| Dataset | Meta-Path |
|---|---|
| Amazon | |
| Yelp | |
| Amazon | Yelp | ||
|---|---|---|---|
| Entity | Number | Entity | Number |
| User | 6170 | User | 16,239 |
| Item | 2753 | Business | 14,284 |
| View | 3857 | Compliment | 11 |
| Category | 22 | Category | 511 |
| Brand | 334 | City | 47 |
| Relation | Number | Relation | Number |
| user–item | 195,791 | User-Business | 198,397 |
| Item-View | 5694 | User-User | 158,590 |
| Item-Categoty | 5508 | User-Compliment | 76,875 |
| Item-Brand | 2753 | Business-City | 14,267 |
| Business-Category | 40,009 | ||
| Density = 1.15% | Density = 0.086% | ||
| Dataset/Ratio | DANER-No | DANER-Local | DANER-Global | DANER-Add | DANER-Concate |
|---|---|---|---|---|---|
| Amazon/20% | 0.819 | 0.691 | 0.69 | 0.687 | 0.672 |
| Amazon/30% | 0.823 | 0.697 | 0.696 | 0.693 | 0.689 |
| Amazon/40% | 0.849 | 0.70 | 0.701 | 0.698 | 0.695 |
| Yelp/20% | 0.837 | 0.793 | 0.792 | 0.799 | 0.784 |
| Yelp/30% | 0.858 | 0.795 | 0.805 | 0.85 | 0.795 |
| Yelp/40% | 0.86 | 0.799 | 0.809 | 0.809 | 0.798 |
| Dataset/Ratio | DANER-No | DANER-Local | DANER-Global | DANER-Add | DANER-Concate |
|---|---|---|---|---|---|
| Amazon/20% | 1.066 | 0.941 | 0.937 | 0.935 | 0.934 |
| Amazon/30% | 1.071 | 0.947 | 0.945 | 0.945 | 0.944 |
| Amazon/40% | 1.075 | 0.949 | 0.948 | 0.95 | 0.946 |
| Yelp/20% | 1.065 | 1.017 | 1.015 | 1.016 | 1.009 |
| Yelp/30% | 1.073 | 1.024 | 1.03 | 1.025 | 1.019 |
| Yelp/40% | 1.08 | 1.029 | 1.031 | 1.028 | 1.022 |
| Dataset/Ratio | RegSVD | SVD++ | NeuCF | FMG | DANER |
|---|---|---|---|---|---|
| Amazon/20% | 0.728 | 0.715 | 0.702 | 0.711 | 0.672 |
| Amazon/30% | 0.731 | 0.726 | 0.722 | 0.717 | 0.689 |
| Amazon/40% | 0.749 | 0.781 | 0.739 | 0.722 | 0.695 |
| Yelp/20% | 0.833 | 0.818 | 0.808 | 0.796 | 0.784 |
| Yelp/30% | 0.835 | 0.819 | 0.814 | 0.81 | 0.795 |
| Yelp/40% | 0.841 | 0.825 | 0.828 | 0.819 | 0.798 |
| Dataset/Ratio | RegSVD | SVD++ | NeuCF | FMG | DANER |
|---|---|---|---|---|---|
| Amazon/20% | 0.957 | 0.949 | 0.954 | 0.947 | 0.934 |
| Amazon/30% | 0.961 | 0.954 | 0.957 | 0.949 | 0.944 |
| Amazon/40% | 0.986 | 0.966 | 0.963 | 0.954 | 0.946 |
| Yelp/20% | 1.066 | 1.051 | 1.027 | 1.025 | 1.008 |
| Yelp/30% | 1.068 | 1.054 | 1.032 | 1.032 | 1.019 |
| Yelp/40% | 1.075 | 1.060 | 1.037 | 1.034 | 1.022 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zuo, X.; Jia, T.; He, X.; Yang, B.; Wang, Y. Exploiting Dual-Attention Networks for Explainable Recommendation in Heterogeneous Information Networks. Entropy 2022, 24, 1718. https://doi.org/10.3390/e24121718
Zuo X, Jia T, He X, Yang B, Wang Y. Exploiting Dual-Attention Networks for Explainable Recommendation in Heterogeneous Information Networks. Entropy. 2022; 24(12):1718. https://doi.org/10.3390/e24121718
Chicago/Turabian StyleZuo, Xianglin, Tianhao Jia, Xin He, Bo Yang, and Ying Wang. 2022. "Exploiting Dual-Attention Networks for Explainable Recommendation in Heterogeneous Information Networks" Entropy 24, no. 12: 1718. https://doi.org/10.3390/e24121718
APA StyleZuo, X., Jia, T., He, X., Yang, B., & Wang, Y. (2022). Exploiting Dual-Attention Networks for Explainable Recommendation in Heterogeneous Information Networks. Entropy, 24(12), 1718. https://doi.org/10.3390/e24121718







