Planar Gas Expansion under Intensive Nanosecond Laser Evaporation into Vacuum as Applied to Time-of-Flight Analysis
Abstract
:1. Introduction
2. Formulation of the Problem
3. Methods of the Analysis
3.1. DSMC
3.2. BGK Model Equation
3.3. Analytical Continuum Solution
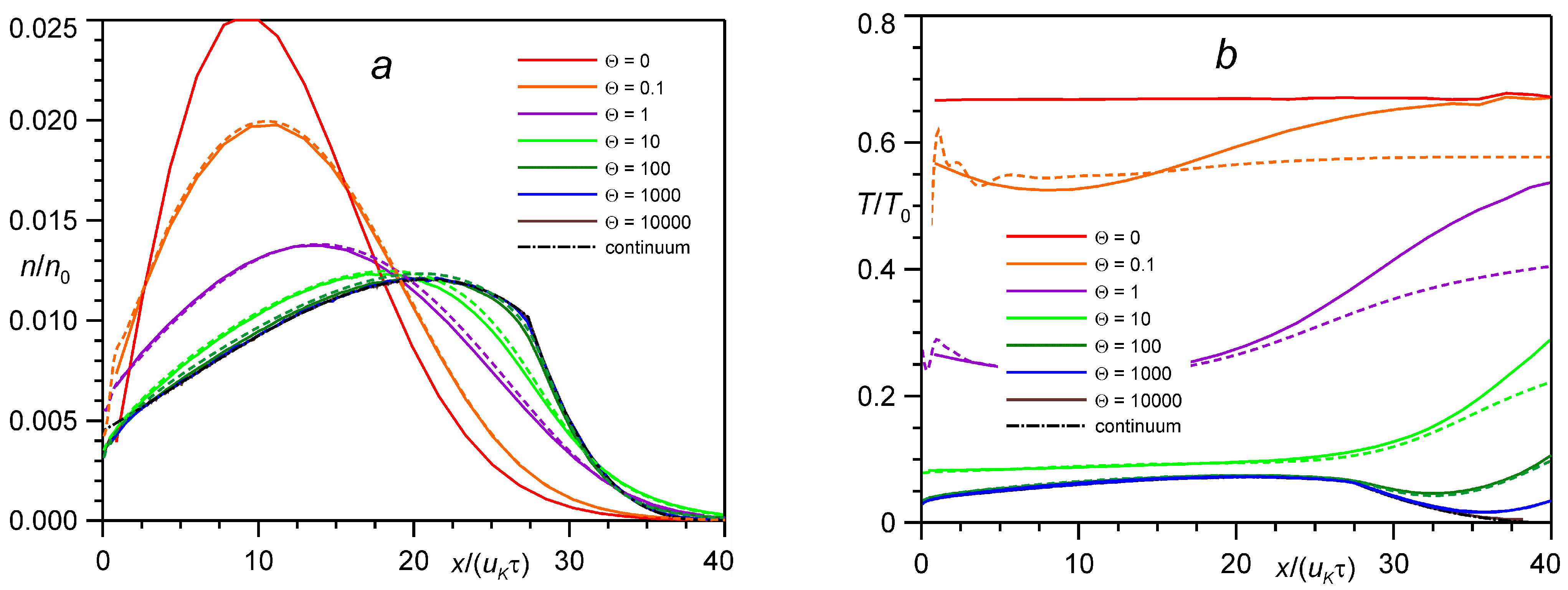
4. Results and Discussion
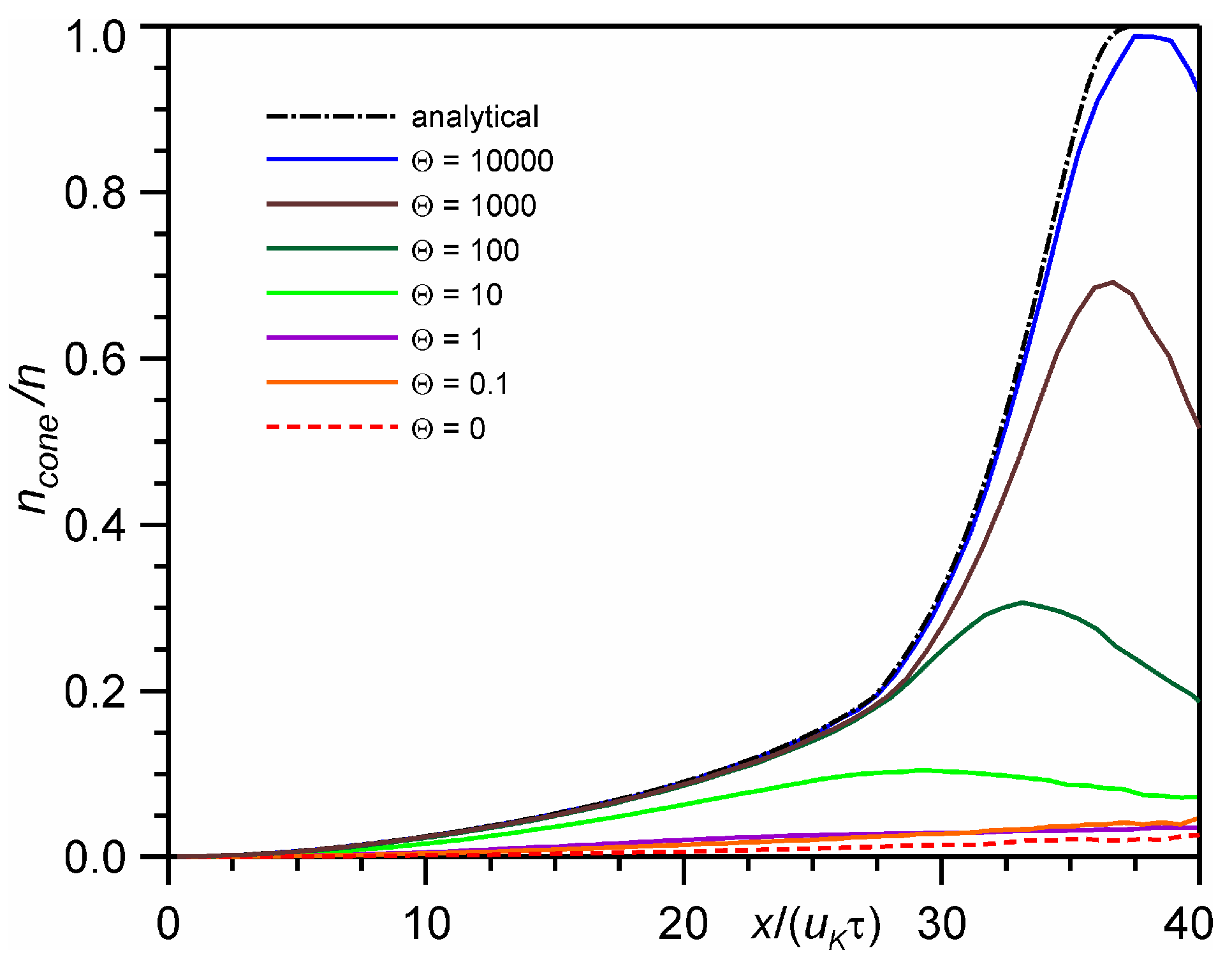
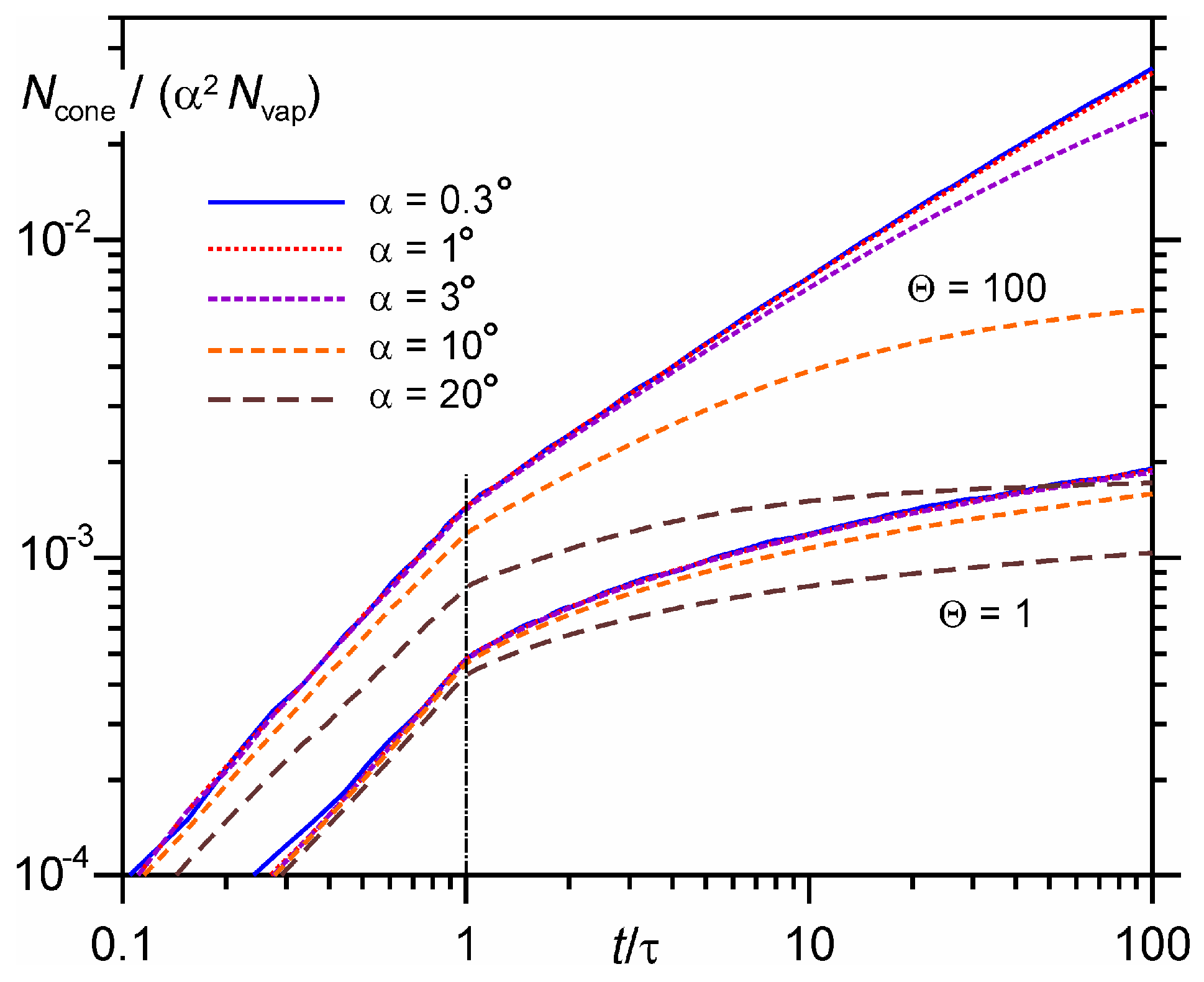
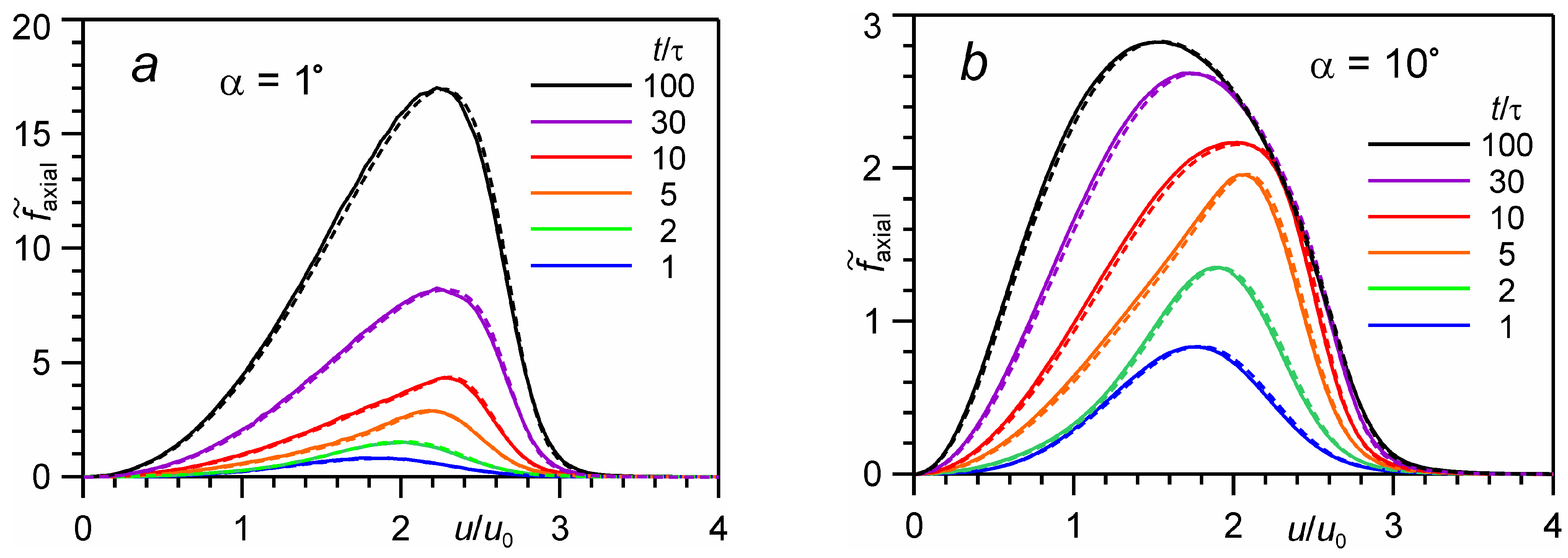
4.1. Distribution of Molecules in the Velocity Cone
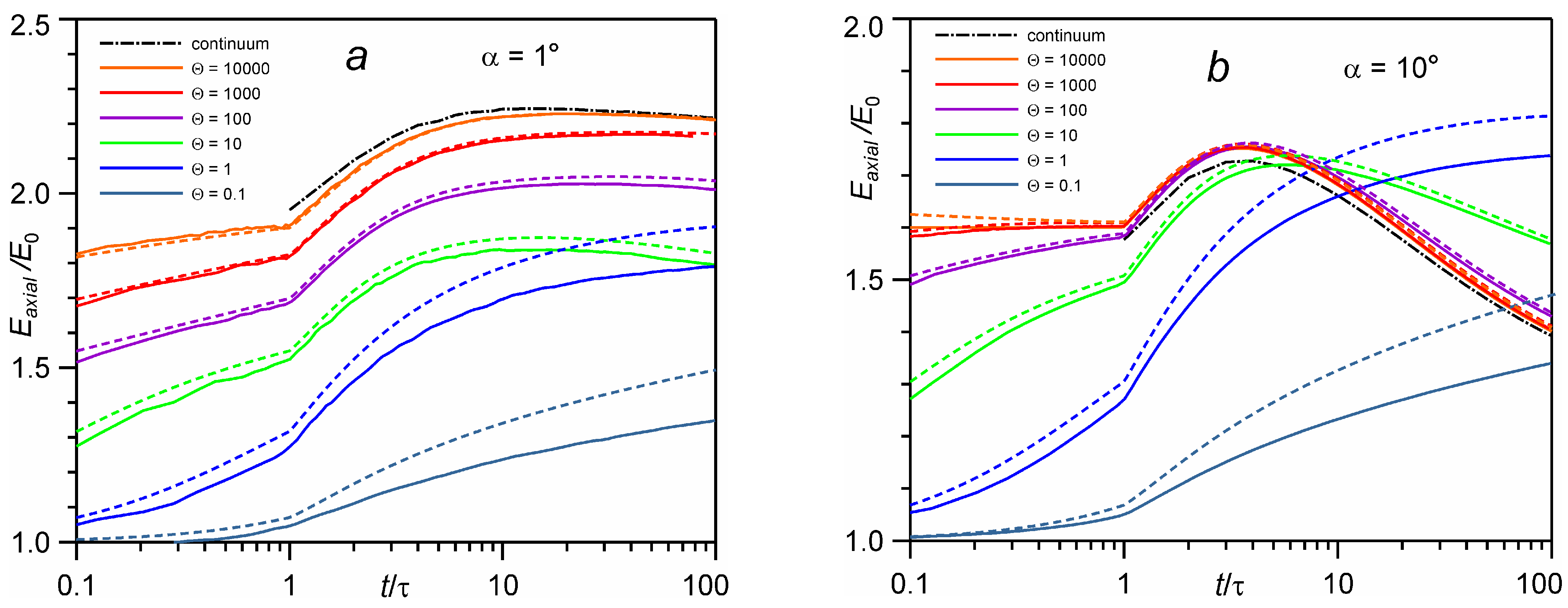
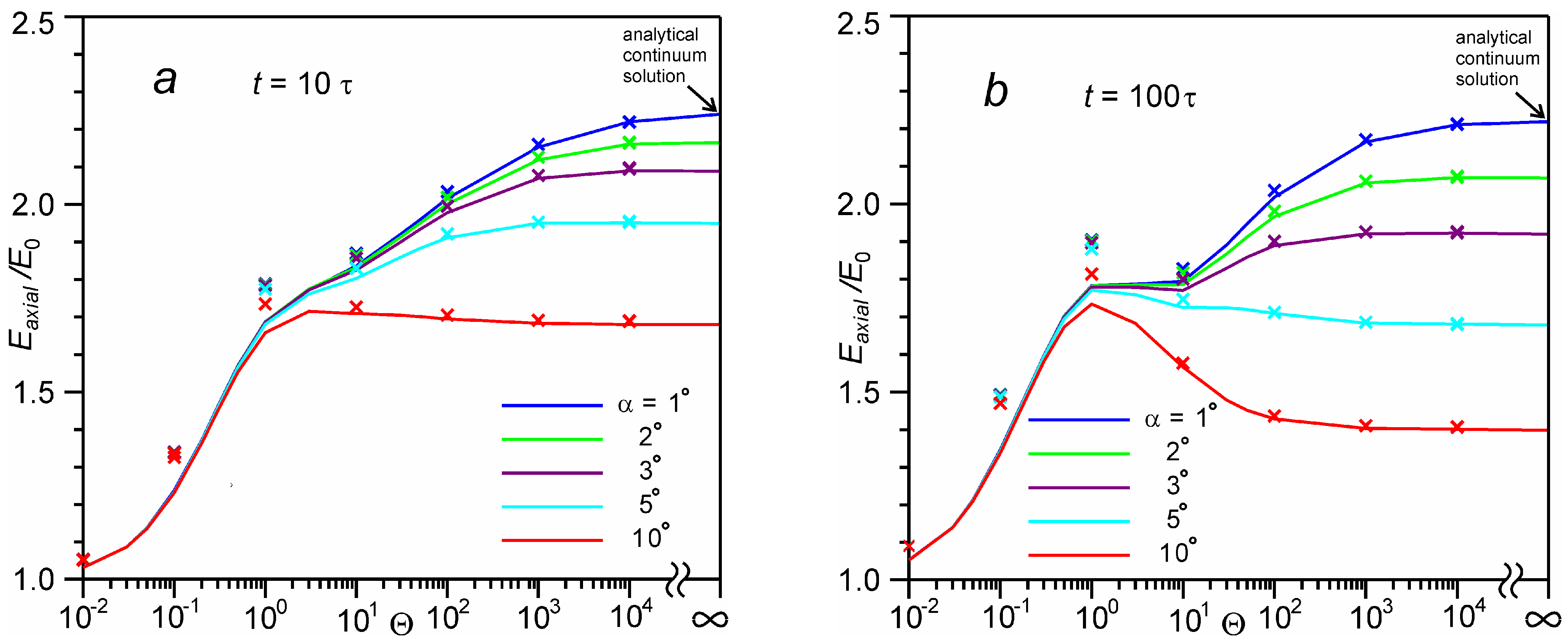
4.2. Temporal Evolution of Average Energy of Molecules
4.3. Generalizing Dependences on Average Energy of Molecules
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bäuerle, D. Laser Processing and Chemistry, 4th ed.; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Kell, R.; Dreyfus, R.W. On the effect of Knudsen-layer formation on studies of vaporization, sputtering, and desorption. Surf. Sci. 1988, 198, 263–276. [Google Scholar] [CrossRef]
- Braun, R.; Hess, P. Time-of-flight investigation of infrared laser-induced multilayer desorption of benzene. J. Chem. Phys. 1993, 99, 8330–8340. [Google Scholar] [CrossRef]
- Krajnovich, D.J. Laser sputtering of highly oriented pyrolytic graphite at 248 nm. J. Chem. Phys. 1995, 102, 726–743. [Google Scholar] [CrossRef]
- Claeyssens, F.; Henley, S.J.; Ashfold, M.N.R. Comparison of the ablation plumes arising from ArF laser ablation of graphite, silicon, copper, and aluminum in vacuum. J. Appl. Phys. 2003, 94, 2203–2211. [Google Scholar] [CrossRef]
- Morozov, A.A. Analytical formula for interpretation of time-of-flight distributions for neutral particles under pulsed laser evaporation in vacuum. J. Phys. D Appl. Phys. 2015, 48, 195501. [Google Scholar] [CrossRef] [Green Version]
- Bauer, W.; Perram, G. Laser ablated Ti velocity distribution dynamics. J. Opt. Soc. Am. B 2018, 35, 27–37. [Google Scholar] [CrossRef]
- Skočić, M.; Dojić, D.; Bukvić, S. Consideration of optical time of flight measurement in laser induced plasmas. Spectrochim. Acta B 2020, 165, 105786. [Google Scholar] [CrossRef]
- Irimiciuc, S.A.; Chertopalov, S.; Lancok, J.; Craciun, V. Langmuir probe technique for plasma characterization during pulsed laser deposition process. Coatings 2021, 11, 762. [Google Scholar] [CrossRef]
- Morozov, A.A.; Mironova, M.L. Numerical analysis of time-of-flight distributions of neutral particles for pulsed laser ablation of binary substances into vacuum. Appl. Phys. A 2017, 123, 783. [Google Scholar] [CrossRef]
- Bird, G.A. Molecular Gas Dynamics and Direct Simulation of Gas Flows; Clarendon Press: Oxford, UK, 1994. [Google Scholar]
- NoorBatcha, I.; Lucchese, R.R.; Zeiri, Y. Effects of gas-phase collisions on particles rapidly desorbed from surfaces. Phys. Rev. B 1987, 36, 4978–4981. [Google Scholar] [CrossRef]
- Feil, H.; Baller, T.S.; Dieleman, J. Effects of post-desorption collisions on the energy distribution of SiCl molecules pulsed-laser desorbed from Cl-covered Si surfaces: Monte-Carlo simulations compared to experiments. Appl. Phys. A 1992, 55, 554–560. [Google Scholar] [CrossRef]
- Sibold, D.; Urbassek, H.M. Effect of gas-phase collisions in pulsed-laser desorption: A three-dimensional Monte Carlo simulation study. J. Appl. Phys. 1993, 73, 8544–8551. [Google Scholar] [CrossRef]
- Morozov, A.A. Dynamics of gas cloud expansion under pulsed laser evaporation into vacuum. J. Phys. Conf. Ser. 2018, 1105, 012116. [Google Scholar] [CrossRef]
- Itina, T.E.; Tokarev, V.N.; Marine, W.; Autric, M. Monte Carlo simulation study of the effects of nonequilibrium chemical reactions during pulsed laser desorption. J. Chem. Phys. 1997, 106, 8905–8912. [Google Scholar] [CrossRef]
- Petrov, V.A.; Ranjbar, O.A.; Zhilyaev, P.A.; Volkov, A.N. Kinetic simulations of laser-induced plume expansion from a copper target into a vacuum or argon background gas based on ab initio calculation of Cu–Cu, Ar–Ar, and Ar–Cu interactions. Phys. Fluids 2020, 32, 102010. [Google Scholar] [CrossRef]
- Konomi, I.; Motohiro, T.; Kobayashi, T.; Asaoka, T. Considerations on the determining factors of the angular distribution of emitted particles in laser ablation. Appl. Surf. Sci. 2010, 256, 4959–4965. [Google Scholar] [CrossRef]
- Urbassek, H.M.; Sibold, D. Gas-phase segregation effects in pulsed laser desorption from binary targets. Phys. Rev. Lett. 1993, 70, 1886–1889. [Google Scholar] [CrossRef]
- Morozov, A.A.; Starinskiy, S.V.; Bulgakov, A.V. Pulsed laser ablation of binary compounds: Effect of time delay in component evaporation on ablation plume expansion. J. Phys. D Appl. Phys. 2021, 54, 175203. [Google Scholar] [CrossRef]
- Itina, T.E.; Patrone, L.; Marine, W.; Autric, M. Numerical analysis of TOF measurements in pulsed laser ablation. Appl. Phys. A 1999, 69, S59–S65. [Google Scholar] [CrossRef]
- Garrelie, F.; Aubreton, J.; Catherinot, A. Monte Carlo simulation of laser-induced plasma plume expansion under vacuum: Comparison with experiments. J. Appl. Phys. 1998, 83, 5075–5082. [Google Scholar] [CrossRef]
- Morozov, A.A. Interpretation of time-of-flight distributions for neutral particles under pulsed laser evaporation using direct Monte Carlo simulation. J. Chem. Phys. 2013, 139, 234706. [Google Scholar] [CrossRef] [PubMed]
- Bykov, N.Y.; Bulgakova, N.M.; Bulgakov, A.V.; Loukianov, G.A. Pulsed laser ablation of metals in vacuum: DSMC study versus experiment. Appl. Phys. A 2004, 79, 1097–1100. [Google Scholar] [CrossRef]
- Morozov, A.A. Analysis of time-of-flight distributions under pulsed laser ablation in vacuum based on the DSMC calculations. Appl. Phys. A 2013, 111, 1107–1111. [Google Scholar] [CrossRef]
- Morozov, A.A.; Evtushenko, A.B.; Bulgakov, A.V. Gas-dynamic acceleration of laser-ablation plumes: Hyperthermal particle energies under thermal vaporization. Appl. Phys. Lett. 2015, 106, 054107. [Google Scholar] [CrossRef]
- Ellegaard, O.; Schou, J.; Urbassek, H.M. Monte–Carlo description of gas flow from laser-evaporated silver. Appl. Phys. A 1999, 69, S577–S581. [Google Scholar] [CrossRef]
- Morozov, A.A. Effect of temporal evolution of the evaporation surface temperature on the plume expansion under pulsed laser ablation. J. Phys. Conf. Ser. 2020, 1677, 012143. [Google Scholar] [CrossRef]
- Morozov, A.A. Effect of evaporation-flux nonuniformity along the irradiation-spot radius on the plume expansion dynamics during pulsed laser ablation in vacuum. Thermophys. Aeromech. 2022, 29, 437–448. [Google Scholar] [CrossRef]
- Itina, T.E.; Marine, W.; Autric, M. Nonstationary effects in pulsed laser ablation. J. Appl. Phys. 1999, 85, 7905–7908. [Google Scholar] [CrossRef] [Green Version]
- Gusarov, A.V.; Smurov, I. Influence of atomic collisions in vapour phase on pulsed laser ablation. Appl. Surf. Sci. 2000, 168, 96–99. [Google Scholar] [CrossRef]
- Volkov, A.N. Splitting of laser-induced neutral and plasma plumes: Hydrodynamic origin of bimodal distributions of vapor density and plasma emission intensity. J. Phys. D Appl. Phys. 2021, 54, 37LT01. [Google Scholar] [CrossRef]
- Morozov, A.A.; Frolova, A.A.; Titarev, V.A. On different kinetic approaches for computing planar gas expansion under pulsed evaporation into vacuum. Phys. Fluids 2020, 32, 112005. [Google Scholar] [CrossRef]
- Morozov, A.A.; Titarev, V.A. Dynamics of planar gas expansion during nanosecond laser evaporation into a low-pressure background gas. Phys. Fluids 2022, 34, 096101. [Google Scholar] [CrossRef]
- Titarev, V.A.; Morozov, A.A. Arbitrary Lagrangian-Eulerian discrete velocity method with application to laser-induced plume expansion. Appl. Math. Comput. 2022, 429, 127241. [Google Scholar] [CrossRef]
- Miotello, A.; Kelly, R. Critical assessment of thermal models for laser sputtering at high fluences. Appl. Phys. Lett. 1995, 67, 3535–3537. [Google Scholar] [CrossRef]
- Bulgakova, N.M.; Bulgakov, A.V. Pulsed laser ablation of solids: Transition from normal vaporization to phase explosion. Appl. Phys. A 2001, 73, 199–208. [Google Scholar] [CrossRef]
- Sone, Y.; Sugimoto, H. Kinetic theory analysis of steady evaporating flows from a spherical condensed phase into a vacuum. Phys. Fluids A 1993, 5, 1491–1511. [Google Scholar] [CrossRef]
- Titov, E.V.; Levin, D.A. Extension of the DSMC method to high pressure flows. Int. J. Comput. Fluid Dyn. 2007, 21, 351–368. [Google Scholar] [CrossRef]
- Bird, G.A.; Gallis, M.A.; Torczynski, J.R.; Rader, D.J. Accuracy and efficiency of the sophisticated direct simulation Monte Carlo algorithm for simulating noncontinuum gas flows. Phys. Fluids 2009, 21, 017103. [Google Scholar] [CrossRef]
- Bhatnagar, P.; Gross, E.; Krook, M. A model for collision processes in gases. I. Small amplitude processes in charged and neutral one-component systems. Phys. Rev. 1954, 94, 511–525. [Google Scholar] [CrossRef]
- Drikakis, D.; Rider, W. High Resolution Methods for Incompressible and Low Speed Flows; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Toro, E.F. Riemann Solvers and Numerical Methods for Fluid Dynamics, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Hirt, C.W.; Amsden, A.A.; Cook, J.L. An arbitrary Lagrangian-Eulerian computing method for all flow speeds. J. Comput. Phys. 1974, 14, 227. [Google Scholar] [CrossRef]
- Boscheri, W.; Loubère, R.; Dumbser, M. Direct Arbitrary-Lagrangian-Eulerian ADER-MOOD finite volume schemes for multidimensional hyperbolic conservation laws. J. Comput. Phys. 2015, 292, 56. [Google Scholar] [CrossRef]
- Titarev, V. Efficient deterministic modelling of three-dimensional rarefied gas flows. Commun. Comput. Phys. 2012, 12, 162. [Google Scholar] [CrossRef]
- Titarev, V.; Dumbser, M.; Utyuzhnikov, S. Construction and comparison of parallel implicit kinetic solvers in three spatial dimensions. J. Comput. Phys. 2014, 256, 17. [Google Scholar] [CrossRef]
- Titarev, V. Application of the Nesvetay code for solving three-dimensional high-altitude aerodynamics problems. Comput. Math. Math. Phys. 2020, 60, 737. [Google Scholar] [CrossRef]
- Florinski, V.; Balsara, D.; Garain, S.; Gurski, K. Technologies for supporting high-order geodesic mesh frameworks for and space sciences. Comput. Astrophys. Cosmol. 2020, 7, 1. [Google Scholar] [CrossRef] [Green Version]
- Sibold, D.; Urbassek, H.M. Gas-dynamic study of pulsed desorption flows into a vacuum. Phys. Fluids A 1992, 4, 165–177. [Google Scholar] [CrossRef]
- Stanukovich, K.P. Unsteady Motion of Continuous Media; Pergamon: New York, NY, USA, 1960. [Google Scholar]
- Moizhes, B.Y.; Nemchinsky, V.A. Formation of a jet during vaporization in vacuum. Sov. Phys. Tech. Phys. 1982, 27, 438–441. [Google Scholar]
- Morozov, A.A. Evolution of the back flux in the case of pulsed evaporation into vacuum. Dokl. Phys. 2004, 49, 134–137. [Google Scholar] [CrossRef]
- Morozov, A.A. Thermal model of pulsed laser ablation: Back flux contribution. Appl. Phys. A 2004, 79, 997–999. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morozov, A.; Titarev, V. Planar Gas Expansion under Intensive Nanosecond Laser Evaporation into Vacuum as Applied to Time-of-Flight Analysis. Entropy 2022, 24, 1738. https://doi.org/10.3390/e24121738
Morozov A, Titarev V. Planar Gas Expansion under Intensive Nanosecond Laser Evaporation into Vacuum as Applied to Time-of-Flight Analysis. Entropy. 2022; 24(12):1738. https://doi.org/10.3390/e24121738
Chicago/Turabian StyleMorozov, Alexey, and Vladimir Titarev. 2022. "Planar Gas Expansion under Intensive Nanosecond Laser Evaporation into Vacuum as Applied to Time-of-Flight Analysis" Entropy 24, no. 12: 1738. https://doi.org/10.3390/e24121738
APA StyleMorozov, A., & Titarev, V. (2022). Planar Gas Expansion under Intensive Nanosecond Laser Evaporation into Vacuum as Applied to Time-of-Flight Analysis. Entropy, 24(12), 1738. https://doi.org/10.3390/e24121738








