Boltzmann Configurational Entropy Revisited in the Framework of Generalized Statistical Mechanics
Abstract
:1. Introduction
2. Occupational Counting in the Generalized Statistics
3. Boltzmann Entropy of Degree
4. Connection with the Shannon Entropy of Degree
5. Some Particular Cases
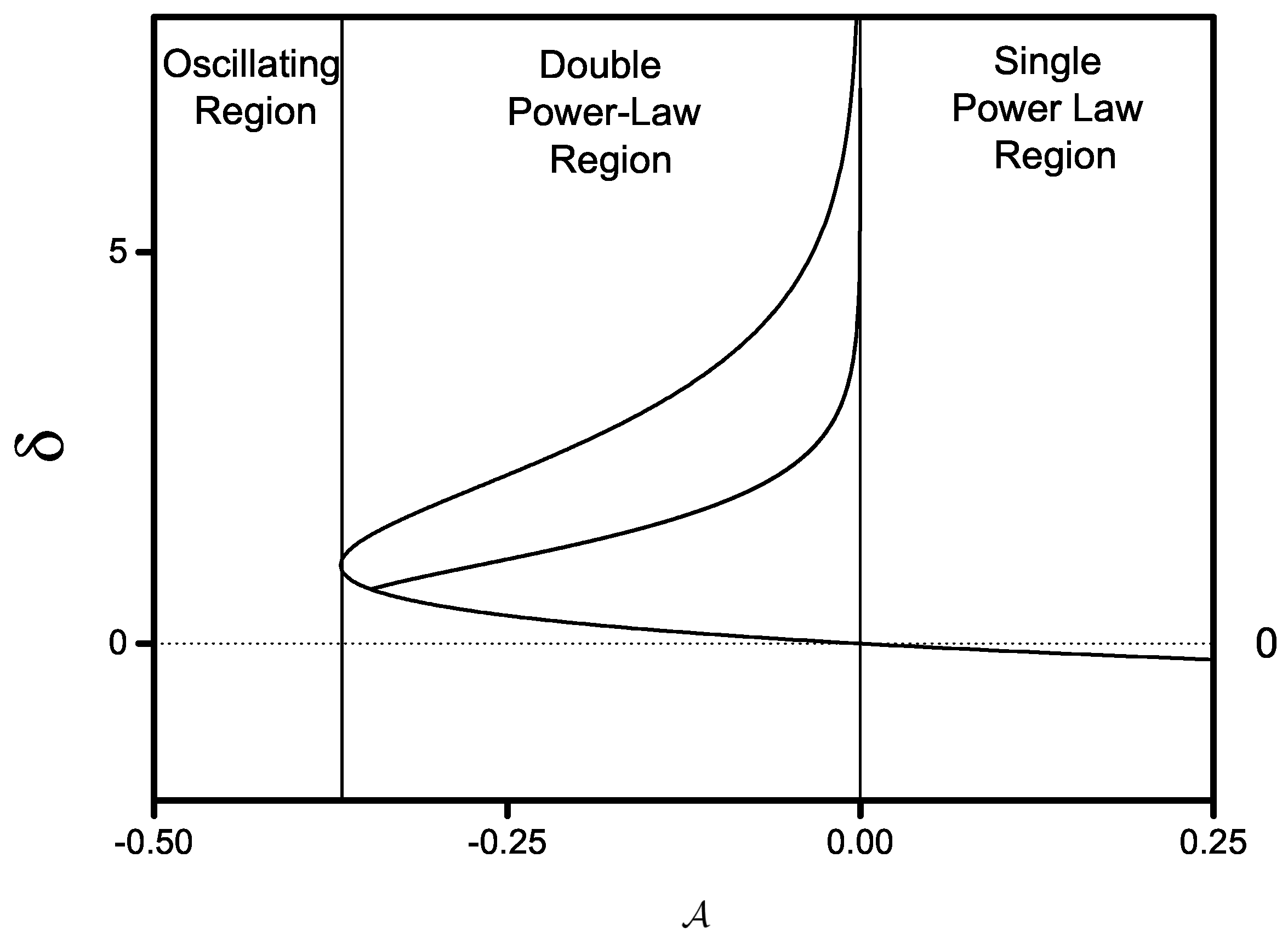
5.1. -Deformed Boltzmann Entropy
5.2. q-Deformed Boltzmann Entropy
6. Conclusions
Funding
Conflicts of Interest
Appendix A. Asymptotic Approximation of
- ,
- ,
- ,
References
- Ji, X.; Du, J. Diffusion and heat conductivity in the weakly ionized plasma with power-law q-distributions in nonextensive statistics. Physica A 2019, 523, 292–300. [Google Scholar] [CrossRef] [Green Version]
- Modanese, G. Common origin of power-law tails in income distributions and relativistic gases. Phys. Lett. A 2016, 380, 29–32. [Google Scholar] [CrossRef] [Green Version]
- Campagnano, C.; Zilberberg, O.; Gornyi, I.V.; Feldman, O.E.; Potter, A.C.; Gefen, Y. Hanbury brown–twiss interference of anyons. Phys. Rev. Lett. 2012, 109, 106802–106805. [Google Scholar] [CrossRef] [Green Version]
- Shen, Y.; Ai, Q.; Long, G.L. The relation between properties of Gentile statistics and fractional statistics of anyon. Physica A 2010, 389, 1565–1570. [Google Scholar] [CrossRef]
- Lavagno, A.; Swamy, P.N. Thermostatistics of deformed bosons and fermions. Found. Phys. 2009, 40, 814–828. [Google Scholar] [CrossRef] [Green Version]
- Bagarello, F. Quons, Coherent states and intertwining operators. Phys. Lett. A 2009, 373, 2637–2642. [Google Scholar] [CrossRef] [Green Version]
- Kibler, M.R. Miscellaneous applications of quons. Symmetry Integr. Geom. Methods Appl. 2007, 3, 92. [Google Scholar] [CrossRef] [Green Version]
- Greenberg, O.W. Particles with small violations of Fermi or Bose statistics. Phys. Rev. D 1991, 43, 4111–4120. [Google Scholar] [CrossRef]
- Acharya, R.; Narayana Swamy, P. Statistical mechanics of anyons. J. Phys. A Math. Theor. 1994, 27, 7247–7263. [Google Scholar] [CrossRef]
- Scarfone, A.M.; Narayana Swamy, P. An interacting particles system revisited in the framework of the q-deformed algebra. J. Phys. A Math. Theor. 2008, 41, 275211. [Google Scholar] [CrossRef]
- Scarfone, A.M.; Narayana Swamy, P. An interacting ensemble of particles in the context of quantum algebra. J. Stat. Mech. Theor. Exp. 2009, 2009, 2055. [Google Scholar] [CrossRef]
- Kaniadakis, G. Non-linear kinetics underlying generalized statistics. Physica A 2001, 296, 405–425. [Google Scholar] [CrossRef] [Green Version]
- Algin, A.; Senay, M. General thermostatistical properties of a q-deformed fermion gas in two dimension. J. Phys. Conf. Ser. 2016, 766, 012008. [Google Scholar] [CrossRef]
- Wilczek, F. (Ed.) Fractional Statistics and Anyon Superconductivity; World Scientific: Singapore, 1990. [Google Scholar]
- Stern, A. Anyons and the quantum Hall effect—A pedagogical review. Ann. Phys. 2008, 323, 204–249. [Google Scholar] [CrossRef] [Green Version]
- Ezawa, Z.F.; Iwazaki, A. Quantum Hall liquid, Josephson effect, and hierarchy in a double-layer electron system. Phys. Rev. B 1993, 1993 47, 7295–7311. [Google Scholar] [CrossRef]
- Haldane, F.D.M. “Spinon gas” description of the S = 1/2 Heisenberg chain with inverse-square exchange: Exact spectrum and thermodynamics. Phys. Rev. Lett. 1991, 66, 1529–1532. [Google Scholar] [CrossRef]
- Wu, Y.S. Statistical distribution for generalized ideal gas of fractional-statistics particles. Phys. Rev. Lett. 1994, 73, 922–925. [Google Scholar] [CrossRef] [PubMed]
- Rüegg, A.; Fiete, G.A. Topological order and semions in a strongly correlated quantum spin hall insulator. Phys. Rev. Lett. 2012, 108, 046401. [Google Scholar]
- Gentile, G., Jr. Osservazioni sopra le statistiche intermedie. Nuovo Cim. 1940, 17, 493–497. [Google Scholar] [CrossRef]
- Hoyuelos, M. Exotic statistics for particles without spin. J. Stat. Mech. Theor. Exp. 2018, 2018, 73103. [Google Scholar] [CrossRef] [Green Version]
- Kaniadakis, G.; Quarati, P. Classical model of bosons and fermions. Phys. Rev. E 1994, 49, 5103–5110. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kaniadakis, G.; Quarati, P.; Scarfone, A.M. Nonlinear canonical quantum system of collectively interacting particles via an exclusion-inclusion principle. Phys. Rev. E 1998, 58, 5574–5585. [Google Scholar] [CrossRef] [Green Version]
- Rossani, A.; Scarfone, A.M. Generalized kinetic theory of electrons and phonons: Models, equilibrium and stability. Physica B 2003, 334, 292–297. [Google Scholar] [CrossRef] [Green Version]
- Scarfone, A.M. Canonical quantization of nonlinear many-body systems. Phys. Rev. E 2006, 71, 051103. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Suyari, H. Mathematical structures derived from the q-multinomial coefficient in Tsallis statistics. Physica A 2006, 368, 63–82. [Google Scholar] [CrossRef]
- Niven, R.K.; Suyari, H. Combinatorial basis and non-asymptotic form of the Tsallis entropy function. Eur. Phys. J. B 2008, 61, 75–82. [Google Scholar] [CrossRef]
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics; Springer: New York, NY, USA, 2009. [Google Scholar]
- Kaniadakis, G. Statistical mechanics in the context of special relativity. Phys. Rev. E 2002, 66, 056125. [Google Scholar] [CrossRef] [Green Version]
- Kaniadakis, G. Statistical mechanics in the context of special relativity. II. Phys. Rev. E 2005, 72, 036108. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wada, T.; Suyari, H. The κ-Generalizations of Stirling approximation and multinominal coefficients. Entropy 2013, 15, 5144–5153. [Google Scholar] [CrossRef]
- Scarfone, A.M. Entropic forms and related algebras. Entropy 2013, 15, 624–649. [Google Scholar] [CrossRef] [Green Version]
- Wada, T. Thermodynamic stability conditions for nonadditive composable entropies. Cont. Mech. Thermodyn. 2004, 16, 263–267. [Google Scholar] [CrossRef] [Green Version]
- Suyari, H.; Wada, T. κ-generalization of Gauss’ law of error. Phys. Lett. A 2006, 348, 89–93. [Google Scholar]
- Scarfone, A.M.; Wada, T. Canonical partition function for anomalous systems described by the κ-entropy. Prog. Theor. Phys. Suppl. 2006, 162, 45–52. [Google Scholar] [CrossRef] [Green Version]
- Cravero, M.; Iabichino, G.; Kaniadakis, G.; Miraldi, E.; Scarfone, A.M. A κ-entropic approach to the analysis of the fracture problem. Physica A 2004, 340, 410–417. [Google Scholar] [CrossRef]
- Ourabah, K.; Tribeche, M. Planck radiation law and Einstein coefficients reexamined in Kaniadakis κ statistics. Phis. Rev. E 2014, 89, 062130. [Google Scholar]
- Lapenta, G.; Markidis, S.; Marocchino, A.; Kaniadakis, G. Relaxation of relativistic plasmas under the effect of wave-particle interactions. Astrophys. J. 2007, 666, 949–954. [Google Scholar] [CrossRef]
- Wada, T.; Scarfone, A.M. Asymptotic solutions of a nonlinear diffusive equation in the framework of κ-generalized statistical mechanics. Eur. Phys. J. B 2009, 70, 65–71. [Google Scholar] [CrossRef] [Green Version]
- Silva, R. The H-theorem in κ-statistics: Influence on the molecular chaos hypothesis. Phys. Lett. A 2006, 352, 17–20. [Google Scholar] [CrossRef] [Green Version]
- Pereira, F.I.M.; Silva, R.; Alcaniz, J.S. Non-Gaussian statistics and the relativistic nuclear equation of state. Nucl. Phys. A 2009, 828, 136–148. [Google Scholar] [CrossRef] [Green Version]
- Casas, G.A.; Nobre, F.D.; Curado, E.M.F. Entropy production and nonlinear Fokker-Planck equations. Phys. Rev. E 2012, 86, 061136. [Google Scholar] [CrossRef] [Green Version]
- Kaniadakis, G. Theoretical Foundations and Mathematical Formalism of the Power-Law Tailed Statistical Distributions. Entropy 2013, 15, 3983–4010. [Google Scholar] [CrossRef] [Green Version]
- Kaniadakis, G.; Baldi, M.M.; Deisboeck, T.S.; Grisolia, G.; Hristopulos, D.T.; Scarfone, A.M.; Sparavigna, A.; Wada, T.; Lucia, U. The κ-statistics approach to epidemiology. Sci. Rep. 2020, 10, 19949. [Google Scholar] [CrossRef] [PubMed]
- Sharma, B.D.; Taneja, I.J. Entropy of type (α,β) and other generalized additive measures in information theory. Metrika 1975, 22, 205–215. [Google Scholar] [CrossRef]
- Mittal, D.P. On some functional equations concerning entropy, directed divergence and inaccuracy. Metrika 1975, 22, 35–46. [Google Scholar] [CrossRef]
- Evans, L.C. Entropy and Partial Differential Equations; UC Berkeley: Berkeley, CA, USA, 2001. [Google Scholar]
- Scarfone, A.M.; Wada, T. Lie symmetries and related group-invariant solutions of a nonlinear Fokker-Planck equation based on the Sharma–Taneja–Mittal entropy. Braz. J. Phys. 2009, 39, 475–482. [Google Scholar] [CrossRef] [Green Version]
- Li, S.-N.; Cao, B.-Y. Mathematical and information-geometrical entropy for phenomenological Fourier and non-Fourier heat conduction. Phys. Rev. E 2017, 96, 032131. [Google Scholar] [CrossRef] [Green Version]
- Essex, C.; Schulzky, C.; Franz, A.; Hoffmann, K.H. Tsallis and Rényi entropies in fractional diffusion and entropy production. Physica A 2000, 284, 299–308. [Google Scholar] [CrossRef]
- Kac, V.; Cheung, P. Quantum Calculus; Springer: New York, NY, USA, 2001. [Google Scholar]
- Pathria, R.K. Statistical Mechanics; Elsevier: Amsterdam, The Netherlands, 1996. [Google Scholar]
- Kaniadakis, G.; Lissia, M.; Scarfone, A.M. Two-parameter deformations of logarithm, exponential, and entropy: A consistent framework for generalized statistical mechanics. Phys. Rev. E 2005, 71, 046128. [Google Scholar] [CrossRef] [Green Version]
- Kaniadakis, G.; Scarfone, A.M.; Sparavigna, A.; Wada, T. Composition law of κ-entropy for statistically independent systems. Phys. Rev. E 2017, 95, 052112. [Google Scholar] [CrossRef] [Green Version]
- Scarfone, A.M. Legendre structure of the thermostatistics theory based on the Sharma–Taneja–Mittal entropy. Physica A 2006, 365, 63–70. [Google Scholar] [CrossRef] [Green Version]
- Nivanen, L.; Le Mehaute, A.; Wang, Q.A. Generalized algebra within a nonextensive statistics. Rep. Math. Phys. 2003, 52, 437–444. [Google Scholar] [CrossRef] [Green Version]
- Borges, E.P. A possible deformed algebra and calculus inspired in nonextensive thermostatistics. Physica A 2004, 340, 95–101. [Google Scholar] [CrossRef] [Green Version]
- Deppman, A.; Oliveira Andrade, E., II. Emergency of Tsallis statistics in fractal networks. PLoS ONE 2021, 16, e0257855. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Scarfone, A.M. Boltzmann Configurational Entropy Revisited in the Framework of Generalized Statistical Mechanics. Entropy 2022, 24, 140. https://doi.org/10.3390/e24020140
Scarfone AM. Boltzmann Configurational Entropy Revisited in the Framework of Generalized Statistical Mechanics. Entropy. 2022; 24(2):140. https://doi.org/10.3390/e24020140
Chicago/Turabian StyleScarfone, Antonio Maria. 2022. "Boltzmann Configurational Entropy Revisited in the Framework of Generalized Statistical Mechanics" Entropy 24, no. 2: 140. https://doi.org/10.3390/e24020140
APA StyleScarfone, A. M. (2022). Boltzmann Configurational Entropy Revisited in the Framework of Generalized Statistical Mechanics. Entropy, 24(2), 140. https://doi.org/10.3390/e24020140





