An Experimental and Numerical Investigation on Bubble Growth in Polymeric Foams
Abstract
:1. Introduction
2. Experiments
2.1. Materials
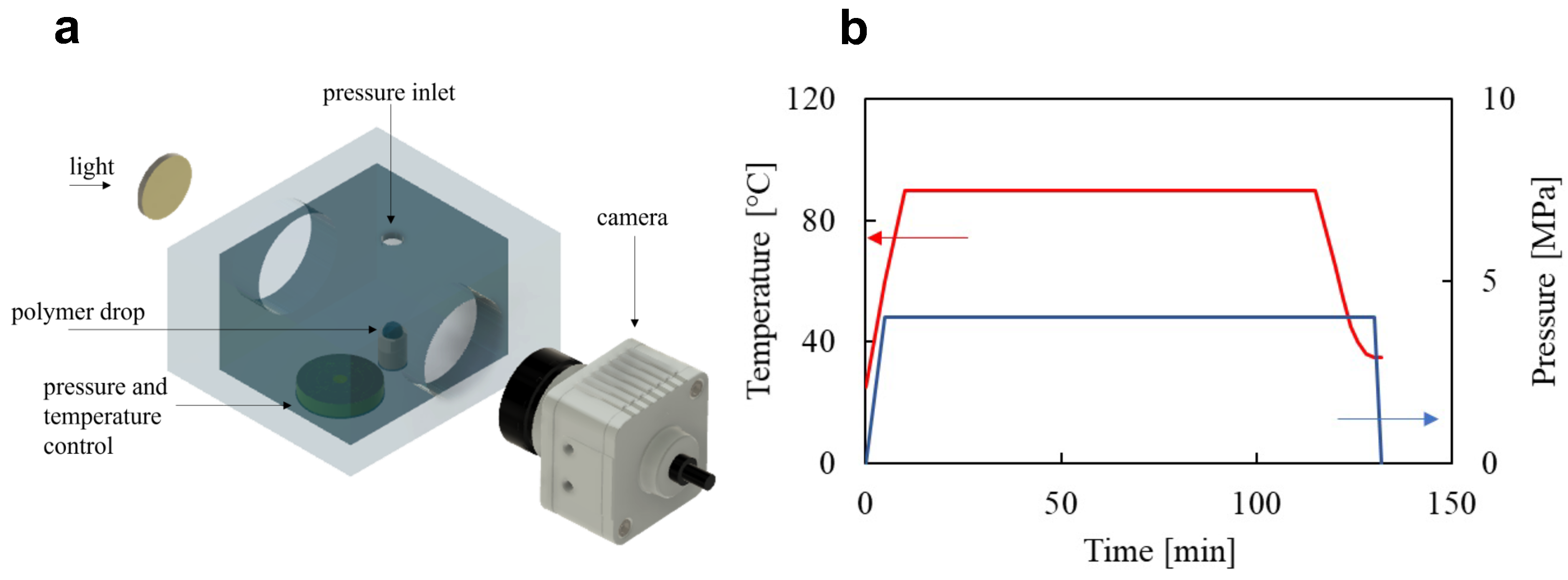
2.2. Foaming Equipment and Procedure
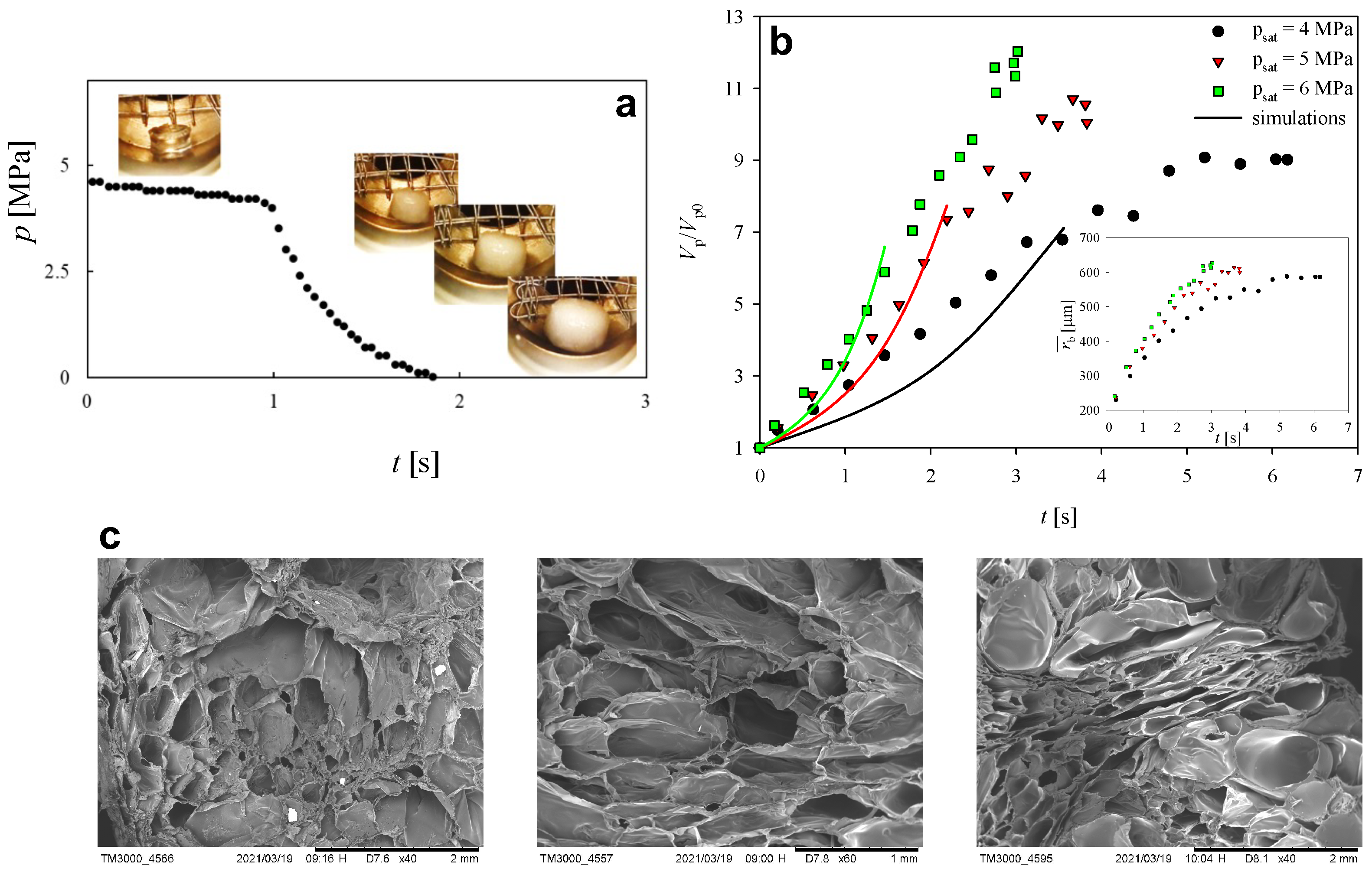
2.3. Experimental Results
3. Direct Numerical Simulations
3.1. Mathematical Model
3.2. Single Bubble Growth
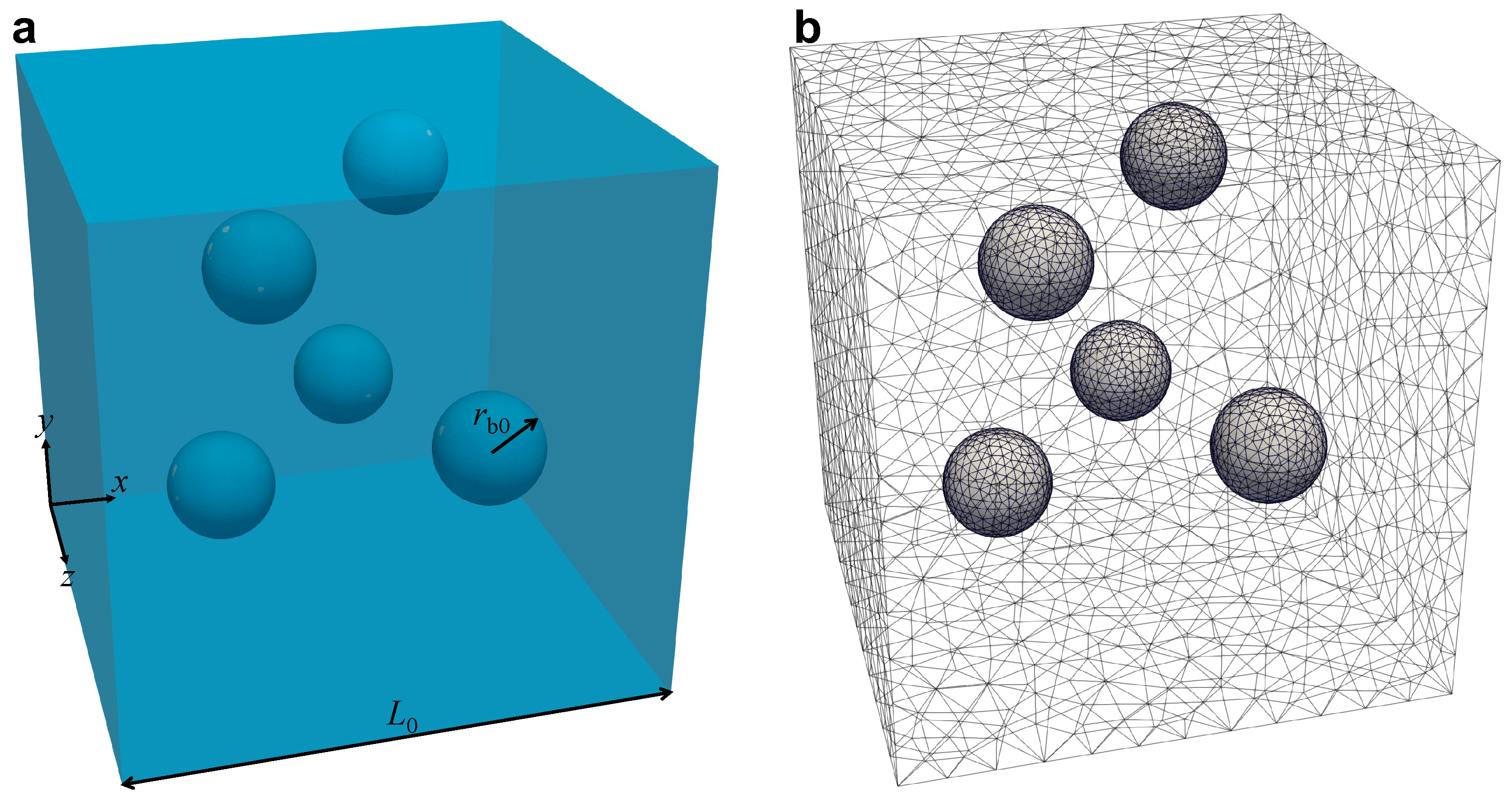
3.3. Numerical Technique
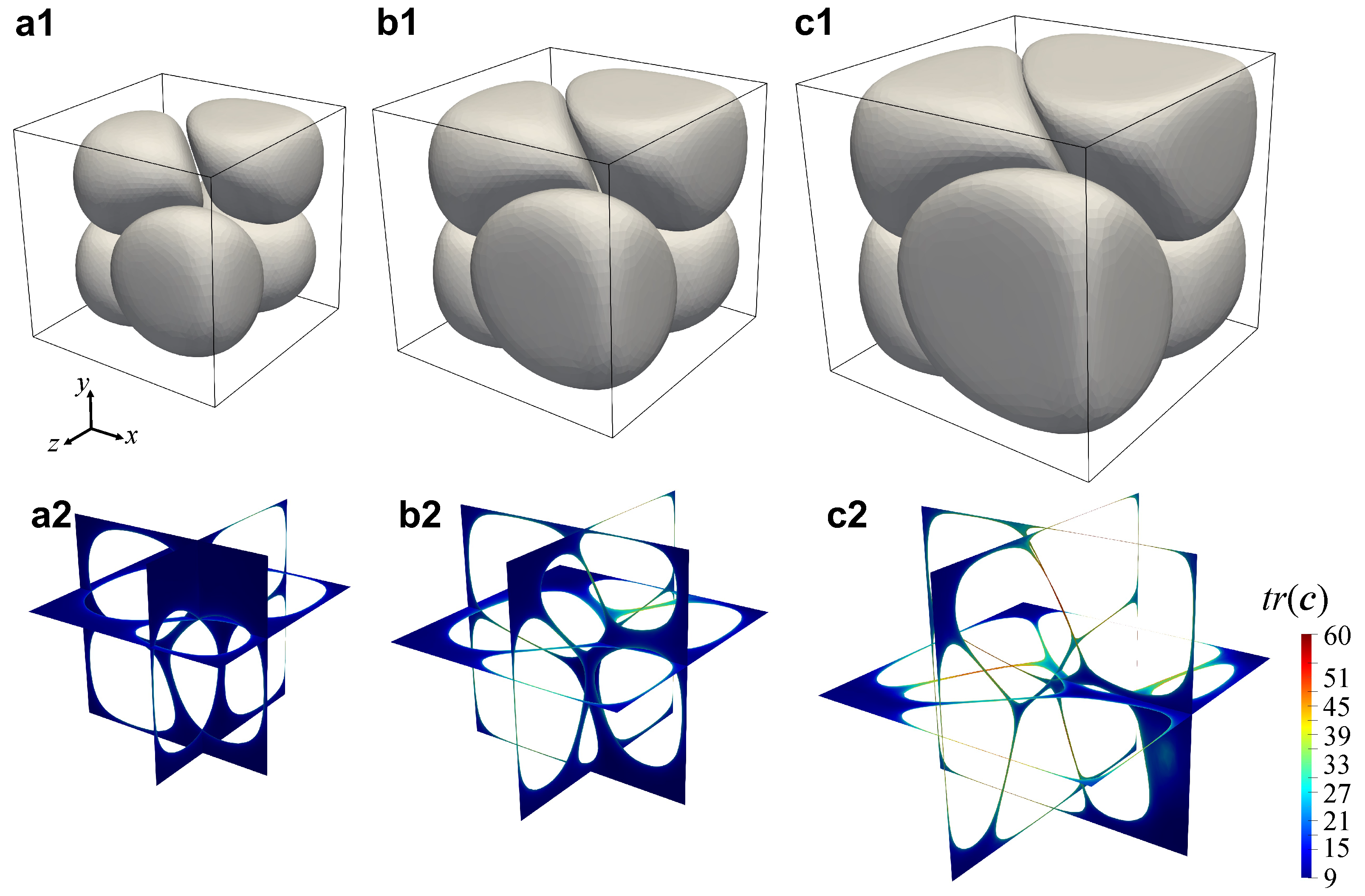
3.4. Numerical Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lee, S.T.; Park, C.B. Foam Extrusion: Principles and Practice; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Naguib, H.E.; Park, C.B.; Panzer, U.; Reichelt, N. Strategies for achieving ultra low-density polypropylene foams. Polym. Eng. Sci. 2002, 42, 1481–1492. [Google Scholar] [CrossRef]
- Lombardi, L.; Tammaro, D. Effect of polymer swell in extrusion foaming of low-density polyethylene. Phys. Fluids 2021, 33, 033104. [Google Scholar] [CrossRef]
- Lakes, R. Materials with structural hierarchy. Nature 1993, 361, 511–515. [Google Scholar] [CrossRef]
- Chen, Q.; Pugno, N.M. Bio-mimetic mechanisms of natural hierarchical materials: A review. J. Mech. Behav. Biomed. Mater. 2013, 19, 3–33. [Google Scholar] [CrossRef] [PubMed]
- Tammaro, D.; D’Avino, G.; Di Maio, E.; Pasquino, R.; Villone, M.M.; Gonzales, D.; Groombridge, M.; Grizzuti, N.; Maffettone, P.L. Validated modeling of bubble growth, impingement and retraction to predict cell-opening in thermoplastic foaming. Chem. Eng. J. 2016, 287, 492–502. [Google Scholar] [CrossRef]
- Tammaro, D.; Lombardi, L.; Scherillo, G.; Di Maio, E.; Ahuja, N.; Mensitieri, G. Modelling Sorption Thermodynamics and Mass Transport of n-Hexane in a Propylene-Ethylene Elastomer. Polymers 2021, 13, 1157. [Google Scholar] [CrossRef] [PubMed]
- Di Caprio, M.R.; Tammaro, D.; Di Maio, E.; Cavalca, S.; Parenti, V.; Fangareggi, A.; Iannace, S. A pressure vessel for studying gas foaming of thermosetting polymers: Sorption, synthesis and processing. Polym. Test. 2017, 62, 137–142. [Google Scholar] [CrossRef]
- Sannino, A.; Esposito, A.; Villone, M.M.; Hulsen, M.A.; D’Avino, G. Bubble impingement in the presence of a solid particle: A computational study. Comput. Fluids 2018, 170, 349–356. [Google Scholar] [CrossRef]
- Dabo, M.; Roland, T.; Dalongeville, G.; Gauthier, C.; Kékicheff, P. Ad-hoc modeling of closed-cell foam microstructures for structure-properties relationships. Eur. J. Mech. A Solids 2019, 75, 128–141. [Google Scholar] [CrossRef]
- Mitrias, C.; Egelmeers, T.R.; Jaensson, N.O.; Hulsen, M.A.; Anderson, P.D. Simulation of bubble growth during the foaming process and mechanics of the solid foam. Rheol. Acta 2019, 58, 131–144. [Google Scholar] [CrossRef]
- Everitt, S.; Harlen, O.; Wilson, H. Bubble growth in a two-dimensional viscoelastic foam. J. Non-Newton. Fluid Mech. 2006, 137, 46–59. [Google Scholar] [CrossRef] [Green Version]
- Tammaro, D.; Gatta, R.D.; Villone, M.M.; Maffettone, P.L. Continuous 3D printing of hierarchically structured micro-foamed objects. Adv. Eng. Mater. 2021, 8, 2101226. [Google Scholar] [CrossRef]
- Wong, A.; Park, C. A visualization system for observing plastic foaming processes under shear stress. Polym. Test. 2012, 31, 417–424. [Google Scholar] [CrossRef]
- Spitael, P.; Macosko, C.W. Strain hardening in polypropylenes and its role in extrusion foaming. Polym. Eng. Sci. 2004, 44, 2090–2100. [Google Scholar] [CrossRef]
- Tammaro, D.; Astarita, A.; Di Maio, E.; Iannace, S. Polystyrene foaming at high pressure drop rates. Ind. Eng. Chem. Res. 2016, 55, 5696–5701. [Google Scholar] [CrossRef] [Green Version]
- Pinto, J.; Escudero, J.; Solórzano, E.; Rodriguez-Perez, M. A novel route to produce structural polymer foams with a controlled solid skin-porous core structure based on gas diffusion mechanisms. J. Sandw. Struct. Mater. 2020, 22, 822–832. [Google Scholar] [CrossRef]
- Everitt, S.; Harlen, O.; Wilson, H.; Read, D. Bubble dynamics in viscoelastic fluids with application to reacting and non-reacting polymer foams. J. Non-Newton. Fluid Mech. 2003, 114, 83–107. [Google Scholar] [CrossRef]
- Villone, M.M.; Hulsen, M.A.; Anderson, P.D.; Maffettone, P.L. Simulations of deformable systems in fluids under shear flow using an arbitrary Lagrangian Eulerian technique. Comput. Fluids 2014, 90, 88–100. [Google Scholar] [CrossRef]
- Hu, H.H.; Patankar, N.A.; Zhu, M.Y. Direct numerical simulations of fluid–solid systems using the arbitrary Lagrangian–Eulerian technique. J. Comput. Phys. 2001, 169, 427–462. [Google Scholar] [CrossRef]
- Jaensson, N.O.; Hulsen, M.A.; Anderson, P.D. Stokes–Cahn–Hilliard formulations and simulations of two-phase flows with suspended rigid particles. Comput. Fluids 2015, 111, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Larson, R.G. Constitutive Equations for Polymer Melts and Solutions: Butterworths Series in Chemical Engineering; Butterworth-Heinemann: Oxford, UK, 2013. [Google Scholar]

| ηs [Pa s−1] | 5691.58 Pa s−1 | ||
| i | 1 | 2 | 3 |
| 4.13 | 0.52 | 0.083 | |
| 0.82 | 0.53 | 0.48 | |
| [Pa s−1] | 32,258.0 | 41,419.0 | 27,964.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tammaro, D.; Villone, M.M.; D’Avino, G.; Maffettone, P.L. An Experimental and Numerical Investigation on Bubble Growth in Polymeric Foams. Entropy 2022, 24, 183. https://doi.org/10.3390/e24020183
Tammaro D, Villone MM, D’Avino G, Maffettone PL. An Experimental and Numerical Investigation on Bubble Growth in Polymeric Foams. Entropy. 2022; 24(2):183. https://doi.org/10.3390/e24020183
Chicago/Turabian StyleTammaro, Daniele, Massimiliano M. Villone, Gaetano D’Avino, and Pier Luca Maffettone. 2022. "An Experimental and Numerical Investigation on Bubble Growth in Polymeric Foams" Entropy 24, no. 2: 183. https://doi.org/10.3390/e24020183
APA StyleTammaro, D., Villone, M. M., D’Avino, G., & Maffettone, P. L. (2022). An Experimental and Numerical Investigation on Bubble Growth in Polymeric Foams. Entropy, 24(2), 183. https://doi.org/10.3390/e24020183









