Helstrom Bound for Squeezed Coherent States in Binary Communication
Abstract
:1. Introduction
2. Squeezed Coherent States from Holomorphic Hermite Polynomials
3. Helstrom Bound for Squeezed Coherent States
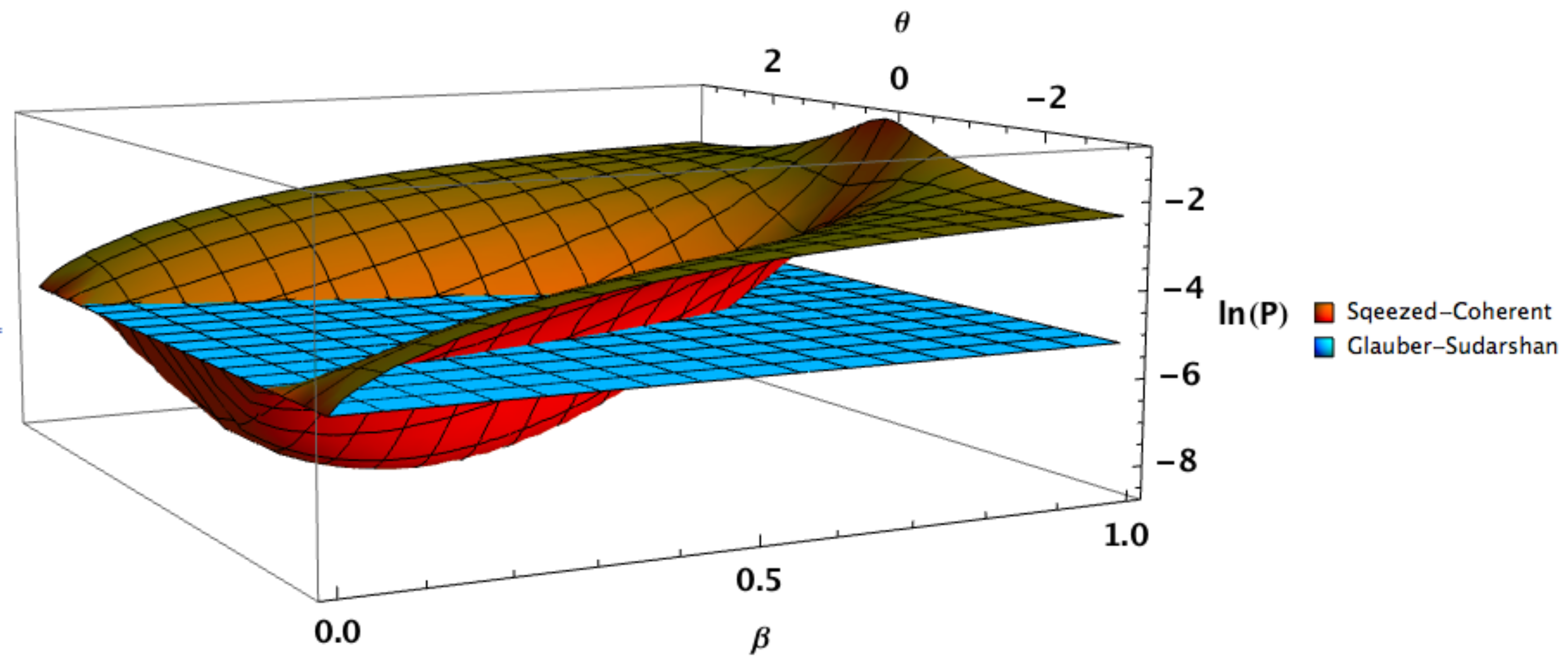
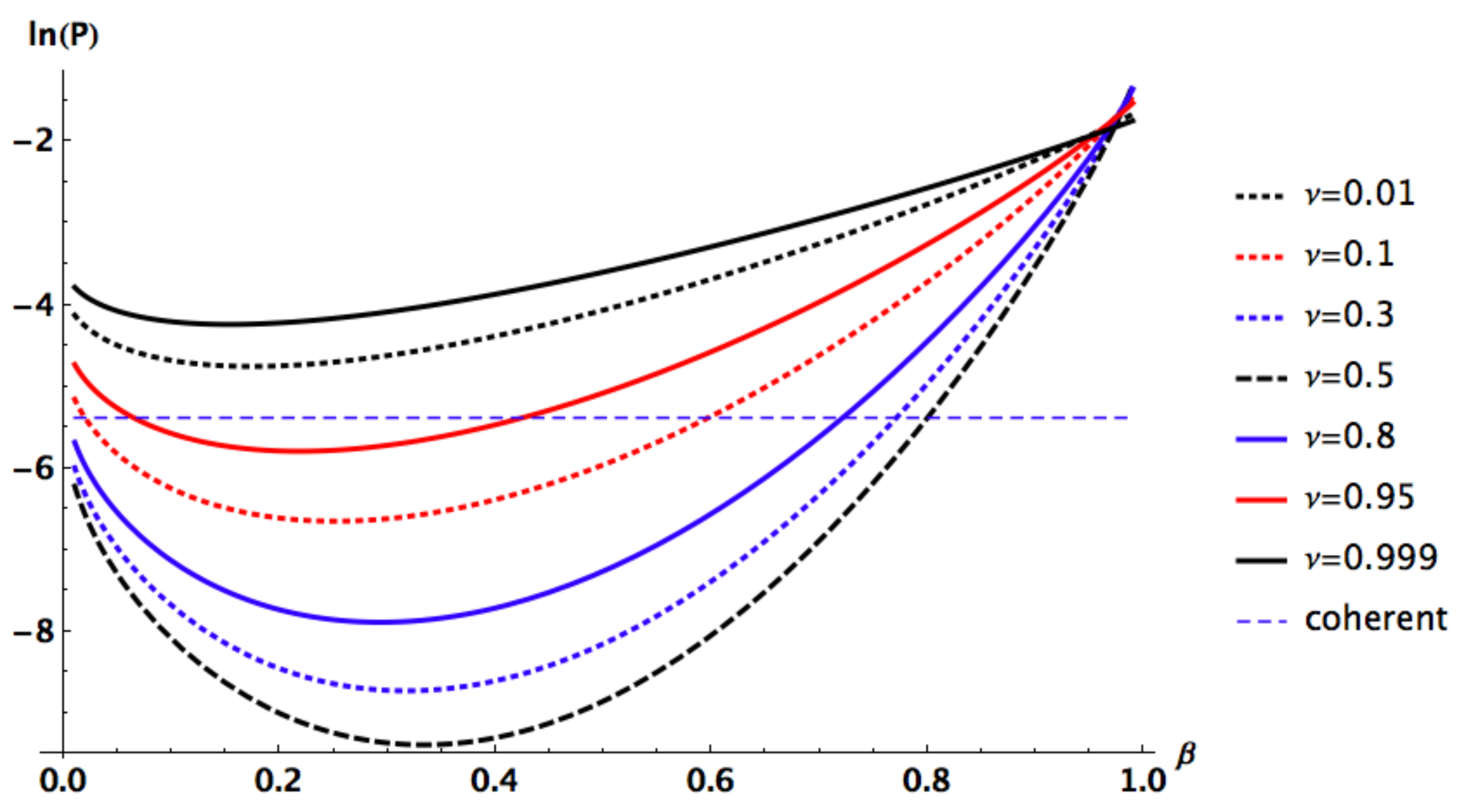
3.1. Case 1: Glauber-Sudarshan Alphabet
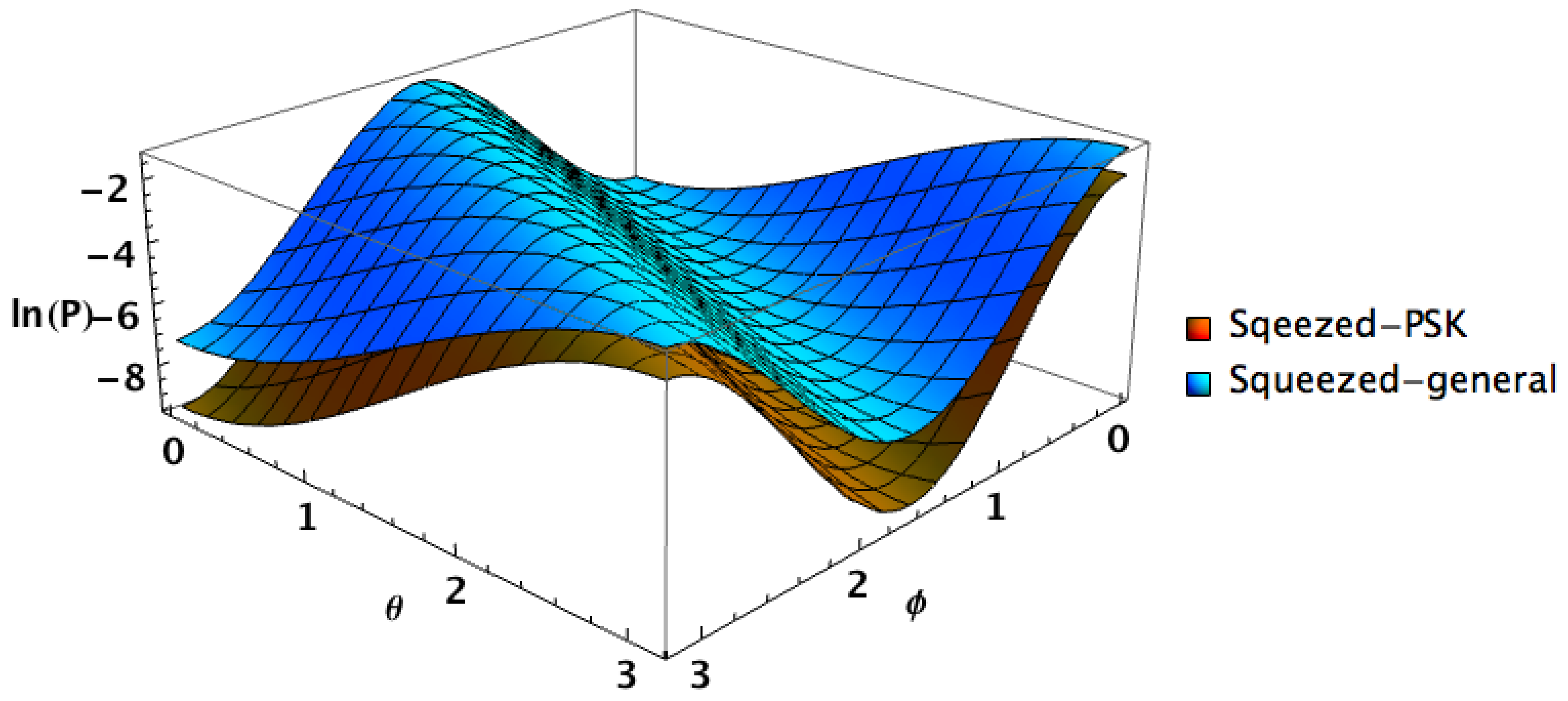
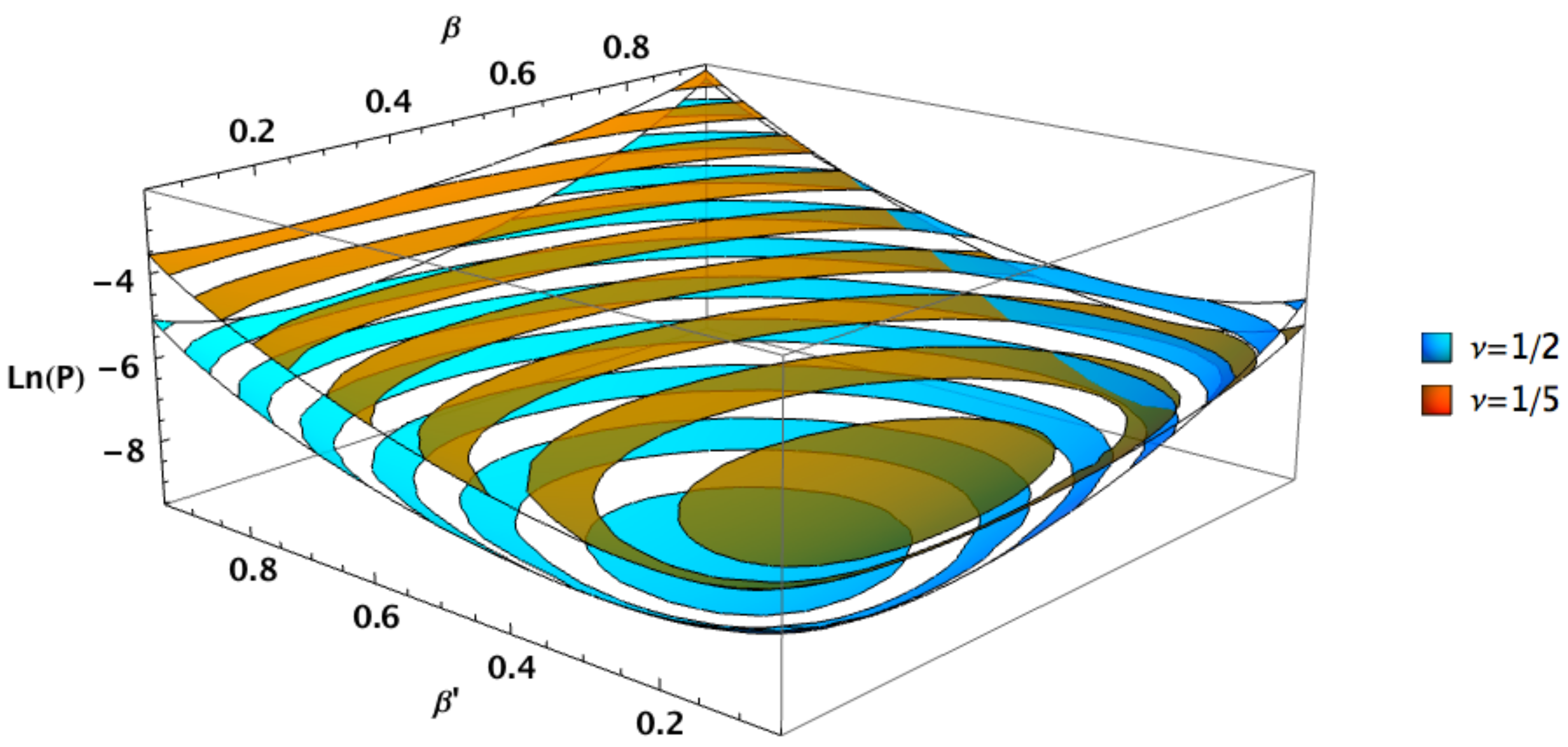
3.2. Case 2: Squeezed-Coherent PSK Encoding
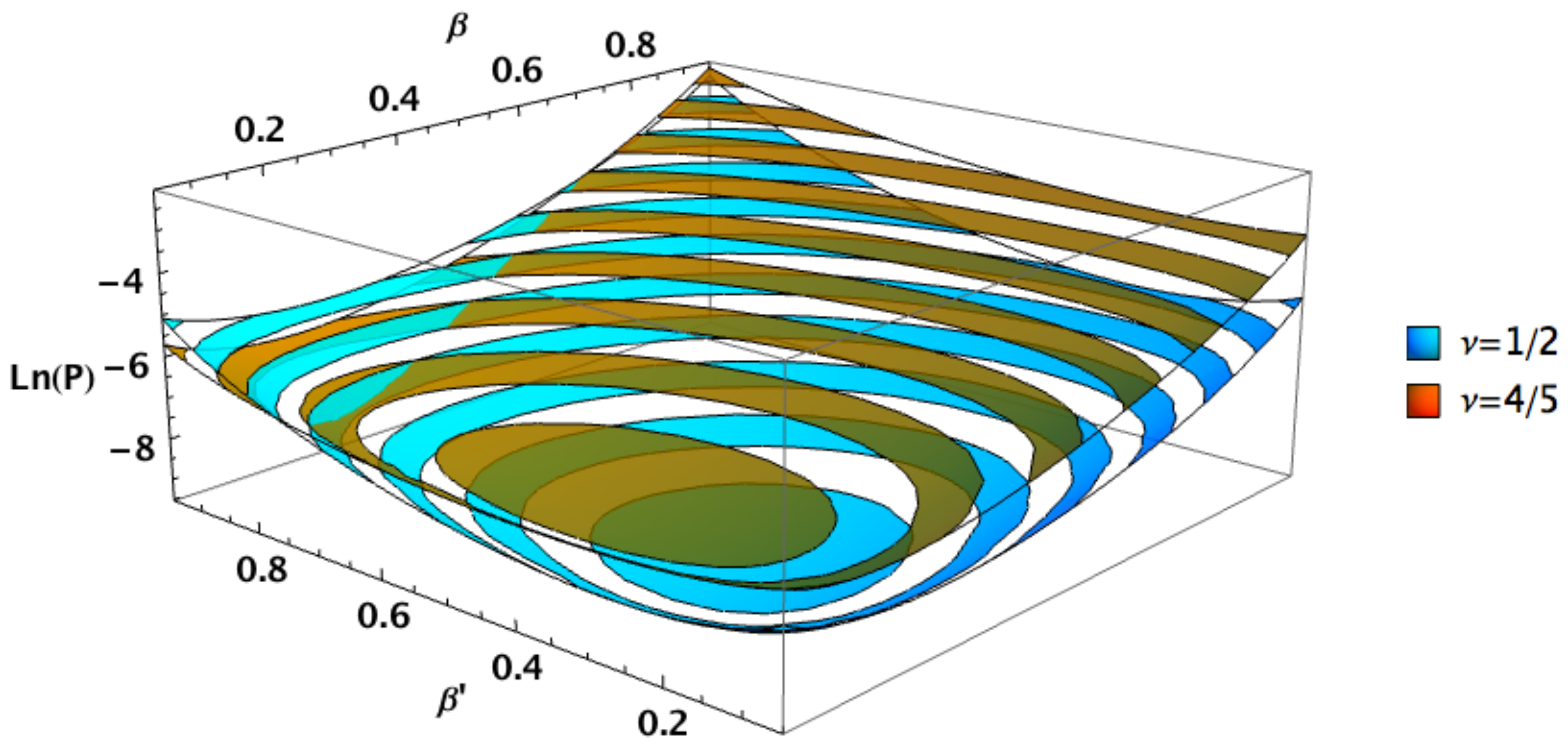
3.3. Case 3: Optimal Squeezed-Coherent PSK Encoding
3.4. Case 4: General Squeezed-Coherent Alphabet
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. The Modulus Squared of the Overlap of Two Arbitrary Squeezed States
References
- Holevo, A.S. Statistical decision theory for quantum systems. J. Multivar. Anal. 1973, 3, 337–394. [Google Scholar] [CrossRef] [Green Version]
- Holevo, A.S. Probabilistic and Statistical Aspects of Quantum Theory; Springer Science & Business Media: Berlin & Heidelberg, Germany, 2011. [Google Scholar]
- Helstrom, C.W. Quantum detection and estimation theory. In Mathematics in Science and Engineering; Academic Press: New York, NY, USA, 1976; pp. 1–309. [Google Scholar]
- Glauber, R.J. Photons correlations. Phys. Rev. Lett. 1963, 10, 84–86. [Google Scholar] [CrossRef] [Green Version]
- Schrödinger, E. Der steatite Übergang von der Mikro-Zur Makromechanik. Die Naturwissenshaften 1926, 14, 664–666. [Google Scholar] [CrossRef]
- Cook, R.L.; Martin, P.J.; Geremia, J.M. Optical coherent state discrimination using a closed-loop quantum measurement. Nature 2007, 446, 774–777. [Google Scholar] [CrossRef] [PubMed]
- Gazeau, J.-P. Coherent States in Quantum Physics, 1st ed.; Wiley-VCH: Berlin, Germany, 2009. [Google Scholar]
- Paris, M.G.A. Nearly ideal binary communication in squeezed channels. Phys. Rev. A 2001, 64, 014304. [Google Scholar] [CrossRef] [Green Version]
- Lawrie, B.J.; Lett, P.D.; Marino, A.M.; Pooser, R.C. Quantum sensing with squeezed light. ACS Photonics 2019, 6, 1307–1318. [Google Scholar] [CrossRef]
- Tse, M.; Yu, H.; Kijbunchoo, N.; Fernandez-Galiana, A.; Dupej, P.; Barsotti, L.; Blair, C.D.; Brown, D.D.; Dwyer, S.E.; Effler, A.; et al. Quantum-enhanced advanced LIGO detectors in the era of gravitational-wave astronomy. Phys. Rev. Lett. 2019, 123, 231107. [Google Scholar] [CrossRef] [Green Version]
- Walls, D.F. Squeezed states of light. Nature 1983, 306, 141–146. [Google Scholar] [CrossRef]
- Lvovsky, A.I. Squeezed light. In Photonics: Scientific Foundations, Technology and Applications; Andrews, D.L., Ed.; John Wiley & Sons: Hoboken, NJ, USA, 2015; pp. 121–163. [Google Scholar]
- Schnabel, R. Squeezed states of light and their applications in laser interferometers. Phys. Rep. 2017, 684, 1–51. [Google Scholar] [CrossRef] [Green Version]
- Slusher, R.; Hollberg, L.; Yurke, B.; Mertz, J.; Valley, J. Observation of squeezed states generated by four wave mixing in an optical cavity. Phys. Rev. Lett. 1985, 55, 2409. [Google Scholar] [CrossRef]
- Wu, L.-A.; Kimble, H.; Hall, J.; Wu, H. Generation of Squeezed States by Parametric Down Conversion. Phys. Rev. Lett. 1986, 57, 2520–2523. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dodonov, V.; Marchiolli, M.; Korennoy, Y.A.; Man’ko, V.; Moukhin, Y. Dynamical squeezing of photon-added coherent states. Phys. Rev. A 1998, 58, 4087. [Google Scholar] [CrossRef] [Green Version]
- Curado, E.M.F.; Faci, S.; Gazeau, J.-P.; Noguera, D. Lowering Helstrom Bound with non-standard coherent states. J. Opt. Soc. Am. B 2021, 38, 3556–3566. [Google Scholar] [CrossRef]
- Chesi, G.; Olivares, S.; Paris, M.G.A. Squeezing-enhanced phase-shift-keyed binary communication in noisy channels. Phys. Rev. A 2018, 97, 032315. [Google Scholar] [CrossRef] [Green Version]
- Yuen, H. Two-photon coherent states of the radiation field. Phys. Rev. A 1976, 13, 2226. [Google Scholar] [CrossRef] [Green Version]
- Hirota, O. Generalized quantum measurement theory and its application in quantum communication theory (Optical communication by two-photon laser). Electron. Commun. Jpn. 1977, 60, 701–708. [Google Scholar]
- Hirota, O.; Shioya, I.; Ikehara, S.; Suematsu, Y. Optimal Control of Quantum Noise (Optical Communication by Two-Photon Laser Part II). IECE Trans. 1978, 61, 273–279. [Google Scholar]
- Yuen, H.; Shapiro, J. Optical Communication with Two-Photon Coherent States—Part I: Quantum-State Propagation and Quantum Noise Reduction. IEEE Trans. Inf. Theory 1978, 24, 657–668. [Google Scholar] [CrossRef]
- Shapiro, J.; Yuen, H.; Mata, A. Optical communication with two-photon coherent states—Part II: Photoemissive detection and structured receiver performance. IEEE Trans. Inf. Theory 1979, 25, 179–192. [Google Scholar] [CrossRef]
- Yuen, H.; Shapiro, J. Optical communication with two-photon coherent states—Part III: Quantum measurements realizable with photoemissive detectors. IEEE Trans. Inf. Theory 1980, 26, 78–92. [Google Scholar] [CrossRef]
- Hirota, O. Squeezed Light; Elsevier: Amsterdam, The Netherlands, 1992. [Google Scholar]
- Gong, J.J.; Arvind, P.K. Expansion coefficients of a squeezed coherent state in the number state basis. Am. J. Phys. 1990, 58, 1003–1006. [Google Scholar] [CrossRef]
- Gazeau, J.-P.; Szafraniec, F.H. Holomorphic Hermite polynomials and a non-commutative plane. J. Phys. A Math. Theor. 2011, 44, 495201. [Google Scholar] [CrossRef]
- Ali, S.T.; Górska, K.; Horzela, A.; Szafraniec, F.H. Squeezed states and Hermite polynomials in a complex variable. J. Math. Phys. 2014, 55, 012107. [Google Scholar] [CrossRef] [Green Version]
- Eijndhoven, S.J.L.; Meyers, J.L.H. New orthogonality relations for the Hermite polynomials and related Hilbert spaces. J. Math. Anal. Appl. 1990, 146, 89–98. [Google Scholar] [CrossRef] [Green Version]
- Górska, K.; Horzela, A.; Szafraniec, F.H. Coherence, squeezing and entanglement: An example of peaceful coexistence. In Coherent States and Their Applications; Antoine, J.P., Bagarello, F., Gazeau, J.P., Eds.; Springer: Cham, Switzerland, 2018; pp. 89–117. [Google Scholar]
- Górska, K.; Horzela, A.; Szafraniec, F.H. Holomorphic Hermite polynomials in two variables. J. Math. Anal. Appl. 2019, 470, 750–769. [Google Scholar] [CrossRef] [Green Version]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Curado, E.M.F.; Faci, S.; Gazeau, J.-P.; Noguera, D. Helstrom Bound for Squeezed Coherent States in Binary Communication. Entropy 2022, 24, 220. https://doi.org/10.3390/e24020220
Curado EMF, Faci S, Gazeau J-P, Noguera D. Helstrom Bound for Squeezed Coherent States in Binary Communication. Entropy. 2022; 24(2):220. https://doi.org/10.3390/e24020220
Chicago/Turabian StyleCurado, Evaldo M. F., Sofiane Faci, Jean-Pierre Gazeau, and Diego Noguera. 2022. "Helstrom Bound for Squeezed Coherent States in Binary Communication" Entropy 24, no. 2: 220. https://doi.org/10.3390/e24020220





