Reduced System Complexity of Heart Rate Dynamics in Patients with Hyperthyroidism: A Multiscale Entropy Analysis
Abstract
:1. Introduction
2. Methods
2.1. Subjects
2.2. Study Protocol and Procedures
2.3. Linear Analysis
2.4. Multiscale Entropy Analysis
2.5. Assays
2.6. Statistical Analysis
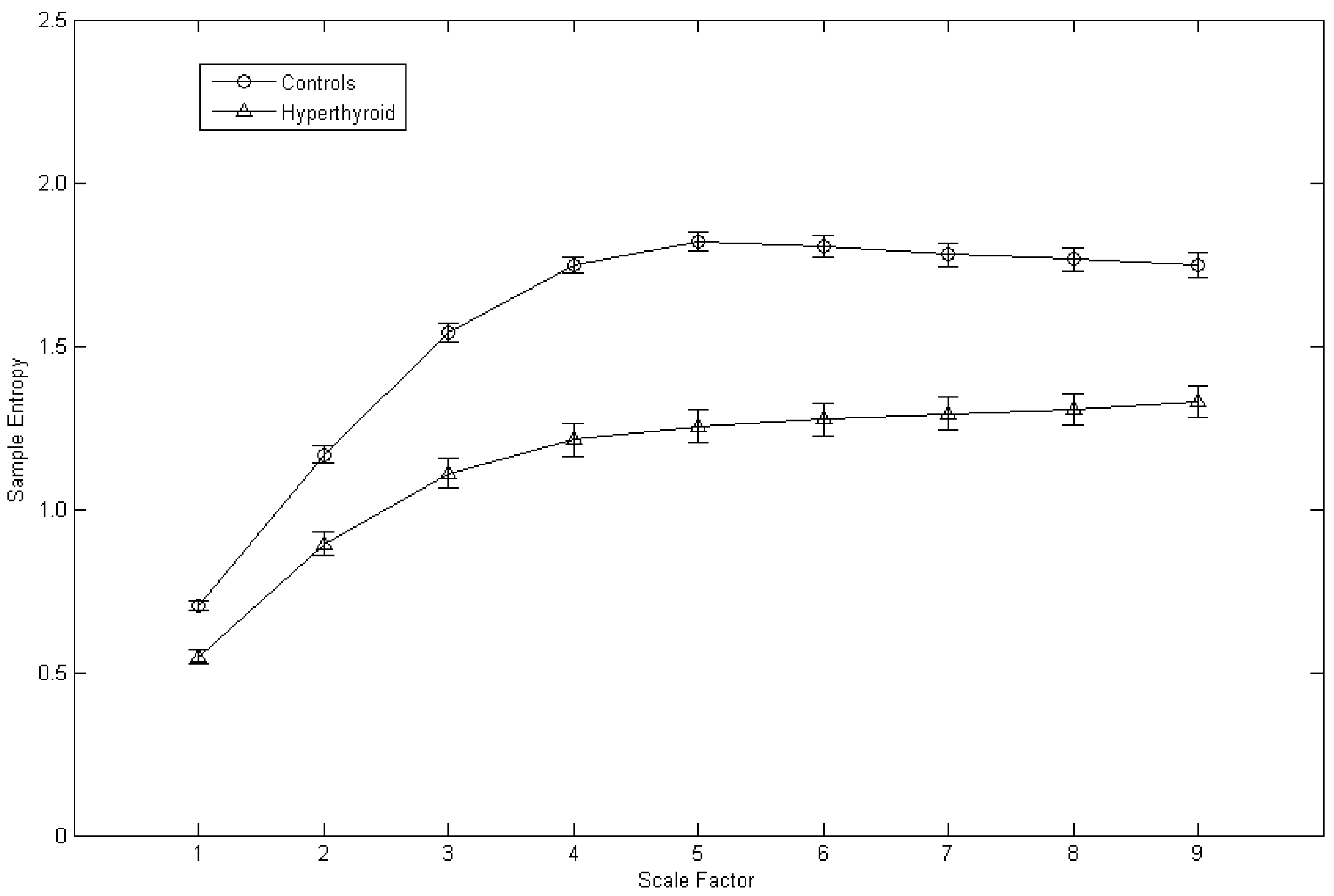
3. Results
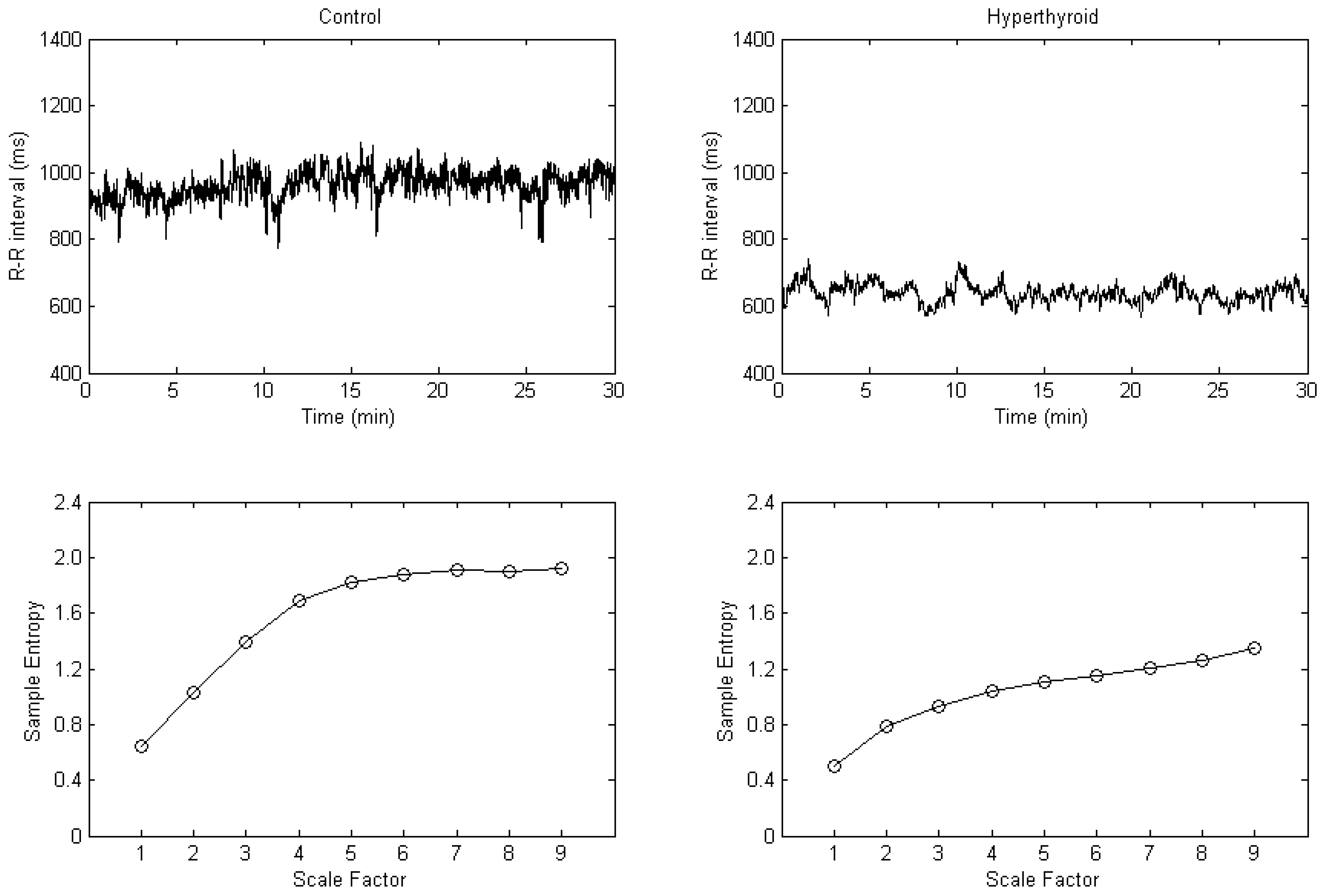
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cacciatori, V.; Bellavere, F.; Pezzarossa, A.; Dellera, A.; Gemma, M.L.; Thomaseth, K.; Castello, R.; Moghetti, P.; Muggeo, M. Power spectral analysis of heart rate in hyperthyroidism. J. Clin. Endocrinol. Metab. 1996, 81, 2828–2835. [Google Scholar]
- Burggraaf, J.; Tulen, J.H.; Lalezari, S.; Schoemaker, R.C.; De Meyer, P.H.; Meinders, A.E.; Cohen, A.F.; Pijl, H. Sympathovagal imbalance in hyperthyroidism. Am. J. Physiol. Endocrinol. Metab. 2001, 281, E190–E195. [Google Scholar] [CrossRef]
- Chen, J.-L.; Chiu, H.-W.; Tseng, Y.-J.; Chu, W.-C. Hyperthyroidism is characterized by both increased sympathetic and decreased vagal modulation of heart rate: Evidence from spectral analysis of heart rate variability. Clin. Endocrinol. 2006, 64, 611–616. [Google Scholar] [CrossRef]
- Peng, C.-K.; Costa, M.; Goldberger, A.L. Adaptive data analysis of complex fluctuations in physiologic time series. Adv. Adapt. Data Anal. 2009, 1, 61–70. [Google Scholar] [CrossRef] [PubMed]
- Costa, M.; Goldberger, A.L.; Peng, C.-K. Multiscale entropy analysis of biological signals. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2005, 71, 021906. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Costa, M.; Priplata, A.A.; Lipsitz, L.A.; Wu, Z.; Huang, N.E.; Goldberger, A.L.; Peng, C.-K. Noise and poise: Enhancement of postural complexity in the elderly with a stochastic-resonance-based therapy. Europhys. Lett. 2007, 77, 68008. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Norris, P.R.; Stein, P.K.; Morris, J.A., Jr. Reduced heart rate multiscale entropy predicts death in critical illness: A study of physiologic complexity in 285 trauma patients. J. Crit. Care 2008, 23, 399–405. [Google Scholar] [CrossRef]
- Papaioannou, V.E.; Chouvarda, I.; Maglaveras, N.; Dragoumanis, C.; Pneumatikos, I. Changes of heart and respiratory rate dynamics during weaning from mechanical ventilation: A study of physiologic complexity in surgical critically ill patients. J. Crit. Care 2011, 26, 262–272. [Google Scholar] [CrossRef] [PubMed]
- Yang, A.C.; Tsai, S.-J.; Yang, C.-H.; Kuo, C.-H.; Chen, T.-J.; Hong, C.-J. Reduced physiologic complexity is associated with poor sleep in patients with major depression and primary insomnia. J. Affect. Disord. 2011, 131, 179–185. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.-H.; Huang, P.-W.; Tang, S.-C.; Shieh, J.-S.; Lai, D.-M.; Wu, A.-Y.; Jeng, J.-S. Complexity of heart rate variability can predict stroke-in-evolution in acute ischemic stroke patients. Sci. Rep. 2015, 5, 17552. [Google Scholar] [CrossRef]
- Tsai, C.-H.; Ma, H.-P.; Lin, Y.-T.; Hung, C.-S.; Huang, S.-H.; Chuang, B.-L.; Lin, C.; Lo, M.-T.; Peng, C.-K.; Lin, Y.-H. Usefulness of heart rhythm complexity in heart failure detection and diagnosis. Sci. Rep. 2020, 10, 14916. [Google Scholar] [CrossRef]
- Zeiler, F.A.; Ercole, A.; Placek, M.M.; Hutchinson, P.J.; Stocchetti, N.; Czosnyka, M.; Smielewski, P. Association between physiological signal complexity and outcomes in moderate and severe traumatic brain injury: A CENTER-TBI exploratory analysis of multi-scale entropy. J. Neurotrauma 2021, 38, 272–282. [Google Scholar] [PubMed]
- Escudero, J.; Abasolo, D.; Hornero, R.; Espino, P.; Lopez, M. Analysis of electroencephalograms in Alzheimer’s disease patients with multiscale entropy. Physiol. Meas. 2006, 27, 1091–1106. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Takahashi, T.; Cho, R.Y.; Murata, T.; Mizuno, T.; Kikuchi, M.; Mizukami, K.; Kosaka, H.; Takahashi, K.; Wada, Y. Age-related variation in EEG complexity to photic stimulation: A multiscale entropy analysis. Clin. Neurophysiol. 2009, 120, 476–483. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Catarino, A.; Churches, O.; Baron-Cohen, S.; Andrade, A.; Ring, H. Atypical EEG complexity in autism spectrum conditions: A multiscale entropy analysis. Clin. Neurophysiol. 2011, 122, 2375–2383. [Google Scholar] [CrossRef] [PubMed]
- Weng, W.-C.; Chang, C.-F.; Wong, L.C.; Lin, J.-H.; Lee, W.-T.; Shieh, J.-S. Altered resting-state EEG complexity in children with Tourette syndrome: A preliminary study. Neuropsychology 2017, 31, 395–402. [Google Scholar] [CrossRef]
- Chu, Y.-J.; Chang, C.-F.; Weng, W.-C.; Fan, P.-C.; Shieh, J.-S.; Lee, W.-T. Electroencephalography complexity in infantile spasms and its association with treatment response. Clin. Neurophysiol. 2021, 132, 480–486. [Google Scholar] [CrossRef]
- Yu, W.-Y.; Low, I.; Chen, C.; Fuh, J.-L.; Chen, L.-F. Brain dynamics altered by photic stimulation in patients with Alzheimer’s disease and mild cognitive impairment. Entropy 2021, 23, 427. [Google Scholar] [CrossRef]
- Ahmadi, S.; Siragy, T.; Nantel, J. Regularity of kinematic data between single and dual-task treadmill walking in people with Parkinson’s disease. J. Neuroeng. Rehabil. 2021, 18, 20. [Google Scholar] [CrossRef]
- Busa, M.A.; Jones, S.L.; Hamill, J.; van Emmerik, R.E. Multiscale entropy identifies differences in complexity in postural control in women with multiple sclerosis. Gait Posture 2016, 45, 7–11. [Google Scholar] [CrossRef]
- O’Keeffe, C.; Taboada, L.P.; Feerick, N.; Gallagher, L.; Lynch, T.; Reilly, R.B. Complexity based measures of postural stability provide novel evidence of functional decline in fragile X premutation carriers. J. Neuroeng. Rehabil. 2019, 16, 87. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.-L.; Chen, P.-F.; Wang, H.-M. Decreased complexity of glucose dynamics in diabetes: Evidence from multiscale entropy analysis of continuous glucose monitoring system data. Am. J. Physiol. Regul. Integr. Comp. Physiol. 2014, 307, R179–R183. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Task Force of the European Society of Cardiology and the North American Society of Pacing and Electrophysiology Heart rate variability: Standards of measurement, physiological interpretation and clinical use. Circulation 1996, 93, 1043–1065. [CrossRef] [Green Version]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Akselrod, S.; Gordon, D.; Ubel, F.A.; Shannon, D.C.; Berger, A.C.; Cohen, R.J. Power spectrum analysis of heart rate fluctuation: A quantitative probe of beat-to-beat cardiovascular control. Science 1981, 213, 220–222. [Google Scholar] [CrossRef]
- Sassi, R.; Cerutti, S.; Lombardi, F.; Malik, M.; Huikuri, H.V.; Peng, C.K.; Schmidt, G.; Yamamoto, Y. Advances in heart rate variability signal analysis: Joint position statement by the e-Cardiology ESC Working Group and the European Heart Rhythm Association co-endorsed by the Asia Pacific Heart Rhythm Society. Europace 2015, 17, 1341–1353. [Google Scholar] [CrossRef]
- Javorka, M.; Trunkvalterova, Z.; Tonhajzerova, I.; Javorkova, J.; Javorka, K.; Baumert, M. Short-term heart rate complexity is reduced in patients with type 1 diabetes mellitus. Clin. Neurophysiol. 2008, 119, 1071–1081. [Google Scholar] [CrossRef]
- Liu, S.-H.; Lo, L.-W.; Tsai, T.-Y.; Cheng, W.-H.; Lin, Y.-J.; Chang, S.-L.; Hu, Y.-F.; Chung, F.-P.; Chao, T.-F.; Liao, J.-N.; et al. Circadian rhythm dynamics on multiscale entropy identifies autonomic dysfunction associated with risk of ventricular arrhythmias and near syncope in chronic kidney disease. J. Cardiol. 2020, 76, 542–548. [Google Scholar] [CrossRef]
- Schulz, S.; Koschke, M.; Bar, K.J.; Voss, A. The altered complexity of cardiovascular regulation in depressed patients. Physiol. Meas. 2010, 31, 303–321. [Google Scholar] [CrossRef]
- Leistedt, S.J.; Linkowski, P.; Lanquart, J.P.; Mietus, J.E.; Davis, R.B.; Goldberger, A.L.; Costa, M.D. Decreased neuroautonomic complexity in men during an acute major depressive episode: Analysis of heart rate dynamics. Transl. Psychiatry 2011, 1, e27. [Google Scholar] [CrossRef]
- Tang, S.-C.; Jen, H.-I.; Lin, Y.-H.; Hung, C.-S.; Jou, W.-J.; Huang, P.-W.; Shieh, J.-S.; Ho, Y.-L.; Lai, D.-M.; Wu, A.-Y.; et al. Complexity of heart rate variability predicts outcome in intensive care unit admitted patients with acute stroke. J. Neurol. Neurosurg. Psychiatry 2015, 86, 95–100. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Riordan, W.P., Jr.; Norris, P.R.; Jenkins, J.M.; Morris, J.A., Jr. Early loss of heart rate complexity predicts mortality regardless of mechanism, anatomic location, or severity of injury in 2178 trauma patients. J. Surg. Res. 2009, 156, 283–289. [Google Scholar] [CrossRef] [PubMed]
- Ho, Y.-L.; Lin, C.; Lin, Y.-H.; Lo, M.-T. The prognostic value of non-linear analysis of heart rate variability in patients with congestive heart failure—A pilot study of multiscale entropy. PLoS ONE 2011, 6, e18699. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tsai, C.-H.; Huang, J.-W.; Lin, C.; Ma, H.-P.; Lo, M.-T.; Liu, L.D.; Lin, L.-Y.; Lin, C.-T.; Hung, C.-S.; Peng, C.-K.; et al. Heart rhythm complexity predicts long-term cardiovascular outcomes in peritoneal dialysis patients: A prospective cohort study. J. Am. Heart Assoc. 2020, 9, e013036. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Zhan, P.; Shi, J.; Hu, M.; Wang, G.; Wang, W. Heart rhythm complexity as predictors for the prognosis of end-stage renal disease patients undergoing hemodialysis. BMC Nephrol. 2020, 21, 536. [Google Scholar] [CrossRef]
| Controls | Hyperthyroid | p-Value | |
|---|---|---|---|
| Mean RRI (ms) | 865 ± 16 | 608 ± 14 | <0.001 |
| SDNN (ms) | 54 ± 4 | 25 ± 2 | <0.001 |
| RMSSD (ms) | 42 ± 4 | 9 ± 1 | <0.001 |
| TP (ms2) | 3054 ± 488 | 772 ± 143 | <0.001 |
| VLF (ms2) | 1566 ± 214 | 598 ± 112 | <0.001 |
| LF (ms2) | 748 ± 146 | 133 ± 28 | <0.001 |
| HF (ms2) | 740 ± 165 | 40 ± 9 | <0.001 |
| LF% (nu) | 50.49 ± 1.67 | 77.31 ± 1.78 | <0.001 |
| HF% (nu) | 49.51 ± 1.67 | 22.69 ± 1.78 | <0.001 |
| LF/HF | 1.10 ± 0.07 | 4.63 ± 0.49 | <0.001 |
| CI | 14.08 ± 0.21 | 10.21 ± 0.37 | <0.001 |
| S1 | 0.70 ± 0.01 | 0.55 ± 0.02 | <0.001 |
| S2 | 1.17 ± 0.03 | 0.89 ± 0.04 | <0.001 |
| S3 | 1.54 ± 0.03 | 1.11 ± 0.05 | <0.001 |
| S4 | 1.75 ± 0.03 | 1.21 ± 0.05 | <0.001 |
| S5 | 1.82 ± 0.03 | 1.25 ± 0.05 | <0.001 |
| S6 | 1.81 ± 0.03 | 1.27 ± 0.05 | <0.001 |
| S7 | 1.78 ± 0.04 | 1.29 ± 0.05 | <0.001 |
| S8 | 1.77 ± 0.04 | 1.31 ± 0.05 | <0.001 |
| S9 | 1.75 ± 0.04 | 1.33 ± 0.05 | <0.001 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.-L.; Shen, H.-S.; Peng, S.-Y.; Wang, H.-M. Reduced System Complexity of Heart Rate Dynamics in Patients with Hyperthyroidism: A Multiscale Entropy Analysis. Entropy 2022, 24, 258. https://doi.org/10.3390/e24020258
Chen J-L, Shen H-S, Peng S-Y, Wang H-M. Reduced System Complexity of Heart Rate Dynamics in Patients with Hyperthyroidism: A Multiscale Entropy Analysis. Entropy. 2022; 24(2):258. https://doi.org/10.3390/e24020258
Chicago/Turabian StyleChen, Jin-Long, Hsuan-Shu Shen, Shih-Yi Peng, and Hung-Ming Wang. 2022. "Reduced System Complexity of Heart Rate Dynamics in Patients with Hyperthyroidism: A Multiscale Entropy Analysis" Entropy 24, no. 2: 258. https://doi.org/10.3390/e24020258
APA StyleChen, J.-L., Shen, H.-S., Peng, S.-Y., & Wang, H.-M. (2022). Reduced System Complexity of Heart Rate Dynamics in Patients with Hyperthyroidism: A Multiscale Entropy Analysis. Entropy, 24(2), 258. https://doi.org/10.3390/e24020258






