Learning Competitive Swarm Optimization
Abstract
:1. Introduction
- Adjustment of parameters. Shi and Eberhart [22] indicated that the performance of the PSO method depends primarily on the inertia weight. In their opinion, the best results give inertial weight, which decreases linearly from 0.9 to 0.4. Zhang et al. [23] and Niu et al. [24] proposed to use a random inertia weight. In contrast to Zhang et al. [23] and Niu et. al. [24], Clerc [25] suggested that all coefficients should rather be constant and proved that inertia weight w = 0.729 and factors c1 = c2 = 1.494 can increase the rate of convergence. Venter and Sobieszczański [26] found that the PSO method is more effective when the acceleration coefficients are constant but different. According to them, the social coefficient should be greater than the cognitive one, and they proved that c2 = 2.5 and c1 = 1.5 produce superior performance. Nonlinear, dynamically changing coefficients were proposed by Borowska [27]. In this approach, the values of coefficients were affected by the performance of PSO and the number of iterations. In order to more efficiently control the searching process, Ratnaweera et al. [28] recommended time-varying coefficients (TVACs). An approach based on fuzzy systems was proposed by Chen [29].
- Topology. Topological structure has a great influence on the performance of the PSO algorithm. According to Kennedy and Mendes [30], a proper topology significantly improves the exploration ability of PSO. Lin et al. [31] and Borowska [32] indicated that the ring topology can help maintain swarm diversity and improve the algorithm’s adaptability. An approach based on multi-swarm structure was proposed by Chen et al. [33] and Niu [24]. In turn, a two-layer cascading structure was recommended by Gong et al. [34]. To alleviate premature convergence, Mendes et al. [35] introduced a fully informed swarm in which particles are updated based on the best locations of their neighbors. A PSO variant with adaptive time-varying topology connectivity (PSO-ATVTC) was developed by Lim et al. [36]. Carvalho et al. [37] proposed a particle topology based on the clan structure. The dynamic Clan PSO topology was described by Bastos-Filho et al. [38]. Shen et al. [39] proposed a multi-stage search strategy supplemented by mutual repulsion and attraction among particles. The proposed algorithm increases the entropy of the particle population and leads to a more balanced search process.
- Combining PSO with other methods. In order to obtain higher-quality solutions and enhance the performance of PSO, in many papers, researchers merge two or more different methods or their advantageous elements. Ali et al. [40] and Sharma et al. [41] combined PSO with genetic operators. A modified particle swarm optimization algorithm with simulated annealing strategy (SA) was proposed by Shieh et al. [42]. A PSO method with ant colony optimization (ACO) was developed by Holden et al. [43]. Cooperation of many swarms and four other methods for improving the efficiency of PSO was applied by Liu and Zhou [44]. Not only did the authors combine multi-population-based particle swarm optimization with the simulated annealing method but also with co-evolution theory, quantum behavior theory and mutation strategy. A different approach was presented by Cheng et al. [45]. To improve the exploration ability of PSO, they used a multi-swarm framework combining the feedback mechanism with the convergence strategy and the mutation strategy. The proposed approach helps reach a balance between exploration and exploitation and reduces the risk of premature convergence.
- Adaptation of learning strategy. This approach allows particles to acquire knowledge from high-quality exemplars. In order to increase the adaptability of PSO, Ye et al. [46] developed dynamic learning strategy. A comprehensive learning strategy based on historical knowledge about particle position was recommended by Liang et al. [47] and was also developed by Lin et al. [48]. Instead of individual learning of particles based on their historical knowledge, Cheng and Jin [49] introduced a social learning mechanism using sorting of swarm and learning from demonstrators (any better particles) of the current swarm. The method turned out to be effective and computationally efficient. A learning strategy with operators of the genetic algorithm (GA) and a modified updating equation based on exemplars was proposed by Gong et al. [34]. To enhance diversity and improve the efficiency of PSO, Lin et al. [31] merged PSO with genetic operators and also connected them with global learning strategy and ring topology. Learning strategy with genetic operators and interlaced ring topology was also proposed by Borowska [32]. To improve the searching process, Niu et al. [50] recommended applying learning multi-swarm PSO based on a symbiosis.
2. The PSO Method
| Algorithm 1 Pseudo code of the PSO algorithm. |
| Determine the size of the swarm |
| for j = 1 to size of the swarm do |
| Generate an initial position and velocity of the particle, |
| Evaluate the particle; |
| Determine the pbest (personal best position) of the particle |
| end |
| Select the gbest (the best position) found in the swarm |
| while termination criterion is not met do |
| for j = 1 to size of the swarm do |
| Update the velocity and position of each particle according to Equations (1) and (2) |
| Evaluate new position of the particle; |
| Update the pbest (personal best position) of each particle |
| end |
| Update the gbest (the best position) found in the swarm |
| end |
3. The Proposed LCSO Algorithm
| Algorithm 2 Pseudo code of the LCSO algorithm. FEs is the number of fitness evaluations. The termination condition is the maximum number of fitness evaluations (maxFEs). |
| Determine the size of the swarm; |
| Determine the number of sub-swarms; |
| Determine number of particles in the sub-swarms; |
| Randomly initialize position and velocity of the particles in sub-swarms; |
| t = 0; |
| while termination criterion (FEs ≤ maxFEs) is not met do |
| Evaluate the particles fitness; |
| Parallel in each sub-swarm organize tournament independently: |
| while sub-swarm ≠ Ø do |
| Randomly select three particles, compare their fitness and determine winner Xw, runner-up Xr and loser Xl |
| Update runner-up’s position according to (3) and (4) |
| Update loser’s position according to (5) and (6) |
| end |
| Organize tournament between sub-swarms: |
| Randomly select one particle from the winners of each sub-swarm |
| while set of selected winners ≠ Ø do |
| Randomly select three particles |
| compare fitness of the selected particles to determine winner Xw, runner-up Xr and loser Xl |
| Update runner-up’s position according to (3) and (4) |
| Update loser’s position according to (5) and (6) |
| end |
| t = t + 1; |
| end |
| output the best solution |
4. Results
- The use of sub-swarms helps maintain the diversity of the population and keep the balance between the global exploration and local exploitation;
- Particles learning from the winners can effectively search space for a better position;
- Good information found by sub-swarm is not lost;
- Particles can learn from the useful information found by other sub-swarms;
- In each iteration, the position and velocity of only two out of three particles is updated which significantly reduces the cost of computations;
- Particles do not need to remember their personal best position; instead, the competition mechanism is applied;
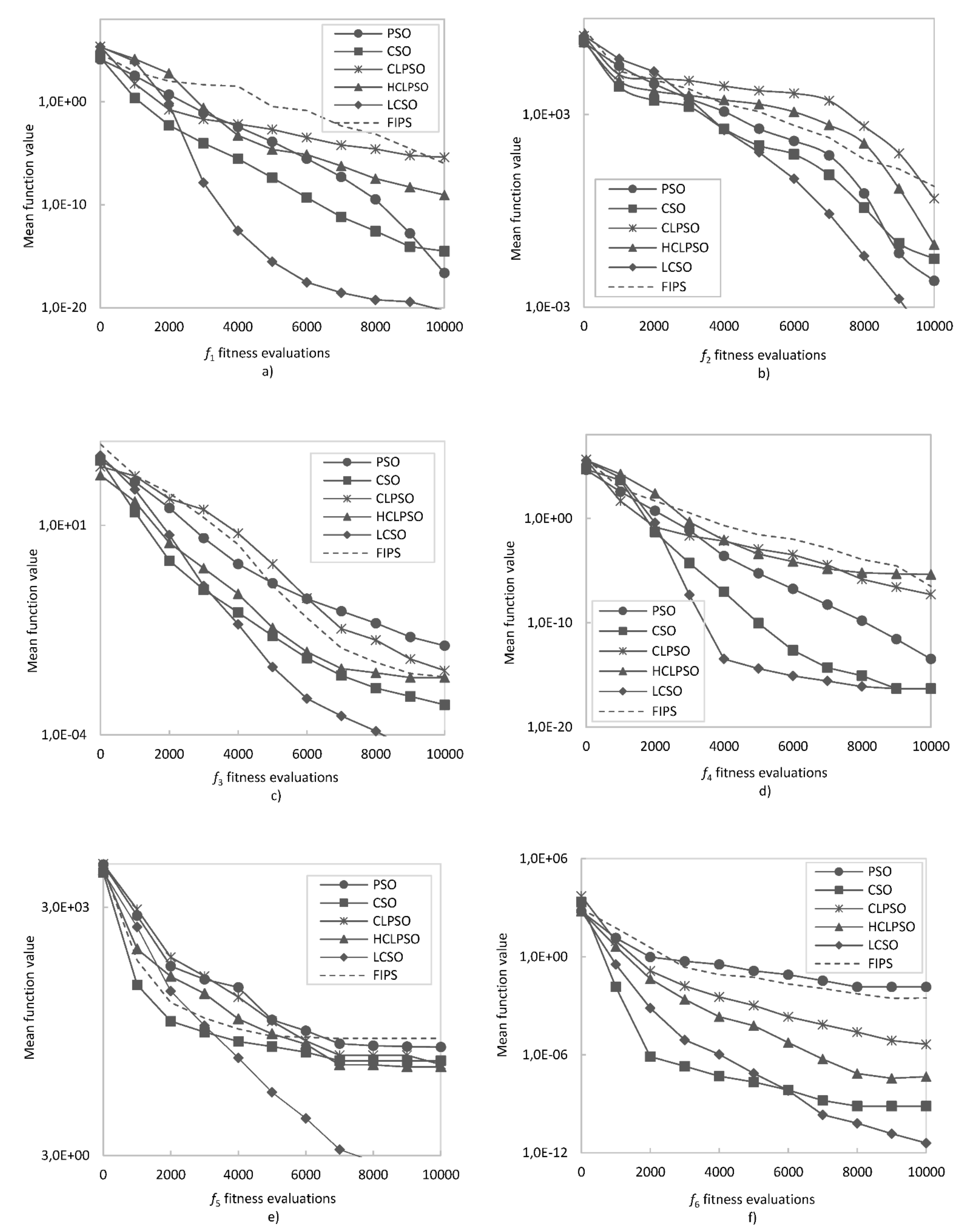
- LCSO can obtain better results and convergence than the other algorithms.
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kennedy, J.; Eberhart, R.C.; Shi, Y. Swarm Intelligence; Morgan Kaufmann Publishers: San Francisco, CA, USA, 2001. [Google Scholar]
- Xu, X.; Hao, J.; Zheng, Y. Multi-objective artificial bee colony algorithm for multi-stage resource leveling problem in sharing logistics network. Comput. Ind. Eng. 2020, 142, 106338. [Google Scholar] [CrossRef]
- Lei, D.; Liu, M. An artificial bee colony with division for distributed unrelated parallel machine scheduling with preventive maintenance. Comput. Ind. Eng. 2020, 141, 106320. [Google Scholar] [CrossRef]
- Borowska, B. An improved CPSO algorithm. In Proceedings of the International Scientific and Technical Conference Computer Sciences and Information Technologies CSIT, Lviv, Ukraine, 6–10 September 2016; pp. 1–3. [Google Scholar] [CrossRef]
- Dorigo, M.; Blum, C. Ant colony optimization theory: A survey. Theor. Comput. Sci. 2005, 344, 243–278. [Google Scholar]
- Nanda, S.J.; Panda, G. A survey on nature inspired metaheuristic algorithms for partitional clustering. Swarm Evol. Comput. 2014, 16, 1–18. [Google Scholar]
- Ismkhan, H. Effective heuristics for ant colony optimization to handle large-scale problems. Swarm Evol. Comput. 2017, 32, 140–149. [Google Scholar] [CrossRef]
- Jain, M.; Singh, V.; Rani, A. A novel nature inspired algorithm for optimization: Squirrel search algorithm. Swarm Evol. Comput. 2019, 44, 148–175. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C. Particle Swarm Optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- You, Z.; Lu, C. A heuristic fault diagnosis approach for electro-hydraulic control system based on hybrid particle swarm optimization and Levenberg–Marquardt algorithm. J. Ambient Intell. Humaniz. Comput. 2018. [Google Scholar] [CrossRef]
- Yu, J.; Mo, B.; Tang, D.; Liu, H.; Wan, J. Remaining useful life prediction for lithium-ion batteries using a quantum particle swarm optimization-based particle filter. Qual. Eng. 2017, 29, 536–546. [Google Scholar] [CrossRef]
- Fernandes Junior, F.E.; Yen, G. Particle swarm optimization of deep neural networks architectures for image classification. Swarm Evol. Comput. 2019, 49, 62–74. [Google Scholar] [CrossRef]
- Ignat, A.; Lazar, E.; Petreus, D. Energy Management for an Islanded Microgrid Based on Particle Swarm Optimization. In Proceedings of the International Symposium for Design and Technology of Electronics Packages, Cluj-Napoca, Romania, 23–26 October 2019. [Google Scholar]
- Abo-Elnaga, Y.; Nasr, S. Modified Evolutionary Algorithm and Chaotic Search for Bilevel Programming Problems. Symmetry 2020, 12, 767. [Google Scholar] [CrossRef]
- Goshu, N.N.; Kassa, S.M. A systematic sampling evolutionary (SSE) method for stochastic bilevel programming problems. Comput. Oper. Res. 2020, 120, 104942. [Google Scholar] [CrossRef]
- Zhang, X.; Lu, D.; Zhang, X.; Wang, Y. Antenna array design by a contraction adaptive particle swarm optimization algorithm. EURASIP J. Wirel. Commun. Netw. 2019, 57. [Google Scholar] [CrossRef] [Green Version]
- Hu, Z.; Chang, J.; Zhou, Z. PSO Scheduling Strategy for Task Load in Cloud Computing. Hunan Daxue Xuebao/J. Hunan Univ. Nat. Sci. 2019, 46, 117–123. [Google Scholar]
- Chen, X.; Xiao, S. Multi-Objective and Parallel Particle Swarm Optimization Algorithm for Container-Based Microservice Scheduling. Sensors 2021, 21, 6212. [Google Scholar] [CrossRef]
- Nadolski, S.; Borowska, B. Application of the PSO algorithm with sub-domain approach for the optimization of radio telescope array. J. Appl. Comput. Sci. 2008, 16, 7–14. [Google Scholar]
- Michaloglou, A.; Tsitsas, N.L. Feasible Optimal Solutions of Electromagnetic Cloaking Problems by Chaotic Accelerated Particle Swarm Optimization. Mathematics 2021, 9, 2725. [Google Scholar] [CrossRef]
- Cheng, R.; Jin, Y. A competitive swarm optimizer for large scale optimization. IEEE Trans. Cybern. 2015, 45, 191–204. [Google Scholar] [CrossRef] [PubMed]
- Shi, Y.; Eberhart, R.C. Empirical study of particle swarm optimization. In Proceedings of the Congress on Evolutionary Computation, Washington, DC, USA, 6–9 July 1999; pp. 1945–1949. [Google Scholar]
- Zhang, L.; Yu, H.; Hu, S. A new approach to improve particle swarm optimization. In Proceedings of the International Conference on Genetic and Evolutionary Computation, Chicago, IL, USA, 12–16 July 2003; Springer: Berlin, Germany, 2003; pp. 134–139. [Google Scholar]
- Niu, B.; Zhu, Y.; He, X.; Wu, H. MCPSO: A multi-swarm cooperative particle swarm optimizer. Appl. Math. Comput. 2007, 185, 1050–1062. [Google Scholar] [CrossRef] [Green Version]
- Clerc, M. The swarm and the queen: Towards a deterministic and adaptive particle swarm optimization. In Proceedings of the ICEC, Washington, DC, USA, 6–9 July 1999; pp. 1951–1957. [Google Scholar]
- Venter, G.; Sobieszczanski-Sobieski, J. Particle swarm optimization. In Proceedings of the 43rd AIAA/ASME/ASCE/AHS/ASC Structure, Structure Dynamics and Materials Conference, Denver, CO, USA, 22–25 April 2002; pp. 22–25. [Google Scholar]
- Borowska, B. Social strategy of particles in optimization problems. In Advances in Intelligent Systems and Computing; Springer: Berlin/Heidelberg, Germany, 2020; Volume 991, pp. 537–546. [Google Scholar] [CrossRef]
- Ratnaweera, A.; Halgamuge, S.K.; Watson, H.C. Self-organizing hierarchical particle swarm optimizer with time-varying acceleration coefficients. IEEE Trans. Evol. Comput. 2004, 8, 240–255. [Google Scholar] [CrossRef]
- Chen, T.; Shen, Q.; Su, P.; Shang, C. Fuzzy rule weight modification with particle swarm optimization. Soft Comput. 2016, 20, 2923–2937. [Google Scholar] [CrossRef] [Green Version]
- Kennedy, J.; Mendes, R. Population structure and particle swarm performance. In Proceedings of the 2002 Congress on Evolutionary Computation, Honolulu, HI, USA, 12–17 May 2002; Volume 2, pp. 1671–1676. [Google Scholar]
- Lin, A.; Sun, W.; Yu, H.; Wu, G.; Tang, H. Global genetic learning particle swarm optimization with diversity enhanced by ring topology. Swarm Evol. Comput. 2019, 44, 571–583. [Google Scholar] [CrossRef]
- Borowska, B. Genetic learning particle swarm optimization with interlaced ring topology. In Lecture Notes in Computer Science, Proceedings of the Computational Science—ICCS 2020, Amsterdam, The Netherlands, 3–5 June 2020; Krzhizhanovskaya, V.V., Závodszky, G., Lees, H., Eds.; Springer: Cham, Switzerland, 2020; Volume 12141, pp. 136–148. [Google Scholar] [CrossRef]
- Chen, Y.; Li, L.; Peng, H.; Xiao, J.; Wu, Q.T. Dynamic multi-swarm differential learning particle swarm optimizer. Swarm Evol. Comput. 2018, 39, 209–221. [Google Scholar] [CrossRef]
- Gong, Y.J.; Li, J.J.; Zhou, Y.C.; Li, Y.; Chung, H.S.H.; Shi, Y.H.; Zhang, J. Genetic learning particle swarm optimization. IEEE Trans. Cybern. 2016, 46, 2277–2290. [Google Scholar] [CrossRef] [Green Version]
- Mendes, R.; Kennedy, J.; Neves, J. The fully informed particle swarm: Simpler, maybe better. IEEE Trans. Evol. Comput. 2004, 8, 204–210. [Google Scholar] [CrossRef]
- Lim, W.H.; Isa, N.A.M. Particle swarm optimization with adaptive time-varying topology connectivity. Appl. Soft Comput. 2014, 24, 623–642. [Google Scholar] [CrossRef]
- Carvalho, D.F.; Bastos-Filho, C.J.A. Clan Particle Swarm Optimization. In Proceedings of the 2008 IEEE Congress on Evolutionary Computation (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1–6 June 2008; pp. 3044–3051. [Google Scholar] [CrossRef]
- Bastos-Filho, C.J.A.; Carvalho, D.F.; Figueiredo, E.M.N.; Miranda, P.B.C. Dynamic Clan Particle Swarm Optimization. In Proceedings of the Ninth International Conference on Intelligent Systems Design and Applications, Pisa, Italy, 30 November–2 December 2009; pp. 249–254. [Google Scholar] [CrossRef]
- Shen, Y.; Cai, W.; Kang, H.; Sun, X.; Chen, Q.; Zhang, H. A Particle Swarm Algorithm Based on a Multi-Stage Search Strategy. Entropy 2021, 23, 1200. [Google Scholar] [CrossRef]
- Ali, A.F.; Tawhid, M.A. A hybrid particle swarm optimization and genetic algorithm with population partitioning for large scale optimization problems. Ain Shams Eng. J. 2017, 8, 191–206. [Google Scholar] [CrossRef] [Green Version]
- Sharma, M.; Chhabra, J.K. Sustainable automatic data clustering using hybrid PSO algorithm with mutation. Sustain. Comput. Inform. Syst. 2019, 23, 144–157. [Google Scholar] [CrossRef]
- Shieh, H.L.; Kuo, C.C.; Chiang, C.M. Modified particle swarm optimization algorithm with simulated annealing behavior and its numerical verification. Appl. Math. Comput. 2011, 218, 4365–4383. [Google Scholar] [CrossRef]
- Holden, N.; Freitas, A. A hybrid particle swarm/ant colony algorithm for the classification of hierarchical biological data. In Proceedings of the 2005 IEEE Swarm Intelligence Symposium, Pasadena, CA, USA, 8–10 June 2005; pp. 100–107. [Google Scholar]
- Liu, F.; Zhou, Z. An improved QPSO algorithm and its application in the high-dimensional complex problems. Chomometrics Intell. Lab. Syst. 2014, 132, 82–90. [Google Scholar] [CrossRef]
- Cheng, R.; Sun, C.; Jin, Y. A multi-swarm evolutionary framework based on a feedback mechanism. In Proceedings of the IEEE Congress on Evolutionary Computation, Cancun, Mexico, 20–23 June 2013; pp. 718–724. [Google Scholar] [CrossRef]
- Ye, W.; Feng, W.; Fan, S. A novel multi-swarm particle swarm optimization with dynamic learning strategy. Appl. Soft Comput. 2017, 61, 832–843. [Google Scholar] [CrossRef]
- Liang, J.; Qin, K.; Suganthan, P.N.; Baskar, S. Comprehensive learning particle swarm optimizer for global optimization of multimodal functions. IEEE Trans. Evol. Comput. 2006, 10, 281–295. [Google Scholar] [CrossRef]
- Lin, A.; Sun, W.; Yu, H.; Wu, G.; Tang, H. Adaptive comprehensive learning particle swarm optimization with cooperative archive. Appl. Soft Comput. J. 2019, 77, 533–546. [Google Scholar] [CrossRef]
- Cheng, R.; Jin, Y. A social learning particle swarm optimization algorithm for scalable optimization. Inf. Sci. 2015, 291, 43–60. [Google Scholar]
- Niu, B.; Huang, H.; Tan, L.; Duan, Q. Symbiosis-based alternative learning multi-swarm particle swarm optimization. IEEE/ACM Trans. Comput. Biol. Bioinform. 2017, 14, 4–14. [Google Scholar] [CrossRef] [PubMed]
- Shi, Y.; Eberhart, R. A Modified Particle Swarm Optimizer; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Igel, C.; Hansen, N.; Roth, S. Covariance matrix adaptation for multi-objective optimization. Evol. Comput. 2007, 15, 1–28. [Google Scholar] [CrossRef] [PubMed]
- Lynn, N.; Suganthan, P.N. Heterogeneous comprehensive learning particle swarm optimization with enhanced exploration and exploitation. Swarm Evol. Comput. 2015, 24, 11–24. [Google Scholar] [CrossRef]




| Function | Formula | Fmin | Range |
|---|---|---|---|
| Sphere | 0 | [−100, 100]n | |
| Schwefel 1.2 | 0 | [−100, 100]n | |
| Quartic | 0 | [−100, 100]n | |
| Schwefel 2.22 | 0 | [−10; 10]n | |
| Rosenbrock | 0 | [−30, 30]n | |
| Griewank | 0 | [−600, 600]n | |
| Rastrigin | 0 | [−5.12, 5.12]n | |
| Ackley | 0 | [−32, 32]n | |
| Zakharov | 0 | [−10, 10]n | |
| Schwefel | 0 | [−400, 400]n | |
| Weierstrass | a = 0.5, b = 3, kmax = 20 | 0 | [−0.5, 0.5]n |
| Rotated Rastrigin | 0 | [−5.12, 5.12]n | |
| Rotated Griewank | 0 | [−600, 600]n | |
| Rotated Schwefel | 0 | [−400, 400]n | |
| Rotated Weierstrass | a = 0.5, b = 3, kmax = 20, | 0 | [−0.5, 0.5]n |
| Rotated Ackley | 0 | [−32, 32]n |
| Algorithm | Inertia Weight w | Acceleration Coefficients c1, c2, c | Other Parameters |
|---|---|---|---|
| CLPSO | w = 0.9–0.4 | c = 1.496 | - |
| FIPS | c = 2.05 | χ = 0.729 | |
| PSO | w = 0.9–0.4 | c1 = 2.0, c2 = 2.0 | - |
| HCLPSO | w = 0.99–0.2 | c1 = 2.5–0.5, c2 = 0.5–2.5, c = 3–1.5 | - |
| CSO | w = 0.7298 | c = 1.49618 | pm = 0.01, sg = 7 |
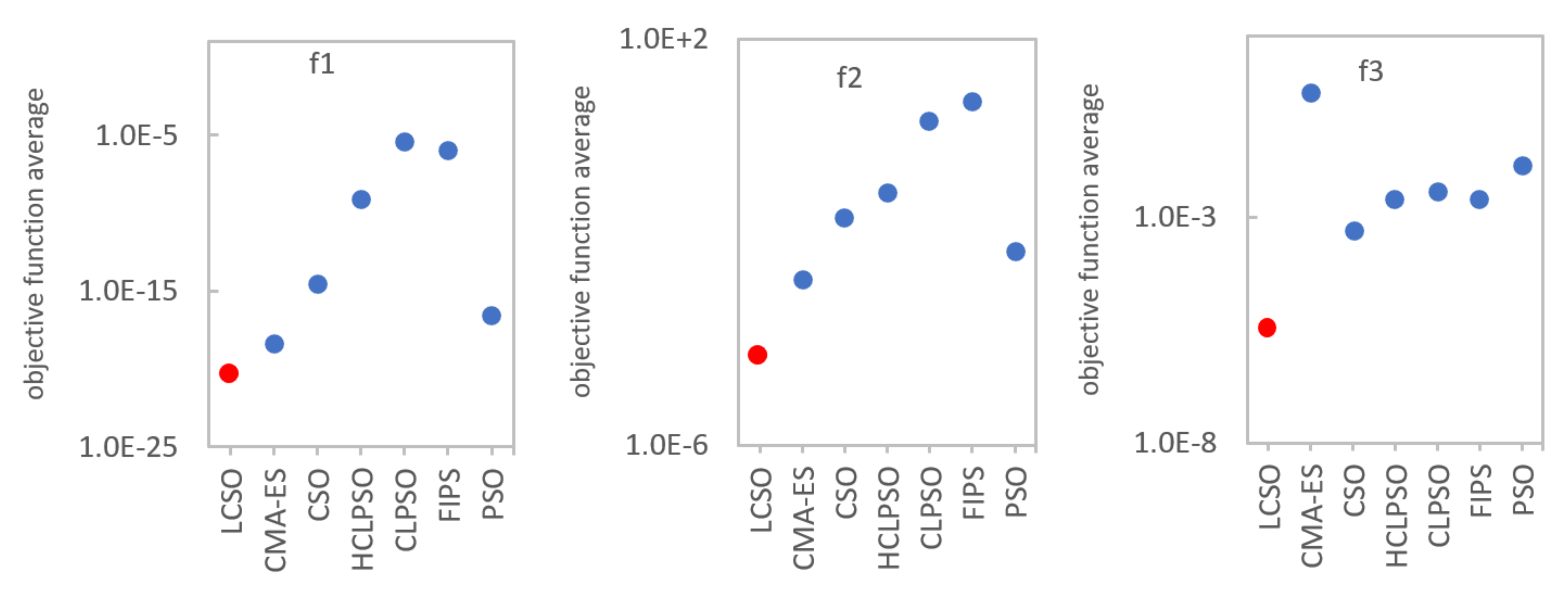
| Function | CLPSO | PSO | HCLPSO | CSO | CMA-ES | FIPS | LCSO | |
|---|---|---|---|---|---|---|---|---|
| f1 | Mean | 4.15E-06 | 2.43E-17 | 8.93E-10 | 3.22E-15 | 4.16E-19 | 1.03E-06 | 5.24E-21 |
| Std | 3.81E-06 | 3.15E-17 | 7.11E-10 | 3.75E-15 | 4.07E-19 | 1.59E-06 | 2.19E-21 | |
| f2 | Mean | 2.43E-01 | 6.54E-03 | 8.93E-02 | 3.22E-02 | 1.78E-03 | 4.88E-00 | 5.63E-05 |
| Std | 3.15E-01 | 4.81E-03 | 7.11E-02 | 3.75E-02 | 4.02E-04 | 5.37E-00 | 4.39E-05 | |
| f3 | Mean | 3.42E-03 | 1.34E-02 | 2.33E-03 | 5.22E-04 | 5.21E-01 | 2.41E+03 | 3.61E-06 |
| Std | 5.17E-03 | 9.06E-03 | 7.94E-04 | 5.08E-04 | 2.79E-03 | 1.47E+03 | 6.42E-06 | |
| f4 | Mean | 5.16E-08 | 3.44E-14 | 4.33E-06 | 4.88E-17 | 3.25E-07 | 3.17E-07 | 4.86E-17 |
| Std | 1.04E-07 | 2.80E-14 | 1.13E-05 | 4.63E-16 | 2.81E-07 | 4.54E-07 | 3.40E-16 | |
| f5 | Mean | 3.78E+01 | 6.14E+01 | 3.53E+01 | 4.20E+01 | 1.02E+01 | 2.82E+01 | 2.54E+00 |
| Std | 1.86E+01 | 5.80E+01 | 5.14E+00 | 3.15E+01 | 1.61E+00 | 2.14E+01 | 5.72E+00 | |
| f6 | Mean | 4.43E-06 | 1.45E-02 | 4.61E-08 | 7.21E-10 | 3.34E-09 | 2.93E-03 | 3.98E-12 |
| Std | 1.01E-05 | 1.29E-02 | 5.42E-08 | 5.36E-10 | 1.02E-10 | 4.18E-03 | 3.41E-11 | |
| f7 | Mean | 1.34E+00 | 4.38E+01 | 4.78E-04 | 3.80E-04 | 1.8E+01 | 7.32E+01 | 6.54E-06 |
| Std | 6.16E-01 | 8.75E+00 | 7.05E-05 | 2.52E-04 | 7.35E-01 | 2.25E+01 | 3.77E-05 | |
| f8 | Mean | 5.12E-01 | 2.24E+00 | 1.15E-09 | 4.60E-10 | 7.35E-12 | 5.74E+00 | 8.12E-08 |
| Std | 8.39E-01 | 1.46E+00 | 3.67E-10 | 1.88E-09 | 1.14E-12 | 6.18E-01 | 7.93E-09 | |
| f9 | Mean | 3.97E-01 | 1.56E+00 | 6.30E-02 | 5.61E-02 | 1.39E-01 | 2.25E-01 | 3.08E-03 |
| Std | 3.12E-01 | 1.25E+00 | 5.47E-02 | 3.95E-02 | 2.61E-02 | 2.43E-01 | 2.95E-03 | |
| f10 | Mean | 1.71E-03 | 1.86E+03 | 2.08E-03 | 6.53E+03 | 1.25E-03 | 6.62E+02 | 3.15E-05 |
| Std | 1.59E-03 | 2.07E+02 | 1.37E-03 | 3.87E+03 | 1.94E-03 | 4.94E+02 | 4.39E-05 | |
| f11 | Mean | 2.39E-05 | 1.89E-03 | 4.38E-04 | 3.15E-03 | 2.32E-03 | 5.29E-04 | 5.37E-07 |
| Std | 2.12E-05 | 1.67E-03 | 3.65E-04 | 1.97E-03 | 1.85E-03 | 1.92E-04 | 3.71E-07 | |
| f12 | Mean | 1.89E+02 | 5.94E+01 | 5.98E+01 | 1.92E+01 | 2.74E+01 | 2.21E+02 | 7.67E+00 |
| Std | 5.14E+01 | 6.73E+00 | 4.26E+01 | 5.07E+00 | 1.30E-01 | 2.80E+01 | 4.02E+00 | |
| f13 | Mean | 3.44E-03 | 7.68E-02 | 7.53E-03 | 5.41E-09 | 2.28E-08 | 6.67E-04 | 9.16E-12 |
| Std | 4.96E-03 | 8.39E-02 | 8.66E-03 | 7.92E-09 | 3.46E-09 | 1.02E-03 | 7.85E-11 | |
| f14 | Mean | 6.23E+03 | 4.66E+03 | 6.83E+03 | 7.78E+03 | 1.15E+03 | 7.65E+03 | 4.59E+02 |
| Std | 4.18E+03 | 3.19E+03 | 3.99E+03 | 3.54E+03 | 3.29E+03 | 3.61E+03 | 6.34E+02 | |
| f15 | Mean | 3.27E+01 | 2.55E+01 | 6.45E+01 | 1.83E-01 | 2.12E+01 | 4.07E+01 | 3.47E-03 |
| Std | 3.39E+01 | 3.12E+01 | 4.73E+01 | 2.78E-01 | 1.96E+00 | 8.65E+00 | 2.51E-03 | |
| f16 | Mean | 8.27E-01 | 2.25E+00 | 2.31E+00 | 5.11E-10 | 1.76E+00 | 2.71E-03 | 5.09E-14 |
| Std | 6.54E-02 | 6.58E-01 | 5.15E-02 | 5.16E-10 | 5.04E-01 | 2.03E-03 | 6.71E-14 |
| Function | t-Value between CLPSO and LCSO | t-Value between PSO and LCSO | t-Value between HCLPSO and LCSO | t-Value between CSO and LCSO | t-Value between FIPS and LCSO | Two-Tailed p between CLPSO and LCSO | Two-Tailed p between PSO and LCSO | Two-Tailed p between HCLPSO and LCSO | Two-Tailed p between CSO and LCSO | Two-Tailed p between FIPS and LCSO |
|---|---|---|---|---|---|---|---|---|---|---|
| f1 | 6.16E+00 | 4.36E+00 | 7.10E+00 | 4.86E+00 | 3.66E+00 | 1.60E-08 | 3.18E-05 | 1.95E-10 | 4.51E-06 | 4.02E-04 |
| f2 | 4.36E+00 | 7.62E+00 | 7.10E+00 | 4.85E+00 | 5.14E+00 | 3.18E-05 | 1.59E-11 | 1.99E-10 | 4.67E-06 | 1.40E-06 |
| f3 | 3.74E+00 | 8.36E+00 | 1.66E+01 | 5.77E+00 | 9.27E+00 | 3.12E-04 | 4.21E-13 | 3.50E-30 | 9.19E-08 | 4.55E-15 |
| f4 | 2.82E+00 | 6.94E+00 | 2.16E+00 | N/A | 3.95E+00 | 5.89E-03 | 4.28E-10 | 3.30E-02 | N/A | 1.47E-04 |
| f5 | 1.02E+01 | 5.71E+00 | 2.41E+01 | 6.97E+00 | 6.55E+00 | 3.47E-17 | 1.19E-07 | 6.31E-43 | 3.67E-10 | 2.64E-09 |
| f6 | 2.49E+00 | 6.36E+00 | 4.81E+00 | 7.55E+00 | 3.97E+00 | 1.45E-02 | 6.49E-09 | 5.44E-06 | 2.26E-11 | 1.40E-04 |
| f7 | 1.23E+01 | 2.83E+01 | 6.95E+00 | 4.66E+00 | 1.84E+01 | 1.35E-21 | 5.57E-49 | 4.01E-10 | 1.00E-05 | 1.45E-33 |
| f8 | 3.45E+00 | 8.68E+00 | N/A | N/A | 5.25E+01 | 8.23E-04 | 8.84E-14 | N/A | N/A | 1.35E-73 |
| f9 | 7.14E+00 | 7.04E+00 | 6.19E+00 | 7.57E+00 | 5.17E+00 | 1.63E-10 | 2.60E-10 | 1.43E-08 | 2.05E-11 | 1.26E-06 |
| f10 | 5.97E+00 | 5.08E+01 | 8.45E+00 | 9.55E+00 | 7.58E+00 | 3.81E-08 | 3.10E-72 | 2.70E-13 | 1.18E-15 | 1.97E-11 |
| f11 | 6.23E+00 | 6.40E+00 | 6.78E+00 | 9.04E+00 | 1.56E+01 | 1.15E-08 | 5.35E-09 | 9.11E-10 | 1.44E-14 | 3.01E-28 |
| f12 | 1.93E+01 | 3.61E+01 | 6.67E+00 | 9.76E+00 | 4.13E+01 | 4.12E-35 | 1.84E-58 | 1.51E-09 | 4.01E-16 | 8.48E-64 |
| f13 | 3.80E+00 | 5.01E+00 | 4.76E+00 | 3.75E+00 | 3.58E+00 | 2.52E-04 | 2.38E-06 | 6.62E-06 | 3.00E-04 | 5.39E-04 |
| f14 | 7.48E+00 | 7.07E+00 | 8.64E+00 | 1.11E+01 | 1.07E+01 | 3.26E-11 | 2.25E-10 | 1.09E-13 | 3.95E-19 | 2.93E-18 |
| f15 | 5.28E+00 | 4.48E+00 | 7.47E+00 | 3.54E+00 | 2.58E+01 | 7.69E-07 | 2.06E-05 | 3.39E-11 | 6.20E-04 | 1.94E-45 |
| f16 | 6.93E+01 | 1.87E+01 | 2.46E+02 | 5.42E+00 | 7.31E+00 | 4.80E-85 | 3.78E-34 | 1.53E-138 | 4.21E-07 | 7.22E-11 |
| Function | D = 100 | D = 500 | D = 1000 |
|---|---|---|---|
| f1 | 1.97E-23 | 2.03E-11 | 2.14E-09 |
| f2 | 4.62E-01 | 7.39E+01 | 2.17E+02 |
| f3 | 1.95E-01 | 1.38E+04 | 2.01E+05 |
| f4 | 5.16E-02 | 8.41E+00 | 3.56E+02 |
| f5 | 9.38E+01 | 5.22E+02 | 9.72E+02 |
| f6 | 1.02E-18 | 5.46E-12 | 3.65E-10 |
| f7 | 1.06E-13 | 3.71E-08 | 5.29E-06 |
| f8 | 5.12E-14 | 2.24E-05 | 4.15E-03 |
| f9 | 7.06E-07 | 4.67E-04 | 5.07E-02 |
| f10 | 3.18E+04 | 1.82E+05 | 3.94E+05 |
| f11 | 1.37E-02 | 2.56E+01 | 4.61E+03 |
| f12 | 1.25E-12 | 3.77E-09 | 6.29E-08 |
| f13 | 1.03E-14 | 6.32E-09 | 5.07E-08 |
| f14 | 2.56E+04 | 1.69E+05 | 3.83E+05 |
| f15 | 1.42E+01 | 3.70E+02 | 7.26E+02 |
| f16 | 2.07E-13 | 3.24E-07 | 4.19E-06 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Borowska, B. Learning Competitive Swarm Optimization. Entropy 2022, 24, 283. https://doi.org/10.3390/e24020283
Borowska B. Learning Competitive Swarm Optimization. Entropy. 2022; 24(2):283. https://doi.org/10.3390/e24020283
Chicago/Turabian StyleBorowska, Bożena. 2022. "Learning Competitive Swarm Optimization" Entropy 24, no. 2: 283. https://doi.org/10.3390/e24020283
APA StyleBorowska, B. (2022). Learning Competitive Swarm Optimization. Entropy, 24(2), 283. https://doi.org/10.3390/e24020283






