Solving Generalized Polyomino Puzzles Using the Ising Model
Abstract
:1. Introduction
2. Combinatorial Optimization Problem and the Ising Model
2.1. The Ising Model and the QUBO Problem
2.2. Hopfield Neural Network for Solving Combinatorial Optimization Problems
- Express the objective function to be minimized in a quadratic form for binary variables.
- Compare the quadratic form to be minimized with the energy function in Equation (4) and obtain the values of and , which make them coincide.
- Construct a Hopfield neural network with the obtained values of and .
- Select one neuron randomly and update it using Equations (1) and (2).
- Perform Step 4 several times to minimize the free energy in Equation (3).
- Obtain the output values of the neurons and binarize them based on some criteria. The solution is obtained if the output values of the neurons after the binarization operation satisfy the constraint conditions. In this study, the binarization is performed based on whether the output value is greater than or equal to 0.5.
3. Solving Pentomino Puzzles with the Ising Model
3.1. Pentomino Puzzle
3.2. Improvement of the Hamiltonian Function
3.2.1. Constraint on the Number of Times Each Pentomino Is Used
3.2.2. Constraint on the Overlap of the Pentominoes on the Board
3.2.3. Inhibition of Bubbles
3.2.4. Encouragement for Combinations of Pentominoes That Contact Each Other
3.2.5. Encouragement for Pentominoes That Contact the Borders of the Board
3.2.6. Broad Restriction on All Pairs of Neurons
3.2.7. Hamiltonian for the Pentomino Puzzle
3.3. Computer Experiments
3.3.1. Experimental Parameters
3.3.2. Probability of Finding the Optimal Solution
4. Allowing Zero or Multiple Usage of Polyomino and Arbitrarily Shaped Board
4.1. Target Problem
- Each pentomino can be used zero or more times;
- An arbitrarily shaped board is the subject of the problem.
4.2. Hamiltonian for the Generalized Polyomino Puzzle
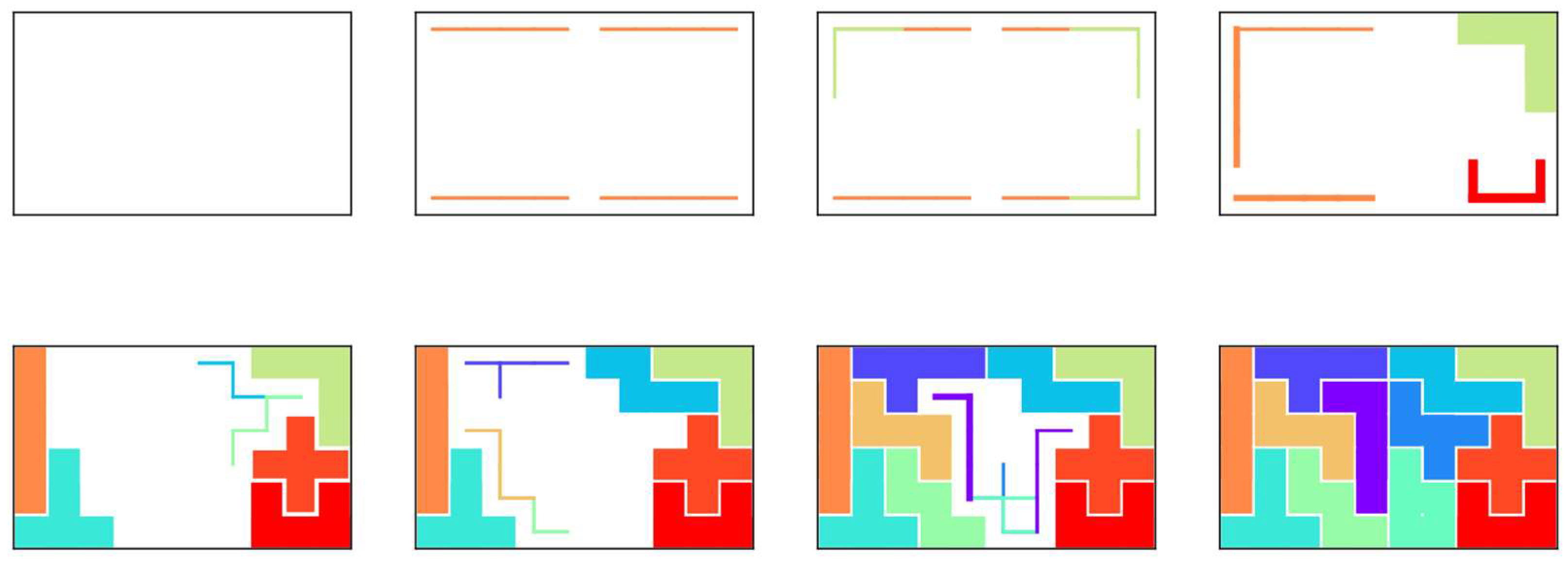
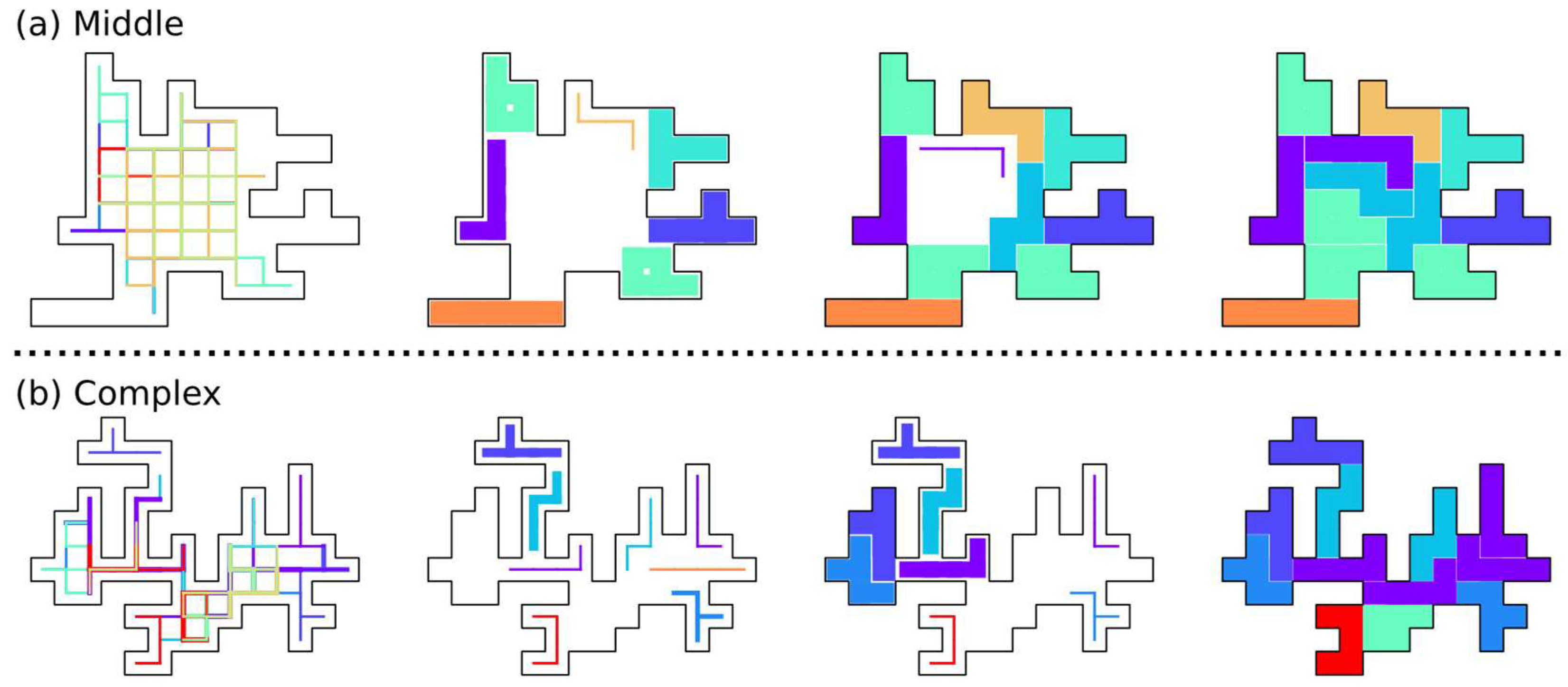
4.3. Generation of Arbitrarily Shaped Boards
4.4. Computer Experiments
4.4.1. Experimental Parameters
4.4.2. Probability of Finding an Optimal Solution
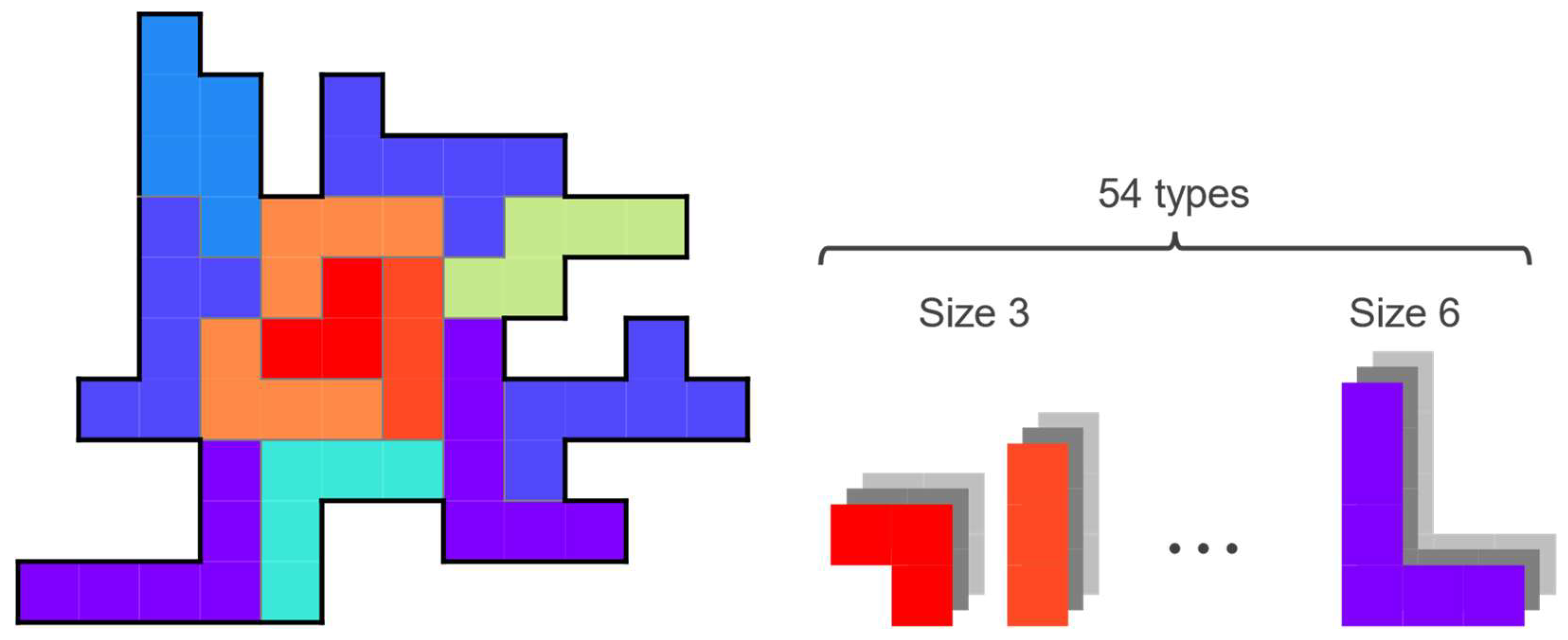
5. Accepting Various Sizes of Polyominoes
5.1. Set of Polyominoes
5.2. Computer Experiments
5.2.1. Experimental Parameters
5.2.2. Probability of Finding an Optimal Solution
5.2.3. Size of the Placed Polyominoes
5.2.4. Performance with the Reduced Types of Polyominoes
6. Discussion
6.1. Optimization of the Coefficients of the Hamiltonian
6.2. Proposal of a New Term That Minimizes the Total Number of Polyominoes Placed
6.3. Possibility of Application for Drug Discovery
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Golomb, S.W. Checker boards and polyominoes. Am. Math. Mon. 1954, 61, 675–682. [Google Scholar] [CrossRef]
- Golomb, S.W. Tiling with sets of polyominoes. J. Combin. Theory 1970, 9, 60–71. [Google Scholar] [CrossRef] [Green Version]
- Golomb, S.W. Tiling with polyominoes. J. Combin. Theory 1966, 1, 280–296. [Google Scholar] [CrossRef] [Green Version]
- Golomb, S.W. Polyominoes; Charles Scribner’s Sons: New York, NY, USA, 1965. [Google Scholar]
- Akiyama, Y.; Yamashita, A.; Kajiura, M.; Aiso, H. Combinatorial optimization with Gaussian Machines. Proc. Int. Jt. Conf. Neural Netw. 1989, 1, 533–540. [Google Scholar]
- Takefuji, Y.; Lee, Y.C. A parallel algorithm for tiling problems. IEEE Trans. Neural Netw. 1990, 1, 143–145. [Google Scholar] [CrossRef] [PubMed]
- Manabe, S.; Asai, H. A neuro-based optimization algorithm for tiling problems with rotation. Neural Process. Lett. 2001, 13, 267–275. [Google Scholar] [CrossRef]
- Eagle, A.; Kato, T.; Minato, Y. Solving tiling puzzles with quantum annealing. arXiv 2019, arXiv:1904.01770. [Google Scholar]
- Lenz, W. Beiträge zum Verständnis der magnetischen Eigenschaften in festen Körpern. Z. Phys. 1920, 21, 613–615. [Google Scholar]
- Hopfield, J.J. Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. USA 1982, 79, 2554–2558. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hopfield, J.J. Neurons with graded response have collective computational properties like those of two-state neurons. Proc. Natl. Acad. Sci. USA 1984, 81, 3088–3092. [Google Scholar] [CrossRef] [Green Version]
- Hopfield, J.J.; Tank, D.W. “Neural” computation of decisions in optimization problems. Biol. Cybern. 1985, 52, 141–152. [Google Scholar] [CrossRef] [PubMed]
- Lucas, A. Ising formulations of many NP problems. Front. Phys. 2014, 2, 5. [Google Scholar] [CrossRef] [Green Version]
- Rosenberg, G.; Haghnegahdar, P.; Goddard, P.; Carr, P.; Wu, K.; De Prado, M.L. Solving the optimal trading trajectory problem using a quantum annealer. IEEE J. Sel. Top. Signal Process. 2016, 10, 1053–1060. [Google Scholar] [CrossRef] [Green Version]
- Banchi, L.; Fingerhuth, M.; Babej, T.; Ing, C.; Arrazola, J.M. Molecular docking with Gaussian boson sampling. Sci. Adv. 2020, 6, eaax1950. [Google Scholar] [CrossRef]
- Johnson, M.W.; Amin, M.H.; Gildert, S.; Lanting, T.; Hamze, F.; Dickson, N.; Harris, R.; Berkley, A.J.; Johansson, J.; Bunyk, P.; et al. Quantum annealing with manufactured spins. Nature 2011, 473, 194–198. [Google Scholar] [CrossRef] [PubMed]
- McMahon, P.L.; Marandi, A.; Haribara, Y.; Hamerly, R.; Langrock, C.; Tamate, S.; Inagaki, T.; Takesue, H.; Utsunomiya, S.; Aihara, K.; et al. A fully programmable 100-spin coherent Ising machine with all-to-all connections. Science 2016, 354, 614–617. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Goto, H.; Tatsumura, K.; Dixon, A.R. Combinatorial optimization by simulating adiabatic bifurcations in nonlinear Hamiltonian systems. Sci. Adv. 2019, 5, eaav2372. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rosenthal, J.S.; Dote, A.; Dabiri, K.; Tamura, H.; Chen, S.; Sheikholeslami, A. Jump Markov chains and rejection-free Metropolis algorithm. Comput. Stat. 2021, 36, 2789–2811. [Google Scholar] [CrossRef]
- Akiyama, Y.; Yamashita, A.; Kajiura, M.; Anzai, Y.; Aiso, H. The Gaussian machine: A stochastic neural network for solving assignment problems. J. Neural Netw. Comput. 1991, 2, 43–51. [Google Scholar]
- Haselgrove, C.B.; Haselgrove, J. A computer program for pentominoes. Eureka 1960, 23, 16–18. [Google Scholar]
- Kajiura, M.; Akiyama, Y.; Anzai, Y. Solving large scale puzzles with neural networks. IEEE International Workshop on Tools for Artificial Intelligence, Fairfax, VA, USA, 23–25 October 1989; 1989; pp. 562–569. [Google Scholar]
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A next-generation hyperparameter optimization framework. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 2623–2631. [Google Scholar]
- Yanagisawa, K.; Komine, S.; Suzuki, S.D.; Ohue, M.; Ishida, T.; Akiyama, Y. Spresso: An ultrafast compound pre-screening method based on compound decomposition. Bioinformatics 2017, 33, 3836–3843. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zsoldos, Z.; Reid, D.; Simon, A.; Sadjad, S.B.; Johnson, A.P. eHiTS: A new fast, exhaustive flexible ligand docking system. J. Mol. Graph. Model. 2007, 26, 198–212. [Google Scholar] [CrossRef] [PubMed]
- Irwin, J.J.; Sterling, T.; Mysinger, M.M.; Bolstad, E.S.; Coleman, R.G. ZINC: A free tool to discover chemistry for biology. J. Chem. Inf. Model. 2012, 52, 1757–1768. [Google Scholar] [CrossRef] [PubMed]













| Problem | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| Pentomino puzzle | 4.29 | 2.16 | 8.38 | 0.246 | 0.0358 | 1.95 |
| Problem | B | C | D | E | F |
|---|---|---|---|---|---|
| Original | 3.09 | 5.64 | 0.777 | 0.430 | 4.76 |
| Middle | 1.17 | 3.98 | 0.511 | 0.671 | 2.36 |
| Complex | 2.66 | 3.31 | 0.129 | 0.164 | 4.83 |
| Name | Size of Polyomino | No. of Types |
|---|---|---|
| monomino | 1 | 1 |
| domino | 2 | 1 |
| tromino | 3 | 2 |
| tetromino | 4 | 5 |
| pentomino | 5 | 12 |
| hexomino | 6 | 35 |
| heptomino | 7 | 108 |
| octomino | 8 | 369 |
| Problem | B | C | D | E | F |
|---|---|---|---|---|---|
| Original | 3.38 | 5.70 | 0.615 | 0.518 | 3.91 |
| Middle | 1.41 | 5.05 | 0.647 | 0.328 | 3.31 |
| Complex | 1.81 | 5.56 | 0.482 | 0.407 | 3.29 |
| Parameter | Range |
|---|---|
| A | [0,5] |
| B | [0,5] |
| C | [0,10] |
| D | [0,1] |
| E | [0,1] |
| F | [0,5] |
| Problem | B | C | D | E | F | G |
|---|---|---|---|---|---|---|
| Original | 3.21 | 5.86 | 0.640 | 0.489 | 3.61 | 2.59 |
| Middle | 1.33 | 4.97 | 0.606 | 0.344 | 2.96 | 2.67 |
| Complex | 2.16 | 5.68 | 0.469 | 0.384 | 3.34 | 2.37 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Takabatake, K.; Yanagisawa, K.; Akiyama, Y. Solving Generalized Polyomino Puzzles Using the Ising Model. Entropy 2022, 24, 354. https://doi.org/10.3390/e24030354
Takabatake K, Yanagisawa K, Akiyama Y. Solving Generalized Polyomino Puzzles Using the Ising Model. Entropy. 2022; 24(3):354. https://doi.org/10.3390/e24030354
Chicago/Turabian StyleTakabatake, Kazuki, Keisuke Yanagisawa, and Yutaka Akiyama. 2022. "Solving Generalized Polyomino Puzzles Using the Ising Model" Entropy 24, no. 3: 354. https://doi.org/10.3390/e24030354
APA StyleTakabatake, K., Yanagisawa, K., & Akiyama, Y. (2022). Solving Generalized Polyomino Puzzles Using the Ising Model. Entropy, 24(3), 354. https://doi.org/10.3390/e24030354








