Theil Entropy as a Non-Lineal Analysis for Spectral Inequality of Physiological Oscillations
Abstract
:1. Introduction
2. Materials and Methods
2.1. Signals and Clinical Datasets
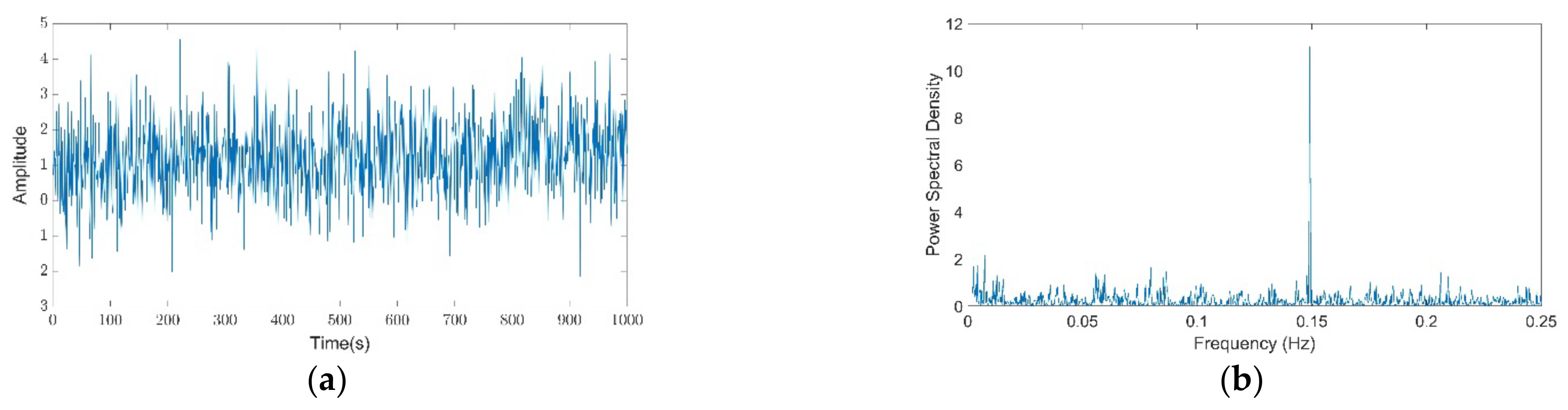
2.1.1. Synthetic Signals
2.1.2. RR Intervals
2.1.3. Image Intensity Data Collection
2.2. Theil Entropy
2.3. Spectral Density Analysis
2.3.1. Welch Periodogram
2.3.2. Lomb–Scargle Periodogram
2.3.3. Burg Periodogram
3. Results
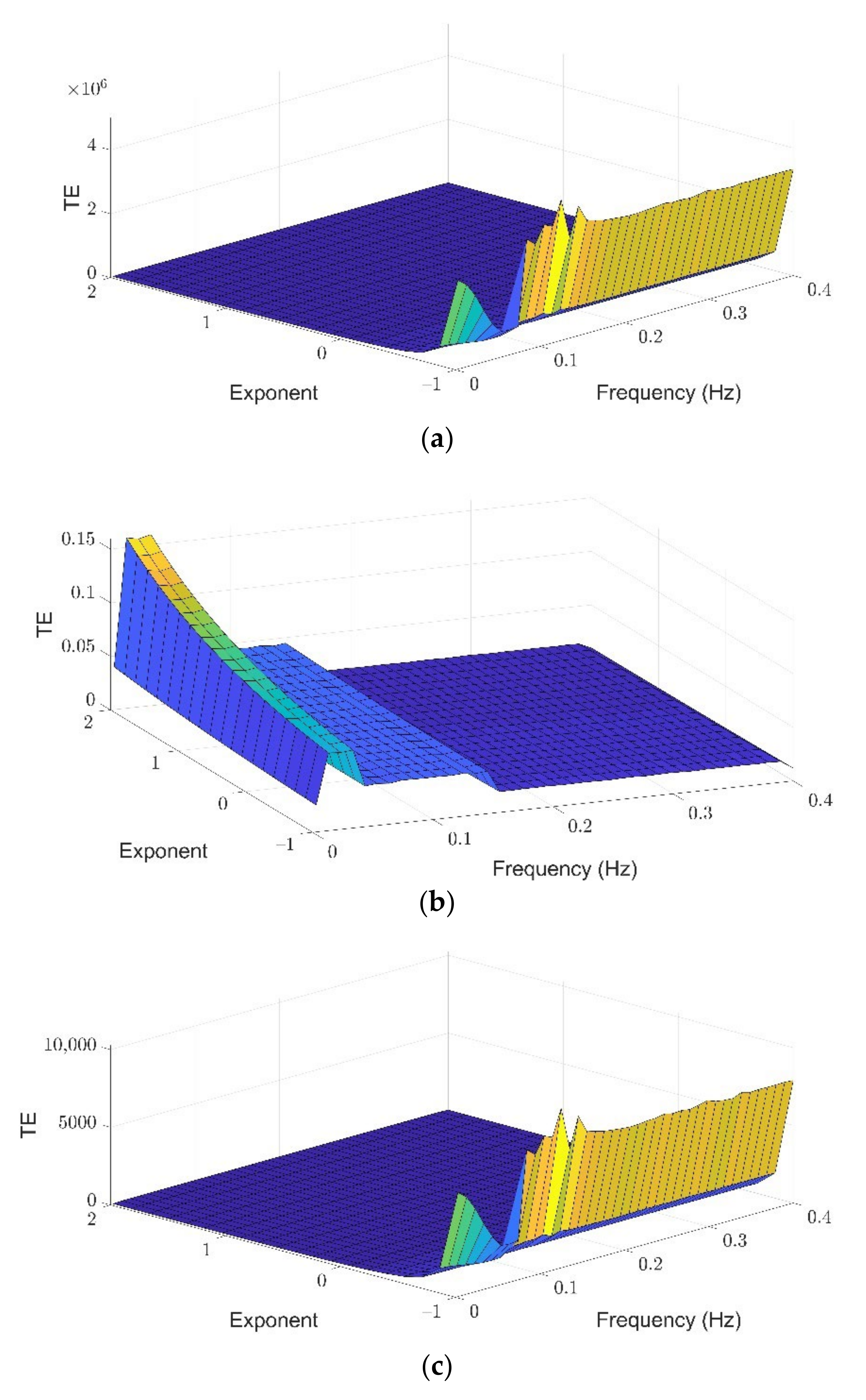
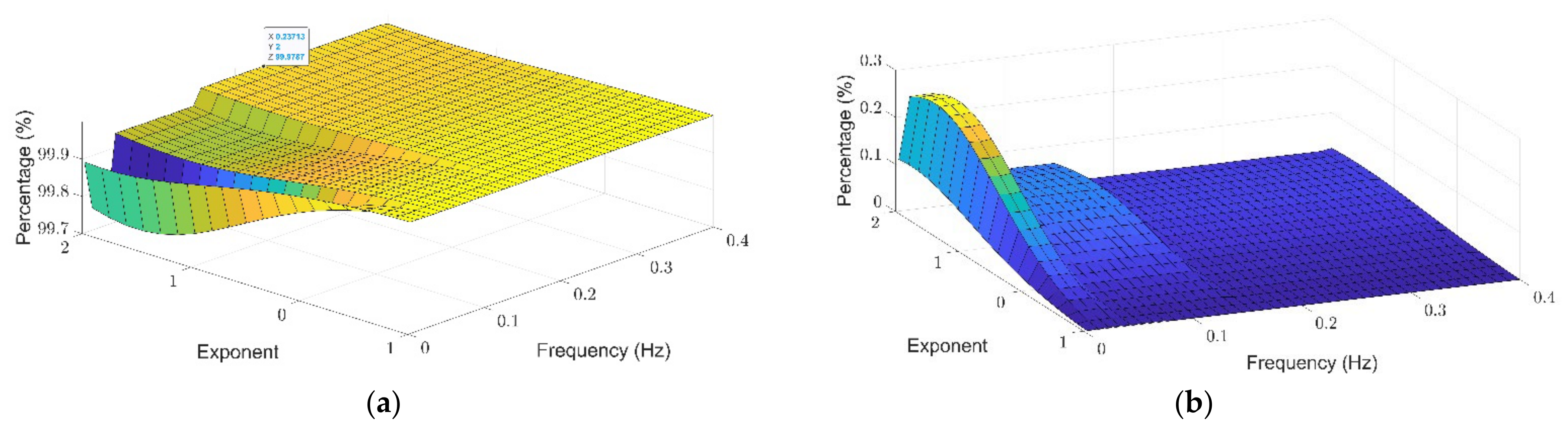
3.1. Theil Entropy Analysis of Synthetic Signals Shows the Potential of This Method to Account for Inequality Distribution of Power Spectra
3.2. Theil Entropy Effectively Captures Inequality Distribution of Heart Rate Variations in Response to Stress
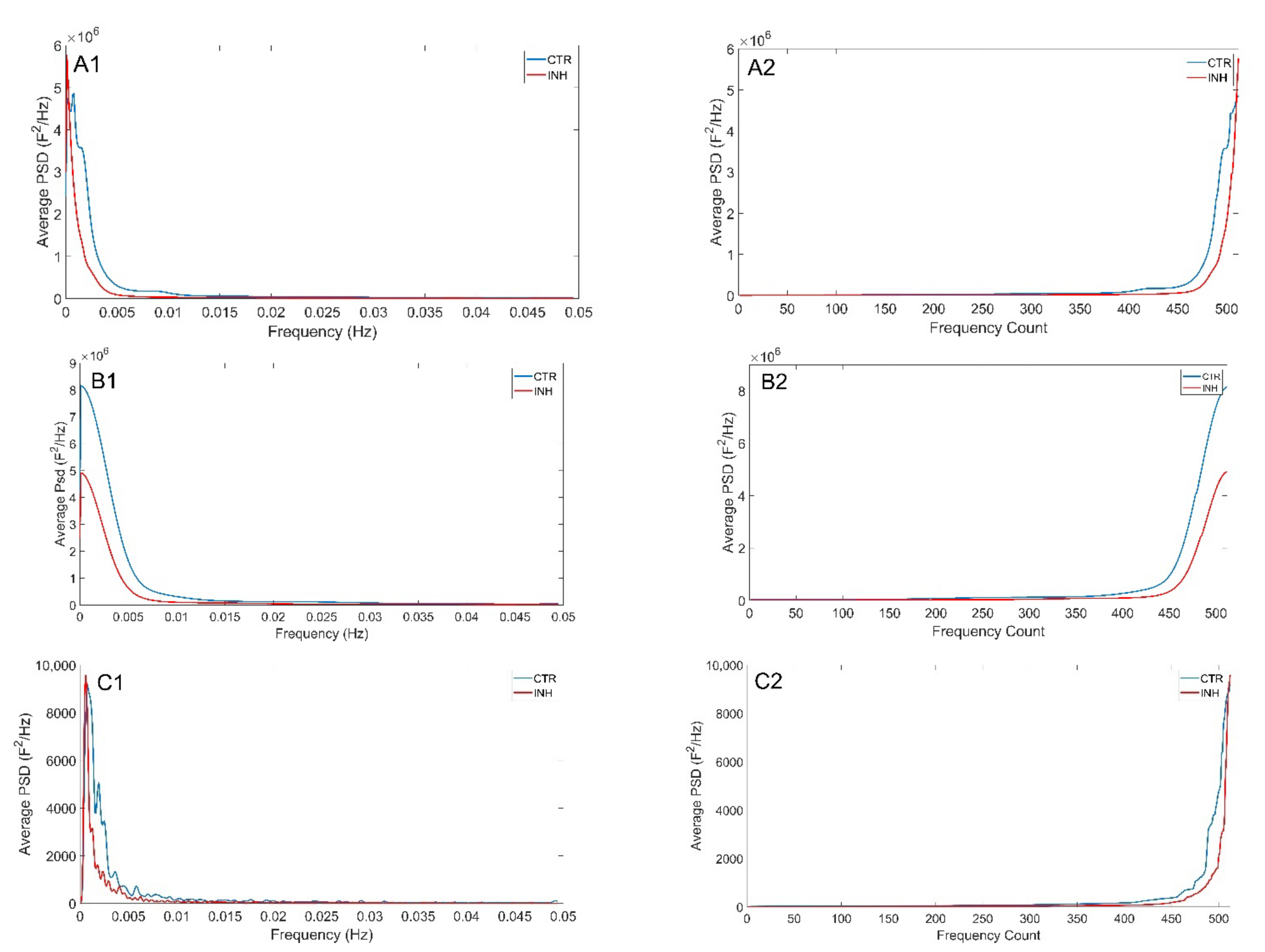
3.3. Theil Entropy Analysis Reveals Inequality Distribution of Calcium Oscillations in the Developing Brain
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Faust, O.; Hagiwara, Y.; Hong, T.J.; Lih, O.S.; Acharya, U.R. Deep learning for healthcare applications based on physiological signals: A review. Comput. Methods Programs Biomed. 2018, 161, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Gomez-Pilar, J.; Poza, J.; Gómez, C.; Northoff, G.; Lubeiro, A.; Cea-Cañas, B.B.; Molina, V.; Hornero, R. Altered predictive capability of the brain network EEG model in schizophrenia during cognition. Schizophr. Res. 2018, 201, 120–129. [Google Scholar] [CrossRef] [PubMed]
- Rezek, I.; Roberts, S. Stochastic complexity measures for physiological signal analysis. IEEE Trans. Biomed. Eng. 1998, 45, 1186–1191. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yu, X.; Mei, Z.; Chen, C.; Chen, W. Ranking Power Spectra: A Proof of Concept. Entropy 2019, 21, 1057. [Google Scholar] [CrossRef] [Green Version]
- Johnson, R.; Shore, J. Which is the better entropy expression for speech processing: -S log S or log S? IEEE Trans. Acoust. Speech Signal Process. 1984, 32, 129–137. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.D. Entropy for the Complexity of Physiological Signal Dynamics. Adv. Exp. Med. Biol. 2017, 1028, 39–53. [Google Scholar] [CrossRef]
- Bernardo, A.F.B.; Vanderlei, L.C.; Garner, D.M. HRV Analysis: A Clinical and Diagnostic Tool in Chronic Obstructive Pulmonary Disease. Int. Sch. Res. Not. 2014, 2014, 673232. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. ACM SIGMOBILE Mob. Comput. Commun. Rev. 2001, 5, 3–55. [Google Scholar] [CrossRef]
- Życzkowski, K. Rényi extrapolation of Shannon entropy. Open Syst. Inf. Dyn. 2003, 10, 297–310. [Google Scholar] [CrossRef] [Green Version]
- Wu, B.-F.; Wang, K.-C. Robust endpoint detection algorithm based on the adaptive band-partitioning spectral entropy in adverse environments. IEEE Trans. Speech Audio Process. 2005, 13, 762–775. [Google Scholar]
- Zhang, Y.; Zhang, Q.; Melodia, T. A frequency-domain entropy-based detector for robust spectrum sensing in cognitive radio networks. IEEE Commun. Lett. 2010, 14, 533–535. [Google Scholar] [CrossRef] [Green Version]
- Smith, C.R.; Grandy, W.T., Jr. Maximum-Entropy and Bayesian Methods in Inverse Problems; Springer Science & Business Media: New York, NY, USA, 2013; Volume 14. [Google Scholar]
- Shorrocks, A.F. The Class of Additively Decomposable Inequality Measures. Econometrica 1980, 48, 613–625. [Google Scholar] [CrossRef] [Green Version]
- Gini, C. Measurement of Inequality of Incomes. Econ. J. 1921, 31, 124–126. [Google Scholar] [CrossRef]
- Sen, A. On Economic Inequality; Oxford University Press: Oxford, NY, USA, 1973. [Google Scholar]
- Sánchez-Hechavarría, M.E.; Ghiya, S.; Carrazana-Escalona, R.; Cortina-Reyna, S.; Andreu-Heredia, A.; Acosta-Batista, C.; Saá-Muñoz, N.A. Introduction of Application of Gini Coefficient to Heart Rate Variability Spectrum for Mental Stress Evaluation. Arq. Bras. Cardiol. 2019, 113, 725–733. [Google Scholar] [CrossRef] [PubMed]
- You, K.-J.; Noh, G.-J.; Shin, H.-C. Spectral Gini Index for Quantifying the Depth of Consciousness. Comput. Intell. Neurosci. 2016, 2016, 2304356. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Viehweger, A.; Riffert, T.; Dhital, B.; Knösche, T.R.; Anwander, A.; Stepan, H.; Sorge, I.; Hirsch, F.W. The Gini coefficient: A methodological pilot study to assess fetal brain development employing postmortem diffusion MRI. Pediatr. Radiol. 2014, 44, 1290–1301. [Google Scholar] [CrossRef]
- Tamponi, M.; Crivelli, P.; Montella, R.; Sanna, F.; Gabriele, D.; Poggiu, A.; Sanna, E.; Marini, P.; Meloni, G.B.; Sverzellati, N.; et al. Exploring the variability of radiomic features of lung cancer lesions on unenhanced and contrast-enhanced chest CT imaging. Phys. Medica 2021, 82, 321–331. [Google Scholar] [CrossRef]
- Muelas, M.W.; Mughal, F.; O’Hagan, S.; Day, P.J.; Kell, D.B. The role and robustness of the Gini coefficient as an unbiased tool for the selection of Gini genes for normalising expression profiling data. Sci. Rep. 2019, 9, 17960. [Google Scholar] [CrossRef]
- Ávila, D.; Aedo, E.; Sánchez-Hechavarria, M.; Ávila, C.; Ávila, A. Glycine Receptor Inhibition Differentially Affect Selected Neuronal Populations of the Developing Embryonic Cortex, as Evidenced by the Analysis of Spontaneous Calcium Oscillations. Int. J. Mol. Sci. 2020, 21, 8013. [Google Scholar] [CrossRef]
- Sánchez-Torres, R.M. Desigualdad del ingreso en Colombia: Un estudio por departamentos. Cuadernos de Economía 2017, 36, 139–178. [Google Scholar] [CrossRef]
- Bourguignon, F. Decomposable Income Inequality Measures. Econometrica 1979, 47, 901–920. [Google Scholar] [CrossRef] [Green Version]
- Gisbert, F.J.G. Desigualdad, Diversidad y Convergencia: [Algunos] Instrumentos de Medida; Instituto Valenciano de Investigaciones Económicas [IVIE]: Valencia, Spain, 1998; Available online: https://dialnet.unirioja.es/servlet/libro?codigo=46706 (accessed on 27 March 2021).
- Litchfield, J.A. Inequality: Methods and Tools. In Inequality, Poverty, and Socio-Economic Performance; The World Bank: Washington, DC, USA, 1999. [Google Scholar]
- Schröder, C.; Cowell, F. Measuring Inequality, London School of Economics Perspectives in Economic Analysis. J. Econ. 2011, 104, 281–285. [Google Scholar] [CrossRef]
- Muszyńska, J.; Wędrowska, E. Income inequality of households in Poland: A subgroup decomposition of generalized entropy measures. Ekonometria 2018, 22, 43–64. [Google Scholar] [CrossRef] [Green Version]
- Mookherjee, D.; Shorrocks, A. A decomposition analysis of the trend in UK income inequality. Econ. J. 1982, 92, 886–902. [Google Scholar] [CrossRef]
- Shorrocks, A.F. Inequality Decomposition by Population Subgroups. Econometrica 1984, 52, 1369–1385. [Google Scholar] [CrossRef]
- Electrophysiology, T.F. Heart rate variability: Standards of measurement, physiological interpretation, and clinical use. Circulation 1996, 93, 1043–1065. [Google Scholar] [CrossRef] [Green Version]
- Sanchez-Hechavarria, M.; Escalona, R.C. RR intervals of 13 healthy subjects in rest and mental stress: Open Primary Database. 2020. Available online: https://www.researchgate.net/publication/338657618_RR_intervals_of_13_healthy_subjects_in_rest_and_mental_stress_Open_Primary_Database (accessed on 9 January 2021).
- Avila, A.; Vidal, P.M.; Dear, T.N.; Harvey, R.J.; Rigo, J.-M.; Nguyen, L. Glycine Receptor α2 Subunit Activation Promotes Cortical Interneuron Migration. Cell Rep. 2013, 4, 738–750. [Google Scholar] [CrossRef] [PubMed]
- Ramshur, J. Design, evaluation, and application of Heart Rate Variability Analysis Software [HRVAS]. Ph.D. Thesis, University of Memphis, Memphis, TN, USA, 2010. [Google Scholar]
- Yates, R.D.; Goodman, D.J. Probability and Stochastic Processes: A Friendly Introduction for Electrical and Computer Engineers; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Estévez, M.; Machado, C.; Leisman, G.; Estévez-Hernández, T.; Arias-Morales, A.; Machado, A.; Montes-Brown, J. Spectral analysis of heart rate variability. Int. J. Disabil. Hum. Dev. 2016, 15, 5–17. [Google Scholar] [CrossRef] [Green Version]
- Lévy-Leduc, C.; Moulines, E.; Roueff, F. Frequency estimation based on the cumulated Lomb–Scargle periodogram. J. Time Ser. Anal. 2008, 29, 1104–1131. [Google Scholar] [CrossRef]
- Thong, T.; McNames, J.; Aboy, M. Lomb-Wech periodogram for non-uniform sampling. In Proceedings of the 26th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, San Francisco, CA, USA, 1–5 September 2004; IEEE: New York, NY, USA, 2004; pp. 271–274. [Google Scholar]
- Boardman, A.; Schlindwein, F.S.; Rocha, A.P. A study on the optimum order of autoregressive models for heart rate variability. Physiol. Meas. 2002, 23, 325. [Google Scholar] [CrossRef]
- Van Dongen, H.P.; Olofsen, E.; VanHartevelt, J.H.; Kruyt, E.W. Searching for biological rhythms: Peak detection in the periodogram of unequally spaced data. J. Biol. Rhythm. 1999, 14, 617–620. [Google Scholar] [CrossRef] [PubMed]
- Pytharouli, S.I.; Stiros, S.C. Spectral analysis of unevenly spaced or discontinuous data using the “normperiod” code. Comput. Struct. 2008, 86, 190–196. [Google Scholar] [CrossRef]
- Ruf, T. The Lomb-Scargle periodogram in biological rhythm research: Analysis of incomplete and unequally spaced time-series. Biol. Rhythm. Res. 1999, 30, 178–201. [Google Scholar] [CrossRef]
- Jenkins, S.P. Distributionally-sensitive inequality indices and the GB2 income distribution. Rev. Income Wealth 2009, 55, 392–398. [Google Scholar] [CrossRef]
- Akselrod, S.; Gordon, D.; Ubel, F.A.; Shannon, D.C.; Berger, A.C.; Cohen, R.J. Power spectrum analysis of heart rate fluctuation: A quantitative probe of beat-to-beat cardiovascular control. Science 1981, 213, 220–222. [Google Scholar] [CrossRef]
- Billman, G.E.; Huikuri, H.V.; Sacha, J.; Trimmel, K. An introduction to heart rate variability: Methodological considerations and clinical applications. Front. Physiol. 2015, 6, 55. [Google Scholar] [CrossRef] [Green Version]
- Bravi, A.; Longtin, A.; Seely, A.J. Review and classification of variability analysis techniques with clinical applications. Biomed. Eng. Online 2011, 10, 90. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shaffer, F.; Ginsberg, J.P. An Overview of Heart Rate Variability Metrics and Norms. Front. Public Health 2017, 5, 258. [Google Scholar] [CrossRef] [Green Version]
- Roach, D.; Sheldon, R. Origins of the power of the low frequency heart rate variability bandwidth. J. Electrocardiol. 2018, 51, 422–427. [Google Scholar] [CrossRef]
- Del Paso, G.A.R.; Langewitz, W.; Mulder, L.J.; Van Roon, A.; Duschek, S. The utility of low frequency heart rate variability as an index of sympathetic cardiac tone: A review with emphasis on a reanalysis of previous studies. Psychophysiology 2013, 50, 477–487. [Google Scholar] [CrossRef]
- Bates, M.E.; Buckman, J.F.; Vaschillo, E.G.; Fonoberov, V.A.; Fonoberova, M.; Vaschillo, B.; Mun, E.Y.; Mezić, A.; Mezić, I. The redistribution of power: Neurocardiac signaling, alcohol and gender. PLoS ONE 2011, 6, e28281. [Google Scholar] [CrossRef] [PubMed]
- Atkinson, A.B.; Bourguignon, F. Introduction: Income distribution today. Handb. Income Distrib. 2015, 2, xvii–64. [Google Scholar]
- Velázquez, J.J.N. La desigualdad económica medida a través de las curvas de Lorenz//Economic inequality measurement through Lorenz curves. Revista Métodos Cuantitativos Economía Empresa 2006, 2, 67–108. [Google Scholar]
- Sitthiyot, T.; Holasut, K. A simple method for measuring inequality. Palgrave Commun. 2020, 6, 112. [Google Scholar] [CrossRef]

| Method | Exponent | Rest | Mental Stress | p | RB | ||||
|---|---|---|---|---|---|---|---|---|---|
| X | SD | CV | X | SD | CV | ||||
| Burg | −1 | 328.48 | 430.19 | 130.97 | 83.45 | 71.6 | 85.8 | 0.99 | 0.74 |
| 0 | 2.57 | 0.63 | 24.51 | 2.37 | 0.34 | 14.41 | 0.89 | 0.39 | |
| 1 | 1.2 | 0.22 | 18.5 | 1.32 | 0.19 | 14.59 | 0.05 * | −0.54 | |
| 2 | 2 | 0.86 | 43.01 | 2.34 | 0.79 | 33.83 | 0.21 | −0.28 | |
| Welch | −1 | 189.03 | 171.03 | 90.48 | 56.98 | 40.77 | 71.55 | 0.99 | 0.69 |
| 0 | 2.48 | 0.63 | 25.45 | 2.25 | 0.63 | 28.01 | 0.91 | 0.41 | |
| 1 | 1.07 | 0.19 | 17.61 | 1.21 | 0.13 | 11 | 0 * | −0.89 | |
| 2 | 1.38 | 0.44 | 32.19 | 1.83 | 0.39 | 21.44 | 0 * | −0.85 | |
| Lomb-Scargle | −1 | 780.01 | 624.44 | 80.06 | 33,059.8 | 100,850.69 | 305.06 | 0.42 | −0.08 |
| 0 | 1.45 | 0.44 | 30.07 | 1.85 | 0.5 | 26.96 | <0.001 * | −0.96 | |
| 1 | 1.09 | 0.35 | 31.9 | 1.6 | 0.33 | 20.84 | <0.001 * | −1 | |
| 2 | 2.29 | 1.35 | 59.01 | 6.02 | 2.88 | 47.9 | <0.001 * | −1 | |
| Theil | Exp | Rest | Mental Stress | p | RB | ||||
|---|---|---|---|---|---|---|---|---|---|
| X | SD | CV | X | SD | CV | ||||
| VLF | −1 | 0.001 | 0.0004 | 40.00 | 0.001 | 0.0005 | 50.00 | 0.5 | −0.011 |
| 0 | 0.0006 | 0.0002 | 33.33 | 0.0007 | 0.0004 | 57.14 | 0.271 | −0.209 | |
| 1 | 0.0004 | 0.0003 | 75.00 | 0.0007 | 0.0008 | 114.29 | 0.42 | −0.077 | |
| 2 | 0.0002 | 0.0003 | 150 | 0.0009 | 0.002 | 222.2 | 0.294 | −0.187 | |
| LF | −1 | 0.005 | 0.003 | 60.00 | 0.005 | 0.003 | 60.00 | 0.658 | 0.121 |
| 0 | 0.018 | 0.009 | 50.00 | 0.026 | 0.016 | 61.54 | 0.122 | −0.385 | |
| 1 | 0.067 | 0.043 | 64.18 | 0.132 | 0.085 | 64.39 | 0.029 * | −0.604 | |
| 2 | 0.282 | 0.250 | 88.65 | 0.691 | 0.474 | 68.59 | 0.024 * | −0.626 | |
| HF | −1 | 0.054 | 0.043 | 79.63 | 0.084 | 0.058 | 69.05 | 0.007 * | −0.758 |
| 0 | 0.102 | 0.062 | 60.78 | 0.107 | 0.054 | 50.47 | 0.249 | −0.231 | |
| 1 | 0.226 | 0.171 | 75.66 | 0.143 | 0.061 | 42.66 | 0.892 | 0.385 | |
| 2 | 0.550 | 0.510 | 92.72 | 0.203 | 0.096 | 47.29 | 0.966 | 0.560 | |
| TI | −1 | 0.06 | 0.043 | 71.67 | 0.09 | 0.057 | 63.33 | 0.009 * | −0.736 |
| 0 | 0.121 | 0.064 | 52.89 | 0.133 | 0.056 | 42.11 | 0.207 | −0.275 | |
| 1 | 0.294 | 0.167 | 56.80 | 0.276 | 0.121 | 43.84 | 0.473 | −0.033 | |
| 2 | 0.832 | 0.444 | 53.36 | 0.895 | 0.522 | 58.32 | 0.368 | −0.121 | |
| TB | −1 | 0.086 | 0.047 | 54.65 | 0.139 | 0.046 | 33.09 | <0.001 * | −0.912 |
| 0 | 0.059 | 0.045 | 76.27 | 0.105 | 0.035 | 33.33 | 0.002 * | −0.868 | |
| 1 | 0.05 | 0.049 | 98.00 | 0.099 | 0.038 | 38.38 | 0.002 * | −0.868 | |
| 2 | 0.110 | 0.060 | 54.54 | 0.110 | 0.047 | 42.72 | 0.002 * | −0.846 | |
| TI + TB | −1 | 0.146 | 0.081 | 55.48 | 0.229 | 0.094 | 41.05 | <0.001 * | −0.978 |
| 0 | 0.179 | 0.081 | 45.25 | 0.238 | 0.085 | 35.71 | 0.004 * | −0.802 | |
| 1 | 0.344 | 0.161 | 46.80 | 0.375 | 0.133 | 35.47 | 0.271 * | −0.209 | |
| 2 | 0.883 | 0.439 | 49.71 | 1.005 | 0.527 | 52.43 | 0.368 * | −0.121 | |
| Theil | Exp | Rest | Mental Stress | p | RB | ||||
|---|---|---|---|---|---|---|---|---|---|
| X | SD | CV | X | SD | CV | ||||
| VLF | −1 | 0.017 | 0.006 | 35.29 | 0.019 | 0.011 | 57.89 | 0.42 | −0.077 |
| 0 | 0.011 | 0.003 | 27.27 | 0.01 | 0.002 | 20.00 | 0.607 | 0.077 | |
| 1 | 0.007 | 0.002 | 28.57 | 0.01 | 0.008 | 80.00 | 0.368 | −0.121 | |
| 2 | 0.005 | 0.004 | 80.00 | 0.016 | 0.028 | 175.00 | 0.368 | −0.121 | |
| LF | −1 | 0.001 | 0.0007 | 70.00 | 0.003 | 0.002 | 66.67 | 0.02 * | −0.648 |
| 0 | 0.005 | 0.003 | 60.00 | 0.013 | 0.01 | 76.92 | 0.004 * | −0.802 | |
| 1 | 0.019 | 0.017 | 89.47 | 0.064 | 0.047 | 73.44 | 0.003 * | −0.824 | |
| 2 | 0.085 | 0.108 | 127.06 | 0.318 | 0.234 | 73.58 | 0.005 * | −0.78 | |
| HF | −1 | 0.04 | 0.033 | 82.50 | 0.062 | 0.043 | 69.35 | 0.005 * | −0.78 |
| 0 | 0.073 | 0.038 | 52.05 | 0.082 | 0.039 | 47.56 | 0.207 | −0.275 | |
| 1 | 0.151 | 0.083 | 54.97 | 0.114 | 0.05 | 43.86 | 0.927 | 0.451 | |
| 2 | 0.334 | 0.236 | 70.66 | 0.169 | 0.087 | 51.48 | −0.78 | 0.648 | |
| TI | −1 | 0.059 | 0.031 | 52.54 | 0.083 | 0.038 | 45.78 | 0.002 * | −0.868 |
| 0 | 0.089 | 0.04 | 44.94 | 0.105 | 0.041 | 39.05 | 0.108 | −0.407 | |
| 1 | 0.177 | 0.087 | 49.15 | 0.188 | 0.085 | 45.21 | 0.446 | −0.055 | |
| 2 | 0.424 | 0.234 | 55.19 | 0.503 | 0.3 | 59.64 | 0.249 | −0.231 | |
| TB | −1 | 0.072 | 0.045 | 62.50 | 0.131 | 0.032 | 24.43 | <0.001 * | −0.956 |
| 0 | 0.053 | 0.044 | 83.02 | 0.099 | 0.026 | 26.26 | <0.001 * | −0.912 | |
| 1 | 0.047 | 0.047 | 100.00 | 0.093 | 0.03 | 32.26 | 0.002 * | −0.868 | |
| 2 | 0.3 | 0.057 | 19.00 | 0.101 | 0.036 | 35.64 | 0.003 * | −0.824 | |
| TI + TB | −1 | 0.131 | 0.071 | 54.20 | 0.214 | 0.064 | 29.91 | <0.001 * | −0.956 |
| 0 | 0.142 | 0.068 | 47.89 | 0.203 | 0.059 | 29.06 | <0.001 * | −0.956 | |
| 1 | 0.224 | 0.092 | 41.07 | 0.28 | 0.087 | 31.07 | 0.013 * | −0.692 | |
| 2 | 0.473 | 0.23 | 48.63 | 0.604 | 0.291 | 48.18 | 0.108 | −0.407 | |
| Theil | Exp | Basal | Mental Stress | p | RB | ||||
|---|---|---|---|---|---|---|---|---|---|
| X | SD | CV | X | SD | CV | ||||
| VLF | −1 | 0.309 | 0.341 | 110.36 | 0.17 | 0.105 | 61.76 | 0.936 | 0.473 |
| 0 | 0.035 | 0.021 | 60.00 | 0.04 | 0.023 | 57.50 | <0.001 * | −1 | |
| 1 | 0.01 | 0.015 | 150.00 | 0.022 | 0.045 | 204.55 | 0.207 | −0.275 | |
| 2 | 0.004 | 0.009 | 225.00 | 0.031 | 0.099 | 319.35 | 0.227 | −0.253 | |
| LF | −1 | 0.018 | 0.008 | 44.44 | 0.014 | 0.005 | 35.71 | 0.945 | 0.495 |
| 0 | 0.048 | 0.009 | 18.75 | 0.076 | 0.02 | 26.32 | 0.473 | −0.033 | |
| 1 | 0.152 | 0.091 | 59.87 | 0.416 | 0.13 | 31.25 | <0.001 * | −1 | |
| 2 | 0.599 | 0.707 | 118.03 | 2.345 | 0.955 | 40.72 | <0.001 * | −1 | |
| HF | −1 | 0.121 | 0.041 | 33.88 | 0.168 | 0.081 | 48.21 | 0.007 * | −0.758 |
| 0 | 0.173 | 0.036 | 20.81 | 0.177 | 0.048 | 27.12 | 0.02 * | −0.648 | |
| 1 | 0.264 | 0.101 | 38.26 | 0.196 | 0.05 | 25.51 | 0.945 | 0.495 | |
| 2 | 0.431 | 0.291 | 67.52 | 0.229 | 0.094 | 41.05 | 0.971 | 0.582 | |
| TI | −1 | 0.449 | 0.352 | 78.40 | 0.352 | 0.092 | 26.14 | 0.58 | 0.055 |
| 0 | 0.256 | 0.056 | 21.88 | 0.292 | 0.067 | 22.95 | <0.001 * | −0.934 | |
| 1 | 0.426 | 0.426 | 100.00 | 0.634 | 0.152 | 23.97 | <0.001 * | −1 | |
| 2 | 1.034 | 0.678 | 65.57 | 2.605 | 0.931 | 35.74 | <0.001 * | −1 | |
| TB | −1 | 0.345 | 0.27 | 78.26 | 0.305 | 0.074 | 24.26 | 0.554 | 0.033 |
| 0 | 0.098 | 0.047 | 47.96 | 0.165 | 0.035 | 21.21 | 0.002 * | −0.868 | |
| 1 | 0.063 | 0.051 | 80.95 | 0.143 | 0.044 | 30.77 | <0.001 * | −0.978 | |
| 2 | 0.059 | 0.064 | 108.47 | 0.157 | 0.055 | 35.03 | <0.001 * | −0.978 | |
| TI + TB | −1 | 0.793 | 0.594 | 74.91 | 0.657 | 0.14 | 21.31 | 0.554 | 0.033 |
| 0 | 0.354 | 0.083 | 23.45 | 0.457 | 0.094 | 20.57 | <0.001 * | −0.956 | |
| 1 | 0.488 | 0.157 | 32.17 | 0.777 | 0.182 | 23.42 | <0.001 * | −1 | |
| 2 | 1.094 | 0.731 | 66.82 | 2.763 | 0.978 | 35.40 | <0.001 * | −1 | |
| Method. | Exp | Control | Under Inhibition | p | RB | ||||
|---|---|---|---|---|---|---|---|---|---|
| X | SD | CV | X | SD | CV | ||||
| Burg | −1 | 13.442 | 16.813 | 125.08 | 9.652 | 5.795 | 60.04 | 0.294 | 0.084 |
| 0 | 2.032 | 0.878 | 43.21 | 2.267 | 0.591 | 26.07 | 0.148 | −0.161 | |
| 1 | 2.01 | 0.727 | 36.17 | 2.386 | 0.602 | 25.23 | 0.016 * | −0.326 | |
| 2 | 8.084 | 5.482 | 67.81 | 10.794 | 6.094 | 56.46 | 0.027 * | −0.292 | |
| Welch | −1 | 9.076 | 11.91 | 131.23 | 5.595 | 3.658 | 65.38 | 0.562 | 0.023 |
| 0 | 1.73 | 0.771 | 44.57 | 1.749 | 0.48 | 27.44 | 0.342 | −0.063 | |
| 1 | 1.481 | 0.472 | 31.87 | 1.643 | 0.33 | 20.09 | 0.116 | −0.183 | |
| 2 | 3.188 | 1.374 | 43.10 | 3.769 | 1.087 | 28.84 | 0.042 * | −0.262 | |
| Lomb | −1 | 4.791 × 10 25 | 2.443 × 10 26 | 500.99 | 9.448 × 10 24 | 1.616 × 10 25 | 171.04 | 0.643 | 0.054 |
| 0 | 2.256 | 0.719 | 31.87 | 2.366 | 0.418 | 17.67 | 0.148 | −0.161 | |
| 1 | 2.003 | 0.591 | 29.51 | 2.282 | 0.431 | 18.89 | 0.013 * | −0.337 | |
| 2 | 8.357 | 5.095 | 60.97 | 11.272 | 4.813 | 42.70 | 0.004 * | −0.398 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carrazana-Escalona, R.; Sánchez-Hechavarría, M.E.; Ávila, A. Theil Entropy as a Non-Lineal Analysis for Spectral Inequality of Physiological Oscillations. Entropy 2022, 24, 370. https://doi.org/10.3390/e24030370
Carrazana-Escalona R, Sánchez-Hechavarría ME, Ávila A. Theil Entropy as a Non-Lineal Analysis for Spectral Inequality of Physiological Oscillations. Entropy. 2022; 24(3):370. https://doi.org/10.3390/e24030370
Chicago/Turabian StyleCarrazana-Escalona, Ramón, Miguel Enrique Sánchez-Hechavarría, and Ariel Ávila. 2022. "Theil Entropy as a Non-Lineal Analysis for Spectral Inequality of Physiological Oscillations" Entropy 24, no. 3: 370. https://doi.org/10.3390/e24030370







