A Maximal Correlation Framework for Fair Machine Learning
Abstract
:1. Introduction
- We present a universal framework justified by an information–theoretic view that can inherently handle the popular fairness criteria, namely independence and separation, while seamlessly adopting both discrete and continuous cases, which uses the maximal correlation to construct measures of fairness associated with different criteria; then, we use these measures to further develop fair learning algorithms in a fast, efficient, and effective manner.
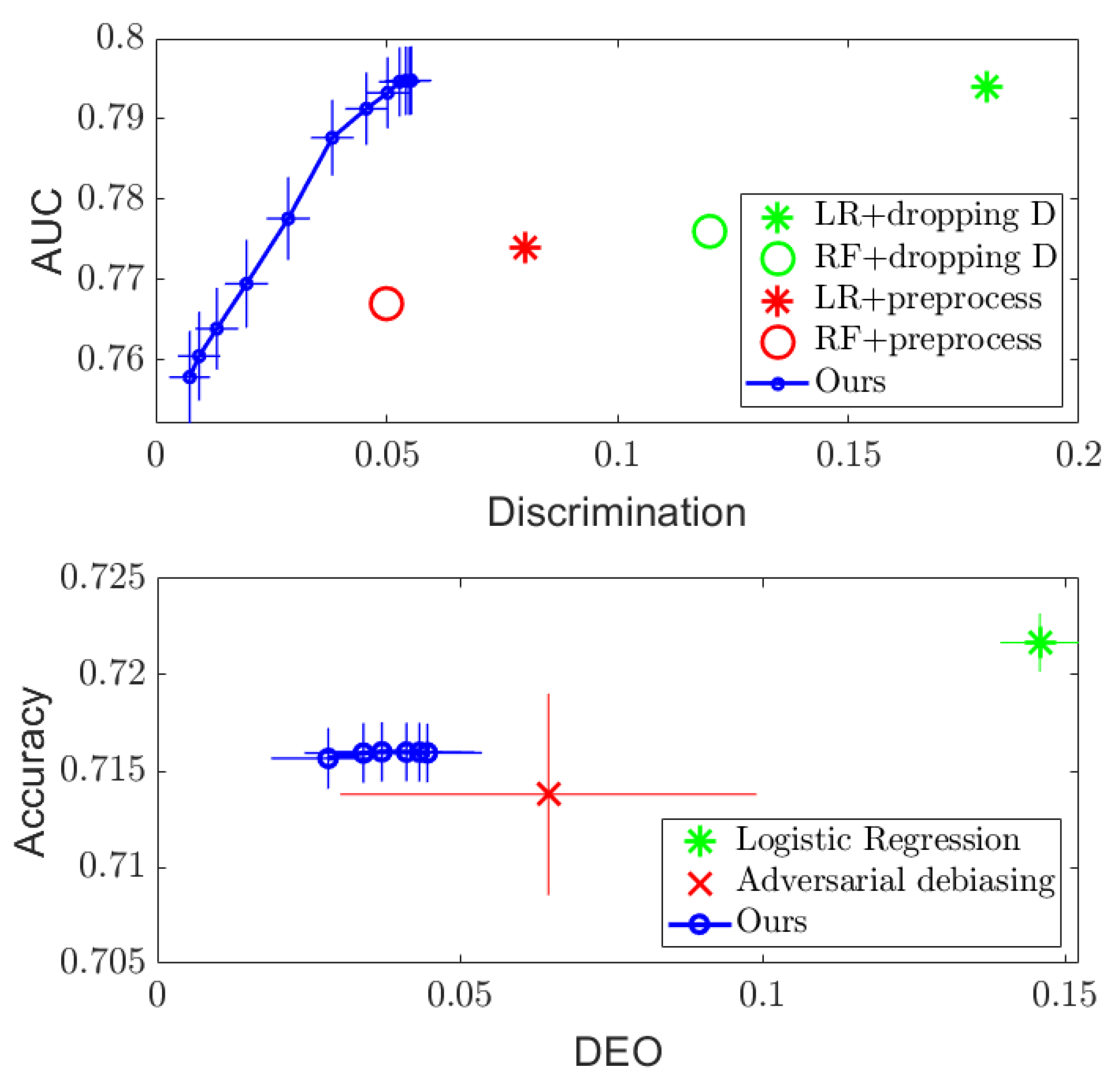
- We show empirically that these algorithms can provide the desired smooth tradeoff curve between the performance and the measures of fairness on several standard datasets (COMPAS, Adult, and Communities and Crimes), so that a desired level of fairness can be achieved.
- Finally, we perform experiments to illustrate that our algorithms can be used to impose fairness on a model originally trained without any fairness constraint in the few-shot regime, which further demonstrates the versatility of our algorithms in a post-processing setup.
2. Background
2.1. Fairness Objectives in Machine Learning
2.2. Maximal Correlation
2.3. Related Work
3. Maximal Correlation for Fairness
3.1. Maximal Correlation for Discrete Learning
3.1.1. Independence
3.1.2. Separation
3.2. Maximal Correlation for Continuous Learning
3.2.1. Independence
3.2.2. Separation
3.2.3. Few-Shot Learning
4. Experimental Results
4.1. Discrete Case
4.2. Continuous Case
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Effect of the Regularizer in Discrete Case




References
- Selbst, A.D.; Boyd, D.; Friedler, S.A.; Venkatasubramanian, S.; Vertesi, J. Fairness and abstraction in sociotechnical systems. In Proceedings of the Conference on Fairness, Accountability, and Transparency, Atlanta, GA, USA, 29–31 January 2019; pp. 59–68. [Google Scholar]
- Bellamy, R.K.; Dey, K.; Hind, M.; Hoffman, S.C.; Houde, S.; Kannan, K.; Lohia, P.; Martino, J.; Mehta, S.; Mojsilovic, A.; et al. AI Fairness 360: An extensible toolkit for detecting, understanding, and mitigating unwanted algorithmic bias. arXiv 2018, arXiv:1810.01943. [Google Scholar]
- Barocas, S.; Hardt, M.; Narayanan, A. Fairness and Machine Learning. 2019. Available online: http://www.fairmlbook.org (accessed on 14 February 2022).
- EEOC. Department of Labor, & Department of Justice. Uniform Guidelines on Employee Selection Procedures; Federal Register: Washington, DC, USA, 1978.
- Locatello, F.; Abbati, G.; Rainforth, T.; Bauer, S.; Schölkopf, B.; Bachem, O. On the fairness of disentangled representations. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; pp. 14584–14597. [Google Scholar]
- Gölz, P.; Kahng, A.; Procaccia, A.D. Paradoxes in Fair Machine Learning. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; pp. 8340–8350. [Google Scholar]
- Corbett-Davies, S.; Goel, S. The measure and mismeasure of fairness: A critical review of fair machine learning. arXiv 2018, arXiv:1808.00023. [Google Scholar]
- Calmon, F.; Wei, D.; Vinzamuri, B.; Ramamurthy, K.N.; Varshney, K.R. Optimized pre-processing for discrimination prevention. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 3992–4001. [Google Scholar]
- Mary, J.; Calauzenes, C.; El Karoui, N. Fairness-aware learning for continuous attributes and treatments. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; pp. 4382–4391. [Google Scholar]
- Kamiran, F.; Calders, T. Data preprocessing techniques for classification without discrimination. Knowl. Inf. Syst. 2012, 33, 1–33. [Google Scholar] [CrossRef] [Green Version]
- Zemel, R.; Wu, Y.; Swersky, K.; Pitassi, T.; Dwork, C. Learning fair representations. In Proceedings of the International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; pp. 325–333. [Google Scholar]
- Feldman, M.; Friedler, S.A.; Moeller, J.; Scheidegger, C.; Venkatasubramanian, S. Certifying and Removing Disparate Impact. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Sydney, Australia, 10–13 August 2015; pp. 259–268. [Google Scholar]
- Sattigeri, P.; Hoffman, S.C.; Chenthamarakshan, V.; Varshney, K.R. Fairness gan. arXiv 2018, arXiv:1805.09910. [Google Scholar]
- Xu, D.; Yuan, S.; Zhang, L.; Wu, X. Fairgan: Fairness-aware generative adversarial networks. In Proceedings of the 2018 IEEE International Conference on Big Data (Big Data), Seattle, WA, USA, 10–13 December 2018; pp. 570–575. [Google Scholar]
- Kamiran, F.; Karim, A.; Zhang, X. Decision Theory for Discrimination-Aware Classification. In Proceedings of the IEEE International Conference on Data Mining, Brussels, Belgium, 10–13 December 2012; pp. 924–929. [Google Scholar] [CrossRef] [Green Version]
- Hardt, M.; Price, E.; Srebro, N. Equality of Opportunity in Supervised Learning. In Proceedings of the Advances in Neural Information Processing Systems 29, Barcelona, Spain, 5–10 December 2016; pp. 3315–3323. [Google Scholar]
- Pleiss, G.; Raghavan, M.; Wu, F.; Kleinberg, J.; Weinberger, K.Q. On fairness and calibration. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 5680–5689. [Google Scholar]
- Wei, D.; Ramamurthy, K.N.; Du Pin Calmon, F. Optimized Score Transformation for Fair Classification. arXiv 2019, arXiv:1906.00066. [Google Scholar]
- Kamishima, T.; Akaho, S.; Asoh, H.; Sakuma, J. Fairness-Aware classifier with Prejudice Remover Regularizer. In Machine Learning and Knowledge Discovery in Databases; Springer: Berlin/Heidelberg, Germany, 2012; pp. 35–50. [Google Scholar]
- Zhang, B.H.; Lemoine, B.; Mitchell, M. Mitigating unwanted biases with adversarial learning. In Proceedings of the 2018 AAAI/ACM Conference on AI, Ethics, and Society, New Orleans, LA, USA, 2–3 February 2018; pp. 335–340. [Google Scholar]
- Celis, L.E.; Huang, L.; Keswani, V.; Vishnoi, N.K. Classification with fairness constraints: A meta-algorithm with provable guarantees. In Proceedings of the Conference on Fairness, Accountability, and Transparency, Atlanta, GA, USA, 29–31 January 2019; pp. 319–328. [Google Scholar]
- Angwin, J.; Larson, J.; Mattu, S.; Kirchner, L. Machine Bias: There’s Software Used across the Country to Predict Future Criminals. And It’s Biased against Blacks; ProPublica: New York, NY, USA, 2016. [Google Scholar]
- Chouldechova, A. Fair prediction with disparate impact: A study of bias in recidivism prediction instruments. Big Data 2017, 5, 153–163. [Google Scholar] [CrossRef] [PubMed]
- Hirschfeld, H.O. A connection between correlation and contingency. Proc. Camb. Phil. Soc. 1935, 31, 520–524. [Google Scholar] [CrossRef]
- Gebelein, H. Das statistische Problem der Korrelation als Variations-und Eigenwertproblem und sein Zusammenhang mit der Ausgleichsrechnung. Z. Angew. Math. Mech. 1941, 21, 364–379. [Google Scholar] [CrossRef]
- Rényi, A. On Measures of Dependence. Acta Math. Acad. Sci. Hung. 1959, 10, 441–451. [Google Scholar] [CrossRef]
- Huang, S.L.; Makur, A.; Wornell, G.W.; Zheng, L. On Universal Features for High-Dimensional Learning and Inference. Preprint. 2019. Available online: http://allegro.mit.edu/~gww/unifeatures (accessed on 14 February 2022).
- Lee, J.; Sattigeri, P.; Wornell, G. Learning New Tricks From Old Dogs: Multi-Source Transfer Learning From Pre-Trained Networks. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; pp. 4372–4382. [Google Scholar]
- Wang, L.; Wu, J.; Huang, S.L.; Zheng, L.; Xu, X.; Zhang, L.; Huang, J. An efficient approach to informative feature extraction from multimodal data. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 5281–5288. [Google Scholar]
- Rezaei, A.; Fathony, R.; Memarrast, O.; Ziebart, B. Fairness for robust log loss classification. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 5511–5518. [Google Scholar]
- Zafar, M.B.; Valera, I.; Rogriguez, M.G.; Gummadi, K.P. Fairness constraints: Mechanisms for fair classification. In Proceedings of theArtificial Intelligence and Statistics, PMLR, Fort Lauderdale, FL, USA, 20–22 April 2017; pp. 962–970. [Google Scholar]
- Grari, V.; Ruf, B.; Lamprier, S.; Detyniecki, M. Fairness-Aware Neural Réyni Minimization for Continuous Features. arXiv 2019, arXiv:1911.04929. [Google Scholar]
- Baharlouei, S.; Nouiehed, M.; Beirami, A.; Razaviyayn, M. Rènyi Fair Inference. arXiv 2019, arXiv:1906.12005. [Google Scholar]
- Moyer, D.; Gao, S.; Brekelmans, R.; Galstyan, A.; Ver Steeg, G. Invariant representations without adversarial training. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 3–8 December 2018; pp. 9084–9093. [Google Scholar]
- Cho, J.; Hwang, G.; Suh, C. A fair classifier using mutual information. In Proceedings of the 2020 IEEE International Symposium on Information Theory (ISIT), Los Angeles, CA, USA, 21–26 June 2020; pp. 2521–2526. [Google Scholar]
- Horn, R.A.; Johnson, C.R. Matrix Analysis; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Breiman, L.; Friedman, J.H. Estimating Optimal Transformations for Multiple Regression and Correlation. J. Am. Stat. Assoc. 1985, 80, 580–598. [Google Scholar] [CrossRef]
- Gao, W.; Oh, S.; Viswanath, P. Demystifying Fixed k-Nearest Neighbor Information Estimators. IEEE Trans. Inf. Theory 2018, 64, 5629–5661. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Scott, D.W. Nonparametric density estimation for high-dimensional data—Algorithms and applications. Wiley Interdiscip. Rev. Comput. Stat. 2019, 11, e1461. [Google Scholar] [CrossRef] [Green Version]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.; Bu, Y.; Sattigeri, P.; Panda, R.; Wornell, G.W.; Karlinsky, L.; Schmidt Feris, R. A Maximal Correlation Framework for Fair Machine Learning. Entropy 2022, 24, 461. https://doi.org/10.3390/e24040461
Lee J, Bu Y, Sattigeri P, Panda R, Wornell GW, Karlinsky L, Schmidt Feris R. A Maximal Correlation Framework for Fair Machine Learning. Entropy. 2022; 24(4):461. https://doi.org/10.3390/e24040461
Chicago/Turabian StyleLee, Joshua, Yuheng Bu, Prasanna Sattigeri, Rameswar Panda, Gregory W. Wornell, Leonid Karlinsky, and Rogerio Schmidt Feris. 2022. "A Maximal Correlation Framework for Fair Machine Learning" Entropy 24, no. 4: 461. https://doi.org/10.3390/e24040461
APA StyleLee, J., Bu, Y., Sattigeri, P., Panda, R., Wornell, G. W., Karlinsky, L., & Schmidt Feris, R. (2022). A Maximal Correlation Framework for Fair Machine Learning. Entropy, 24(4), 461. https://doi.org/10.3390/e24040461







