Next Article in Journal
Epistemic Communities under Active Inference
Next Article in Special Issue
Information Inequalities via Submodularity and a Problem in Extremal Graph Theory
Previous Article in Journal
Application of Convolutional Neural Network for Fingerprint-Based Prediction of Gender, Finger Position, and Height
Previous Article in Special Issue
Statistical Divergences between Densities of Truncated Exponential Families with Nested Supports: Duo Bregman and Duo Jensen Divergences
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Entropy
Volume 24
Issue 4
10.3390/e24040477
entropy-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Contingency Table Analysis and Inference via Double Index Measures

by
Christos Meselidis
* and
Alex Karagrigoriou
Laboratory of Statistics and Data Analysis, Department of Statistics and Actuarial-Financial Mathematics, University of the Aegean, Karlovasi, GR-83200 Samos, Greece
*
Author to whom correspondence should be addressed.
Entropy 2022, 24(4), 477; https://doi.org/10.3390/e24040477
Submission received: 20 February 2022 / Revised: 17 March 2022 / Accepted: 28 March 2022 / Published: 29 March 2022
(This article belongs to the Special Issue Information and Divergence Measures)
Browse Figures
Versions Notes

Abstract

In this work, we focus on a general family of measures of divergence for estimation and testing with emphasis on conditional independence in cross tabulations. For this purpose, a restricted minimum divergence estimator is used for the estimation of parameters under constraints and a new double index (dual) divergence test statistic is introduced and thoroughly examined. 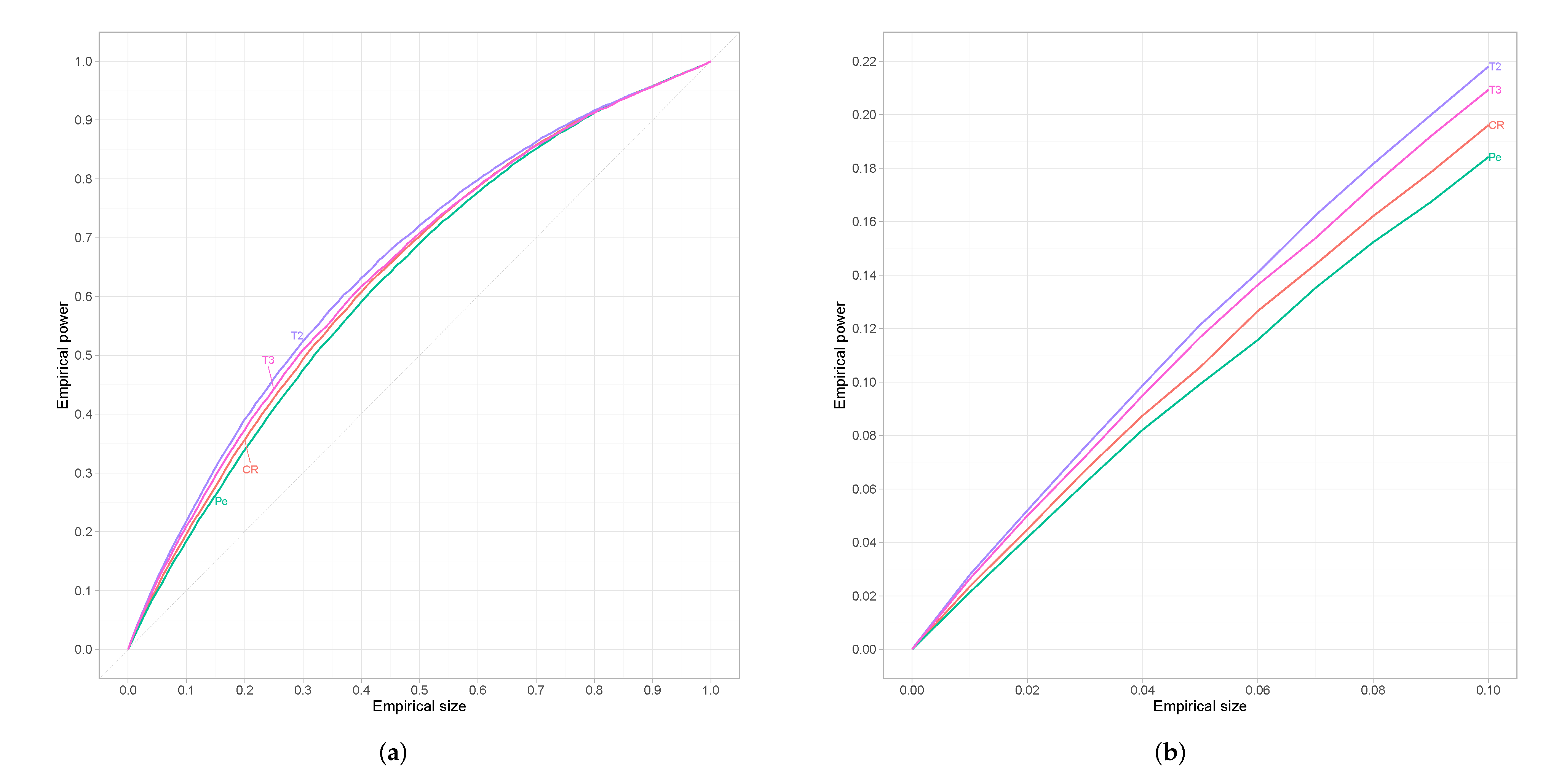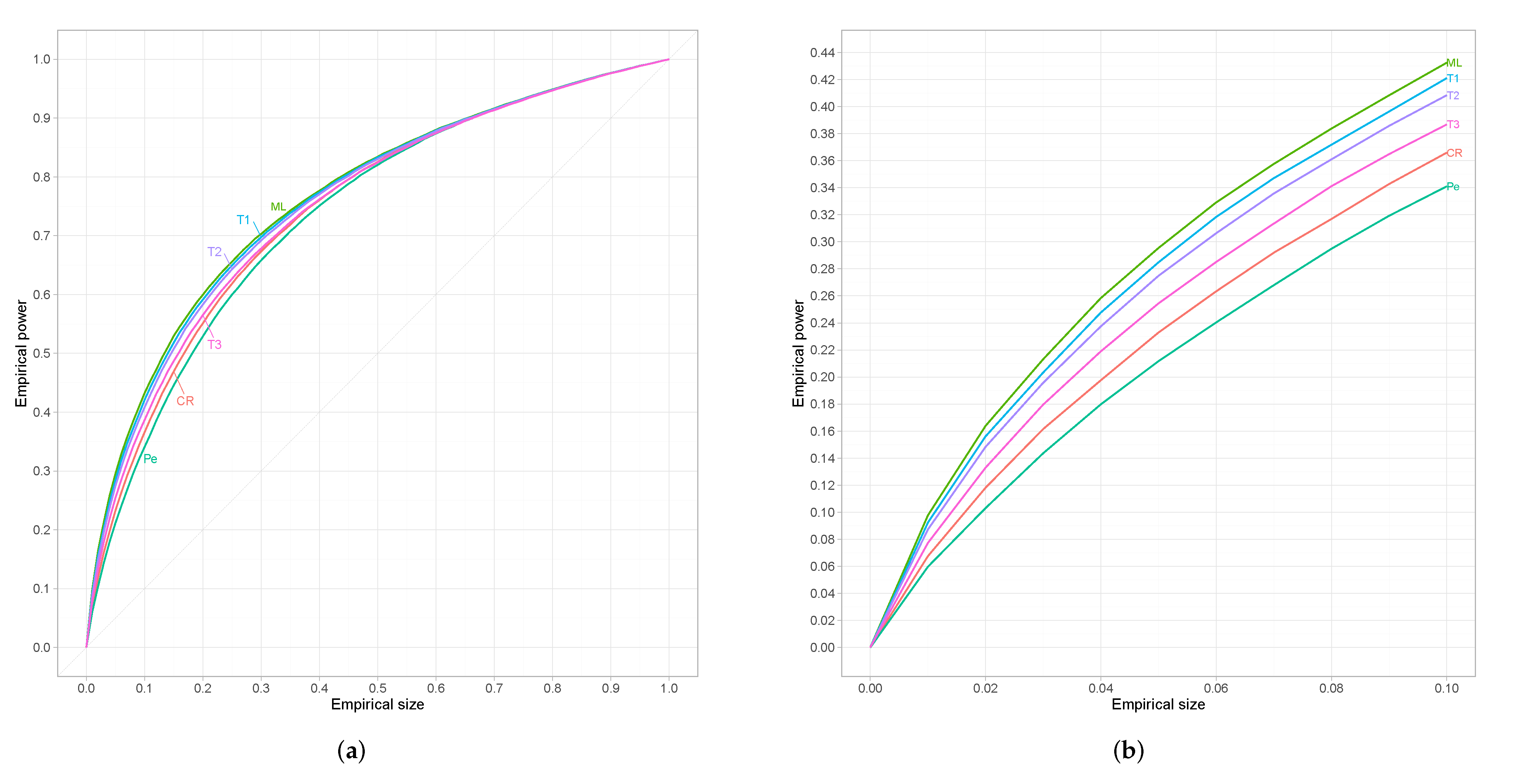The associated asymptotic theory is provided and the advantages and practical implications are explored via simulation studies.
Keywords: double index divergence test statistic; multivariate data analysis; conditional independence; cross tabulations double index divergence test statistic; multivariate data analysis; conditional independence; cross tabulations

Share and Cite

MDPI and ACS Style

Meselidis, C.; Karagrigoriou, A. Contingency Table Analysis and Inference via Double Index Measures. Entropy 2022, 24, 477. https://doi.org/10.3390/e24040477

AMA Style

Meselidis C, Karagrigoriou A. Contingency Table Analysis and Inference via Double Index Measures. Entropy. 2022; 24(4):477. https://doi.org/10.3390/e24040477

Chicago/Turabian Style

Meselidis, Christos, and Alex Karagrigoriou. 2022. "Contingency Table Analysis and Inference via Double Index Measures" Entropy 24, no. 4: 477. https://doi.org/10.3390/e24040477

APA Style

Meselidis, C., & Karagrigoriou, A. (2022). Contingency Table Analysis and Inference via Double Index Measures. Entropy, 24(4), 477. https://doi.org/10.3390/e24040477

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop