The Exergy Losses Analysis in Adiabatic Combustion Systems including the Exhaust Gas Exergy
Abstract
:1. Introduction
2. Numerical Modeling
2.1. Eulerian Stochastic Fields Method
2.1.1. Manifold Generation
2.1.2. Coupling FGM to LES
2.1.3. The Eulerian Stochastic Field (ESF) Method
2.1.4. Numerical Solution Procedure
2.2. The Exergy Losses of Adiabatic Turbulent Flame
2.2.1. Exergy Losses during Combustion
2.2.2. Exergy Losses at the Exhaust Gas
3. Results and Discussion
3.1. Experimental and Numerical Setup
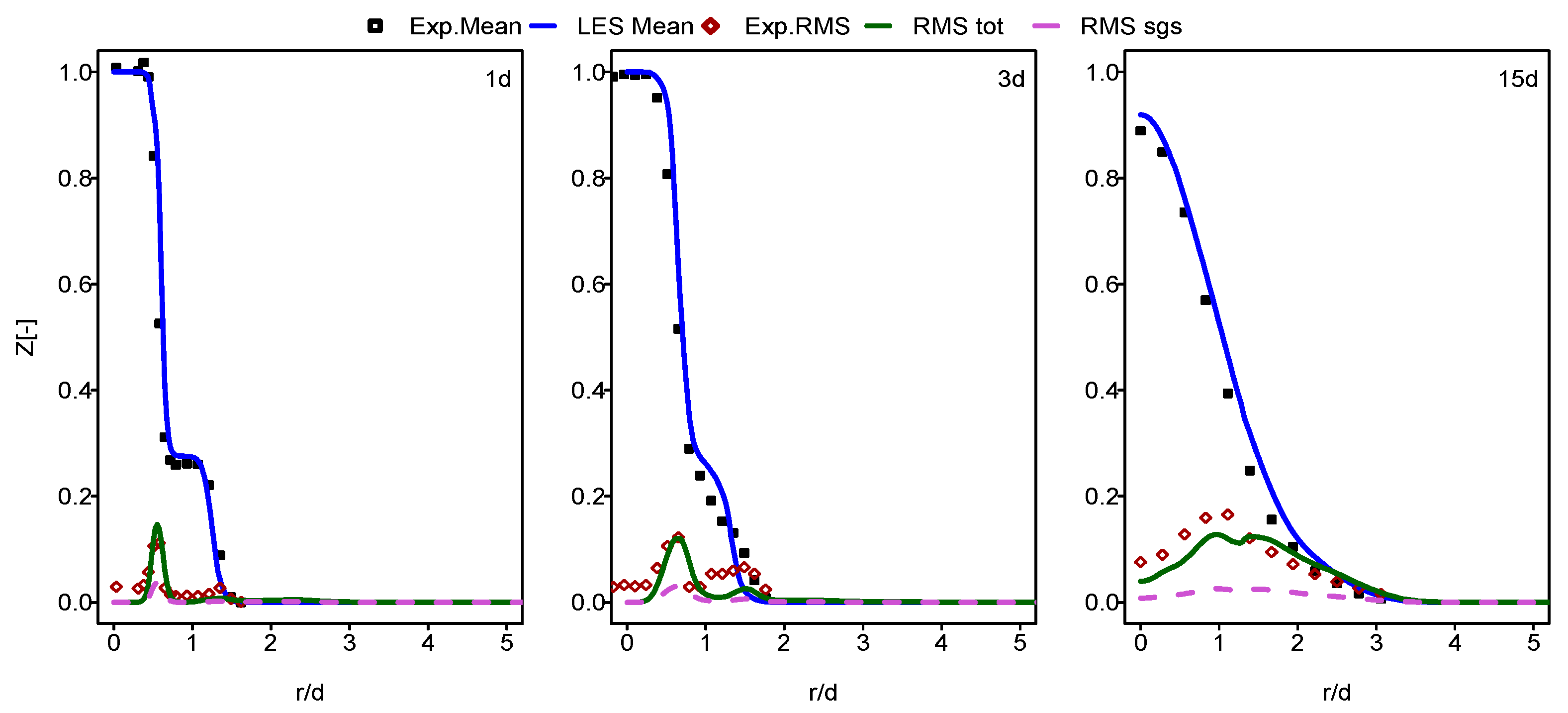
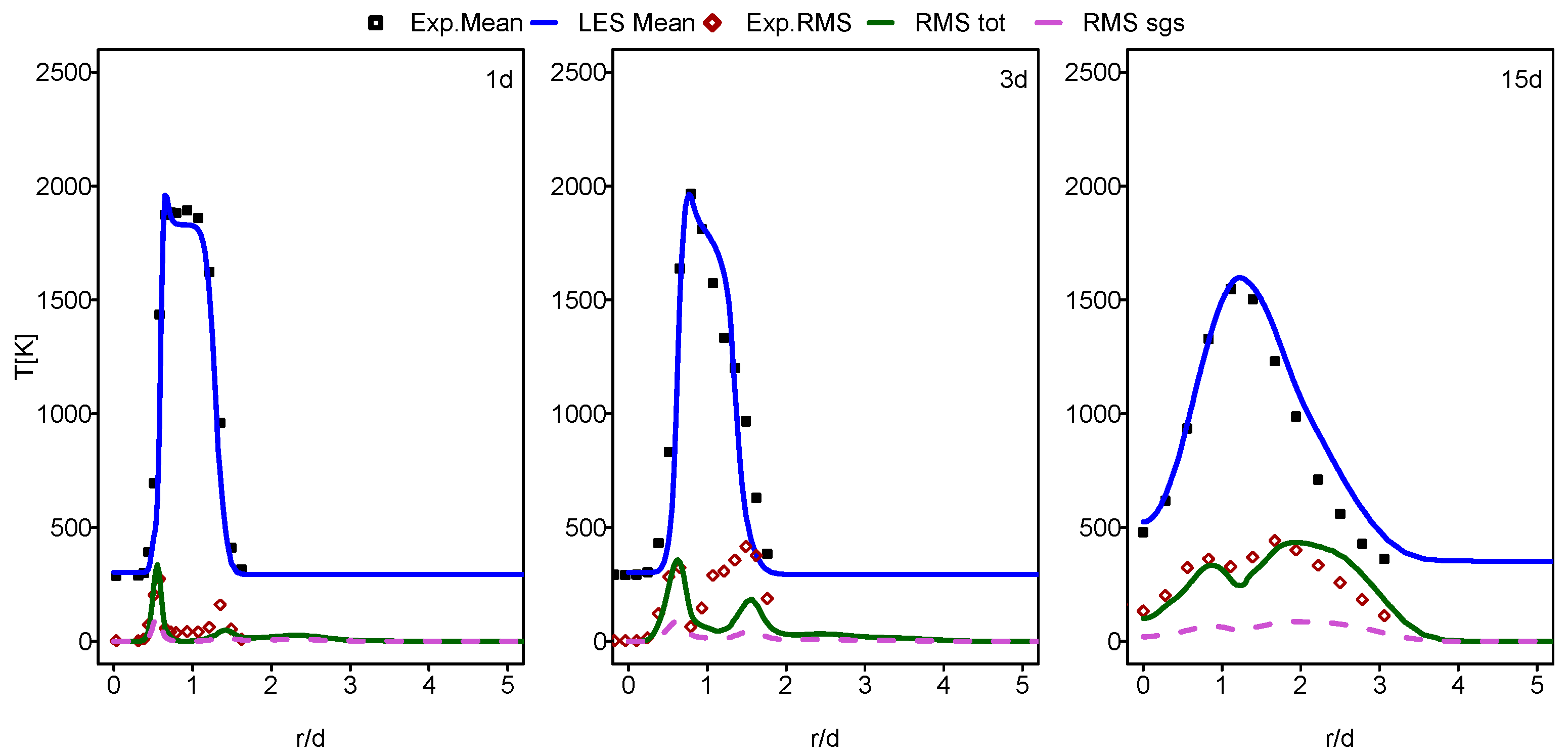
3.2. Validation
3.3. Exergy Losses Analysis
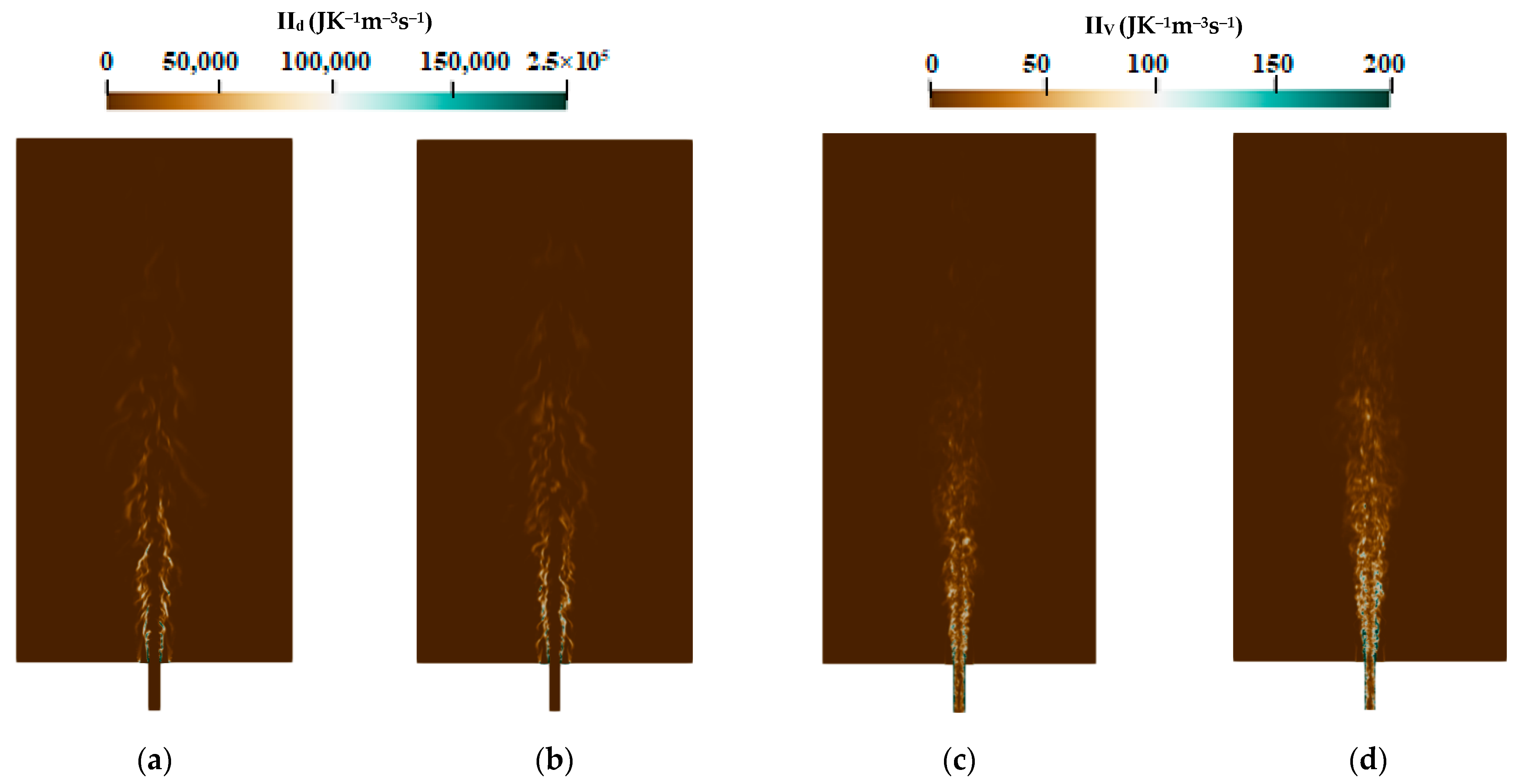
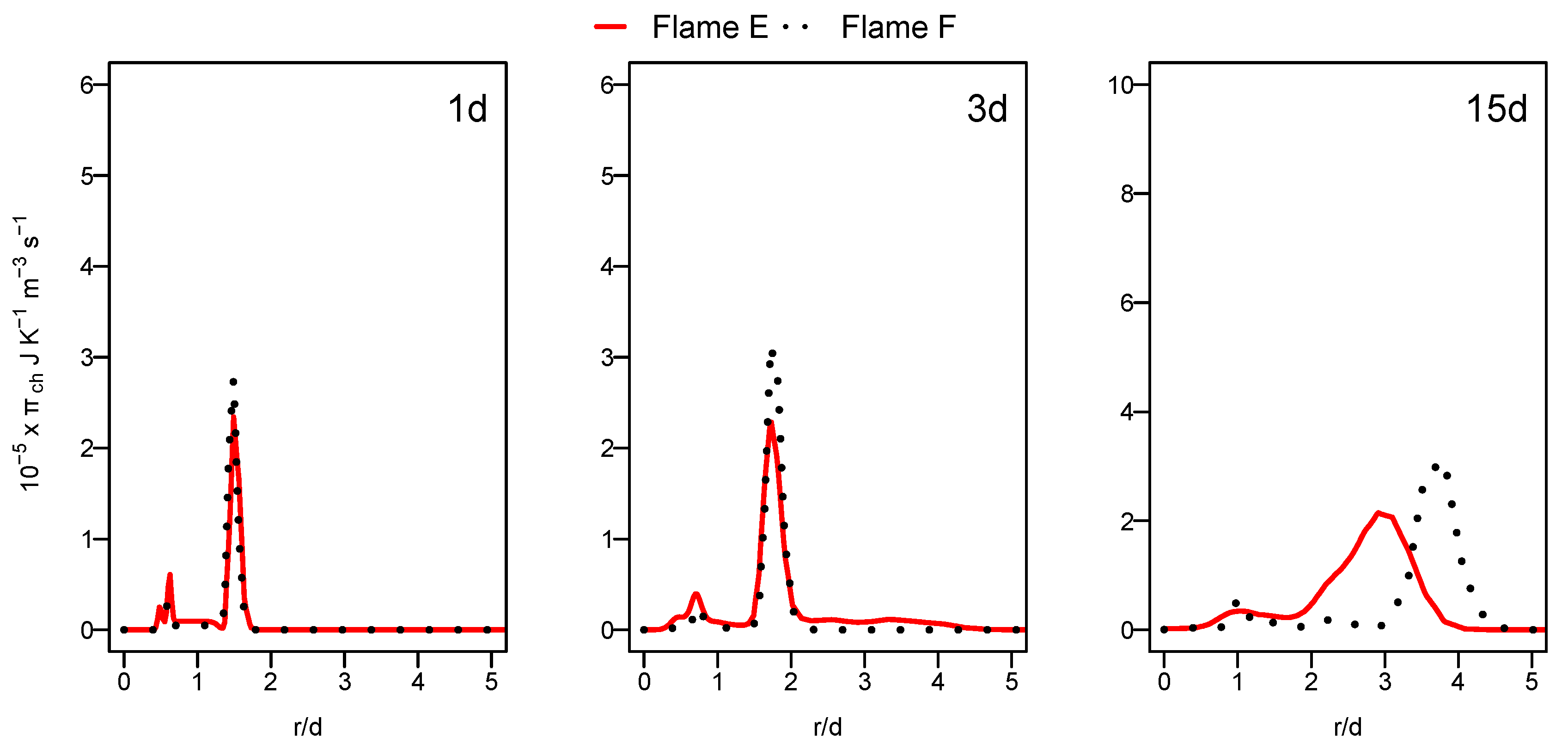
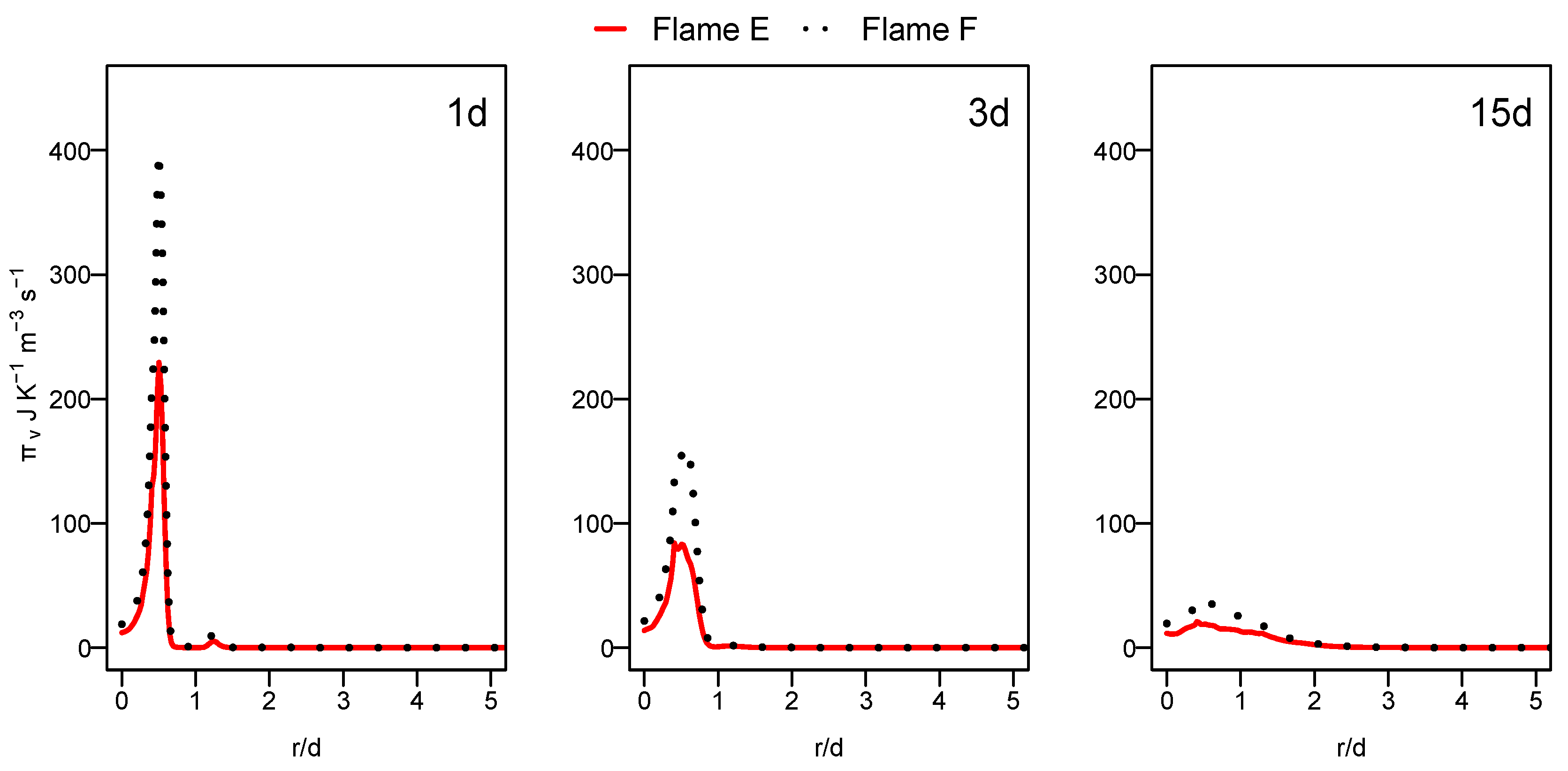
3.3.1. Entropy Generation during Combustion
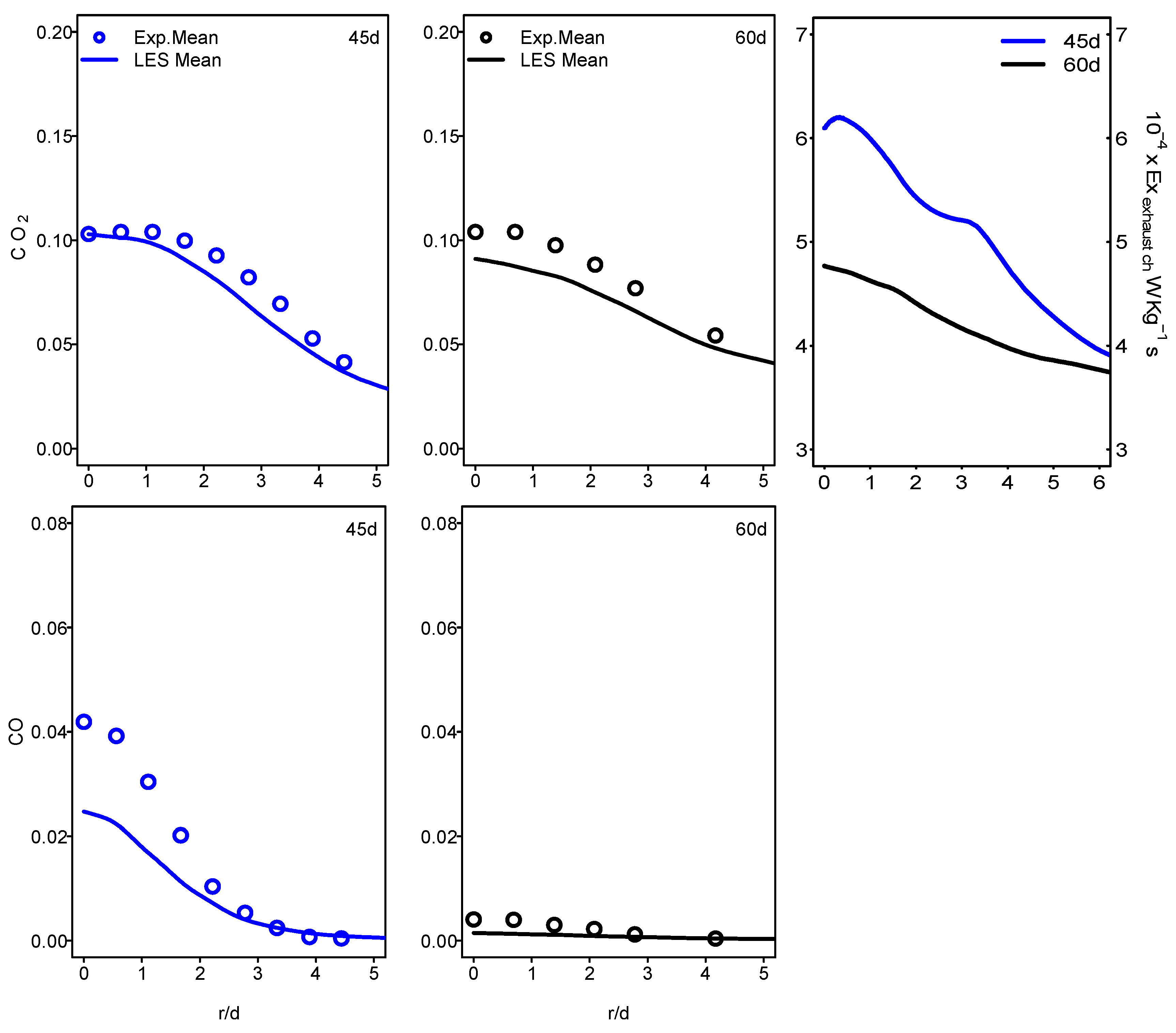
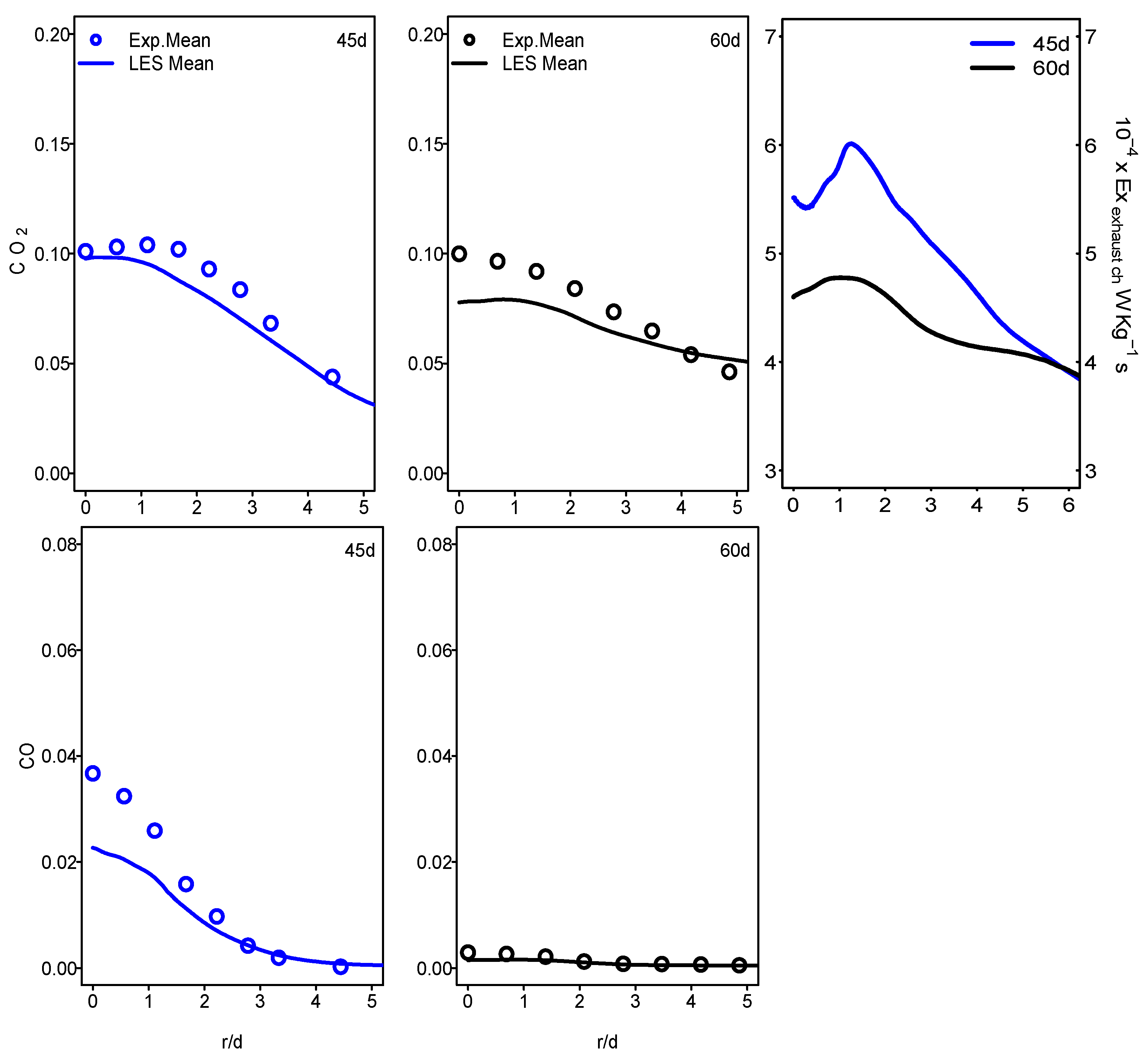
3.3.2. Exhaust Gases Exergy
4. Conclusions
- The exergy destroyed inside the combustion chamber increases with the increase in the mass flow rate along with the Re-number for flame F in comparison to flame E.
- The heat transfer and chemical reaction processes have higher contributions in entropy production compared to those of mass diffusion and viscous dissipation.
- With the increase in the jet velocity for flame F, inducing more concentrations and temperature gradients, further increase in entropy generation was expected compared to flame E. However, the lower predictivity of the ESF in the case of flame F leads to a slight difference in entropy generation, especially for the heat transfer entropy source term.
- The analysis of the chemical exergy content of exhaust gases decreases, going towards the combustion chamber outlet.
- Downstream from the burner, the temperature continues to decrease. The same decrease in the chemical exergy of the exhaust gases can be related to the temperature. This leads to the fact that cooling the exhaust gases can increase the exhaust gases exergy recovery.
- A strong link was found between the combustion emissions and the chemical exergy of the exhaust gases since its evolution follows the mass fractions of exhaust gases species.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nishida, K.; Takagi, T.; Kinoshita, S. Analysis of entropy generation and exergy loss during combustion. Proc. Comb. Inst 2002, 29, 869–874. [Google Scholar] [CrossRef]
- Keenan, J.G. Availability and irreversibility in thermodynamics. Brit. J. Appl. Phys 1951, 2, 183–192. [Google Scholar] [CrossRef]
- Bejan, A. Fundamentals of exergy analysis, entropy generation minimization, and the generation of flow architecture. Int. J. Energy Res. 2002, 26, 545–565. [Google Scholar] [CrossRef]
- Som, S.K.; Datta, A. Thermodynamic irreversibilities and exergy balance in combustion processes. Prog. Energy Combust. Sci. 2008, 34, 351–376. [Google Scholar] [CrossRef]
- Sciacovelli, A.; Verda, V.; Sciubba, E. Entropy generation analysis as a design tool—A review. Renew. Sust. Energ. Rev. 2015, 43, 1167–1181. [Google Scholar] [CrossRef]
- Caton, J.A. Implications of fuel selection for an SI engine: Results from the first and second laws of thermodynamics. Fuel 2010, 89, 3157–3166. [Google Scholar] [CrossRef]
- Caton, J.A. A cycle simulation including the second law of thermodynamics for a spark-ignition engine: Implications of the use of multiple-zones for combustion. SAE Tech. Paper 2002, 111, 281–299. [Google Scholar]
- Javaheri, A.; Esfahanian, V.; Salavati-Zadeh, A.; Darzi, M. Energetic and exergetic analyses of a variable compression ratio spark ignition gas engine. Energy Convers. Manag. 2014, 88, 739–748. [Google Scholar] [CrossRef]
- Özkan, M.; Özkan, D.B.; Özener, O.; Yılmaz, H. Experimental study on energy and exergy analyses of a diesel engine performed with multiple injection strategies: Effect of pre-injection timing. Appl. Therm. Eng. 2013, 53, 21–30. [Google Scholar] [CrossRef]
- Taghavifar, H.; Khalilarya, S.; Jafarmadar, S. Exergy analysis of combustion n in VGT-modified diesel engine with detailed chemical kinetics mechanism. Energy 2015, 93, 740–748. [Google Scholar] [CrossRef]
- Rakopoulos, C.D.; Giakoumis, E.G. Simulation and exergy analysis of transient diesel-engine operation. Energy 1997, 22, 875–885. [Google Scholar] [CrossRef]
- Sayin, C.; Hosoz, M.; Canakci, M.; Kilicaslan, I. Energy and exergy analyses of a gasoline engine. Int. J. Energy Res. 2007, 31, 259–273. [Google Scholar] [CrossRef]
- Feng, H.; Liu, D.; Yang, X.; An, M.; Zhang, W.; Zhang, X. Availability analysis of using iso-octane/n-butanol blends in spark-ignition engines. Renew. Energy 2016, 96, 281–294. [Google Scholar] [CrossRef]
- Teh, K.Y.; Miller, S.L.; Edwards, C.F. Thermodynamic requirements for maximum internal combustion engine cycle efficiency. Part 1: Optimal combustion strategy. Int. J. Engine Res. 2008, 9, 449–465. [Google Scholar] [CrossRef]
- Teh, K.Y.; Miller, S.L.; Edwards, C.F. Thermodynamic requirements for maximum internal combustion engine cycle efficiency. Part 2: Work extraction and reactant preparation strategies. Int. J. Engine Res. 2008, 9, 467–481. [Google Scholar] [CrossRef]
- Bhatti, S.S.; Verma, S.; Tyagi, S.K. Energy and exergy-based performance evaluation of variable compression ratio spark ignition engine based on experimental work. Therm. Sci. Eng. Prog. 2019, 9, 332–339. [Google Scholar] [CrossRef]
- da Costa, Y.J.R.; de Lima, A.G.B.; Filho, C.R.B.; de Araujo Lima, L. Energetic and exergetic analyses of a dual-fuel diesel engine. Renew. Sustain. Energy Rev. 2012, 16, 4651–4660. [Google Scholar] [CrossRef]
- Li, Y.; Jia, M.; Chang, Y.; Kokjohn, S.L.; Reitz, R.D. Thermodynamic energy and exergy analysis of three different engine combustion regimes. Appl. Energy 2016, 180, 849–858. [Google Scholar] [CrossRef]
- Sanli, B.G.; Özcanli, M.; Serin, H. Assessment of thermodynamic performance of an IC engine using microalgae biodiesel at various ambient temperatures. Fuel 2020, 277, 118108. [Google Scholar] [CrossRef]
- Punov, P.; Evtimov, T.; Chiriac, R.; Clenci, A.; Danel, Q.; Descombes, G. Progress in high performance, low emissions, and exergy recovery in internal combustion engines. Int. J. Energy Res 2017, 41, 1229–1241. [Google Scholar] [CrossRef]
- Safari, M.; Sheikhi, M.R.H.; Janbozorgi, M.; Metghalchi, H.; Sheikhi, R.H. Entropy transport equation in large eddy simulation for exergy analysis of turbulent combustion systems. Entropy 2010, 12, 434–444. [Google Scholar] [CrossRef]
- Safari, M.; Hadi, F.; Sheikhi, M.R.H. Progress in the Prediction of entropy generation in turbulent reacting flows using large eddy simulation. Entropy 2014, 16, 5159–5177. [Google Scholar] [CrossRef] [Green Version]
- Pope, S. PDF methods for turbulent reactive flows. Prog. Energy Combust. Sci 1985, 11, 119–192. [Google Scholar] [CrossRef]
- Pope, S.B. A monte carlo method for the PDF equations of turbulent reactive flow. Combust. Sci. Technol. 1981, 25, 159–174. [Google Scholar] [CrossRef]
- Agrebi, S.; Dreßler, L.; Nicolai, H.; Ries, F.; Nishad, K.; Sadiki, A. Analysis of Local Exergy Losses in Combustion Systems Using a Hybrid Filtered Eulerian Stochastic Field Coupled with Detailed Chemistry Tabulation: Cases of Flames D and E. Energies 2021, 14, 6315. [Google Scholar] [CrossRef]
- Ries, F.; Li, Y.; Nishad, K.; Janicka, J.; Sadiki, A. Entropy generation analysis and thermodynamic optimization of jet impinge-ment cooling using large eddy simulation. Entropy 2019, 19, 129. [Google Scholar] [CrossRef] [Green Version]
- Valencia, G.; Fontalvo, A.; Cárdenas, Y.; Duarte, J.; Isaza, C. Energy and Exergy Analysis of Different Exhaust Waste Heat Recovery Systems for Natural Gas Engine Based on ORC. Energies 2019, 12, 2378. [Google Scholar] [CrossRef] [Green Version]
- Rosen, M.A.; Dincer, I. On exergy and environmental impact. Int. J. Energy Res. 1997, 21, 643–654. [Google Scholar] [CrossRef]
- Valero, A.; Usón, S.; Torres, C.; Stanek, W. Theory of Exergy Cost and Thermo-ecological Cost. In Thermodynamics for Sustainable Management of Natural Resources. Green Energy and Technology; Stanek, W., Ed.; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Valero, A.; Valero, A.; Stanek, W. Assessing the exergy degradation of the natural capital: From Szargut’s updated reference environment to the new thermogeological-cost methodology. Energy 2018, 163, 1140–1149. [Google Scholar] [CrossRef]
- Veiga, J.P.S.; Romanelli, T.L. Mitigation of greenhouse gas emissions using exergy. J. Clean. Prod. 2020, 260, 121092. [Google Scholar] [CrossRef]
- Vihervaara, P.; Franzese, P.P.; Buonocore, E. Information, energy, and eco-exergy as indicators of ecosystem complexity. Ecol. Model. 2019, 395, 23–27. [Google Scholar] [CrossRef]
- Wu, J.; Wang, N. Exploring avoidable carbon emissions by reducing exergy destruction based on advanced exergy analysis: A case study. Energy 2020, 206, 118246. [Google Scholar] [CrossRef]
- Rosen, M.A. Exergy Analysis as a Tool for Addressing Climate Change. Eur. J. Sustain. Dev. Res. 2021, 5, 0148. [Google Scholar] [CrossRef]
- Prasad, V.N. Large Eddy Simulation of Partially Premixed Turbulent Combustion. Ph.D. Thesis, Imperial College London, University of London, London, UK, 2011. [Google Scholar]
- Jones, W.; Prasad, V. Large eddy simulation of the Sandia flame series (D–F) using the Eulerian stochastic field method. Combust. Flame 2010, 157, 1621–1636. [Google Scholar] [CrossRef]
- Yifan, D.U.A.N.; Zhixun, X.I.A.; Likun, M.A.; Zhenbing, L.U.O.; Huang, X.; Xiong, D.E.N.G. LES of the Sandia flame series D-F using the Eulerian stochastic field method coupled with tabulated chemistry. Chin. J. Aeronaut 2020, 33, 116–133. [Google Scholar]
- Bilger, R.W.; Stårner, S.H.; Kee, R.J. On reduced mechanisms for methane-air combustion in non-premixed flames. Combust. Flame 1990, 80, 135–149. [Google Scholar] [CrossRef]
- Mahmoud, R.; Jangi, M.; Ries, F.; Fiorina, B.; Janicka, J.; Sadiki, A. Combustion characteristics of a non-premixed oxy-flame applying a hybrid filtered eulerian stochastic field/flamelet progress variable approach. Appl. Sci. 2019, 9, 1320. [Google Scholar] [CrossRef] [Green Version]
- Goodwin, D.; Moffat, H.K. Cantera. Available online: http://code.google.com/p/cantera/ (accessed on 28 June 2021).
- Nicoud, F.; Toda, H.B.; Cabrit, O.; Bose, S.; Lee, J. Using singular values to build a subgrid-scale model for large eddy simula-tions. Phys. Fluids 2011, 23, 085106. [Google Scholar] [CrossRef] [Green Version]
- Valiño, L. A field monte carlo formulation for calculating the probability density function of a single scalar in a turbulent flow. Flow Turbul. Combust. 1998, 60, 157–172. [Google Scholar] [CrossRef]
- Dopazo, C.; O’Brien, E.E. Functional formulation of non-isothermal turbulent reactive flows. Phys. Fluids 1974, 17, 1968–1975. [Google Scholar] [CrossRef] [Green Version]
- Dressler, L.; Filho, F.L.S.; Ries, F.; Nicolai, H.; Janicka, J.; Sadiki, A. Numerical prediction of turbulent spray flame characteristics using the filtered eulerian stochastic field approach coupled to tabulated chemistry. Fluids 2021, 6, 50. [Google Scholar] [CrossRef]
- Jones, W.P.; Navarro-Martinez, S.; Röhl, O. Large eddy simulation of hydrogen auto-ignition with a probability density function method. Proc. Combust. Inst. 2007, 31, 1765–1771. [Google Scholar] [CrossRef]
- Avdić, A.; Kuenne, G.; di Mare, F.; Janicka, J. LES combustion modeling using the Eulerian stochastic field method coupled with tabulated chemistry. Combust. Flame 2017, 175, 201–219. [Google Scholar] [CrossRef]
- Frost, V.A. Model of a turbulent, diffusion-controlled flame jet. Fluid Mech. Soviet Res. 1975, 4, 124–133. [Google Scholar]
- O’Brien, E.E. The probability density function (pdf) approach to reacting turbulent flows. In Turbulent Reacting Flows; Springer: Berlin/Heidelberg, Germany, 1980; pp. 185–218. [Google Scholar]
- Villermaux, J.; Falk, L. A generalized mixing model for initial contacting of reactive fluids. Chem. Eng. Sci. 1994, 49, 5127–5140. [Google Scholar] [CrossRef]
- Kloeden, P.E.; Platen, E. Numerical Solution of Stochastic Differential Equations; Springer Science & Business Media: New York, NY, USA, 1992. [Google Scholar]
- Picciani, M.A. Investigation of Numerical Resolution Requirements of the Eulerian Stochastic Fields and the Thickened Sto-chastic Field Approach. Ph.D. Thesis, University of Southampton, Southampton, UK, 2018. [Google Scholar]
- Muradoglu, M.; Jenny, P.; Pope, S.B.; Caughey, D.A. A consistent hybrid finite-volume/particle method for the PDF equations of turbulent reactive flows. J. Comput. Phys. 1999, 154, 342–371. [Google Scholar] [CrossRef] [Green Version]
- Garmory, A. Micro-mixing Effects in Atmospheric Reacting Flows. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 2008. [Google Scholar]
- Sahoo, B.B.; Dabi, M.; Saha, U.K. A Compendium of Methods for Determining the Exergy Balance Terms Applied to Reciprocating Internal Combustion Engines. J. Energy Resour. Technol. 2021, 143, 120801. [Google Scholar] [CrossRef]
- Dimitrova, Z.; Marechal, F. Energy Integration on Multi-periods for Vehicle Thermal Powertrains. Can. J. Chem. Eng. 2017, 95, 235–264. [Google Scholar] [CrossRef]
- Khaliq, A.; Trivedi, S.K. Second Law Assessment of a Wet Ethanol Fuelled HCCI Engine Combined with Organic Rankine Cycle. ASME J. Energy Resour. Technol. 2012, 134, 022201. [Google Scholar] [CrossRef]
- Salek, F.; Babaie, M.; Ghodsi, A.; Hosseini, S.V.; Zare, A. Energy and Exergy Analysis of a Novel Turbo-compounding System for Supercharging and Mild Hybridization of a Gasoline Engine. J. Therm. Anal. Calorim 2020, 145, 817–828. [Google Scholar] [CrossRef]
- Ntziachristos, L.; Samaras, Z.; Zervas, E.; Dorlhene, P. Effects of a Catalysed and an Additized Partied Filter on the Emissions of a Diesel Passenger Car Operating on Low Sulphur Fuels. Atmos. Environ. 2005, 39, 4925–4936. [Google Scholar] [CrossRef]
- Moran, M.J.; Shapiro, H.N.; Boettner, D.D.; Bailey, M.B. Fundamentals of Engineering Thermodynamics; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- TNF Workshop. Available online: http://www.ca.sandia.gov/TNF (accessed on 28 June 2021).







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Agrebi, S.; Dreßler, L.; Nishad, K. The Exergy Losses Analysis in Adiabatic Combustion Systems including the Exhaust Gas Exergy. Entropy 2022, 24, 564. https://doi.org/10.3390/e24040564
Agrebi S, Dreßler L, Nishad K. The Exergy Losses Analysis in Adiabatic Combustion Systems including the Exhaust Gas Exergy. Entropy. 2022; 24(4):564. https://doi.org/10.3390/e24040564
Chicago/Turabian StyleAgrebi, Senda, Louis Dreßler, and Kaushal Nishad. 2022. "The Exergy Losses Analysis in Adiabatic Combustion Systems including the Exhaust Gas Exergy" Entropy 24, no. 4: 564. https://doi.org/10.3390/e24040564
APA StyleAgrebi, S., Dreßler, L., & Nishad, K. (2022). The Exergy Losses Analysis in Adiabatic Combustion Systems including the Exhaust Gas Exergy. Entropy, 24(4), 564. https://doi.org/10.3390/e24040564





