Information Architecture for Data Disclosure
Abstract
:1. Introduction
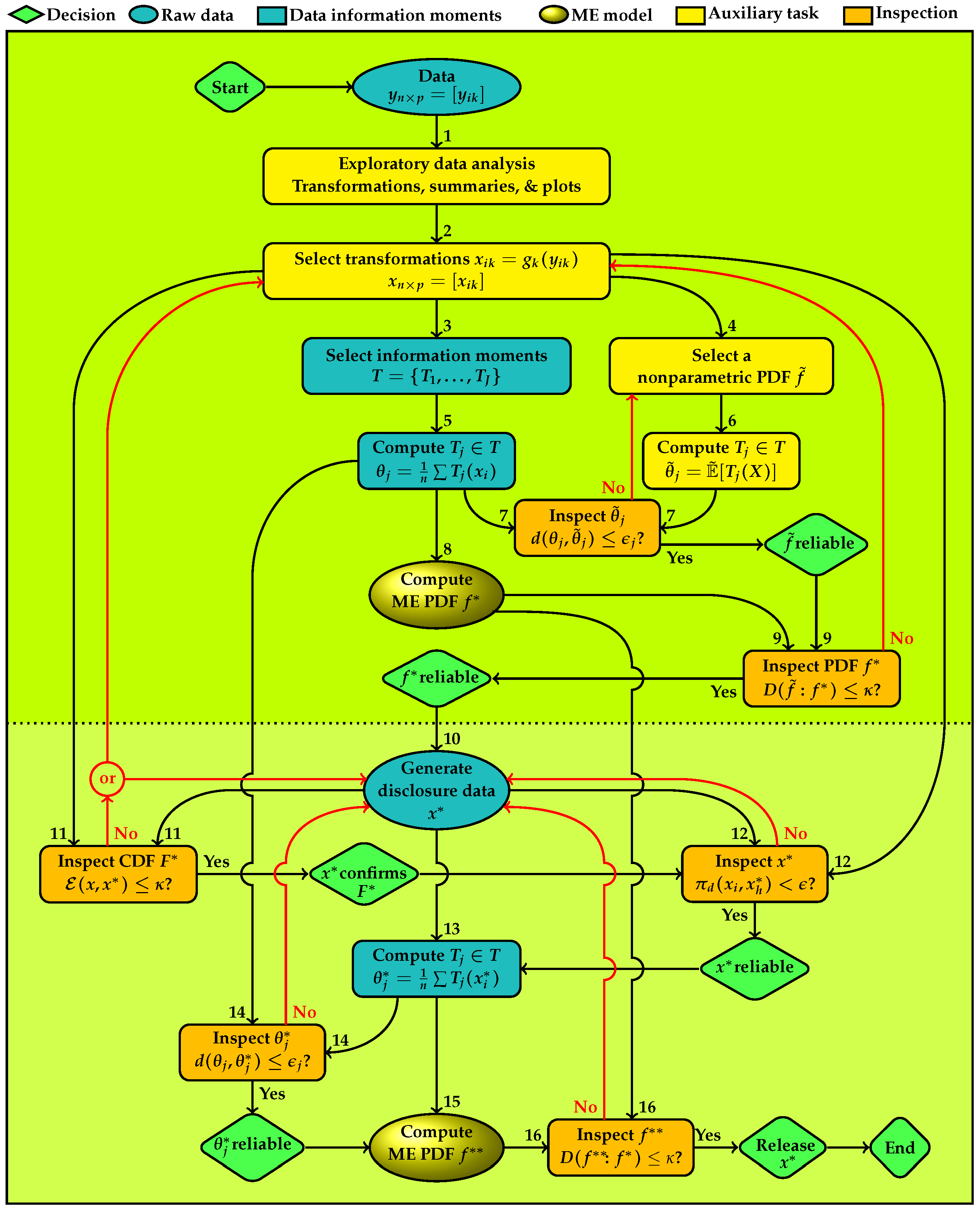
2. Information Architecture
- (a)
- The essential statistical aspects, such as underlying distribution and information moments of the actual and disclosure data sets are about the same.
- (b)
- The individual points in the actual and disclosure data sets are not similar.
- Task 1
- starts the process with an exploratory data analysis of the raw data. Various distribution plots and scatter plots are produced for the following purposes.
- (a)
- To explore the distributional features of the data that provide clues for selecting a transformation for specifying the set of information moments T for an ME model , as a parametric representation of f, which is used for generating a replica for disclosure.
- (b)
- To explore a suitable nonparametric PDF that represents f for checking the adequacy of .
- Task 2
- specifies transformations of the original data to , where , hereafter is called the actual data, are one-to-one functions on ℜ which transforms the coordinates of . The identity function is included when a transformation is not needed.
- Task 3
- specifies the set of information moments for deriving the parametric ME model to represent f.
- Task 4
- provides a nonparametric PDF , for representing f. For continuous variables, is a multivariate kernel density estimate or histogram. For the discrete and categorical variables, is the distribution of relative frequencies. This distribution serves as an intermediary for examining suitability of the information moments for developing an ME model for the data. This mediation is necessary for the continuous variables because the information moments of the raw data given in (2) are based on the usual empirical distribution, which does not possess a continuous PDF for confirming a continuous ME model.
- Task 5
- computes the specified moment information. For example, equal weights of data points giveThese information moments can include usual moments such as various power and cross-product moments, quantiles such as median where is an indicator function, and/or more complex type such as those shown in Table A1, Table A2 and Table A3 in the Appendix A [29,31]. In the case of frequency tables, represent univariate and multivariate marginal frequencies of contingency tables. The information architecture for disclosure accomplishes data protection via creating a statistical copy of for disclosure, both of which possess approximately the same information moments as the actual data.
- Task 6
- computes the information moments of given byfor continuous variables and for discrete variables and the integral changes to summation. The idea is that if is a good representation of the information characteristics of the data then its information moments should be approximately the same as those given in (2).
- Task 7
- has two input links to inspect the Euclidean distance between each information moment of the nonparametric PDF and the corresponding data information moment. If any is not confirmed, has to be revised and the information moments of the revised should be examined. The revision can include, for example, changing the grid used for computing the information moments and the bandwidth of the kernel density, type of the kernel function, the bins of histogram or the type of empirical PDF. If all individual ’s are confirmed, then the empirical PDF is reliable for using to inspect the adequacy of the ME model for the data. The first decision node shown at the right side of this node in Figure 1) displays this conclusion.
- Task 8
- computes the ME model for , shown as , implied by the set of data information moments .
- Task 9
- has two input links to inspect the information divergence between the multivariate PDF of the ME model, and the nonparametric PDF that represents the data. The multivariate divergence examines entire set of moments T and lower dimensional divergence measures examine respective subsets of marginal information moments. This task serves two purposes.
- (a)
- The information divergence measure between two distributions is inclusive of all information moments of reflected of and , hence provides an aggregate measure of discrepancy between their sets of moments.
- (b)
- The information divergence examines the adequacy of the ME PDF for representing the nonparametric PDF of the data.
If is not confirmed, then selection of information moments has to be revised for which revisiting data exploratory analysis becomes necessary. The revision can include reexamining transformations, selection of the information moments and the nonparametric PDF. Upon the revision, all preceding nodes have to be revisited. If is confirmed, the role of ends. We conclude that the information moments represent the statistical characteristics of the data. By the Entropy Concentration Theorem (Jaynes [32]), if the data generating distribution is governed by the selected information moments, then the ME distribution closely approximates types of distributions that satisfy the moments. This property makes reliable for inferential purposes. The second decision node shown below ME model in Figure 1 displays this conclusion.Then the process proceeds with using the ME model for generating disclosure data. - Task 10
- uses to generate the statistical copy for disclosure, which will be subject to four inspections for approval to release.
- Task 11
- uses to reaffirm the ME model via the energy statistic which measures the difference between two distributions based on the pairwise Euclidean distance on , defined byDistances between data points in the actual and disclosure data sets, , are assessed in terms of the difference between their average and the average of distances within each data set and . For measuring the model fit should be low. If the value of is not negligible, a new set of data has to be generated and reexamined. If regeneration does not produce a satisfactory result, selection of information moments has to be revised for which revisiting data exploratory analysis becomes necessary. Upon the revision, all preceding nodes must be revisited. If the ME model is confirmed, the process continues with further inspections of the disclosure data. The third decision node shown below the disclosure data in Figure 1 displays this conclusion.
- Task 12
- inspects the proportion of distances between the points in the actual and disclosure data,where is the indicator function of condition A. This measure is used for controlling the disclosure risk of . The disclosure data is synthetic, generated from the ME model for the actual data. There is not a one-to-one correspondence between the points in the two data sets. However, there still can be a disclosure risk, for example, when each disclosure data point is very close to an actual data point. If does not produce a satisfactory result, a new set of disclosure data ought to be generated and reexamined. If is confirmed, the fourth decision node reflects this conclusion and the process continues with the information moments.
- Task 13
- computes the information moments of the disclosure data, denoted as . As noted before, T includes marginal and joint moments of various types.
- Task 14
- uses two input links for to inspect each information moment of the release data with the corresponding information moment of the actual data. If the closeness of the pairs of all information moments is not confirmed, a new version of disclosure data has to be generated and reexamined through Tasks 11–14. If are confirmed individually, then the set of disclosure data moments is reliable. The fifth decision node at the east of this node in Figure 1 displays this conclusion and the process proceeds with computation of the ME model for the disclosure data for further inspections.
- Task 15
- computes the ME model implied by the set of data information moments for the inspection the entire set as a whole.
- Task 16
- serves the purpose of examining the information discrepancy between and . The multivariate divergence examines entire T and the marginal divergence measures examines subsets of marginal information moments. If the closeness of the two ME models is not confirmed, a new set of data has to be generated and reexamined through Tasks 11–16. With approval of the sixth decision node in southeast corner of Figure 1 displays the following conclusion: is a statistical replica of and ready for disclosure. Then the process ends.
3. Implementation of the Information Architecture
3.1. ME Information Moments
3.2. Discrepancy Measures
3.2.1. Energy Statistic
3.2.2. Kullback–Leibler Information Divergence
3.3. Semi-Parametric Measures
4. Disclosure of Financial Data
4.1. Mortgage Data
4.1.1. Exploratory Analysis
4.1.2. Information Moments and ME Model
4.1.3. Disclosure Data and Inspections
4.2. Bank Data
4.2.1. Exploratory Analysis
4.2.2. Information Moments and ME Model
4.2.3. Disclosure Data and Inspections
5. Concluding Remarks
“If the information incorporated into the maximum-entropy analysis includes all the constraints actually operative in the random experiment, then the distribution predicted by maximum entropy is overwhelmingly the most likely to be observed experimentally, because it can be realized in overwhelmingly the greatest number of ways.Conversely, if the experiment fails to confirm the maximum-entropy prediction, and this disagreement persists on indefinite repetition of the experiment, then we will conclude that the physical mechanism of the experiment must contain additional constraints which were not taken into account in the maximum-entropy calculations. The observed deviations then provide a clue as to the nature of these new constraints.”(Jaynes [47])
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| ME Model | Density | Information Moments |
|---|---|---|
| Generalized error, (Laplace , Normal ) | ||
| Student-t, (Cauchy ), | ||
| Logistic, | ||
| Asymmetric Laplace, | ||
| Exponential | ||
| Pareto Type II [], | ||
| Gamma [], | ||
| Beta [], | ||
| Family and Transformation | Density | Information Moments |
|---|---|---|
| Location-scale transformation | ||
| Log and exponential transformations | ||
| Logistic, | ||
| Log-Gamma, | ||
| Lognormal, | ||
| Power transformations | ||
| Generalized Gamma, (Weibull , Half-normal ), Generalized normal | ||
| Pareto Type IV, ( Pareto Type III) | ||
| Inverted beta, | ||
| ME Model | Density | Information Moments |
|---|---|---|
References
- Franconi, L.; Stander, J. A Model-based method for disclosure limitation of business microdata. Statistician 2002, 51, 51–61. [Google Scholar] [CrossRef]
- Ichim, D. Disclosure control of business microdata: A density-based approach. Int. Stat. Rev. 2009, 77, 196–211. [Google Scholar] [CrossRef]
- Duncan, G.T.; Elliot, M.; Salazar-Gonzales, J. Statistical Confidentiality: Principles and Practice; Springer: New York, NY, USA, 2011. [Google Scholar]
- Liu, L.; Kinney, S.; Slavković, A.S. Special Issue: A New Generation of Statisticians Tackles Data Privacy. Chance 2020, 33, 4–5. [Google Scholar] [CrossRef]
- Duncan, G.T.; Lambert, D. The risk of disclosure for microdata. J. Bus. Econ. Stat. 1989, 7, 207–217. [Google Scholar]
- Kadane, J.B.; Krishnan, R.; Shmueli, G. A data disclosure policy for count data based on the COM-Poisson distribution. Manag. Sci. 2006, 52, 1610–1617. [Google Scholar] [CrossRef] [Green Version]
- Fienberg, S.E. Confidentiality and Disclosure Limitation. Encycl. Soc. Meas. 2005, 1, 463–469. [Google Scholar]
- Carlson, M.; Salabasis, M. A data-swapping technique using ranks—A method for disclosure control (with comments). Res. Off. Stat. 2002, 6, 35–67. [Google Scholar]
- Dalenius, R.T.; Reiss, S.P. Data swapping: A technique for disclosure control. J. Stat. Plan. Inference 1982, 6, 73–85. [Google Scholar] [CrossRef]
- Duncan, G.T.; Pearson, R.W. Enhancing access to microdata while protecting confidentiality. Stat. Sci. 1991, 6, 219–239. [Google Scholar]
- Moore, R.A. Controlled Data-Swapping Techniques for Masking Public Use Micro-Data Sets; Bureau of the Census, Statistical Research Division, Statistical Research Report Series, No RR96/04; US Bureau of the Census: Washington, DC, USA, 1996.
- Muralidhar, K.; Batra, D.; Kirs, P. Accessibility, security, and accuracy in statistical databases: The case for the multiplicative fixed data perturbation approach. Manag. Sci. 1995, 41, 1549–1564. [Google Scholar] [CrossRef]
- Muralidhar, K.; Parsa, R.; Sarathy, R. A general additive data perturbation method for database security. Manag. Sci. 1999, 45, 1399–1415. [Google Scholar] [CrossRef]
- Muralidhar, K.; Sarathy, R. Data Shuffling—A new Masking Approach for Numerical Data. Manag. Sci. 2006, 52, 658–670. [Google Scholar] [CrossRef]
- Reiter, J.P. Releasing multiple imputed, synthetic, public-use microdata: An illustration and empirical study. J. R. Stat. Soc. A 2005, 168, 185–205. [Google Scholar] [CrossRef]
- Duncan, G.T.; Stokes, L. Data masking for disclosure limitation. WIRES Comput. Stat. 2009, 1, 83–92. [Google Scholar] [CrossRef]
- McKay-Bowen, C. The art of data privacy. Significance 2022, 19, 14–19. [Google Scholar] [CrossRef]
- Hu, J.M.; Savitsky, T.; Williams, M. Risk-weighted data synthesizers for microdata dissemination. Chance 2020, 33, 29–36. [Google Scholar] [CrossRef]
- Karr, A.F.; Kohnen, C.N.; Oganian, A.; Reiter, J.P.; Sanil, A.P. A framework for evaluating the utility of data altered to protect confidentiality. Am. Stat. 2006, 60, 224–232. [Google Scholar] [CrossRef]
- Keller-McNulty, S.; Nakhleh, C.W.; Singpurwalla, N.D. A paradigm for masking (camouflaging) information. Int. Stat. Rev. 2005, 73, 331–349. [Google Scholar] [CrossRef]
- Sankar, L.; Rajagopalan, S.R.; Poor, H.V. Utility-Privacy Tradeoffs in Databases: An Information-Theoretic Approach. IEEE Trans. Inf. Forensics Secur. 2013, 8, 838–852. [Google Scholar] [CrossRef] [Green Version]
- Trottini, M. A decision-theoretic approach to data disclosure problems. Res. Off. Stat. 2001, 4, 7–22. [Google Scholar]
- Trottini, M. Decision Models for Data Disclosure Limitation. Ph.D. Dissertation, Department of Statistics, Carnegie Mellon University, Pittsburgh, PA, USA, 2003. [Google Scholar]
- Keeney, R.L.; Raiffa, H. Decisions with Multiple Objectives-Preferences and Value Tradeoffs; Wiley: New York, NY, USA, 1976. [Google Scholar]
- Cox, L.H.; Karr, A.F.; Kinney, S.K. Risk-utility for statistical disclosure limitation: How to think, but not how to act? Int. Stat. Rev. 2011, 79, 160–183. [Google Scholar] [CrossRef]
- Dwork, C. Differential privacy. In 33rd International Colloquium on Automata, Languages and Programming, Part II (ICALP 2006); Bugliesi, M., Preneel, B., Sassone, V., Wegener, I., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 1–12. [Google Scholar]
- Snoke, J.; McKay Bowen, C. How statisticians should grapple with privacy in a changing data landscape. Chance 2020, 33, 6–13. [Google Scholar] [CrossRef]
- Polettini, S. Maximum entropy simulation for microdata protection. Stat. Comput. 2003, 13, 307–320. [Google Scholar] [CrossRef]
- Ebrahimi, N.; Soofi, E.S.; Soyer, R. Multivariate maximum entropy identification, transformation, and dependence. J. Multivar. Anal. 2008, 99, 1217–1231. [Google Scholar] [CrossRef] [Green Version]
- Awan, J.; Reimherr, M.; Slavković, A.S. Formal privacy for modern nonparametric statistics. Chance 2020, 33, 43–49. [Google Scholar] [CrossRef]
- Bajgiran, A.H.; Mardikoraem, M.; Soofi, E.S. Maximum entropy distributions with quantile information. Eur. J. Oper. Res. 2021, 290, 196–209. [Google Scholar] [CrossRef]
- Jaynes, E.T. On the rationale of maximum-entropy methods. Proc. IEEE 1982, 70, 939–952. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; Wiley: New York, NY, USA, 2006; p. 35. [Google Scholar]
- Darbellay, G.A.; Vajda, I. Entropy expressions for multivariate continuous distributions. IEEE Trans. Inf. Theory 2000, 46, 709–712. [Google Scholar] [CrossRef]
- Aulogiaris, G.; Zografos, K. A maximum entropy characterization of symmetric Kotz type and Burr multivariate distributions. Test 2004, 13, 65–83. [Google Scholar] [CrossRef]
- Zografos, K. On maximum entropy characterization of Pearson’s Type II and VII multivariate distributions. J. Multivar. Anal. 1999, 71, 67–75. [Google Scholar] [CrossRef] [Green Version]
- Ebrahimi, N.; Hamedani, G.G.; Soofi, E.S.; Volkmer, H. A Class of models for uncorrelated random variables. J. Multivar. Anal. 2010, 101, 1859–1871. [Google Scholar] [CrossRef] [Green Version]
- Sarathy, R.; Muralidhar, K.; Parsa, R. Perturbing Nonnormal Confidential Attributes: The Copula Approach. Manag. Sci. 2002, 48, 1613–1627. [Google Scholar] [CrossRef]
- Rizzo, M.L.; Székely, G.J. Energy distance. WIREs Comput. Stat. 2016, 8, 27–38. [Google Scholar] [CrossRef]
- Baringhaus, L.; Franz, C. On a new multivariate two-sample test. J. Multivar. Anal. 2004, 88, 190–206. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- McCulloch, R.E. Local model influence. J. Am. Stat. Assoc. 1989, 84, 473–478. [Google Scholar] [CrossRef]
- Ebrahimi, N.; Jalali, N.Y.; Soofi, E.S. Comparison, utility, and partition of dependence under absolutely continuous and singular distributions. J. Multivar. Anal. 2014, 131, 32–50. [Google Scholar] [CrossRef]
- Hall, P.; Morton, S.C. On the estimation of entropy. Ann. Inst. Math. Stat. 1993, 45, 69–88. [Google Scholar] [CrossRef]
- Soyer, R.; Xu, F. Assessment of mortgage default risk via Bayesian reliability models. Appl. Stoch. Model. Bus. Ind. 2010, 26, 308–330. [Google Scholar] [CrossRef]
- Kotz, S.; Balakrishnan, N.; Johnson, N.L. Continuous Multivariate Distributions: Volume I: Models and Applications, 2nd ed.; Wiley: New York, NY, USA, 2000. [Google Scholar]
- Jaynes, E.T. Prior Probabilities. IEEE Trans. Sys. Sci. Cyber. 1968, 4, 227–241. [Google Scholar] [CrossRef]
- Mazzuchi, T.A.; Soofi, E.S.; Soyer, R. Bayes estimate and inference for entropy and information index of fit. Econ. Rev. 2008, 27, 428–456. [Google Scholar] [CrossRef]








| Information Moment | Entropy | KL Divergence | K Index | Coin | |||
|---|---|---|---|---|---|---|---|
| Actual | Kernel | ||||||
| Loan | 0.563 | 0.564 | 0.009 | 0.017 | 0.565 | ||
| Mean | 11.117 | 11.111 | |||||
| Variance | 0.180 | 0.189 | |||||
| Income | 0.594 | 0.609 | 0.016 | 0.031 | 0.588 | ||
| Mean | 10.394 | 10.389 | |||||
| Variance | 0.192 | 0.203 | |||||
| Bivariate | 0.925 | 0.866 | 0.072 | 0.134 | 0.683 | ||
| Covariance | 0.123 | 0.118 | |||||
| Information Moment | Energy Stat | Euclidean Dist | ||
|---|---|---|---|---|
| Actual | Disclosure | |||
| Loan | 0.134 | 0.027 | ||
| Mean | 11.117 | 11.115 | ||
| Variance | 0.180 | 0.188 | ||
| Income | 0.065 | 0.026 | ||
| Mean | 10.394 | 10.397 | ||
| Variance | 0.192 | 0.191 | ||
| Bivariate | 0.201 | <0.001 | ||
| Covariance | 0.123 | 0.119 | ||
| Entropy | KL Divergence | K Index | Coin | ||
|---|---|---|---|---|---|
| Loan | 0.563 | 0.583 | <0.001 | 0.001 | 0.514 |
| Income | 0.595 | 0.593 | <0.001 | <0.001 | 0.504 |
| Bivariate | 868 | 0.923 | 0.004 | 0.007 | 0.542 |
| Mutual info | 0.290 | 0.253 | |||
| M index | 0.440 | 0.397 | |||
| Coin index | 0.832 | 0.815 | |||
| Information Moment | Entropy | KL Divergence | K Index | Coin | |||
|---|---|---|---|---|---|---|---|
| Actual | Kernel | ||||||
| Asset | 2.044 | 2.085 | 0.016 | 0.031 | 0.589 | ||
| Mean | 6.473 | 6.461 | |||||
| Score | 1.774 | 1.787 | 0.014 | 0.027 | 0.582 | ||
| Mean | 5.470 | 5.457 | |||||
| Bivariate | 3.625 | 3.766 | 0.283 | 0.432 | 0.828 | ||
| Log-sum-expo | 1.161 | 1.518 | |||||
| Information Moment | Energy Stat | Euclidean Dist | ||
|---|---|---|---|---|
| Actual | Disclosure | |||
| Asset | 0.460 | 0.006 | ||
| Mean | 6.473 | 6.376 | ||
| Score | 0.655 | 0.008 | ||
| Mean | 5.470 | 5.481 | ||
| Bivariate | 2.529 | <0.001 | ||
| Log-sum-expo | 1.161 | 1.495 | ||
| Entropy | KL Divergence | K Index | Coin | ||
|---|---|---|---|---|---|
| Asset | 2.044 | 2.119 | 0.005 | 0.010 | 0.550 |
| Score | 1.774 | 1.903 | 0.009 | 0.018 | 0.568 |
| Bivariate | 3.625 | 3.829 | 0.002 | 0.005 | 0.535 |
| Mutual info | 0.193 | 0.193 | |||
| M index | 0.320 | 0.320 | |||
| Coin index | 0.783 | 0.783 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pflughoeft, K.A.; Soofi, E.S.; Soyer, R. Information Architecture for Data Disclosure. Entropy 2022, 24, 670. https://doi.org/10.3390/e24050670
Pflughoeft KA, Soofi ES, Soyer R. Information Architecture for Data Disclosure. Entropy. 2022; 24(5):670. https://doi.org/10.3390/e24050670
Chicago/Turabian StylePflughoeft, Kurt A., Ehsan S. Soofi, and Refik Soyer. 2022. "Information Architecture for Data Disclosure" Entropy 24, no. 5: 670. https://doi.org/10.3390/e24050670
APA StylePflughoeft, K. A., Soofi, E. S., & Soyer, R. (2022). Information Architecture for Data Disclosure. Entropy, 24(5), 670. https://doi.org/10.3390/e24050670






