Inference of Molecular Regulatory Systems Using Statistical Path-Consistency Algorithm
Abstract
:1. Introduction
2. Methods
2.1. Information Theory
2.2. Path-Consistency Algorithm
| Algorithm 1: PC algorithm using PMI (PCA-PMI). |
|
2.3. Statistical Path-Consistency Algorithm (SPCA)
- Case 1: Edge appears in all the inferred N networks.
- Case 2: Edge appears in part of the networks but disappears in the other networks.
- Case 3: Edge disappears in all the inferred N networks.
| Algorithm 2: Statistical path-consistent Algorithm (SPCA). |
| Input: : molecular (gene or protein) activity dataset with n variables and m observations. : node set. N: number of different variable orders. : threshold value. M: number of edges in the output network. Output: Network G(V, E). E is the set of selected edges.
|
2.4. Accuracy Measures
2.5. Experimental Datasets
3. Results
3.1. Dependence of Network Structure on Variable Orders
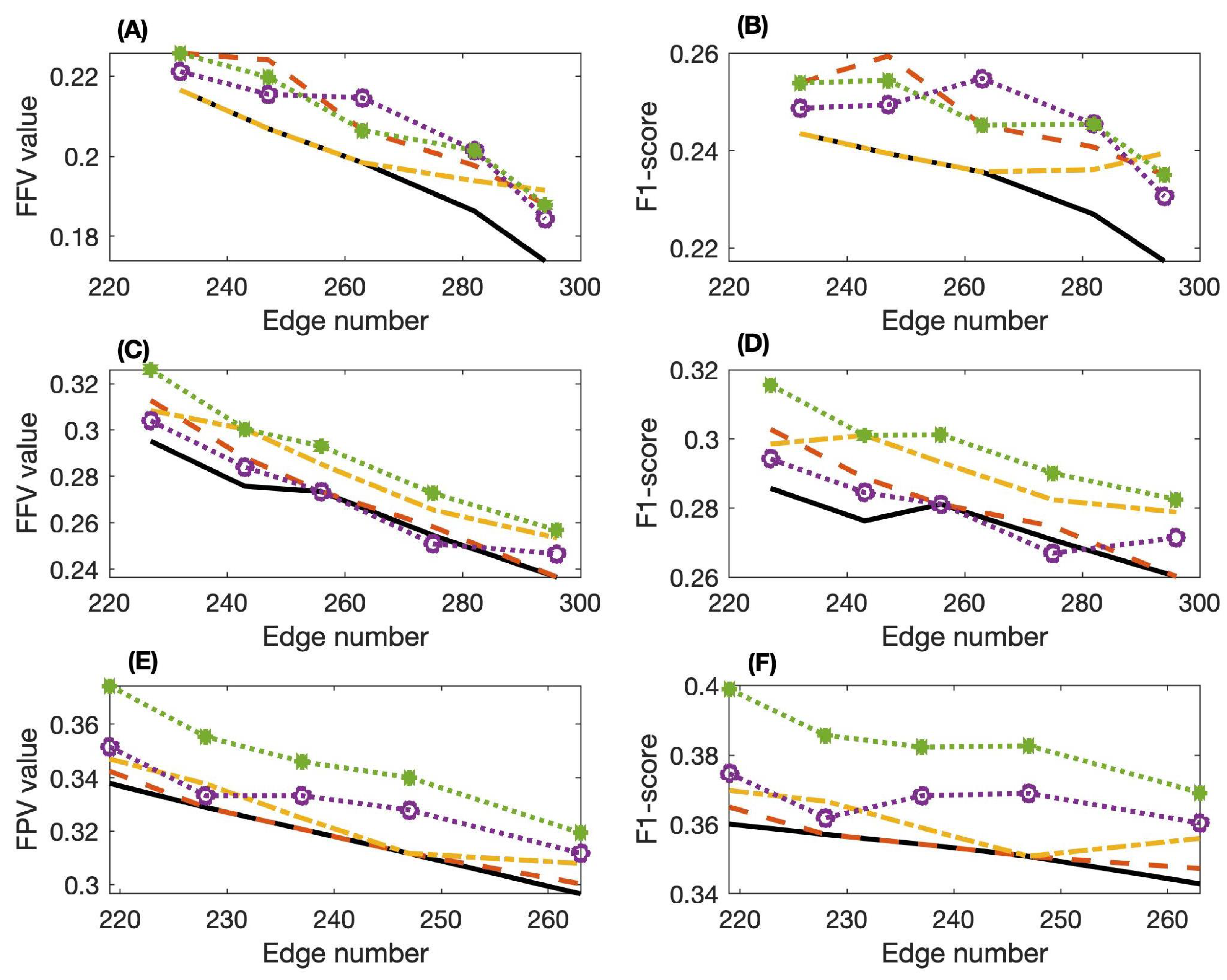
3.2. Effectiveness of SPCA
3.3. Map Kinase Network
3.4. Reconstruction of Cancer-Specific Gene Regulatory Network
4. Discussions and Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| SPCA | Statistical Path-Consistency Algorithm |
| MAP | Mitogen-Activated Protein |
| DREAM | Dialogue for Reverse Engineering Assessments and Methods |
| CMI | Conditional Mutual Information |
| PCA | Path-Consistency Algorithm |
| AUC | Area Under ROC Curve |
| AML | Acute Myeloid Leukemia |
References
- Haas, R.; Zelezniak, A.; Iacovacci, J.; Kamrad, S.; Townsend, S.; Ralser, M. Designing and interpreting ‘multi-omic’ experiments that may change our understanding of biology. Curr. Opin. Syst. Biol. 2017, 6, 37–45. [Google Scholar] [CrossRef] [PubMed]
- Vogel, C.; Marcotte, E.M. Insights into the regulation of protein abundance from proteomic and transcriptomic analyses. Nat. Rev. Genet. 2012, 13, 227–232. [Google Scholar] [CrossRef] [PubMed]
- Saintantoine, M.M.; Singh, A. Network inference in systems biology: Recent developments, challenges, and applications. Curr. Opin. Biotechnol. 2020, 63, 89–98. [Google Scholar] [CrossRef] [Green Version]
- Karlebach, G.; Shamir, R. Modelling and analysis of gene regulatory networks. Nat. Rev. Mol. Cell Biol. 2008, 9, 770–780. [Google Scholar] [CrossRef] [PubMed]
- Basso, K.; Margolin, A.A.; Stolovitzky, G.; Klein, U.; Dallafavera, R.; Califano, A. Reverse engineering of regulatory networks in human b cells. Nat. Genet. 2005, 37, 382–390. [Google Scholar] [CrossRef] [PubMed]
- De Smet, R.; Marchal, K. Advantages and limitations of current network inference methods. Nat. Rev. Microbiol. 2010, 8, 717–729. [Google Scholar] [CrossRef]
- Li, H.; Xie, L.; Zhang, X.; Wang, Y. Wisdom of crowds for robust gene network inference. Nat. Methods 2012, 9, 796–804. [Google Scholar]
- Laehnemann, D.; Kster, J.; Szczurek, E.; McCarthy, D.J.; Hicks, S.C.; Robinson, M.D.; Vallejos, C.A.; Campbell, K.R.; Beerenwinkel, N.; Mahfouz, A.; et al. Eleven grand challenges in single-cell data science. Genome Biol. 2020, 21, 31. [Google Scholar] [CrossRef]
- Dai, H.; Jin, Q.Q.; Li, L.; Chen, L.N. Reconstructing gene regulatory networks in single-cell transcriptomic data analysis. Zool Res. 2020, 41, 599–604. [Google Scholar] [CrossRef]
- Stumpf, M.P.H. Inferring better gene regulation networks from single-cell data. Curr. Opin. Syst. Biol. 2021, 27, 100342. [Google Scholar] [CrossRef]
- Maetschke, S.R.; Madhamshettiwar, P.B.; Davis, M.J.; Ragan, M.A. Supervised, semi-supervised and unsupervised inference of gene regulatory networks. Brief. Bioinform. 2013, 15, 195–211. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huynthu, V.A.; Sanguinetti, G. Gene regulatory network inference: An Introductory Survey. Methods Mol. Biol. 2019, 1883, 1–23. [Google Scholar]
- Zhao, M.; He, W.; Tang, J.; Zou, Q.; Guo, F. A comprehensive overview and critical evaluation of gene regulatory network inference technologies. Brief Bioinform. 2021, 22, bbab009. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Li, W.; Zeng, M.; Zheng, R.; Li, M. Network-based methods for predicting essential genes or proteins: A survey. Brief Bioinform. 2020, 21, 566–583. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z. Quantifying Gene Regulatory Relationships with Association Measures: A Comparative Study. Front Genet. 2017, 8, 96. [Google Scholar] [CrossRef] [Green Version]
- Stuart, J.M.; Segal, E.; Koller, D.; Kim, S.M. A gene-coexpression network for global discovery of conserved genetic modules. Science 2003, 302, 249–255. [Google Scholar] [CrossRef] [Green Version]
- Casadiego, J.; Nitzan, M.; Hallerberg, S.; Timme, M. Model-free inference of direct network interactions from nonlinear collective dynamics. Nat. Commun. 2017, 8, 2192. [Google Scholar] [CrossRef]
- Peng, C.; Zou, L.; Huang, D.S. Discovery of relationships between long non-oding RNAs and genes in human diseases based on tensor completion. IEEE Access 2018, 6, 59152–59162. [Google Scholar] [CrossRef]
- Yuan, L.; Guo, L.; Yuan, C.; Zhang, Y.; Han, K.; Nandi, A.K.; Honig, B.; Huang,, D. Integration of multi-omics data for gene regulatory network inference and application to breast cancer. IEEE/ACM Trans. Comput. Biol. Bioinf. 2019, 16, 782–791. [Google Scholar] [CrossRef] [Green Version]
- Skinnider, M.A.; Squair, J.W.; Foster, L.J. Evaluating measures of association for single-cell transcriptomics. Nat. Methods 2019, 16, 381–386. [Google Scholar] [CrossRef]
- Yang, B.; Bao, W.; Huang, D.S.; Chen, Y. Inference of large-scale time-delayed gene regulatory network with parallel MapReduce cloud platform. Sci. Rep. 2018, 8, 17787. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, B.; Chen, Y.; Zhang, W.; Lv, J.; Bao, W.; Huang, D. Hscvfnt: Inference of time-delayed gene regulatory network based on complex-valued flexible neural tree model. Int. J. Mol. Sci. 2018, 19, 3178. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Meyer, P.E.; Kontos, K.; Lafitte, F.; Bontempi, G. Information-theoretic inference of large transcriptional regulatory networks. EURASIP J. Bioinf. Syst. Biol. 2007, 2007, 8. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, X.; Zhao, X.; He, K.; Lu, L.; Cao, Y.; Liu, J.; Hao, J.; Liu, Z.; Chen, L. Inferring gene regulatory networks from gene expression data by path consistency algorithm based on conditional mutual information. Bioinformatics 2012, 28, 98–104. [Google Scholar] [CrossRef] [PubMed]
- Guo, X.; Zhang, H.; Tian, T. Development of stock correlation networks using mutual information and financial big data. PLoS ONE 2018, 13, e0195941. [Google Scholar] [CrossRef]
- Yan, Y.; Wu, B.; Tian, T.; Zhang, H. Development of Stock Networks Using Part Mutual Information and Australian Stock Market Data. Entropy 2020, 22, 773. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, J.; Hao, J.; Zhao, X.; Chen, L. Conditional mutual inclusive information enables accurate quantification of associations in gene regulatory networks. Nucleic Acids Res. 2015, 43, e31. [Google Scholar] [CrossRef] [Green Version]
- Zhao, J.; Zhou, Y.; Zhang, X.; Chen, L. Part mutual information for quantifying direct associations in networks. Proc. Natl. Acad. Sci. USA 2016, 113, 5130–5135. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Xie, L.; Wang, Y. Output Regulation of Boolean Control Networks. IEEE Trans Auto Control 2017, 62, 2993–2998. [Google Scholar] [CrossRef]
- Ouyang, H.; Fang, J.; Shen, L.; Dougherty, E.R.; Liu, W. Learning restricted Boolean network model by time-series data. EURASIP J. Bioinform. Syst. Biol. 2014, 2014, 10. [Google Scholar] [CrossRef] [Green Version]
- Cantone, I.; Marucci, L.; Iorio, F.; Ricci, M.A.; Belcastro, V.; Bansal, M.; Santini, S.; Di Bernardo, M.; Di Bernardo, D.; Cosma, M.P. A yeast synthetic network for in vivo assessment of reverse-engineering and modeling approaches. Cell 2019, 137, 172–181. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chan, T.E.; Stumpf, M.P.; Babtie, A.C. Gene regulatory network inference from single-cell data using multivariate information measures. Cell Syst. 2017, 5, 251–267. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kishan, K.C.; Li, R.; Cui, F.; Haake, A.R. GNE: A deep learning framework for gene network inference by aggregating biological information. BMC Syst. Biol. 2019, 13, 38. [Google Scholar]
- Ma, B.; Fang, M.; Jiao, X. Inference of gene regulatory networks based on nonlinear ordinary differential equations. Bioinformatics 2020, 36, 4885–4893. [Google Scholar] [CrossRef]
- Specht, A.T.; Li, J. LEAP: Constructing gene co-expression networks for single-cell RNA-sequencing data using pseudo-time ordering. Bioinformatics 2016, 33, 764–766. [Google Scholar] [CrossRef] [Green Version]
- Matsumoto, H.; Kiryu, H.; Furusawa, C.; Gunawan, R. SCODE: An efficient regulatory network inference algorithm from single-cell RNA-seq during differentiation. Bioinformatics 2017, 33, 2314–2321. [Google Scholar] [CrossRef]
- Matsumoto, H.; Kiryu, H. SCOUP: Probabilistic model based on the Ornstein–Uhlenbeck process to analyze single-cell expression data during differentiation. BMC Bioinform. 2016, 17, 232. [Google Scholar] [CrossRef] [Green Version]
- Bonnaffoux, A.; Herbach, U.; Richard, A.; Guillemin, A.; Gonin-Giraud, S.; Gros, P.A.; Gandrillon, O. WASABI: A dynamic iterative framework for gene regulatory network inference. BMC Bioinform. 2019, 20, 220. [Google Scholar] [CrossRef] [Green Version]
- Andrea, O.; Laleh, H.; Mueller, N.S.; Theis, F.J. Reconstructing gene regulatory dynamics from high-dimensional single-cell snapshot data. Bioinformatics 2015, 31, 89–96. [Google Scholar]
- Wang, J.; Wu, Q.; Hu, X.T.; Tian, T. An integrated platform for reverse-engineering protein-gene interaction network. Methods 2016, 110, 3–13. [Google Scholar] [CrossRef]
- Wei, J.; Hu, X.; Zou, X.; Tian, T. Reverse-engineering of gene networks for regulating early blood development from single-cell measurements. BMC Med. Genom. 2017, 10, 72. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.; Cui, T.; Zhang, X.; Tian, T. A non-linear reverse-engineering method for inferring genetic regulatory networks. PeerJ 2020, 8, e9065. [Google Scholar] [CrossRef] [PubMed]
- Yan, Y.; Jiang, F.; Zhang, X.; Tian, T. Integrated inference of asymmetric protein interaction networks using dynamic model and individual patient proteomics data. Symmetry 2021, 13, 1097. [Google Scholar] [CrossRef]
- Huynh-Thu, V.A.; Irrthum, A.; Wehenkel, L.; Geurts, P. Inferring regulatory networks from expression data using tree-based methods. PLoS ONE 2010, 5, e12776. [Google Scholar] [CrossRef]
- Yang, B.; Bao, W. RNDEtree: Regulatory network with differential equation based on flexible neural tree with novel criterion function. IEEE Access 2019, 7, 58255–58263. [Google Scholar] [CrossRef]
- Ye, Y.; Bar-Joseph, Z. Deep learning for inferring gene relationships from single-cell expression data. Proc. Natl. Acad. Sci. USA 2019, 116, 27151–27158. [Google Scholar]
- Yan, Y.; Zhang, X.; Tian, T. Inference method for reconstructing regulatory networks using statistical path-consistency algorithm and mutual information. Lect. Notes Comput. Sci. 2020, 12464, 45–56. [Google Scholar]
- Colombo, D.; Maathuis, M.H. Order-independent constraint-based causal structure learning. J. Mach. Learn Res. 2014, 15, 3741–3782. [Google Scholar]
- Janzing, D.; Balduzzi, D.; Grosse-Wentrup, M.; Schölkopf, B. Quantifying causal influences. Ann. Stat. 2013, 41, 2324–2358. [Google Scholar] [CrossRef]
- Marbach, D.; Prill, R.J.; Schaffter, T.; Mattiussi, C.; Floreano, D.; Stolovitzky, G. Revealing strengths and weaknesses of methods for gene network inference. Proc. Nat. Acad. Sci. USA 2010, 107, 6286–6291. [Google Scholar] [CrossRef] [Green Version]
- Ronen, M.; Rosenberg, R.; Shraiman, B.I. Assigning numbers to the arrows: Parameterizing a gene regulation network by using accurate expression kinetics. Proc. Natl. Acad. Sci. USA 2002, 99, 10555–10560. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Greenfield, A.; Madar, A.; Ostrer, H.; Bonneau, R. DREAM4: Combining genetic and dynamic information to identify biological networks and dynamical models. PLoS ONE 2014, 5, e13397. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cargnello, M.; Roux, P.P. Activation and function of the mapks and their substrates, the mapk-activated protein kinases. Microbiol. Mol. Biol. Rev. 2011, 75, 50–83. [Google Scholar] [CrossRef] [Green Version]
- Tian, T.; Song, J. Mathematical modelling of the MAP kinase pathway based on proteomics dataset. PLoS ONE 2012, 7, e42230. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pozniak, Y.; Balintlahat, N.; Rudolph, J.D.; Lindskog, C.; Katzir, R.; Avivi, C.; Ponten, F.; Ruppin, E.; Barshack, I.; Geiger, T. System-wide clinical proteomics of breast cancer reveals global remodeling of tissue homeostasis. Cell Syst. 2016, 2, 172–184. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kanehisa, M.; Goto, S.; Kawashima, S.; Okuno, Y.; Hattori, M. The kegg resource for deciphering the genome. Nucleic Acids Res. 2004, 32 (Suppl. 1), 277–280. [Google Scholar] [CrossRef] [Green Version]
- Lawrence, R.T.; Perez, E.M.; Hernandez, D.; Miller, C.P.; Haas, K.M.; Irie, H.Y.; Lee, S.I.; Blau, C.A.; Villén, J. The proteomic landscape of triple-negative breast cancer. Cell Rep. 2015, 11, 630–644. [Google Scholar] [CrossRef] [Green Version]
- McLendon, R.; Friedman, A.D.B.; Van Meir, E.G.; Brat, D.J.; Mastrogianakis, G.M.; Olson, J.J.; Mikkelsen, T.; Lehman, N.; Aldape, K. Comprehensive genomic characterization defines human glioblastoma genes and core pathways. Nature 2008, 455, 1061–1068. [Google Scholar]
- Cancer Genome Atlas Research Network. Genomic and epigenomic landscapes of adult de novo acute myeloid leukemia. N. Engl. J. Med. 2013, 368, 2059. [Google Scholar] [CrossRef] [Green Version]
- Kalisch, M.; Maechler, M.; Colombo, D. Causal inference using graphical models with the r package pcalg. J. Stat. Softw. 2012, 47, 1–26. [Google Scholar] [CrossRef] [Green Version]
- Liu, K.; Liu, Z.; Hao, J.; Chen, L.; Zhao, X.M. Identifying dysregulated pathways in cancers from pathway interaction networks. Bmc Bioinform. 2012, 13, 126. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, Y.; Liang, M.; Zhang, Z. Regression analysis of combined gene expression regulation in acute myeloid leukemia. PLoS Comput. Biol. 2014, 10, 1003908. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.; Liao, Q.; Liu, B. A comprehensive review and evaluation of computational methods for identifying protein complexes from protein-sprotein interaction networks. Brief. Bioinform. 2020, 21, 1531–1548. [Google Scholar] [CrossRef] [PubMed]






| Dataset | No. of Genes | No. of Samples | Max Degree | Min Degree | No. of Edges | Density |
|---|---|---|---|---|---|---|
| Dataset 1 | 100 | 100 | 26 | 1 | 169 | 0.03483 |
| Dataset 2 | 100 | 100 | 38 | 1 | 242 | 0.04988 |
| Dataset 3 | 100 | 100 | 16 | 1 | 192 | 0.03957 |
| Dataset 4 | 100 | 100 | 16 | 1 | 207 | 0.04267 |
| Dataset 5 | 100 | 100 | 18 | 1 | 191 | 0.03937 |
| Mean Edge Number | Min Edge Number | Max Edge Number | Variation Ratio | |
|---|---|---|---|---|
| 0.05 | 105 | 95 | 113 | 17.14% |
| 0.03 | 155 | 136 | 161 | 16.13% |
| 0.02 | 197 | 186 | 209 | 11.68% |
| 0.016 | 250 | 234 | 262 | 11.12% |
| Dataset | Edge Ranges | PCI-PMI | PC-Stable | SPCA(MW) | SPCA(APMI) | SPCA(MPMI) |
|---|---|---|---|---|---|---|
| 1 | 232∼294 | 0.6441 | 0.6484 | 0.6475 | 0.6537 | 0.6523 |
| 2 | 227∼296 | 0.5828 | 0.5902 | 0.5978 | 0.5988 | 0.6025 |
| 3 | 219∼263 | 0.6980 | 0.6991 | 0.7021 | 0.7024 | 0.7124 |
| 4 | 236∼279 | 0.6565 | 0.6507 | 0.6611 | 0.6628 | 0.6679 |
| 5 | 243∼297 | 0.6902 | 0.6882 | 0.6914 | 0.6919 | 0.6999 |
| Dataset | Edge Ranges | PCI-PMI | PC-Stable | SPCA(MW) | SPCA(APMI) | SPCA(MPMI) |
|---|---|---|---|---|---|---|
| 1 | 232∼294 | 0.1964 | 0.2084 | 0.2015 | 0.2074 | 0.2083 |
| 2 | 227∼296 | 0.2671 | 0.2738 | 0.2826 | 0.2718 | 0.2898 |
| 3 | 219∼263 | 0.3192 | 0.3208 | 0.3259 | 0.3316 | 0.3470 |
| 4 | 236∼279 | 0.3064 | 0.2919 | 0.3104 | 0.3041 | 0.3200 |
| 5 | 243∼297 | 0.3462 | 0.3296 | 0.3505 | 0.3436 | 0.3614 |
| Dataset | Edge Ranges | PCI-PMI | PC-Stable | SPCA(MW) | SPCA(APMI) | SPCA(MPMI) |
|---|---|---|---|---|---|---|
| 1 | 232∼294 | 0.2325 | 0.2468 | 0.2388 | 0.2458 | 0.2468 |
| 2 | 227∼296 | 0.2671 | 0.2738 | 0.2826 | 0.2718 | 0.2898 |
| 3 | 219∼263 | 0.3530 | 0.3549 | 0.3605 | 0.3669 | 0.3838 |
| 4 | 236∼279 | 0.3462 | 0.3296 | 0.3505 | 0.3436 | 0.3614 |
| 5 | 243∼297 | 0.2964 | 0.2881 | 0.2962 | 0.2946 | 0.3036 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, Y.; Jiang, F.; Zhang, X.; Tian, T. Inference of Molecular Regulatory Systems Using Statistical Path-Consistency Algorithm. Entropy 2022, 24, 693. https://doi.org/10.3390/e24050693
Yan Y, Jiang F, Zhang X, Tian T. Inference of Molecular Regulatory Systems Using Statistical Path-Consistency Algorithm. Entropy. 2022; 24(5):693. https://doi.org/10.3390/e24050693
Chicago/Turabian StyleYan, Yan, Feng Jiang, Xinan Zhang, and Tianhai Tian. 2022. "Inference of Molecular Regulatory Systems Using Statistical Path-Consistency Algorithm" Entropy 24, no. 5: 693. https://doi.org/10.3390/e24050693
APA StyleYan, Y., Jiang, F., Zhang, X., & Tian, T. (2022). Inference of Molecular Regulatory Systems Using Statistical Path-Consistency Algorithm. Entropy, 24(5), 693. https://doi.org/10.3390/e24050693








