Electron Kinetic Entropy across Quasi-Perpendicular Shocks
Abstract
1. Introduction
2. Method
2.1. Data
2.2. Shock Parameter Calculations
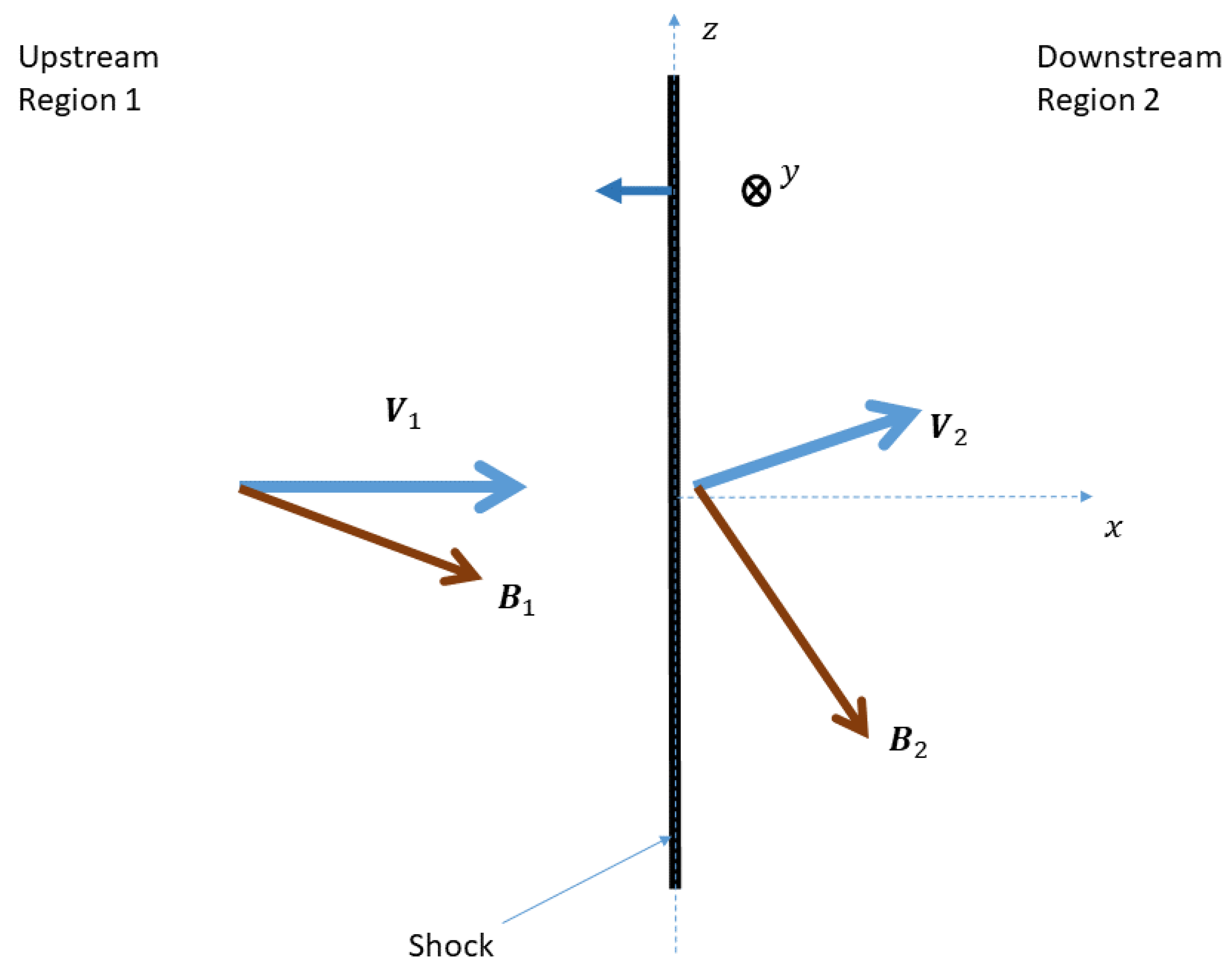
2.2.1. Shock Normal
2.2.2. Upstream Shock Parameters
2.3. Electron Distribution Function Corrections
2.3.1. Spacecraft Potential
2.3.2. Secondary Electrons
2.3.3. Extrapolation to Zero Energy
2.3.4. Density and Temperature
2.4. Electron Entropy Calculation
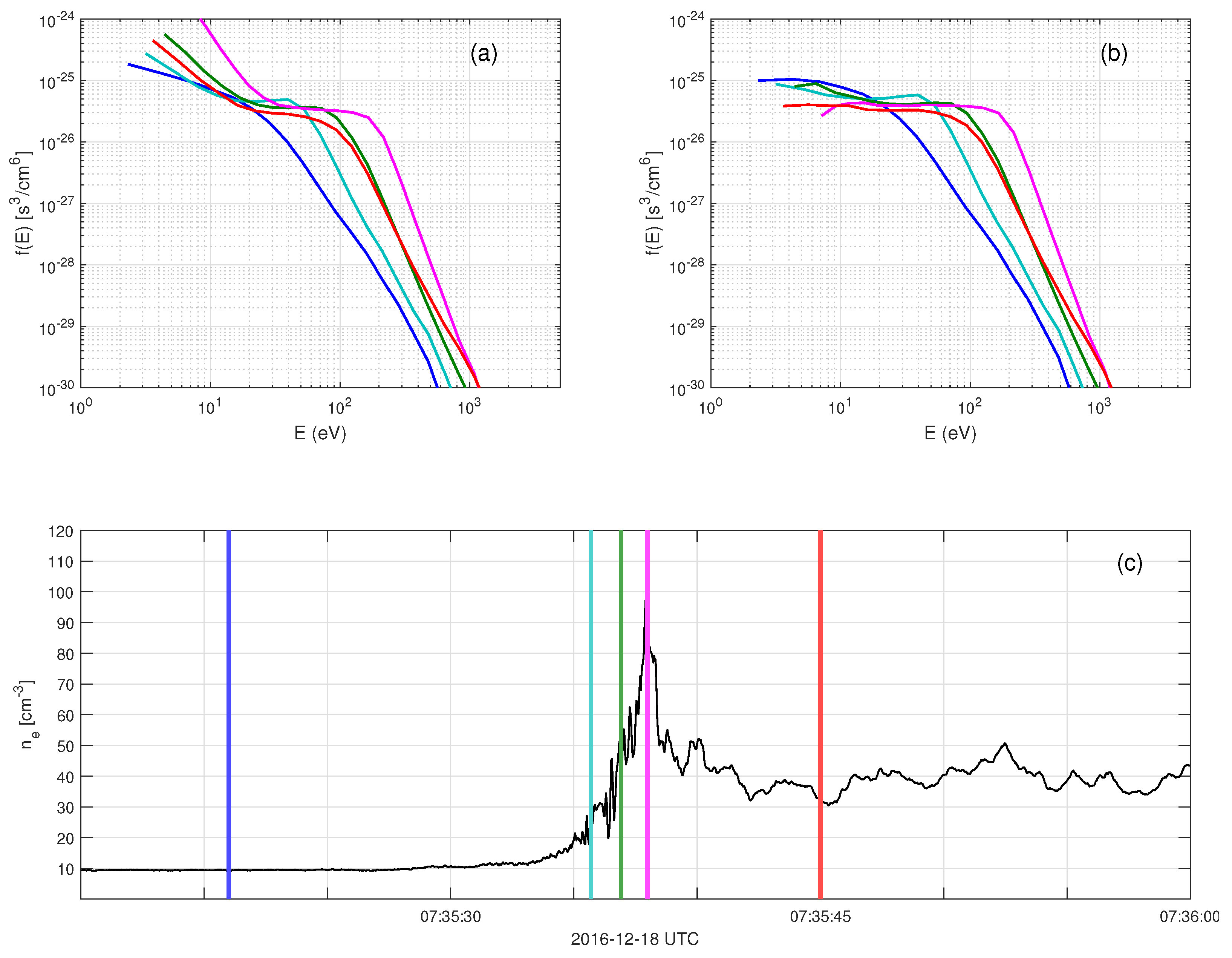
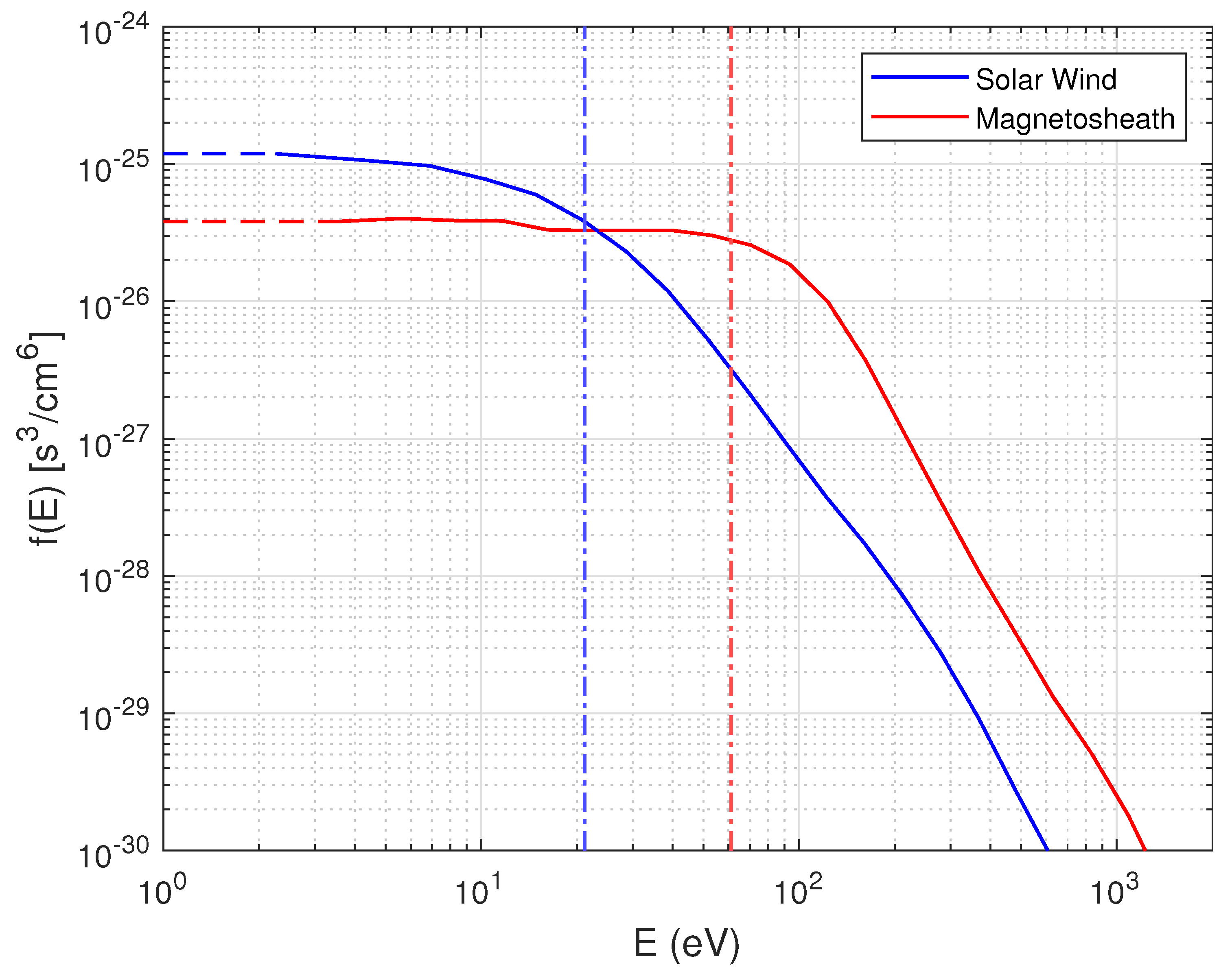
3. Results
4. Discussion
5. Conclusions
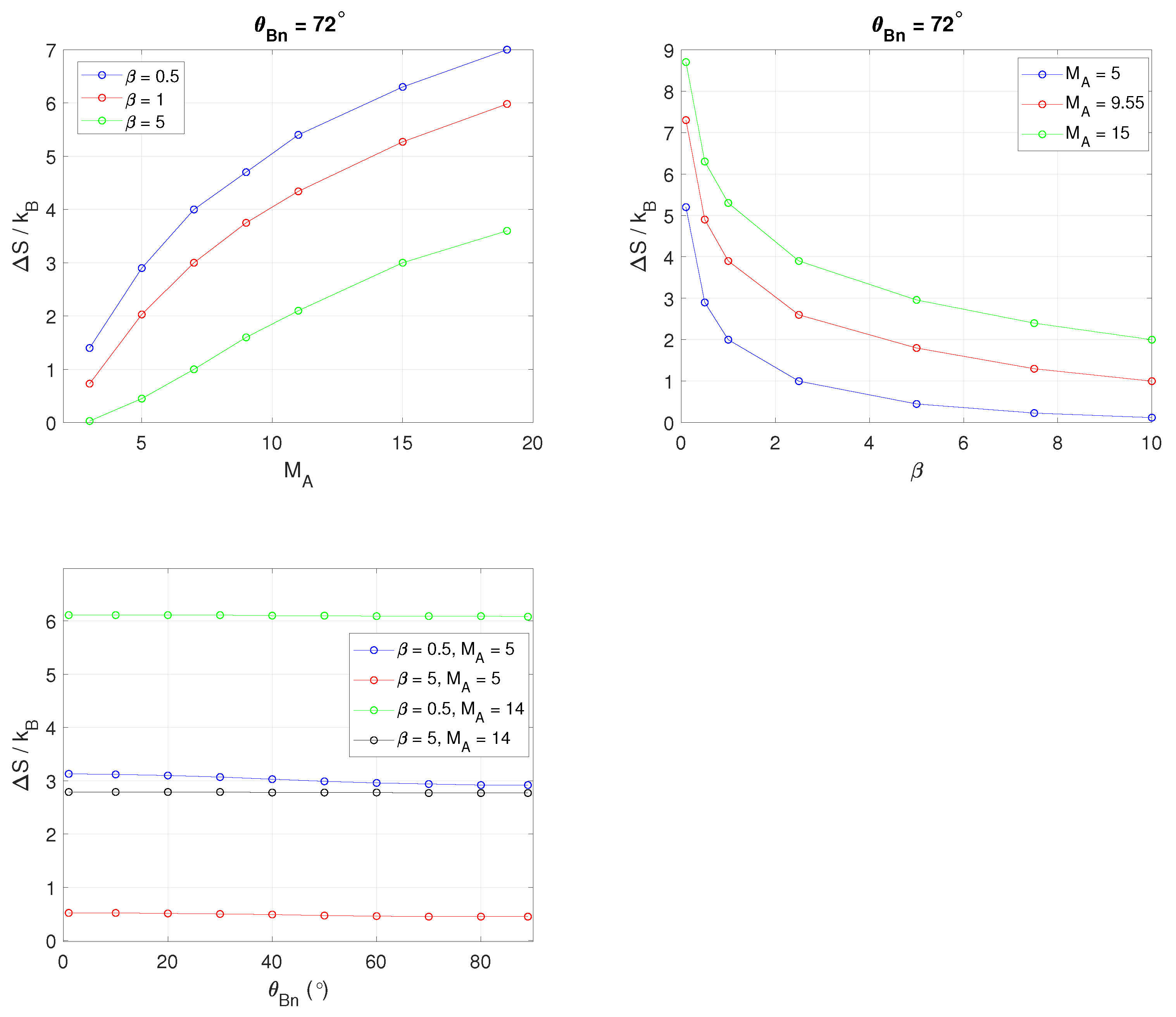
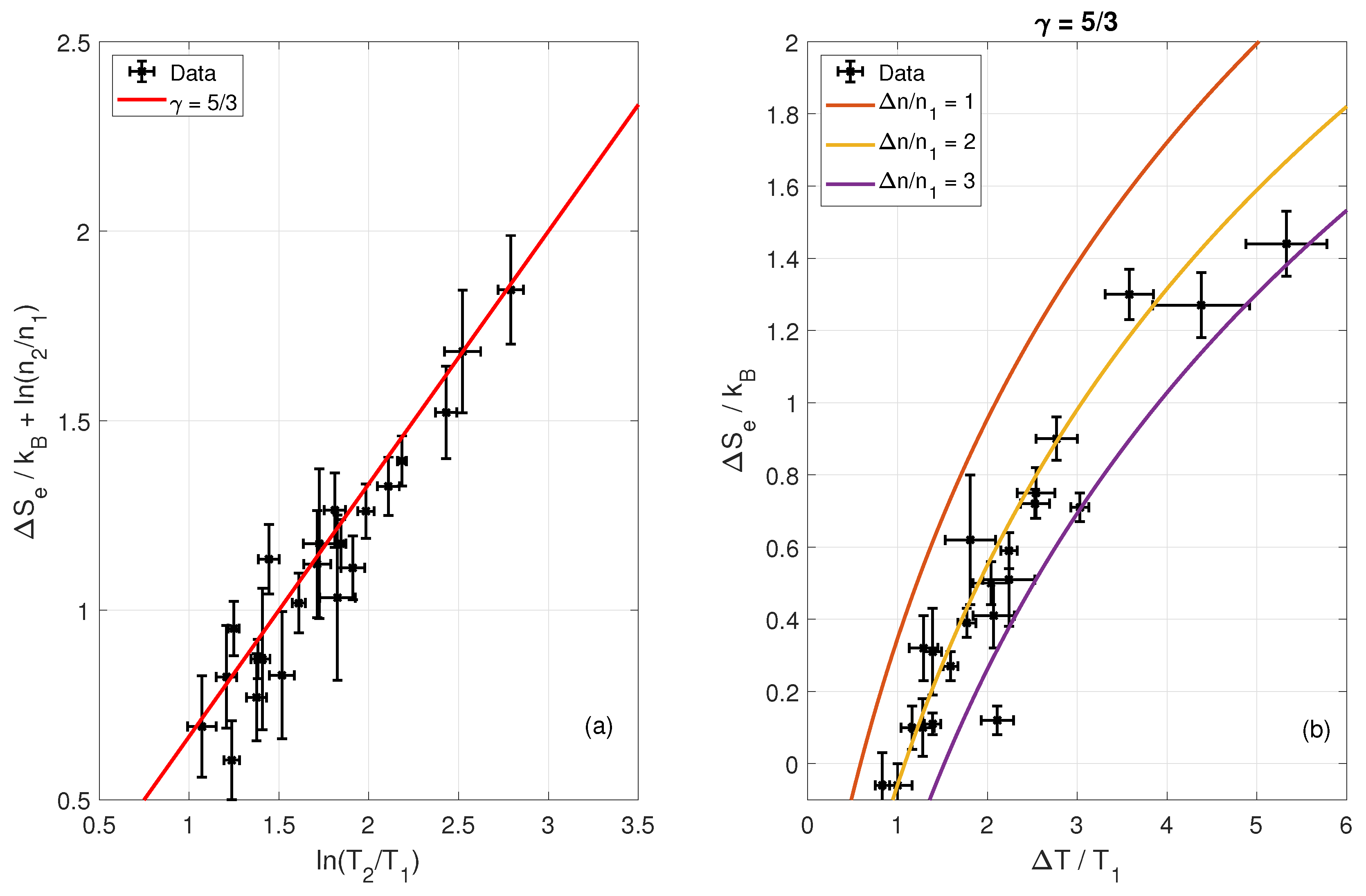
- In total, 20 out of 22 crossings display an increase in the electron kinetic entropy going from the solar wind to the magnetosheath in the range .
- Two crossings display a slight decrease, and , but within error margins, they are still consistent with entropy not decreasing across the shock.
- We observe that displays a strong dependence on the change in electron temperature across the shock, , and the upstream electron plasma beta, . Shocks with high are found to have high . Shocks with small upstream are found to generate more entropy than shocks with large upstream .
- For the parameters, , , , , and , no clear trend is observed, and more crossings need to be analyzed.
- The effective adiabatic index of electrons is calculated for each shock crossing, using the analytical expression relating entropy change to the change in density and temperature, see Equation (13). We find that all shocks have an effective adiabatic index that is in the vicinity of . This suggests the electrons behave similarly to a monatomic gas with three degrees of freedom.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Analytical Calculation of Total Entropy Change across Collisionless Shock
References
- Schwartz, S.J.; Henley, E.; Mitchell, J.; Krasnoselskikh, V. Electron Temperature Gradient Scale at Collisionless Shocks. Phys. Rev. Lett. 2011, 107, 215002. [Google Scholar] [CrossRef] [PubMed]
- See, V.; Cameron, R.F.; Schwartz, S.J. Non-Adiabatic Electron Behaviour Due to Short-Scale Electric Field Structures at Collisionless Shock Waves. Ann. Geophys. 2013, 31, 639–646. [Google Scholar] [CrossRef][Green Version]
- Chen, L.J.; Wang, S.; Wilson, L.B.; Schwartz, S.; Bessho, N.; Moore, T.; Gershman, D.; Giles, B.; Malaspina, D.; Wilder, F.D.; et al. Electron Bulk Acceleration and Thermalization at Earth’s Quasiperpendicular Bow Shock. Phys. Rev. Lett. 2018, 120, 225101. [Google Scholar] [CrossRef] [PubMed]
- Parks, G.K.; Lee, E.; McCarthy, M.; Goldstein, M.; Fu, S.Y.; Cao, J.B.; Canu, P.; Lin, N.; Wilber, M.; Dandouras, I.; et al. Entropy Generation across Earth’s Collisionless Bow Shock. Phys. Rev. Lett. 2012, 108, 061102. [Google Scholar] [CrossRef]
- Liang, H.; Cassak, P.A.; Servidio, S.; Shay, M.A.; Drake, J.F.; Swisdak, M.; Argall, M.R.; Dorelli, J.C.; Scime, E.E.; Matthaeus, W.H.; et al. Decomposition of Plasma Kinetic Entropy into Position and Velocity Space and the Use of Kinetic Entropy in Particle-in-Cell Simulations. Phys. Plasmas 2019, 26, 082903. [Google Scholar] [CrossRef]
- Liang, H.; Barbhuiya, M.H.; Cassak, P.A.; Pezzi, O.; Servidio, S.; Valentini, F.; Zank, G.P. Kinetic Entropy-Based Measures of Distribution Function Non-Maxwellianity: Theory and Simulations. J. Plasma Phys. 2020, 86, 825860502. [Google Scholar] [CrossRef]
- Cassak, P.A. Inside the Black Box: Magnetic Reconnection and the Magnetospheric Multiscale Mission. Space Weather 2016, 14, 186–197. [Google Scholar] [CrossRef]
- Howes, G.G. Laboratory Space Physics: Investigating the Physics of Space Plasmas in the Laboratory. Phys. Plasmas 2018, 25, 055501. [Google Scholar] [CrossRef]
- Anderson, J.D. Modern Compressible Flow: With Historical Perspective; McGraw-Hill: Boston, MA, USA, 2004. [Google Scholar]
- Blundell, S.J.; Blundell, K.M. Concepts in Thermal Physics; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Tidman, D.A.; Krall, N.A. Shock Waves in Collisionless Plasmas; Wiley: Hoboken, NJ, USA, 1971. [Google Scholar]
- Burch, J.; Moore, T.; Torbert, R.; Giles, B. Magnetospheric multiscale overview and science objectives. Space Sci. Rev. 2016, 199, 5–21. [Google Scholar] [CrossRef]
- Krasnoselskikh, V.V.; Lembège, B.; Savoini, P.; Lobzin, V.V. Nonstationarity of Strong Collisionless Quasiperpendicular Shocks: Theory and Full Particle Numerical Simulations. Phys. Plasmas 2002, 9, 1192–1209. [Google Scholar] [CrossRef]
- Lalti, A.; Khotyaintsev, Y.; Graham, D.B.; Vaivads, A.; Steinvall, K.; Russell, C.T. Source of Whistler Precursor Waves At Quasi-Perpendicular Super-Critical Shocks. arXiv 2020, arXiv:2011.10593. [Google Scholar]
- Oka, M.; Terasawa, T.; Seki, Y.; Fujimoto, M.; Kasaba, Y.; Kojima, H.; Shinohara, I.; Matsui, H.; Matsumoto, H.; Saito, Y.; et al. Whistler critical Mach number and electron acceleration at the bow shock: Geotail observation. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Amano, T.; Katou, T.; Kitamura, N.; Oka, M.; Matsumoto, Y.; Hoshino, M.; Saito, Y.; Yokota, S.; Giles, B.L.; Paterson, W.R.; et al. Observational Evidence for Stochastic Shock Drift Acceleration of Electrons at the Earth’s Bow Shock. Phys. Rev. Lett. 2020, 124, 065101. [Google Scholar] [CrossRef] [PubMed]
- Balogh, A.; Treumann, R.A. Basic Equations and Models. In Physics of Collisionless Shocks: Space Plasma Shock Waves; Balogh, A., Treumann, R.A., Eds.; ISSI Scientific Report Series; Springer: New York, NY, USA, 2013; pp. 45–123. [Google Scholar] [CrossRef]
- Raptis, S.; Karlsson, T.; Plaschke, F.; Kullen, A.; Lindqvist, P.A. Classifying Magnetosheath Jets Using MMS: Statistical Properties. J. Geophys. Res. Space Phys. 2020, 125, e2019JA027754. [Google Scholar] [CrossRef]
- Russell, C.; Anderson, B.; Baumjohann, W.; Bromund, K.; Dearborn, D.; Fischer, D.; Le, G.; Leinweber, H.; Leneman, D.; Magnes, W.; et al. The magnetospheric multiscale magnetometers. Space Sci. Rev. 2016, 199, 189–256. [Google Scholar] [CrossRef]
- Pollock, C.; Moore, T.; Jacques, A.; Burch, J.; Gliese, U.; Saito, Y.; Omoto, T.; Avanov, L.; Barrie, A.; Coffey, V.; et al. Fast plasma investigation for magnetospheric multiscale. Space Sci. Rev. 2016, 199, 331–406. [Google Scholar] [CrossRef]
- Lindqvist, P.A.; Olsson, G.; Torbert, R.; King, B.; Granoff, M.; Rau, D.; Needell, G.; Turco, S.; Dors, I.; Beckman, P.; et al. The spin-plane double probe electric field instrument for MMS. Space Sci. Rev. 2016, 199, 137–165. [Google Scholar] [CrossRef]
- Ergun, R.; Tucker, S.; Westfall, J.; Goodrich, K.; Malaspina, D.; Summers, D.; Wallace, J.; Karlsson, M.; Mack, J.; Brennan, N.; et al. The axial double probe and fields signal processing for the MMS mission. Space Sci. Rev. 2016, 199, 167–188. [Google Scholar] [CrossRef]
- King, J.H.; Papitashvili, N.E. Solar Wind Spatial Scales in and Comparisons of Hourly Wind and ACE Plasma and Magnetic Field Data. J. Geophys. Res. Space Phys. 2005, 110. [Google Scholar] [CrossRef]
- Paschmann, G.; Daly, P.W. Analysis Methods for Multi-Spacecraft Data; International Space Science Institute: Bern, Switzerland, 1998. [Google Scholar]
- Gershman, D.J.; Avanov, L.A.; Boardsen, S.A.; Dorelli, J.C.; Gliese, U.; Barrie, A.C.; Schiff, C.; Paterson, W.R.; Torbert, R.B.; Giles, B.L.; et al. Spacecraft and Instrument Photoelectrons Measured by the Dual Electron Spectrometers on MMS. J. Geophys. Res. Space Phys. 2017, 122, 11548–11558. [Google Scholar] [CrossRef]
- Schwartz, S.J.; Thomsen, M.F.; Bame, S.J.; Stansberry, J. Electron Heating and the Potential Jump across Fast Mode Shocks. J. Geophys. Res. Space Phys. 1988, 93, 12923–12931. [Google Scholar] [CrossRef]
- Pudovkin, M.I.; Meister, C.V.; Besser, B.P.; Biernat, H.K. The effective polytropic index in a magnetized plasma. J. Geophys. Res. Space Phys. 1997, 102, 27145–27150. [Google Scholar] [CrossRef]
- Kivelson, M.G.; Russel, C.T. Introduction to Space Physics; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]


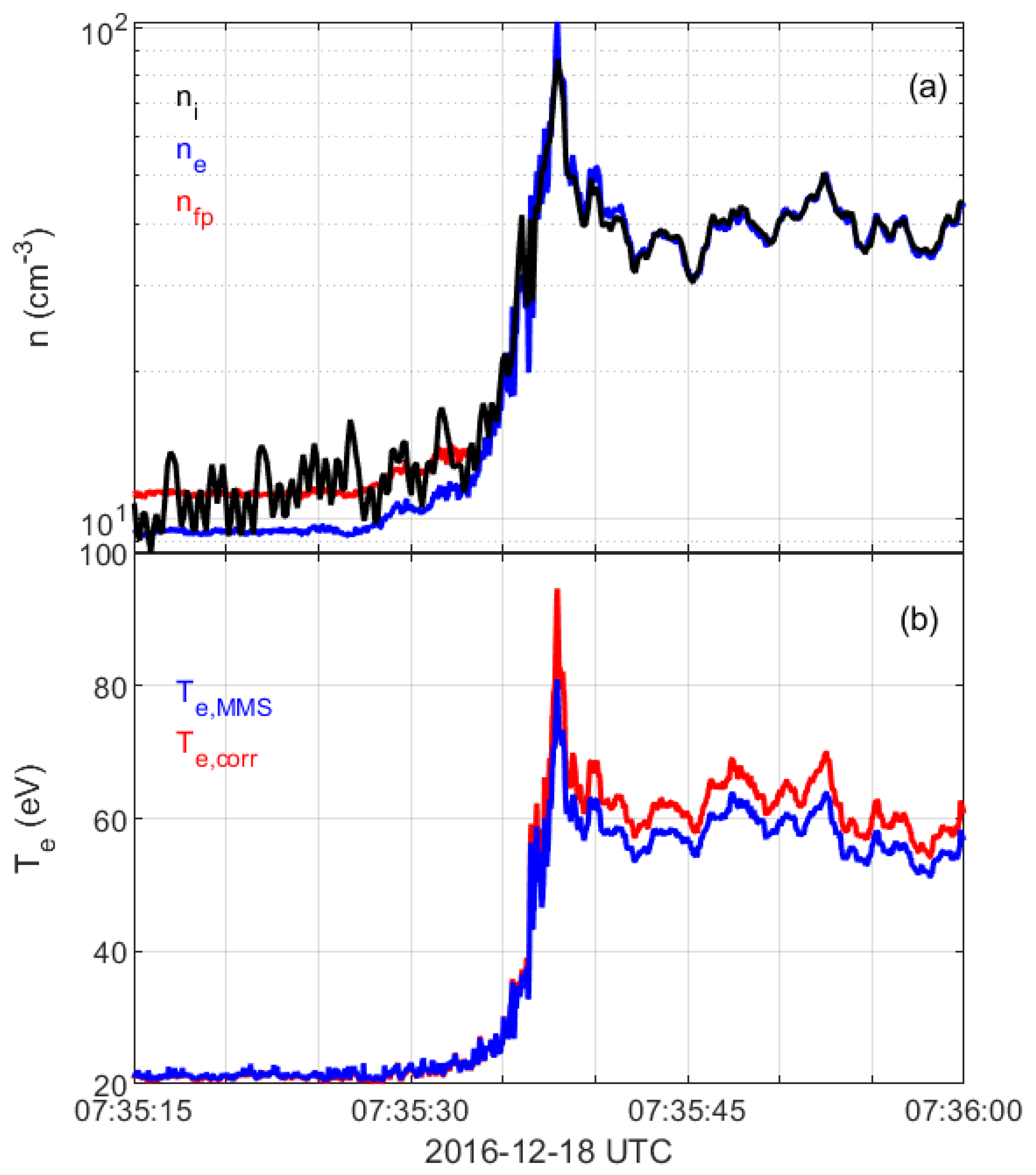


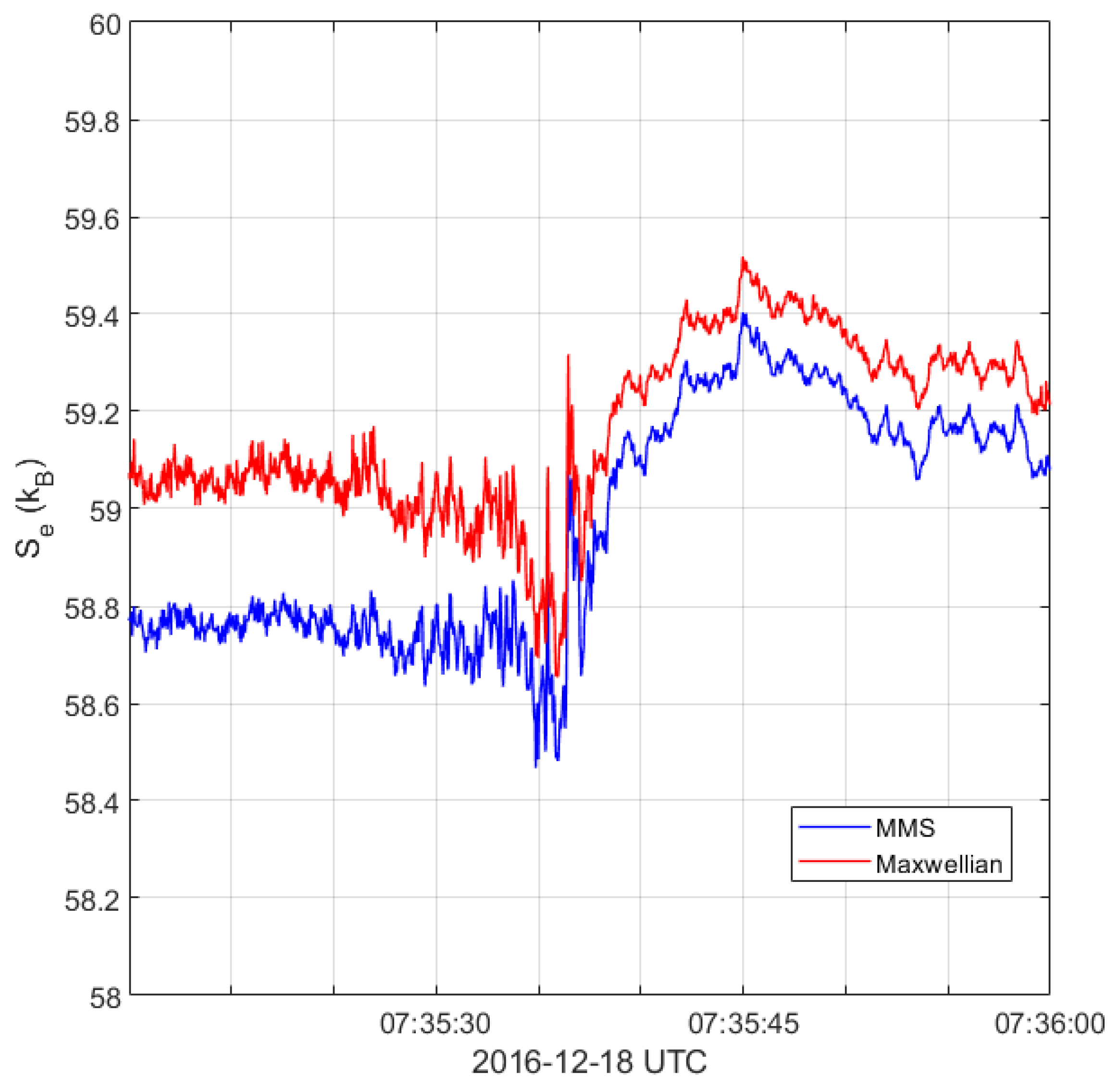
| Crossing | (GSE) | ||||
|---|---|---|---|---|---|
| 1. 2016-11-10 17:10 | 12.4 | 379 | 24.1 | 19.2 | 0.88 0.44 0.18 |
| 2. 2016-11-10 16:59 | 7.0 | 373 | 43.8 | 17.3 | 0.81 0.58 0.07 |
| 3. 2016-12-06 10:55 | 8.0 | 343 | 24.8 | 11.6 | 0.97 0.24 0.02 |
| 4. 2016-12-09 10:29 | 7.9 | 617 | 6.9 | 13.0 | 0.99 0.15 −0.06 |
| 5. 2016-12-18 07:36 | 6.2 | 439 | 11.3 | 21.0 | 0.99 −0.09 0.03 |
| 6. 2017-01-01 09:11 | 3.9 | 486 | 9.2 | 16.5 | 0.99 −0.13 0.07 |
| 7. 2017-01-15 06:43 | 5.0 | 324 | 19.1 | 10.4 | 0.88 0.26 0.39 |
| 8. 2017-01-18 05:39 | 17.1 | 374 | 21.7 | 17.8 | 0.95 −0.32 0.003 |
| 9. 2017-01-31 10:07 | 9.1 | 645 | 11.0 | 16.4 | 0.94 −0.24 0.24 |
| 10. 2017-10-18 04:34 | 3.3 | 404 | 4.7 | 15.8 | 0.80 0.55 0.25 |
| 11. 2017-11-02 04:27 | 9.9 | 317 | 17.0 | 13.2 | 0.73 0.66 0.15 |
| 12. 2017-11-24 23:20 | 9.1 | 396 | 7.3 | 12.0 | 0.86 0.48 0.20 |
| 13. 2017-11-28 18:01 | 5.2 | 405 | 11.3 | 11.8 | 0.99 0.03 0.05 |
| 14. 2017-12-26 22:10 | 3.2 | 460 | 7.1 | 14.9 | 0.94 −0.07 0.33 |
| 15. 2018-01-24 04:05 | 2.4 | 369 | 5.9 | 9.8 | 0.92 −0.35 0.16 |
| 16. 2018-11-16 00:11 | 4.3 | 361 | 7.5 | 9.5 | 0.80 0.57 0.18 |
| 17. 2018-11-18 17:47 | 5.6 | 310 | 17.6 | 7.5 | 0.84 0.43 0.32 |
| 18. 2018-11-27 04:18 | 3.4 | 299 | 16.3 | 11.7 | 0.95 0.22 0.24 |
| 19. 2018-12-16 20:16 | 4.0 | 325 | 11.5 | 12.4 | 0.96 0.14 0.25 |
| 20. 2018-12-25 07:56 | 4.6 | 325 | 9.9 | 12.3 | 0.98 0.16 0.11 |
| 21. 2019-12-17 21:44 | 3.5 | 327 | 9.6 | 12.0 | 0.89 0.15 0.42 |
| 22. 2020-04-17 18:19 | 3.4 | 297 | 8.8 | 8.2 | 0.63 −0.78 −0.04 |
| # | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 6.0 | 7.1 | 1.2 | 63 | 2.5 ± 0.1 | 2.2 ± 0.1 | 0.59 ± 0.05 | 1.64 ± 0.03 |
| 2 | 4.9 | 13.6 | 6.2 | 89 | 2.1 ± 0.4 | 1.0 ± 0.2 | −0.06 ± 0.06 | 1.65 ± 0.11 |
| 3 | 5.2 | 7.9 | 1.8 | 79 | 2.4 ± 0.5 | 2.2 ± 0.3 | 0.51 ± 0.13 | 1.68 ± 0.09 |
| 4 | 6.0 | 9.9 | 0.6 | 85 | 2.9 ± 0.4 | 5.3 ± 0.5 | 1.44 ± 0.09 | 1.66 ± 0.04 |
| 5 | 5.4 | 10.9 | 2.5 | 61 | 2.4 ± 0.2 | 1.8 ± 0.1 | 0.39 ± 0.04 | 1.63 ± 0.04 |
| 6 | 5.1 | 14.7 | 4.0 | 64 | 2.0 ± 0.4 | 1.4 ± 0.1 | 0.31 ± 0.12 | 1.62 ± 0.09 |
| 7 | 5.2 | 10.5 | 3.3 | 89 | 2.0 ± 0.2 | 1.3 ± 0.1 | 0.10 ± 0.08 | 1.68 ± 0.09 |
| 8 | 4.2 | 4.8 | 0.5 | 59 | 1.9 ± 0.5 | 2.5 ± 0.2 | 0.75 ± 0.07 | 1.70 ± 0.05 |
| 9 | 5.4 | 10.8 | 0.9 | 77 | 2.5 ± 0.2 | 4.4 ± 0.5 | 1.27 ± 0.09 | 1.67 ± 0.06 |
| 10 | 4.2 | 7.1 | 2.8 | 59 | 2.6 ± 0.3 | 1.2 ± 0.1 | 0.10 ± 0.06 | 1.56 ± 0.06 |
| 11 | 3.2 | 4.4 | 0.9 | 64 | 1.7 ± 0.2 | 1.6 ± 0.1 | 0.27 ± 0.04 | 1.76 ± 0.05 |
| 12 | 4.0 | 4.6 | 0.4 | 84 | 2.1 ± 0.3 | 3.6 ± 0.3 | 1.30 ± 0.07 | 1.63 ± 0.04 |
| 13 | 7.5 | 11.3 | 2.0 | 75 | 3.4 ± 0.2 | 3.0 ± 0.1 | 0.71 ± 0.04 | 1.64 ± 0.02 |
| 14 | 6.1 | 15.5 | 4.1 | 84 | 2.3 ± 0.4 | 1.8 ± 0.3 | 0.62 ± 0.18 | 1.57 ± 0.09 |
| 15 | 8.8 | 18.2 | 4.1 | 79 | 3.1 ± 0.2 | 2.0 ± 0.2 | 0.50 ± 0.06 | 1.58 ± 0.04 |
| 16 | 5.1 | 8.2 | 1.5 | 83 | 2.4 ± 0.2 | 2.8 ± 0.2 | 0.90 ± 0.06 | 1.63 ± 0.04 |
| 17 | 4.9 | 7.8 | 1.7 | 70 | 2.8 ± 0.3 | 2.1 ± 0.2 | 0.12 ± 0.04 | 1.79 ± 0.06 |
| 18 | 5.1 | 13.7 | 6.7 | 67 | 2.7 ± 0.2 | 0.83 ± 0.1 | −0.06 ± 0.09 | 1.49 ± 0.05 |
| 19 | 6.1 | 11.3 | 3.6 | 72 | 2.3 ± 0.5 | 1.3 ± 0.2 | 0.32 ± 0.09 | 1.55 ± 0.08 |
| 20 | 5.8 | 10.3 | 2.3 | 87 | 2.5 ± 0.2 | 2.5 ± 0.2 | 0.72 ± 0.04 | 1.64 ± 0.03 |
| 21 | 5.3 | 11.7 | 3.8 | 52 | 2.6 ± 0.2 | 1.4 ± 0.1 | 0.11 ± 0.03 | 1.63 ± 0.04 |
| 22 | 5.6 | 10.2 | 2.5 | 65 | 2.7 ± 0.4 | 2.1 ± 0.2 | 0.41 ± 0.09 | 1.65 ± 0.07 |
| # | ||||
|---|---|---|---|---|
| 1 | 0.74 | 0.56 | 739 | 0.59 ± 0.05 |
| 2 | 1.2 | 1.01 | 224 | −0.06 ± 0.06 |
| 3 | 1.9 | 1.6 | 178 | 0.51 ± 0.13 |
| 4 | 44 | 29 | 121 | 1.44 ± 0.09 |
| 5 | 1.05 | 0.85 | 271 | 0.39 ± 0.04 |
| 6 | 1.5 | 1.2 | 121 | 0.31 ± 0.12 |
| 7 | 28 | 34 | 130 | 0.10 ± 0.08 |
| 8 | 0.44 | 0.34 | 716 | 0.75 ± 0.07 |
| 9 | 2.2 | 2.3 | 192 | 1.27 ± 0.09 |
| 10 | 0.42 | 0.33 | 117 | 0.10 ± 0.06 |
| 11 | 0.47 | 0.37 | 143 | 0.27 ± 0.04 |
| 12 | 2.0 | 2.7 | 482 | 1.30 ± 0.07 |
| 13 | 2.1 | 1.8 | 294 | 0.71 ± 0.04 |
| 14 | 7.2 | 7.2 | 82 | 0.62 ± 0.18 |
| 15 | 4.4 | 4.1 | 261 | 0.50 ± 0.06 |
| 16 | 3.4 | 2.6 | 203 | 0.90 ± 0.06 |
| 17 | 1.06 | 0.82 | 293 | 0.12 ± 0.04 |
| 18 | 1.6 | 1.4 | 194 | −0.06 ± 0.09 |
| 19 | 1.7 | 1.5 | 441 | 0.32 ± 0.09 |
| 20 | 8.6 | 8.8 | 302 | 0.72 ± 0.04 |
| 21 | 0.88 | 0.72 | 171 | 0.11 ± 0.03 |
| 22 | 1.12 | 0.93 | 231 | 0.41 ± 0.09 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lindberg, M.; Vaivads, A.; Raptis, S.; Lindqvist, P.-A.; Giles, B.L.; Gershman, D.J. Electron Kinetic Entropy across Quasi-Perpendicular Shocks. Entropy 2022, 24, 745. https://doi.org/10.3390/e24060745
Lindberg M, Vaivads A, Raptis S, Lindqvist P-A, Giles BL, Gershman DJ. Electron Kinetic Entropy across Quasi-Perpendicular Shocks. Entropy. 2022; 24(6):745. https://doi.org/10.3390/e24060745
Chicago/Turabian StyleLindberg, Martin, Andris Vaivads, Savvas Raptis, Per-Arne Lindqvist, Barbara L. Giles, and Daniel Jonathan Gershman. 2022. "Electron Kinetic Entropy across Quasi-Perpendicular Shocks" Entropy 24, no. 6: 745. https://doi.org/10.3390/e24060745
APA StyleLindberg, M., Vaivads, A., Raptis, S., Lindqvist, P.-A., Giles, B. L., & Gershman, D. J. (2022). Electron Kinetic Entropy across Quasi-Perpendicular Shocks. Entropy, 24(6), 745. https://doi.org/10.3390/e24060745







