An Improved Incipient Fault Diagnosis Method of Bearing Damage Based on Hierarchical Multi-Scale Reverse Dispersion Entropy
Abstract
:1. Introduction
- (1)
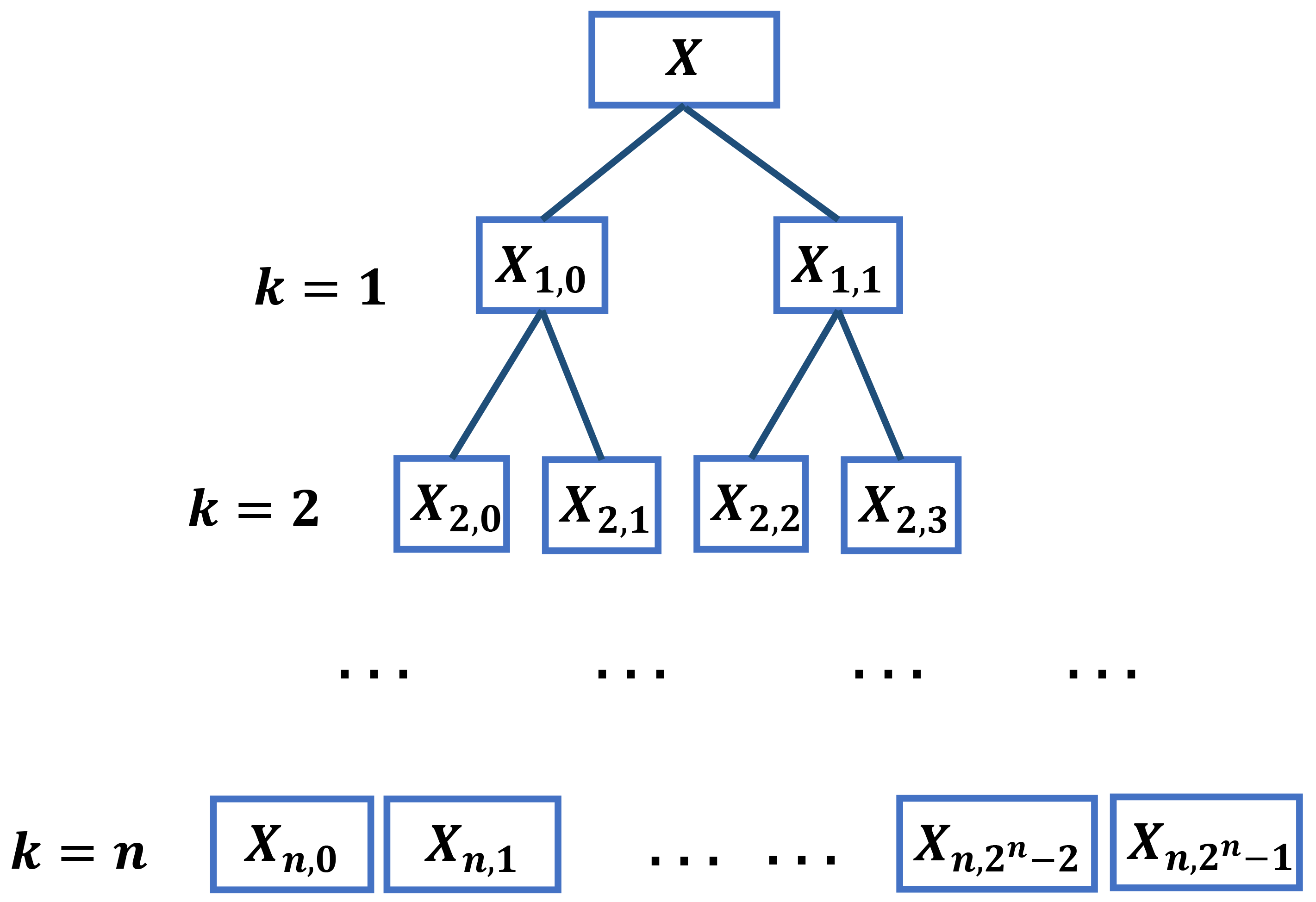
- A new fault extraction approach, named HMRDE, based on MRDE is proposed to extract obvious difference features with various frequency ranges. It introduces hierarchical thought to MRDE and uses hierarchical nodes to analyze the frequency difference features of incipient fault signals for the first time.
- (2)
- HMRDE enhances the disorder difference of each state by calculating the change deviation with a high-frequency operator and reflects this difference by entropy values of hierarchical nodes obviously, which helps classifiers greatly in recognizing incipient faults.
2. Aim Formulation and Methods
2.1. Aim Formulation
2.2. Methods
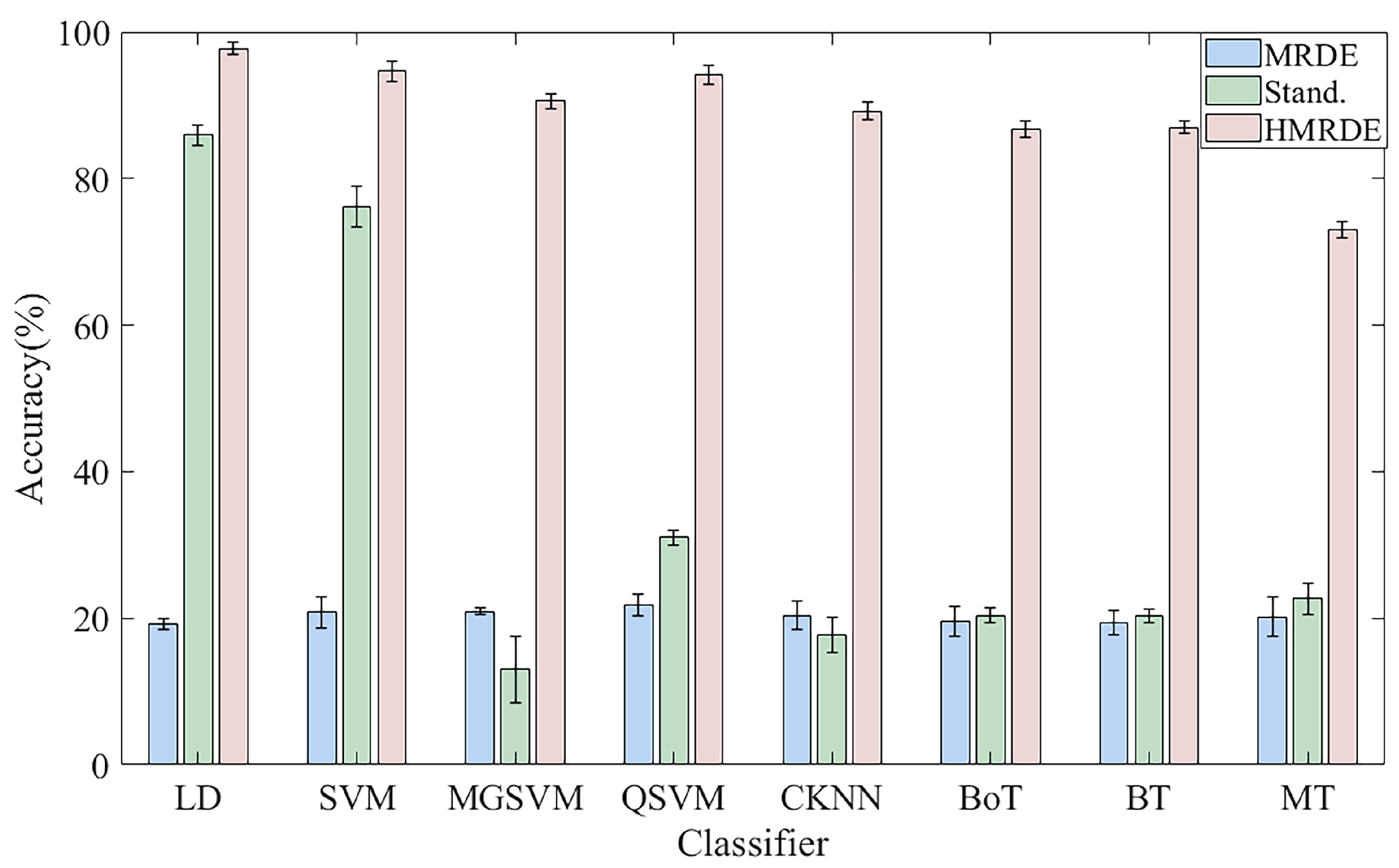
3. Results
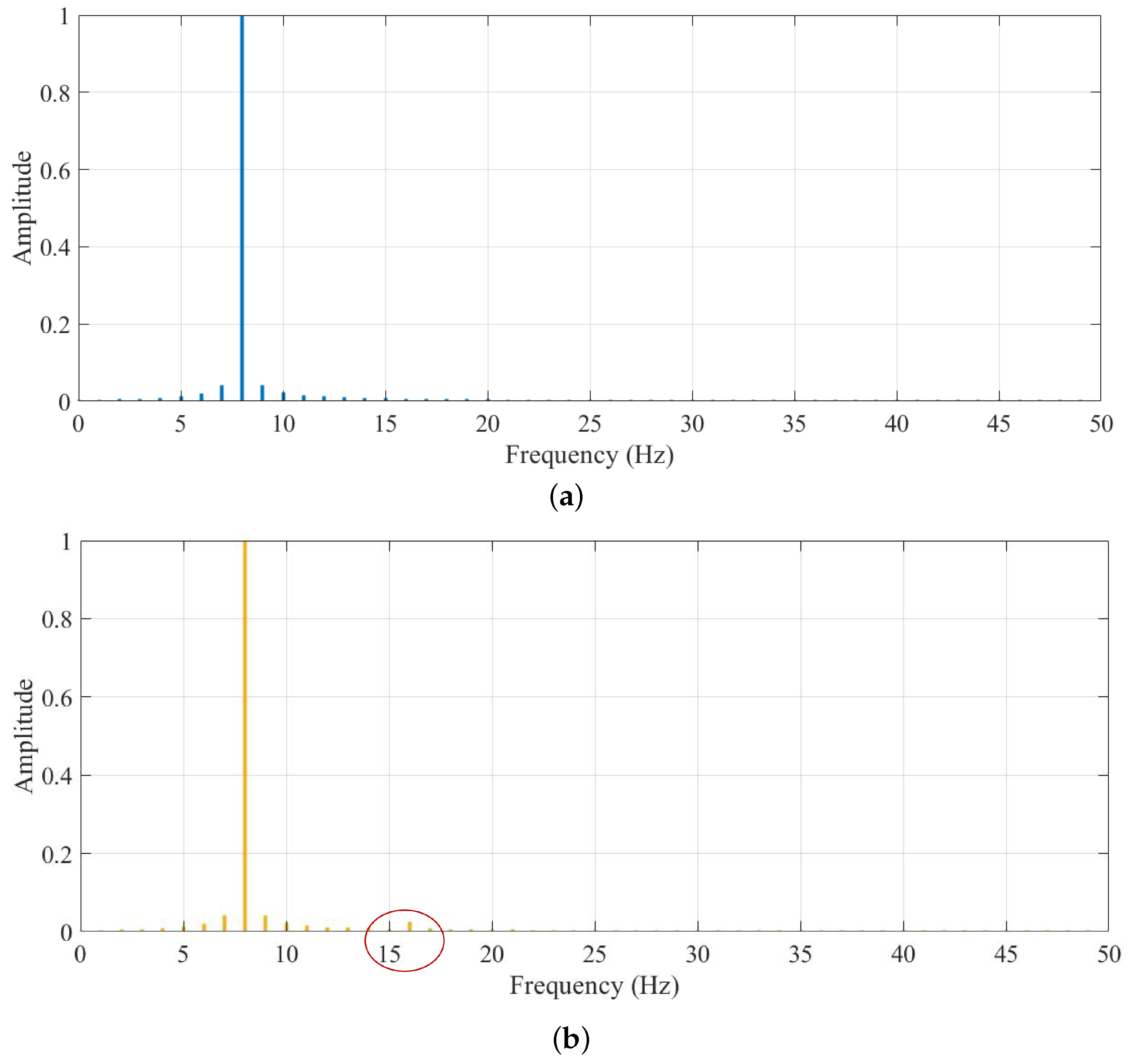
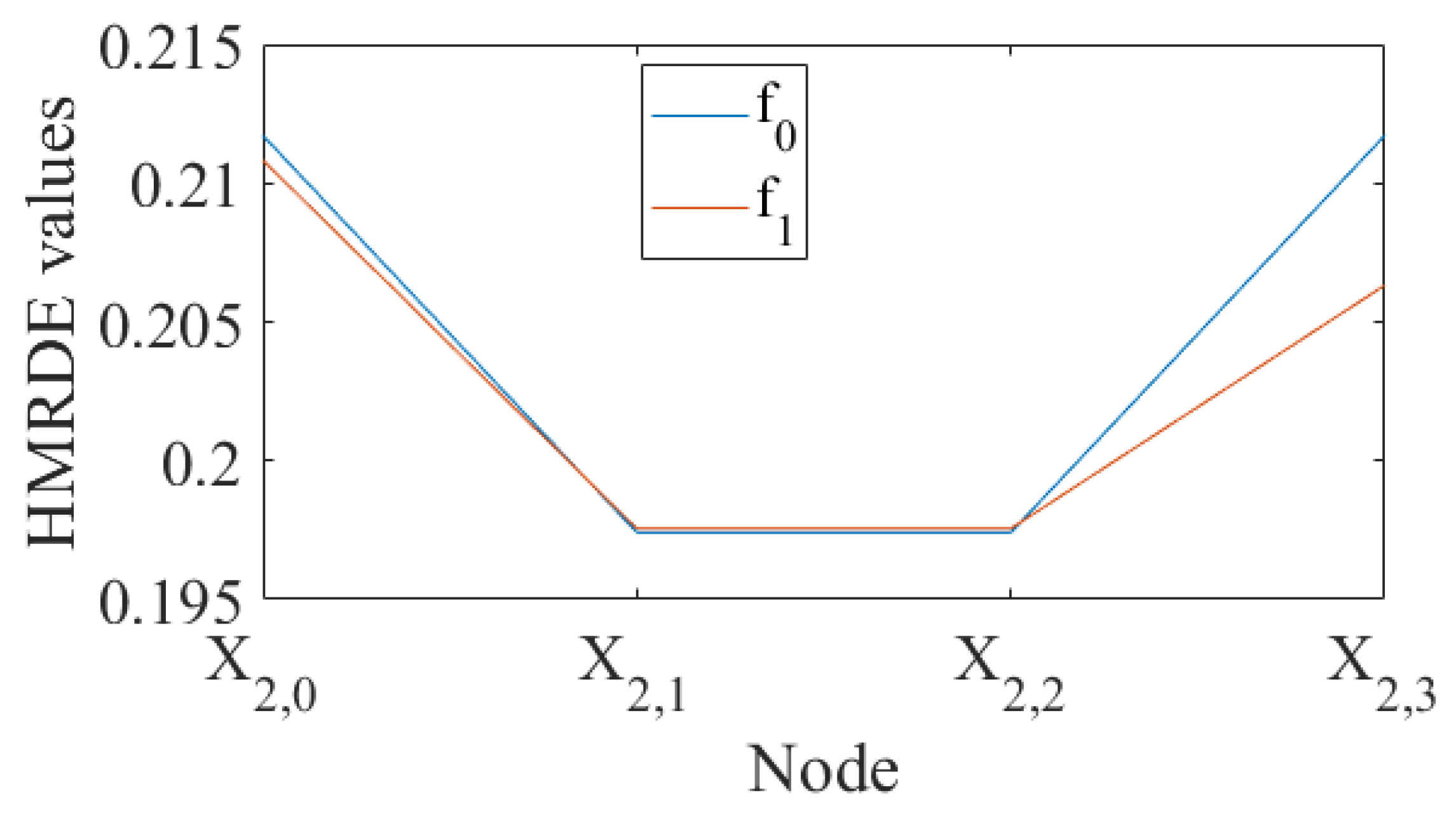
3.1. Case 1: Numeral Example
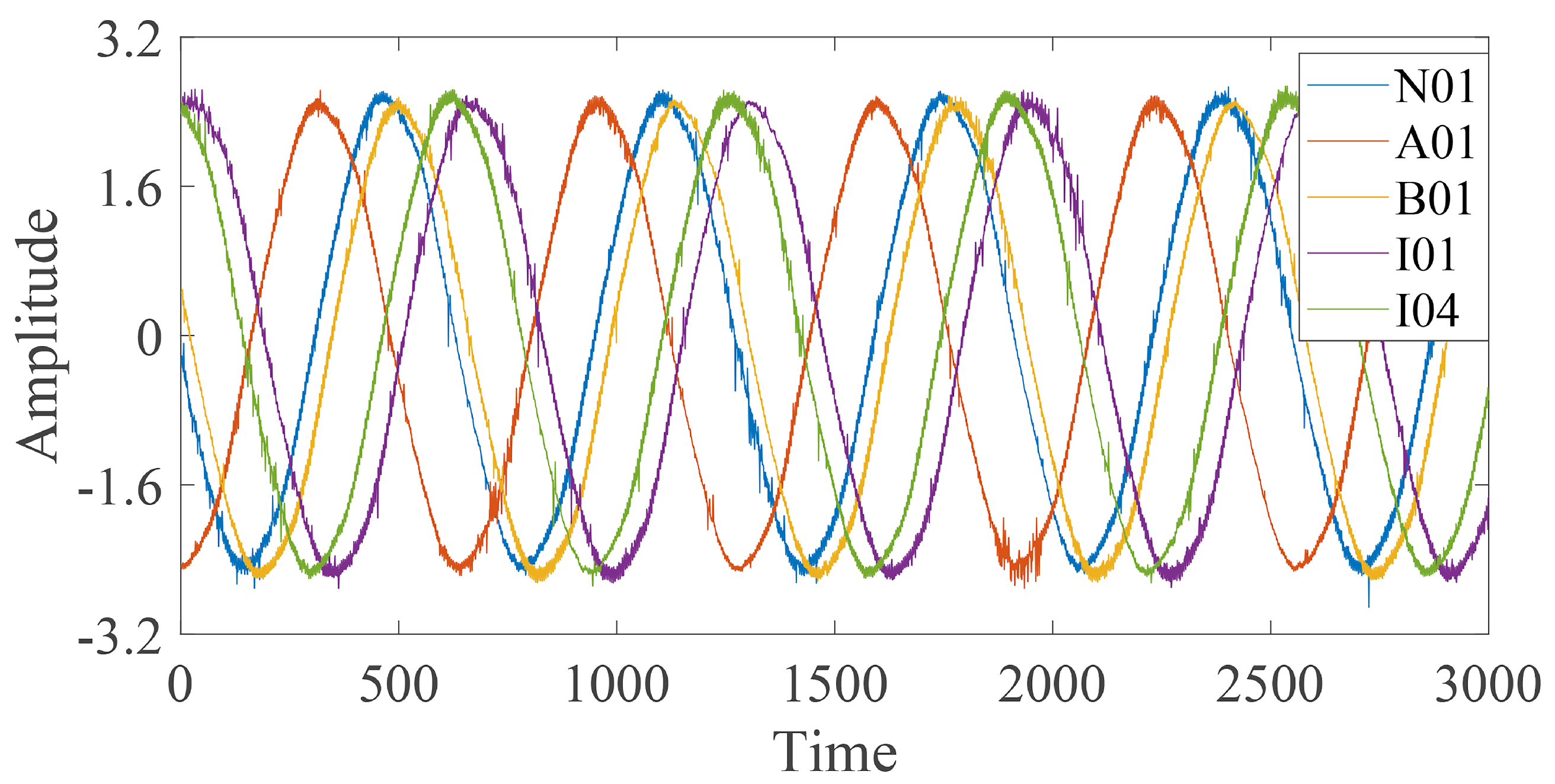
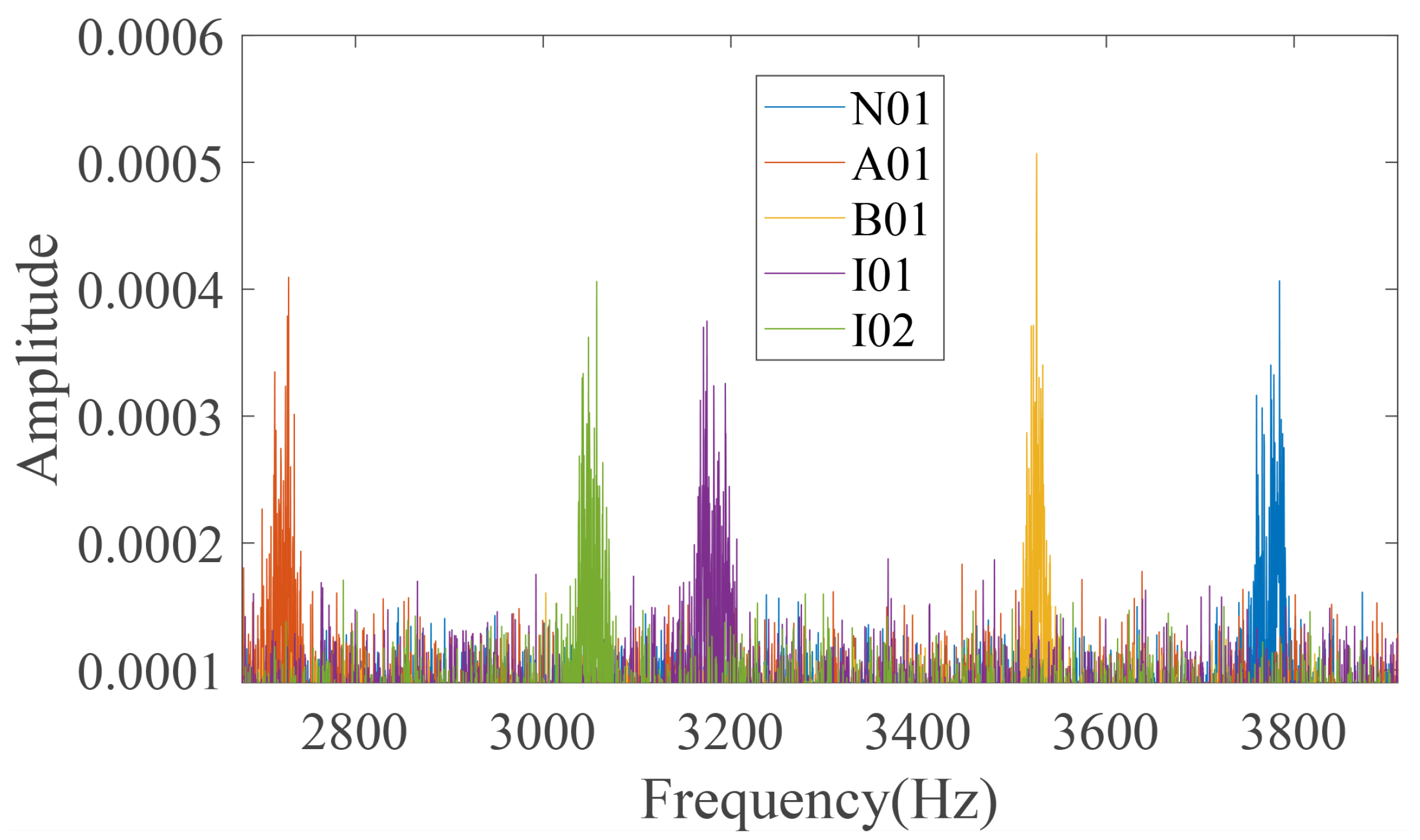
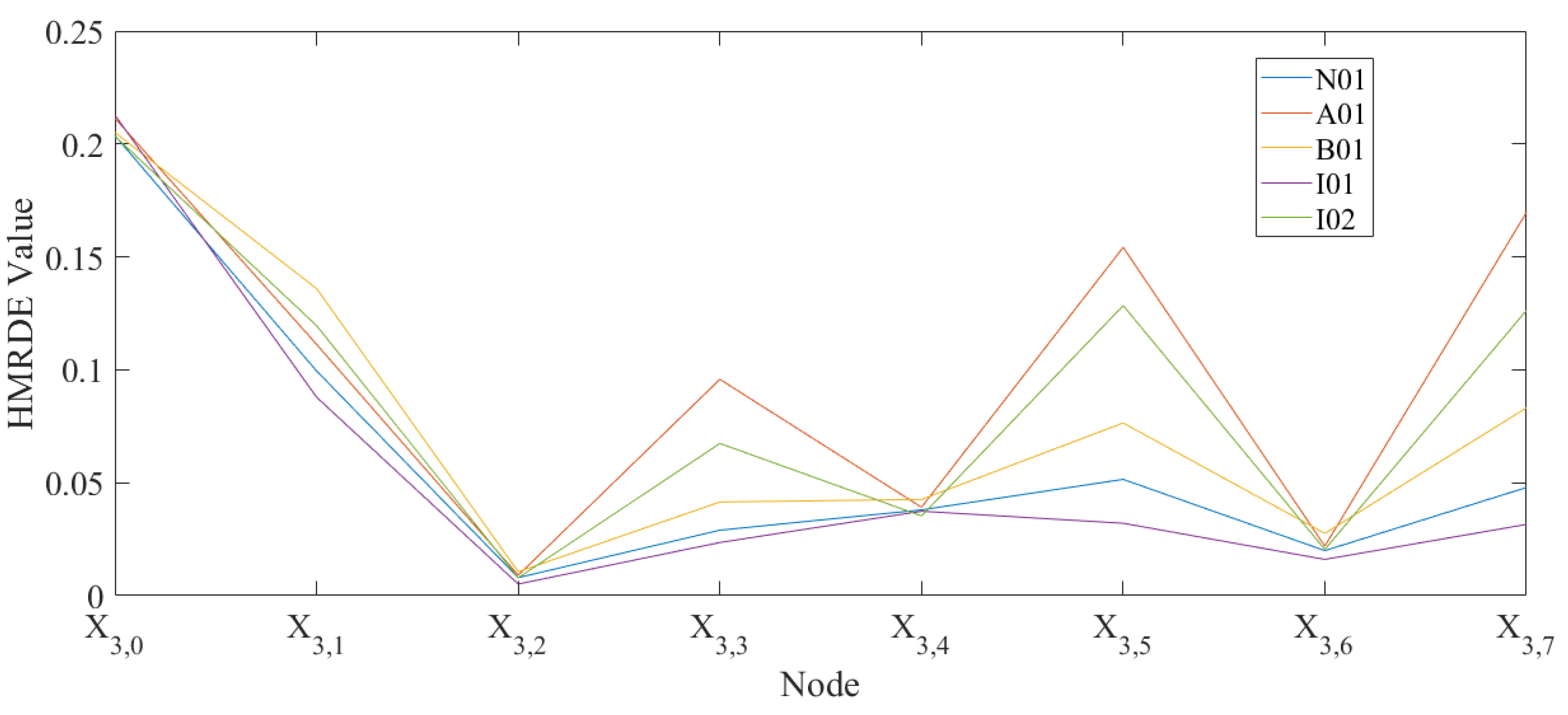
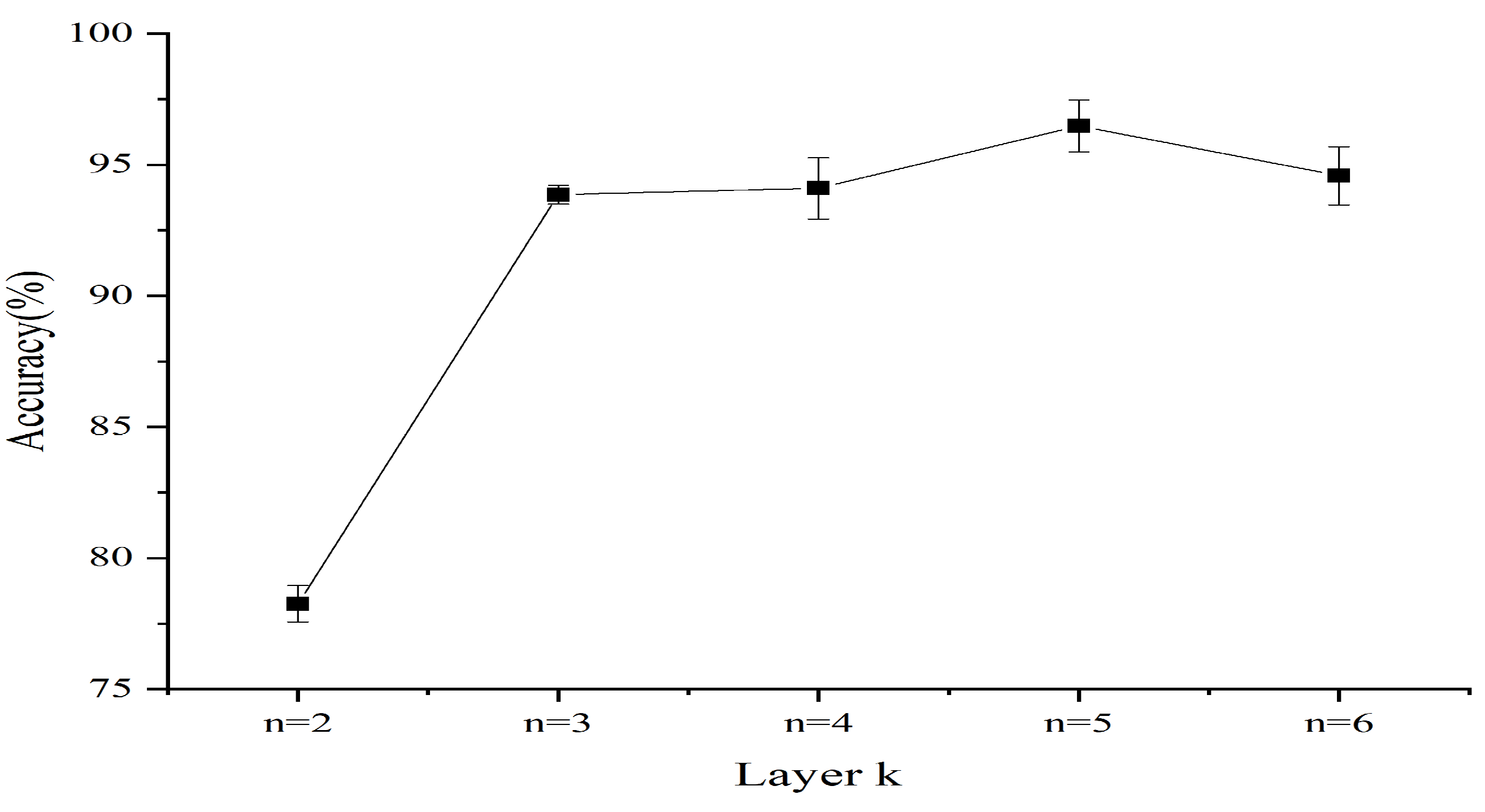
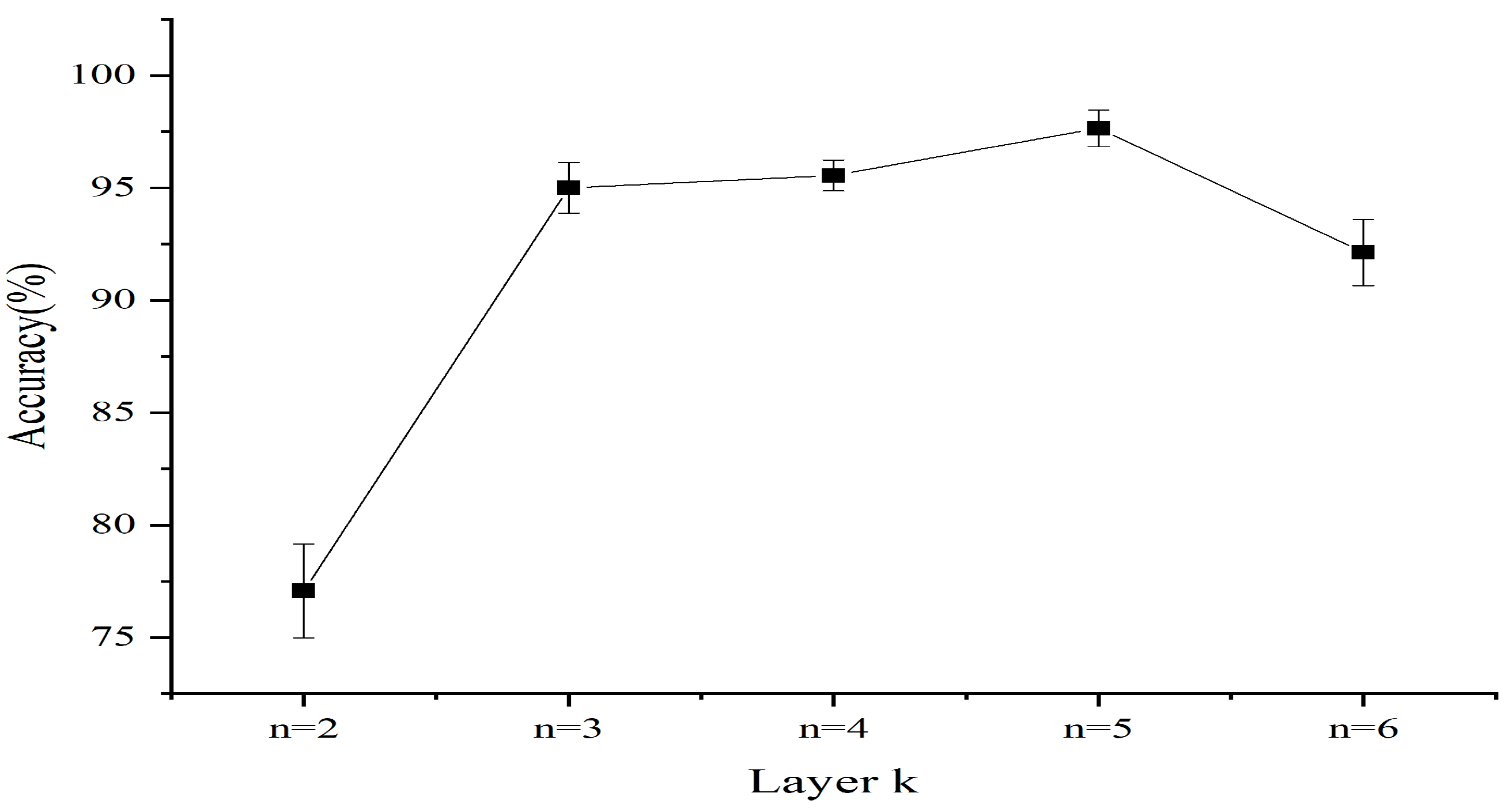
3.2. Case 2: Dataset Provided by Padborn University in Germany
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhao, Q.; Zhou, D. Incipient fault detection and isolation in closed-loop systems. In Proceedings of the 39th Chinese Process Control Conference, Shenyang, China, 27–29 July 2020; pp. 636–641. [Google Scholar]
- Russell, E.; Chiang, L.H.; Braatz, R.D. Data-Driven Methods for Fault Detection and Diagnosis in Chemical Processes; Springer: London, UK, 2000; p. 101. [Google Scholar]
- Zhang, M.; Li, X.; Wang, R. Incipient fault diagnosis of batch process based on deep time series feature extraction. Arab. J. Sci. Eng. 2021, 46, 10125–10136. [Google Scholar] [CrossRef]
- Zhao, H.; Sun, S.; Jin, B. Sequential fault diagnosis based on LSTM neural network. IEEE Access 2018, 6, 12929–12939. [Google Scholar] [CrossRef]
- Yang, J.; Guo, Y.; Zhao, W. Long short-term memory neural network based fault detection and isolation for electro-mechanical actuators. Neurocomputing 2019, 360, 85–96. [Google Scholar] [CrossRef]
- Ivar, Z.; Aimar, K.; Ergo, R.; Anni, M.; Madis, J.; Toomas, T.; Oleg, A.; dC Sergio, R.; Taavo, T. Enhanced efficiency of nitritating-anammox sequencing batch reactor achieved at low decrease rates of oxidation–reduction potential. Environ. Eng. Sci. 2019, 36, 350–360. [Google Scholar]
- Yun, K.; Chong, Y.; Enzhe, S.; Liping, Y.; Quan, D. Fault diagnosis method of diesel engine injector based on hierarchical weighted permutation entropy. In Proceedings of the 2021 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Glasgow, UK, 17–20 May 2021; pp. 1–6. [Google Scholar]
- Xingwei, Y.; Dawei, L.; Jun, Z.; Jianwei, W. Radar jamming detection based on approximate entropy and moving-cut approximate entropy. In Proceedings of the IET International Conference on Information Science and Control Engineering 2012 (ICISCE 2012), Shenzhen, China, 7–9 December 2012; pp. 1–6. [Google Scholar]
- Zhang, H.; He, S. Analysis and comparison of permutation entropy, approximate entropy and sample Entropy. In Proceedings of the 2018 International Symposium on Computer, Consumer and Control (IS3C), Taichung, Taiwan, 6–8 December 2018; pp. 209–212. [Google Scholar]
- Liu, H.; Xie, H.; He, W.; Wang, Z. Characterization and classification of EEG sleep stage based on fuzzy entropy detection and isolation for electro-mechanical actuators. J. Data Acquis. Process. 2010, 25, 484–489. [Google Scholar]
- Zhao, J.; Liu, Y. Approximate entropy based on hilbert transform and its application in bearing fault diagnosis. In Proceedings of the 2018 International Conference on Sensing, Diagnostics, Prognostics, and Control (SDPC), Xi’an, China, 15–17 August 2018; pp. 41–44. [Google Scholar]
- Li, X.; Dai, K.; Wang, Z.; Han, W. Lithium-ion batteries fault diagnostic for electric vehicles using sample entropy analysis method. J. Energy Storage 2020, 27, 101121. [Google Scholar] [CrossRef]
- Zhou, R.; Wang, X.; Wan, J.; Xiong, N. Edm-Fuzzy: An Euclidean Distance Based Multiscale Fuzzy Entropy Technology For Diagnosing Faults Of Industrial Systems. IEEE Trans. Ind. Inform. 2021, 17, 4046–4054. [Google Scholar] [CrossRef]
- Gituku, E.W.; Kimotho, J.K.; Njiri, J.G. Cross-domain bearing fault diagnosis with refined composite multiscale fuzzy entropy and the self organizing fuzzy classifier. Eng. Rep. 2020, 3, 12307. [Google Scholar] [CrossRef]
- An, X.; Pan, L. Bearing fault diagnosis of a wind turbine based on variational mode decomposition and permutation entropy. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2017, 231, 200–206. [Google Scholar] [CrossRef]
- Fadlallah, B.; Chen, B.; Keil, A.; Príncipe, J. Weighted-permutation entropy: A complexity measure for time series incorporating amplitude information. Phys. Rev. E 2013, 23, 022911. [Google Scholar] [CrossRef] [Green Version]
- Rostaghi, M.; Azami, H. Dispersion entropy: A measure for time-series analysis. IEEE Signal Process. Lett. 2016, 23, 610–614. [Google Scholar] [CrossRef]
- Bandt, C. A new kind of permutation entropy used to classify sleep stages from invisible EEG microstructure. Entropy 2017, 19, 197. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Gao, X.; Wang, L. Reverse dispersion entropy: A new complexity measure for sensor signal. Sensors 2019, 19, 5203. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shenghan, Z.; Silin, Q.; Chang, W.; Yiyong, X.; Yang, C. A novel bearing multi-fault diagnosis approach based on weighted permutation entropy and an improved SVM ensemble classifier. Sensors 2018, 18, 1934. [Google Scholar]
- Li, R.; Ran, C.; Luo, J.; Feng, S.; Zhang, B. Rolling bearing fault diagnosis method based on dispersion entropy and SVM. In Proceedings of the 2019 International Conference on Sensing, Diagnostics, Prognostics, and Control (SDPC), Beijing, China, 15–17 August 2019; pp. 596–600. [Google Scholar]
- Songrong, L.; Wenxian, Y.; Youxin, L. Fault diagnosis of a rolling bearing based on adaptive Sparest narrow-band decomposition and refined composite multi-scale dispersion entropy. Entropy 2020, 22, 375. [Google Scholar]
- Jiao, S.; Geng, B.; Li, Y.; Zhang, Q.; Wang, Q. Fluctuation-based reverse dispersion entropy and its applications to signal classification. Appl. Acoust. 2021, 175, 107857. [Google Scholar] [CrossRef]
- Wang, H.; Sun, W.; He, L.; Zhou, J. Intelligent fault diagnosis method for gear transmission systems based on improved multi-scale reverse dispersion entropy and swarm decomposition. IEEE Trans. Instrum. Meas. 2022, 71, 1–13. [Google Scholar] [CrossRef]
- Lessmeier, C.; Kimotho, J.K.; Zimmer, D.; Sextro, W. Condition monitoring of bearing damage in electromechanical drive systems by using motor current signals of electric motors: A benchmark data set for data-driven classification. In Proceedings of the European Conference of the Prognostics and Health Management Society, Bilbao, Spain, 5–8 July 2016; pp. 1–18. [Google Scholar]
- Li, Y.; Li, G.; Yang, Y.; Liang, X.; Xu, M. A fault diagnosis scheme for planetary gearboxes using adaptive multi-scale morphology filter and modified hierarchical permutation entropy. Mech. Syst. Signal Process. 2018, 105, 319–337. [Google Scholar] [CrossRef]
- KAt-DataCenter Website of the Chair of Design and Drive Technology, Paderborn University, Germany. 2016. Available online: http://mb.uni-paderborn.de/kat/datacenter (accessed on 12 December 2021).
- Yang, J.; Yang, Y.; Xie, G. Diagnosis of incipient fault based on sliding-scale resampling strategy and improved deep autoencoder. IEEE Sens. J. 2020, 20, 8336–8348. [Google Scholar] [CrossRef]
- Liu, A.; Yang, Z.; Li, H.; Wang, C.; Liu, X. Intelligent diagnosis of rolling element bearing based on refined composite multiscale reverse dispersion entropy and random forest. Sensors 2022, 22, 2046. [Google Scholar] [CrossRef]
- Li, Z.; Cui, Y.; Li, L.; Chen, R.; Dong, L.; Du, J. Hierarchical amplitude-aware permutation entropy-based fault feature extraction method for rolling bearings. Entropy 2022, 24, 310. [Google Scholar] [CrossRef] [PubMed]
- Ying, W.; Tong, J.; Dong, Z.; Pan, H.; Liu, Q.; Zheng, J. Composite multivariate multi-Scale permutation entropy and laplacian score based fault diagnosis of rolling bearing. Entropy 2022, 24, 160. [Google Scholar] [CrossRef] [PubMed]







| Damage Level | Assigned Percentage | Limits for Bearing |
|---|---|---|
| 1 | 0–2% | ≤2 mm |
| 2 | 2–5% | >2 mm |
| 3 | 5–15% | >4.5 mm |
| 4 | 15–35% | >13.5 mm |
| 5 | >35% | >31.5 mm |
| Code n | Component m | Combination | Characteristic | Level |
|---|---|---|---|---|
| N01 | – | – | – | – |
| A01 | OR | R | distributed | 1 |
| B01 | OR+IR | M | distributed | 1 |
| I01 | IR | M | single point | 1 |
| I02 | IR | R | single point | 1 |
| Condition Number | Rotational Speed (rpm) | Load Torque (Nm) | Radial Force (N) | Name of Setting |
|---|---|---|---|---|
| 1 | 1500 | 0.7 | 1000 | N15M07F10 |
| 2 | 900 | 0.7 | 1000 | N09M07F10 |
| 3 | 1500 | 0.1 | 1000 | N15M01F10 |
| 4 | 1500 | 0.7 | 400 | N15M07F04 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xing, J.; Xu, J. An Improved Incipient Fault Diagnosis Method of Bearing Damage Based on Hierarchical Multi-Scale Reverse Dispersion Entropy. Entropy 2022, 24, 770. https://doi.org/10.3390/e24060770
Xing J, Xu J. An Improved Incipient Fault Diagnosis Method of Bearing Damage Based on Hierarchical Multi-Scale Reverse Dispersion Entropy. Entropy. 2022; 24(6):770. https://doi.org/10.3390/e24060770
Chicago/Turabian StyleXing, Jiaqi, and Jinxue Xu. 2022. "An Improved Incipient Fault Diagnosis Method of Bearing Damage Based on Hierarchical Multi-Scale Reverse Dispersion Entropy" Entropy 24, no. 6: 770. https://doi.org/10.3390/e24060770







