Maximum Power Point Tracking Control for Non-Gaussian Wind Energy Conversion System by Using Survival Information Potential
Abstract
:1. Introduction
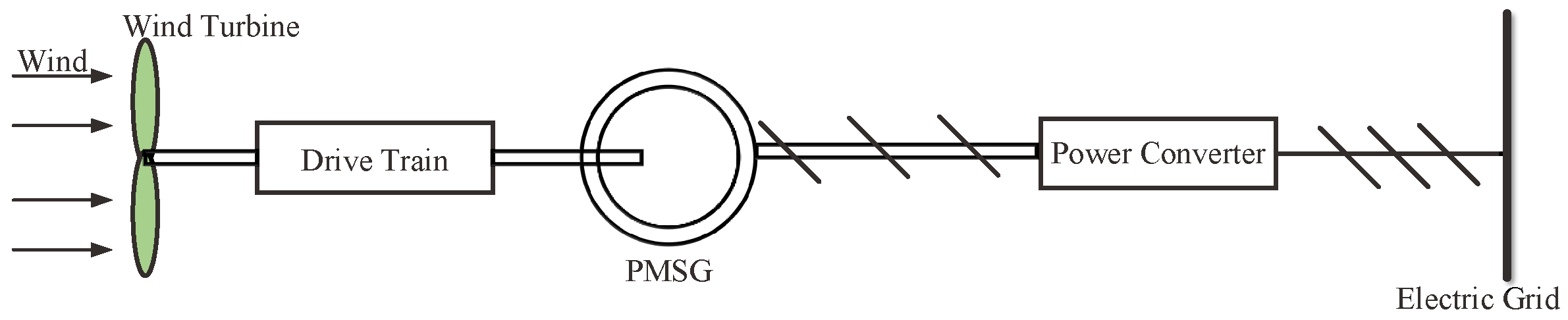
2. System Description
- (A)
- Wind TurbineAccording to the characteristics of the wind turbine [23], the relationship between the wind speed v and output power can be expressed as follows:where is the air density, is the radius of the wind wheel and is the wind energy utilization coefficient. Usually, the conversion rate from wind’s kinetic energy to wind turbine’s mechanical energy is not 100%, so the coefficient is used here to describe the ability of wind turbines to convert wind energy. The larger is, the stronger ability the wind turbine will have.In fact, the wind energy utilization coefficient satisfies where is the wind turbine torque coefficient which can be approximated by a quadratic polynomial function with respect to the tip speed ratio [24] as followswhere {, 1, 2} is the coefficient of the quadratic polynomial. The tip speed ratio depends on the rotor speed of the wind turbine and the wind speed v, and the expression can be written as:Obviously, , .
- (B)
- Drive TrainThe role of the drive train is to transfer the wind turbine mechanical torque to the PMSG. The kinematical equation of the drive train can be expressed as:where is the torque of the wind turbine which can be expressed as:In (4), is the electromagnetic torque of the PMSG, J is the inertia of the rotating part, and is the rotor speed of the wind turbine.
- (C)
- PMSGThe stator voltages of the PMSG in the d-q frame can be expressed as [25]:where and are the d shaft voltage and q shaft voltage in the rotor coordinate system, respectively; and are the d shaft current and q shaft current in the rotor coordinate system, respectively; R is the stator resistance; and are the inductance in the d-q coordinate system, is the electrical angular velocity of the generator; p is the number of pole pairs of the PMSG; and is the flux that is constant due to permanent magnets.
- (D)
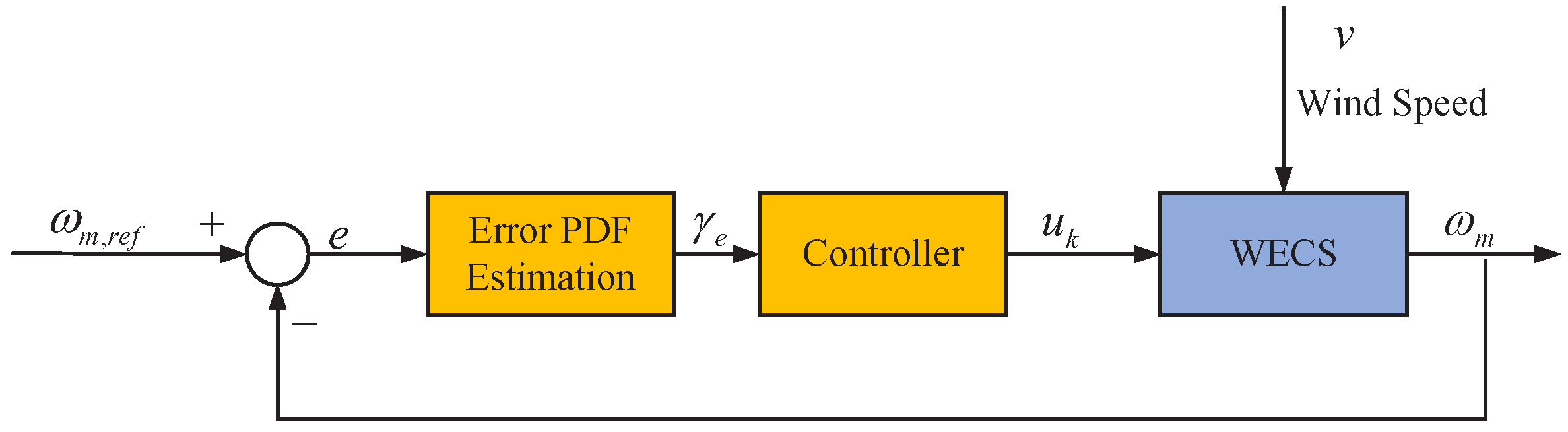
- Power Converter and Electric GridThe job that the power converter does can be divided into three steps: It firstly converts AC voltage from PMSG to DC voltage, then converts DC voltage back to AC but variable voltage, and finally, it puts variable AC voltage into the grid.The wind energy conversion system has partial load mode and full load mode. When the wind speed is lower than the rated wind speed, the wind energy conversion system operates in the partial load mode. When the wind speed is higher than the rated wind speed, the wind energy conversion system operates in the full mode. To explicitly explain our algorithm, we will only consider about the partial load mode. For full load mode, the research method will be quite similarly.In partial load mode, the power electronics dynamic is neglected because it is significantly more rapid than the PMSG-based wind energy conversion system dynamic. As shown in Figure 2, the power converter and the electric grid are equivalent to a parallel connection of a constant value inductance and a variable resistance , and thus in this paper, it is regarded as the equivalent load of the PMSG. In Figure 2, the resistance value of changes with duty ratio of the control pulse of the power converter.According to the Figure 2 and literature [26], the stator voltages of the PMSG equivalent model can be formulated as:On the other hand, the electromagnetic torque in (4) can be expressed as:In order to simplify the system model, assuming that [27], then the electromagnetic torque can be further written as:Substituting (5) and (11) into (4), the dynamic equation of wind turbine speed can be written as:Let = , . Combining (8), (9) and (12), we can get the following nonlinear state space model:where is the control variable, and the detailed expression of , and are shown as followsIn (12), the output y means the output power in the wind energy conversion system, and , , are all known coefficients.According to (16), the output power increases monotonically with the wind turbine rotational speed . If the optimal rotational speed can track , the output power will reach the maximum. Therefore, the output power control of the wind power generation system in the partial load mode can be turned into the control of the wind turbine speed .From the above analysis, it can be seen that the ability of the wind turbine to capture the maximum wind energy is equivalent to controlling the rotational speed of the wind turbine to track the optimal rotational speed. As the wind speed is usually a non-Gaussian random variable, the control theory using only mean or variance is not sufficient.In fact, due to the influence of non-Gaussian random variable v, the wind turbine speed is also a non-Gaussian random variable. Denote the tracking error aswhere is target value. As shown in Figure 3, our objective is to design a controller to make the probability density function (PDF) of power tracking error e get close to an impulse shaped PDF with mean value 0.
3. Controller Design
3.1. Performance Index Function
3.2. SIP Estimation for Tracking Error
3.3. Optimal Control Law
- Step 1:
- Initialize control input ;
- Step 2:
- Select the sliding window width N, the value of the SIP order and the weight and in Equation (24);
- Step 3:
- Calculate the SIP and the performance index value by Equations (23) and (24) respectively;
- Step 4:
- Calculate the and by Equation (28);
- Step 5:
- Solve the optimal control input by Equation (31);
- Step 6:
- According to , update control law;
- Step 7:
- Increase k by 1 to repeat the process from the step 3 to the step 6.
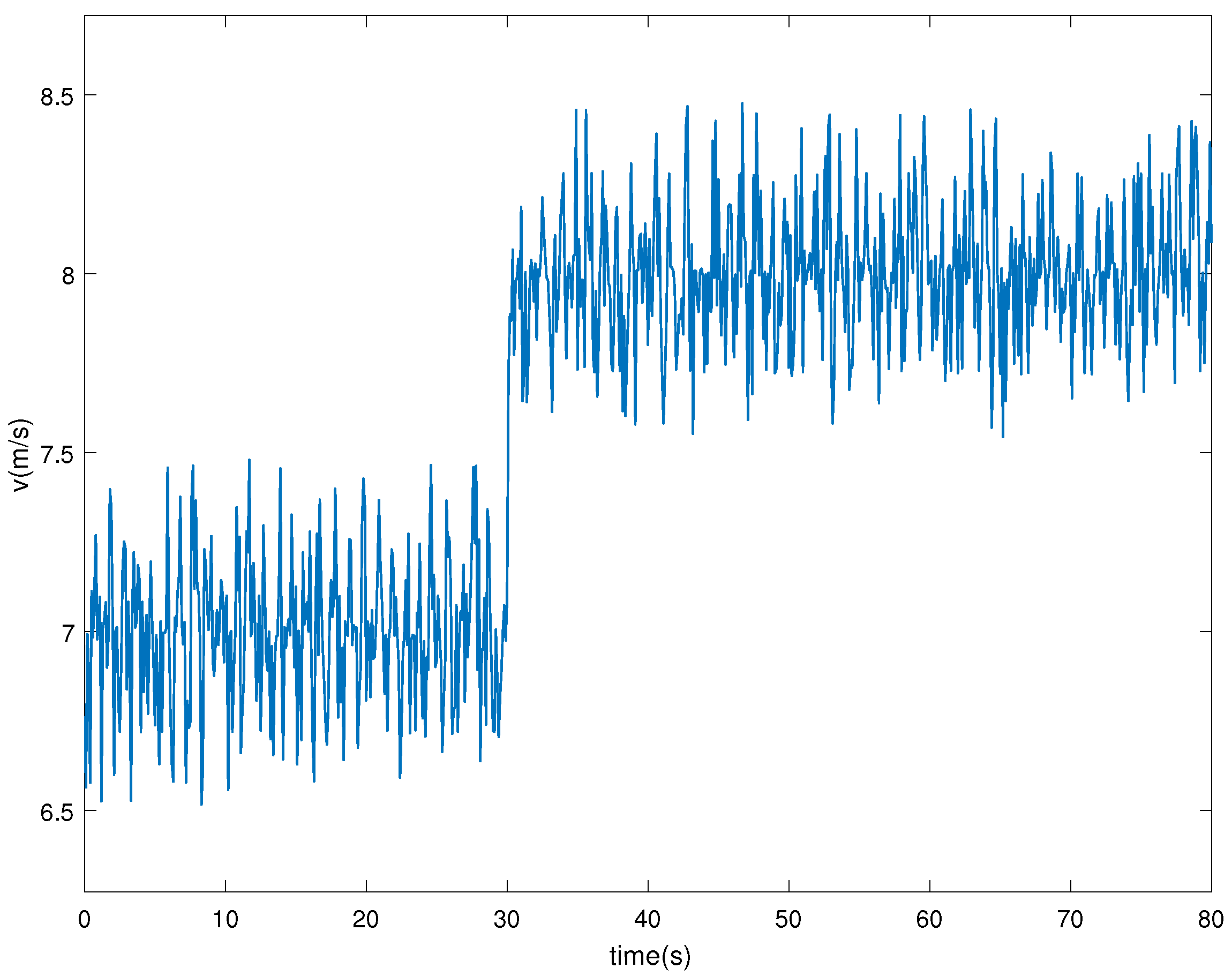
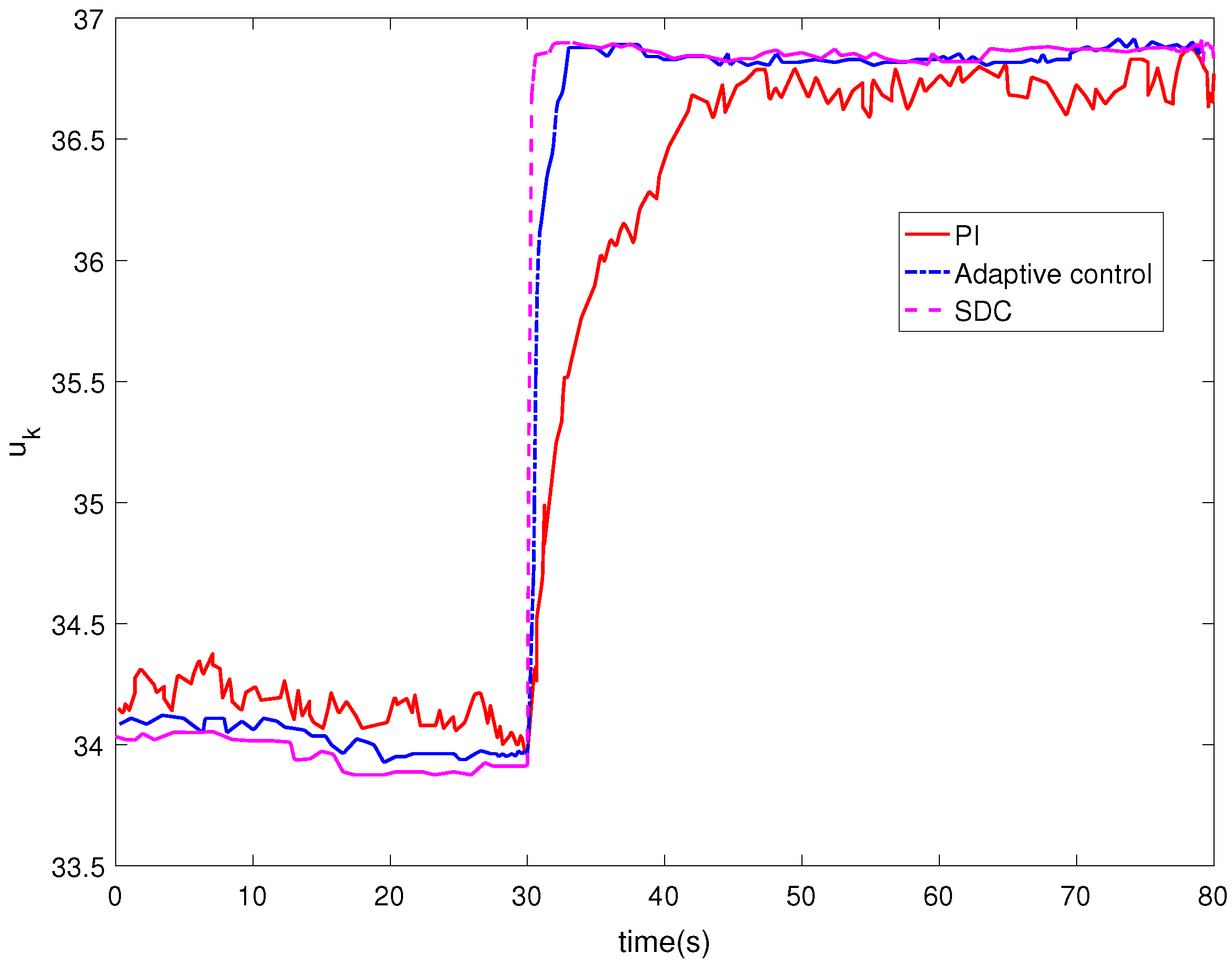
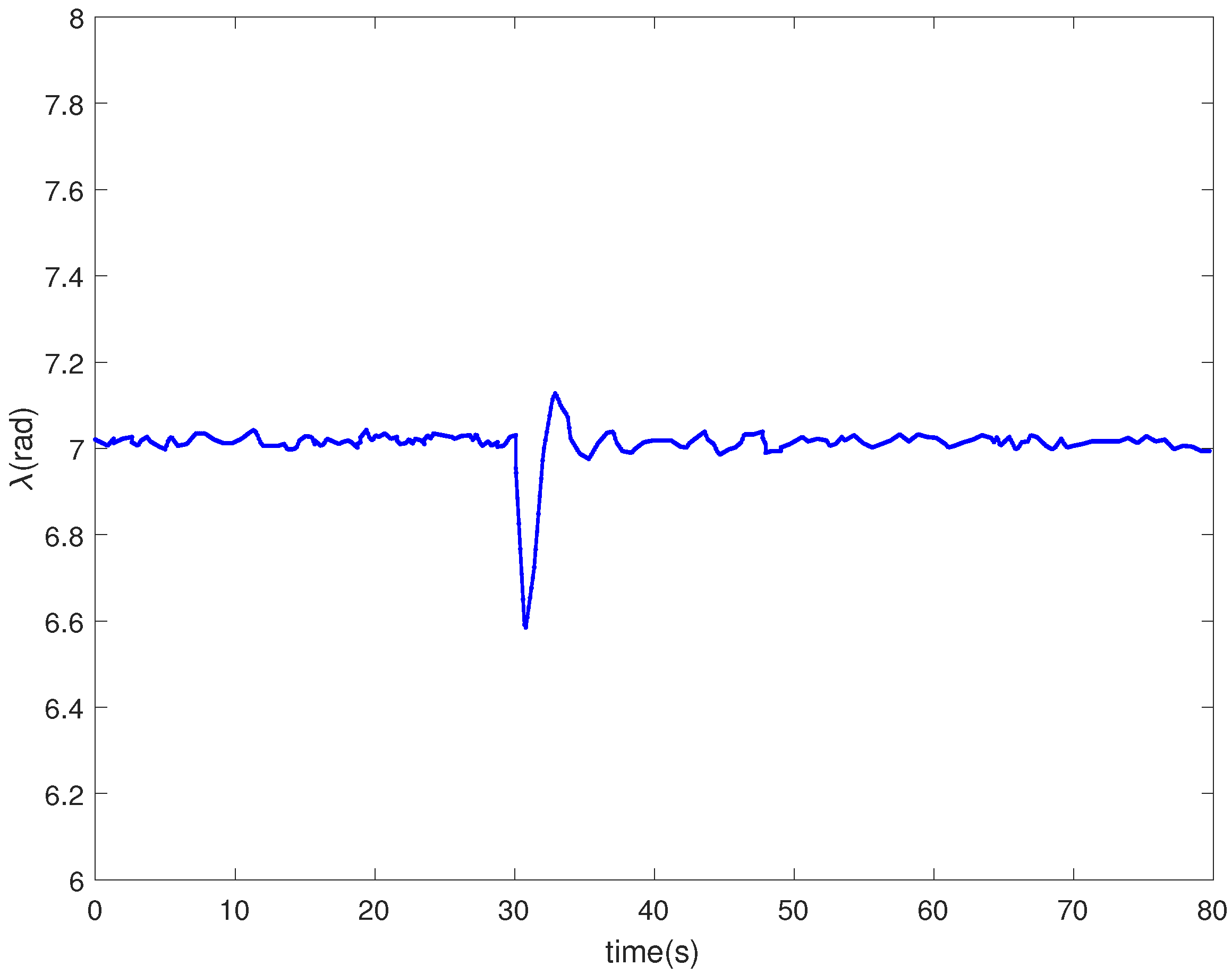
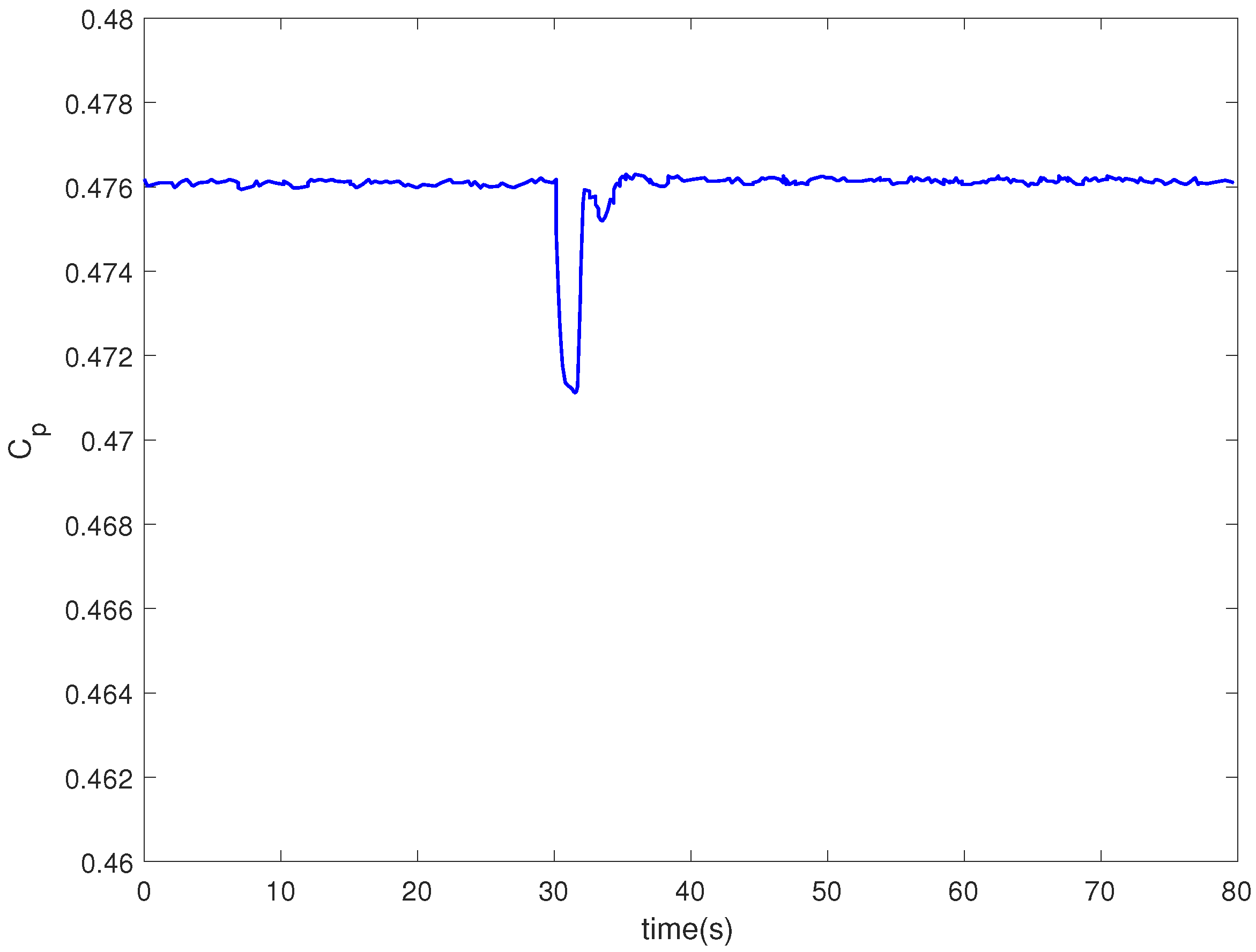
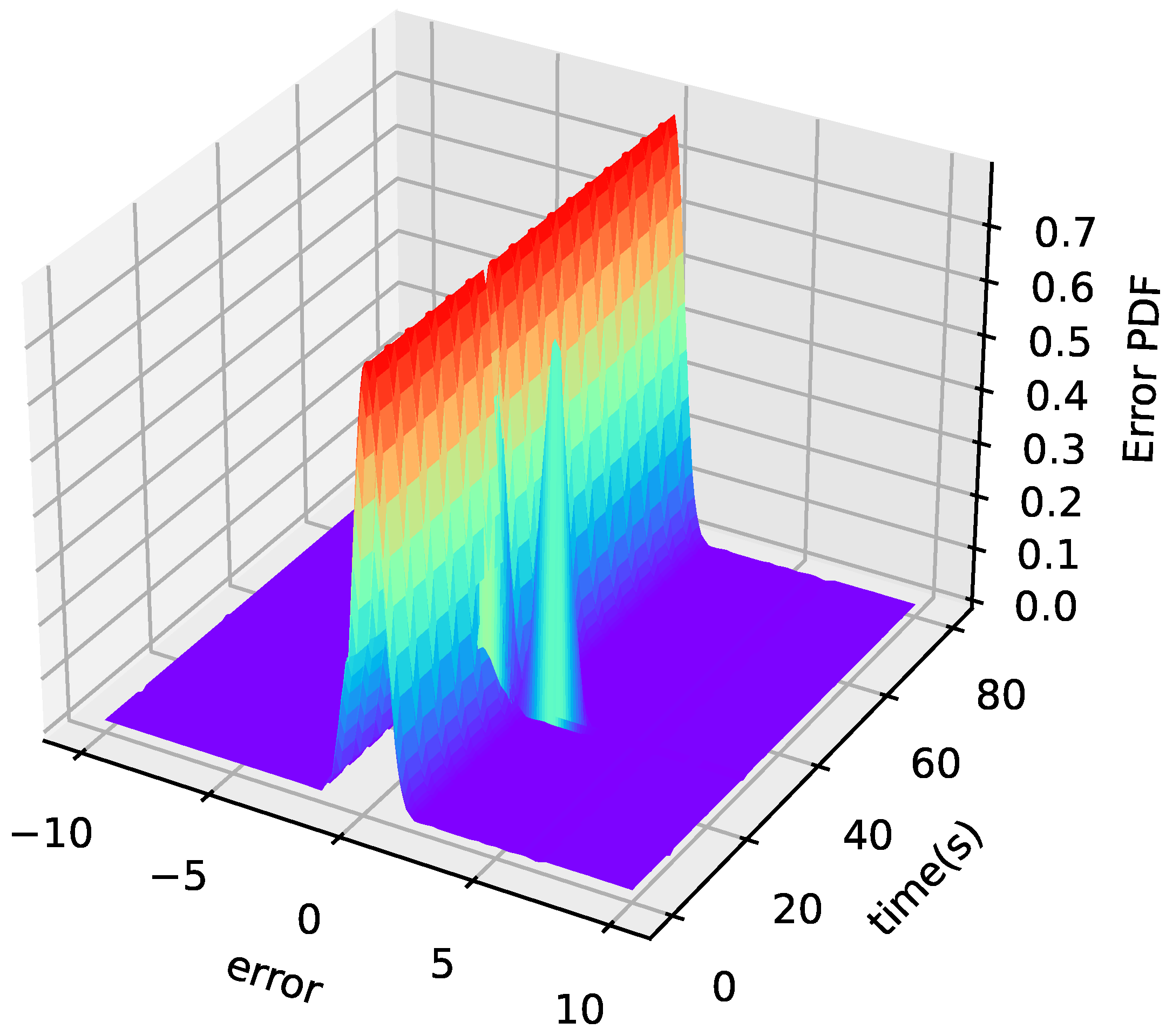
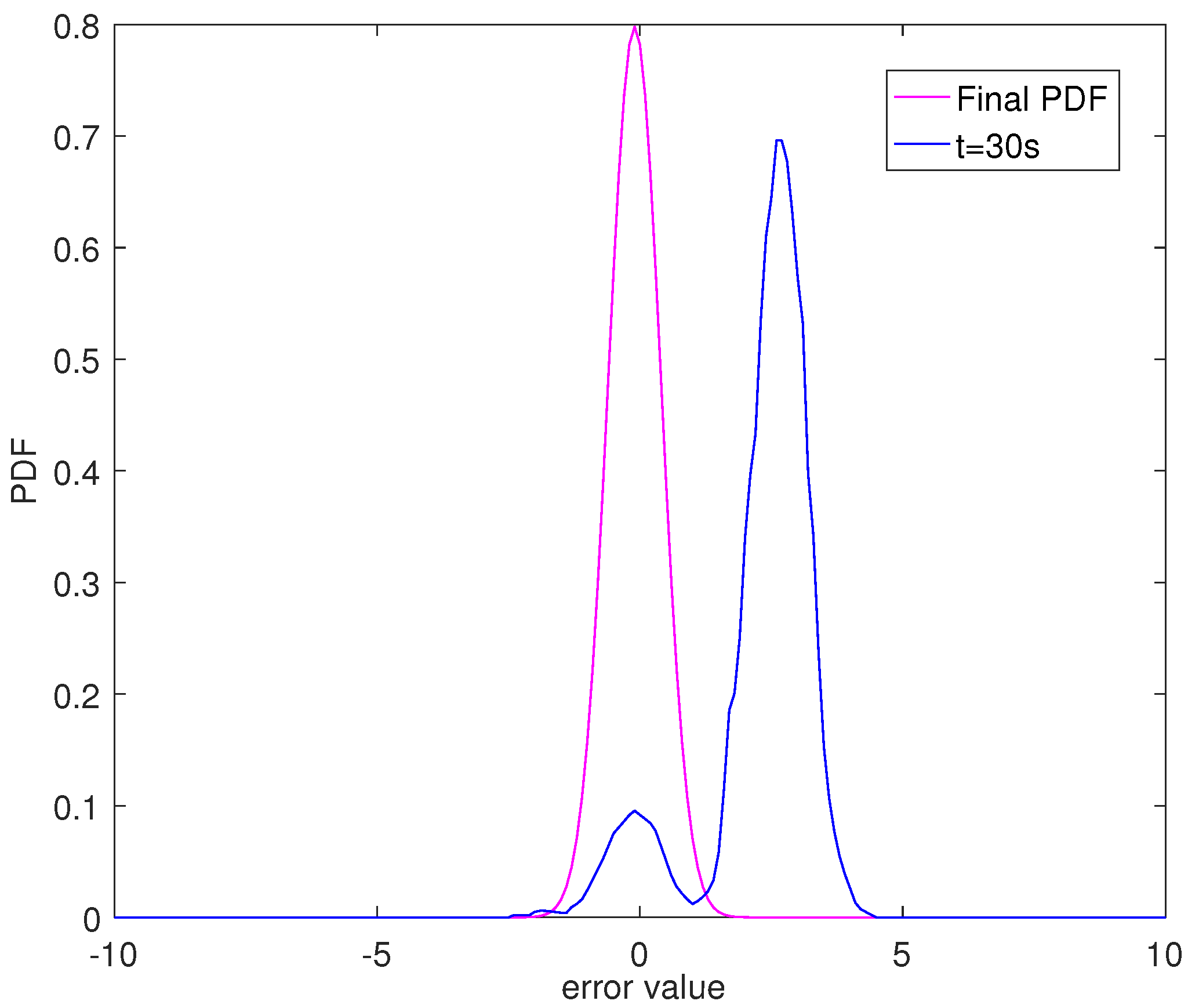
4. Simulation
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Feng, S.; Gong, D.; Zhang, Z.; He, X.; Guo, D. Wind-Chill temperature changes in winter over China during the last 50 years. Acta Geogr. Sinica 2009, 64, 1071–1082. [Google Scholar]
- Li, Y.; Wu, X.; Li, Q.; Tee, K.F. Assessment of onshore wind energy potential under different geographical climate conditions in China. Energy 2018, 152, 498–511. [Google Scholar] [CrossRef]
- Yang, B.; Zhang, X.; Tao, Y.; Shu, H. Grouped grey wolf optimizer for maximum power point tracking of doubly-fed induction generator based wind turbine. Energy Convers. Manag. 2017, 133, 427–443. [Google Scholar] [CrossRef]
- Koutroulis, E.; Kalaitzakis, K. Design of a maximum power tracking system for wind-energy-conversion applications. IEEE Trans. Ind. Electron. 2006, 53, 486–494. [Google Scholar] [CrossRef]
- Rachid, E.; Ahmed, A.D.; Mahdi, D. A novel design of PI current controller for PMSG-based wind turbine considering transient performance specifications and control saturation. IEEE Trans. Ind. Electron. 2018, 65, 8624–8634. [Google Scholar]
- Wang, J.S.; Tse, N.; Gao, Z.W. Synthesis on PI-based pitch controller of large wind turbines generator. Energy Convers. Manag. 2011, 52, 1288–1294. [Google Scholar] [CrossRef]
- José, G.H.; Rubén, S.C.; Roberto, V.B. A novel MPPT PI discrete reverse-acting controller for a wind energy conversion system. Renew. Energy 2021, 178, 904–915. [Google Scholar]
- Rhaili, S.E.; Abbou, A.; Marhraoui, S.; Moutchou, R. Robust sliding mode control with five sliding surfaces of five-phase PMSG based variable speed wind energy conversion system. Renew. Energy 2020, 13, 346–357. [Google Scholar] [CrossRef]
- Chojaa, H.; Derouich, A.; Chehaidia, S.E. Integral sliding mode control for DFIG based WECS with MPPT based on artificial neural network under a real wind profile. Energy Rep. 2021, 7, 4809–4824. [Google Scholar] [CrossRef]
- Darkhan, Z.; Matteo, R.; Ton, D.D. Adaptive super-twisting sliding mode control for maximum power point tracking of PMSG-based wind energy conversion systems. Renew. Energy 2022, 183, 877–889. [Google Scholar]
- Atif, I.; Deng, Y.; Adeel, S. Efficacious pitch angle control of variable-speed wind turbine using fuzzy based predictive controller. Energy Rep. 2020, 6, 423–427. [Google Scholar]
- Riad, A.; Toufik, R.; Djamila, R.; Abdelmounaim, T. Application of nonlinear predictive control for charging the battery using wind energy with permanent magnet synchronous generator. Int. J. Hydrog. Energy 2016, 41, 20964–20973. [Google Scholar]
- Lin, Z.; Chen, Z.; Liu, J. Coordinated mechanical loads and power optimization of wind energy conversion systems with variable-weight model predictive control strategy. Appl. Energy 2019, 236, 307–317. [Google Scholar] [CrossRef]
- Satyajit, D.; Bidyadhar, S. A H∞ Robust active and reactive power control scheme for a PMSG-based wind energy conversion system. IEEE Trans. Energy Convers. 2018, 33, 980–990. [Google Scholar]
- Hadi, D.; Amir, V. Robust control of a permanent magnet synchronous generators based wind energy conversion. In Proceedings of the 2021 7th International Conference on Control, Instrumentation and Automation (ICCIA), Tabriz, Iran, 23–24 February 2021; pp. 1–5. [Google Scholar]
- Amina, M.; Sandrine, L.B.; Helmi, A. Robust control of a wind conversion system based on a hybrid excitation synchronous generator: A comparison between H∞ and CRONE controllers. Math. Comput. Simulat. 2019, 158, 453–476. [Google Scholar]
- Hui, J.; Bakhshai, A. A new adaptive control algorithm for maximum power point tracking for wind energy conversion systems. In Proceedings of the 2008 IEEE Power Electronics Specialists Conference, Rhodes, Greece, 15–19 June 2008; pp. 4003–4007. [Google Scholar]
- Chen, J.; Yao, W.; Zhang, C.; Ren, Y.; Jiang, L. Design of robust MPPT controller for grid-connected PMSG-based wind turbine via perturbation observation based nonlinear adaptive control. Renew. Energy 2019, 134, 478–495. [Google Scholar] [CrossRef]
- Aubrée, R.; Auger, F.; Macé, M.; Loron, L. Design of an efficient small wind-energy conversion system with an adaptive sensorless MPPT strategy. Renew. Energy 2016, 86, 280–291. [Google Scholar] [CrossRef]
- Munteanu, I.; Cutululis, N.A.; Antoneta, I.B. Optimization of variable speed wind power systems based on a LQG approach. Control Eeg. Pract. 2005, 13, 903–912. [Google Scholar] [CrossRef]
- Lescher, F.; Zhao, J.; Martinez, A. LQG multiple model control of a variable speed, pitch regulated wind turbine. Chalmers 2005, 18, 111–117. [Google Scholar]
- Ronilson, R. A sensorless control for a variable speed wind turbine operating at partial load. Renew. Energy 2011, 36, 132–141. [Google Scholar]
- Uehara, A.; Pratap, A.; Goya, T.; Senjyu, T.; Yona, A. A coordinated control method to smooth wind power fluctuations of a PMSG-based WECS. IEEE Trans. Energy Convers. 2011, 26, 550–558. [Google Scholar] [CrossRef]
- Hur, S.; Leithead, W.E. Model predictive and linear quadratic Gaussian control of a wind turbine. Optim. Contr. Appl. Met. 2017, 38, 88–111. [Google Scholar] [CrossRef]
- Tan, K.; Islam, S. Optimum control strategies in energy conversion of PMSG wind turbine system without mechanical sensors. IEEE Trans. Energy Convers. 2004, 19, 392–399. [Google Scholar] [CrossRef]
- Munteanur, I.A.; Cutululis, N.A.; Bratcu, A.I. Optimal Control of Wind Energy Systems; Springer: London, UK, 2008. [Google Scholar]
- Wang, W.; Wu, D.H.; Wang, Y. H∞ gain scheduling control of PMSG-based wind power conversion system. In Proceedings of the 2010 5th IEEE Conference on Industrial Electronics and Applications, Taichung, China, 15–17 June 2010; pp. 712–717. [Google Scholar]
- Zhang, Q.; Wang, H. A novel data-based stochastic distribution control for Non-Gaussian stochastic systems. IEEE Trans. Automat. Contr. 2022, 67, 1506–1513. [Google Scholar] [CrossRef]
- Yin, L.; Wang, H.; Guo, L.; Zhang, H. Data-driven pareto-DE-based intelligent optimal operational control for stochastic processes. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 4443–4452. [Google Scholar] [CrossRef]
- Chen, B.; Zhu, P.; Principe, J.C. Survival Information Potential: A new criterion for adaptive system training. IEEE Trans. Signal Process. 2012, 60, 1184–1194. [Google Scholar] [CrossRef]
- Ren, M.F.; Cheng, T.; Chen, J.H.; Xu, X.Y.; Cheng, L. Single neuron stochastic predictive PID control algorithm for nonlinear and Non-Gaussian systems using the survival information potential criterion. Entropy 2016, 18, 218. [Google Scholar] [CrossRef]
- Abdelhameed, E.H.; Ahmed, H.H. Adaptive maximum power tracking control technique for wind energy conversion systems. In Proceedings of the 2018 Twentieth International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 18–20 December 2018; pp. 146–151. [Google Scholar]
- Chang, T.P. Performance comparison of six numerical methods in estimating Weibull parameters for wind energy application. Appl. Energy 2011, 88, 272–282. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, L.; Lai, L.; Zhu, Z.; Li, T. Maximum Power Point Tracking Control for Non-Gaussian Wind Energy Conversion System by Using Survival Information Potential. Entropy 2022, 24, 818. https://doi.org/10.3390/e24060818
Yin L, Lai L, Zhu Z, Li T. Maximum Power Point Tracking Control for Non-Gaussian Wind Energy Conversion System by Using Survival Information Potential. Entropy. 2022; 24(6):818. https://doi.org/10.3390/e24060818
Chicago/Turabian StyleYin, Liping, Lanlan Lai, Zhengju Zhu, and Tao Li. 2022. "Maximum Power Point Tracking Control for Non-Gaussian Wind Energy Conversion System by Using Survival Information Potential" Entropy 24, no. 6: 818. https://doi.org/10.3390/e24060818
APA StyleYin, L., Lai, L., Zhu, Z., & Li, T. (2022). Maximum Power Point Tracking Control for Non-Gaussian Wind Energy Conversion System by Using Survival Information Potential. Entropy, 24(6), 818. https://doi.org/10.3390/e24060818





