Discrete-Time Memristor Model for Enhancing Chaotic Complexity and Application in Secure Communication
Abstract
:1. Introduction
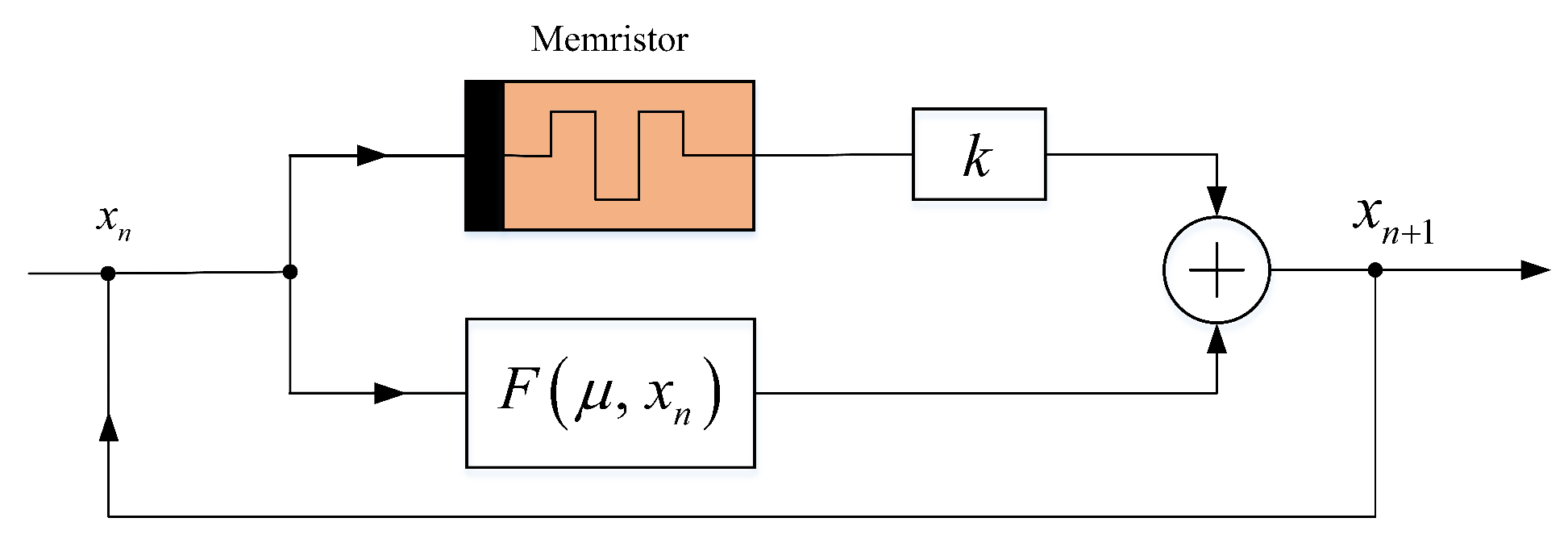
2. Two Dimensional Generalized Discrete Memristor Coupling Model
Memristor Coupled Low-Dimensional Discrete Chaos Model
3. Numerical Example of Two-Dimensional Discrete Memristor Model
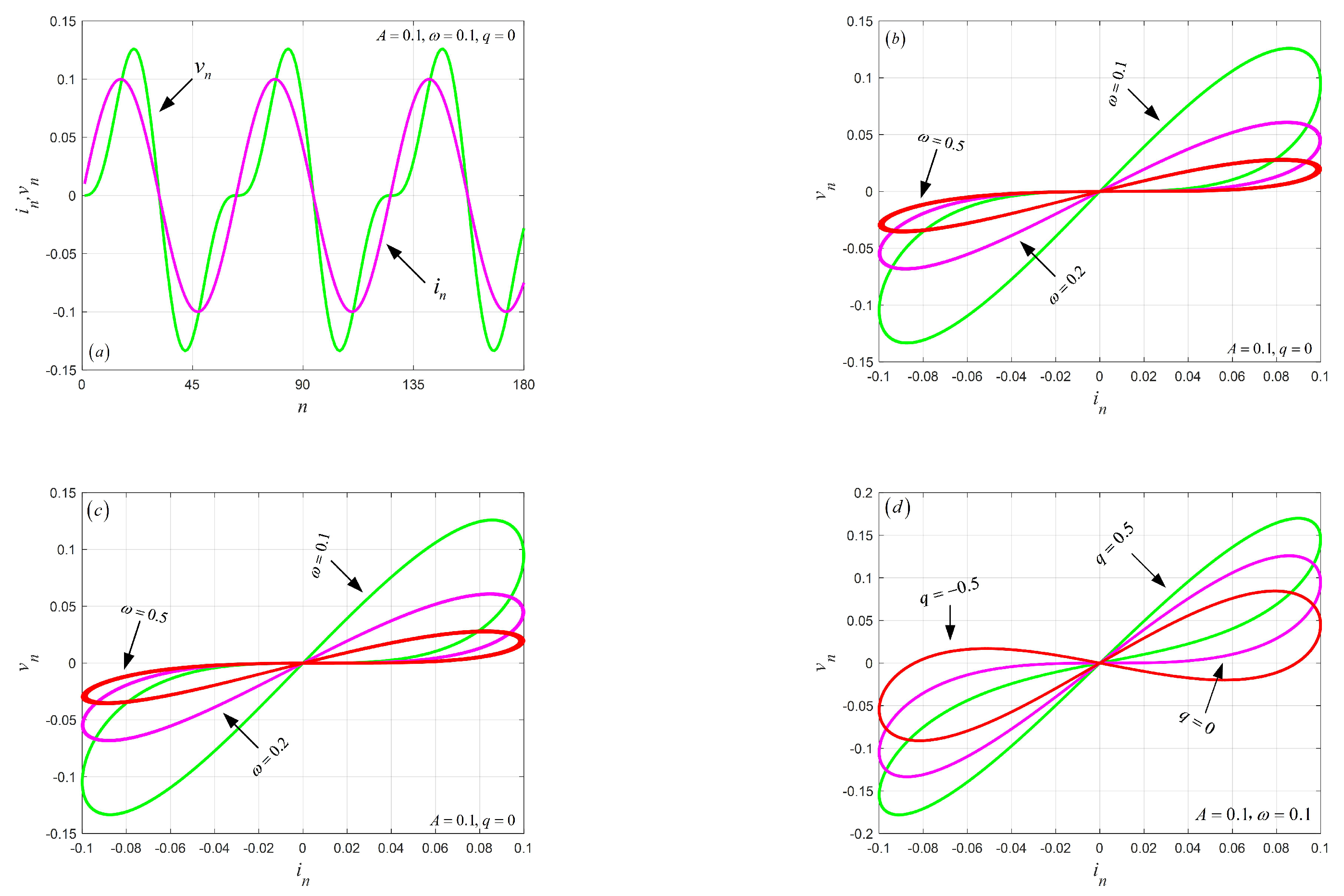
3.1. Numerical Examples
3.2. Bifurcation with Coupling Strength
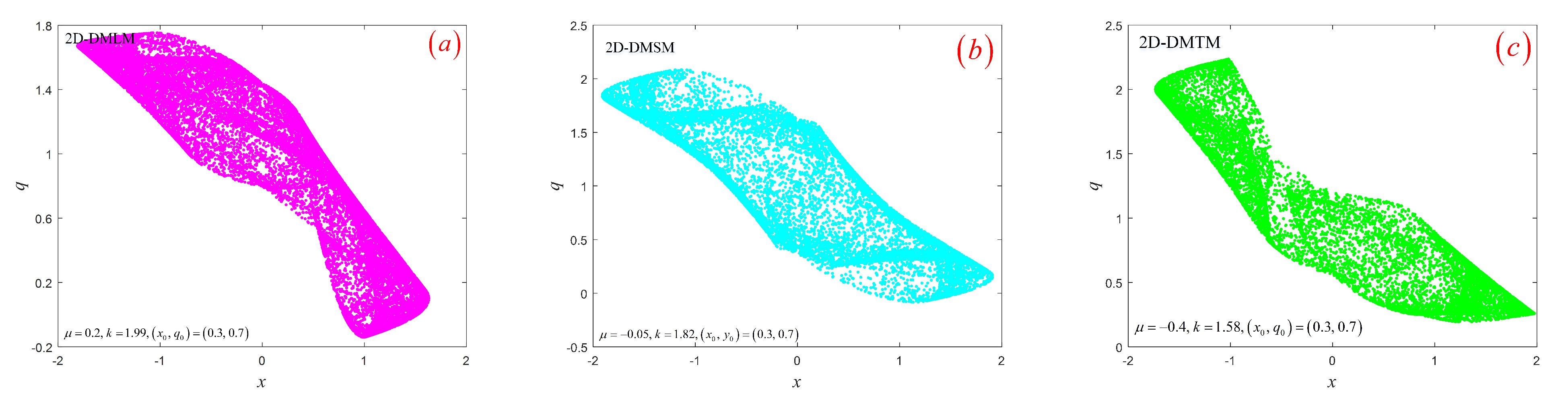
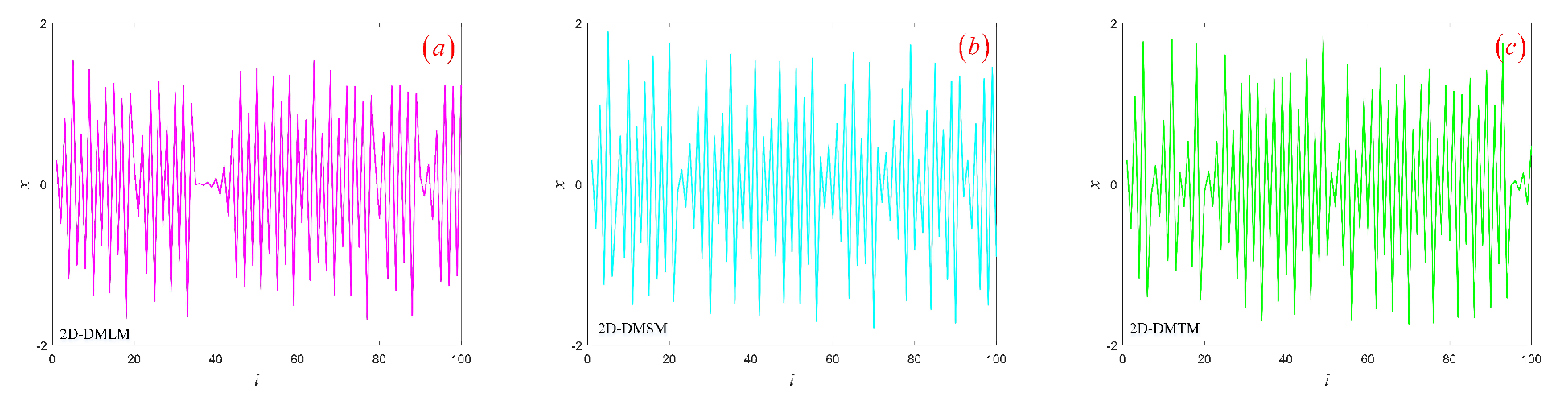
3.3. Hyperchaotic Attractor
4. Application of Hyperchaotic Sequence in Secure Communication
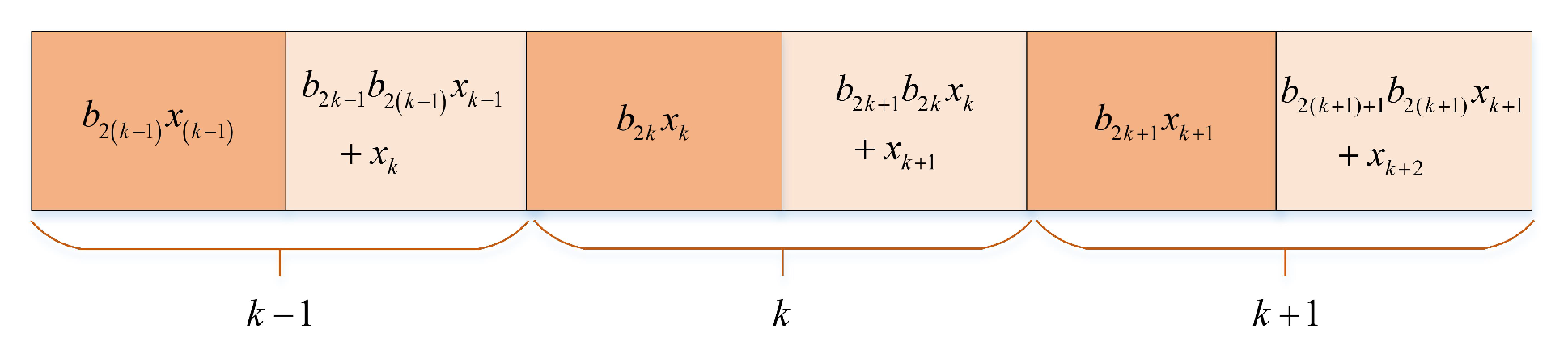
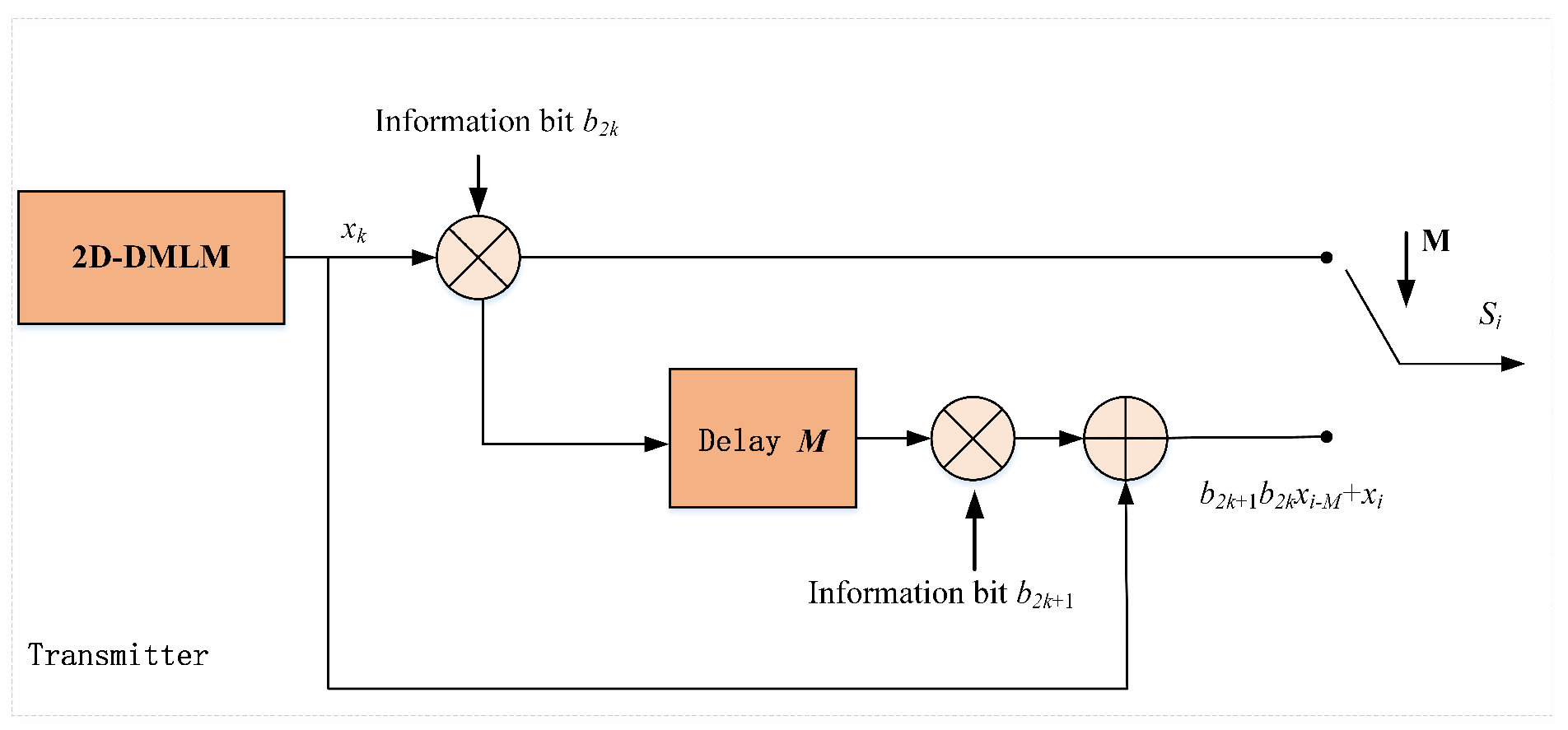
4.1. Transmitter Sructure
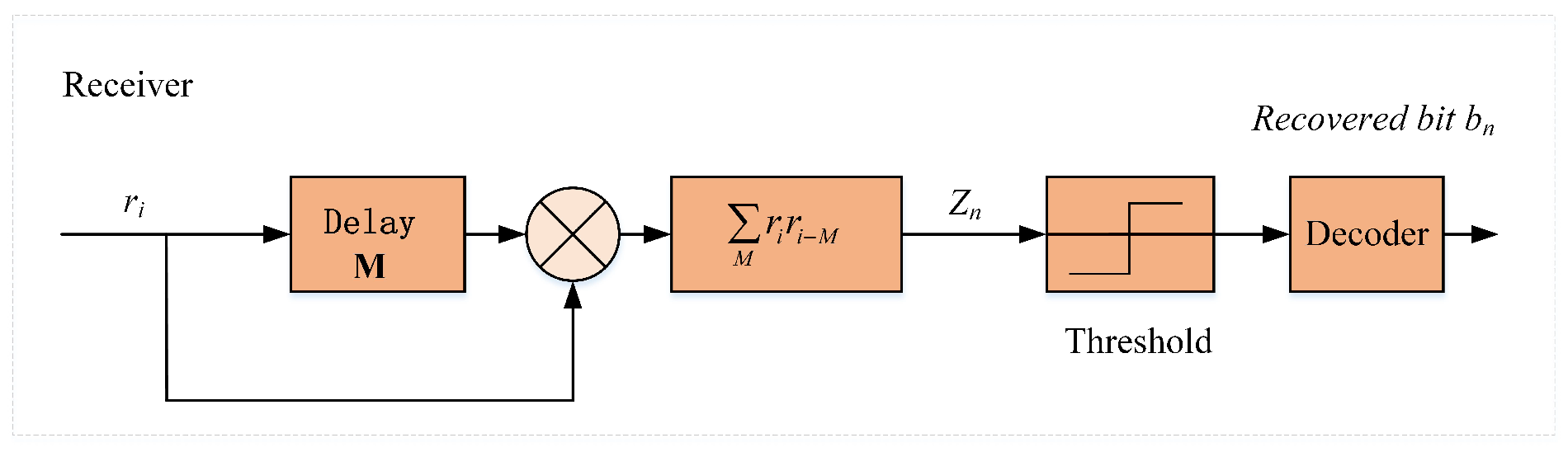
4.2. Receive Structure
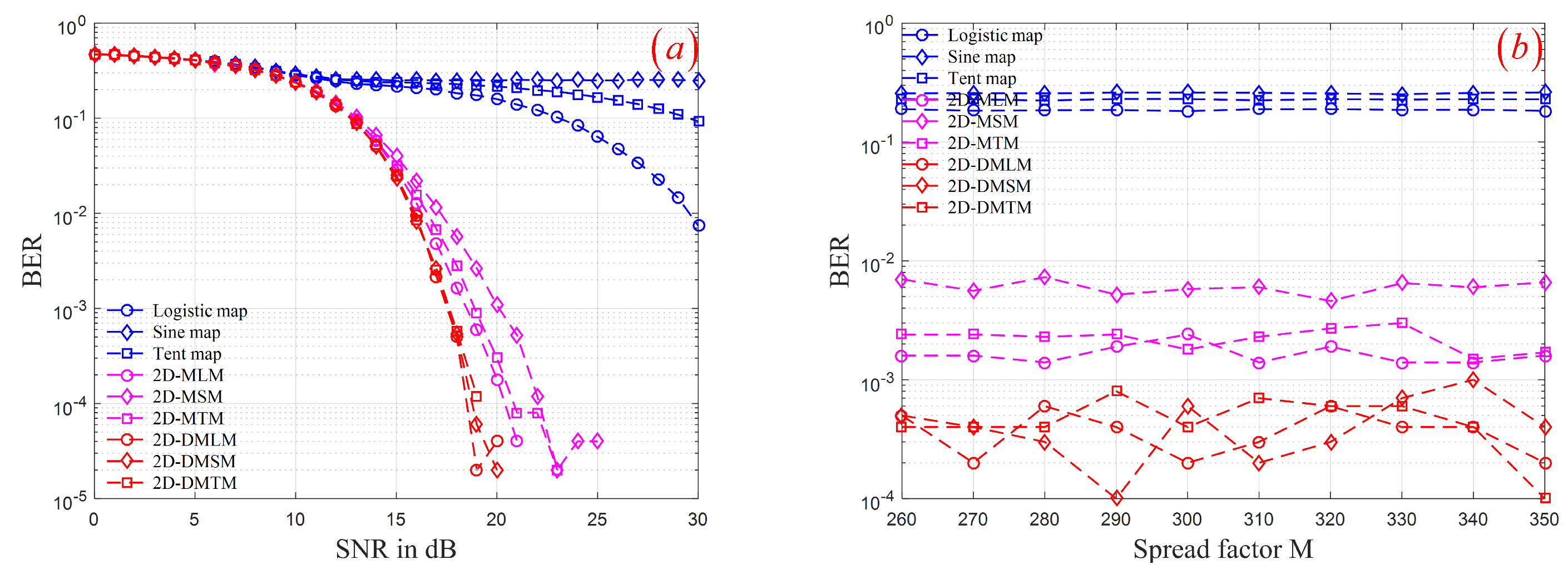
4.3. Simulation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chua, L.O. Memristor-the missing circuit element. IEEE Trans. Circ. Theory 1971, 18, 507–514. [Google Scholar] [CrossRef]
- Chua, L.O.; Kang, S.M. Memristive devices and systems. Proc. IEEE 1976, 64, 209–223. [Google Scholar] [CrossRef]
- Strukov, D.B.; Snider, G.S.; Stewart, D.R.; Williams, R.S. The missing memristor found. Nature 2008, 453, 80–83. [Google Scholar] [CrossRef] [PubMed]
- Adhikari, S.P.; Sah, M.P.; Kim, H.; Chua, L.O. Three fingerprints of memristor. IEEE Trans. Circ. Syst. I Reg. Pap. 2013, 60, 3008–3021. [Google Scholar] [CrossRef]
- Sun, J.; Yao, L.; Zhang, X.; Wang, Y.; Cui, G. Generalised mathematical model of memristor. IET Circ. Device Syst. 2015, 10, 244–249. [Google Scholar] [CrossRef]
- Wang, C.; Xiong, L.; Sun, J.; Yao, W. Memristor-based neural networks with weight simultaneous perturbation training. Nonlinear Dyn. 2018, 93, 2893–2906. [Google Scholar] [CrossRef]
- Duan, S.; Hu, X.; Dong, Z.; Wang, L.; Mazumder, P. Memristor-based cellular nonlinear/neural network: Design, analysis, and applications. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 1202–1213. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhuang, J.; Xia, Y.; Bai, Y.; Cao, J.; Gu, L. Fixed-time synchronization of the impulsive memristor-based neural networks. Commun. Nonlinear Sci. 2019, 77, 40–45. [Google Scholar] [CrossRef]
- Yuan, F.; Li, Y. A chaotic circuit constructed by a memristor, a memcapacitor and a meminductor. Chaos 2019, 29, 101101. [Google Scholar] [CrossRef]
- Fang, Y.; Yue, D.; Li, Y.; Wang, G. The amplitude, frequency and parameter space boosting in a memristor–meminductor-based circuit. Nonlinear Dyn. 2019, 96, 389–405. [Google Scholar]
- Ghenzi, N.; Levy, P. Impact of sub- and supra-threshold switching in the synaptic behavior of TiO2 memristor. Microelectron. Eng. 2018, 193, 13–17. [Google Scholar] [CrossRef]
- Wang, Y.; Ma, J.; Xu, Y.; Wu, F.; Zhou, P. The electrical activity of neurons subject to electromagnetic induction and gaussian white noise. Int. J. Bifurc. Chaos 2017, 27, 1750030. [Google Scholar] [CrossRef]
- Kim, H.; Sah, M.P.; Yang, C.; Cho, S.; Chua, L.O. Memristor emulator for memristor circuit applications. IEEE Trans. Circ. Syst. I Reg. Pap. 2012, 59, 2422–2431. [Google Scholar]
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1976, 20, 130–141. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Luo, Y.; Song, S.; Cao, L.; Liu, J.; Harkin, J. Counteracting dynamical degradation of digital chaotic chebyshev map via perturbation. Int. J. Bifurc. Chaos 2017, 27, 1750033. [Google Scholar] [CrossRef]
- Zheng, J.; Hu, H.P.; Xia, X. Applications of symbolic dynamics in counteracting the dynamical degradation of digital chaos. Nonlinear Dyn. 2018, 94, 1535–1546. [Google Scholar] [CrossRef]
- Zhou, Y.; Bao, L.; Chen, C. Image encryption using a new parametric switching chaotic system. Signal Processing 2013, 93, 3039–3052. [Google Scholar] [CrossRef]
- Hua, Z.; Zhou, B.; Zhou, Y. Sine-transform-based chaotic system with FPGA implementation. IEEE Trans. Ind. Electron. 2017, 65, 2557–2566. [Google Scholar] [CrossRef]
- Hua, Z.; Zhou, Y.; Huang, H. Cosine-transform-based chaotic system for image encryption. Inf. Sci. 2019, 480, 403–419. [Google Scholar] [CrossRef]
- Itoh, M.; Chua, L.O. Memrsitor Oscillator. Int. J. Bifurc. Chaos 2008, 18, 3183–3206. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Z.; Wu, H.; Chen, S.; Bao, B. Two-memristor-based chaotic system and its extreme multistability reconstitution via dimensionality reduction analysis. Chaos Solitons Fractals 2017, 127, 354–363. [Google Scholar] [CrossRef]
- Ma, J.; Wu, F.; Ren, G.; Tang, J. A class of initials-dependent dynamical system. Appl. Math. Comput. 2017, 298, 65–76. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, C.H.; Zhang, X.; Yao, W. Various attractors, coexisting attractors and antimonotonicity in a simple fourth-order memristive Twin-T oscillator. Int. J. Bifurc. Chaos 2018, 28, 1850050. [Google Scholar] [CrossRef] [Green Version]
- Lai, Q.; Kuate, P.; Liu, F.; Iu, H.C. An extremely simple chaotic system with infinitely many coexisting attractors. IEEE Trans. Circ. Syst. II Exp. Briefs 2019, 67, 1129–1133. [Google Scholar] [CrossRef]
- Varshney, V.; Sabarathinam, S.; Awadhesh, P.; Thamilmaran, K. Infinite number of hidden attractors in memristor-based autonomous duffing oscillator. Int. J. Bifurc. Chaos 2019, 67, 1129–1133. [Google Scholar] [CrossRef]
- Peng, Y.; Sun, K.; He, S. A discrete memristor model and its application in Hénon map. Chaos Solitons Fractals 2020, 137, 109873. [Google Scholar] [CrossRef]
- Bao, B.; Rong, K.; Li, H.; Li, K.; Hua, Z.; Zhang, X. Memristor-coupled Logistic hyperchaotic map. IEEE Trans. Circ. Syst. II Exp. Briefs 2021, 68, 2992–2996. [Google Scholar] [CrossRef]
- Deng, Y.; Li, Y. Nonparametric bifurcation mechanism in 2-D hyperchaotic discrete memristor-based map. Nonlinear Dyn. 2021, 104, 4601–4614. [Google Scholar] [CrossRef]
- Chua, L.O. If it’s pinched it’s a memristor. Semicond. Sci. Tech. 2014, 29, 104001. [Google Scholar]
- Richman, J.; Moorman, J. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, 2039–2049. [Google Scholar] [CrossRef] [Green Version]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef]
- Theiler, J. Efficient algorithm for estimating the correlation dimension from a set of discrete points. Phys. Rev. A 1987, 36, 4456–4462. [Google Scholar] [CrossRef]
- Frederickson, P.; Kaplan, J.; Yorke, E.; Yorke, J. The liapunov dimension of strange attractors. J. Differ. Equ. 1983, 49, 185–207. [Google Scholar] [CrossRef] [Green Version]

| CMs | Charge-Controlled | Flux-Controlled |
|---|---|---|
| ideal | ||
| general | ||
| generalized |
| Iterms | k | |||
|---|---|---|---|---|
| 2D-DMLM | 0.200 | 1.99 | (0.3, 0.7) | 0.3028, 0.0731 |
| 2D-DMSM | −0.05 | 1.82 | (0.2, 0.4) | 0.3200, 0.0757 |
| 2D-DMTM | −0.40 | 1.58 | (0.1, 0.6) | 0.2797, 0.1062 |
| Iterms | SE | PE | CorDim | K-YDim |
|---|---|---|---|---|
| 2D-DMLM | 0.7268 | 0.8311 | 1.6163 | 2 |
| 2D-DMSM | 0.7786 | 0.8010 | 1.6315 | 2 |
| 2D-DMTM | 0.7076 | 0.8216 | 1.6295 | 2 |
| Items | Initial Conditions | Control Parameters |
|---|---|---|
| Logistic | ||
| Sine | ||
| Tent | ||
| 2D-MLM | ||
| 2D-MSM | ||
| 2D-MTM | ||
| 2D-DMLM | ||
| 2D-DMLM | ||
| 2D-DMTM |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, W.; Dong, W.; Wang, P.; Wang, Y.; Xing, Y.; Ding, Q. Discrete-Time Memristor Model for Enhancing Chaotic Complexity and Application in Secure Communication. Entropy 2022, 24, 864. https://doi.org/10.3390/e24070864
Yan W, Dong W, Wang P, Wang Y, Xing Y, Ding Q. Discrete-Time Memristor Model for Enhancing Chaotic Complexity and Application in Secure Communication. Entropy. 2022; 24(7):864. https://doi.org/10.3390/e24070864
Chicago/Turabian StyleYan, Wenhao, Wenjie Dong, Peng Wang, Ya Wang, Yanan Xing, and Qun Ding. 2022. "Discrete-Time Memristor Model for Enhancing Chaotic Complexity and Application in Secure Communication" Entropy 24, no. 7: 864. https://doi.org/10.3390/e24070864






