A Model of Interacting Navier–Stokes Singularities
Abstract
:1. Introduction
2. Pinçon Model
2.1. Generalities and Ideas behind the Pinçon Model
2.2. Definition of Pinçon
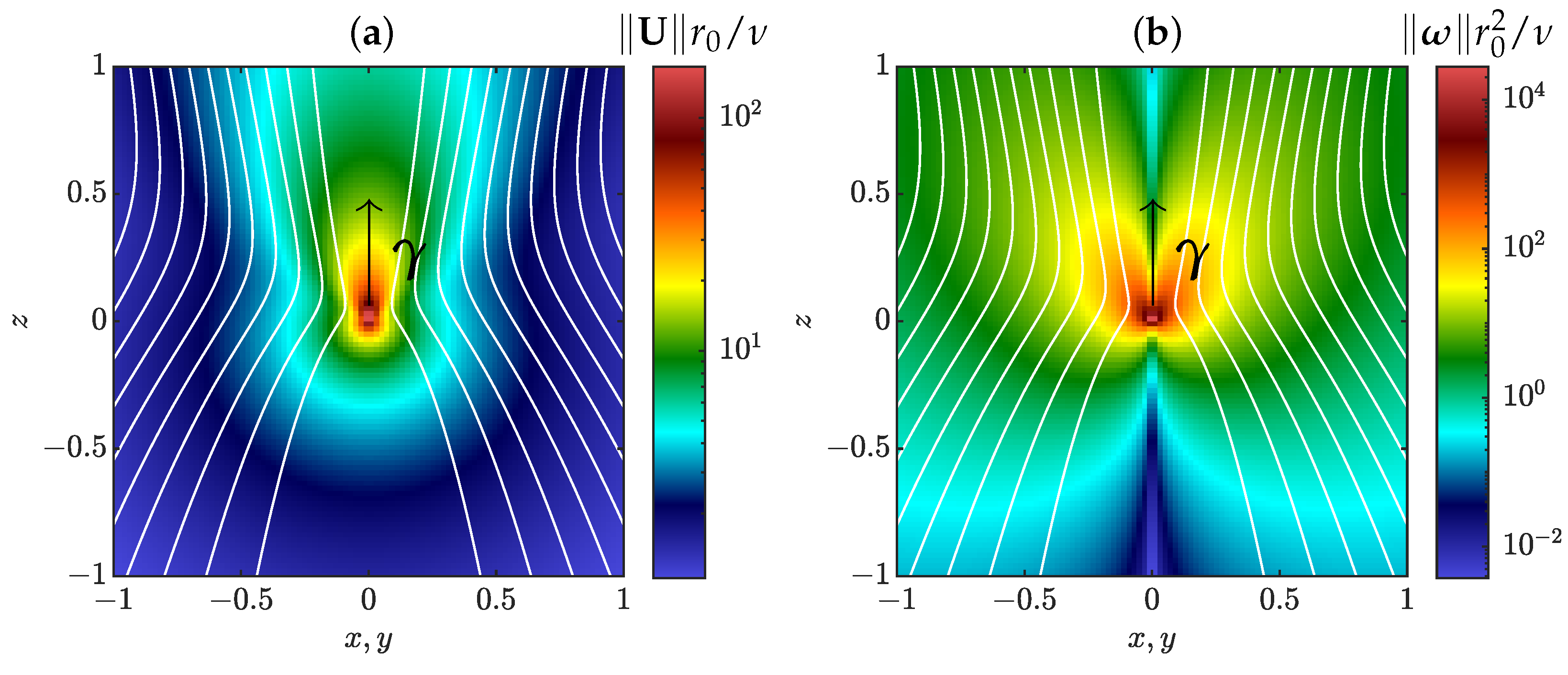
2.3. Properties of Pinçons
2.3.1. Scaling under Coarse-Graining
2.3.2. Potential Vector, Vorticity and Helicity
2.3.3. Generalized Momentum and Coarse-Grained Vorticity
2.4. Interaction of a Pinçon with a Regular Field
- (i)
- the pinçon is dissipative, and requires a force to maintain it; a surrounding fluid can provide the necessary forcing;
- (ii)
- the pinçon lives in an infinite universe and does not fulfill the boundary conditions of a realistic system. To be able to use a pinçon in confined systems, we need to add an external velocity field that will take care of the boundary conditions;
- (iii)
- if we accept that the pinçon describes the very intermittent part of the energy transfer that cannot be resolved, we must also accept the possibility of coexistence and interaction of several pinçons. If we assume that the pinçons are distinct and that they are regular everywhere except at their position, this amounts again to considering the interaction of a pinçon with a regular field.
2.5. Interactions of Pinçons
2.6. Weak Pinçon Limit
3. Dynamics of a Pair of Pinçons
3.1. Interest of Considering a Pair of Pinçons
3.2. Dynamics of a Dipole of Pinçons
3.2.1. Equations
3.2.2. Results at Zero Temperature
3.3. Results at Finite Small Temperature
3.3.1. From Pair of Pinçons to Dipole Equations in the Weak Pinçon Limit
3.3.2. Dynamics at Finite Temperature
3.4. General Dynamics of a Pair of Pinçons
3.4.1. Short Time Dynamics
- (i)
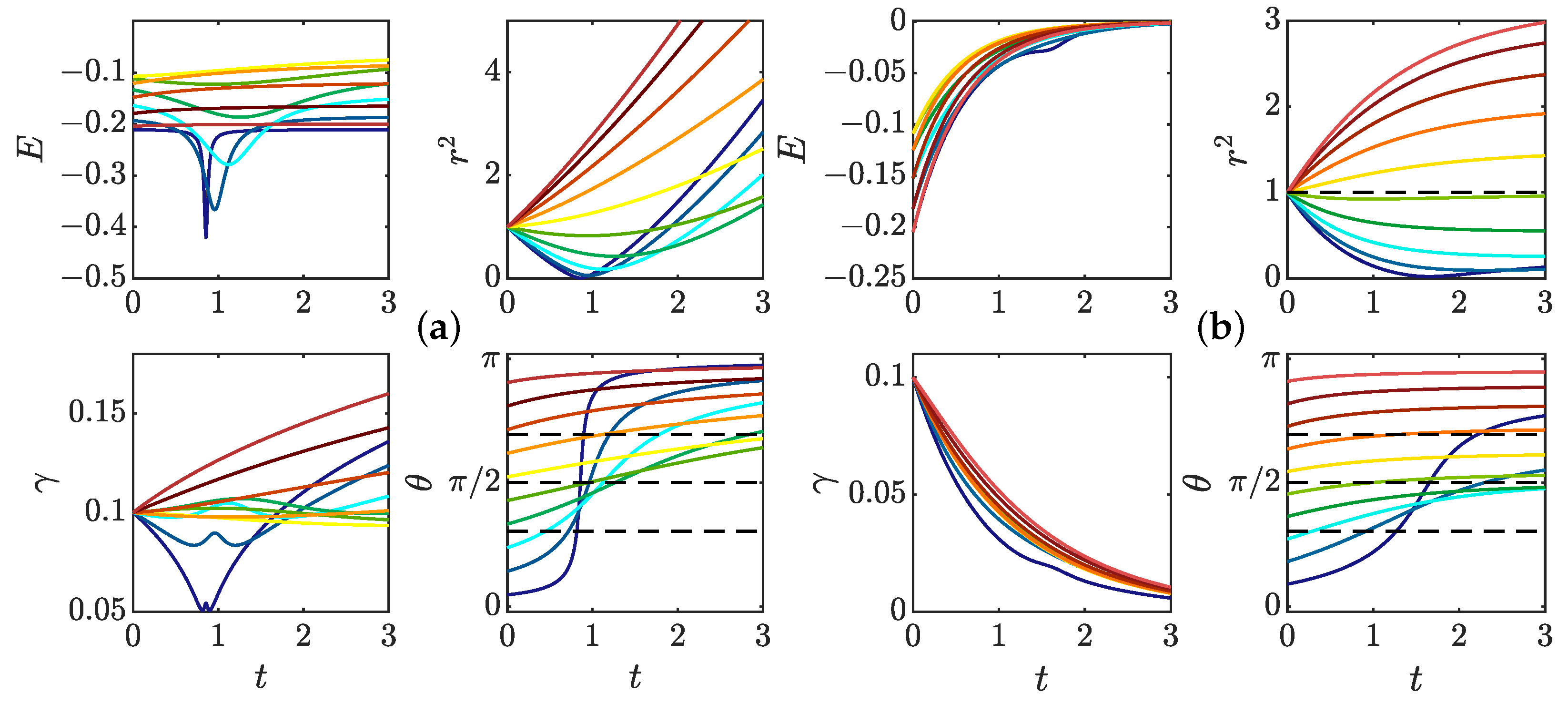
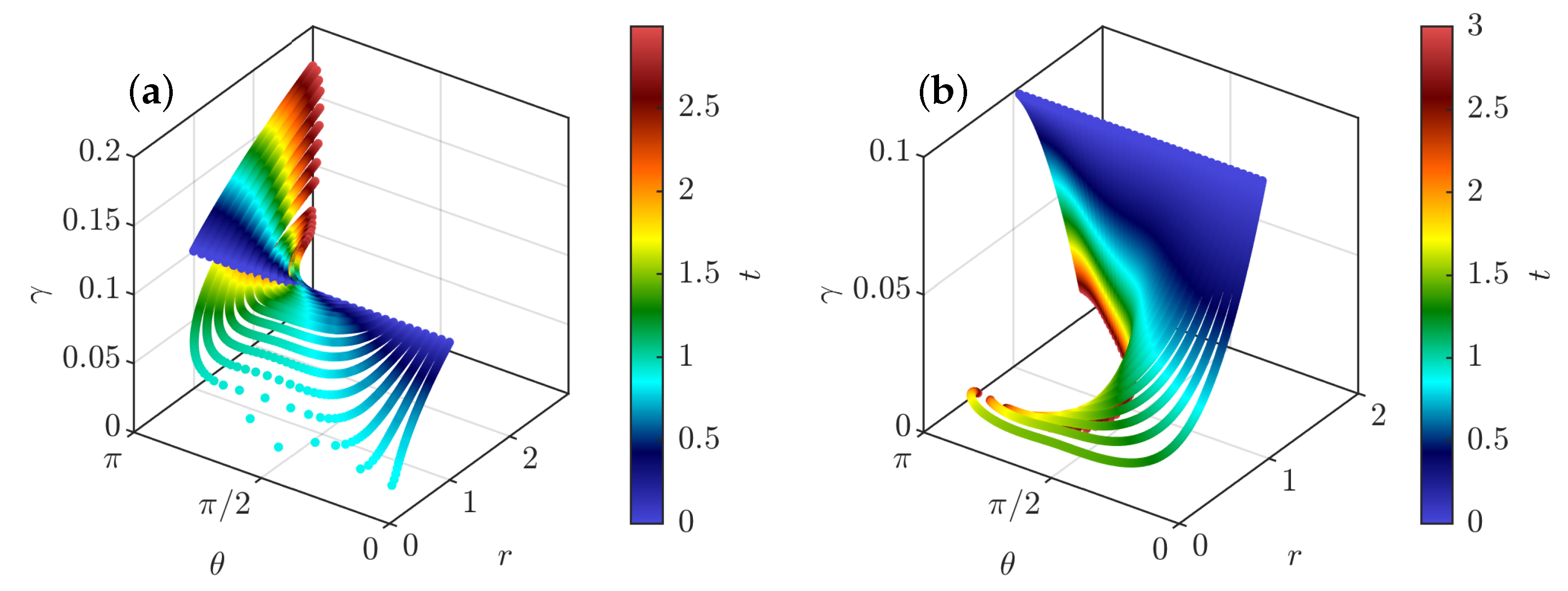
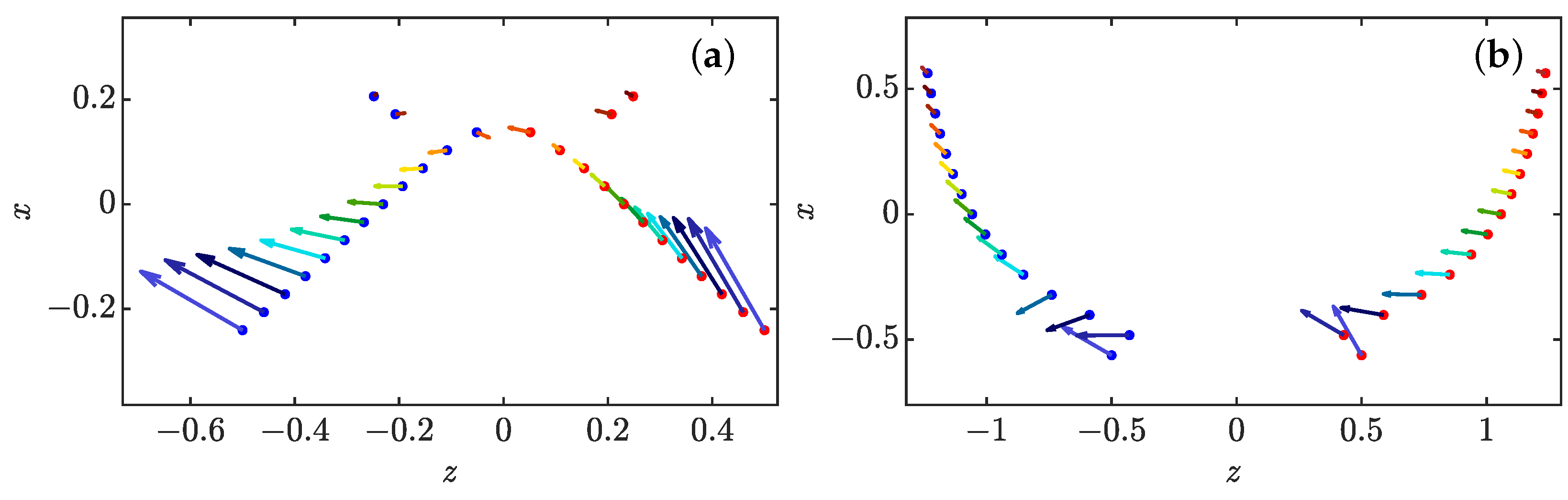
- repelling dipolar expansion, illustrated in Figure 8a. This case corresponds to the case where the two components run away from each other and gradually become a repelling dipole: their mutual angle tends to , while they become anti-parallel to their separation vector and their intensities become equal to each other and tend to 1. In this case, the role of each pinçon is symmetric.
- (ii)
- aligned expansion, illustrated in Figure 8b. In this case, one component grows larger than the other one, while both pinçons become aligned with their separation vector and point in the same direction , , . The component with the lower intensity moves faster and speeds ahead of the other one.
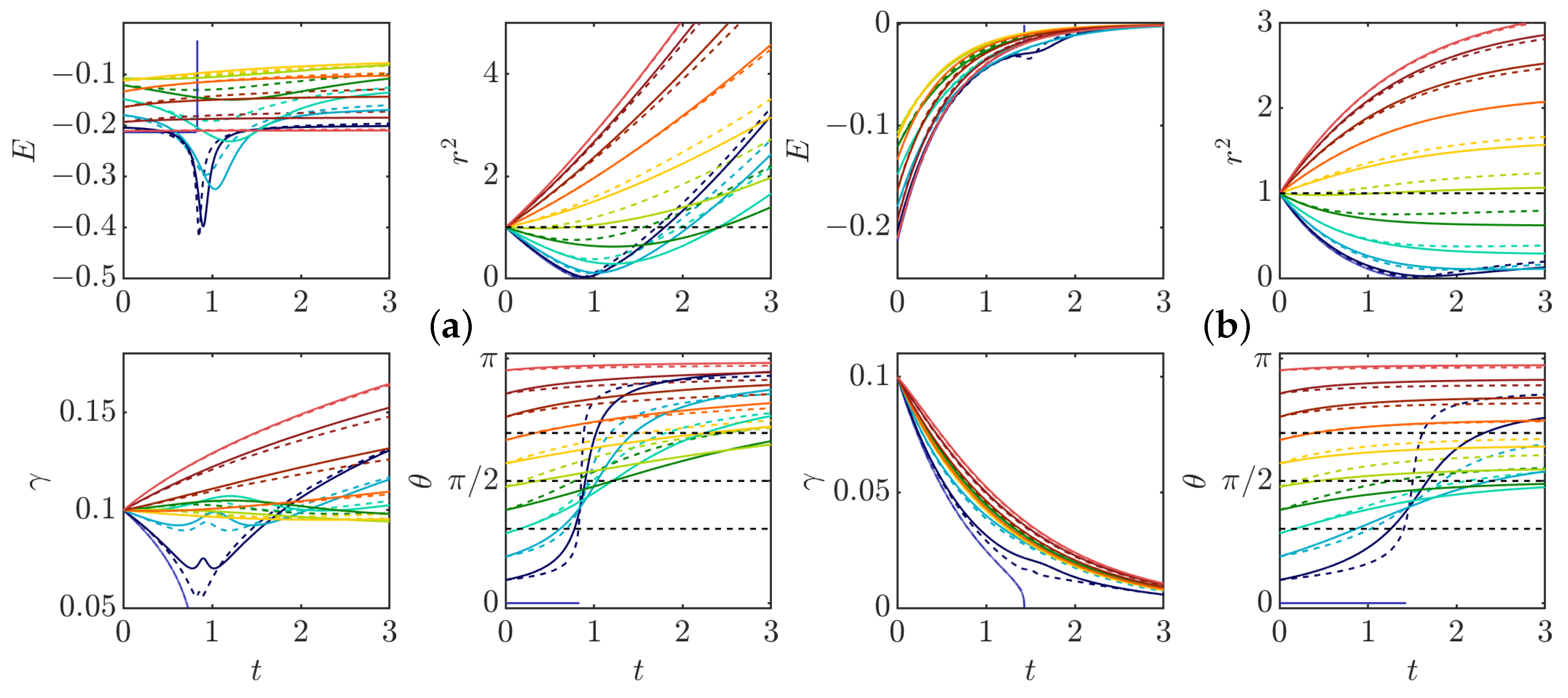
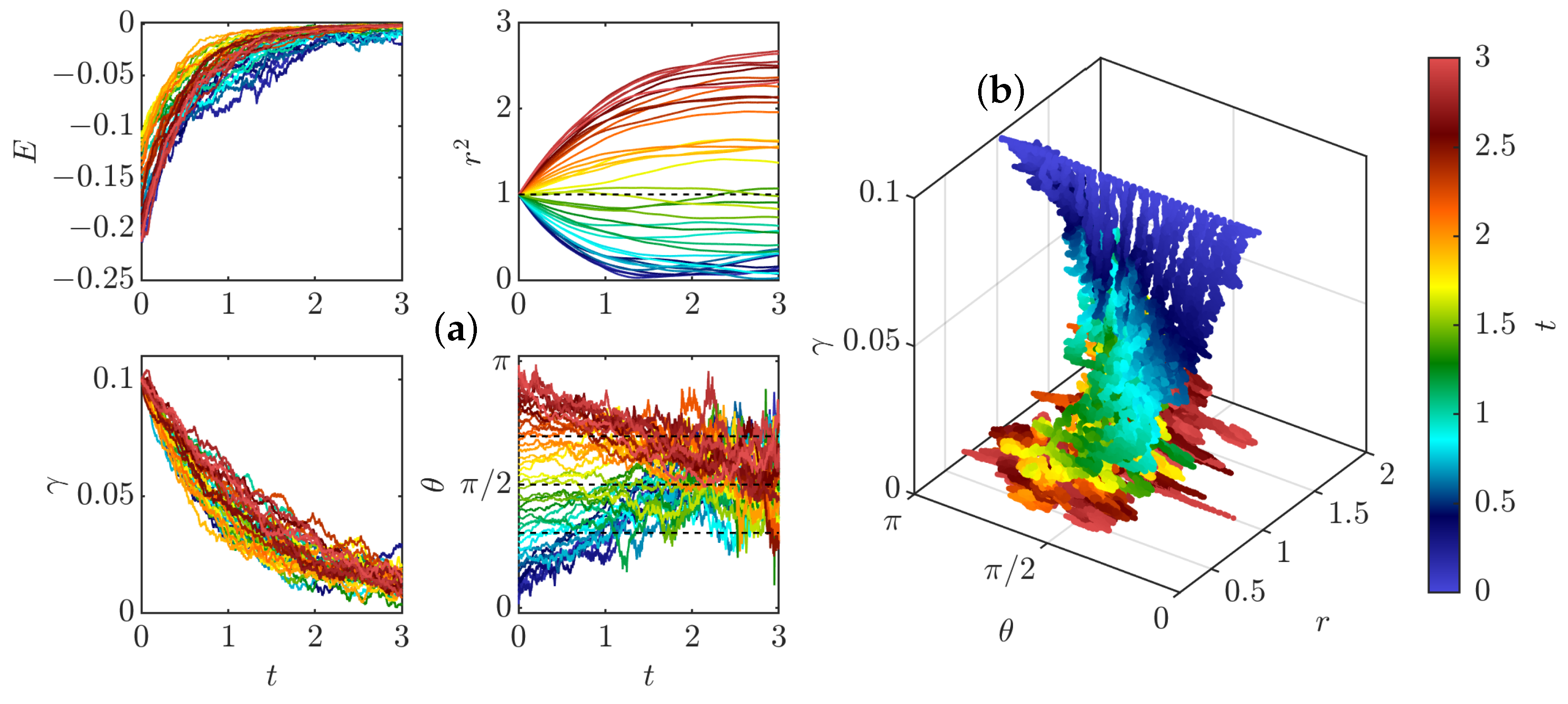
- (iii)
- explosive collapse, illustrated in Figure 9a. In this case, the two pinçons are attracted to each other, while one of the two pinçons rapidly reaches the asymptotic value , corresponding to an infinite dissipation. In contrast with the expansion situations where the pinçons tend to align or anti-align, the collapse case corresponds to intermediate values of and different from . This case can therefore be considered as the generic reconnection event.

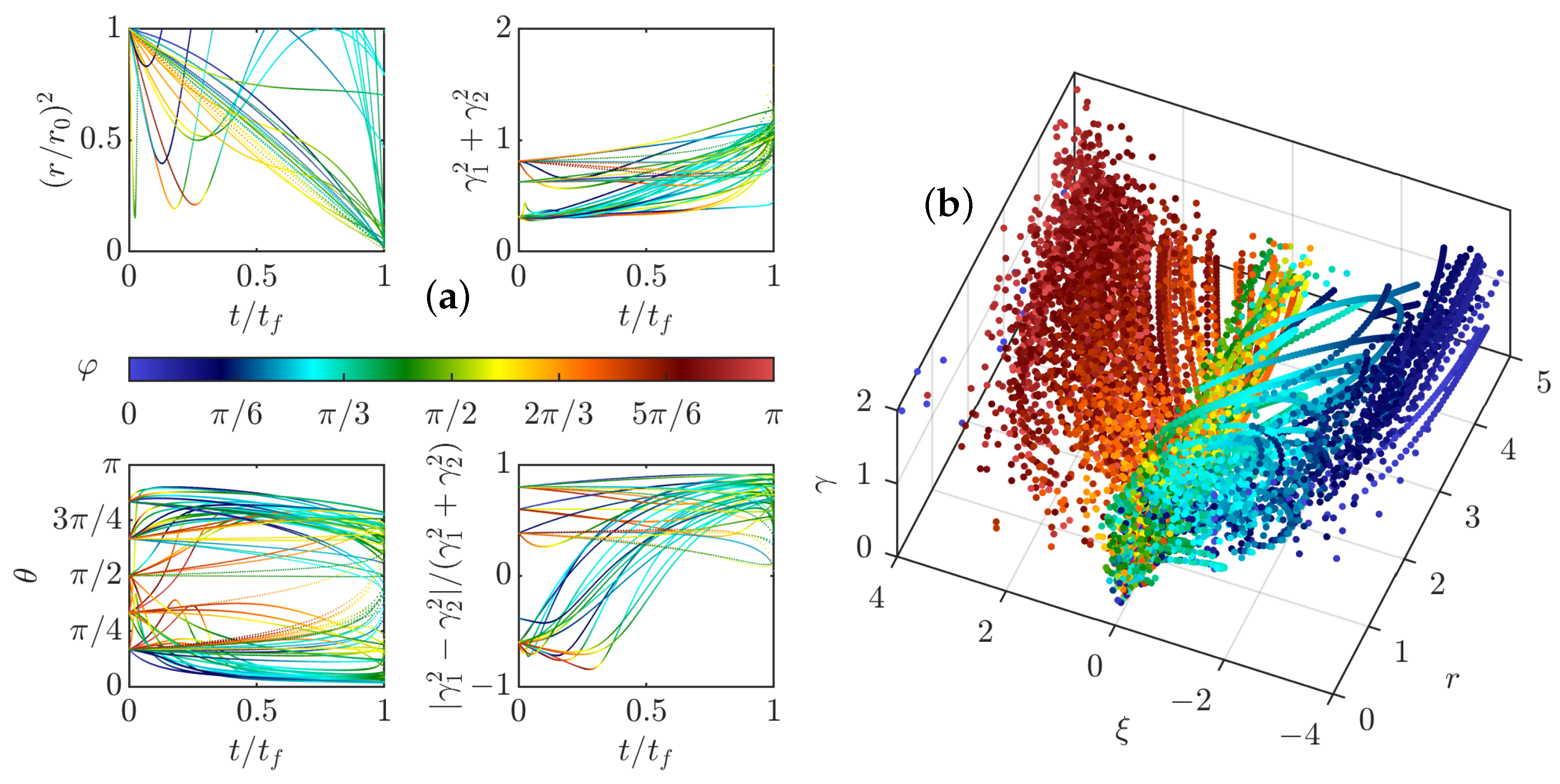
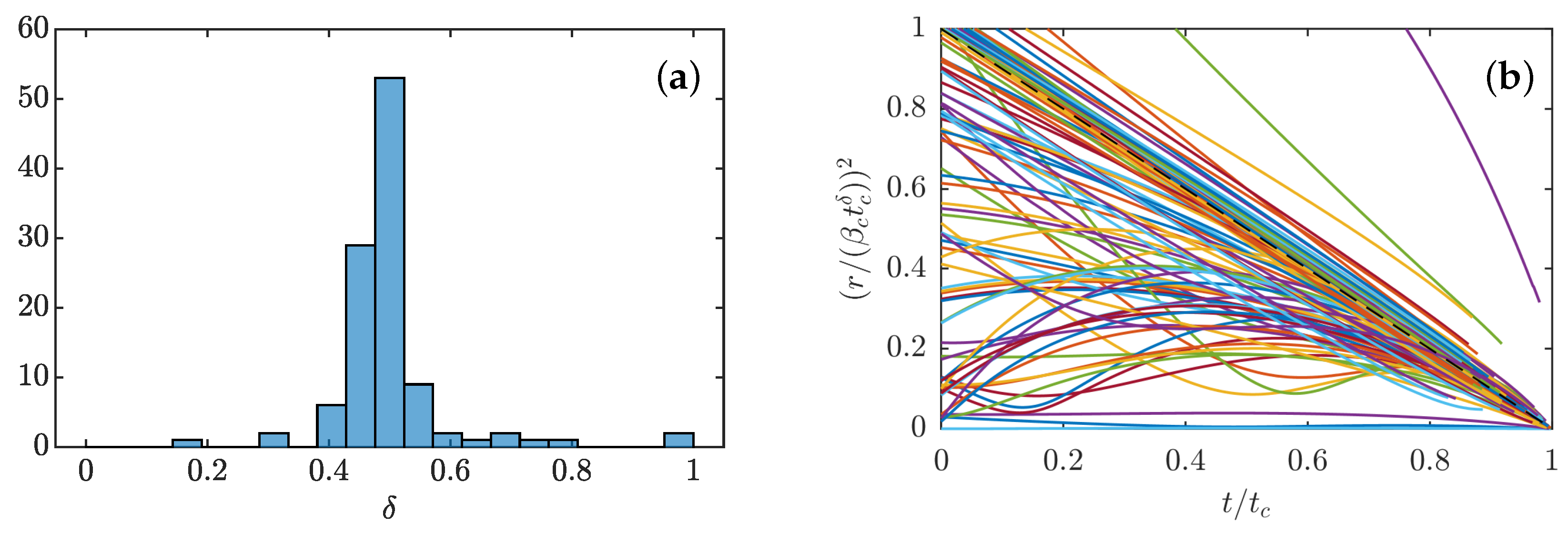
3.4.2. Scaling Laws of Collapse
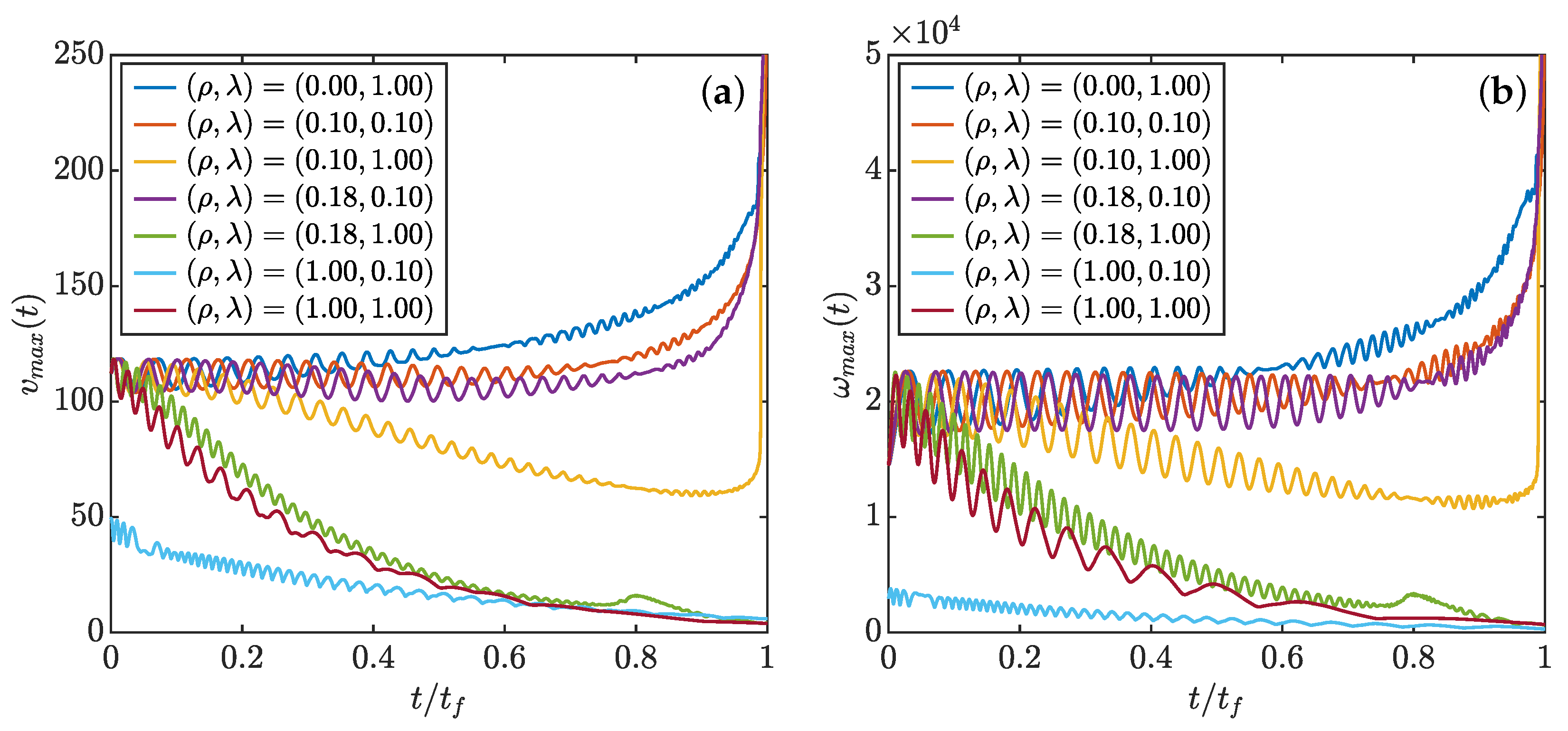
3.4.3. Full Collapse Dynamics
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Useful Properties
Appendix B. Computation of the Generalized Momentum
Appendix C. Velocity Gradient Tensor
Appendix D. Vorton Dynamics
References
- Gibbon, J.D.; Pal, N.; Gupta, A.; Pandit, R. Regularity criterion for solutions of the three-dimensional Cahn-Hilliard-Navier–Stokes equations and associated computations. Phys. Rev. E 2016, 94, 063103. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Constantin, P.; Weinan, E.; Titi, E.S. Onsager’s conjecture on the energy conservation for solutions of Euler’s equation. Commun. Math. Phys. 1994, 165, 207–209. [Google Scholar] [CrossRef]
- Hicks, W. Researches in vortex motion. Part III. On spiral or gyrostatic vortex aggregates. Proc. R. Soc. Lond. 1899, 62, 379387. [Google Scholar]
- Constantin, P.; Majda, A. The Beltrami spectrum for incompressible fluid flows. Commun. Math. Phys. 1988, 115, 435–456. [Google Scholar] [CrossRef]
- Buckmaster, T.; De Lellis, C.; Székelyhidi, L.; Vicol, V. Onsager’s Conjecture for Admissible Weak Solutions. Commun. Pure Appl. Math. 2018, 72, 229–274. [Google Scholar] [CrossRef]
- Lundgren, T.S. Strained spiral vortex model for turbulent fine structure. Phys. Fluids 1982, 25, 2193–2203. [Google Scholar] [CrossRef]
- Gilbert, A.D. A cascade interpretation of Lundgren stretched spiral vortex model for turbulent fine structure. Phys. Fluids A Fluid Dyn. 1993, 5, 2831–2834. [Google Scholar] [CrossRef]
- Chorin, A.J. Equilibrium statistics of a vortex filament with applications. Comm. Math. Phys. 1991, 141, 619–631. [Google Scholar] [CrossRef] [Green Version]
- Koumoutsakos, P. Multiscale flow simulations using particles. Annu. Rev. Fluid Mech. 2005, 37, 457–487. [Google Scholar] [CrossRef]
- Novikov, E.A. Generalized dynamics of three-dimensional vortex singularities /vortons/. Zhurnal Eksperimentalnoi Teor. Fiz. 1983, 84, 975–981. [Google Scholar]
- Aksman, M.J.; Novikov, E.A.; Orszag, S.A. Vorton Method in Three-Dimensional Hydrodynamics. Phys. Rev. Lett. 1985, 54, 2410–2413. [Google Scholar] [CrossRef] [PubMed]
- Alkemade, A.J.Q.; Nieuwstadt, F.T.M.; van Groesen, E. The vorton method. Appl. Sci. Res. 1993, 51, 3–7. [Google Scholar] [CrossRef] [Green Version]
- Pedrizzetti, G. Insight into singular vortex flows. Fluid Dyn. Res. 1992, 10, 101–115. [Google Scholar] [CrossRef]
- Saffman, P.G.; Meiron, D.I. Difficulties with three-dimensional weak solutions for inviscid incompressible flow. Phys. Fluids 1986, 29, 2373–2375. [Google Scholar] [CrossRef]
- Winckelmans, G.; Leonard, A. Weak solutions of the three-dimensional vorticity equation with vortex singularities. Phys. Fluids 1988, 31, 1838–1839. [Google Scholar] [CrossRef]
- Greengard, C.; Thomann, E. Singular vortex systems and weak solutions of the Euler equations. Phys. Fluids 1988, 31, 2810–2813. [Google Scholar] [CrossRef]
- Yeung, P.K.; Sreenivasan, K.R.; Pope, S.B. Effects of finite spatial and temporal resolution in direct numerical simulations of incompressible isotropic turbulence. Phys. Rev. Fluids 2018, 3, 064603. [Google Scholar] [CrossRef]
- Dubrulle, B. Beyond Kolmogorov cascades. J. Fluid Mech. 2019, 867, P1. [Google Scholar] [CrossRef] [Green Version]
- Leray, J. Sur le mouvement d’un liquide visqueux emplissant l’espace. Acta Math. 1934, 63, 193248. [Google Scholar] [CrossRef]
- Sverák, V. On Landau’s solutions of the Navier–Stokes equations. J. Math. Sci. 2011, 179, 208. [Google Scholar] [CrossRef] [Green Version]
- Landau, L.D. A new exact solution of the Navier-Stokes equations. Dokl. Akad. Nauk SSSR 1944, 44, 311314. [Google Scholar]
- Squire, H. XCI. Some viscous fluid flow problems I: Jet emerging from a hole in a plane wall. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1952, 43, 942–945. [Google Scholar] [CrossRef]
- Batchelor, G. An Introduction to Fluid Dynamics; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Tian, G.; Xin, Z. One-point singular solutions to the Navier–Stokes equations. Topol. Methods Nonlinear Anal. 1998, 11, 135–145. [Google Scholar] [CrossRef]
- Cannone, M.; Karch, G. Smooth or singular solutions to the Navier–Stokes system? J. Differ. Equ. 2004, 197, 247–274. [Google Scholar] [CrossRef] [Green Version]
- Eyink, G.L. Turbulence Theory. Course Notes. The Johns Hopkins University. 2007–2008. Available online: https://www.ams.jhu.edu/~eyink/Turbulence/notes.html (accessed on 23 June 2022).
- Kruskal, M.D. The Korteweg-de Vries equation and related evolution equations. In Nonlinear Wave Motion; American Mathematical Society: Providence, RI, USA, 1974; pp. 61–83. [Google Scholar]
- Calogero, F. Motion of poles and zeros of special solutions of nonlinear and linear partial differential equations and related solvablemany-body problems. Il Nuovo C. B (1971–1996) 1978, 43, 177–241. [Google Scholar] [CrossRef]
- Calogero, F. Classical many-body problems amenable to exact treatments. In Lecture Notes in Physics; Springer: Berlin, Germany, 2001; Volume 66. [Google Scholar]
- Saw, E.W.; Kuzzay, D.; Faranda, D.; Guittoneau, A.; Daviaud, F.; Wiertel-Gasquet, C.; Padilla, V.; Dubrulle, B. Experimental characterization of extreme events of inertial dissipation in a turbulent swirling flow. Nat. Comm. 2016, 7, 12466. [Google Scholar] [CrossRef] [Green Version]
- Debue, P.; Valori, V.; Cuvier, C.; Daviaud, F.; Foucaut, J.M.; Laval, J.P.; Wiertel, C.; Padilla, V.; Dubrulle, B. Three-dimensional analysis of precursors to non-viscous dissipation in an experimental turbulent flow. J. Fluid Mech. 2021, 914, A9. [Google Scholar] [CrossRef]
- Nguyen, F.; Laval, J.P.; Dubrulle, B. Characterizing most irregular small-scale structures in turbulence using local Hölder exponents. Phys. Rev. E 2020, 102, 063105. [Google Scholar] [CrossRef]
- Kerr, R.M.; Hussain, F. Simulation of vortex reconnection. Phys. D Nonlinear Phenom. 1989, 37, 474–484. [Google Scholar] [CrossRef]
- Yao, J.; Hussain, F. A physical model of turbulence cascade via vortex reconnection sequence and avalanche. J. Fluid Mech. 2020, 883, A51. [Google Scholar] [CrossRef]
- Yao, J.; Hussain, F. On singularity formation via viscous vortex reconnection. J. Fluid Mech. 2020, 888, R2. [Google Scholar] [CrossRef]
- Kimura, Y.; Moffatt, H.K. A tent model of vortex reconnection under Biot–Savart evolution. J. Fluid Mech. 2018, 834, R1. [Google Scholar] [CrossRef]
- Moffatt, H.K.; Kimura, Y. Towards a finite-time singularity of the Navier–Stokes equations Part 1. Derivation and analysis of dynamical system. J. Fluid Mech. 2019, 861, 930–967. [Google Scholar] [CrossRef] [Green Version]
- Moffatt, H.K.; Kimura, Y. Towards a finite-time singularity of the Navier–Stokes equations. Part 2. Vortex reconnection and singularity evasion. J. Fluid Mech. 2019, 870, R1. [Google Scholar] [CrossRef] [Green Version]
- Moffatt, H.K.; Kimura, Y. Towards a finite-time singularity of the Navier–Stokes equations. Part 2. Vortex reconnection and singularity evasion—CORRIGENDUM. J. Fluid Mech. 2020, 887, E2. [Google Scholar] [CrossRef] [Green Version]
- Kimura, Y.; Moffatt, H.K. Scaling properties towards vortex reconnection under Biot–Savart evolution. Fluid Dyn. Res. 2017, 50, 011409. [Google Scholar] [CrossRef] [Green Version]
- Villois, A.; Proment, D.; Krstulovic, G. Irreversible Dynamics of Vortex Reconnections in Quantum Fluids. Phys. Rev. Lett. 2020, 125, 164501. [Google Scholar] [CrossRef]
- Laval, J.P.; Dubrulle, B.; Nazarenko, S. Fast numerical simulations of 2D turbulence using a dynamic model for subfilter motions. J. Comput. Phys. 2004, 196, 184–207. [Google Scholar] [CrossRef] [Green Version]

| 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Faller, H.; Fery, L.; Geneste, D.; Dubrulle, B. A Model of Interacting Navier–Stokes Singularities. Entropy 2022, 24, 897. https://doi.org/10.3390/e24070897
Faller H, Fery L, Geneste D, Dubrulle B. A Model of Interacting Navier–Stokes Singularities. Entropy. 2022; 24(7):897. https://doi.org/10.3390/e24070897
Chicago/Turabian StyleFaller, Hugues, Lucas Fery, Damien Geneste, and Bérengère Dubrulle. 2022. "A Model of Interacting Navier–Stokes Singularities" Entropy 24, no. 7: 897. https://doi.org/10.3390/e24070897
APA StyleFaller, H., Fery, L., Geneste, D., & Dubrulle, B. (2022). A Model of Interacting Navier–Stokes Singularities. Entropy, 24(7), 897. https://doi.org/10.3390/e24070897






