Numerical Study on Entropy Generation of the Multi-Stage Centrifugal Pump
Abstract
:1. Introduction
2. Entropy Generation Theorem
3. Experimental and Numerical Methods
3.1. Experimental Model
3.2. Grid Generation and Grid Independence Investigation
3.3. Turbulence Model and Boundary Conditions
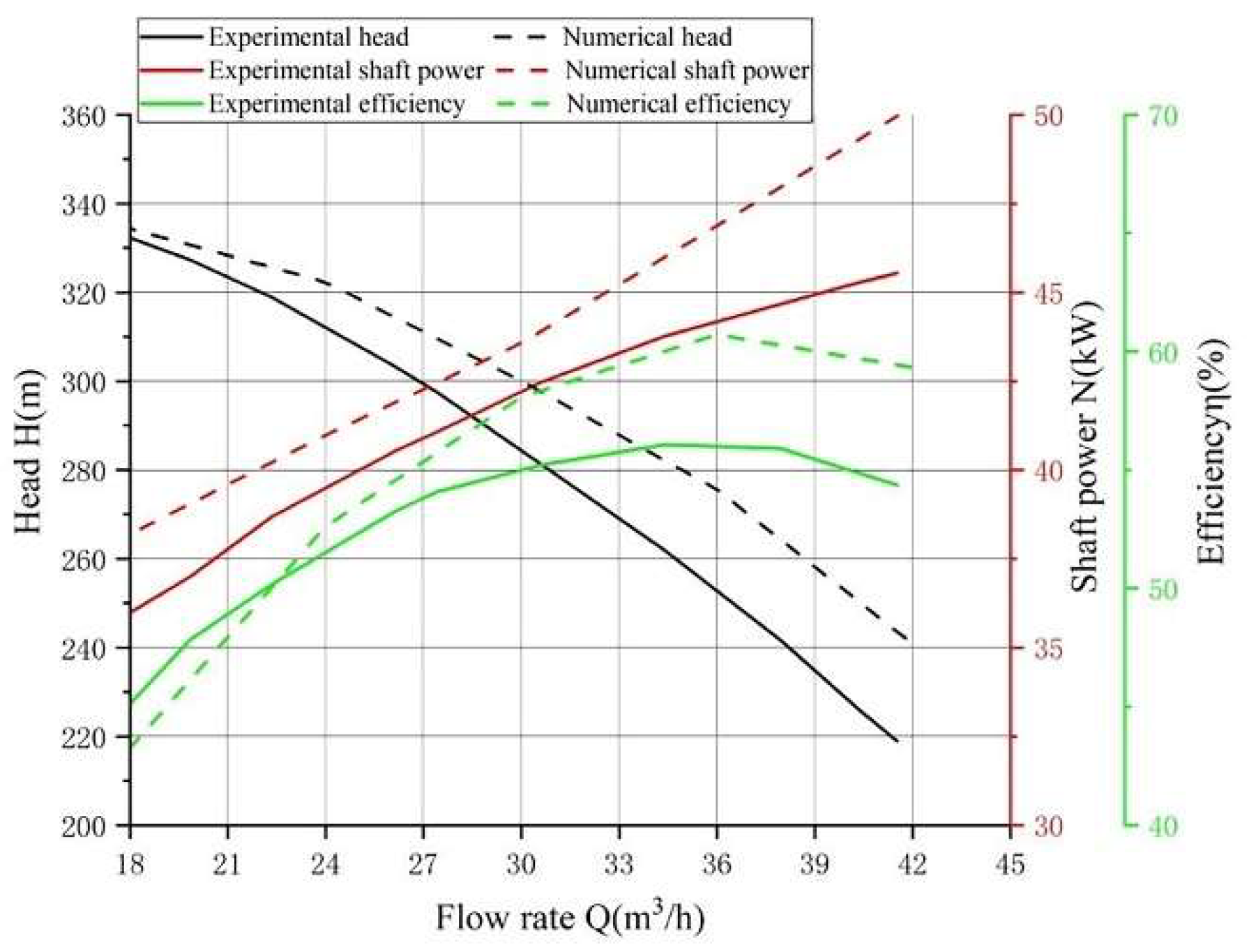
3.4. Validation of the Numerical Results
4. Results and Discussion
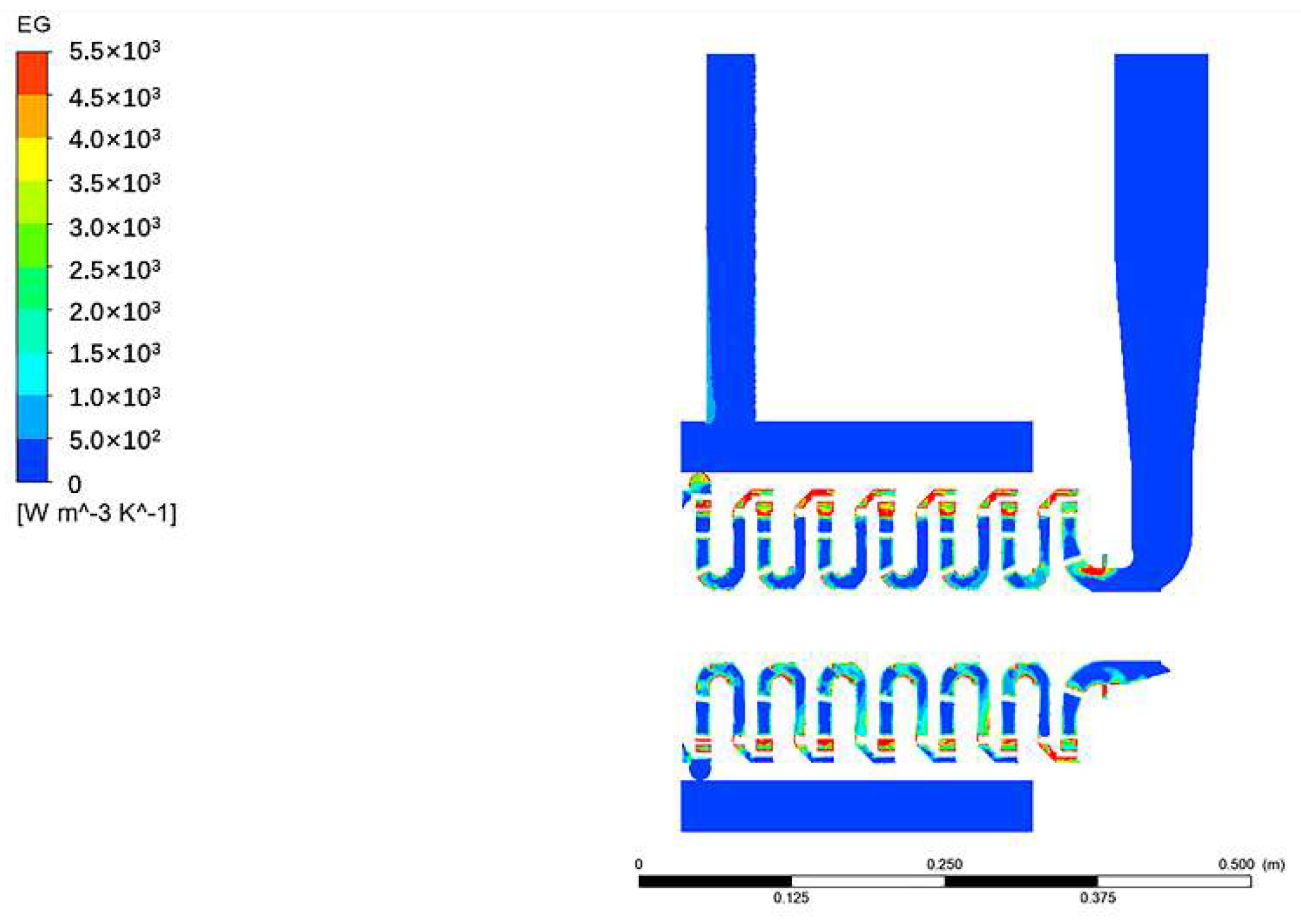
4.1. Entropy Generation of Different Components under the Rated Flow Condition
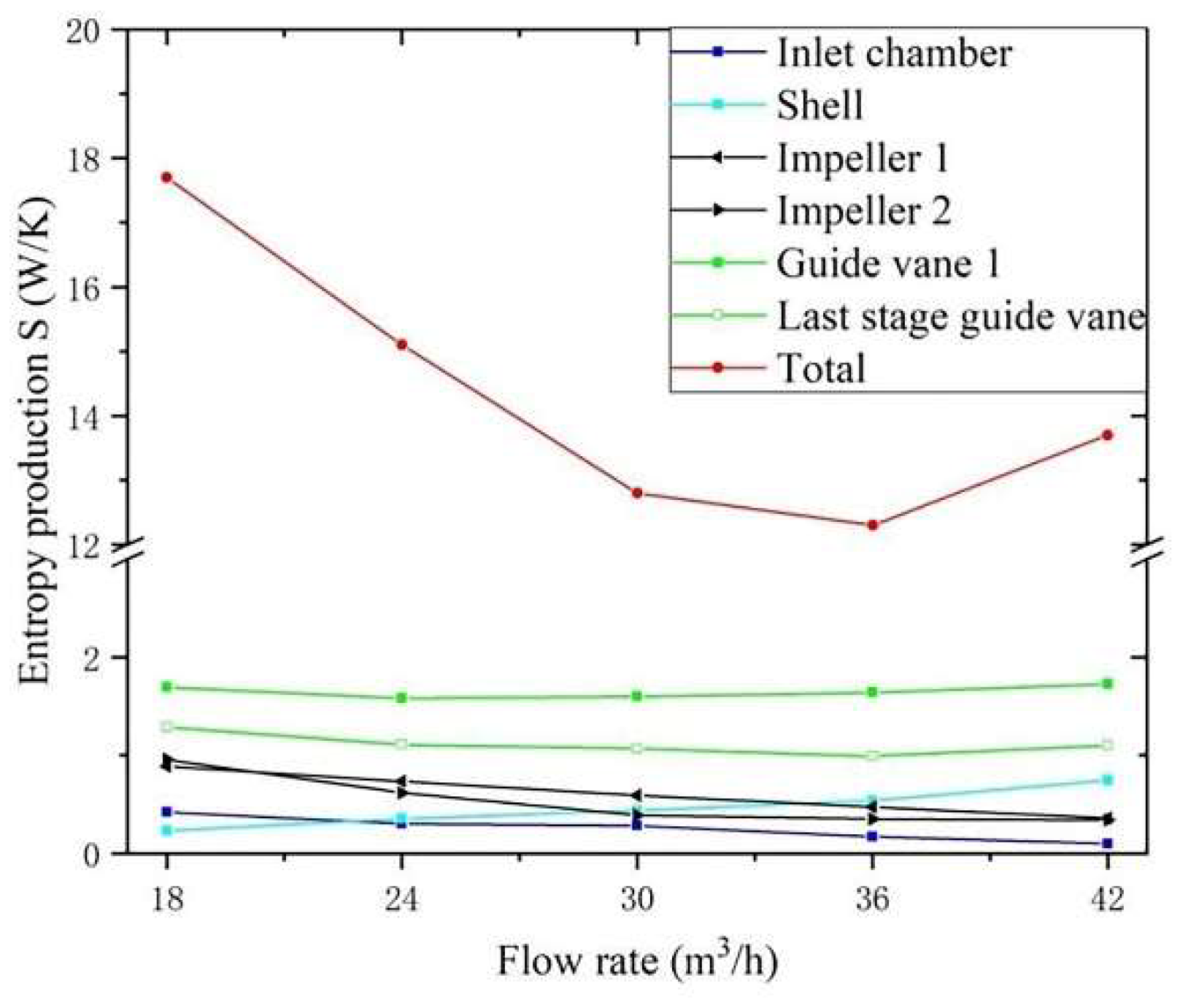
4.2. Entropy Generation of Different Components under Different Flow Conditions
4.3. Entropy Generation of the Impellers and Guide Vanes
5. Conclusions
- Entropy generation of the guide vanes and impellers accounted for 71.2% and 23.3% of the total entropy generation at a flow rate of 1.0 Qd, respectively. The entropy generation of the guide vanes is the biggest entropy generation at about 9 W/K, thus the guide vanes are the main hydraulic loss domains, followed by impellers.
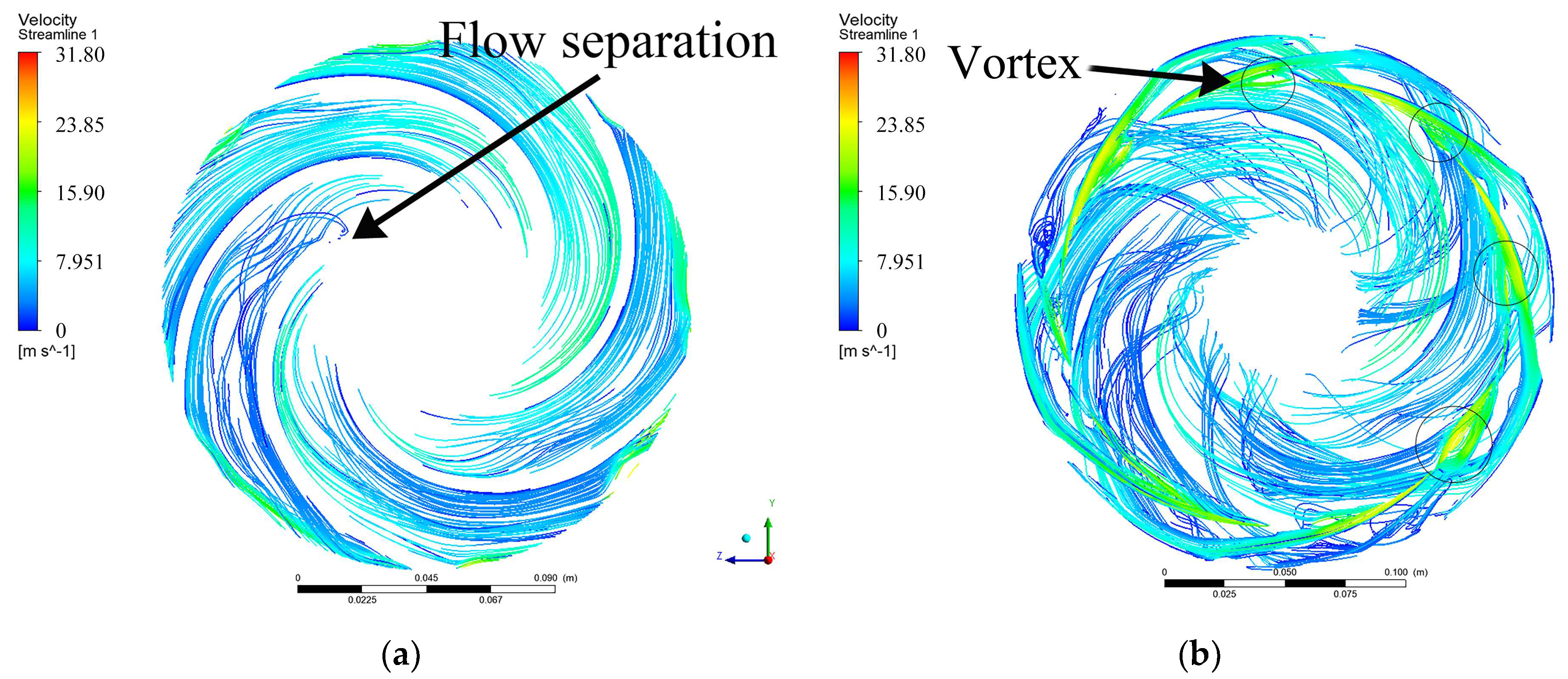
- There are many vortices at the guide vane inlet, which are located on the tongue of the guide vane. Additionally, there are flow separations in the impeller. The fluid impacts the outer edge of the guide vane, which leads to the increase in entropy generation. Furthermore, there is the reflux near the guide vane tongue, which also increases entropy generation.
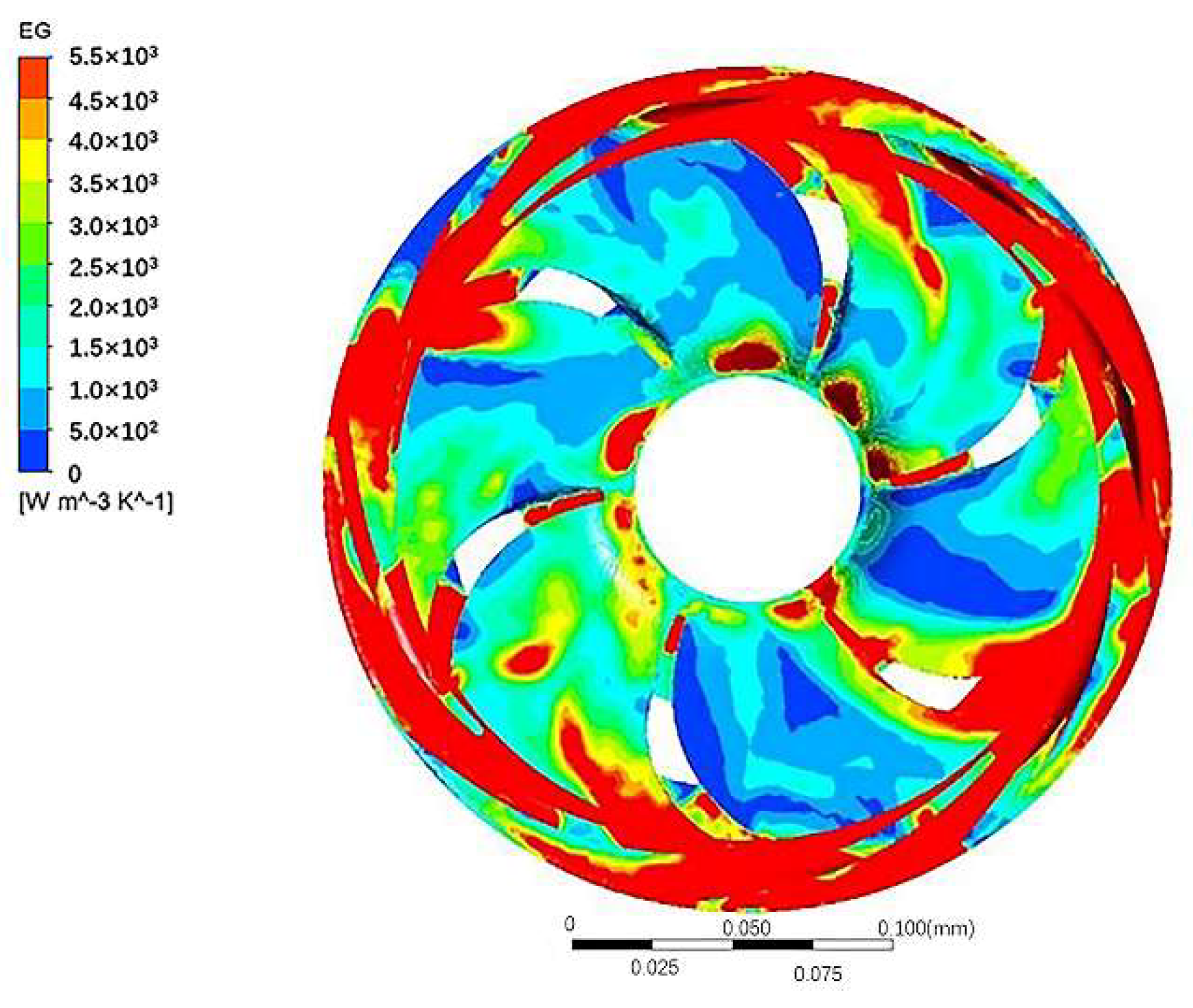
- The entropy generation of the positive guide vane and blade suction surface is greater compared with the reverse guide vane and pressure surface, respectively.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Holbein, P.; Dupont, P. CFD Calculation of a Mixed Flow Pump Characteristic from Shutoff to Maximum Flow. J. Fluids Eng. 2002, 124, 798–802. [Google Scholar] [CrossRef]
- Cao, S.; Peng, G.; Yu, Z. Hydrodynamic Design of Rotodynamic Pump Impeller for Multiphase Pumping by Combined Approach of Inverse Design and CFD Analysis. J. Fluids Eng. 2004, 127, 330–338. [Google Scholar] [CrossRef]
- Guleren, K.M.; Pinarbasi, A. Numerical simulation of the stalled flow within a vaned centrifugal pump. ARCHIVE Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2004, 218, 425–435. [Google Scholar] [CrossRef]
- Jafarzadeh, B.; Hajari, A.; Alishahi, M.M.; Akbari, M.H. The flow simulation of a low-specific-speed high-speed centrifugal pump. Appl. Math. Model. 2011, 35, 242–249. [Google Scholar] [CrossRef]
- Zhou, P.J.; Wang, F.J.; Yang, M. Internal flow numerical simulation of double-suction centrifugal pump using DES model. IOP Conf. Ser. Earth Environ. Sci. 2012, 15, 41–51. [Google Scholar] [CrossRef]
- Feng, J.; Luo, X.; Guo, P.; Wu, G. Influence of tip clearance on pressure fluctuations in an axial flow pump. J. Mech. Sci. Technol. 2016, 30, 1603–1610. [Google Scholar] [CrossRef]
- Zhu, D.S.; Ji, G.F.; Cheng, W.Q. Effect of Multi Stage Centrifugal Pump on the Guide Vane Based on CFD Simulation. J. North Univ. China Nat. Sci. Ed. (China) 2017, 38, 322–326, 332. [Google Scholar] [CrossRef]
- Bejan, A.; Kestin, J. Entropy Generation Through Heat and Fluid Flow. J. Appl. Mech. 1983, 50, 475. [Google Scholar] [CrossRef]
- Spurk, J.H. Fluid Mechanics; Springer: New York, NY, USA, 1997; pp. 67–74. [Google Scholar]
- Kock, F.; Herwig, H. Entropy production calculation for turbulent shear flows and their implementation in CFD codes. Int. J. Heat Fluid Flow 2005, 26, 672–680. [Google Scholar] [CrossRef]
- Zhang, H.C.; Schmandt, B.; Herwig, H. Determination of Loss Coefficients for Micro-Flow Devices: A Method Based on the Second Law Analysis (SLA). In Proceedings of the ASME 2009 2nd Micro/Nanoscale Heat & Mass Transfer International Conference MNHMT, Shanghai, China, 18–21 December 2009; Volume 2. [Google Scholar]
- Chu, S.X.; Liu, L.H. Entropy generation analysis of two-dimensional high-temperature confined jet. Int. J. Therm. Sci. 2009, 48, 998–1006. [Google Scholar] [CrossRef]
- Hou, H.; Zhang, Y.; Li, Z. A numerical research on energy loss evaluation in a centrifugal pump system based on local entropy production method. Therm. Sci. 2016, 2016, 143. [Google Scholar] [CrossRef]
- Hou, H.; Zhang, Y.; Li, Z.; Jiang, T.; Zhang, J.; Xu, C. Numerical analysis of entropy production on a LNG cryogenic submerged pump. J. Nat. Gas Sci. Eng. 2016, 36, 87–96. [Google Scholar] [CrossRef]
- Li, X.; Jiang, Z.; Zhu, Z.; Si, Q.; Li, Y. Entropy generation analysis for the cavitating head-drop characteristic of a centrifugal pump. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2018, 232, 4637–4646. [Google Scholar] [CrossRef]
- Liang, Z.; Xiang, L.; Wei, X.; Chen, S.; Liu, J.; Hao, Z. Numerical study on the flow characteristics of centrifugal compressor impeller with crack damage. Adv. Mech. Eng. 2021, 13, 1–15. [Google Scholar] [CrossRef]
- Yu, A.; Tang, Y.; Tang, Q.; Cai, J.; Zhao, L.; Ge, X. Energy analysis of Francis turbine for various mass flow rate conditions based on entropy production theory. Renew. Energy 2022, 183, 447–458. [Google Scholar] [CrossRef]
- Zhang, F. Study on Flow Loss Characteristics of Side Channel Pump Based on Entropy Production. J. Mech. Eng. 2018, 54, 137. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, Y.; Hou, H.; Zhang, J.; Xu, C. Entropy production diagnostic analysis of energy consumption for cavitation flow in a two-stage LNG cryogenic submerged pump. Int. J. Heat Mass Transf. 2019, 129, 342–356. [Google Scholar] [CrossRef]
- Ghorani, M.M.; Sotoude Haghighi, M.H.; Maleki, A.; Riasi, A. A numerical study on mechanisms of energy dissipation in a pump as turbine (PAT) using entropy generation theory. Renew. Energy 2020, 162, 1036–1053. [Google Scholar] [CrossRef]
- Li, S.; Wu, P.; Wu, D. Hydraulic Optimization and Loss Analyses of a Low Specific-Speed Centrifugal Pump with Variable-Thickness Blades. In Proceedings of the Fluids Engineering Division Summer Meeting, Washington, DC, USA, 10–14 July 2016; p. V01BT27A003. [Google Scholar]
- Pei, J.; Meng, F.; Li, Y.; Yuan, S.; Chen, J. Effects of distance between impeller and guide vane on losses in a low head pump by entropy production analysis. Adv. Mech. Eng. 2016, 8, 11. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Hou, H.; Xu, C.; He, W.; Li, Z. Application of entropy production method to centrifugal pump energy loss evaluation. Paiguan Jixie Gongcheng Xuebao/J. Drain. Irrig. Mach. Eng. 2017, 35, 277–282. [Google Scholar] [CrossRef]
- Li, Y.; Feng, G.; Li, X.; Si, Q.; Zhu, Z. An experimental study on the cavitation vibration characteristics of a centrifugal pump at normal flow rate. J. Mech. Sci. Technol. 2018, 32, 4711–4720. [Google Scholar] [CrossRef]
- Feng, J.; Zhang, Y.; Zhu, G.; Li, Y.; Li, W.; Luo, X. Transition process characteristics of centrifugal pump with power-off based on entropy production theory. Trans. Chin. Soc. Agric. Eng. 2020, 36, 10–17. [Google Scholar]
- Koranteng Osman, M.; Wang, W.; Yuan, J.; Zhao, J.; Wang, Y.; Liu, J. Flow loss analysis of a two-stage axially split centrifugal pump with double inlet under different channel designs. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 5316–5328. [Google Scholar] [CrossRef]
- Ren, Y.; Zhu, Z.C.; Wu, D.H.; Li, X.J. Influence of Guide Ring on Energy Loss in a Multistage Centrifugal Pump. J. Fluids Eng.-Trans. Asme 2019, 141, 061302. [Google Scholar] [CrossRef]
- Wu, T.X.; Wu, D.; Zhang, T.; Huang, H.M.; Wu, Y.Z.; Mou, J. Influence of Diffuser Vane Number on Energy Loss of Multistage Centrifugal Pump. Int. J. Fluid Mach. Syst. 2021, 14, 373–382. [Google Scholar] [CrossRef]
- Spurk, J.H.; Aksel, N. Strömungslehre; Springer: Berlin/Heidelberg, Germany, 1989; Volume 4. [Google Scholar]
- Herwig, H.; Kock, F. Direct and indirect methods of calculating entropy generation rates in turbulent convective heat transfer problems. Heat Mass Transf. 2007, 43, 207–215. [Google Scholar] [CrossRef]
- Callenaere, M.; Franc, J.-P.; Michel, J.-M.; Riondet, M. The cavitation instability induced by the development of a re-entrant jet. J. Fluid Mech. 2001, 444, 223–256. [Google Scholar] [CrossRef]
- Kock, F.; Herwig, H. Local entropy production in turbulent shear flows: A high-Reynolds number model with wall functions. Int. J. Heat Mass Transf. 2004, 47, 2205–2215. [Google Scholar] [CrossRef]
- Sheng-Bo, H.U.; Mo-Ming, S.U. Comparison of Different Turbulence Models for Numerical Simulation of Internal Flow of Centrifugal Compressor. Fluid Mach. 2010, 38, 22–26. [Google Scholar]
- Zhang, M.; Shen, Y. Application of 3-D RNG k-ε turbulence model of meandering river. J. Hydroelectr. Eng. 2007, 26, 86–91. [Google Scholar]
- Zhang, J.; Xu, C.; Zhang, Y.; Zhou, X. Quasi-3D hydraulic design in the application of an LNG cryogenic submerged pump. J. Nat. Gas Sci. Eng. 2016, 29, 89–100. [Google Scholar] [CrossRef]
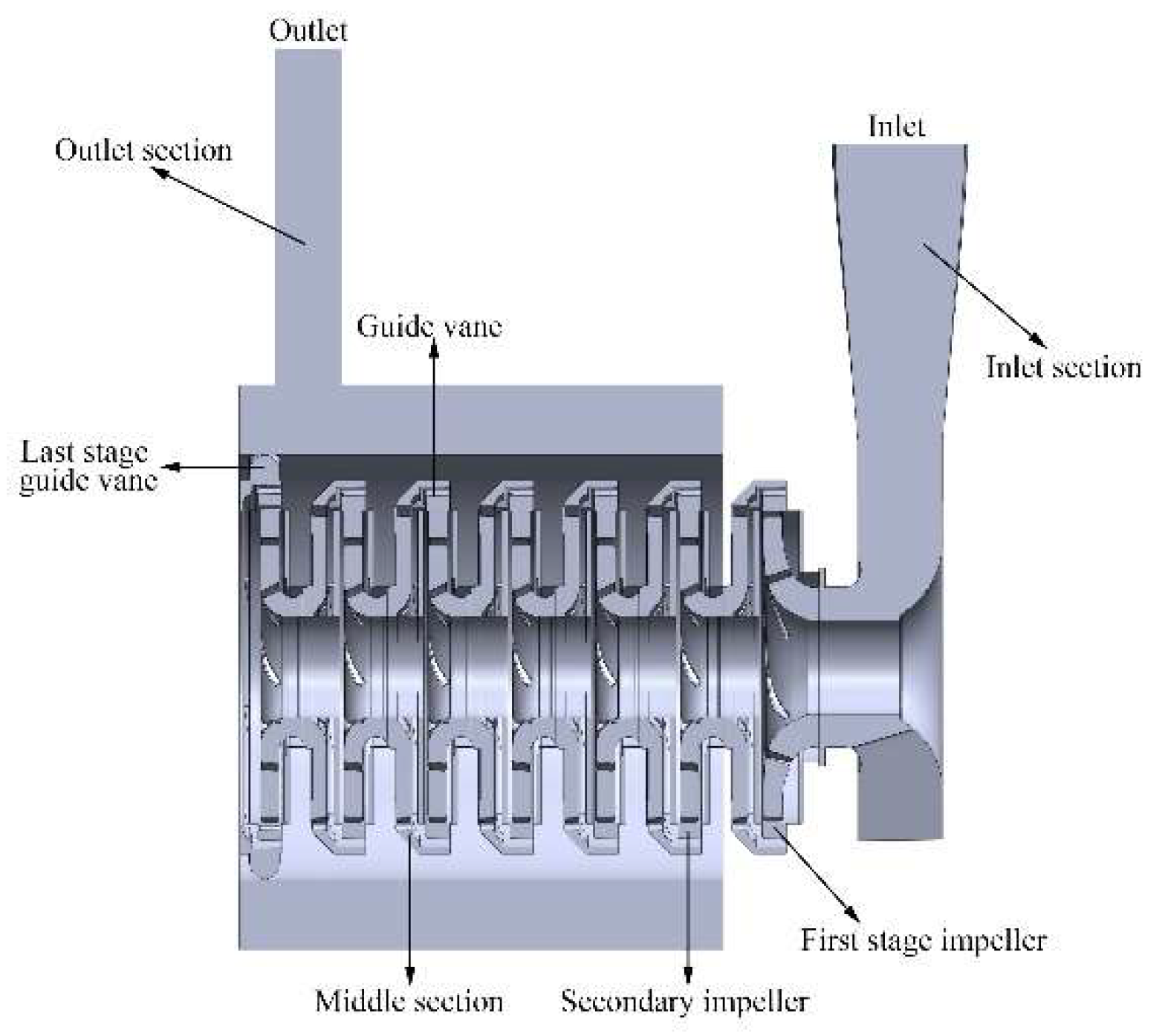

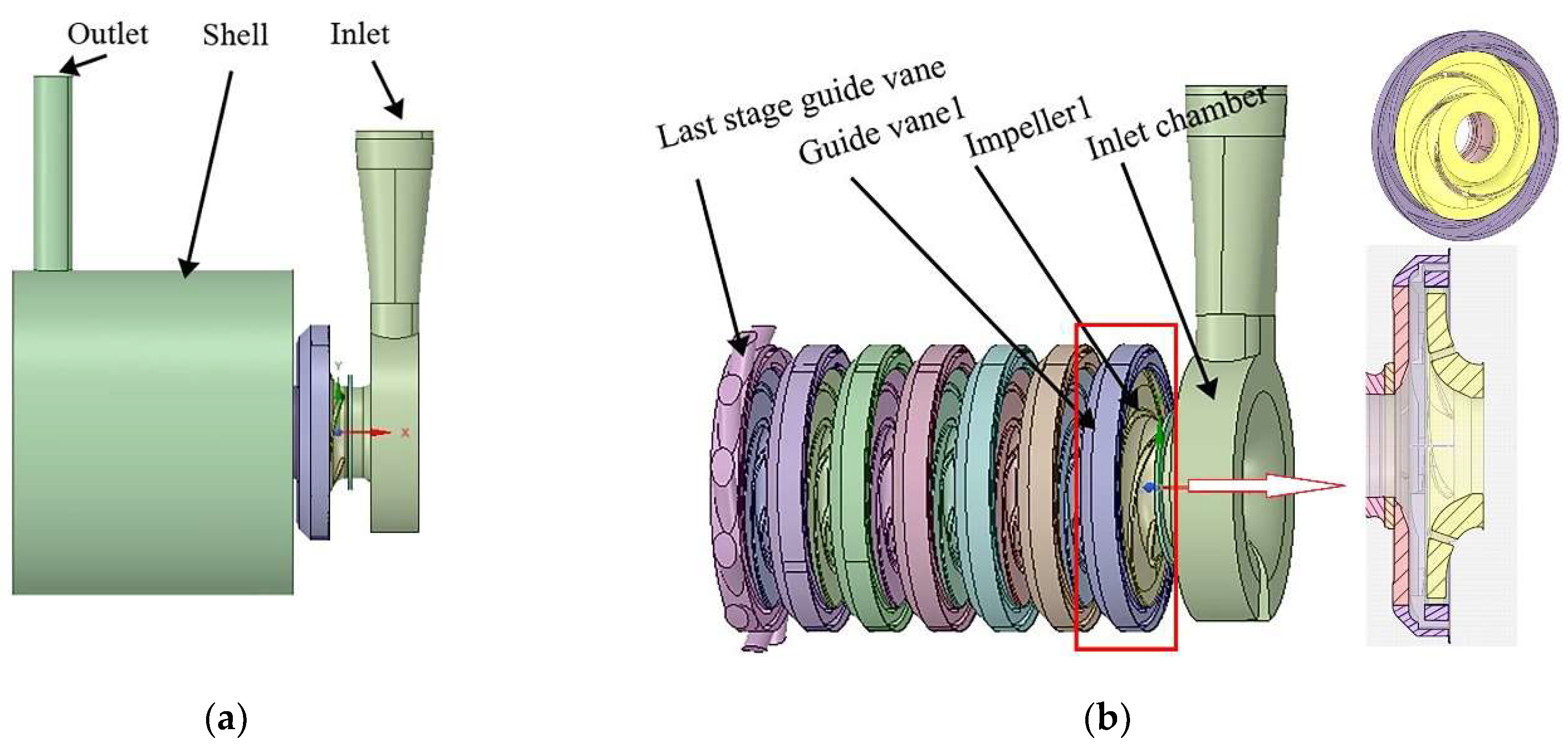


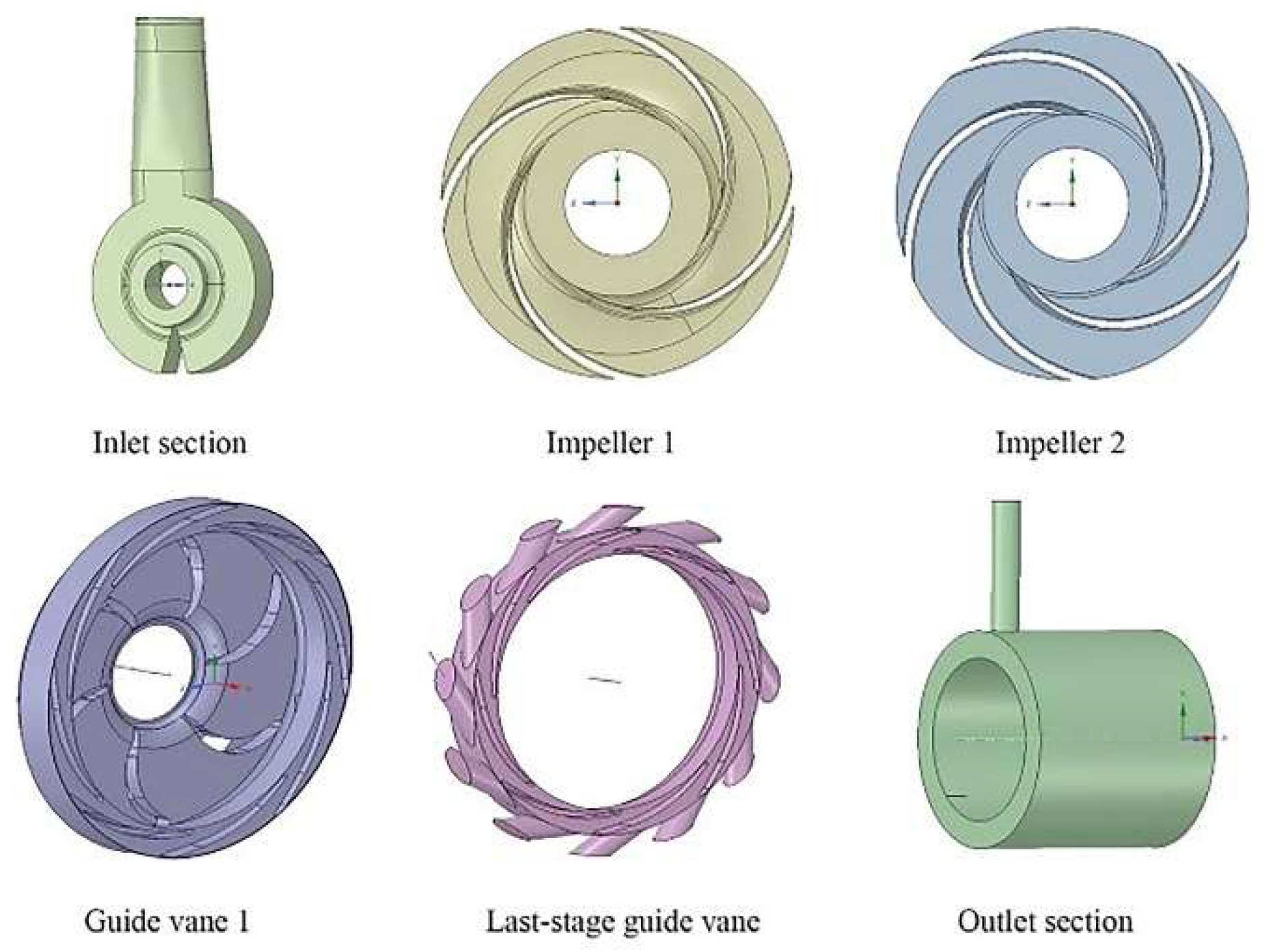



| Rated Flow (m3/h) | Rated Speed (rpm) | Rated Head (m) | Cavitation Allowance (m) | Shaft Power (kw) | Motor Power (kw) |
|---|---|---|---|---|---|
| 30 | 2980 | 252.2 | 30 | 30 | 30 |
| Electromagnetic Flowmeter | Resonant Pressure Transmitter | Motor | Photoelectric Tachometer | Multi-Stage Centrifugal Pump |
|---|---|---|---|---|
| E-mag | EJA430E | Variable-Frequency Adjustable-Speed Three-Phase Roller | Laser Doppler Velocimeter | BB5 Seven-Stage Pump |
| Region | Grids | y+ | Region | Grids | y+ |
|---|---|---|---|---|---|
| Inlet chamber | 564,800 | 90 | Guide vane 1 | 806,900 | 125 |
| Impeller 1 | 437,800 | 144 | Guide vane 2 | 807,000 | 132 |
| Impeller 2 | 504,700 | 122 | Guide vane 3 | 811,200 | 120 |
| Impeller 3 | 504,900 | 121 | Guide vane 4 | 807,000 | 120 |
| Impeller 4 | 502,500 | 123 | Guide vane 5 | 809,800 | 120 |
| Impeller 5 | 507,200 | 123 | Guide vane 6 | 808,700 | 124 |
| Impeller 6 | 503,900 | 123 | Last-stage guide vane | 653,400 | 124 |
| Impeller 7 | 510,000 | 125 | Shell | 293,500 | 180 |
| Total Number of Grids | Head (m) | Relative Error with Experimental Data (%) |
|---|---|---|
| 7,535,621 | 320.6 | 12.1 |
| 8,904,698 | 310.7 | 9.2 |
| 9,833,274 | 300.2 | 6.7 |
| 11,015,236 | 298.3 | 5.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, B.; Liang, Z.; Fan, R.; Chen, S. Numerical Study on Entropy Generation of the Multi-Stage Centrifugal Pump. Entropy 2022, 24, 923. https://doi.org/10.3390/e24070923
Fan B, Liang Z, Fan R, Chen S. Numerical Study on Entropy Generation of the Multi-Stage Centrifugal Pump. Entropy. 2022; 24(7):923. https://doi.org/10.3390/e24070923
Chicago/Turabian StyleFan, Baoxin, Zhaoyu Liang, Ruonan Fan, and Songying Chen. 2022. "Numerical Study on Entropy Generation of the Multi-Stage Centrifugal Pump" Entropy 24, no. 7: 923. https://doi.org/10.3390/e24070923
APA StyleFan, B., Liang, Z., Fan, R., & Chen, S. (2022). Numerical Study on Entropy Generation of the Multi-Stage Centrifugal Pump. Entropy, 24(7), 923. https://doi.org/10.3390/e24070923






