Asymmetric Fractal Characteristics and Market Efficiency Analysis of Style Stock Indices
Abstract
:1. Introduction
2. Literature Review
3. Method
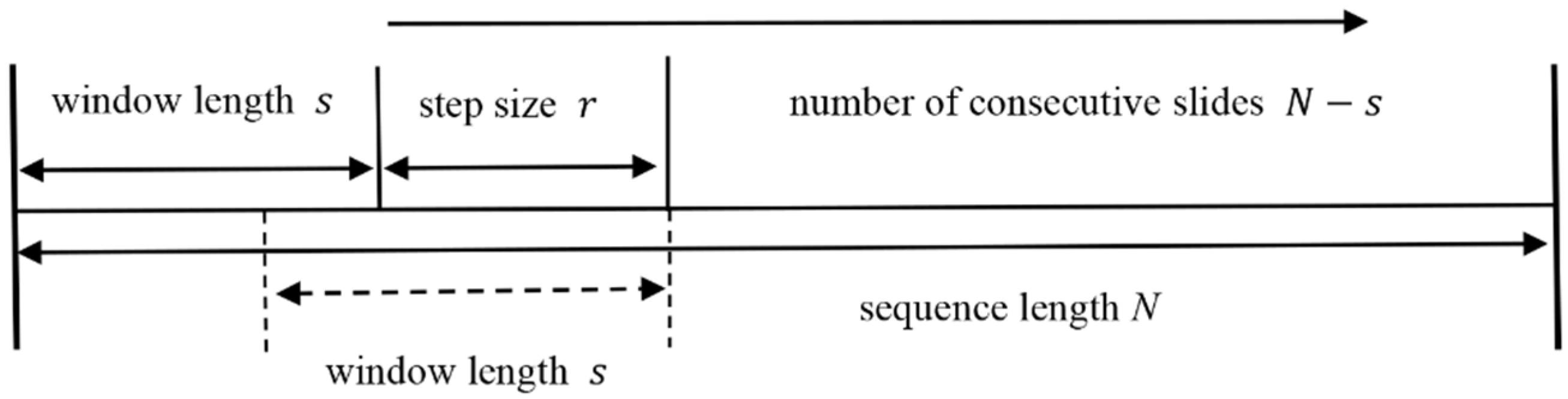
3.1. The A-MFDFA Method and Improvement
- (a)
- If there is no significant change in with the change in the fluctuation order , it indicates that the system exhibits the characteristics of a single fractal. Conversely, if changes significantly with the fluctuation order , it indicates that the system exhibits multifractal characteristics.
- (a)
- For large positive numbers , describes the scaling behavior where large fluctuations dominate. Conversely, for negative or small positive numbers , describes the fractal characteristics dominated by small fluctuations. In particular, when is equal to 2, is the classical Hurst exponent, which measures the overall long memory of the series.
- (c)
- It is worth noting that the correlation in the time series is persistent if , which means that one increment is more likely to be followed by another. However, if , there is inverse persistence, indicating that an increment is more likely to follow a trend transition. When , it means that the sequence follows a random walk process.
3.2. Multifractal Spectrum
3.3. Market Efficiency Indicator
4. Data and Descriptive Statistics
5. Results and Analysis of Style Stock Indices
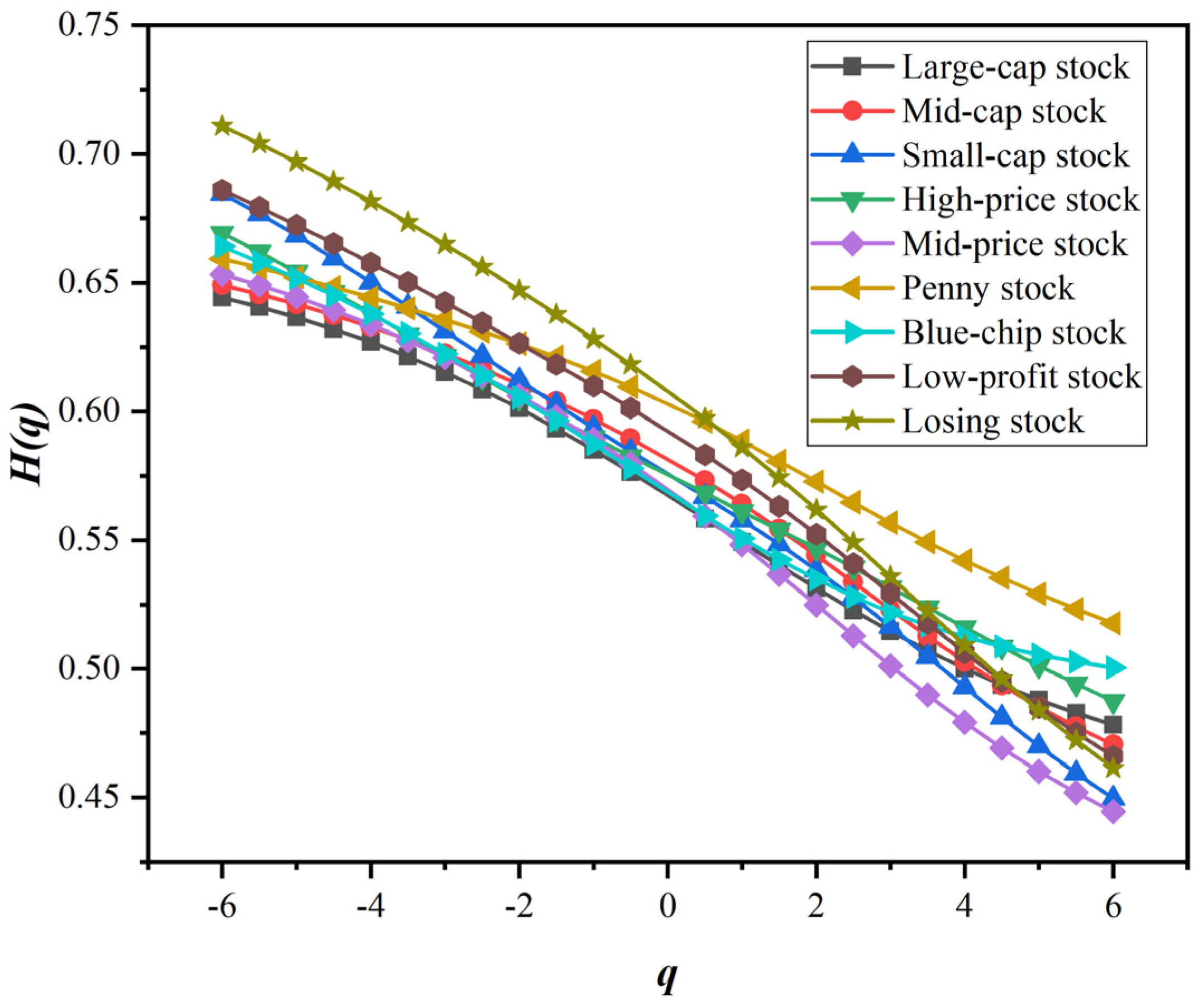
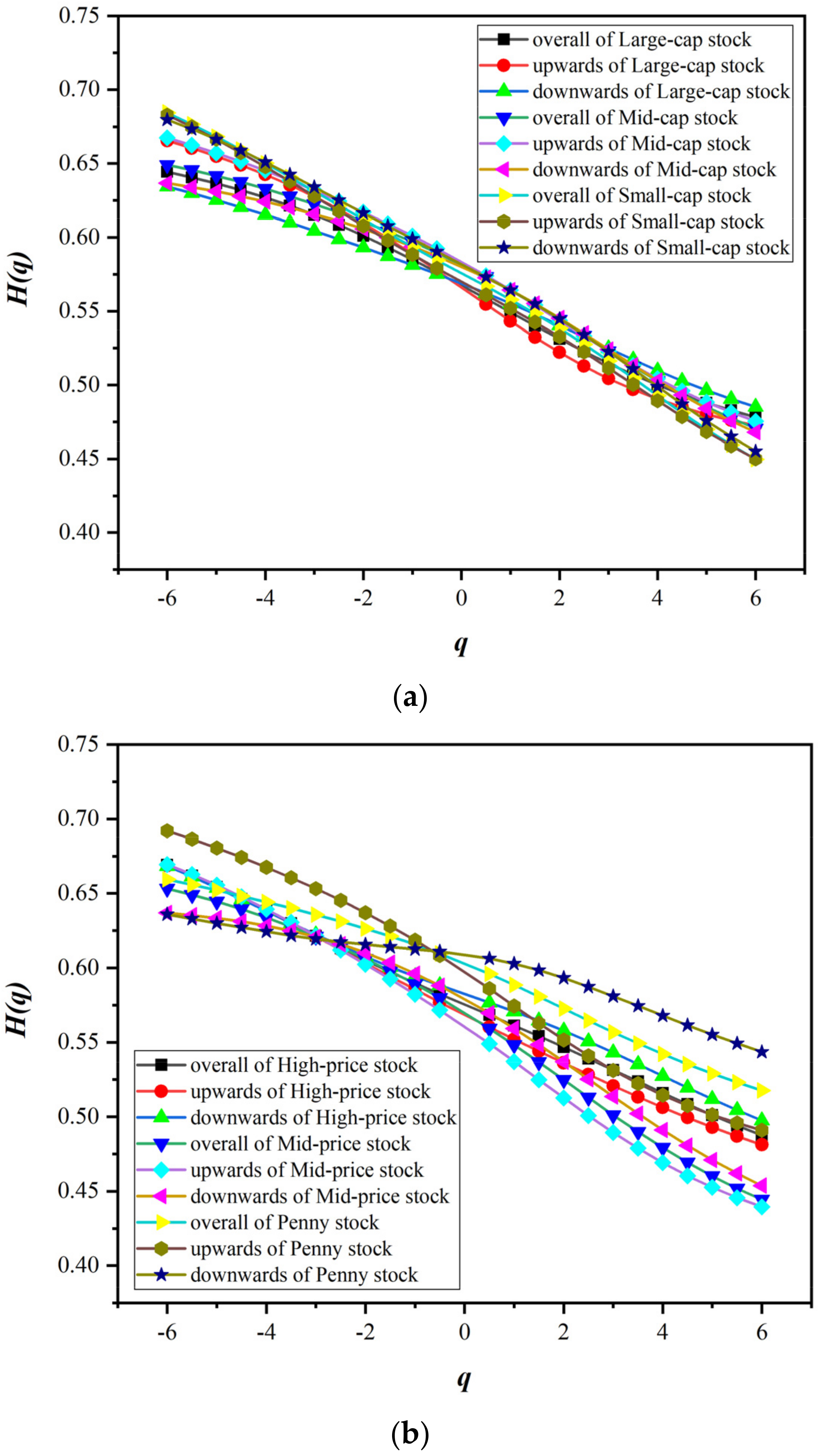
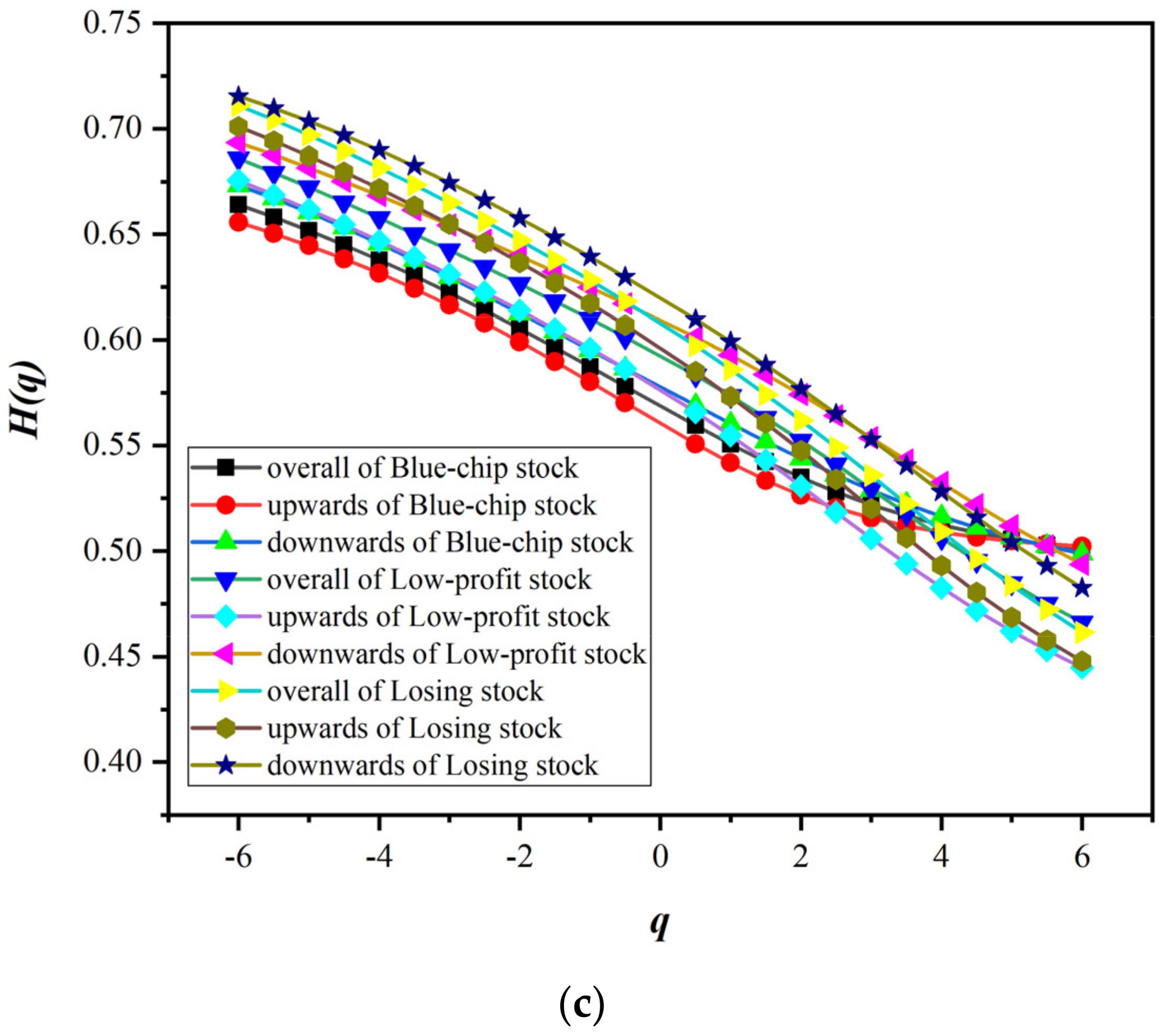
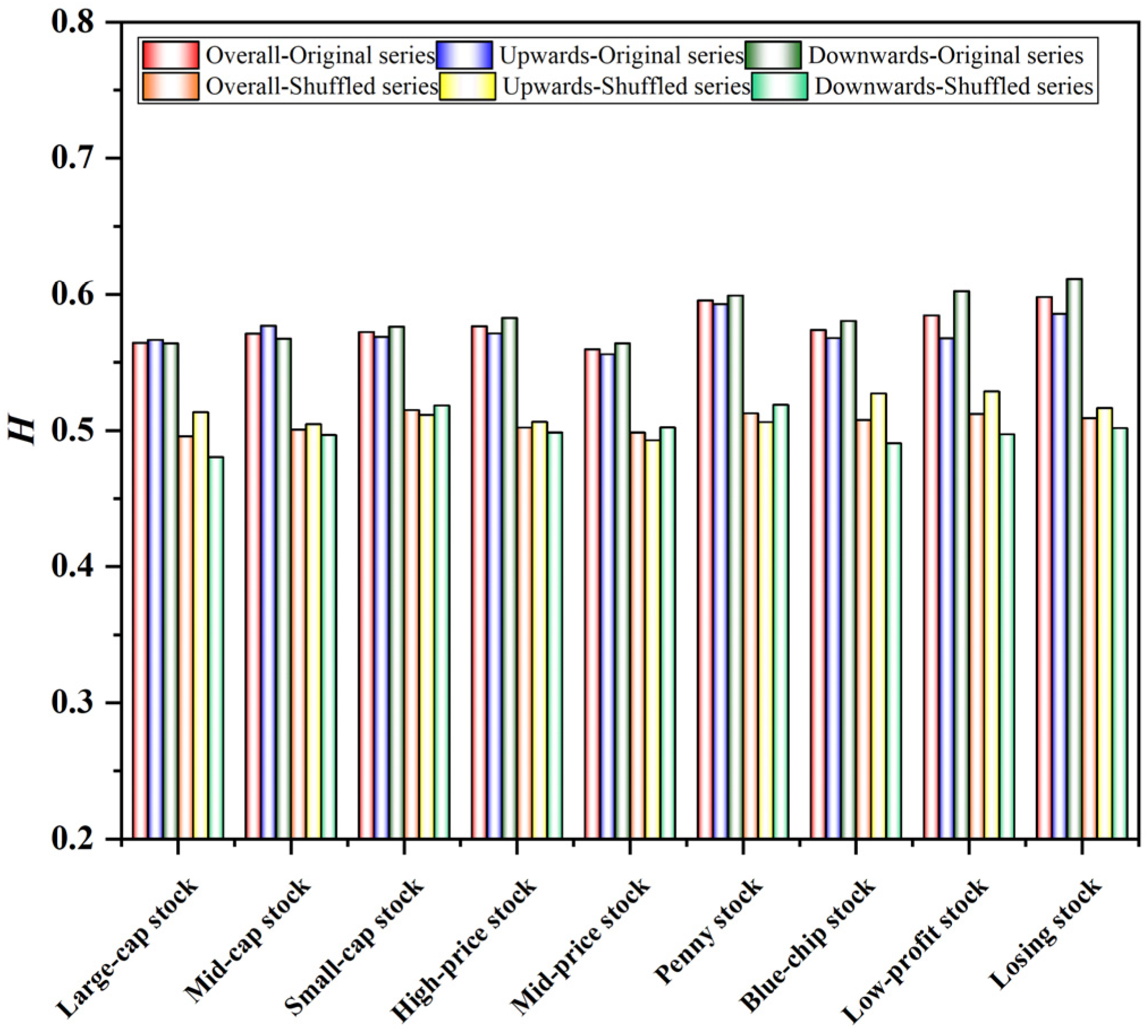
5.1. Asymmetric Multifractal Analysis
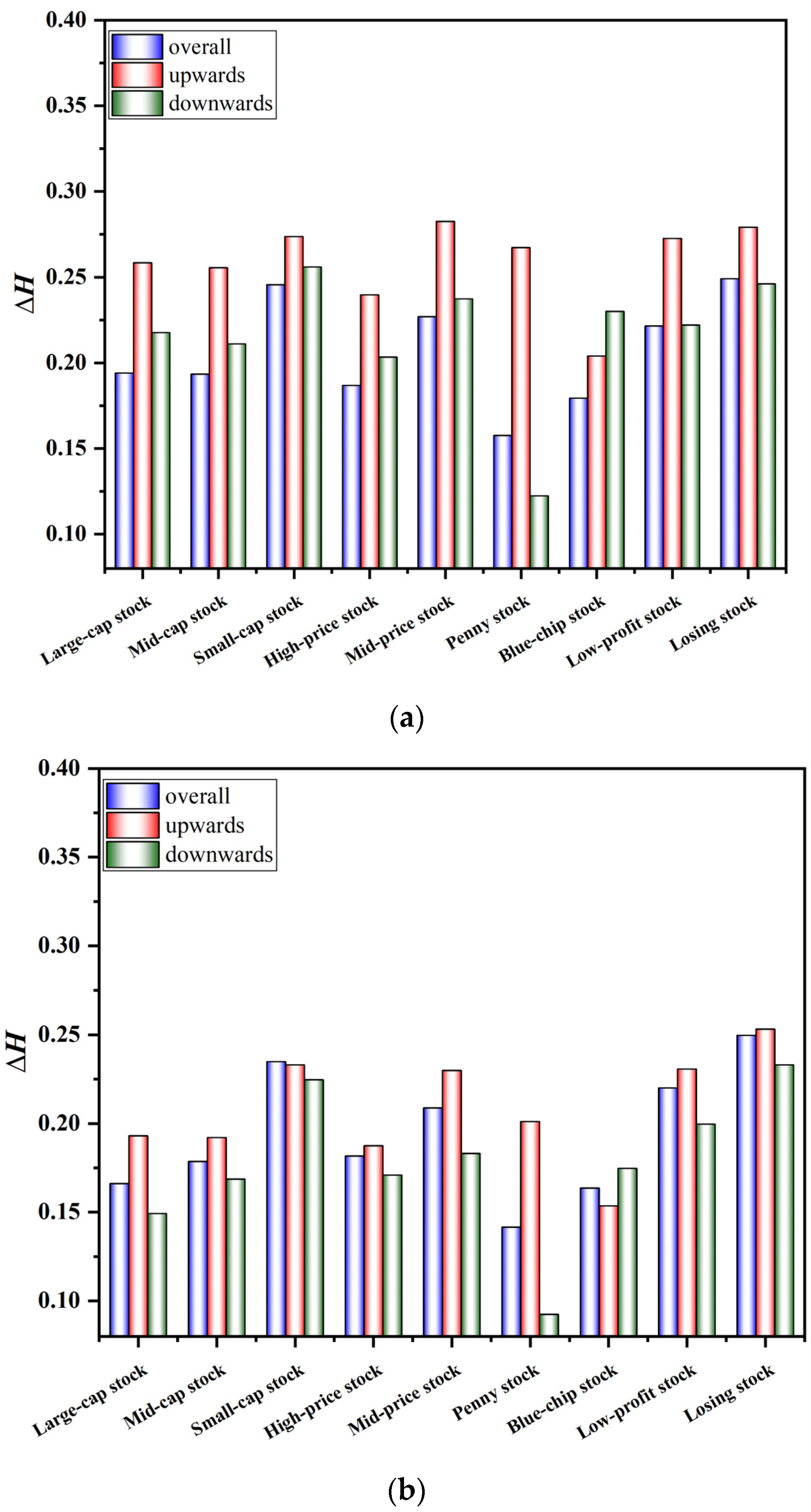
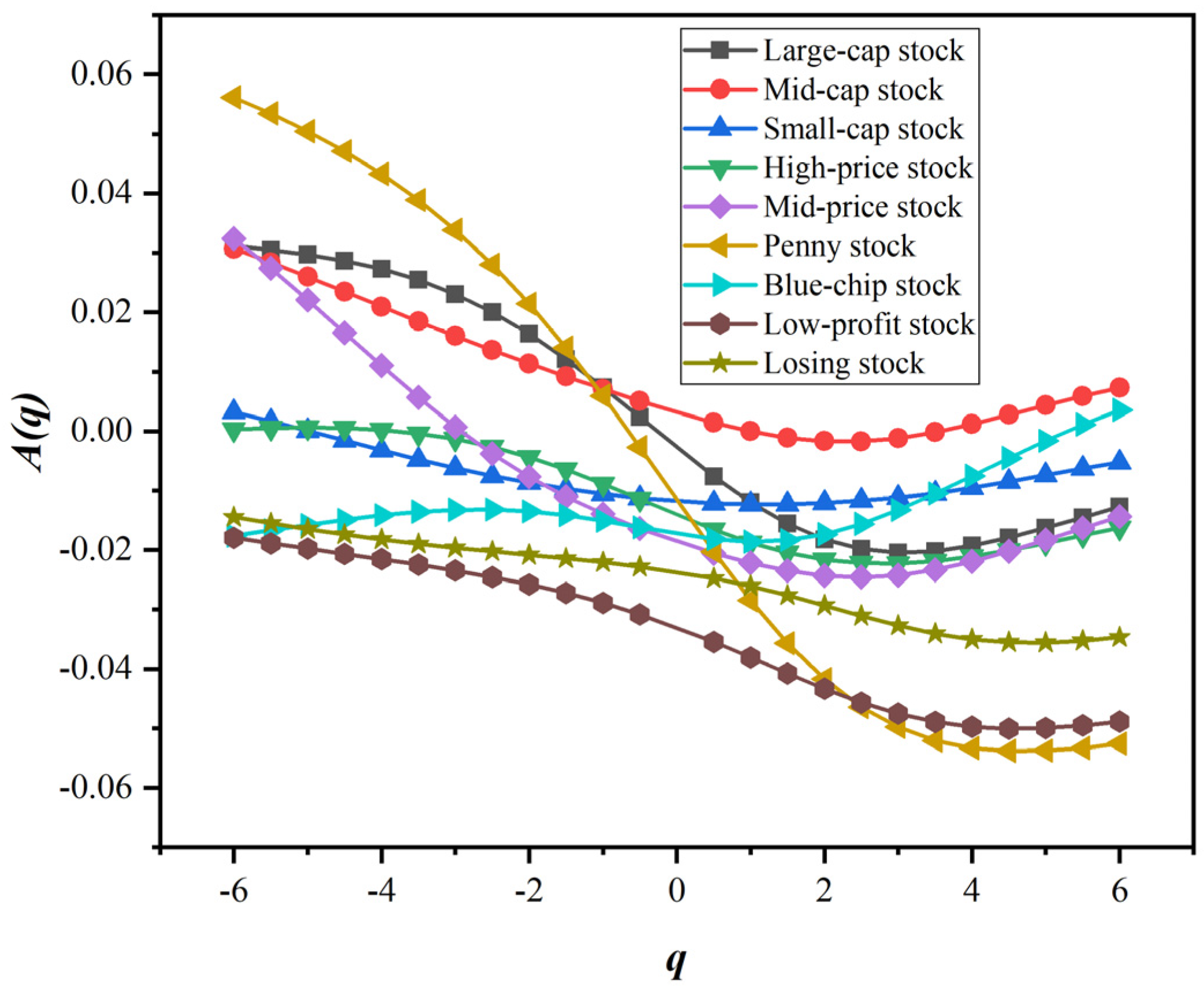
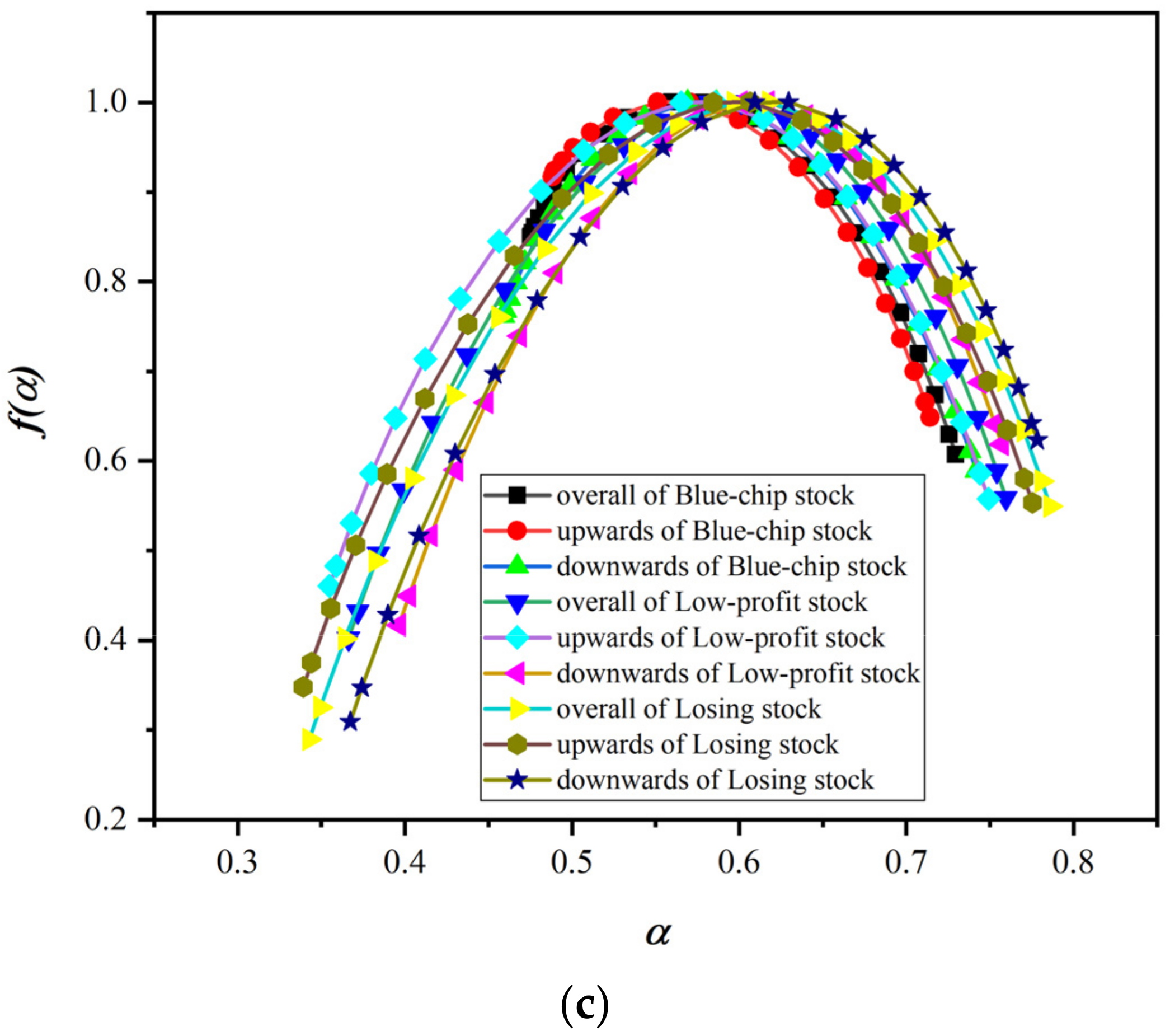
5.2. Variation Analysis of Multifractal Spectrum
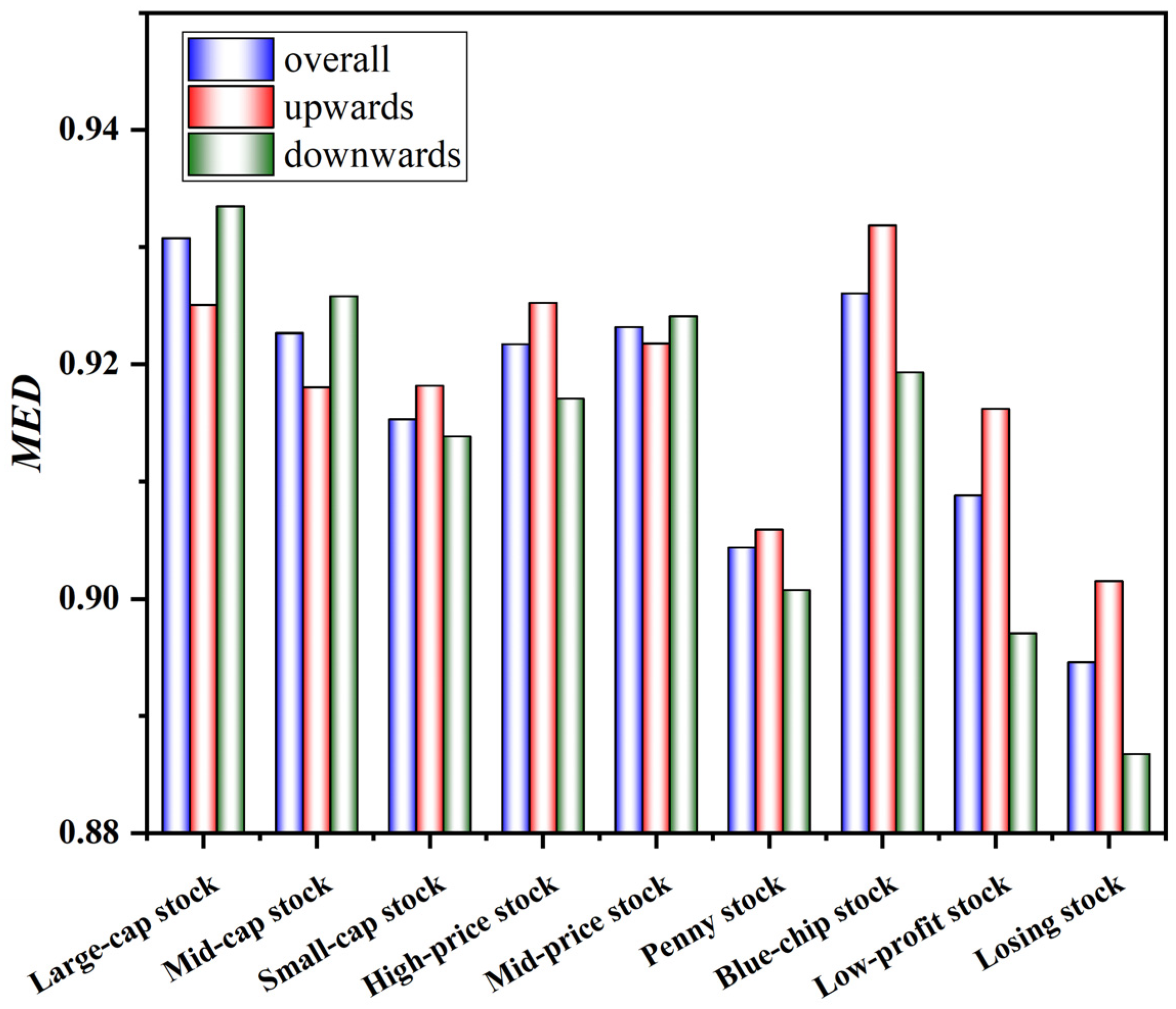
5.3. Efficiency Analysis of Style Indices
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Graham, M.; Peltomaki, J.; Sturludottir, H. Do capital controls affect stock market efficiency? Lessons from Iceland. Int. Rev. Financ. Anal. 2015, 41, 82–88. [Google Scholar] [CrossRef]
- Lim, K.P. Efficiency tests of the UK financial futures markets and the impact of electronic trading systems: A note on relative market efficiency. Appl. Econ. Lett. 2009, 16, 1129–1132. [Google Scholar] [CrossRef]
- Dinga, E.; Oprean-Stan, C.; Tanasescu, C.R.; Bratian, V.; Ionescu, G.M. Entropy-Based Behavioural Efficiency of the Financial Market. Entropy 2021, 23, 1396. [Google Scholar] [CrossRef]
- Malkiel, B.G. The efficient market hypothesis and its critics. J. Econ. Perspect. 2003, 17, 59–82. [Google Scholar] [CrossRef] [Green Version]
- Tran, Q.V. Testing the weak form of Efficient Market Hypothesis for the Czech stock market. Polit. Ekon. 2007, 55, 751–772. [Google Scholar]
- Syed, A.M.; Bajwa, I.A. Earnings announcements, stock price reaction and market efficiency—The case of Saudi Arabia. Int. J. Islamic Middle East. Financ. Manag. 2018, 11, 416–431. [Google Scholar] [CrossRef] [Green Version]
- Tiwari, A.K.; Albulescu, C.T.; Yoon, S.M. A multifractal detrended fluctuation analysis of financial market efficiency: Comparison using Dow Jones sector ETF indices. Phys. A 2017, 483, 182–192. [Google Scholar] [CrossRef]
- Atman, A.P.F.; Goncalves, B.A. Influence of the Investor’s Behavior on the Complexity of the Stock Market. Braz. J. Phys. 2012, 42, 137–145. [Google Scholar] [CrossRef]
- Efremidze, L.; Stanley, D.J.; Kownatzki, C. Entropy trading strategies reveal inefficiencies in Japanese stock market. Int. Rev. Econ. Financ. 2021, 75, 464–477. [Google Scholar] [CrossRef]
- Fan, Q.J. Asymmetric multiscale detrended fluctuation analysis of California electricity spot price. Phys. A 2016, 442, 252–260. [Google Scholar] [CrossRef]
- Liaw, S.S.; Chiu, F.Y.; Wang, C.Y.; Shiau, Y.H. Fractal Analysis of Stock Index and Electrocardiograph. Chin. J. Phys. 2010, 48, 814–828. [Google Scholar]
- Lim, K.P.; Brooks, R. The evolution of stock efficiency over time: A survey of the empirical literature. J. Econ. Surv. 2011, 25, 69–108. [Google Scholar] [CrossRef]
- Frezza, M. A fractal-based approach for modeling stock price variations. Chaos 2018, 28, 091102. [Google Scholar] [CrossRef] [PubMed]
- Lo, A.W. Long-Term-Memory in stock-market prices. Econometrica 1991, 59, 1279–1313. [Google Scholar] [CrossRef]
- Peng, C.K.; Bulcdyrev, S.V.; Havlin, S.; Simons, M.; Stanley, H.E.; Goldberger, A.L. Mosaic organization of DNA nucleotides. Phys. Rev. E 1994, 49, 1685–1689. [Google Scholar] [CrossRef] [Green Version]
- McKenzie, M.D. Non-periodic Australian stock market cycles: Evidence from rescaled range analysis. Econ. Rec. 2001, 77, 393–406. [Google Scholar] [CrossRef]
- Ma, C.Q.; Li, H.Q.; Zou, L.; Wu, Z.J. Long-term memory in emerging markets: Evidence from the Chinese stock market. Int. J. Inf. Technol. Decis. Mak. 2006, 5, 495–501. [Google Scholar] [CrossRef]
- Bratian, V.; Acu, A.M.; Oprean-Stan, C.; Dinga, E.; Ionescu, G.M. Efficient or Fractal Market Hypothesis? A Stock Indexes Modelling Using Geometric Brownian Motion and Geometric Fractional Brownian Motion. Mathematics 2021, 9, 2983. [Google Scholar] [CrossRef]
- Kim, K.; Kim, S.Y.; Lee, M.; Yum, M.K. Hurst exponents in futures exchange markets. Int. J. Mod. Phys. C 2006, 17, 1831–1838. [Google Scholar] [CrossRef]
- Srbek, P. Estimation of the Hurst Exponent in Time Series of Daily Returns of Stock Indices. Polit. Ekon. 2018, 66, 508–524. [Google Scholar] [CrossRef] [Green Version]
- Guharay, S.K.; Thakur, G.S.; Goodman, F.J.; Rosen, S.L.; Houser, D. Integrated data-driven analytics to identify instability signatures in nonstationary financial time series. Appl. Econ. 2016, 48, 1678–1694. [Google Scholar] [CrossRef]
- Jung, N.; Le, Q.A.; Mafwele, B.J.; Lee, H.M.; Chae, S.Y.; Lee, J.W. Fractality and Multifractality in a Stock Market’s Nonstationary Financial Time Series. J. Korean Phys. Soc. 2020, 77, 186–196. [Google Scholar] [CrossRef]
- Lin, X.Q.; Fei, F.Y. Long memory revisit in Chinese stock markets: Based on GARCH-class models and multiscale analysis. Econ. Model. 2013, 31, 265–275. [Google Scholar] [CrossRef]
- Sukpitak, J.; Hengpunya, V. Efficiency of Thai stock markets: Detrended fluctuation analysis. Phys. A 2016, 458, 204–209. [Google Scholar] [CrossRef]
- Bu, L.P.; Shang, P.J. Scaling analysis of stock markets. Chaos 2014, 22, 023107. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Zhou, W.X. Superfamily classification of nonstationary time series based on DFA scaling exponents. J. Phys. A-Math. Theor. 2010, 43, 495005. [Google Scholar] [CrossRef] [Green Version]
- Lahmiri, S. Multifractal in volatility of family business stocks listed on Casablanca stock exchange. Fractals-Complex Geom. Patterns Scaling Nat. Soc. 2017, 25, 1750014. [Google Scholar] [CrossRef]
- Uddin, G.S.; Hernandez, J.A.; Shahzad, S.J.H.; Yoon, S.M. Time-varying evidence of efficiency, decoupling, and diversification of conventional and Islamic stocks. Int. Rev. Financ. Anal. 2018, 56, 167–180. [Google Scholar] [CrossRef]
- Jiang, Z.Q.; Gao, X.L.; Zhou, W.X.; Stanley, H.E. Multifractal cross wavelet analysis. Fractals-Complex Geom. Patterns Scaling Nat. Soc. 2017, 25, 1750054. [Google Scholar] [CrossRef] [Green Version]
- D’Andrea, J. Constructing fractal wavelet frames. Numer. Funct. Anal. Optim. 2012, 33, 906–927. [Google Scholar] [CrossRef]
- Liu, R.P.; Di Matteo, T.; Lux, T. True and apparent scaling: The proximity of the Markov-switching multifractal model to long-range dependence. Phys. A 2007, 383, 35–42. [Google Scholar] [CrossRef] [Green Version]
- Kantelhardt, J.W.; Zschiegner, S.A.; Koscielny-Bunde, E.; Havlin, S.; Bunde, A.; Stanley, H.E. Multifractal detrended fluctuation analysis of nonstationary time series. Phys. A 2002, 316, 87–114. [Google Scholar] [CrossRef] [Green Version]
- Ruan, Q.S.; Wang, Z.L.; Liu, J.; Lv, D.Y. Is Foreign Capital Smarter? Multifractal Evidence from the Shanghai-Hong Kong Stock Connect Program. Fluct. Noise Lett. 2021, 19, 2050047. [Google Scholar] [CrossRef]
- Mensi, W.; Tiwari, A.K.; Al-Yahyaee, K.H. An analysis of the weak form efficiency, multifractality and long memory of global, regional and European stock markets. Q. Rev. Econ. Financ. 2019, 72, 168–177. [Google Scholar] [CrossRef]
- Thompson, J.R.; Wilson, J.R. Multifractal detrended fluctuation analysis: Practical applications to financial time series. Math. Comput. Simul. 2016, 126, 63–88. [Google Scholar] [CrossRef]
- Cai, Y.X.; Hong, J.Q. Dynamic relationship between stock market trading volumes and investor fear gauges movements. Appl. Econ. 2019, 51, 4218–4232. [Google Scholar] [CrossRef]
- Zhang, S.W.; Fang, W. Multifractal Behaviors of Stock Indices and Their Ability to Improve Forecasting in a Volatility Clustering Period. Entropy 2021, 23, 1018. [Google Scholar] [CrossRef]
- Tiwari, A.K.; Aye, G.C.; Gupta, R. Stock market efficiency analysis using long spans of Data: A multifractal detrended fluctuation approach. Financ. Res. Lett. 2019, 28, 398–411. [Google Scholar] [CrossRef] [Green Version]
- Morales, R.; Di Matteo, T.; Gramatica, R.; Aste, T. Dynamical generalized Hurst exponent as a tool to monitor unstable periods in financial time series. Phys. A 2012, 391, 3180–3189. [Google Scholar] [CrossRef] [Green Version]
- Alvarez-Ramirez, J.; Rodriguez, E.; Echeverria, J.C. A DFA approach for assessing asymmetric correlations. Phys. A 2009, 388, 2263–2270. [Google Scholar] [CrossRef]
- Suh, S.; Yoo, E.; Yoon, S.J. Stock market tail risk, tail risk premia, and return predictability. J. Futures Mark. 2021, 41, 1569–1596. [Google Scholar] [CrossRef]
- Xu, C.; Ke, J.C.; Zhao, X.J.; Zhao, X.F. Multiscale Quantile Correlation Coefficient: Measuring Tail Dependence of Financial Time Series. Sustainability 2020, 12, 4908. [Google Scholar] [CrossRef]
- Yang, H.; Cai, J.; Huang, L.; Marcus, A.J. Bank stocks, risk factors, and tail behavior. J. Empir. Financ. 2021, 63, 203–229. [Google Scholar] [CrossRef]
- Lee, M.; Song, J.W.; Park, J.H.; Chang, W. Asymmetric multi-fractality in the US stock indices using index-based model of A-MFDFA. Chaos Solitons Fractals 2017, 97, 28–38. [Google Scholar] [CrossRef]
- Cao, G.X.; Cao, J.; Xu, L.B. Asymmetric multifractal scaling behavior in the Chinese stock market: Based on asymmetric MF-DFA. Phys. A 2013, 392, 797–807. [Google Scholar] [CrossRef]
- Naeem, M.A.; Farid, S.; Ferrer, R.; Shahzad, S.J.H. Comparative efficiency of green and conventional bonds pre- and during COVID-19: An asymmetric multifractal detrended fluctuation analysis. Energy Policy 2021, 153, 112285. [Google Scholar] [CrossRef]
- Kristoufek, L.; Vosvrda, M. Capital Markets Efficiency: Fractal Dimension, Hurst Exponent and Entropy. Polit. Ekon. 2012, 60, 208–221. [Google Scholar] [CrossRef]
- David, S.A.; Inacio, C.M.C.; Quintino, D.D.; Machado, J.A.T. Measuring the Brazilian ethanol and gasoline market efficiency using DFA-Hurst and fractal dimension. Energy Econ. 2020, 85, 104614. [Google Scholar] [CrossRef]
- David, S.A.; Inacio, C.M.C.; Machado, J.A.T. Quantifying the Predictability and Efficiency of the Cointegrated Ethanol and Agricultural Commodities Price Series. Appl. Sci. 2020, 9, 5303. [Google Scholar] [CrossRef] [Green Version]
- Li, D.Y.; Li, R.R.; Sun, Q.K. How the heterogeneity in investment horizons affects market trends. Appl. Econ. 2017, 49, 1473–1482. [Google Scholar] [CrossRef]
- Yalamova, R.; McKelvey, B. Explaining What Leads Up to Stock Market Crashes: A Phase Transition Model and Scalability Dynamics. J. Behav. Financ. 2011, 12, 169–182. [Google Scholar] [CrossRef]
- Wang, Y.D.; Liu, L.; Gu, R.B.; Cao, J.J.; Wang, H.Y. Analysis of market efficiency for the Shanghai stock market over time. Phys. A 2010, 389, 1635–1642. [Google Scholar] [CrossRef]
- Lux, T. Detecting multi-fractal properties in asset returns: The failure of the scaling estimator. Int. J. Mod. Phys. C 2004, 15, 481–491. [Google Scholar] [CrossRef] [Green Version]
- Urquhart, A.; McGroarty, F. Are stock markets really efficient? Evidence of the adaptive market hypothesis. Int. Rev. Financ. Anal. 2016, 47, 39–49. [Google Scholar] [CrossRef] [Green Version]
- Al-Khazali, O.; Mirzaei, A. Stock market anomalies, market efficiency and the adaptive market hypothesis: Evidence from Islamic stock indices. J. Int. Financ. Mark. Inst. Money 2017, 51, 190–208. [Google Scholar] [CrossRef]
- Xiong, X.; Meng, Y.Q.; Li, X.; Shen, D.H. An empirical analysis of the Adaptive Market Hypothesis with calendar effects: Evidence from China. Financ. Res. Lett. 2019, 31, 321–333. [Google Scholar] [CrossRef]
- Urquhart, A.; Hudson, R. Efficient or adaptive markets? Evidence from major stock markets using very long run historic data. Int. Rev. Financ. Anal. 2013, 28, 130–142. [Google Scholar] [CrossRef]



| Factor | Style Stock Indices | ||
|---|---|---|---|
| Equity scale | Large-cap stock | Mid-cap stock | Small-cap stock |
| Share price | High-price stock | Mid-price stock | Penny stock |
| Performance | Blue-chip stock | Low-profit stock | Losing stock |
| Mean | Maximum | Minimum | Std. Dev | Kurtosis | Skewness | Jarque–Bera | |
|---|---|---|---|---|---|---|---|
| Large-cap stock | 1.20 × 10−4 | 0.0407 | −0.0420 | 0.0070 | 7.6066 | −0.3184 | 4.80 × 103 |
| Mid-cap stock | 1.30 × 10−4 | 0.0403 | −0.0404 | 0.0076 | 6.7972 | −0.6361 | 3.56 × 103 |
| Small-cap stock | 1.40 × 10−4 | 0.0399 | −0.0404 | 0.0078 | 6.5100 | −0.6856 | 3.15 × 103 |
| High-price stock | 1.30 × 10−4 | 0.0396 | −0.0413 | 0.0072 | 6.4285 | −0.2931 | 2.69 × 103 |
| Mid-price stock | 1.00 × 10−4 | 0.0412 | −0.0412 | 0.0077 | 6.9325 | −0.5440 | 3.70 × 103 |
| Penny stock | 2.00 × 10−4 | 0.0405 | −0.0403 | 0.0071 | 7.5415 | −0.5761 | 4.88 × 103 |
| Blue-chip stock | 1.80 × 10−4 | 0.0410 | −0.0415 | 0.0074 | 6.7421 | −0.2665 | 3.17 × 103 |
| Low-profit stock | 8.00 × 10−5 | 0.0404 | −0.0421 | 0.0082 | 6.2889 | −0.7054 | 2.85 × 103 |
| Losing stock | 1.00 × 10−4 | 0.0361 | −0.0399 | 0.0074 | 5.7018 | −0.6924 | 2.05 × 103 |
| Overall of large-cap stock | 0.4277 | 0.6850 | 0.2573 | 0.6966 | 0.7558 | −0.0592 |
| Upwards of large-cap stock | 0.4334 | 0.7217 | 0.2883 | 0.7651 | 0.6632 | 0.1019 |
| Downwards of large-cap stock | 0.4260 | 0.6829 | 0.2570 | 0.6447 | 0.7083 | −0.0635 |
| Overall of mid-cap stock | 0.3943 | 0.6880 | 0.2937 | 0.5424 | 0.7669 | −0.2242 |
| Upwards of mid-cap stock | 0.4072 | 0.7215 | 0.3143 | 0.5908 | 0.6753 | −0.0846 |
| Downwards of mid-cap stock | 0.3846 | 0.6655 | 0.2808 | 0.4993 | 0.8272 | −0.3279 |
| Overall of small-cap stock | 0.3430 | 0.7706 | 0.4276 | 0.3596 | −0.4833 | −0.1238 |
| Upwards of small-cap stock | 0.3532 | 0.7703 | 0.4171 | 0.4194 | 0.4758 | −0.0564 |
| Downwards of small-cap stock | 0.3468 | 0.3498 | 0.4035 | 0.7503 | 0.5768 | −0.2271 |
| Overall of high-price stock | 0.4139 | 0.7489 | 0.3349 | 0.5588 | 0.5216 | 0.0373 |
| Upwards of high-price stock | 0.4184 | 0.7444 | 0.3260 | 0.6230 | 0.5456 | 0.0774 |
| Downwards of high-price stock | 0.4202 | 0.7465 | 0.3263 | 0.5364 | 0.5311 | 0.0053 |
| Overall of mid-price stock | 0.3626 | 0.6989 | 0.3363 | 0.5087 | 0.7261 | −0.2175 |
| Upwards of mid-price stock | 0.3716 | 0.7415 | 0.3699 | 0.5926 | 0.5670 | 0.0256 |
| Downwards of mid-price stock | 0.3645 | 0.4636 | 0.2899 | 0.6544 | 0.8952 | −0.4316 |
| Overall of penny stock | 0.4578 | 0.6985 | 0.2407 | 0.6402 | 0.7655 | −0.1253 |
| Upwards of penny stock | 0.4369 | 0.7541 | 0.3172 | 0.6754 | 0.6279 | 0.0475 |
| Downwards of penny stock | 0.4814 | 0.6683 | 0.1868 | 0.6274 | 0.8057 | −0.1783 |
| Overall of blue-chip stock | 0.4753 | 0.7295 | 0.2542 | 0.8490 | 0.6073 | 0.2416 |
| Upwards of blue-chip stock | 0.4896 | 0.7143 | 0.2247 | 0.9242 | 0.6486 | 0.2756 |
| Downwards of blue-chip stock | 0.4591 | 0.7418 | 0.2827 | 0.7621 | 0.5892 | 0.1729 |
| Overall of low-profit stock | 0.3663 | 0.7595 | 0.3932 | 0.4016 | 0.5588 | −0.1572 |
| Upwards of low-profit stock | 0.3549 | 0.7492 | 0.3943 | 0.4603 | 0.5577 | −0.0974 |
| Downwards of low-profit stock | 0.3965 | 0.7570 | 0.3605 | 0.4168 | 0.6185 | −0.2017 |
| Overall of losing stock | 0.3429 | 0.7861 | 0.4431 | 0.2892 | 0.5493 | −0.2601 |
| Upwards of losing stock | 0.3392 | 0.7754 | 0.4362 | 0.3480 | 0.5535 | −0.2055 |
| Downwards of losing stock | 0.3673 | 0.7783 | 0.4109 | 0.3089 | 0.6229 | −0.3141 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, C.; Ke, J.; Peng, Z.; Fang, W.; Duan, Y. Asymmetric Fractal Characteristics and Market Efficiency Analysis of Style Stock Indices. Entropy 2022, 24, 969. https://doi.org/10.3390/e24070969
Xu C, Ke J, Peng Z, Fang W, Duan Y. Asymmetric Fractal Characteristics and Market Efficiency Analysis of Style Stock Indices. Entropy. 2022; 24(7):969. https://doi.org/10.3390/e24070969
Chicago/Turabian StyleXu, Chao, Jinchuan Ke, Zhikai Peng, Wen Fang, and Yu Duan. 2022. "Asymmetric Fractal Characteristics and Market Efficiency Analysis of Style Stock Indices" Entropy 24, no. 7: 969. https://doi.org/10.3390/e24070969
APA StyleXu, C., Ke, J., Peng, Z., Fang, W., & Duan, Y. (2022). Asymmetric Fractal Characteristics and Market Efficiency Analysis of Style Stock Indices. Entropy, 24(7), 969. https://doi.org/10.3390/e24070969






