Entanglement Property of Tripartite GHZ State in Different Accelerating Observer Frames †
Abstract
:1. Introduction
2. Generalization of Single Mode Approximation
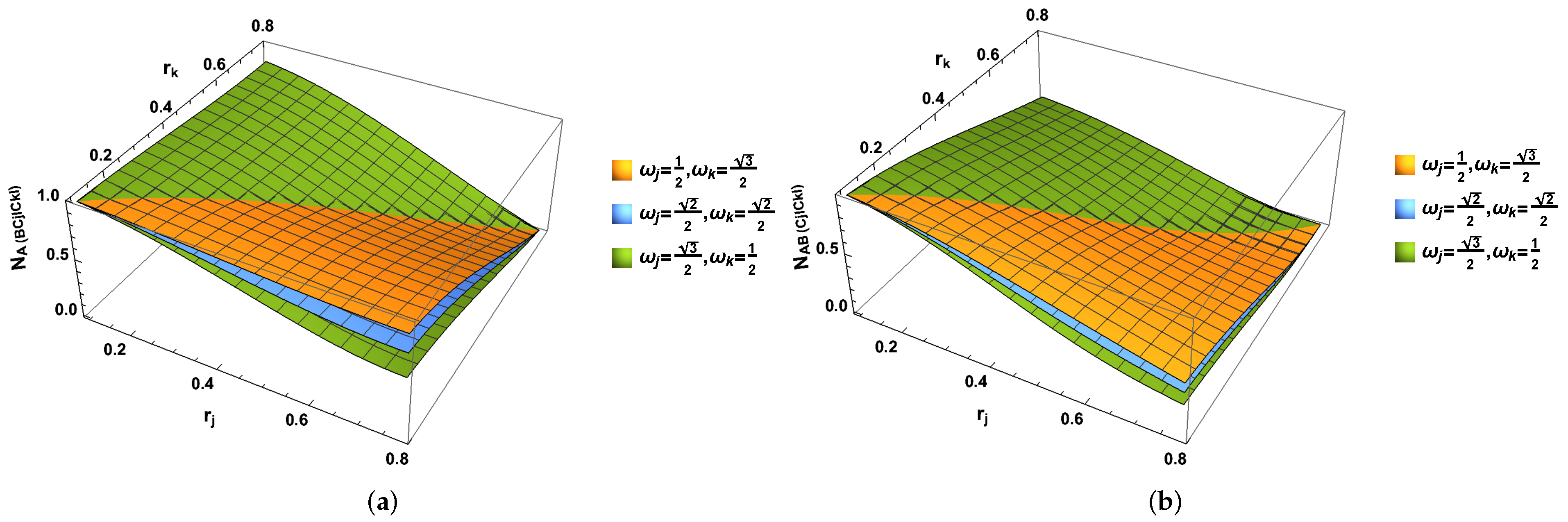
3. Fermionic Entanglement in Two Different Accelerating Observer Frames

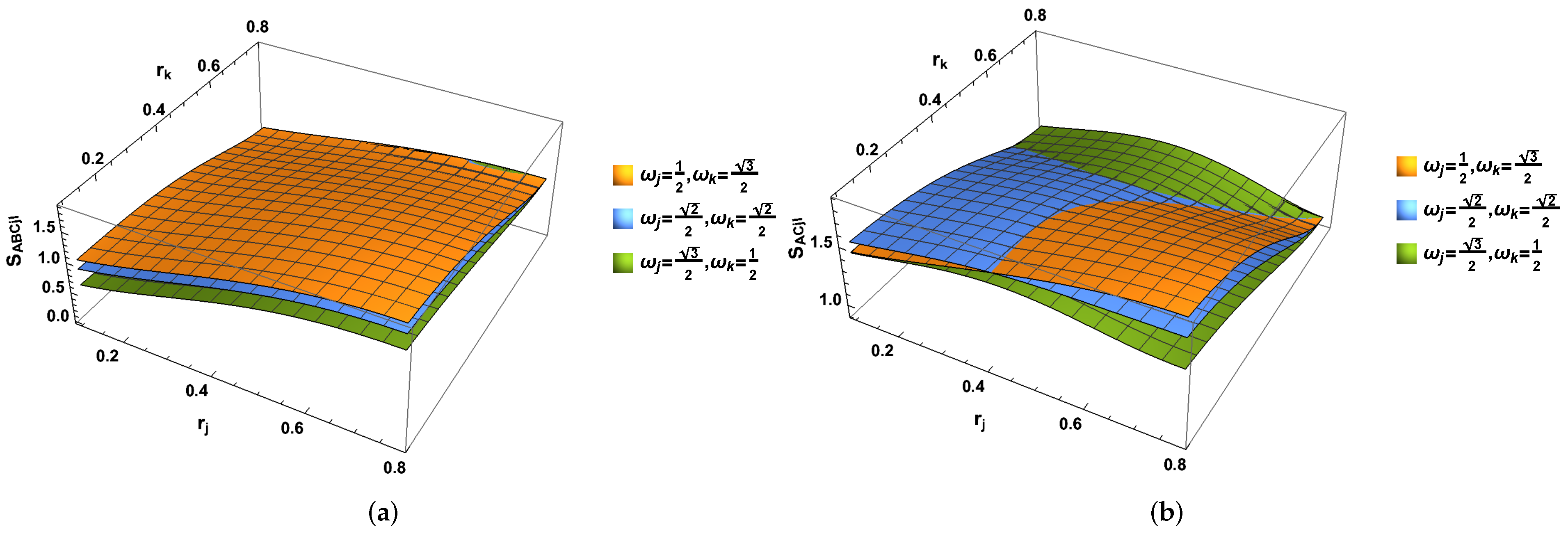
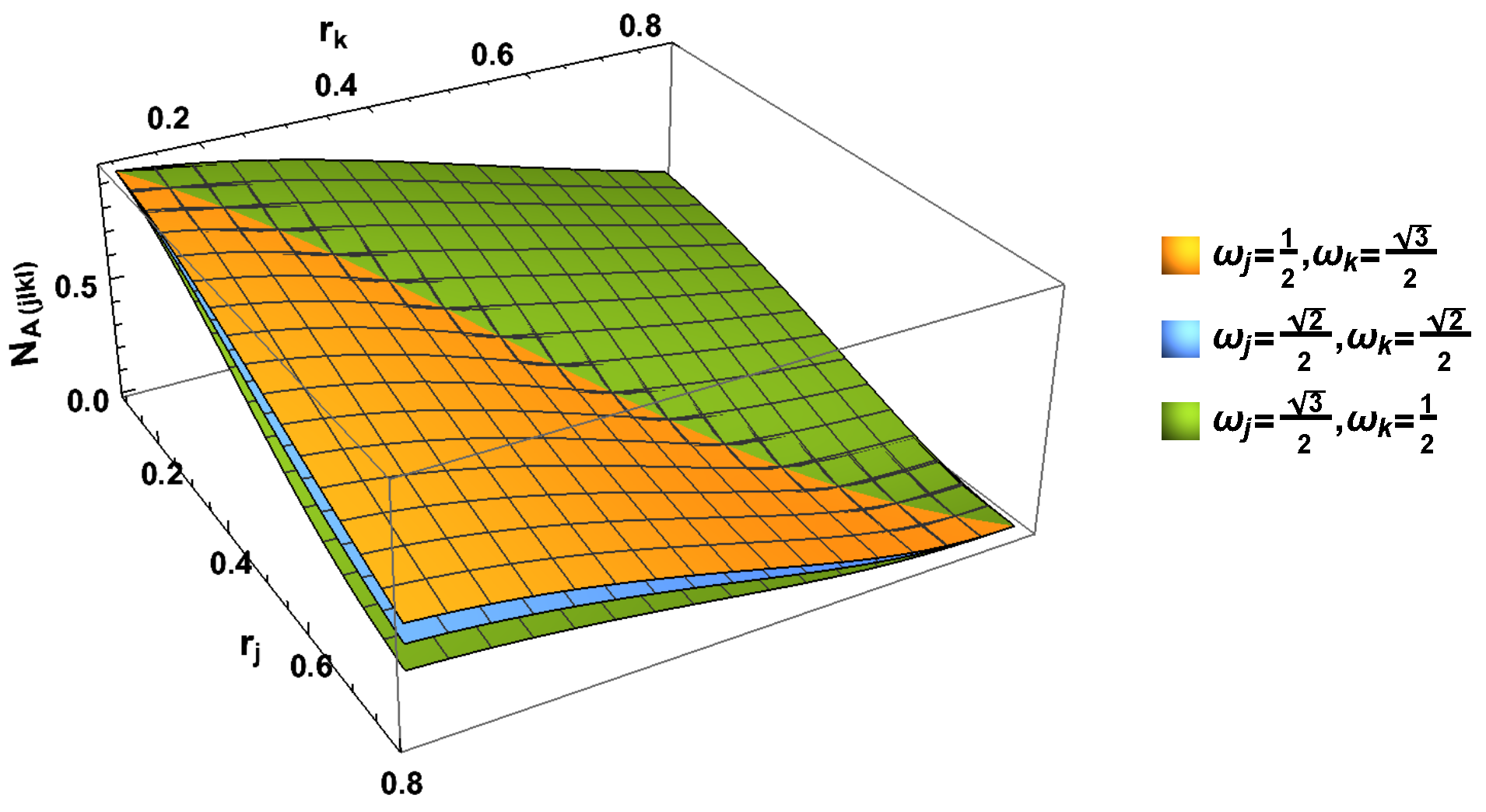
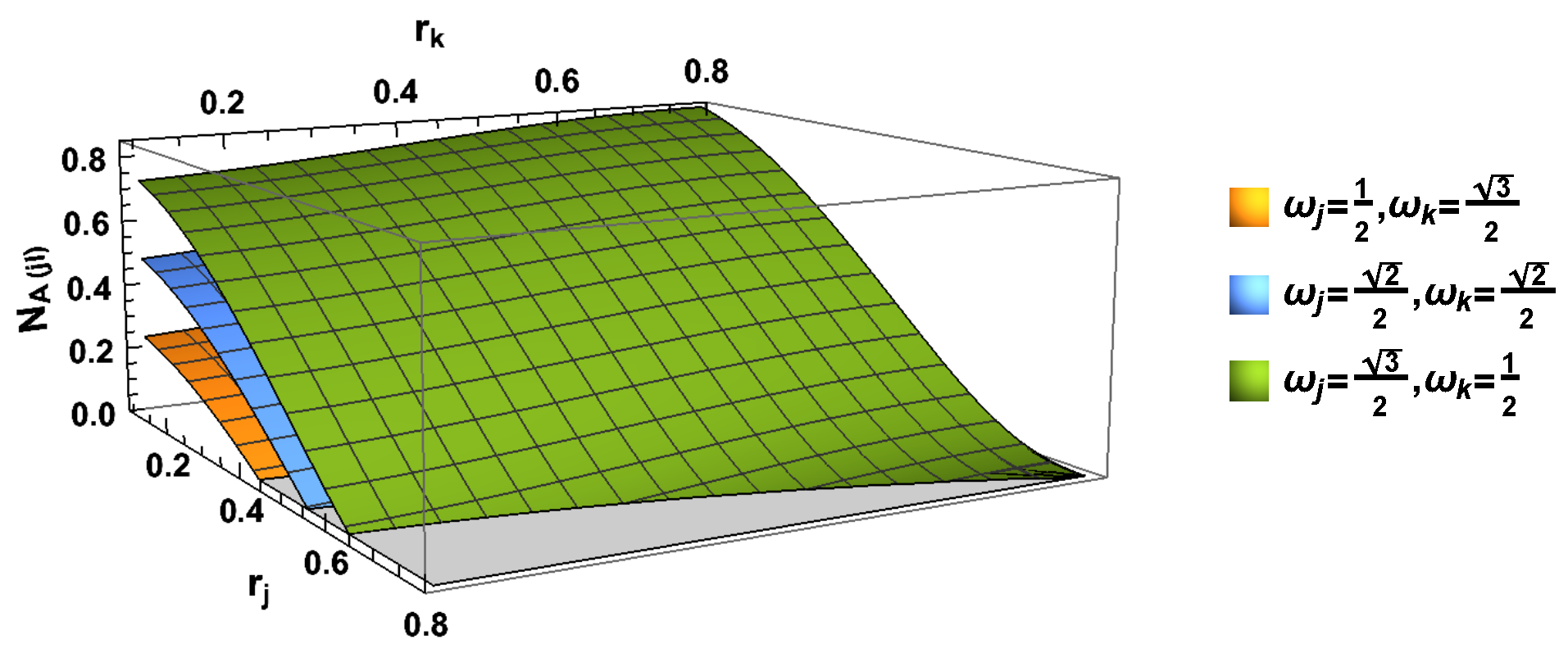
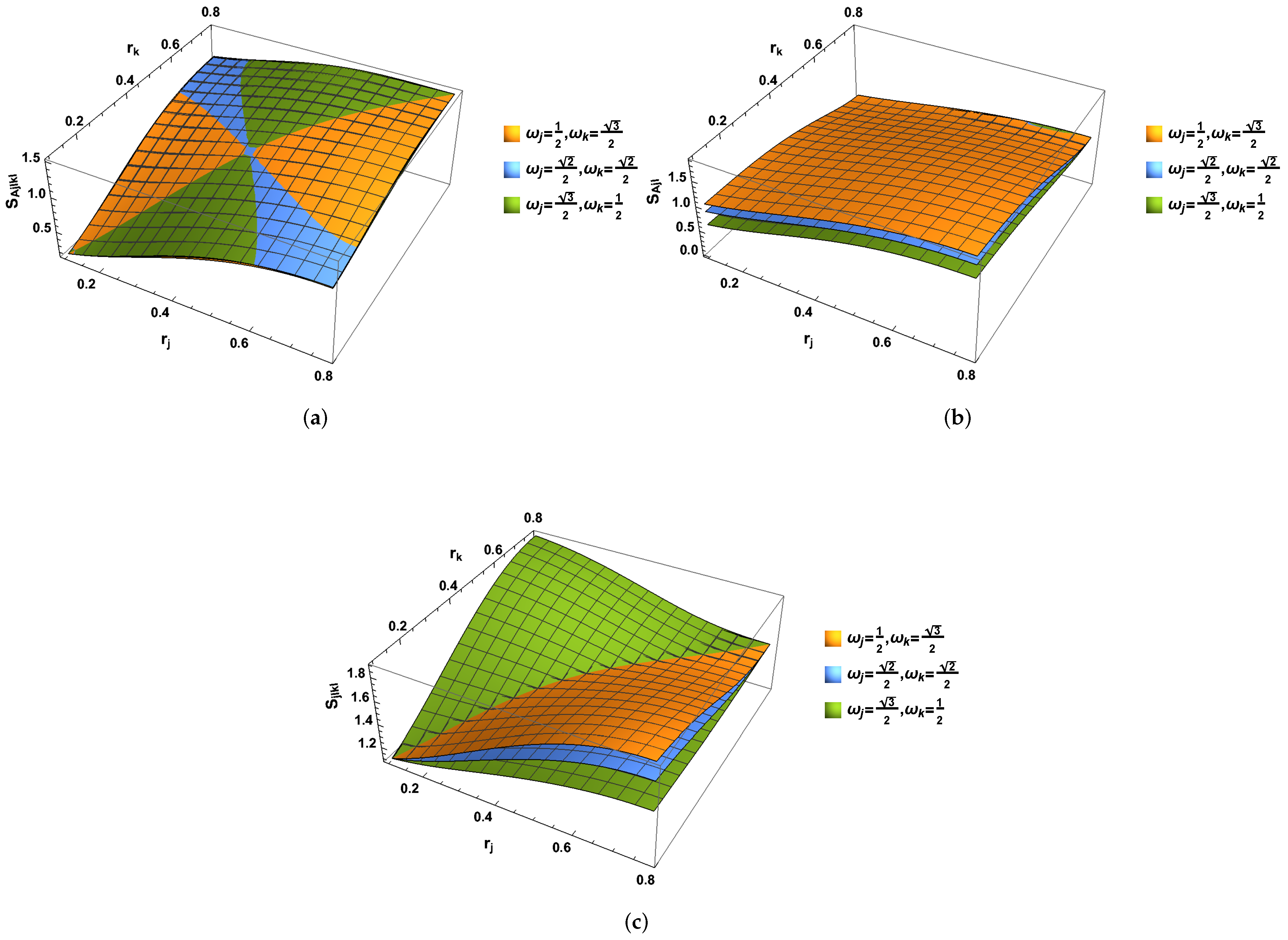
4. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Negative Eigenvalues for NA(BCjICkI) and NB(ACjICkI)
Appendix B. Negative Eigenvalue for NAB(CjICkI) and NCjICkI(AB)
References
- Quezada, L.F.; Dong, S.H. Quantum Key-Distribution Protocols Based on a Quantum Version of the Monty Hall Game. Ann. Phys. 2020, 532, 2000126. [Google Scholar] [CrossRef]
- Quezada, L.F.; Dong, S.H. Quantum version of a generalized Monty Hall game and its possible applications to quantum secure communications. Ann. Phys. 2021, 533, 2000427. [Google Scholar] [CrossRef]
- Castañeda Valle, D.; Quezada, L.F.; Dong, S.H. Bell-GHZ Measurement-Device-Independent Quantum Key Distribution. Ann. Phys. 2021, 533, 2100116. [Google Scholar] [CrossRef]
- Alsing, P.M.; Milburn, G.J. Teleportation with a uniformly accelerated partner. Phys. Rev. Lett. 2003, 91, 180404. [Google Scholar] [CrossRef] [Green Version]
- Bruschi, D.E.; Louko, J.; Martín-Martínez, E.; Dragan, A.; Fuentes, I. Unruh effect in quantum information beyond the single-mode approximation. Phys. Rev. A 2010, 82, 042332. [Google Scholar] [CrossRef] [Green Version]
- Terashima, H.; Ueda, M. Einstein-Podolsky-Rosen correlation in a gravitational field. Phys. Rev. A 2004, 69, 032113. [Google Scholar] [CrossRef] [Green Version]
- Shi, Y. Entanglement in relativistic quantum field theory. Phys. Rev. D 2004, 70, 105001. [Google Scholar] [CrossRef] [Green Version]
- Fuentes-Schuller, I.; Mann, R.B. Alice Falls into a Black Hole: Entanglement in Noninertial Frames. Phys. Rev. Lett. 2005, 95, 120404. [Google Scholar] [CrossRef] [Green Version]
- Alsing, P.M.; Fuentes-Schuller, I.; Mann, R.B.; Tessier, T.E. Entanglement of Dirac fields in noninertial frames. Phys. Rev. A 2006, 74, 032326. [Google Scholar] [CrossRef] [Green Version]
- Ball, J.L.; Fuentes-Schuller, I.; Schuller, F.P. Entanglement in an expanding spacetime. Phys. Lett. A 2006, 359, 550. [Google Scholar] [CrossRef] [Green Version]
- Adesso, G.; Fuentes-Schuller, I.; Ericsson, M. Continuous-variable entanglement sharing in noninertial frames. Phys. Rev. A 2007, 76, 062112. [Google Scholar] [CrossRef] [Green Version]
- Brádler, K. Eavesdropping of quantum communication from a noninertial frame. Phys. Rev. A 2007, 75, 022311. [Google Scholar] [CrossRef] [Green Version]
- Ling, Y.; He, S.; Qiu, W.; Zhang, H. Quantum entanglement of electromagnetic field in non-inertial reference frames. J. Phys. A 2007, 40, 9025. [Google Scholar] [CrossRef] [Green Version]
- Ahn, D.; Moon, Y.; Mann, R.; Fuentes-Schuller, I. The black hole final state for the Dirac fields in Schwarzschild spacetime. J. High Energy Phys. 2008, 8, 62. [Google Scholar] [CrossRef] [Green Version]
- Pan, Q.; Jing, J. Hawking radiation, entanglement, and teleportation in the background of an asymptotically flat static black hole. Phys. Rev. D 2008, 78, 065015. [Google Scholar] [CrossRef] [Green Version]
- Alsing, P.M.; McMahon, D.; Milburn, G.J. Teleportation in a non-inertial frame. J. Opt. B 2004, 6, S834. [Google Scholar] [CrossRef] [Green Version]
- Doukas, J.; Hollenberg, L.C.L. Loss of spin entanglement for accelerated electrons in electric and magnetic fields. Phys. Rev. A 2009, 79, 052109. [Google Scholar] [CrossRef] [Green Version]
- Steeg, G.V.; Menicucci, N.C. Entangling power of an expanding universe. Phys. Rev. D 2009, 79, 044027. [Google Scholar] [CrossRef] [Green Version]
- Leon, J.; Martín-Martxixnez, E. Spin and occupation number entanglement of Dirac fields for noninertial observers. Phys. Rev. A 2009, 80, 012314. [Google Scholar] [CrossRef] [Green Version]
- Adesso, G.; Fuentes-Schuller, I. Correlation loss and multipartite entanglement across a black hole horizon. Quantum Inf. Comput. 2009, 9, 0657. [Google Scholar] [CrossRef]
- Datta, A. Quantum discord between relatively accelerated observers. Phys. Rev. A 2009, 80, 052304. [Google Scholar] [CrossRef] [Green Version]
- Lin, S.Y.; Hu, B.L. Entanglement creation between two causally disconnected objects. Phys. Rev. D 2010, 81, 045019. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Deng, J.; Jing, J. Classical and quantum correlations sharing of Dirac fields in noninertial frames. Phys. Rev. A 2010, 81, 052120. [Google Scholar] [CrossRef] [Green Version]
- Martín-Martxixnez, E.; Garay, L.J.; León, J. Unveiling quantum entanglement degradation near a Schwarzschild black hole. Phys. Rev. D 2010, 82, 064006. [Google Scholar] [CrossRef] [Green Version]
- Mandl, F.; Shaw, G. Quantum Field Theory; Wiley: New York, NY, USA, 1984. [Google Scholar]
- Birrel, N.D.; Davies, P.C.W. Quantum Fields in Curved Space; Cambridge University Press: New York, NY, USA, 1982. [Google Scholar]
- Carroll, S.M. Spacetime and Geometry Addison and Wesley; Addison Wesley Press: New York, NY, USA, 2004; pp. 402–412. [Google Scholar]
- Zepeda, J.L.M.; Paz, J.R.; Aoki, M.A.; Dong, S.H. Pentapartite Entanglement Measures of GHZ and W-Class State in the Noninertial Frame. Entropy 2022, 24, 754. [Google Scholar] [CrossRef] [PubMed]
- Takagi, S. Vacuum noise and stress induced by uniform acceleration: Hawking-Unruh effect in Rindler manifold of arbitrary dimension. Prog. Theor. Phys. Suppl. 1986, 88, 1. [Google Scholar] [CrossRef]
- Jáuregui, R.; Torres, M.; Hacyan, S. Dirac vacuum: Acceleration and external field effects. Phys. Rev. D 1991, 43, 3979. [Google Scholar] [CrossRef] [PubMed]
- McMahon, D.; Alsing, P.M.; Embid, P. The Dirac equation in Rindler space: A pedagogical introduction. no published.
- Greiner, W.; Müller, B.; Rafelski, J. Quantum Electrodynamics of Strong Fields; Springer: New York, NY, USA, 1985; pp. 563–571. [Google Scholar]
- Soffel, M.; Müller, B.; Greiner, W. Dirac particles in Rindler space. Phys. Rev. D 1980, 22, 1935. [Google Scholar] [CrossRef] [Green Version]
- Walls, D.F.; Milburn, G.J. Quantum Optics; Springer: New York, NY, USA, 1994. [Google Scholar]
- Peres, A. Separability Criterion for Density Matrices. Phys. Rev. Lett. 1996, 77, 1413. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Liu, C.; Wang, Q.; Zhang, H.; Hu, L. Tetrapartite entanglement of fermionic systems in noninertial frames. Optik 2016, 127, 9788. [Google Scholar] [CrossRef]
- Torres-Arenas, A.J.; Dong, Q.; Sun, G.H.; Qiang, W.C.; Dong, S.H. Entanglement measures of W-state in noninertial frames. Phys. Lett. B 2019, 789, 93. [Google Scholar] [CrossRef]
- von Neumann, J. Mathematical Foundations of Quantum Mechanics; Princeton University Press: Princeton, NJ, USA, 1996. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, Q.; de Jesus León-Montiel, R.; Sun, G.-H.; Dong, S.-H. Entanglement Property of Tripartite GHZ State in Different Accelerating Observer Frames. Entropy 2022, 24, 1011. https://doi.org/10.3390/e24081011
Dong Q, de Jesus León-Montiel R, Sun G-H, Dong S-H. Entanglement Property of Tripartite GHZ State in Different Accelerating Observer Frames. Entropy. 2022; 24(8):1011. https://doi.org/10.3390/e24081011
Chicago/Turabian StyleDong, Qian, Roberto de Jesus León-Montiel, Guo-Hua Sun, and Shi-Hai Dong. 2022. "Entanglement Property of Tripartite GHZ State in Different Accelerating Observer Frames" Entropy 24, no. 8: 1011. https://doi.org/10.3390/e24081011





