A Dead Reckoning Calibration Scheme Based on Optimization with an Adaptive Quantum-Inspired Evolutionary Algorithm for Vehicle Self-Localization
Abstract
:1. Introduction
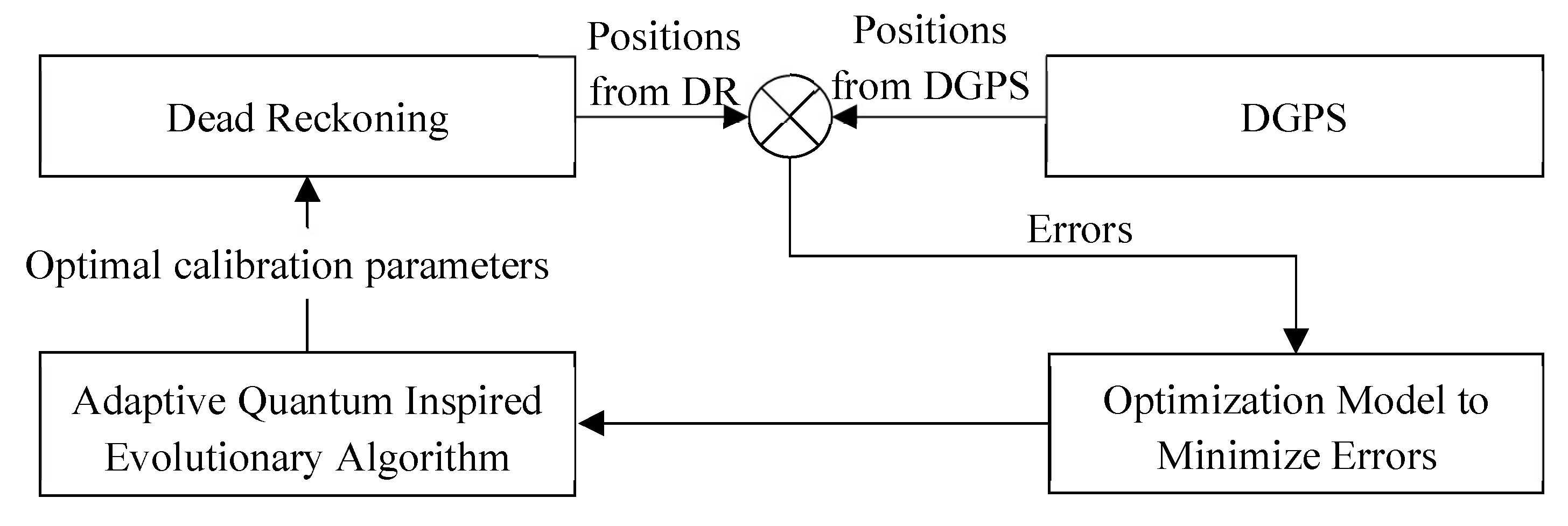
2. An Optimization-Based Dead Reckoning Calibration Scheme
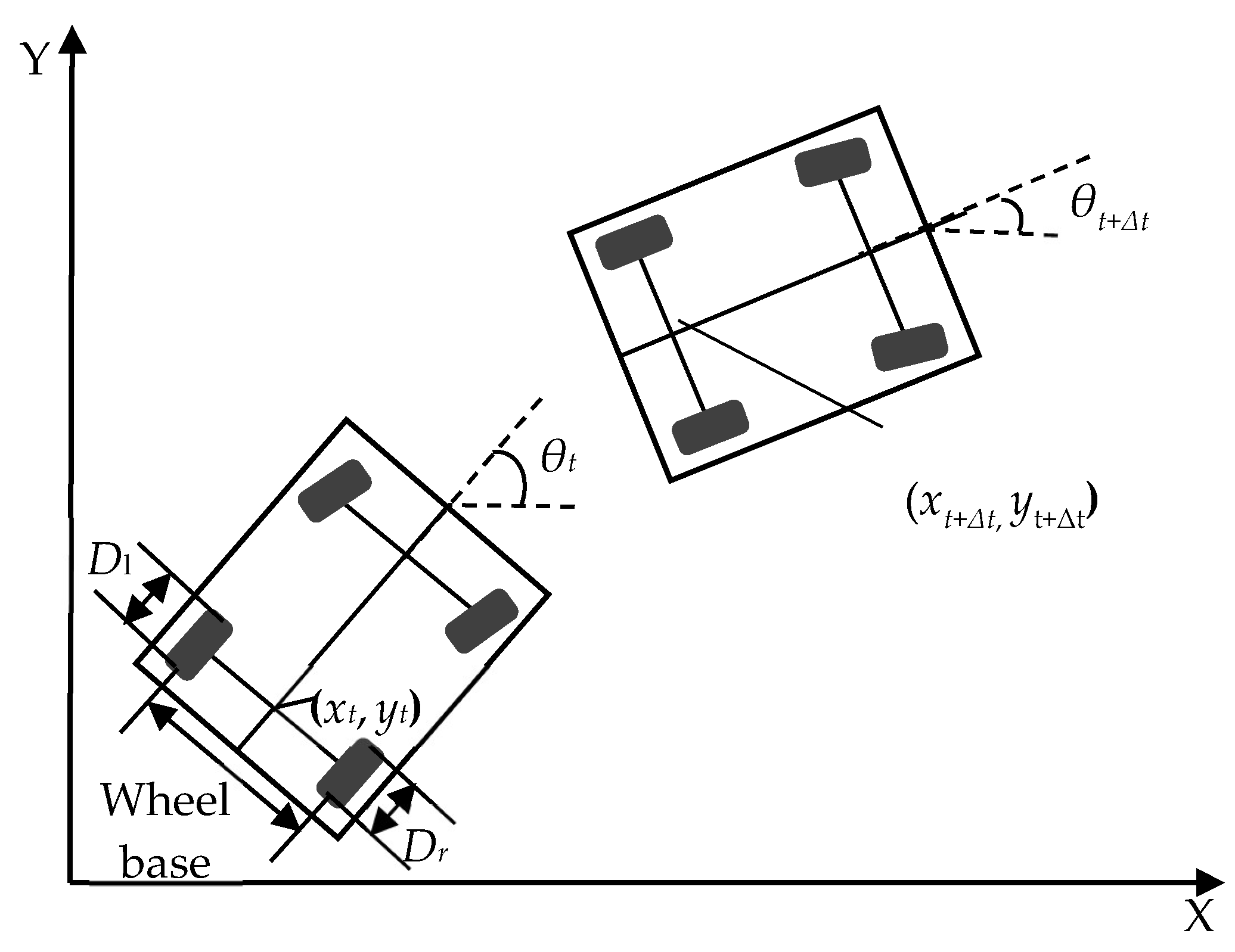
2.1. Dead Reckoning
2.2. Modeling of Systematic Errors for Dead Reckoning
2.3. Optimization Model for Parameter Calibration in Dead Reckoning
3. Optimization Based on an Adaptive Quantum-Inspired Evolutionary Algorithm
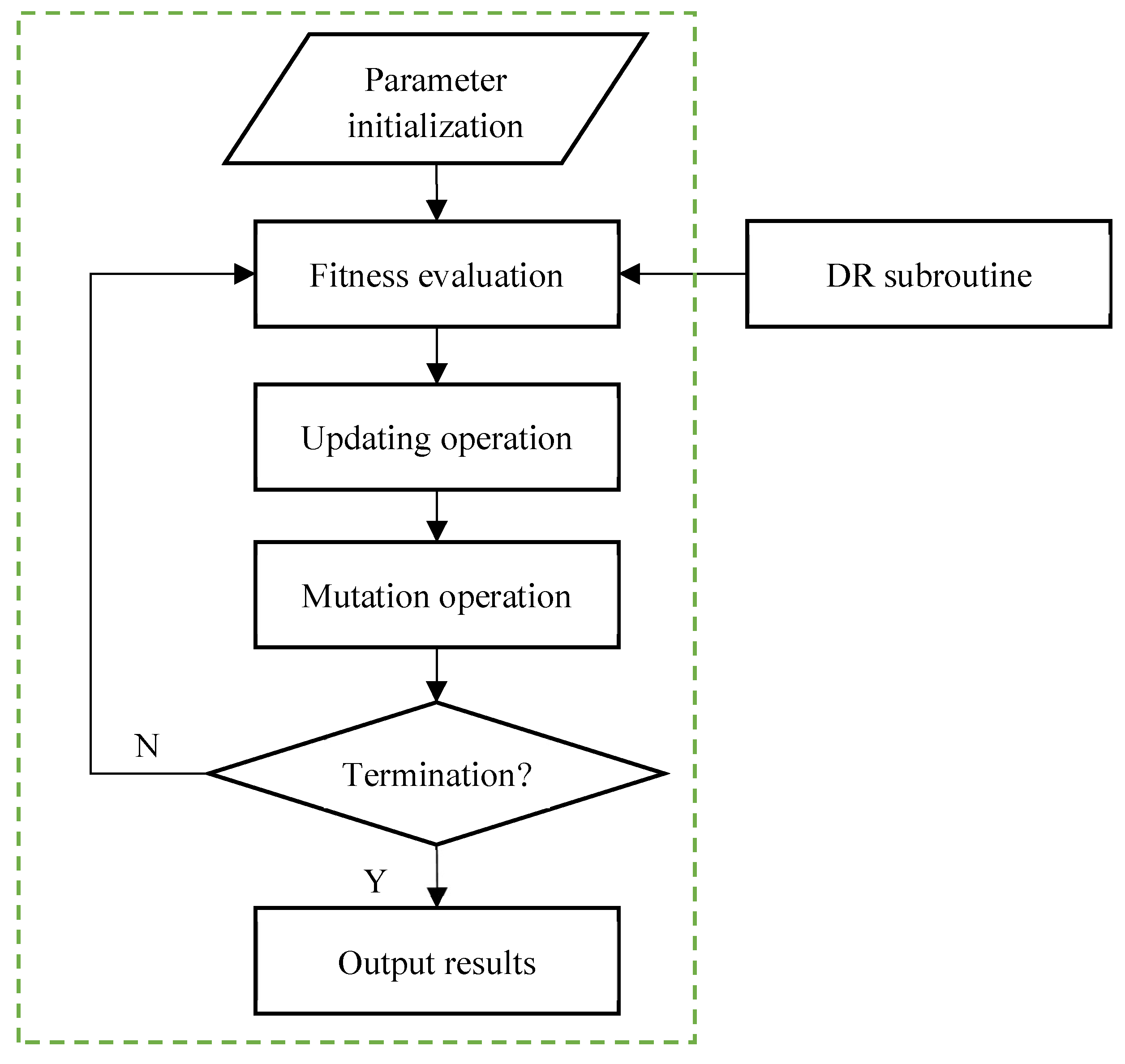
3.1. Process of the Adaptive Quantum-Inspired Evolutionary Algorithm
3.2. Classic Quantum-Inspired Evolutionary Algorithm
3.3. The Adaptive Quantum-Inspired Evolutionary Algorithm
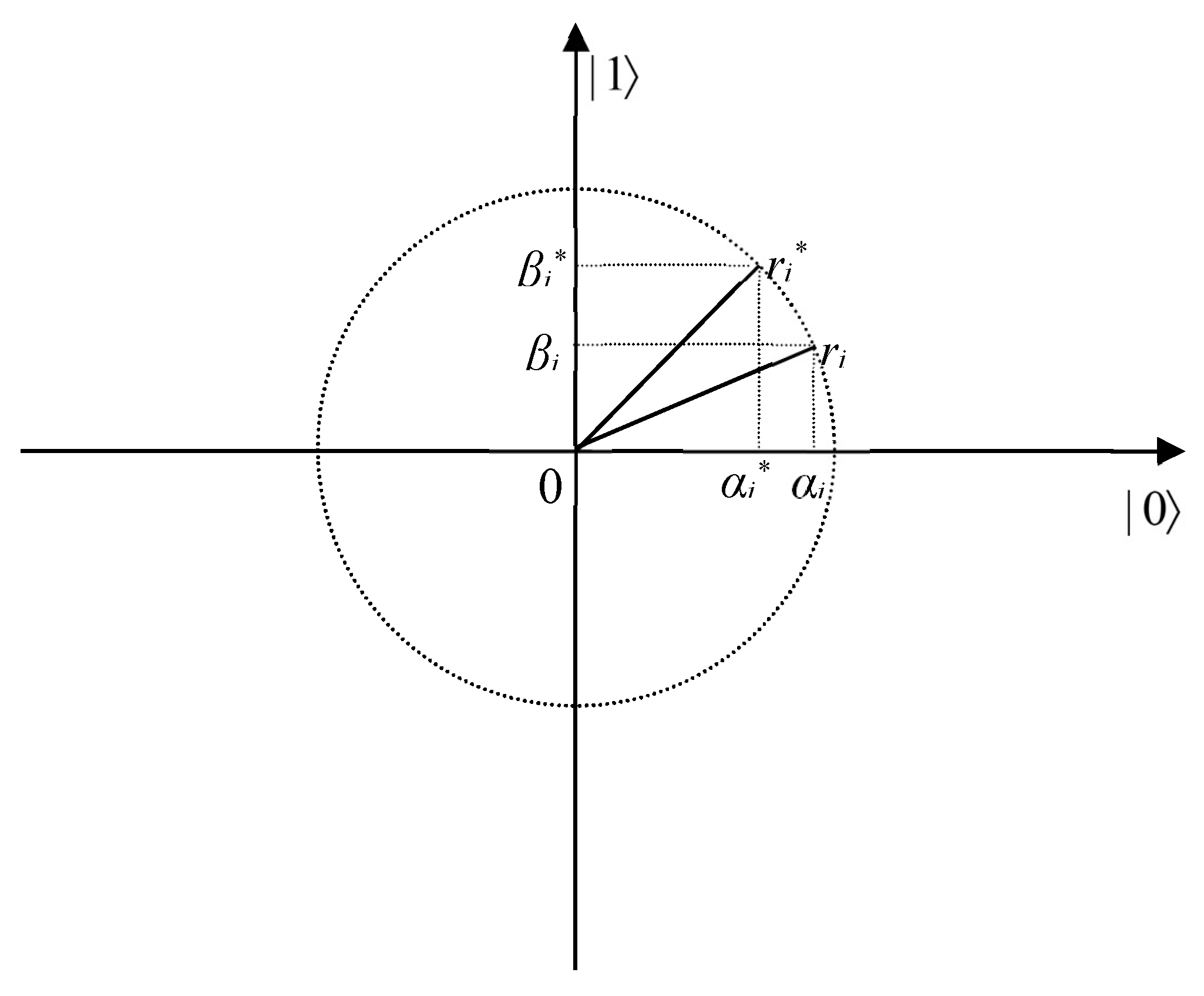
3.3.1. Adaptive Population Updating Operation
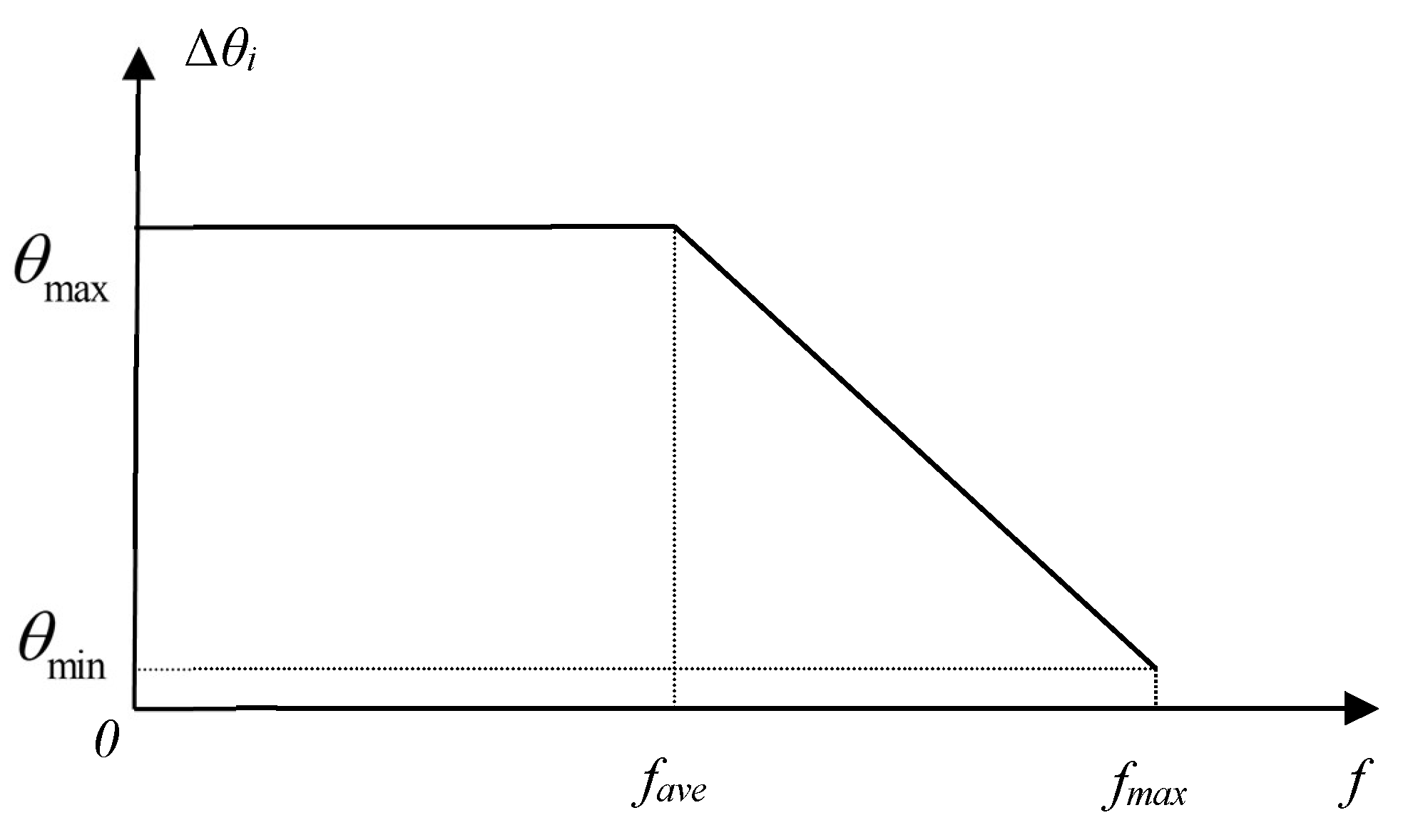
3.3.2. Adaptive Mutation Operation
3.3.3. The Procedures in AQIEA
| Procedure 1. Procedure of AQIEA. |
Begin Proc
End Proc |
| Procedure 2. Procedure of decoding. |
| Begin Proc For (each qj(t) in Q(t))
End Proc |
| Procedure 3. Procedure of population updating. |
| Begin Proc For (each qj(t) in Q(t)) For (each pair of αi and βi in qj(t))
End for End Proc |
| Procedure 4. Procedure of mutation operation. |
| Begin Proc For (each qj(t) in Q(t))
End Proc |
4. Identification of the Optimal Calibration Parameters for Dead Reckoning Based on the AQIEA
4.1. Experimental Setup for Dead Reckoning
4.2. Identification of the Optimal Dead Reckoning Calibration Parameters Based on the AQIEA
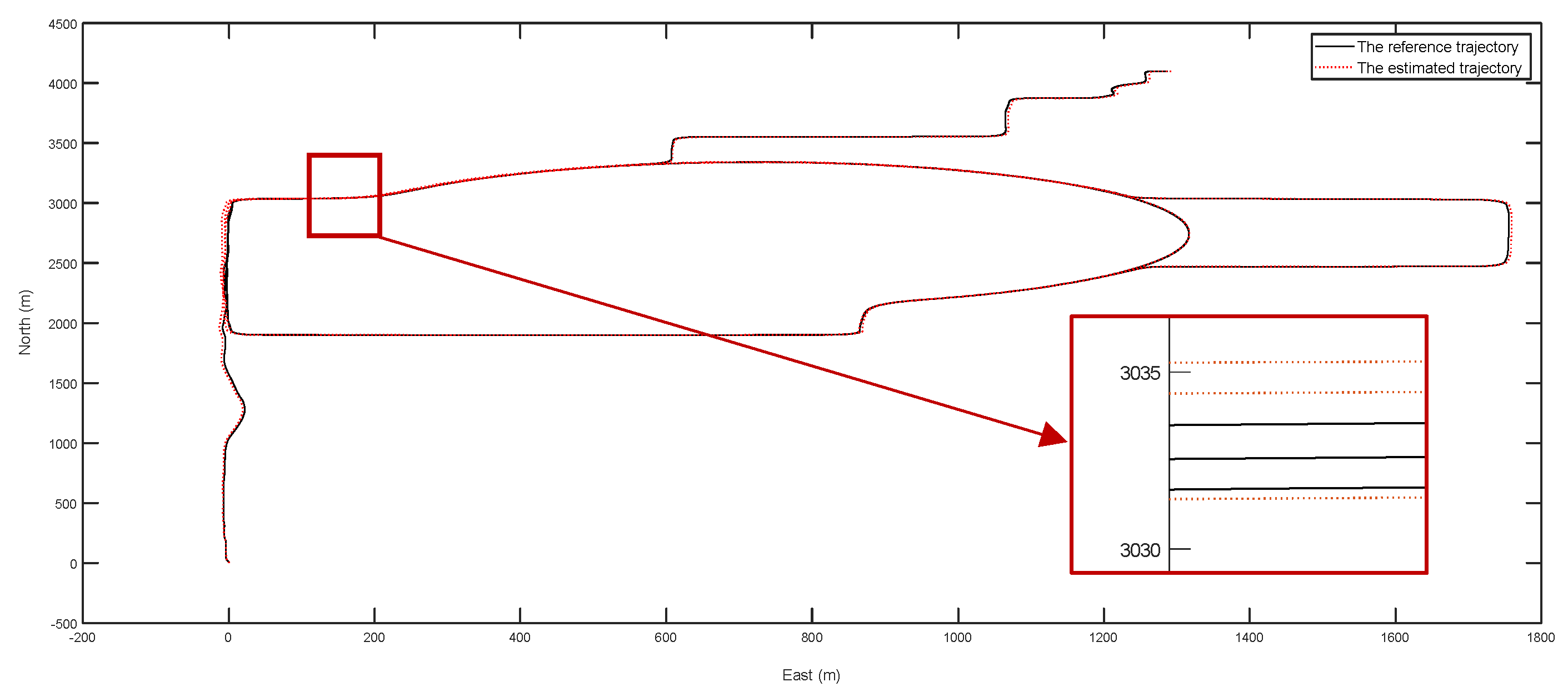
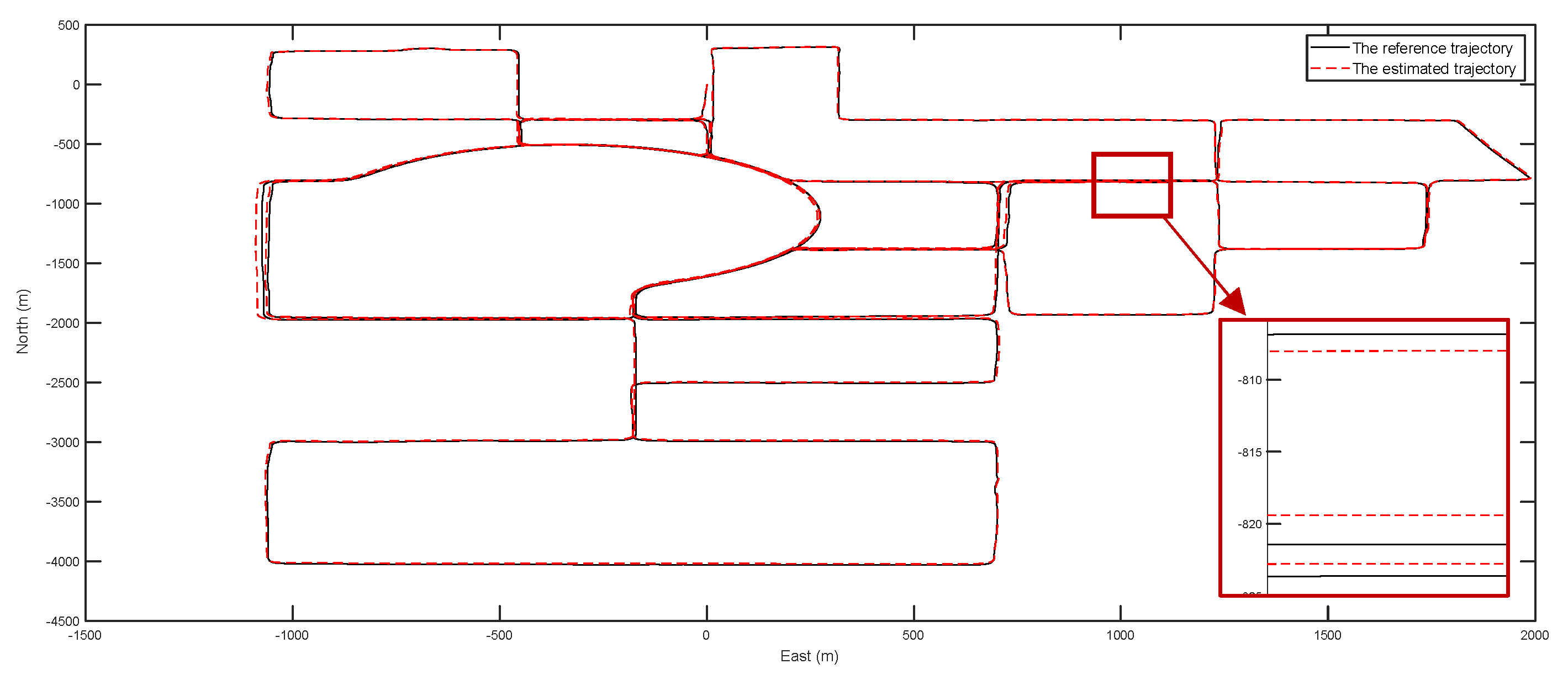
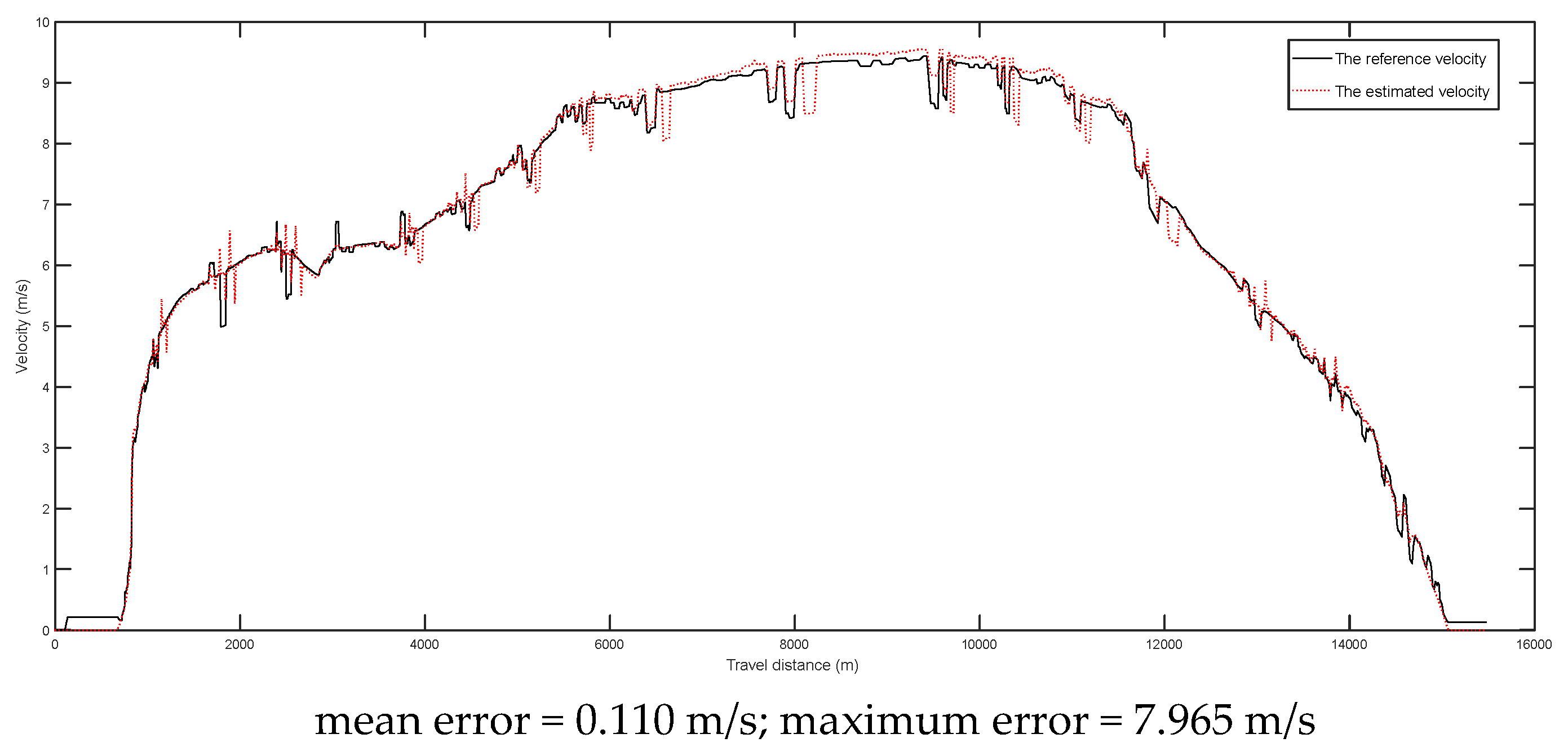
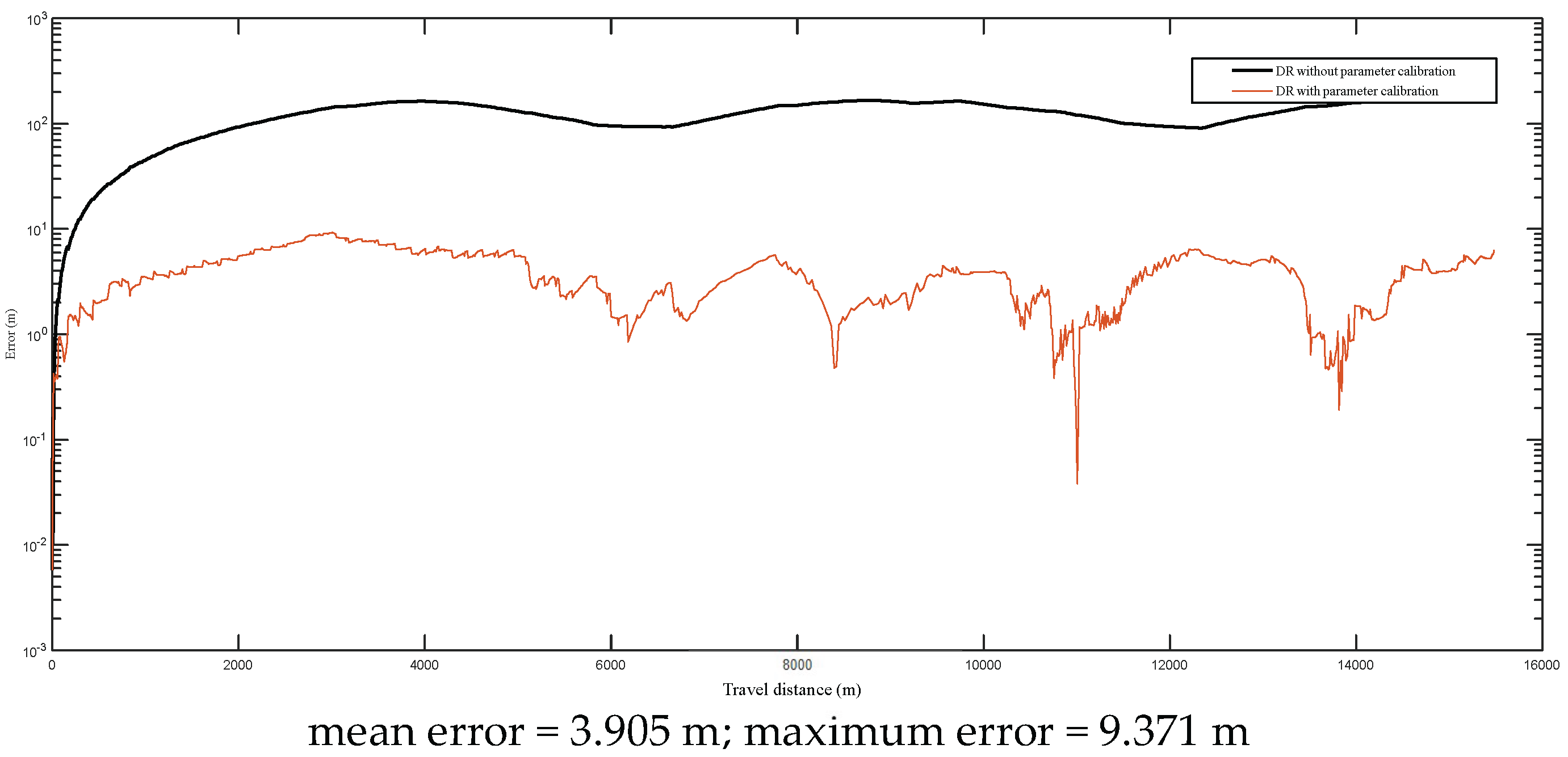
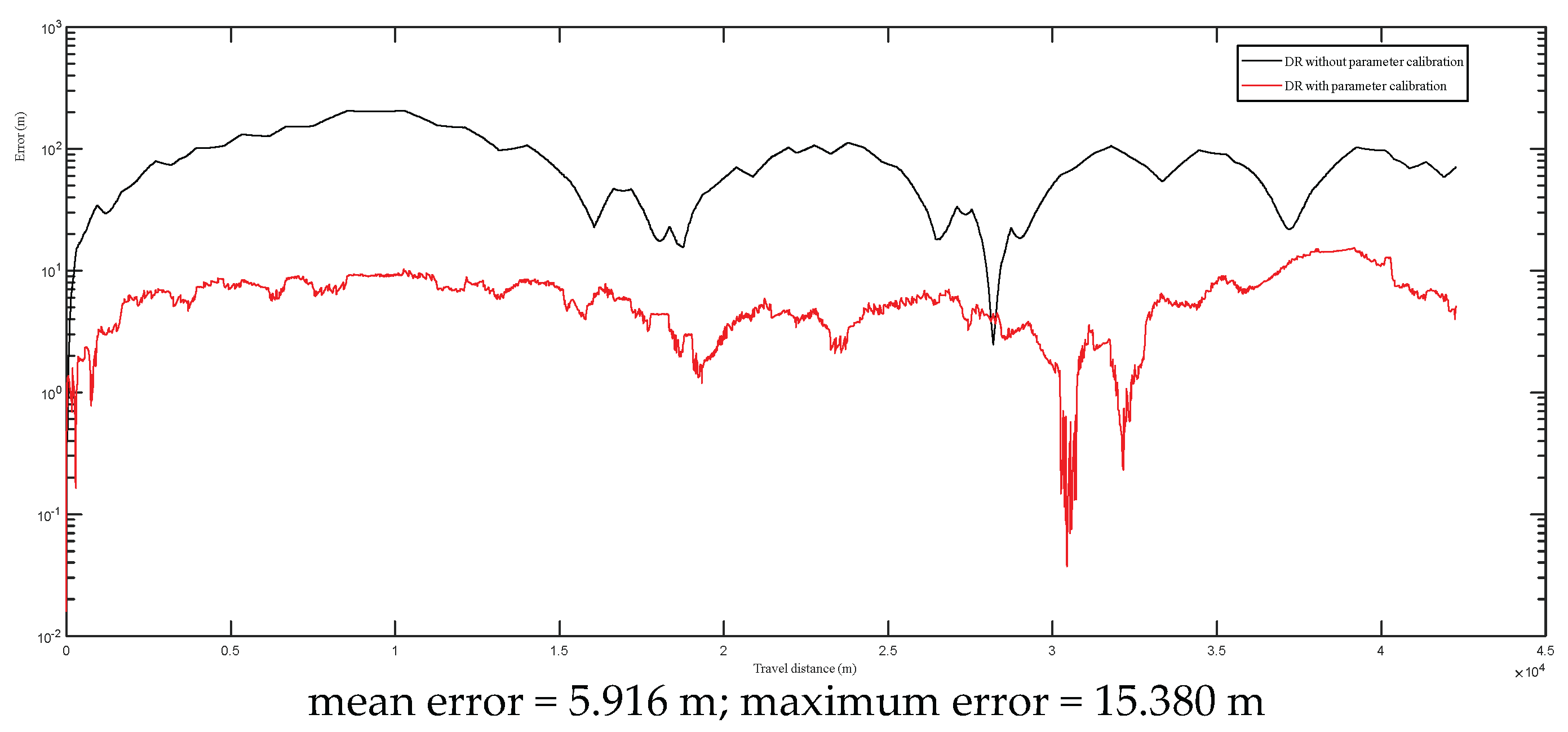
4.3. Experiments for Dead Reckoning with Error Compensation
5. Comparative Study for the AQIEA
5.1. Benchmark Functions
5.2. Results for Comparative Study
6. Conclusions
- (1)
- The newly developed dead reckoning positioning parameter calibration scheme is effective at compensating the systematic errors in dead reckoning. In addition, the design of a special calibration path is not required in this method for the calibration experiment.
- (2)
- The developed adaptive quantum-inspired evolutionary algorithm is effective at identifying the optimal calibration parameters for the dead reckoning.
- (3)
- The adaptive quantum rotation operation and the adaptive quantum mutation operation introduced in this research are effective at improving the computation quality and efficiency of the quantum-inspired evolutionary algorithm.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Quddus, M.A.; Noland, R.B.; Ochieng, W.Y. The effects of navigation sensors and spatial road network data quality on the performance of map matching algorithms. Geoinformatica 2009, 13, 85–108. [Google Scholar] [CrossRef]
- Borenstein, J.; Everett, H.R.; Feng, L.; Wehe, D. Mobile robot positioning: Sensors and techniques. J. Robot. Syst. 1997, 14, 231–249. [Google Scholar] [CrossRef]
- Zhao, L.; Ochieng, W.Y.; Quddus, M.A.; Noland, R.B. An extended Kalman filter algorithm for integrating GPS and low cost dead reckoning system data for vehicle performance and emissions monitoring. J. Navig. 2003, 56, 257–275. [Google Scholar] [CrossRef]
- Borenstein, J.; Feng, L. Measurement and correction of systematic odometry errors in mobile robots. IEEE Trans. Robot. Autom. 1996, 12, 869–880. [Google Scholar] [CrossRef]
- Cho, B.S.; Moon, W.S.; Seo, W.J.; Baek, K.W. A dead reckoning localization system for mobile robots using inertial sensors and wheel revolution encoding. J. Mech. Sci. Technol. 2011, 25, 2907–2917. [Google Scholar] [CrossRef]
- Zhang, J.; Singh, S. Low-drift and real-time lidar odometry and mapping. Auton. Robot. 2017, 41, 401–416. [Google Scholar] [CrossRef]
- Takeyama, K.; Machida, T.; Kojima, Y.; Kubo, N. Improvement of Dead Reckoning in Urban Areas Through Integration of Low-Cost Multisensors. IEEE Trans. Intell. Veh. 2017, 2, 278–287. [Google Scholar] [CrossRef]
- Bento, L.C.; Nunes, U.; Moita, F.; Surrécio, A. Sensor fusion for precise autonomous vehicle navigation in outdoor semi-structured environments. In Proceedings of the IEEE Intelligent Conference on Intelligent Transportation Systems, Vienna, Austria, 16 September 2005. [Google Scholar]
- Surrécio, A.; Nunes, U.; Araújo, R. Fusion of odometry with magnetic sensors using Kalman filters and augmented system models for mobile robot navigation. In Proceedings of the IEEE International Symposium on Industrial Electronics, Dubrovnik, Croatia, 20–23 June 2005. [Google Scholar]
- Philippe, B.; Pascal, B. Data fusion of four ABS sensors and GPS for an enhanced localization of car-like vehicles. In Proceedings of the IEEE International Conference on Robotics and Automation, Seoul, Korea, 21–26 May 2001. [Google Scholar]
- Lee, H.; Jung, J.; Choi, K.; Park, J.; Myung, H. Fuzzy-logic-assisted interacting multiple model (FLAIMM) for mobile robot localization. Robot. Auton. Syst. 2012, 60, 1592–1606. [Google Scholar] [CrossRef]
- Antonelli, G.; Chiaverini, S.; Fusco, G. A calibration method for odometry of mobile robots based on the least-squares technique: Theory and experimental validation. IEEE Trans. Robot. 2005, 21, 994–1004. [Google Scholar] [CrossRef]
- Lee, K.; Jung, C.; Chung, W. Accurate calibration of kinematic parameters for two wheel differential mobile robots. J. Mech. Sci. Technol. 2011, 25, 1603–1611. [Google Scholar] [CrossRef]
- Lee, K.; Chung, W.; Yoo, K. Kinematic parameter calibration of a car-like mobile robot to improve odometry accuracy. Mechatronics 2010, 20, 582–595. [Google Scholar] [CrossRef]
- Dogruer, C.U. Estimation of odometer parameters with MMAE and LSE. In Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Besacon, France, 8–11 July 2014. [Google Scholar]
- Philip, J.M.; Danny, R. Calibrating a 4-wheel mobile robot. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Lausanne, Switzerland, 30 September–5 October 2002; Volume 1, pp. 859–864. [Google Scholar]
- Paulo, A.J.; Bijan, S. Laser interferometry measurements based calibration and error propagation identification for pose estimation in mobile robots. Robotica 2014, 32, 165–174. [Google Scholar]
- Martinelli, A. The odometry error of a mobile robot with a synchronous drive system. IEEE Trans. Robot. Autom. 2002, 18, 399–405. [Google Scholar] [CrossRef]
- Lundquist, C.; Karlsson, R.; Özkan, E. Tire radii estimation using a marginalized particle filter. IEEE Trans. Intell. Transp. Syst. 2014, 15, 663–672. [Google Scholar] [CrossRef]
- Li, F.; Bonnifait, P.; Ibanez-Guzman, J. Map-aided dead-reckoning with lane-level maps and integrity monitoring. IEEE Trans. Intell. Veh. 2018, 3, 81–91. [Google Scholar] [CrossRef]
- Belhajem, I.; Maissa, Y.B.; Tamtaoui, A. Improving low cost sensor based vehicle positioning with Machine Learning. Control Eng. Pract. 2018, 74, 168–176. [Google Scholar] [CrossRef]
- Yu, B.; Dong, L.; Xue, D.; Zhu, H.; Geng, X.; Huang, R.; Wang, J. A hybrid dead reckoning error correction scheme based on extended Kalman filter and map matching for vehicle self-localization. J. Intell. Transp. Syst. Technol. Plan. Oper. 2019, 23, 84–98. [Google Scholar] [CrossRef]
- Han, K.H.; Kim, J.H. Genetic quantum algorithm and its application to combinatorial optimization problem. In Proceedings of the 2000 Congress on Evolutionary Computation, La Jolla, CA, USA, 16–19 July 2000. [Google Scholar]
- Gu, J.W.; Gu, X.S.; Gu, M.Z. A novel parallel quantum genetic algorithm for stochastic job shop scheduling. J. Math. Anal. Appl. 2009, 355, 63–81. [Google Scholar] [CrossRef]
- Li, P.C.; Song, K.P.; Shang, F.H. Double chains quantum genetic algorithm with application to neuro-fuzzy controller design. Adv. Eng. Softw. 2011, 42, 875–886. [Google Scholar] [CrossRef]
- Li, P.C. A quantum-behaved evolutionary algorithm based on the Bloch spherical search. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 763–771. [Google Scholar] [CrossRef]
- Xiong, H.; Wu, Z.; Fan, H.; Li, G.; Jiang, G. Quantum rotation gate in quantum-inspired evolutionary algorithm: A review, analysis and comparison study. Swarm Evol. Comput. 2018, 42, 43–57. [Google Scholar] [CrossRef]
- Chipperfield, A.J.; Fleming, P.J. The MATLAB genetic algorithm toolbox. In Proceedings of the IEEE Colloquium on Applied Control Techniques Using Matlab, London, UK, 26 January 1995. [Google Scholar]




| oi | oi* | s(αiβi) | |||
|---|---|---|---|---|---|
| αiβi > 0 | αiβi < 0 | αi = 0 | βi = 0 | ||
| 1 | 0 | −1 | +1 | ±1 | 0 |
| 0 | 1 | +1 | −1 | 0 | ±1 |
| 0 | 0 | −1 | +1 | ±1 | 0 |
| 1 | 1 | +1 | −1 | 0 | ±1 |
| oi* | s(αiβi) | |||
|---|---|---|---|---|
| αiβi > 0 | αiβi < 0 | αi = 0 | βi = 0 | |
| 0 | −1 | +1 | ±1 | 0 |
| 1 | +1 | −1 | 0 | ±1 |
| Parameter | Name | Value |
|---|---|---|
| Rr | Resolution of encoder for rear right wheel | 4000 pulses/r |
| Rl | Resolution of encoder for rear left wheel | 4000 pulses/r |
| Dr | Nominal diameter of right rear wheel | 0.637 m |
| Dl | Nominal diameter of left rear wheel | 0.637 m |
| No. | Function | Formulation | D | R | O |
|---|---|---|---|---|---|
| f1 | De-Jong’s function | 2 | [−2.048, 2.048] | 0 | |
| f2 | Goldstein–Price function | 2 | [−100, 100] | 3 | |
| f3 | Schaffer’s F6 function | 2 | [−100, 100] | 0 | |
| f4 | Easom’s function | 2 | [−100, 100] | −1 | |
| f5 | Sphere function | 30 | [−5.12, 5.12] | 0 | |
| f6 | Griewank function | 30 | [−600, 600] | 0 | |
| f7 | Ackley function | 30 | [−32, 32] | 0 | |
| f8 | Rastrigin function | 30 | [−5.12, 5.12] | 0 |
| Parameter | CGA | CQIEA | AQIEA |
|---|---|---|---|
| Population size | 60 | 10 | 10 |
| Maximum generation | 5000 for f1~f4 10,000 for f5~f8 | 5000 for f1~f4 10,000 for f5~f8 | 5000 for f1~f4 10,000 for f5~f8 |
| Crossover rate | 0.7 | / | / |
| Mutation rate | 0.01 | / | pmax = 0.1, pmin = 0.01 |
| Quantum rotation angle | / | Given in [23] | θmax = 0.05π, θmin = 0.001π |
| Test Function | Performance | Algorithms | ||
|---|---|---|---|---|
| AQIEA | CGA | CQIEA | ||
| f1 | Best value | 1.0004 × 10−10 | 1.0004 × 10−10 | 8.2224 × 10−8 |
| Worst value | 8.0830 × 10−2 | 1.9749 × 10−1 | 1.0000 | |
| Mean value | 7.3313 × 10−3 | 5.0742 × 10−2 | 7.9007 × 10−2 | |
| Standard deviation | 1.7405 × 10−2 | 6.4377 × 10−2 | 2.5115 × 10−1 | |
| Mean time (s) | 15.8 | 30.2 | 25.3 | |
| f2 | Best value | 3.0000 | 3.0000 | 3.0000 |
| Worst value | 8.4600 × 101 | 5.7482 × 105 | 6.1677 × 107 | |
| Mean value | 9.0448 | 1.9191 × 104 | 2.0560 × 106 | |
| Standard deviation | 1.6197 × 101 | 1.0494 × 105 | 1.1261 × 107 | |
| Mean time (s) | 13.9 | 30.4 | 28.8 | |
| f3 | Best value | 1.8190 × 10−8 | 1.8190 × 10−8 | 1.8190 × 10−8 |
| Worst value | 9.6583 × 10−3 | 1.2439 × 10−1 | 1.2439 × 10−1 | |
| Mean value | 5.9255 × 10−3 | 1.4411 × 10−2 | 1.0522 × 10−2 | |
| Standard deviation | 4.5687 × 10−3 | 3.0204 × 10−2 | 2.1957 × 10−2 | |
| Mean time (s) | 19.9 | 57.2 | 25.8 | |
| f4 | Best value | −1.0000 | −1.0000 | −1.0000 |
| Worst value | −1.0000 | −4.6552 × 10−7 | 0.0000 | |
| Mean value | −1.0000 | −9.6631 × 10−1 | −3.3333 × 10−2 | |
| Standard deviation | 0.0000 | 1.8251 × 10−1 | 1.8257 × 10−1 | |
| Mean time (s) | 13.6 | 30.0 | 28.9 | |
| f5 | Best value | 1.6051 × 10−5 | 4.1621 | 1.2827 × 10−4 |
| Worst value | 2.5806 × 10−2 | 7.3858 | 2.1318 × 10−1 | |
| Mean value | 1.3603 × 10−3 | 5.8291 | 7.9335 × 10−3 | |
| Standard deviation | 4.6669 × 10−3 | 8.3242 × 10−1 | 3.8769 × 10−2 | |
| Mean time (s) | 277.2 | 374.4 | 637.2 | |
| f6 | Best value | 6.2675 × 10−5 | 1.6512 × 101 | 1.9451 × 102 |
| Worst value | 1.8752 × 10−5 | 2.6707 × 101 | 9.4725 × 101 | |
| Mean value | 4.6470 × 10−5 | 2.2313 × 101 | 3.4142 × 101 | |
| Standard deviation | 4.5904 × 10−5 | 2.3307 | 2.1200 × 101 | |
| Mean time (s) | 270.5 | 382.6 | 614.7 | |
| f7 | Best value | 3.3597 × 10−1 | 9.0554 | 9.99160 |
| Worst value | 4.3268 | 1.0766 × 101 | 1.9265 × 101 | |
| Mean value | 2.1113 | 1.0020 × 101 | 1.3341 × 101 | |
| Standard deviation | 7.8542 × 10−1 | 4.2962 × 10−1 | 2.5355 | |
| Mean time (s) | 347.7 | 373.9 | 657.9 | |
| f8 | Best value | 8.1957 | 4.0974 × 101 | 6.6567 × 101 |
| Worst value | 2.4041 × 101 | 8.5433 × 101 | 8.7187 × 101 | |
| Mean value | 1.3444 × 101 | 6.2210 × 101 | 7.9928 × 101 | |
| Standard deviation | 3.9940 | 1.1466 × 101 | 5.1744 | |
| Mean time (s) | 328.6 | 356.7 | 643.1 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, B.; Zhu, H.; Xue, D.; Xu, L.; Zhang, S.; Li, B. A Dead Reckoning Calibration Scheme Based on Optimization with an Adaptive Quantum-Inspired Evolutionary Algorithm for Vehicle Self-Localization. Entropy 2022, 24, 1128. https://doi.org/10.3390/e24081128
Yu B, Zhu H, Xue D, Xu L, Zhang S, Li B. A Dead Reckoning Calibration Scheme Based on Optimization with an Adaptive Quantum-Inspired Evolutionary Algorithm for Vehicle Self-Localization. Entropy. 2022; 24(8):1128. https://doi.org/10.3390/e24081128
Chicago/Turabian StyleYu, Biao, Hui Zhu, Deyi Xue, Liwei Xu, Shijin Zhang, and Bichun Li. 2022. "A Dead Reckoning Calibration Scheme Based on Optimization with an Adaptive Quantum-Inspired Evolutionary Algorithm for Vehicle Self-Localization" Entropy 24, no. 8: 1128. https://doi.org/10.3390/e24081128
APA StyleYu, B., Zhu, H., Xue, D., Xu, L., Zhang, S., & Li, B. (2022). A Dead Reckoning Calibration Scheme Based on Optimization with an Adaptive Quantum-Inspired Evolutionary Algorithm for Vehicle Self-Localization. Entropy, 24(8), 1128. https://doi.org/10.3390/e24081128







