Fixed-Time Leader-Following Consensus Tracking Control for Nonliear Multi-Agent Systems under Jointly Connected Graph
Abstract
:1. Introduction
2. Preliminaries
2.1. Notations
2.2. Definition and Lemmas
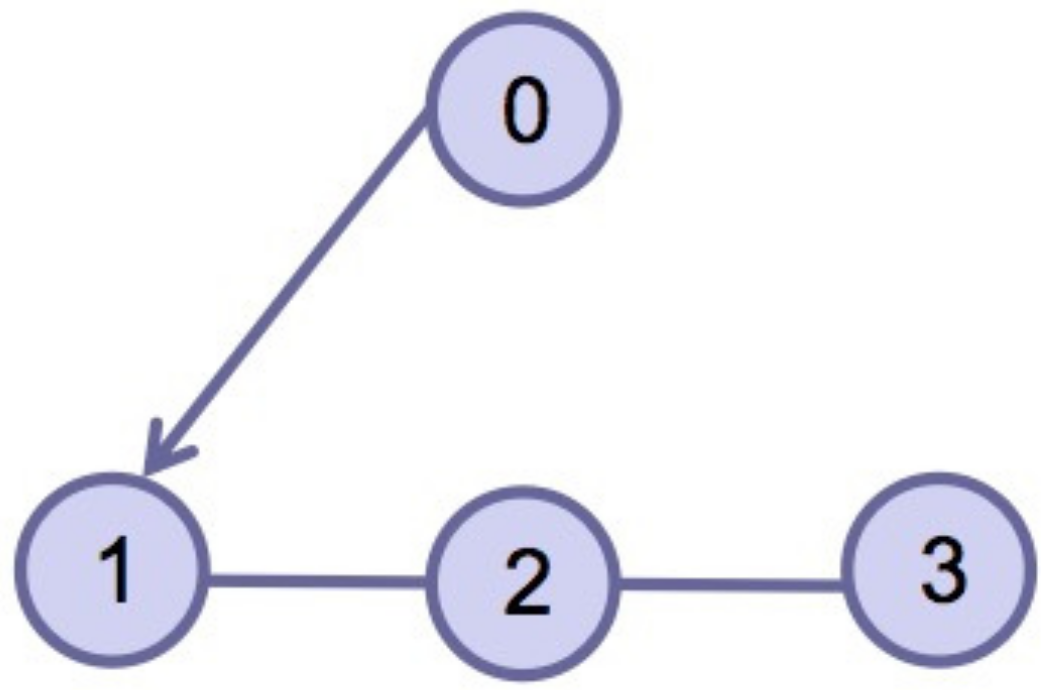
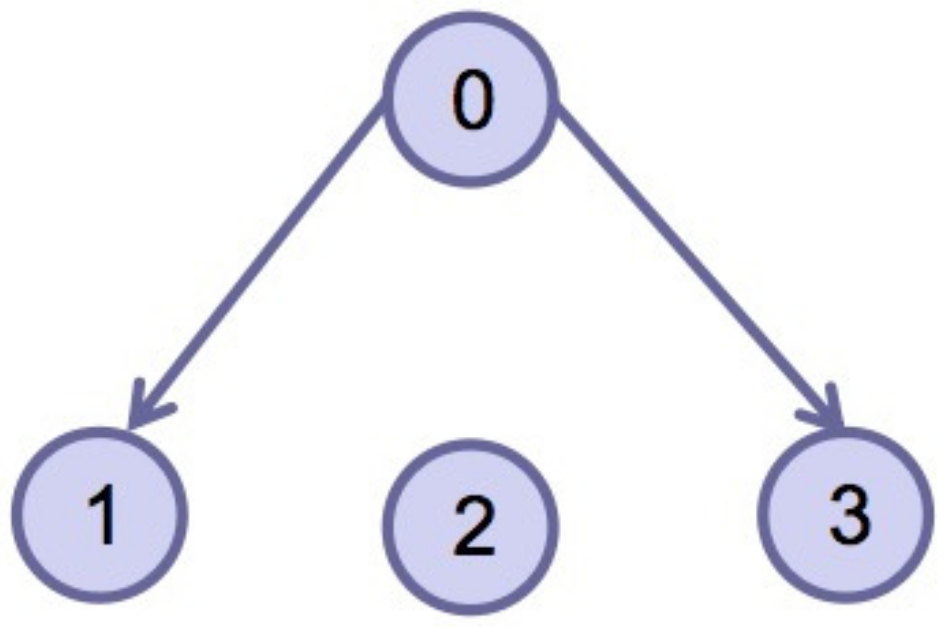
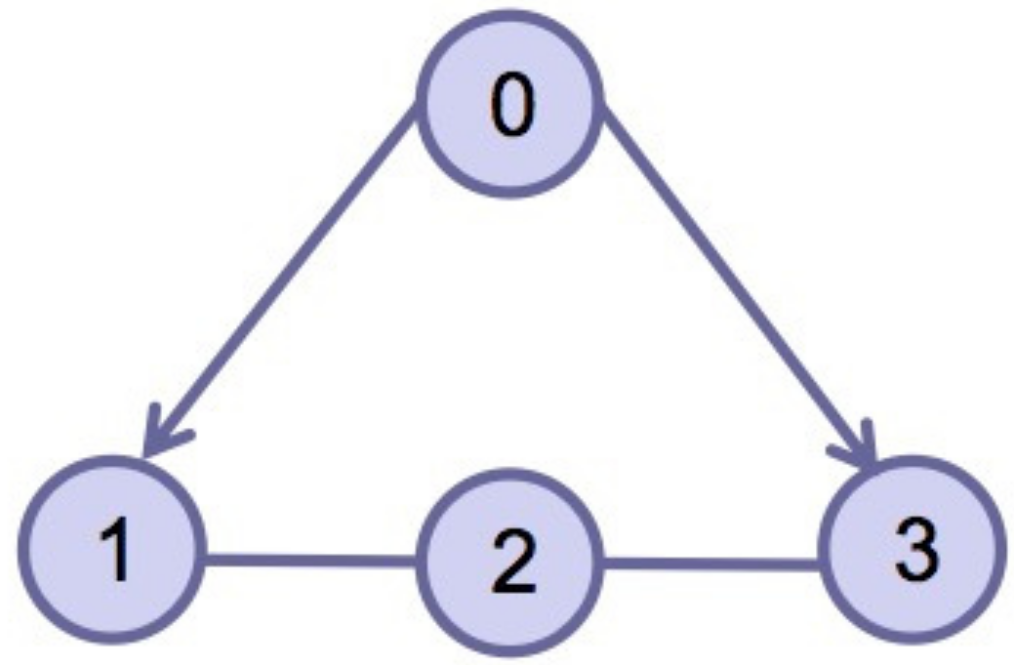
2.3. Algebraic Graph Theory
3. Main Results
3.1. Problem Formulation
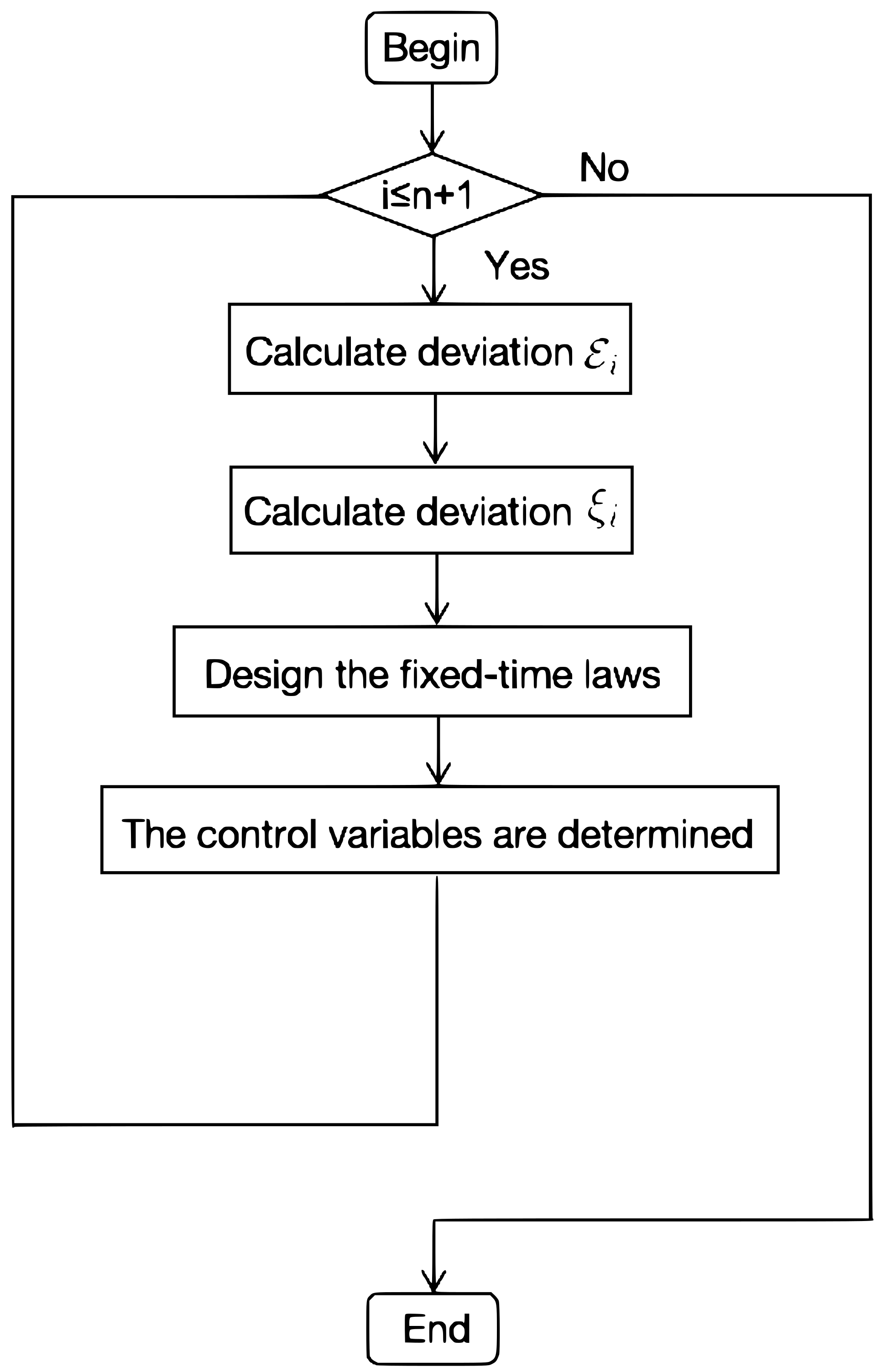
3.2. Fixed-Time Consensus Protocol
4. Simulation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Han, T.; Chi, M.; Guan, Z.H.; Hu, B.; Xiao, J.W.; Huang, Y. Distributed Three-Dimensional Formation Containment Control of Multiple Unmanned Aerial Vehicle Systems: Distributed 3D Formation Containment Control of Multiple UAV Systems. Asian J. Control 2017, 19, 1103–1113. [Google Scholar] [CrossRef]
- Loria, A.; Dasdemir, J.; Jarquin, N.A. Leader–follower formation and tracking control of mobile robots along straight paths. IEEE Trans. Control Syst. Technol. 2015, 24, 727–732. [Google Scholar] [CrossRef]
- Minsky, M. The Society of Mind; JSTOR: New York, NY, USA, 1987. [Google Scholar]
- Zhang, S.; Tepedelenlioǧlu, C.; Banavar, M.K.; Spanias, A. Max consensus in sensor networks: Non-linear bounded transmission and additive noise. IEEE Sens. J. 2016, 16, 9089–9098. [Google Scholar] [CrossRef]
- Jiang, J.; Jiang, Y. Leader-following consensus of linear time-varying multi-agent systems under fixed and switching topologies. Automatica 2020, 113, 108804. [Google Scholar] [CrossRef]
- Li, Z.; Duan, Z. Cooperative Control of Multi-Agent Systems: A Consensus Region Approach; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Guan, Z.H.; Sun, F.L.; Wang, Y.W.; Li, T. Finite-time consensus for leader-following second-order multi-agent networks. IEEE Trans. Circuits Syst. I Regul. Pap. 2012, 59, 2646–2654. [Google Scholar] [CrossRef]
- Li, S.; Du, H.; Lin, X. Finite-time consensus algorithm for multi-agent systems with double-integrator dynamics. Automatica 2011, 47, 1706–1712. [Google Scholar] [CrossRef]
- Wang, L.; Xiao, F. Finite-time consensus problems for networks of dynamic agents. IEEE Trans. Autom. Control 2010, 55, 950–955. [Google Scholar] [CrossRef]
- Zhao, L.; Liu, Y.; Li, F.; Man, Y. Fully distributed adaptive finite-time consensus for uncertain nonlinear multiagent systems. IEEE Trans. Cybern. 2010, 52, 6972–6983. [Google Scholar] [CrossRef]
- Asiri, S.; Liu, D.Y. Finite-time estimation for a class of systems with unknown time-delay using modulating functions-based method. Asian J. Control 2022. [Google Scholar] [CrossRef]
- Li, Y.; Yang, R. Distributed finite-time formation of networked nonlinear systems via dynamic gain control. Asian J. Control 2022. [Google Scholar] [CrossRef]
- Van, M.; Sam Ge, S.; Ceglarek, D. Global finite-time cooperative control for multiple manipulators using integral sliding mode control. Asian J. Control 2021. [Google Scholar] [CrossRef]
- Polyakov, A. Nonlinear feedback design for fixed-time stabilization of linear control systems. IEEE Trans. Autom. Control 2011, 57, 2106–2110. [Google Scholar] [CrossRef]
- Zuo, Z. Nonsingular fixed-time consensus tracking for second-order multi-agent networks. Automatica 2015, 54, 305–309. [Google Scholar] [CrossRef]
- Tian, B.; Lu, H.; Zuo, Z.; Yang, W. Fixed-time leader–follower output feedback consensus for second-order multiagent systems. IEEE Trans. Cybern. 2018, 49, 1545–1550. [Google Scholar] [CrossRef]
- Defoort, M.; Polyakov, A.; Demesure, G.; Djemai, M.; Veluvolu, K. Leader-follower fixed-time consensus for multi-agent systems with unknown non-linear inherent dynamics. IET Control Theory Appl. 2015, 9, 2165–2170. [Google Scholar] [CrossRef]
- Hong, H.; Yu, W.; Wen, G.; Yu, X. Distributed robust fixed-time consensus for nonlinear and disturbed multiagent systems. IEEE Trans. Syst. Man Cybern. Syst. 2016, 47, 1464–1473. [Google Scholar] [CrossRef]
- Shang, Y. Fixed-time group consensus for multi-agent systems with non-linear dynamics and uncertainties. IET Control Theory Appl. 2018, 12, 395–404. [Google Scholar] [CrossRef]
- You, X.; Hua, C.; Li, K.; Jia, X. Fixed-time leader-following consensus for high-order time-varying nonlinear multiagent systems. IEEE Trans. Autom. Control 2020, 65, 5510–5516. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, Y.; Ren, W.; Chen, G. Appointed-time consensus: Accurate and practical designs. Automatica 2018, 89, 425–429. [Google Scholar] [CrossRef]
- Zhao, L.; Sun, Y.; Dai, H.; Zhao, D. Stochastic fixed-time consensus problem of multi-agent systems with fixed and switching topologies. Int. J. Control 2021, 94, 2811–2821. [Google Scholar] [CrossRef]
- Cui, L.; Zhou, Q.; Jin, N. Fixed-time backstepping distributed cooperative control for multiple unmanned aerial vehicles. Asian J. Control 2022. [Google Scholar] [CrossRef]
- Yao, Q. Fixed-time adaptive neural control for nonstrict-feedback uncertain nonlinear systems with output constraints. Asian J. Control 2022. [Google Scholar] [CrossRef]
- Chen, M.; Wang, H.; Liu, X. Adaptive Fuzzy Practical Fixed-Time Tracking Control of Nonlinear Systems. Daptive Fuzzy Pract. Fixed-Time Track. Control Nonlinear Syst. 2021, 29, 664–673. [Google Scholar] [CrossRef]
- Yan, C.; Amir, R.; Ardashir, M.; Sakthivel, R. Deep learned recurrent type-3 fuzzy system: Application for renewable energy modeling/prediction. Energy Rep. 2021, 7, 8115–8127. [Google Scholar]
- Wei, X.; Yu, W.; Wang, H.; Yao, Y.; Mei, F. An observer-based fixed-time consensus control for second-order multi-agent systems with disturbances. IEEE Trans. Circuits Syst. II Express Briefs 2018, 66, 247–251. [Google Scholar] [CrossRef]
- Zuo, Z.; Tian, B.; Defoort, M.; Ding, Z. Fixed-time consensus tracking for multiagent systems with high-order integrator dynamics. IEEE Trans. Autom. Control 2017, 63, 563–570. [Google Scholar] [CrossRef]
- Xu, Y.; Yao, Z.; Lu, R.; Ghosh, B. A novel fixed-time protocol for first-order consensus tracking with disturbance rejection. IEEE Trans. Autom. Control 2021. [Google Scholar] [CrossRef]
- Tian, B.; Shao, X.; Yang, W.; Zhang, W. Fixed time output feedback containment for uncertain nonlinear multiagent systems with switching communication topologies. ISA Trans. 2021, 111, 82–95. [Google Scholar]
- Parsegov, S.; Polyakov, A.; Shcherbakov, P. Fixed-time consensus algorithm for multi-agent systems with integrator dynamics. IFAC Proc. Vol. 2013, 46, 110–115. [Google Scholar] [CrossRef]
- Hardy, G.H.; Littlewood, J.E.; Polya, G. Inequalities; Cambridge University Press: Cambridge, UK, 1952. [Google Scholar]
- Ren, W.; Beard, R.W. Consensus seeking in multiagent systems under dynamically changing interaction topologies. IEEE Trans. Autom. Control 2005, 50, 655–661. [Google Scholar] [CrossRef]




| Notations | |
|---|---|
| The real number set | |
| The positive real number set | |
| n-dimensional real vector space | |
| The column vector of with all elements 1 | |
| The n-dimensional identity matrix | |
| The sign function | |
| The smallest eigenvalue of the matrix | |
| The largest eigenvalue of the matrix |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, M.; Gu, C.; Zhao, L.; Liu, Y. Fixed-Time Leader-Following Consensus Tracking Control for Nonliear Multi-Agent Systems under Jointly Connected Graph. Entropy 2022, 24, 1130. https://doi.org/10.3390/e24081130
Zhao M, Gu C, Zhao L, Liu Y. Fixed-Time Leader-Following Consensus Tracking Control for Nonliear Multi-Agent Systems under Jointly Connected Graph. Entropy. 2022; 24(8):1130. https://doi.org/10.3390/e24081130
Chicago/Turabian StyleZhao, Meng, Chan Gu, Le Zhao, and Yungang Liu. 2022. "Fixed-Time Leader-Following Consensus Tracking Control for Nonliear Multi-Agent Systems under Jointly Connected Graph" Entropy 24, no. 8: 1130. https://doi.org/10.3390/e24081130
APA StyleZhao, M., Gu, C., Zhao, L., & Liu, Y. (2022). Fixed-Time Leader-Following Consensus Tracking Control for Nonliear Multi-Agent Systems under Jointly Connected Graph. Entropy, 24(8), 1130. https://doi.org/10.3390/e24081130





