Free-Energy-Based Discrete Unified Gas Kinetic Scheme for van der Waals Fluid
Abstract
:1. Introduction
2. Numerical Methodology
2.1. Free-Energy Model
2.2. Strang-Splitting DUGKS
2.2.1. Discrete Unified Gas-Kinetic Scheme
2.2.2. Strang-Splitting Scheme
3. Numerical Results
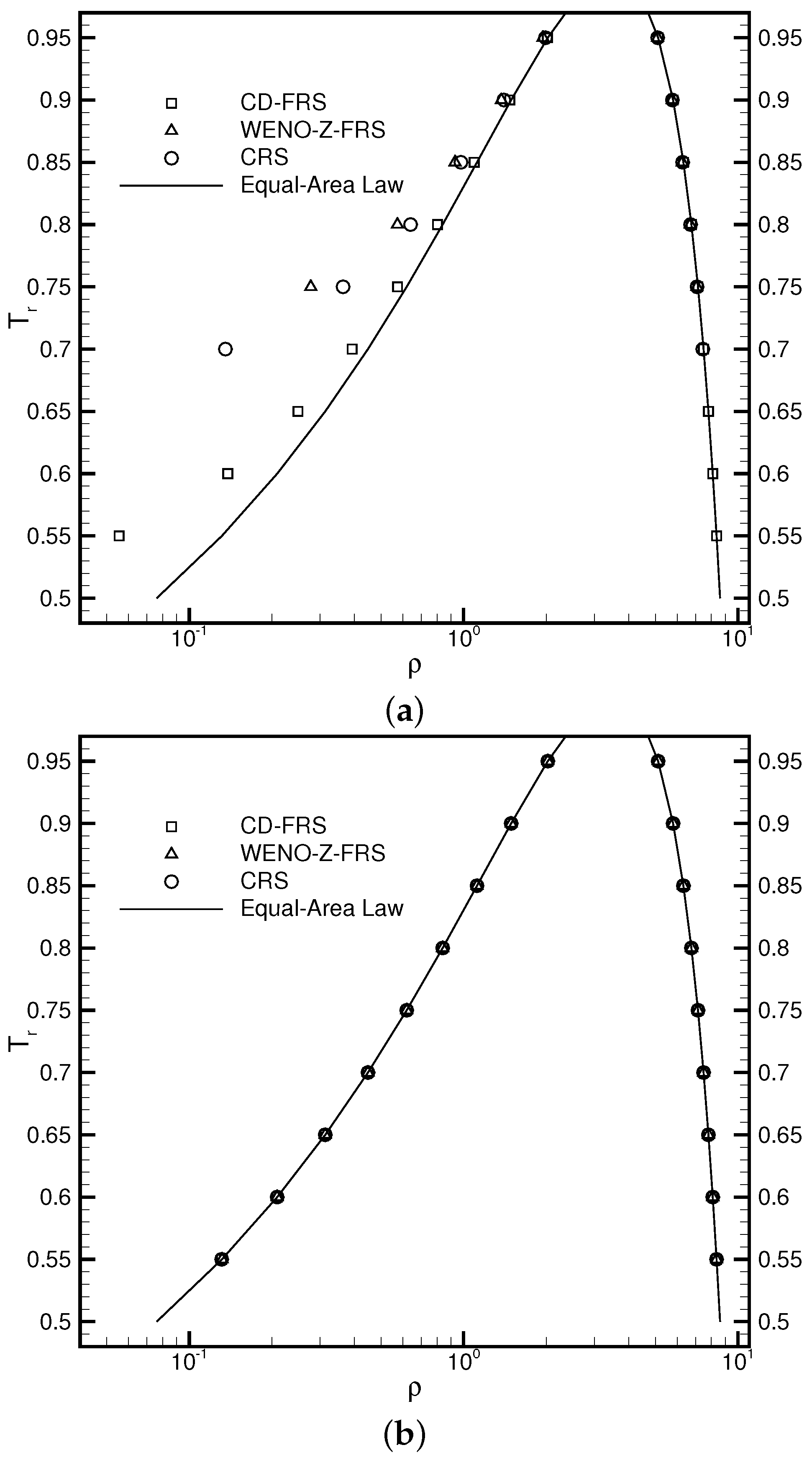
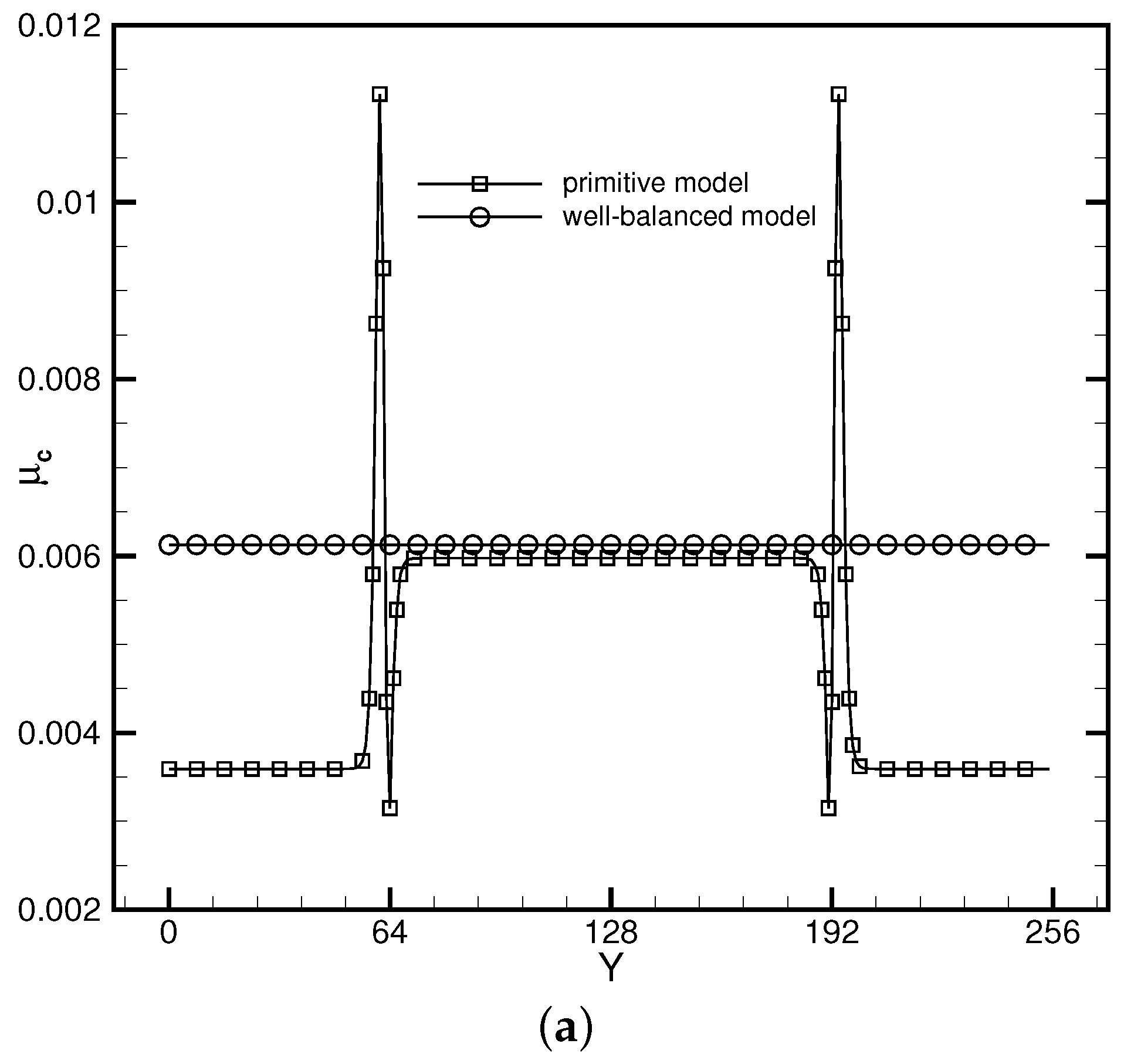
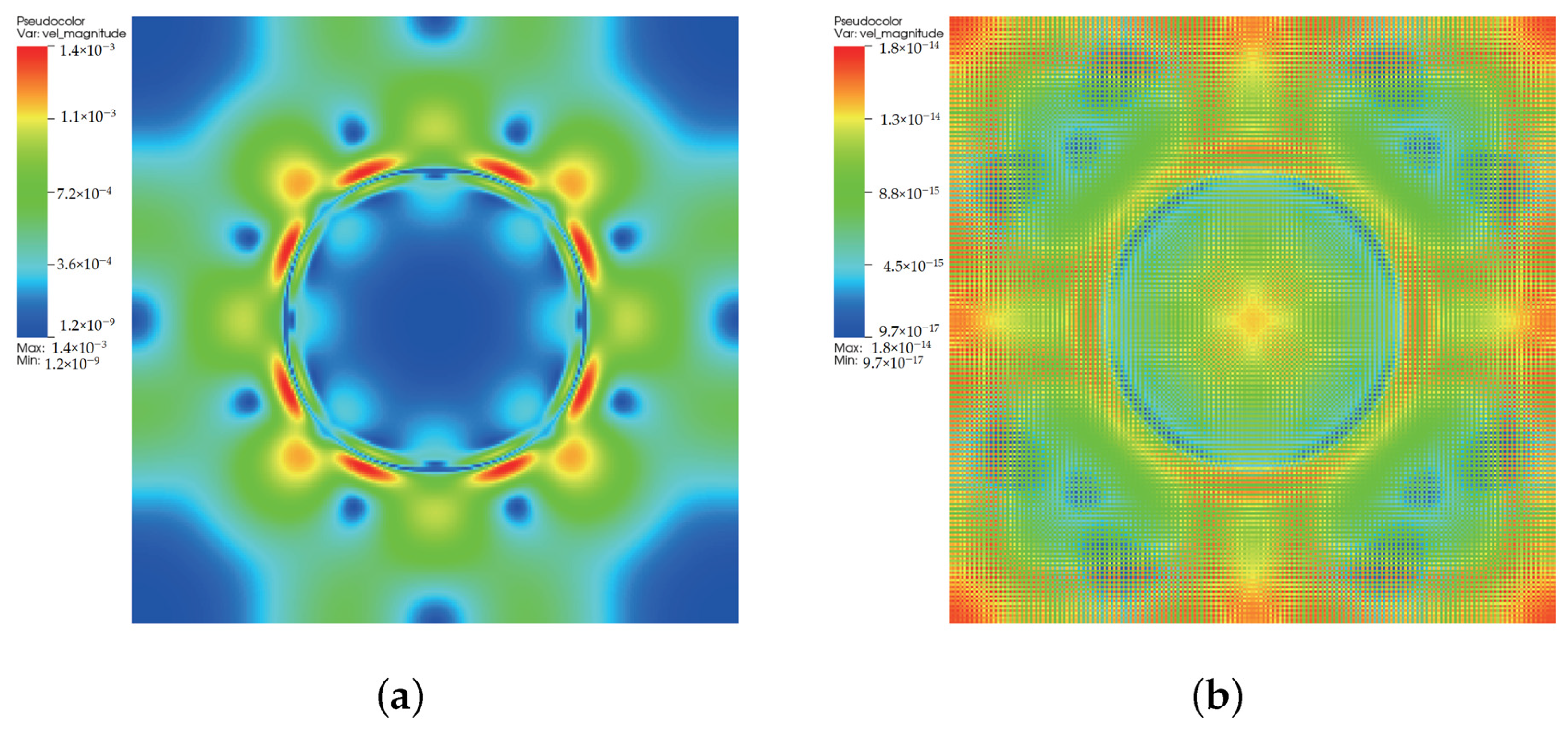
3.1. Flat Interface
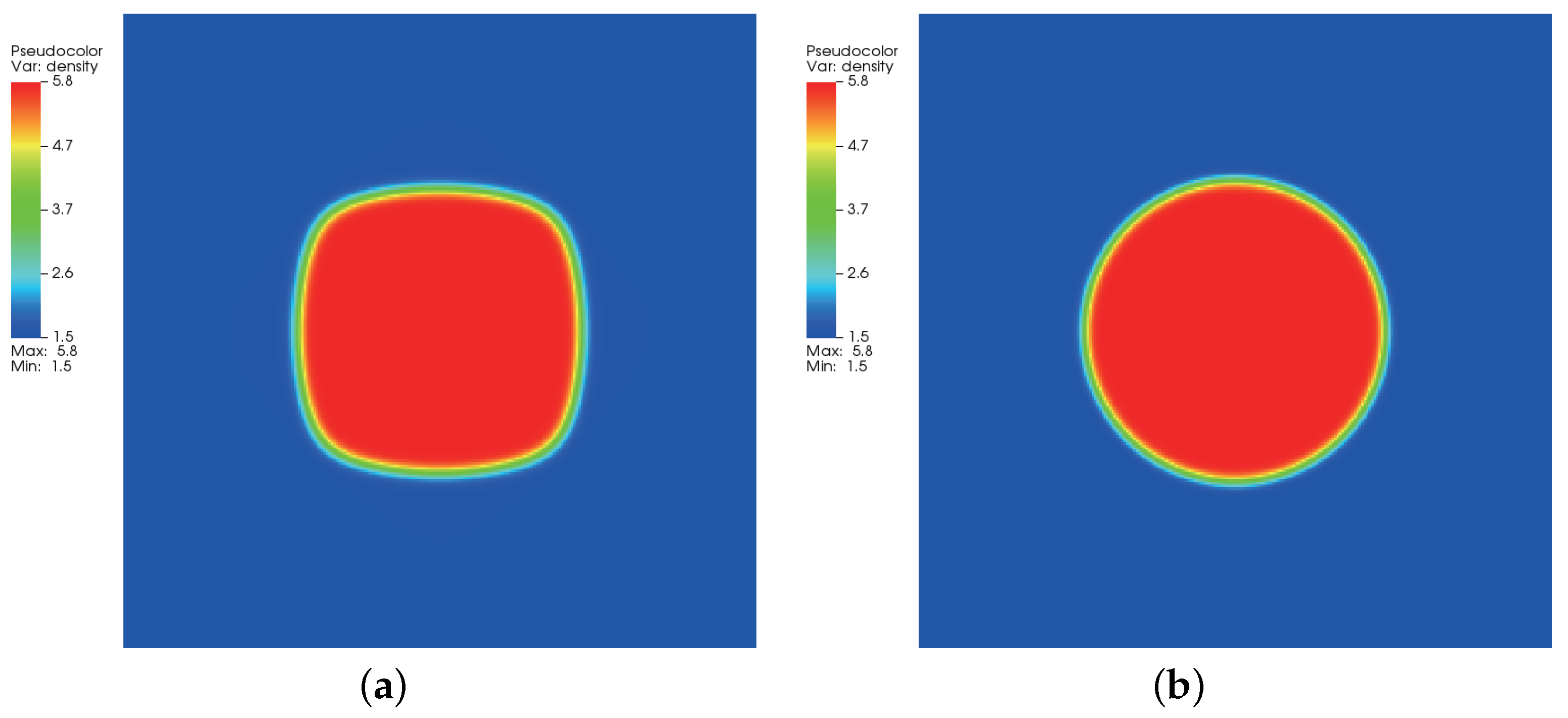
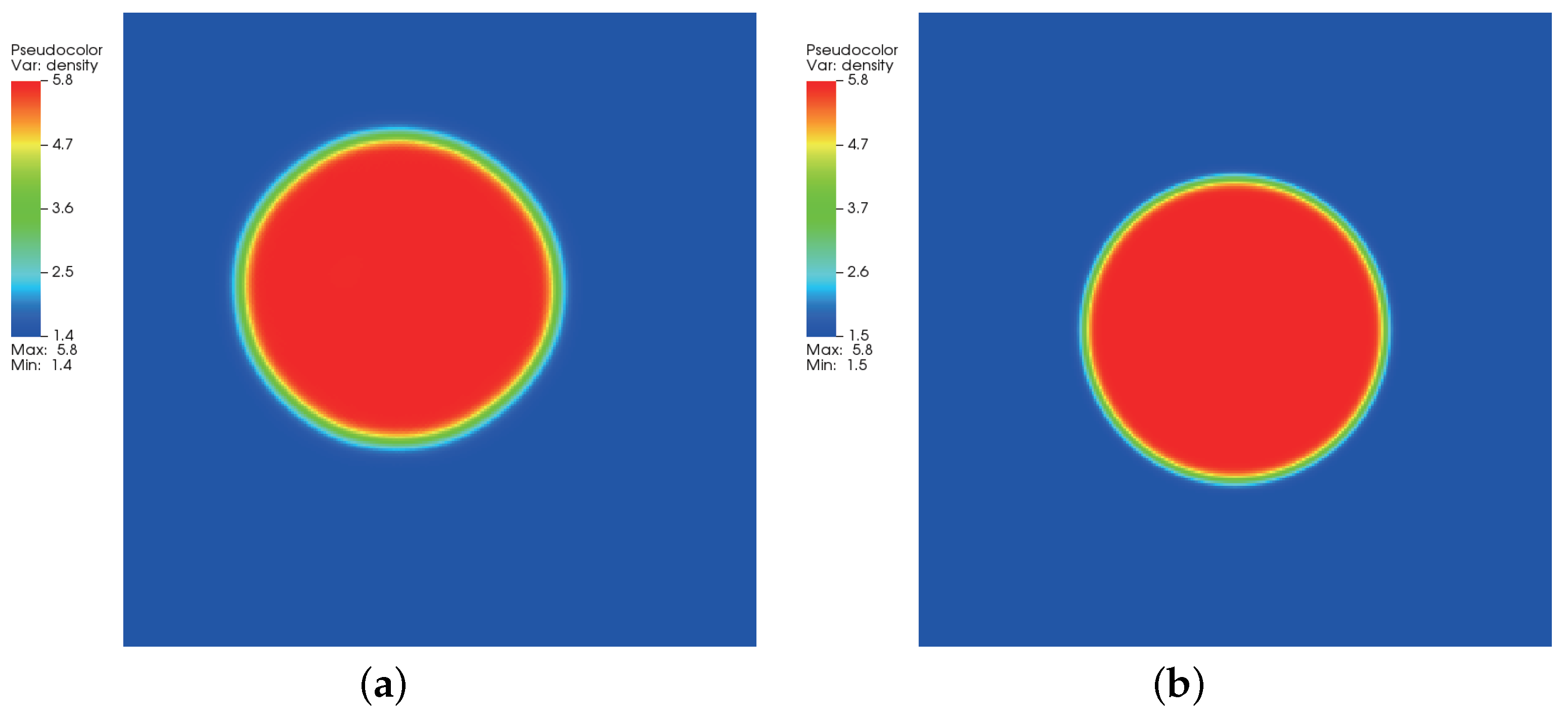
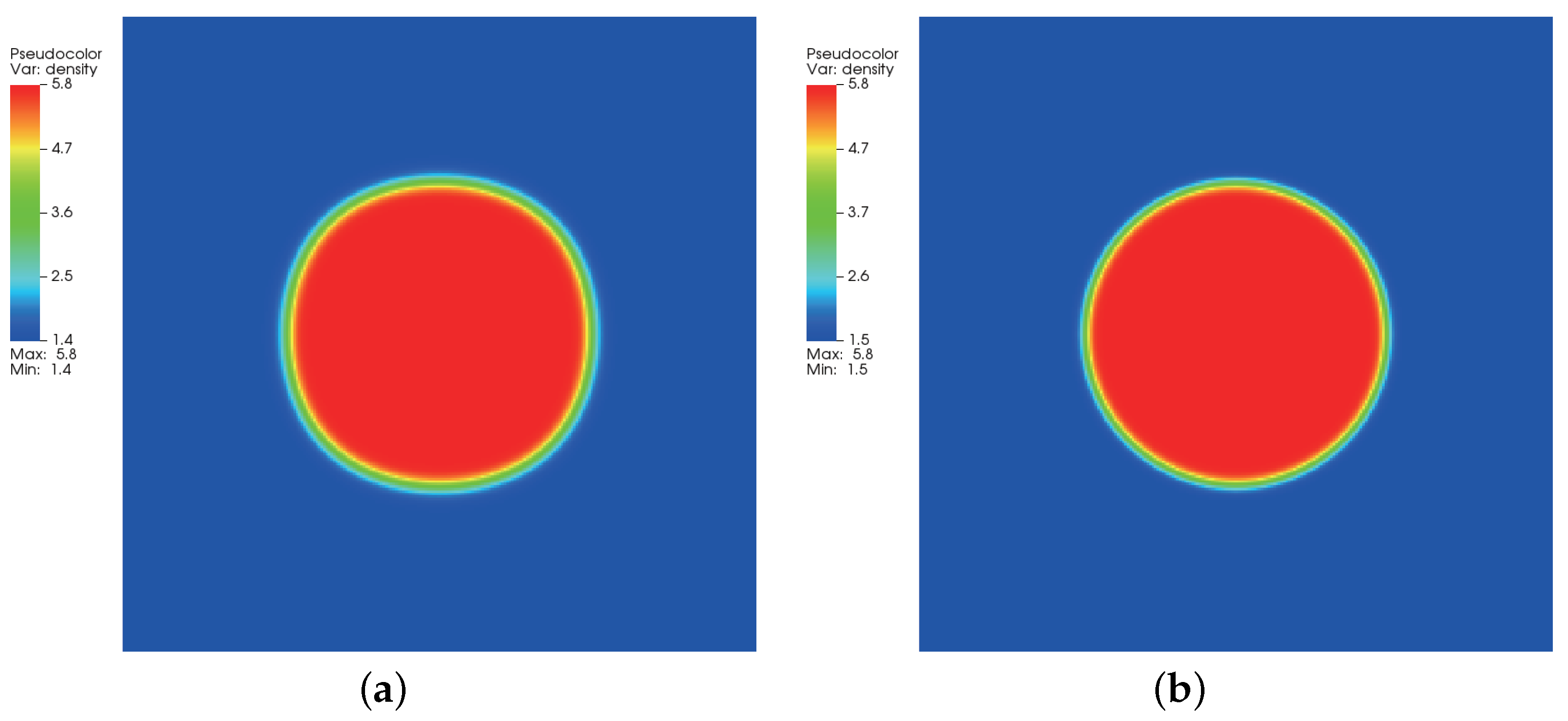
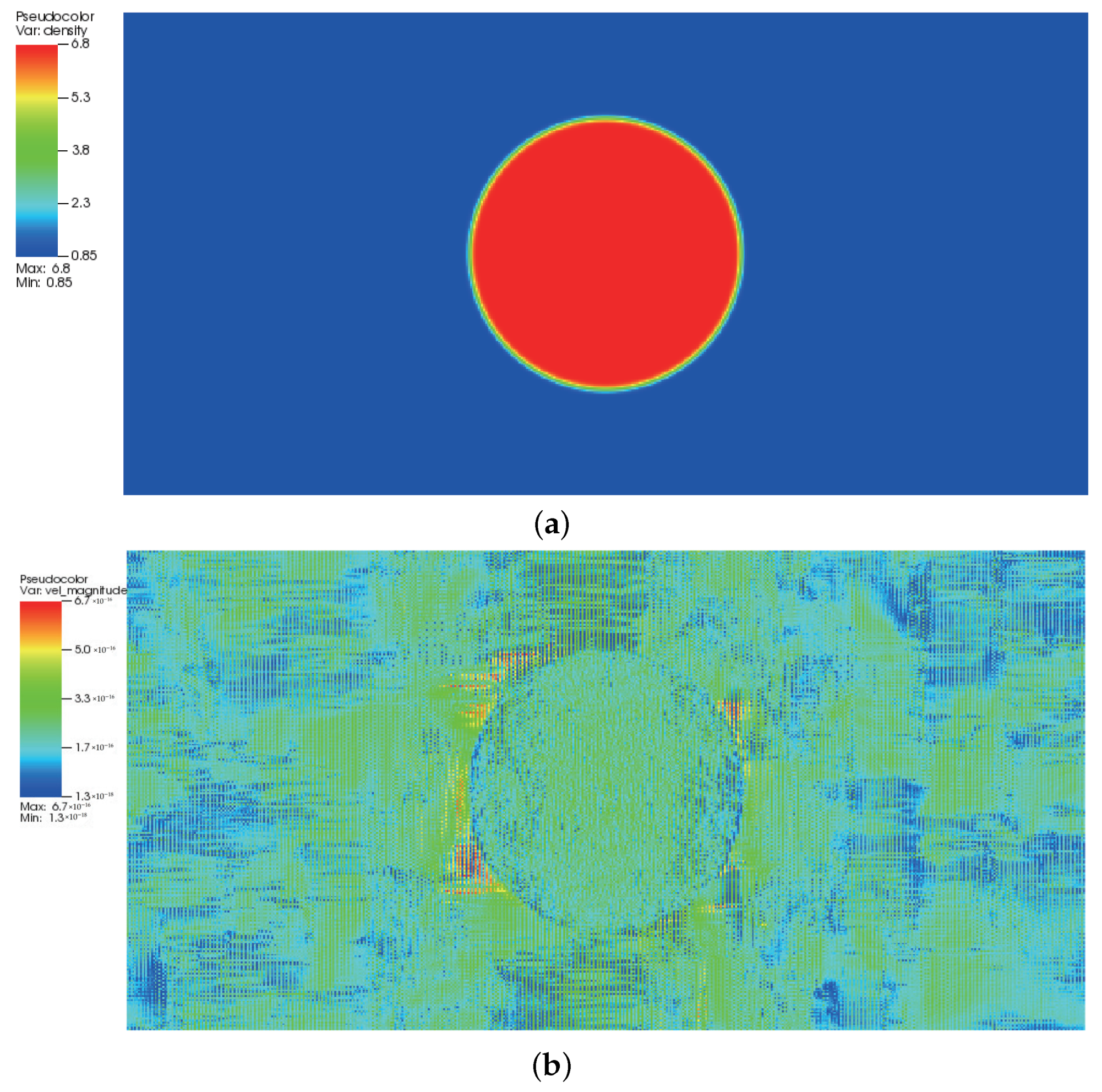
3.2. Quiescent Droplet
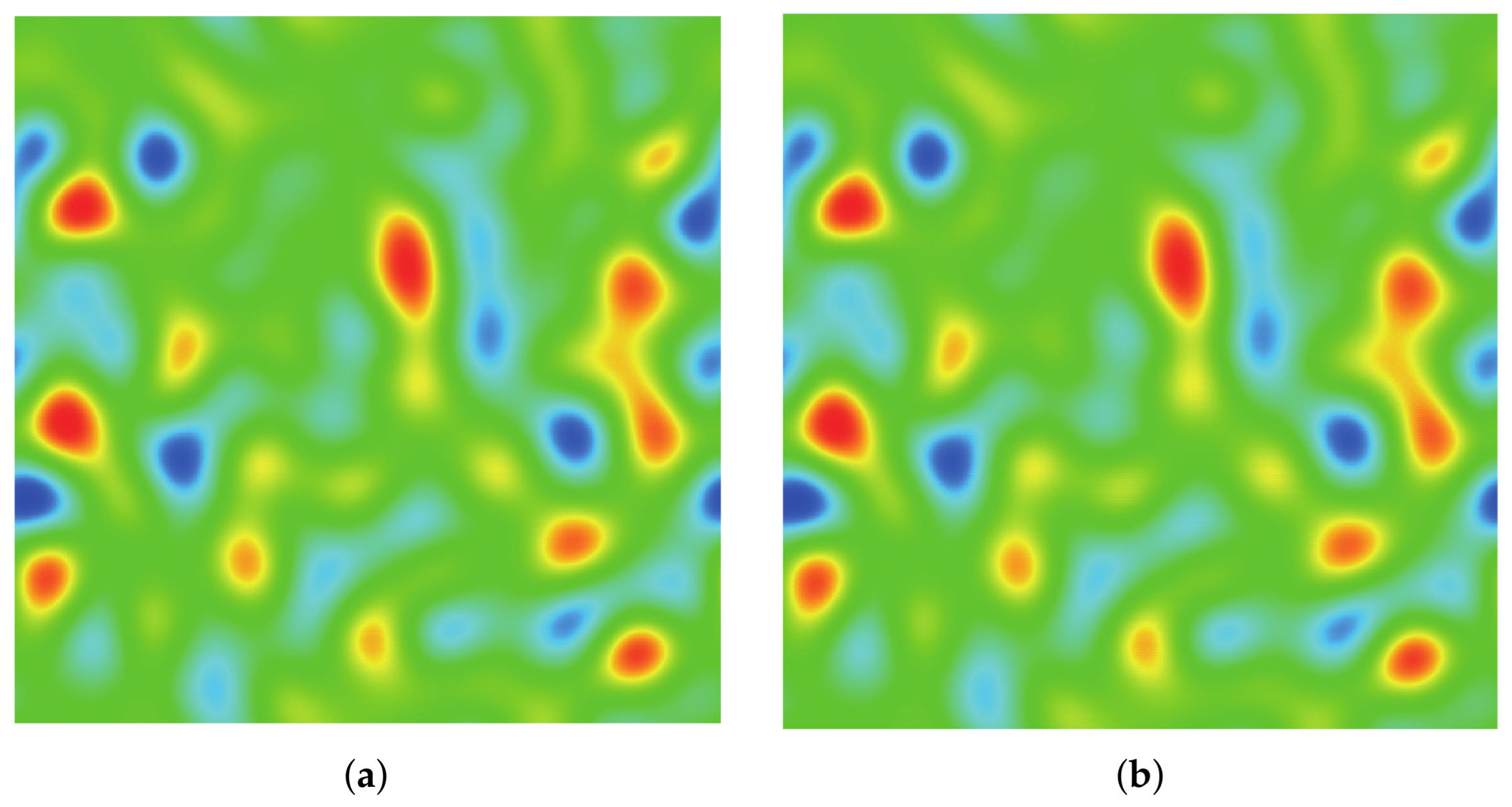
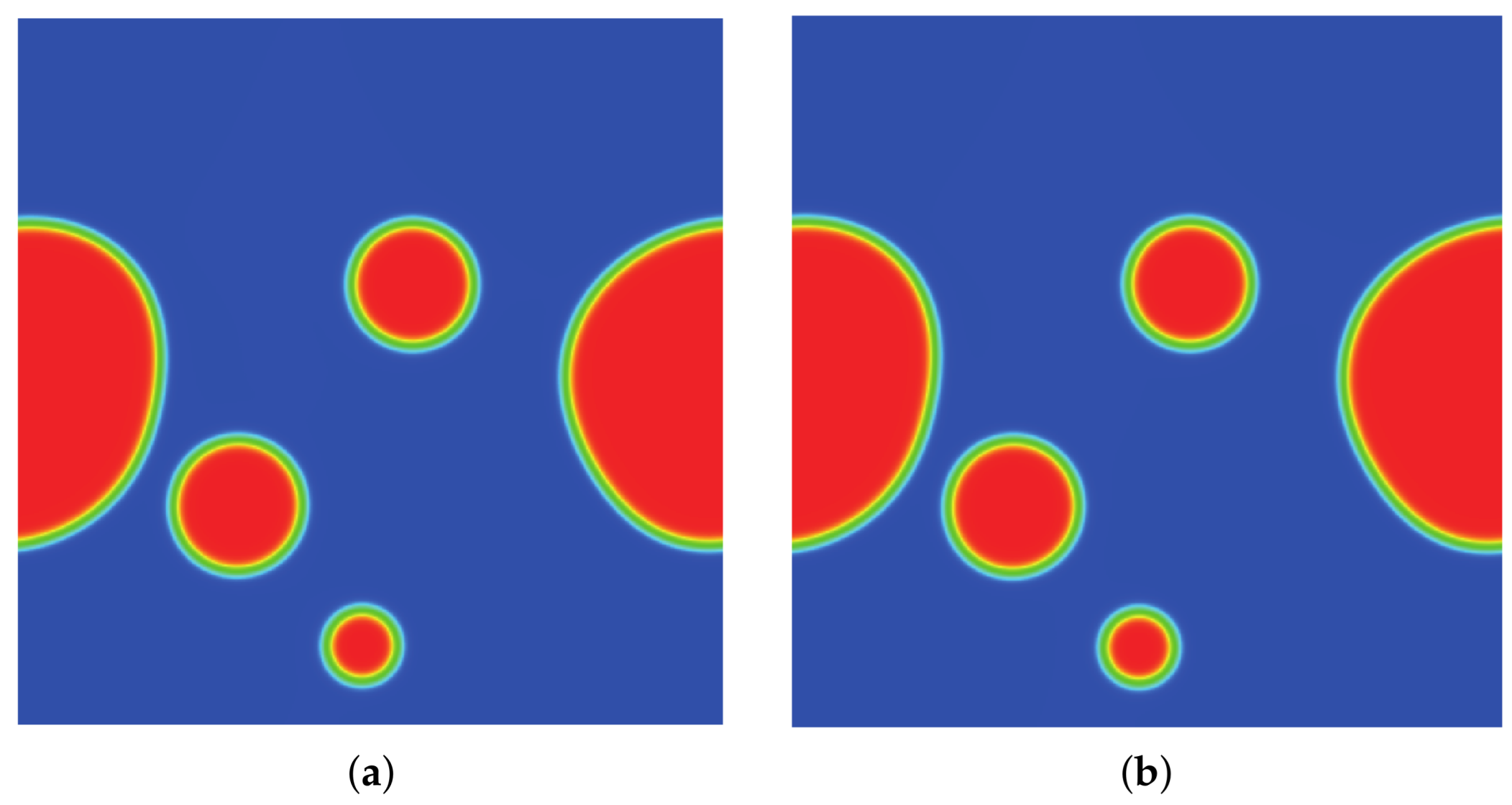
3.3. Spinodal Decomposition
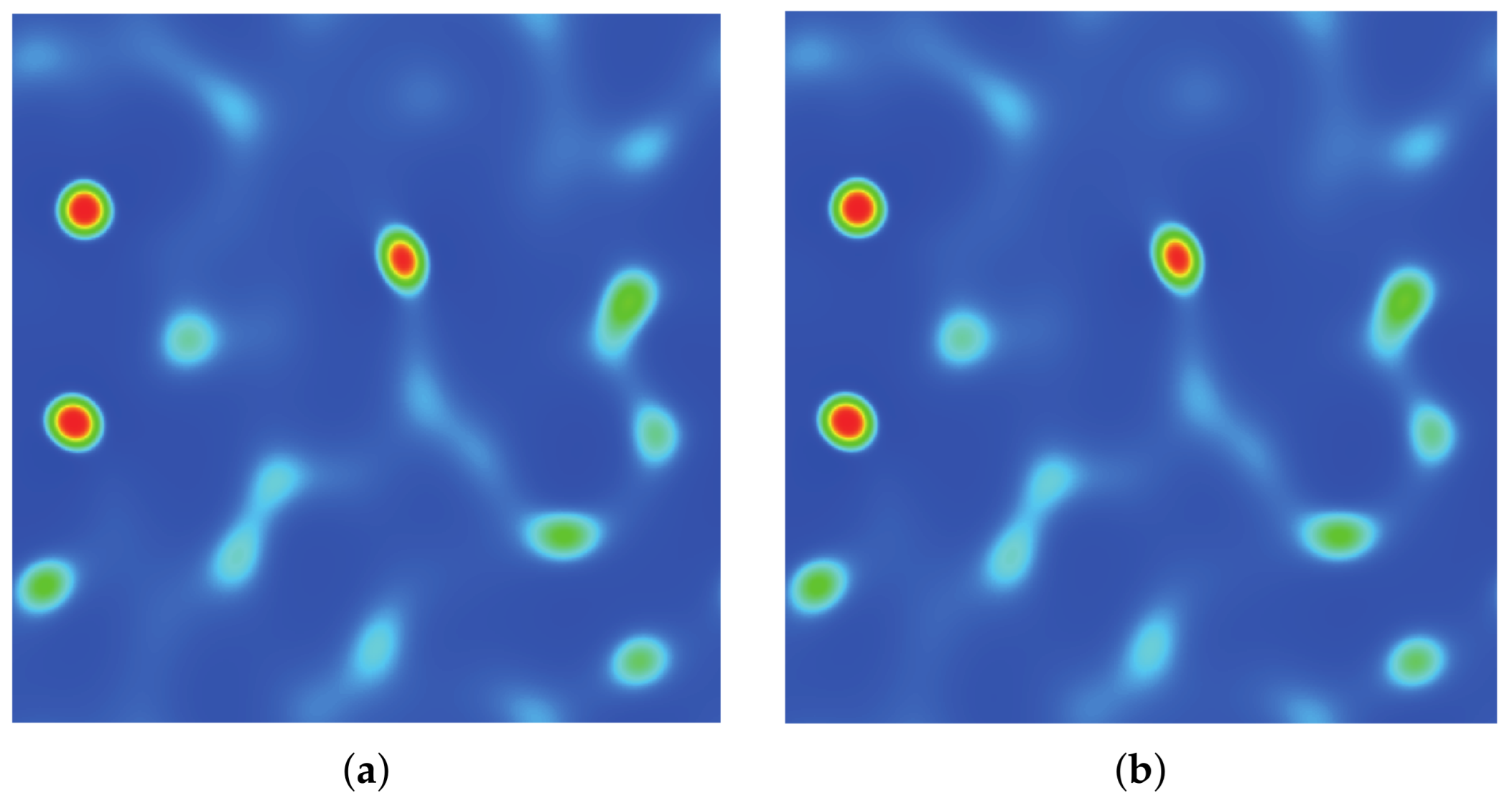
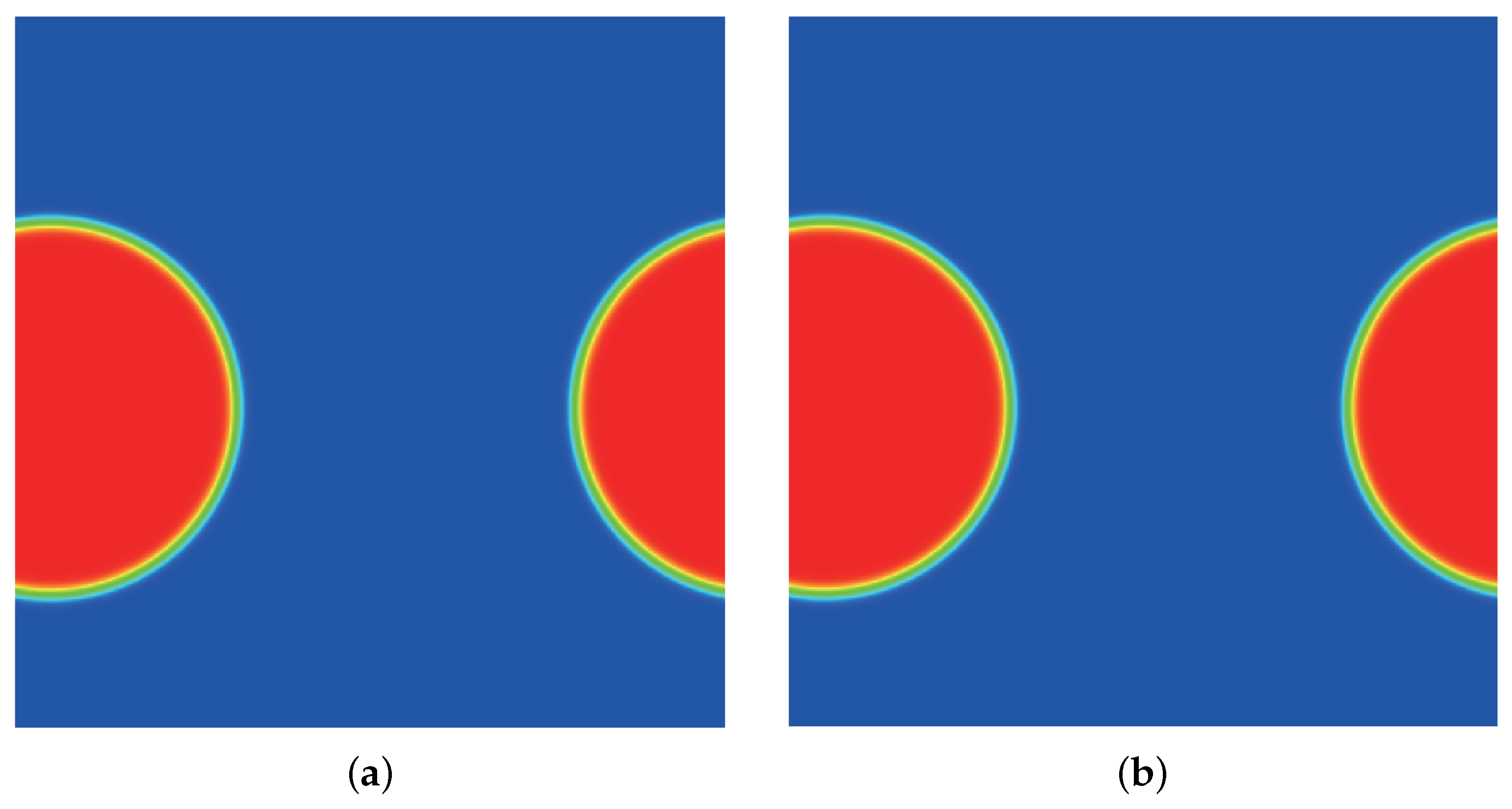
3.4. Droplet Coalescence
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Nondimensionalization of the Boltzmann-BGK Equation
References
- Hirt, C.; Nichols, B. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Unverdi, S.O.; Tryggvason, G. A front-tracking method for viscous, incompressible, multi-fluid flows. J. Comput. Phys. 1992, 100, 25–37. [Google Scholar] [CrossRef]
- Anderson, D.M.; McFadden, G.B.; Wheeler, A.A. Diffuse-interface methods in fluid mechanics. Annu. Rev. Fluid Mech. 1998, 30, 139–165. [Google Scholar] [CrossRef]
- Sethian, J.A.; Smereka, P. Level set methods for fluid interfaces. Annu. Rev. Fluid Mech. 2003, 35, 341–372. [Google Scholar] [CrossRef]
- Guo, Z.; Zheng, C.; Shi, B. Force imbalance in lattice Boltzmann equation for two-phase flows. Phys. Rev. E 2011, 83, 036707. [Google Scholar] [CrossRef]
- Fox, R.O. Large-eddy-simulation tools for multiphase flows. Annu. Rev. Fluid Mech. 2012, 44, 47–76. [Google Scholar] [CrossRef]
- Aidun, C.K.; Clausen, J.R. Lattice-Boltzmann method for complex flows. Annu. Rev. Fluid Mech. 2010, 42, 439–472. [Google Scholar] [CrossRef]
- Gan, Y.; Xu, A.; Zhang, G.; Succi, S. Discrete Boltzmann modeling of multiphase flows: Hydrodynamic and thermodynamic non-equilibrium effects. Soft Matter 2015, 11, 5336–5345. [Google Scholar] [CrossRef]
- Wang, Y.; Shu, C.; Shao, J.; Wu, J.; Niu, X. A mass-conserved diffuse interface method and its application for incompressible multiphase flows with large density ratio. J. Comput. Phys. 2015, 290, 336–351. [Google Scholar] [CrossRef]
- Gunstensen, A.K.; Rothman, D.H.; Zaleski, S.; Zanetti, G. Lattice Boltzmann model of immiscible fluids. Phys. Rev. A 1991, 43, 4320–4327. [Google Scholar] [CrossRef]
- He, X.; Chen, S.; Zhang, R. A lattice Boltzmann scheme for incompressible multiphase flow and its application in simulation of Rayleigh-Taylor instability. J. Comput. Phys. 1999, 152, 642–663. [Google Scholar] [CrossRef]
- Geier, M.; Fakhari, A.; Lee, T. Conservative phase-field lattice Boltzmann model for interface tracking equation. Phys. Rev. E 2015, 91, 063309. [Google Scholar] [CrossRef] [PubMed]
- Shan, X.; Chen, H. Lattice Boltzmann model for simulating flows with multiple phases and components. Phys. Rev. E 1993, 47, 1815–1819. [Google Scholar] [CrossRef] [PubMed]
- Swift, M.R.; Osborn, W.R.; Yeomans, J.M. Lattice Boltzmann simulation of nonideal fluids. Phys. Rev. Lett. 1995, 75, 830–833. [Google Scholar] [CrossRef]
- Yang, K.; Guo, Z. Lattice Boltzmann method for binary fluids based on mass-conserving quasi-incompressible phase-field theory. Phys. Rev. E 2016, 93, 043303. [Google Scholar] [CrossRef]
- Briant, A.J.; Wagner, A.J.; Yeomans, J.M. Lattice Boltzmann simulations of contact line motion. I. Liquid-gas systems. Phys. Rev. E 2004, 69, 031602. [Google Scholar] [CrossRef]
- Briant, A.J.; Yeomans, J.M. Lattice Boltzmann simulations of contact line motion. II. Binary fluids. Phys. Rev. E 2004, 69, 031603. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Wagner, A.J. Symmetric free-energy-based multicomponent lattice Boltzmann method. Phys. Rev. E 2007, 76, 036701. [Google Scholar] [CrossRef]
- Zhang, J.; Kwok, D.Y. A mean-field free energy lattice Boltzmann model for multicomponent fluids. Eur. Phys. J. Spec. Top. 2009, 171, 45–53. [Google Scholar] [CrossRef]
- Wiklund, H.; Lindström, S.; Uesaka, T. Boundary condition considerations in lattice Boltzmann formulations of wetting binary fluids. Comput. Phys. Commun. 2011, 182, 2192–2200. [Google Scholar] [CrossRef]
- Wen, B.; Huang, B.; Qin, Z.; Wang, C.; Zhang, C. Contact angle measurement in lattice Boltzmann method. Comput. Math. Appl. 2018, 76, 1686–1698. [Google Scholar] [CrossRef]
- Yan, Y.; Zu, Y. A lattice Boltzmann method for incompressible two-phase flows on partial wetting surface with large density ratio. J. Comput. Phys. 2007, 227, 763–775. [Google Scholar] [CrossRef]
- Wen, B.; Zhao, L.; Qiu, W.; Ye, Y.; Shan, X. Chemical-potential multiphase lattice Boltzmann method with superlarge density ratios. Phys. Rev. E 2020, 102, 013303. [Google Scholar] [CrossRef] [PubMed]
- Swift, M.R.; Orlandini, E.; Osborn, W.R.; Yeomans, J.M. Lattice Boltzmann simulations of liquid-gas and binary fluid systems. Phys. Rev. E 1996, 54, 5041–5052. [Google Scholar] [CrossRef]
- Inamuro, T.; Konishi, N.; Ogino, F. A Galilean invariant model of the lattice Boltzmann method for multiphase fluid flows using free-energy approach. Comput. Phys. Commun. 2000, 129, 32–45. [Google Scholar] [CrossRef]
- Kalarakis, A.N.; Burganos, V.N.; Payatakes, A.C. Galilean-invariant lattice-Boltzmann simulation of liquid-vapor interface dynamics. Phys. Rev. E 2002, 65, 056702. [Google Scholar] [CrossRef]
- Wagner, A.; Li, Q. Investigation of Galilean invariance of multi-phase lattice Boltzmann methods. Phys. A Stat. Mech. Appl. 2006, 362, 105–110. [Google Scholar] [CrossRef]
- Lee, T.; Fischer, P.F. Eliminating parasitic currents in the lattice Boltzmann equation method for nonideal gases. Phys. Rev. E 2006, 74, 046709. [Google Scholar] [CrossRef]
- Lou, Q.; Guo, Z. Interface-capturing lattice Boltzmann equation model for two-phase flows. Phys. Rev. E 2015, 91, 013302. [Google Scholar] [CrossRef]
- Guo, Z. Well-balanced lattice Boltzmann model for two-phase systems. Phys. Fluids 2021, 33, 031709. [Google Scholar] [CrossRef]
- Guo, Z.; Xu, K.; Wang, R. Discrete unified gas kinetic scheme for all Knudsen number flows: Low-speed isothermal case. Phys. Rev. E 2013, 88, 033305. [Google Scholar] [CrossRef] [PubMed]
- Guo, Z.; Wang, R.; Xu, K. Discrete unified gas kinetic scheme for all Knudsen number flows. II. Thermal compressible case. Phys. Rev. E 2015, 91, 033313. [Google Scholar] [CrossRef] [PubMed]
- Zhu, L.; Guo, Z. Numerical study of nonequilibrium gas flow in a microchannel with a ratchet surface. Phys. Rev. E 2017, 95, 023113. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Cao, Y.; Chen, Q.; Kong, M.; Zheng, L. A conserved discrete unified gas kinetic scheme for microchannel gas flows in all flow regimes. Comput. Fluids 2018, 167, 313–323. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhu, L.; Wang, R.; Guo, Z. Discrete unified gas kinetic scheme for all Knudsen number flows. III. Binary gas mixtures of Maxwell molecules. Phys. Rev. E 2018, 97, 053306. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Zhu, L.; Wang, P.; Guo, Z. Discrete unified gas kinetic scheme for flows of binary gas mixture based on the McCormack model. Phys. Fluids 2019, 31, 017101. [Google Scholar] [CrossRef]
- Wang, P.; Wang, L.P.; Guo, Z. Comparison of the lattice Boltzmann equation and discrete unified gas-kinetic scheme methods for direct numerical simulation of decaying turbulent flows. Phys. Rev. E 2016, 94, 043304. [Google Scholar] [CrossRef]
- Bo, Y.; Wang, P.; Guo, Z.; Wang, L.P. DUGKS simulations of three-dimensional Taylor–Green vortex flow and turbulent channel flow. Comput. Fluids 2017, 155, 9–21. [Google Scholar] [CrossRef]
- Zhang, R.; Zhong, C.; Liu, S.; Zhuo, C. Large-eddy simulation of wall-bounded turbulent flow with high-order discrete unified gas-kinetic scheme. Adv. Aerodyn. 2020, 2, 26. [Google Scholar] [CrossRef]
- Chen, J.; Liu, S.; Wang, Y.; Zhong, C. Conserved discrete unified gas-kinetic scheme with unstructured discrete velocity space. Phys. Rev. E 2019, 100, 043305. [Google Scholar] [CrossRef] [Green Version]
- Zhong, M.; Zou, S.; Pan, D.; Zhuo, C.; Zhong, C. A simplified discrete unified gas–kinetic scheme for compressible flow. Phys. Fluids 2021, 33, 036103. [Google Scholar] [CrossRef]
- Wen, X.; Wang, L.P.; Guo, Z.; Shen, J. An improved discrete unified gas kinetic scheme for simulating compressible natural convection flows. J. Comput. Phys. X 2021, 11, 100088. [Google Scholar] [CrossRef]
- Guo, Z.; Xu, K. Discrete unified gas kinetic scheme for multiscale heat transfer based on the phonon Boltzmann transport equation. Int. J. Heat Mass Transf. 2016, 102, 944–958. [Google Scholar] [CrossRef]
- Luo, X.P.; Wang, C.H.; Zhang, Y.; Yi, H.L.; Tan, H.P. Multiscale solutions of radiative heat transfer by the discrete unified gas kinetic scheme. Phys. Rev. E 2018, 97, 063302. [Google Scholar] [CrossRef]
- Guo, Z.; Xu, K. Progress of discrete unified gas-kinetic scheme for multiscale flows. Adv. Aerodyn. 2021, 3, 6. [Google Scholar] [CrossRef]
- Wang, P.; Zhu, L.; Guo, Z.; Xu, K. A comparative study of LBE and DUGKS methods for nearly incompressible flows. Commun. Comput. Phys. 2015, 17, 657–681. [Google Scholar] [CrossRef]
- Zhang, C.; Yang, K.; Guo, Z. A discrete unified gas-kinetic scheme for immiscible two-phase flows. Int. J. Heat Mass Transf. 2018, 126, 1326–1336. [Google Scholar] [CrossRef]
- Yang, Z.; Zhong, C.; Zhuo, C. Phase-field method based on discrete unified gas-kinetic scheme for large-density-ratio two-phase flows. Phys. Rev. E 2019, 99, 043302. [Google Scholar] [CrossRef]
- Yang, Z.; Liu, S.; Zhuo, C.; Zhong, C. Conservative multilevel discrete unified gas kinetic scheme for modeling multiphase flows with large density ratios. Phys. Fluids 2022, 34, 043316. [Google Scholar] [CrossRef]
- Yang, Z.; Liu, S.; Zhuo, C.; Zhong, C. Pseudopotential-based discrete unified gas kinetic scheme for modeling multiphase fluid flows. Res. Sq. 2022. [Google Scholar] [CrossRef]
- Zeng, W.; Zhang, C.; Guo, Z. Well-balanced discrete unified gas-kinetic scheme for two-phase systems. Phys. Fluids 2022, 34, 052111. [Google Scholar] [CrossRef]
- Jacqmin, D. Calculation of two-phase Navier-Stokes flows using phase-field modeling. J. Comput. Phys. 1999, 155, 96–127. [Google Scholar] [CrossRef]
- Goldstein, H.; Poole, C.; Safko, J. Classical Mechanics, 3rd ed.; Pearson: London, UK, 2001. [Google Scholar]
- Sbragaglia, M.; Chen, H.; Shan, X.; Succi, S. Continuum free-energy formulation for a class of lattice Boltzmann multiphase models. Europhys. Lett. 2009, 86, 24005. [Google Scholar] [CrossRef]
- Wen, B.; Zhou, X.; He, B.; Zhang, C.; Fang, H. Chemical-potential-based lattice Boltzmann method for nonideal fluids. Phys. Rev. E 2017, 95, 063305. [Google Scholar] [CrossRef]
- Li, Q.; Yu, Y.; Huang, R.Z. Achieving thermodynamic consistency in a class of free-energy multiphase lattice Boltzmann models. Phys. Rev. E 2021, 103, 013304. [Google Scholar] [CrossRef]
- Yang, Z.; Zhong, C.; Zhuo, C.; Liu, S. Spatio-temporal error coupling and competition in meso-flux construction of discrete unified gas-kinetic scheme. Comput. Fluids 2022, 244, 105537. [Google Scholar] [CrossRef]
- Borges, R.; Carmona, M.; Costa, B.; Don, W.S. An improved weighted essentially non-oscillatory scheme for hyperbolic conservation laws. J. Comput. Phys. 2008, 227, 3191–3211. [Google Scholar] [CrossRef]
- Tao, S.; Zhang, H.; Guo, Z.; Wang, L.P. A combined immersed boundary and discrete unified gas kinetic scheme for particle–fluid flows. J. Comput. Phys. 2018, 375, 498–518. [Google Scholar] [CrossRef]
- Kumar, A. Isotropic finite-differences. J. Comput. Phys. 2004, 201, 109–118. [Google Scholar] [CrossRef]
- Chen, L.; Kang, Q.; Mu, Y.; He, Y.L.; Tao, W.Q. A critical review of the pseudopotential multiphase lattice Boltzmann model: Methods and applications. Int. J. Heat Mass Transf. 2014, 76, 210–236. [Google Scholar] [CrossRef]
- Wu, M.; Cubaud, T.; Ho, C.M. Scaling law in liquid drop coalescence driven by surface tension. Phys. Fluids 2004, 16, L51–L54. [Google Scholar] [CrossRef] [Green Version]




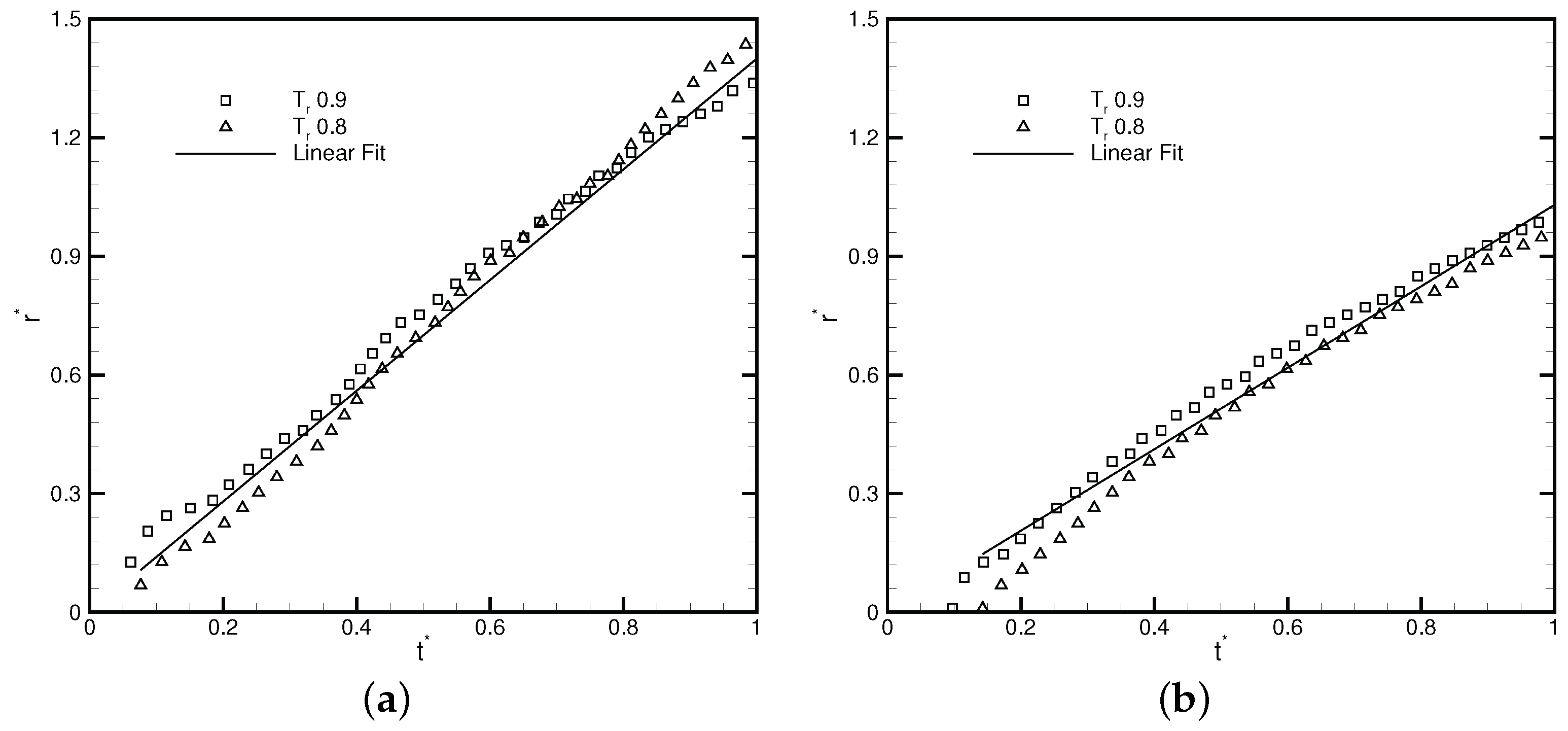

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.; Liu, S.; Zhuo, C.; Zhong, C. Free-Energy-Based Discrete Unified Gas Kinetic Scheme for van der Waals Fluid. Entropy 2022, 24, 1202. https://doi.org/10.3390/e24091202
Yang Z, Liu S, Zhuo C, Zhong C. Free-Energy-Based Discrete Unified Gas Kinetic Scheme for van der Waals Fluid. Entropy. 2022; 24(9):1202. https://doi.org/10.3390/e24091202
Chicago/Turabian StyleYang, Zeren, Sha Liu, Congshan Zhuo, and Chengwen Zhong. 2022. "Free-Energy-Based Discrete Unified Gas Kinetic Scheme for van der Waals Fluid" Entropy 24, no. 9: 1202. https://doi.org/10.3390/e24091202
APA StyleYang, Z., Liu, S., Zhuo, C., & Zhong, C. (2022). Free-Energy-Based Discrete Unified Gas Kinetic Scheme for van der Waals Fluid. Entropy, 24(9), 1202. https://doi.org/10.3390/e24091202









